Automatic Color Correction for Multisource Remote Sensing Images with Wasserstein CNN
Abstract
:1. Introduction
2. Materials and Methods
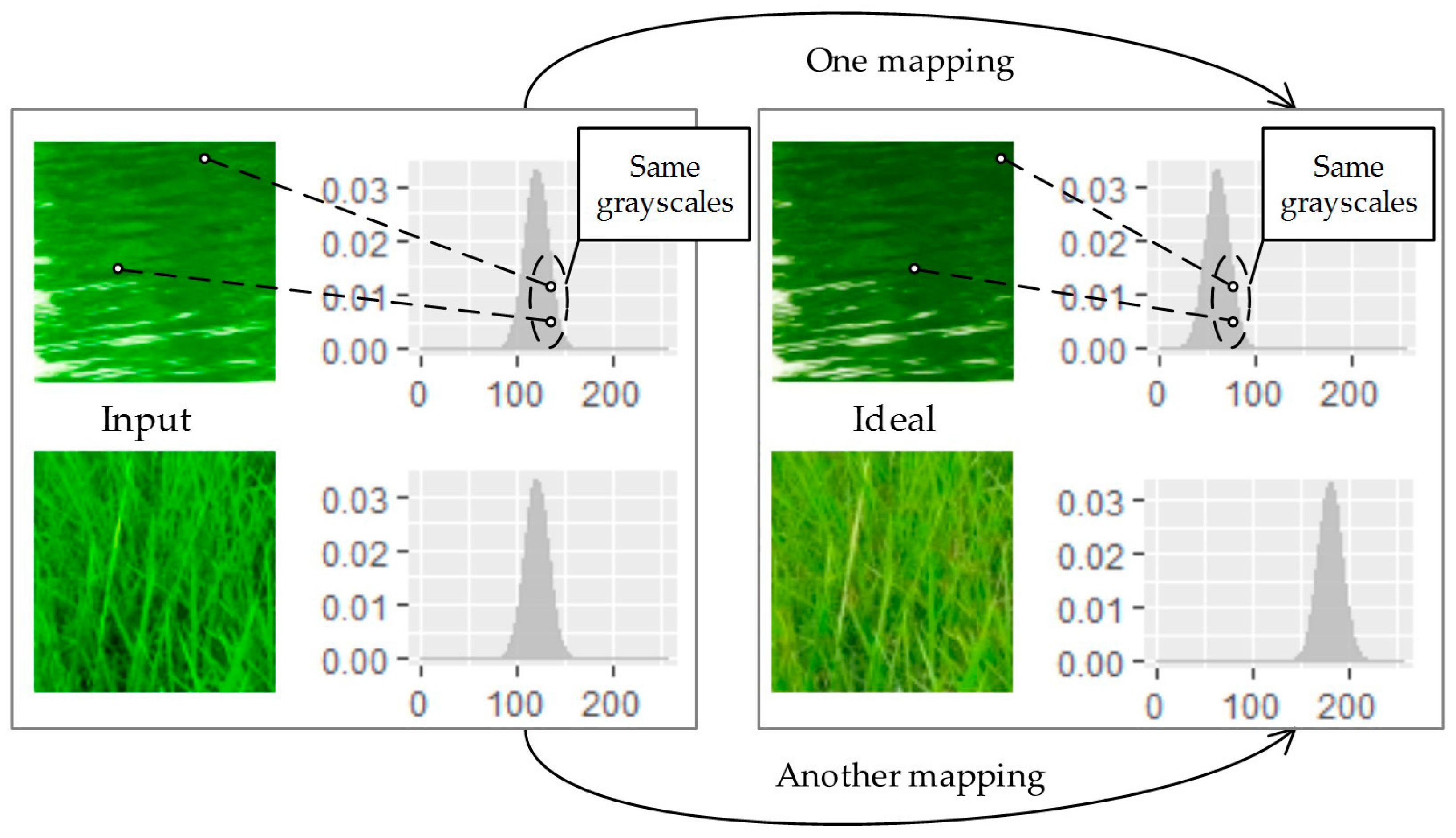
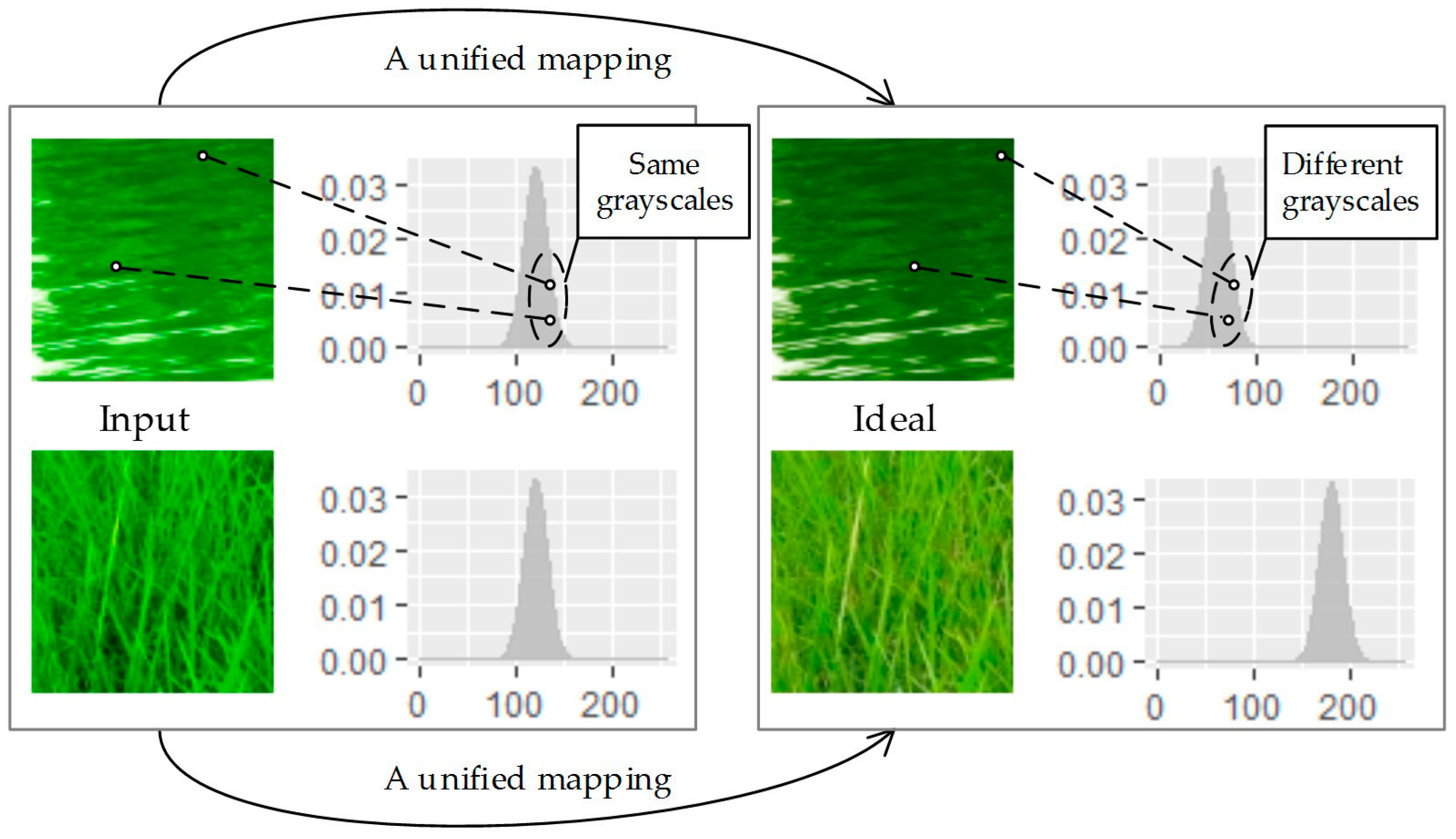
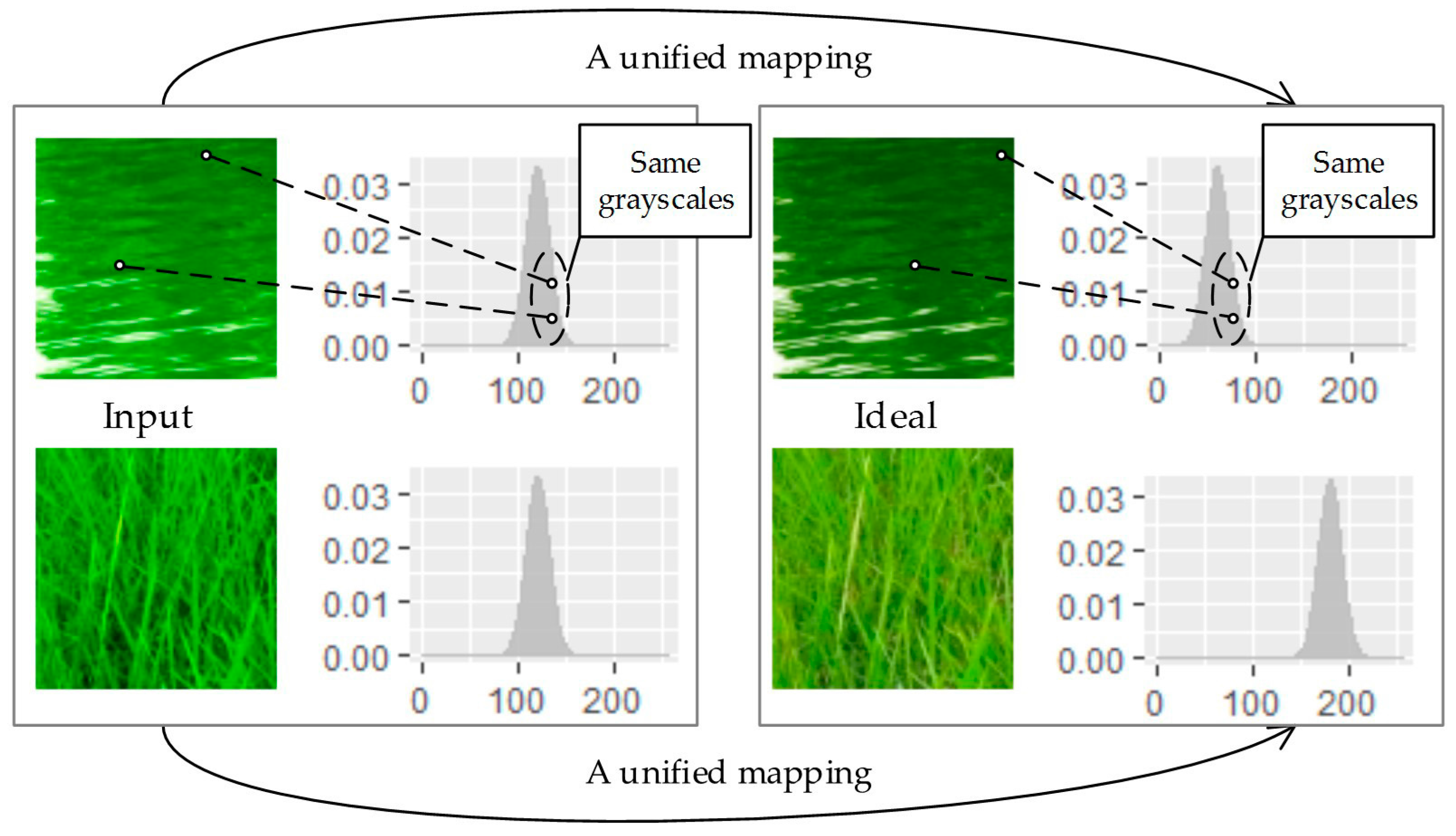
2.1. Analysis
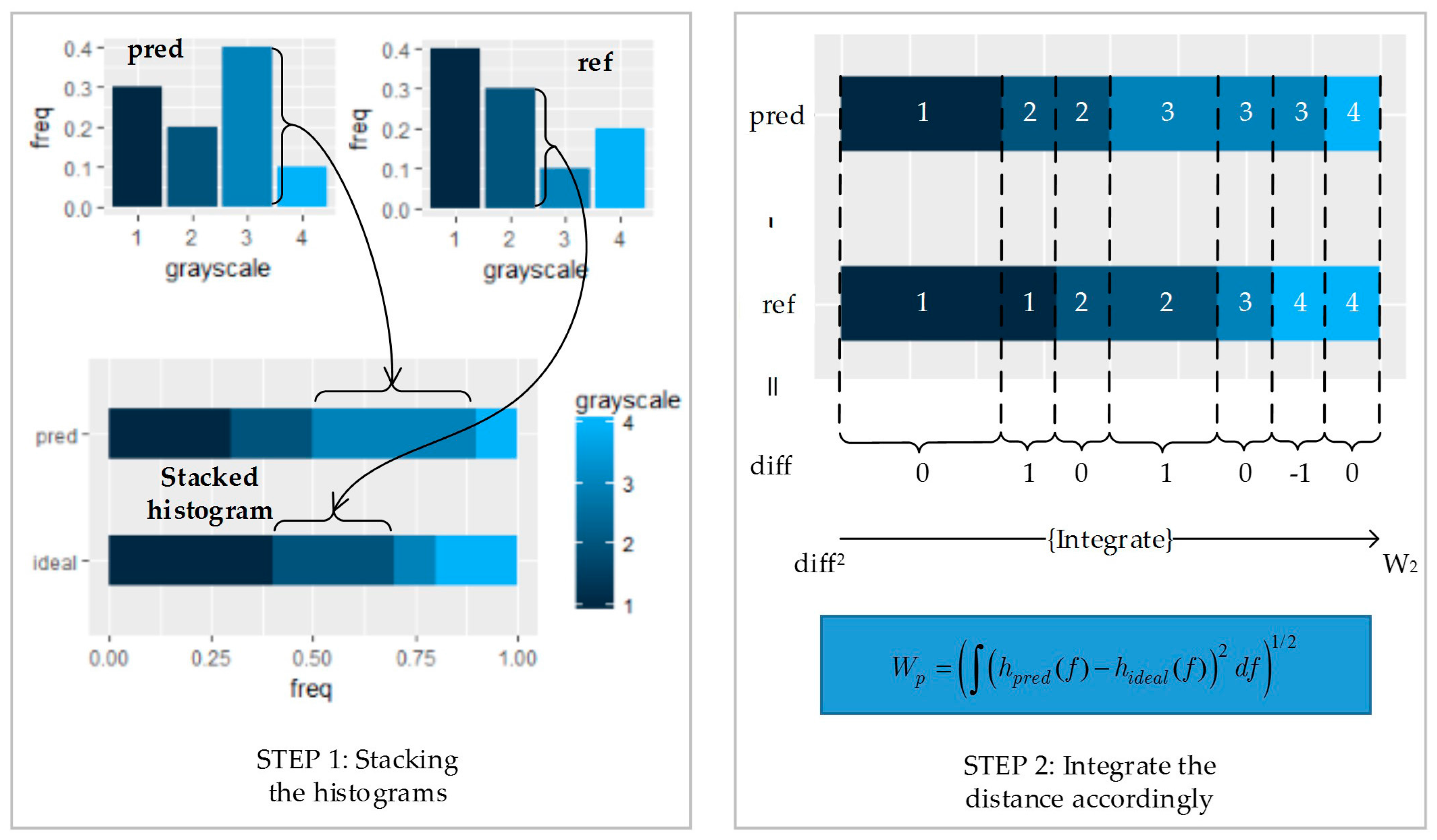
2.2. Optimal Transporting Perspective of View
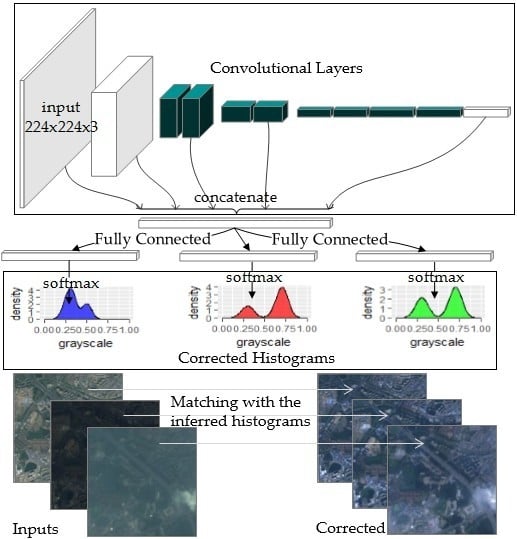
2.3. The Model Structure
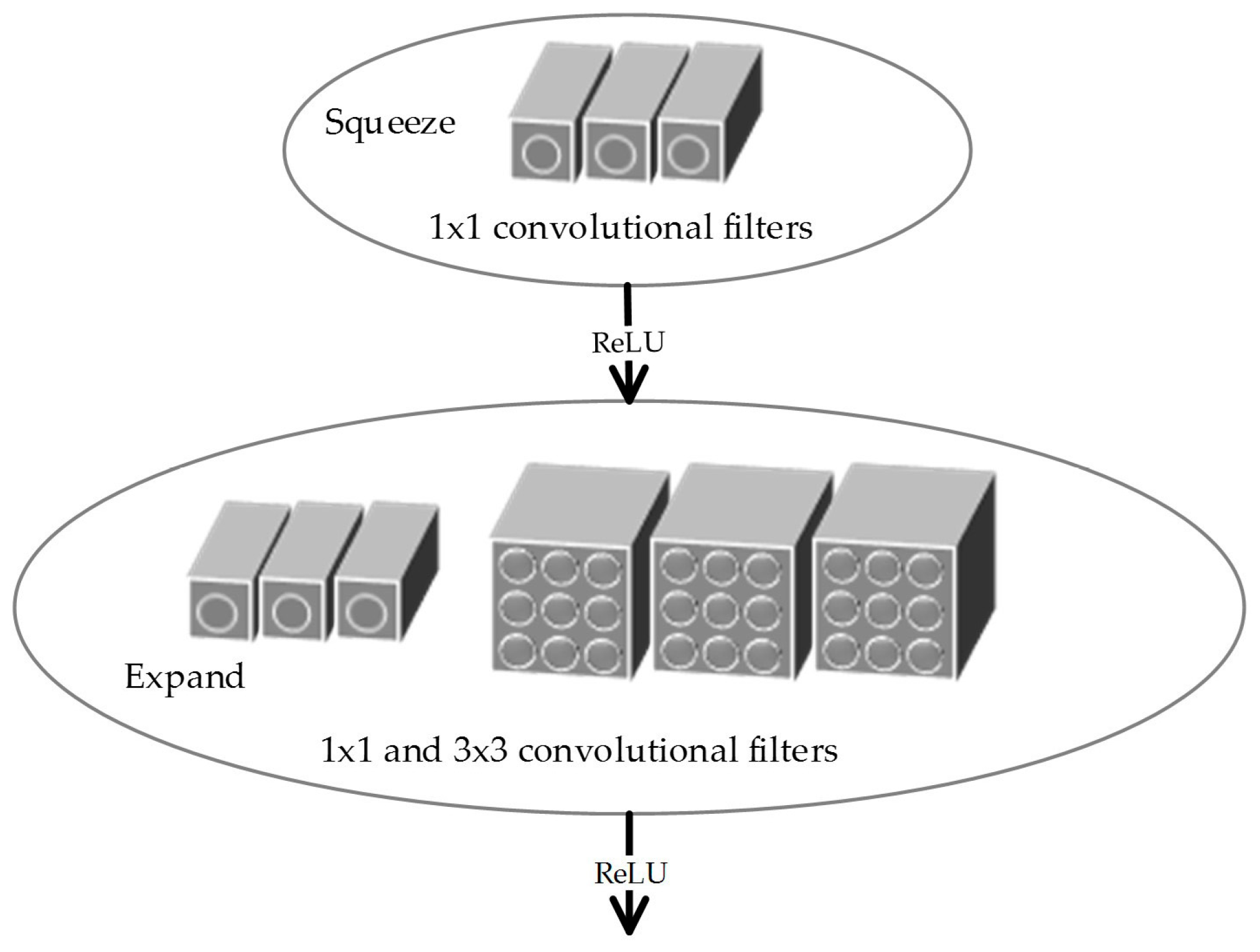
2.3.1. Basic Modules
2.3.2. The Multi-Scale Concatenation and the Histogram Predictors
2.4. Data Augmentation
- Random cropping: A patch of 227 × 227 is cropped at a random position from each 256 × 256 sample. It is worth noting that this implies that no registration is needed in the training process.
- Random flipping: Each sample in the input batch is randomly horizontally and vertically flipped by a chance of 50%.
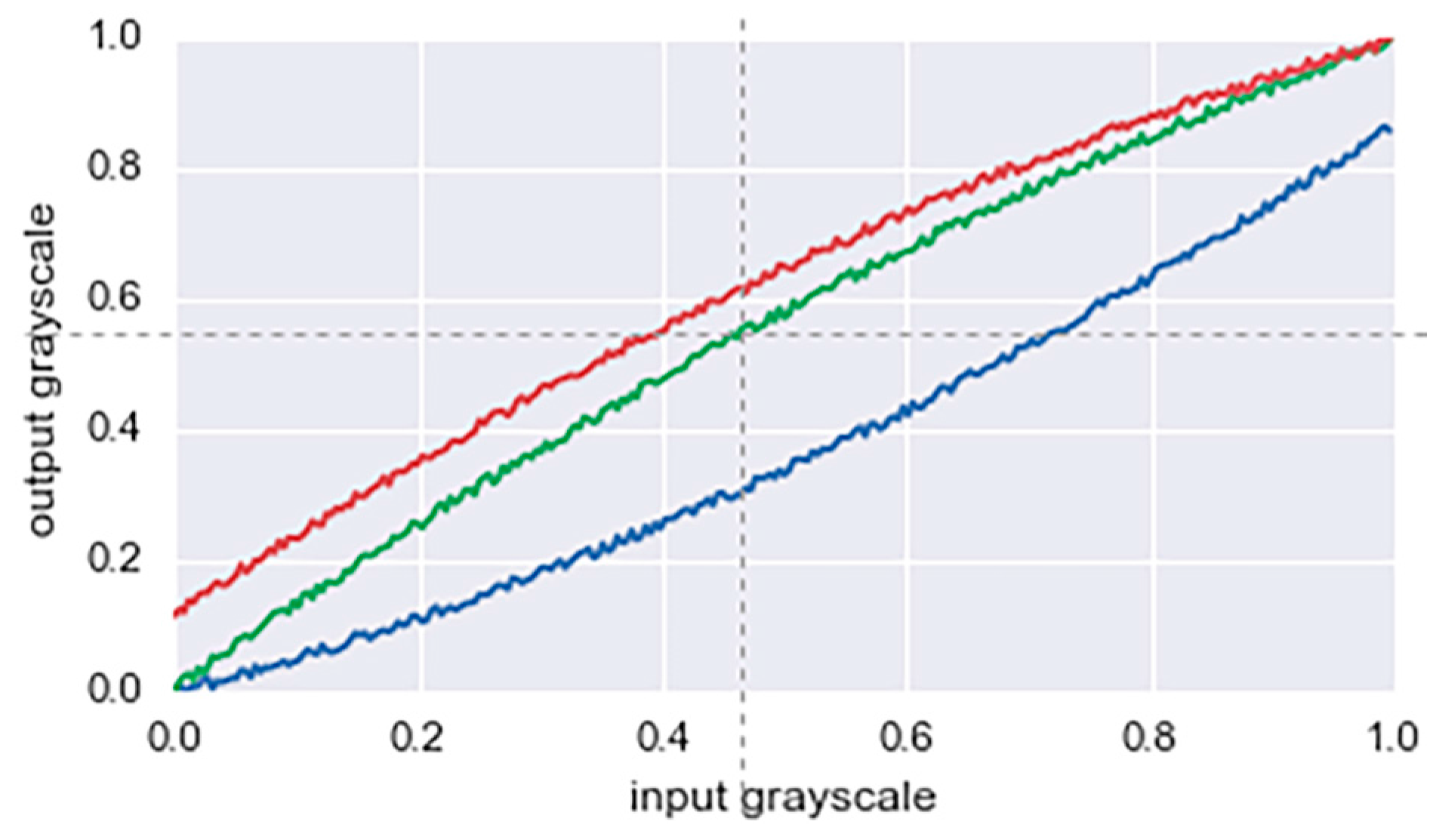
- Random color augmentation: The brightness, saturation, and gamma values of the input color are randomly shifted. Small perturbations are added to each color channel. Figure 8 shows an example of such transformation of the color distribution.
2.5. Algorithm Flow Chart
| Algorithm 1. Training Process of the Automatic Color Matching WCNN, Our Proposed Algorithm. |
| Notations: , the parameters in the WCNN model; , the gradients w.r.t. ; , the predicted color distribution; , the reference color distribution; , the Wasserstein loss. Required constants: , the learning rate; m, the batch size. Required initial values: , the initial parameters. 1: while has not converged do 2: Sample a batch from the input data 3: Sample a batch from the reference data 4: Apply random augmentation to 5: ← 6: ← 7: end while |
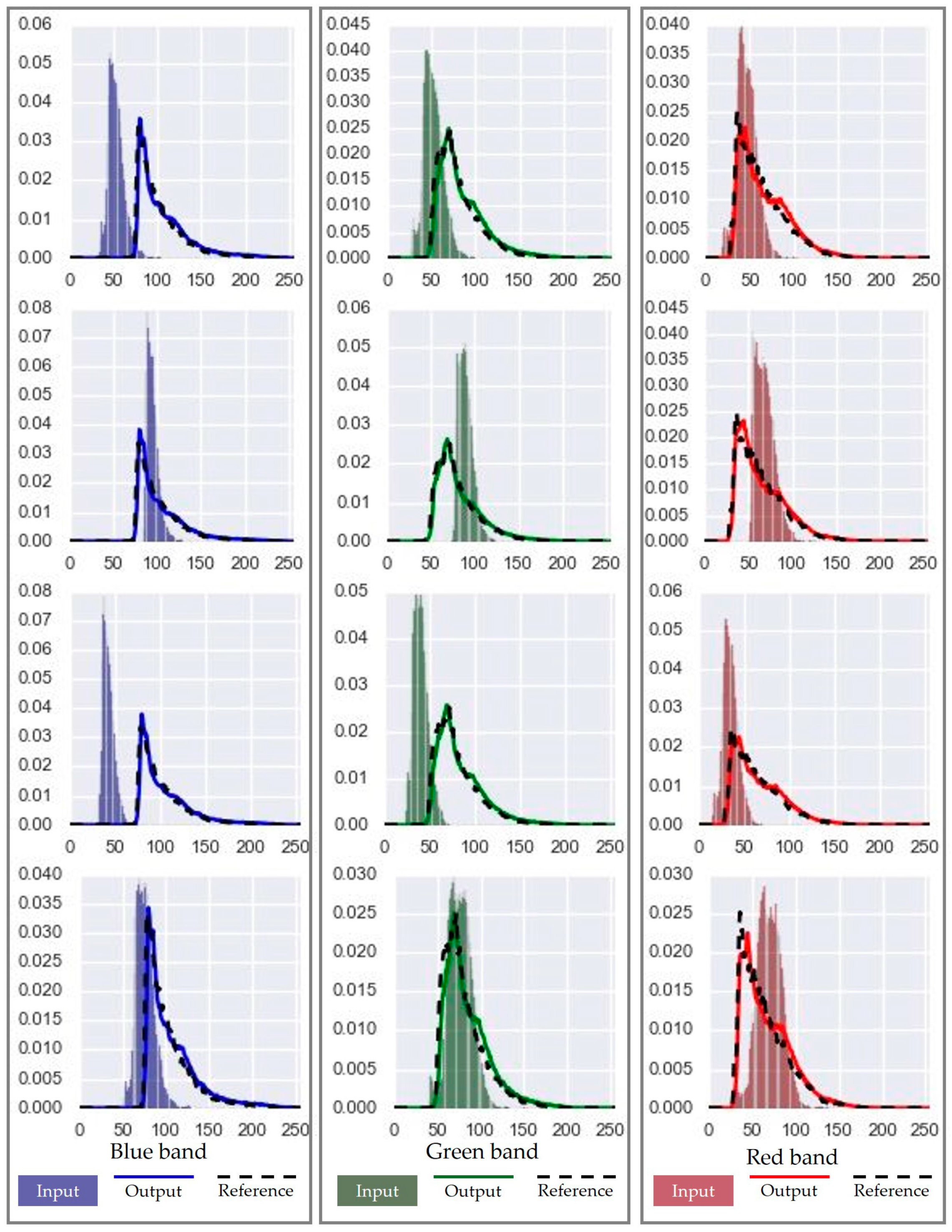
3. Results
4. Discussion
4.1. Comparison between KL Divergence and Wasserstein Distance
4.2. Connection and Comparison with Other Color Matching Methods
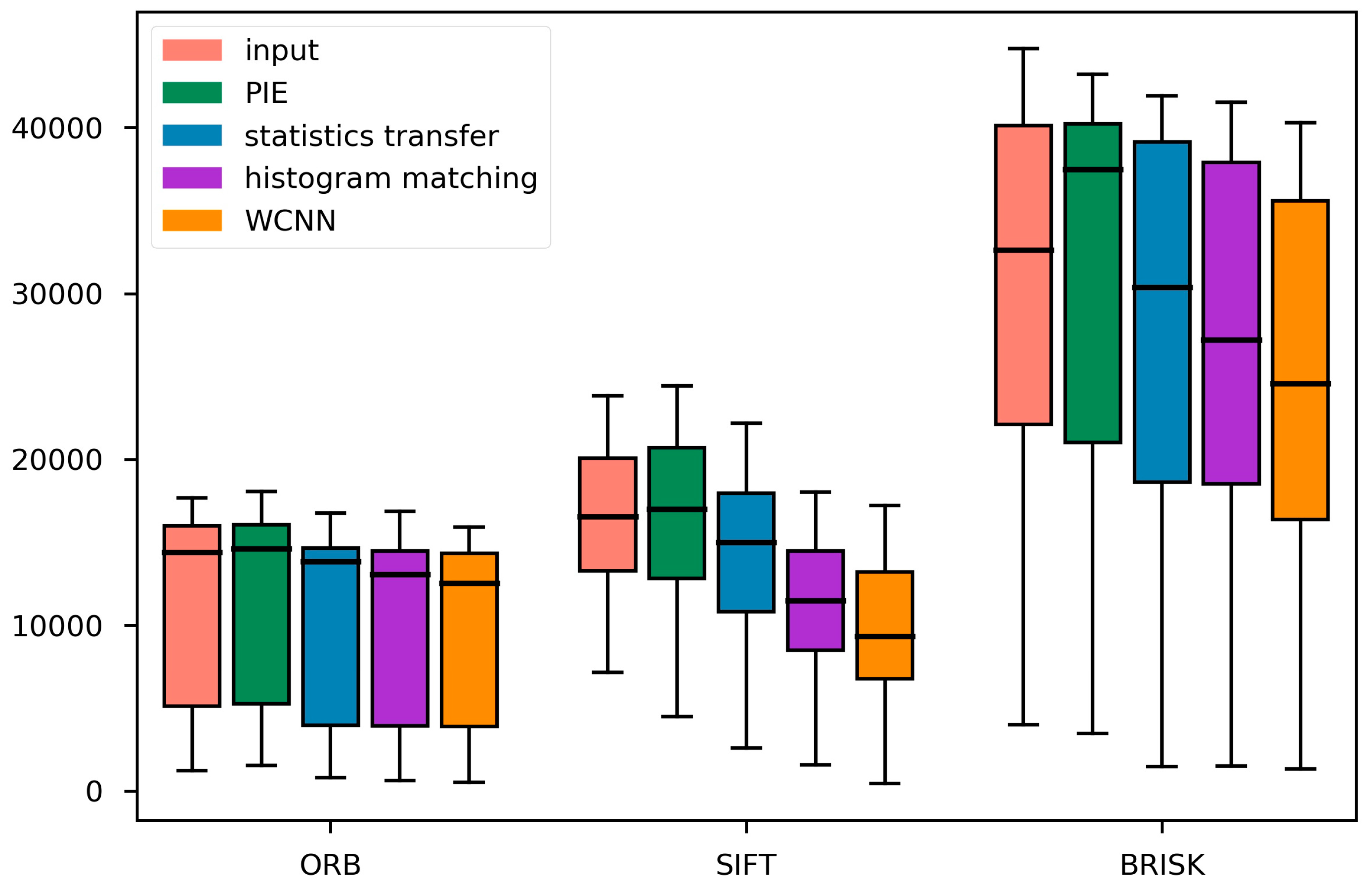
4.3. Processing Time and Memory Comsumption
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Haichao, L.; Shengyong, H.; Qi, Z. Fast seamless mosaic algorithm for multiple remote sensing images. Infrared Laser Eng. 2011, 40, 1381–1386. [Google Scholar]
- Rau, J.; Chen, N.-Y.; Chen, L.-C. True orthophoto generation of built-up areas using multi-view images. Photogramm. Eng. Remote Sens. 2002, 68, 581–588. [Google Scholar]
- Reinhard, E.; Adhikhmin, M.; Gooch, B.; Shirley, P. Color transfer between images. IEEE Comput. Graph. Appl. 2001, 21, 34–41. [Google Scholar] [CrossRef]
- Abadpour, A.; Kasaei, S. A fast and efficient fuzzy color transfer method. In Proceedings of the IEEE Fourth International Symposium on Signal Processing and Information Technology, Rome, Italy, 18–21 Dcember 2004; pp. 491–494. [Google Scholar]
- Kotera, H. A scene-referred color transfer for pleasant imaging on display. In Proceedings of the IEEE International Conference on Image Processing, Genova, Italy, 14 November 2005. [Google Scholar]
- Morovic, J.; Sun, P.-L. Accurate 3d image colour histogram transformation. Pattern Recognit. Lett. 2003, 24, 1725–1735. [Google Scholar] [CrossRef]
- Neumann, L.; Neumann, A. Color style transfer techniques using hue, lightness and saturation histogram matching. In Proceedings of the Computational Aesthetics in Graphics, Visualization and Imaging, Girona, Spain, 18–20 May 2005; pp. 111–122. [Google Scholar]
- Pitie, F.; Kokaram, A.C.; Dahyot, R. N-dimensional probability density function transfer and its application to color transfer. In Proceedings of the Tenth IEEE International Conference on Computer Vision, Beijing, China, 17–21 October 2005; pp. 1434–1439. [Google Scholar]
- Reinhard, E.; Pouli, T. Colour spaces for colour transfer. In Proceedings of the International Workshop on Computational Color Imaging, Milan, Italy, 20–21 April 2011; Springer: Berlin/Heidelberg, Germany; pp. 1–15. [Google Scholar]
- An, X.; Pellacini, F. User-controllable color transfer. In Computer Graphics Forum; Wiley Online Library: Hoboken, NJ, USA, 2010; pp. 263–271. [Google Scholar]
- Pouli, T.; Reinhard, E. Progressive color transfer for images of arbitrary dynamic range. Comput. Graph. 2011, 35, 67–80. [Google Scholar] [CrossRef]
- Tai, Y.-W.; Jia, J.; Tang, C.-K. Local color transfer via probabilistic segmentation by expectation-maximization. In Proceedings of the IEEE Computer Society Conference on Computer Vision and Pattern Recognition, San Diego, CA, USA, 20–26 June 2005; pp. 747–754. [Google Scholar]
- HaCohen, Y.; Shechtman, E.; Goldman, D.B.; Lischinski, D. Non-rigid dense correspondence with applications for image enhancement. ACM Trans. Graph. 2011, 30, 70. [Google Scholar] [CrossRef]
- Kagarlitsky, S.; Moses, Y.; Hel-Or, Y. Piecewise-consistent color mappings of images acquired under various conditions. In Proceedings of the IEEE 12th International Conference on Computer Vision, Kyoto, Japan, 29 September–2 October 2009; pp. 2311–2318. [Google Scholar]
- Bonneel, N.; Sunkavalli, K.; Paris, S.; Pfister, H. Example-based video color grading. ACM Trans. Graph. 2013, 32, 39:1–39:12. [Google Scholar] [CrossRef]
- Wang, Q.; Yan, P.; Yuan, Y.; Li, X. Robust color correction in stereo vision. In Proceedings of the 2011 18th IEEE International Conference on Image Processing, Brussels, Belgium, 11–14 September 2011; pp. 965–968. [Google Scholar]
- Gong, H.; Finlayson, G.D.; Fisher, R.B. Recoding color transfer as a color homography. arXiv, 2016; arXiv:1608.01505. [Google Scholar]
- Liao, D.; Qian, Y.; Li, Z.-N. Semisupervised manifold learning for color transfer between multiview images. In Proceedings of the 2016 23rd International Conference on Pattern Recognition, Cancun, Mexico, 4–8 December 2016; pp. 259–264. [Google Scholar]
- Isola, P.; Zhu, J.-Y.; Zhou, T.; Efros, A.A. Image-to-image translation with conditional adversarial networks. arXiv, 2016; arXiv:1611.07004. [Google Scholar]
- Larsson, G.; Maire, M.; Shakhnarovich, G. Learning representations for automatic colorization. In Proceedings of the European Conference on Computer Vision, Amsterdam, The Netherlands, 8–16 October 2016; pp. 577–593. [Google Scholar]
- Zhang, R.; Isola, P.; Efros, A.A. Colorful image colorization. In Proceedings of the European Conference on Computer Vision, Amsterdam, The Netherlands, 8–16 October 2016; pp. 649–666. [Google Scholar]
- Wang, Q.; Lin, J.; Yuan, Y. Salient band selection for hyperspectral image classification via manifold ranking. IEEE Trans. Neural Netw. Learn. Syst. 2016, 27, 1279–1289. [Google Scholar] [CrossRef] [PubMed]
- Vallet, B.; Lelégard, L. Partial iterates for symmetrizing non-parametric color correction. ISPRS J. Photogramm. Remote Sens. 2013, 82, 93–101. [Google Scholar] [CrossRef]
- Danila, B.; Yu, Y.; Marsh, J.A.; Bassler, K.E. Optimal transport on complex networks. Phys. Rev. E Stat. Nomlin. Soft. Matter Phys. 2006, 74, 046106. [Google Scholar] [CrossRef] [PubMed]
- Villani, C. Optimal Transport: Old and New; Springer: Berlin, Germany, 2008. [Google Scholar]
- Pitié, F.; Kokaram, A. The linear monge-kantorovitch linear colour mapping for example-based colour transfer. In Proceedings of the European Conference on Visual Media Production, London, UK, 27–28 November 2007. [Google Scholar]
- Frogner, C.; Zhang, C.; Mobahi, H.; Araya, M.; Poggio, T.A. Learning with a wasserstein loss. In Proceedings of the Advances in Neural Information Processing Systems, Montreal, QC, Canada, 2015; pp. 2053–2061. [Google Scholar]
- Cuturi, M.; Avis, D. Ground metric learning. J. Mach. Learn. Res. 2014, 15, 533–564. [Google Scholar]
- Iandola, F.N.; Han, S.; Moskewicz, M.W.; Ashraf, K.; Dally, W.J.; Keutzer, K. Squeezenet: Alexnet-level accuracy with 50x fewer parameters and <0.5 mb model size. arXiv, 2016; arXiv:1602.07360. [Google Scholar]
- Long, J.; Shelhamer, E.; Darrell, T. Fully convolutional networks for semantic segmentation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 2015; pp. 3431–3440. [Google Scholar]
- Chen, L.-C.; Papandreou, G.; Kokkinos, I.; Murphy, K.; Yuille, A.L. Semantic image segmentation with deep convolutional nets and fully connected crfs. arXiv, 2014; arXiv:1412.7062. [Google Scholar]




| Input | Reference | Scheme |
|---|---|---|
| Histogram | Histogram | A |
| Image | Image | B |
| Image | Histogram | C |
| Histogram | Image | D |
| Resolution | GF1 | GF2 |
|---|---|---|
| 8 m | 4 m | |
| Band1 | 0.45–0.52 μm | 0.45–0.52 μm |
| Band2 | 0.52–0.59 μm | 0.52–0.59 μm |
| Band3 | 0.63–0.69 μm | 0.63–0.69 μm |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guo, J.; Pan, Z.; Lei, B.; Ding, C. Automatic Color Correction for Multisource Remote Sensing Images with Wasserstein CNN. Remote Sens. 2017, 9, 483. https://doi.org/10.3390/rs9050483
Guo J, Pan Z, Lei B, Ding C. Automatic Color Correction for Multisource Remote Sensing Images with Wasserstein CNN. Remote Sensing. 2017; 9(5):483. https://doi.org/10.3390/rs9050483
Chicago/Turabian StyleGuo, Jiayi, Zongxu Pan, Bin Lei, and Chibiao Ding. 2017. "Automatic Color Correction for Multisource Remote Sensing Images with Wasserstein CNN" Remote Sensing 9, no. 5: 483. https://doi.org/10.3390/rs9050483
APA StyleGuo, J., Pan, Z., Lei, B., & Ding, C. (2017). Automatic Color Correction for Multisource Remote Sensing Images with Wasserstein CNN. Remote Sensing, 9(5), 483. https://doi.org/10.3390/rs9050483