Gated Convolutional Neural Network for Semantic Segmentation in High-Resolution Images
Abstract
:1. Introduction
- A gated network architecture is proposed for adaptive information propagation among feature maps with different level. With this architecture, convolution layers propagate the selected information into the final features. In this way, local and contextual features work with each other for improving the segmentation accuracy.
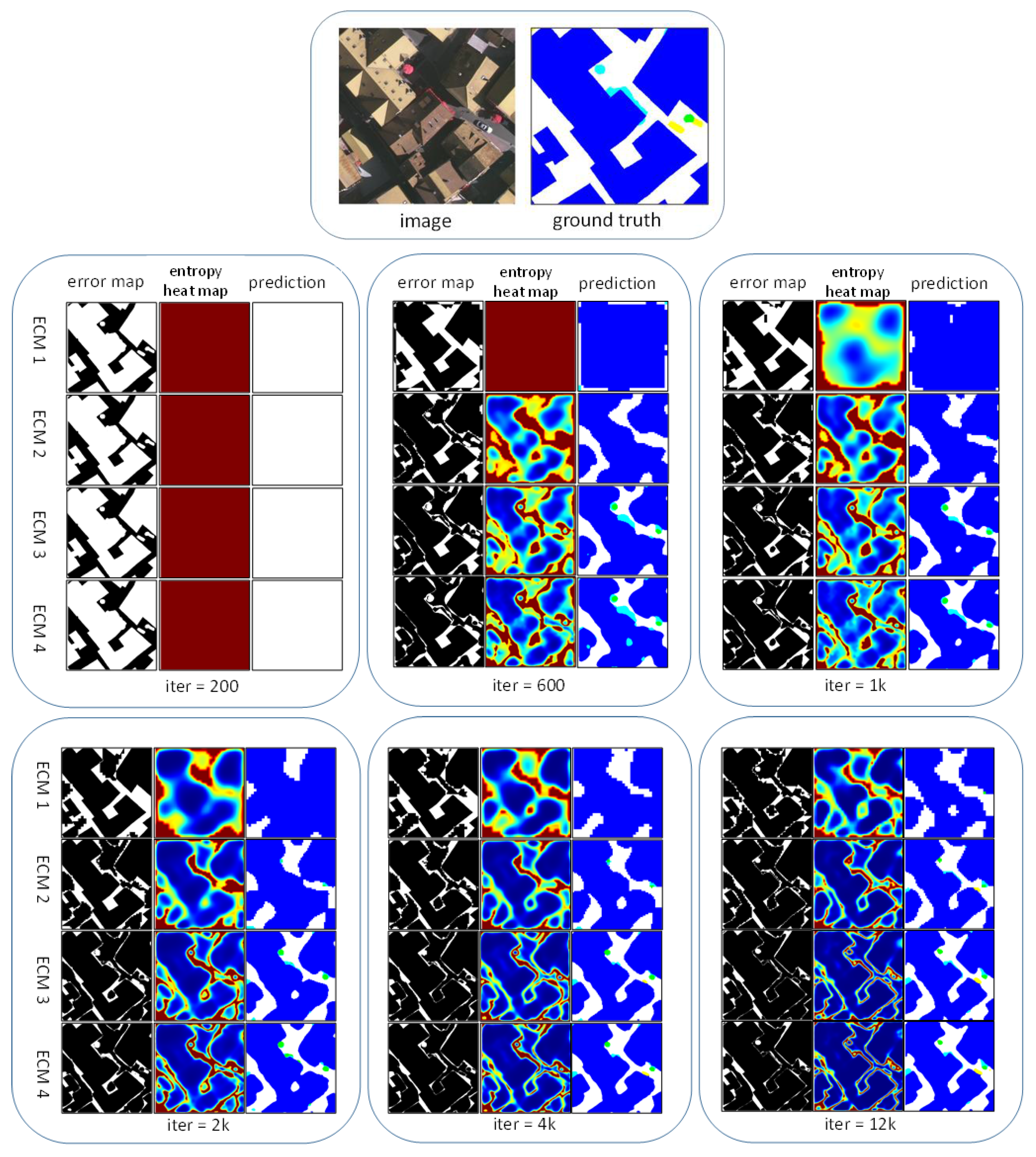
- An entropy control layer is introduced to implement the gate. It is based on the observation that the information entropy of the feature maps before the classifier are closely related to the label-error map of the segmentation, as shown in Figure 1.
- A new deep learning pipeline for semantic segmentation is proposed. It effectively integrates local details and contextual information and can be trained via an end-to-end manner.
- The proposed method achieves state-of-the-art performance among all the published papers on the ISPRS 2D semantic labeling benchmark. Specifically, our method achieves a mean score of 88.7% on five categories (ranking 1st) and overall accuracy 90.3% (ranking 1st). It should be noted that these results are obtained using only RGB images with a single model, without Digital Surface Model (DSM) and model ensemble strategy.
2. Related Work
2.1. Deep Learning
2.2. Semantic Segmentation in Remote Sensing
2.3. Gate in Neural Networks
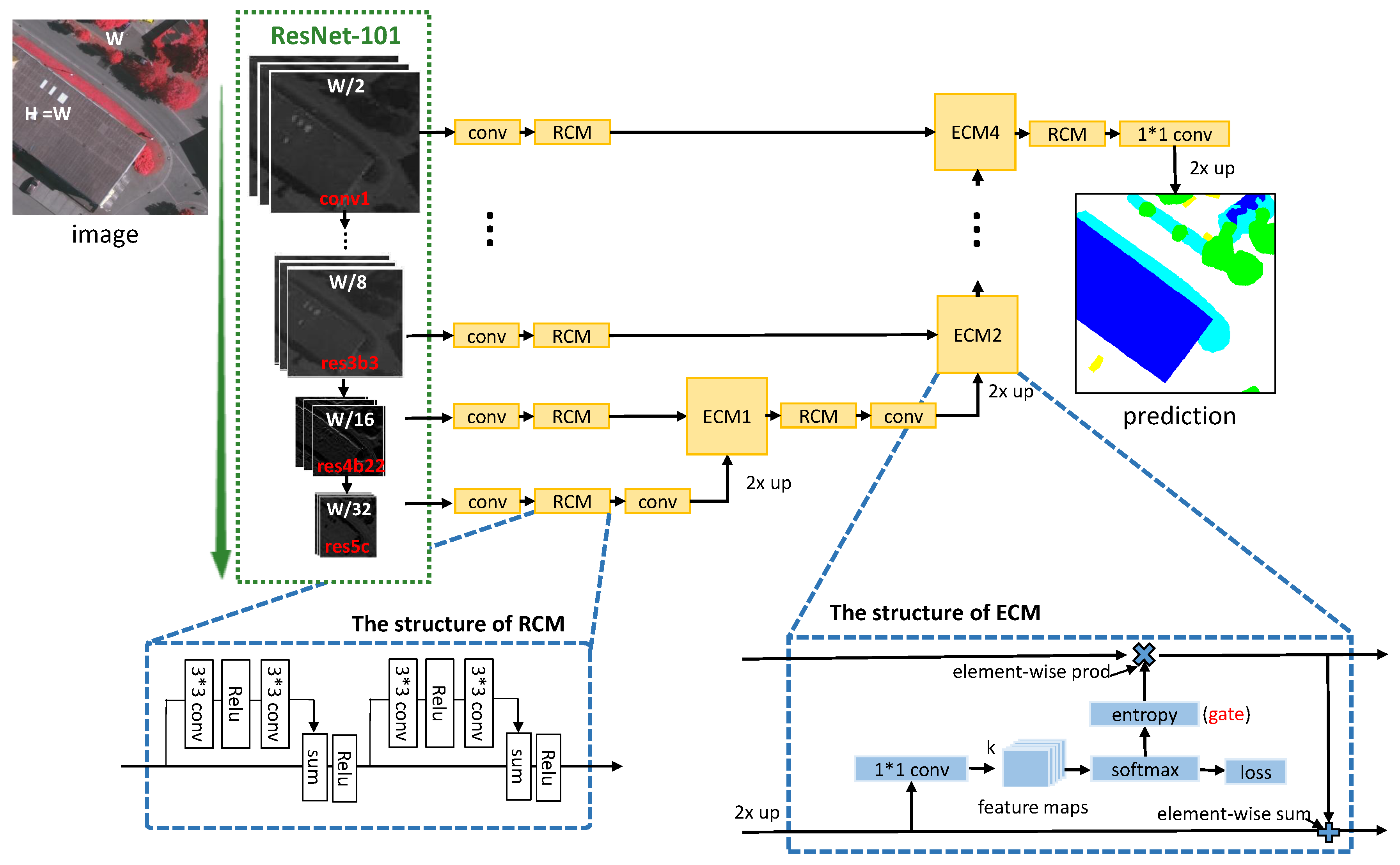
3. Method
3.1. Important Observation
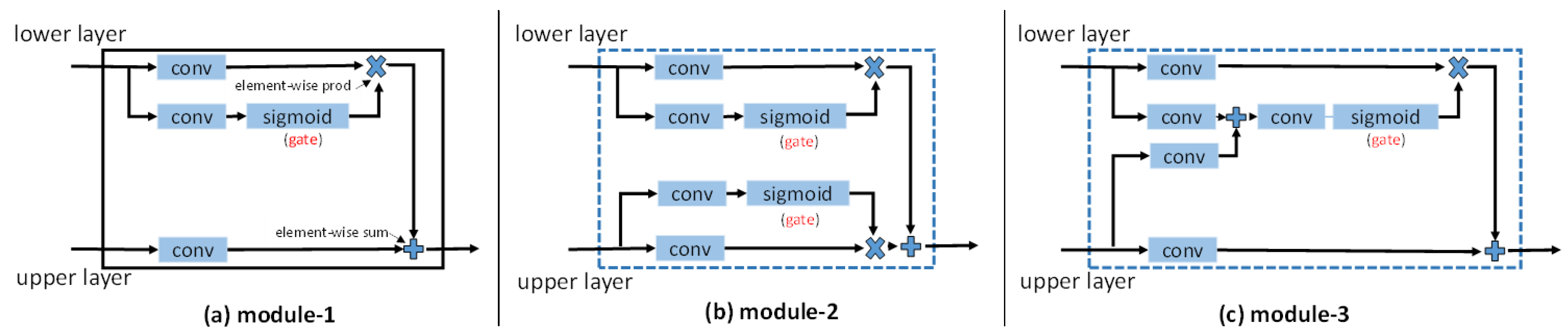
3.2. Gated Segmentation Network
3.2.1. Entropy Control Module
3.2.2. Residual Convolution Module
3.2.3. Model Optimization
| Algorithm 1 The training algorithm for the proposed GSN. |
| Input: Training data x, maximum iteration T. Initialize the parameters θ in convolutional layers, learning rate αt, learning rate policy ploy. Set the initialized iteration t ← 0. Output: The leanred parameter θ. 1: while do 2: . 3: Call network forward to compute the output and loss L. 4: Call network backward to compute the gradients . 5: Update the parameters by . 6: Updates the according to learning rate policy. 7: end while |
3.3. Implementation Details
4. Experiments
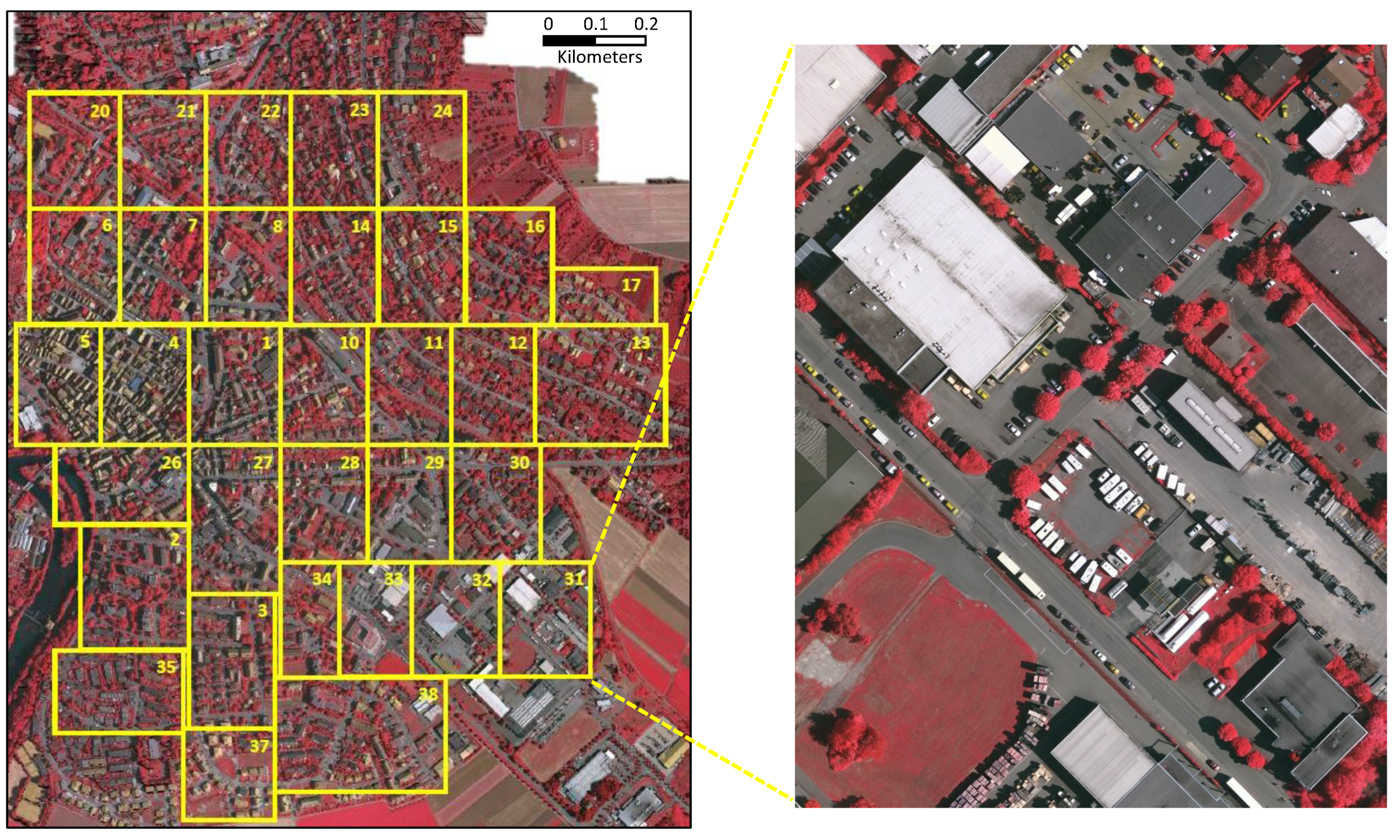
4.1. Dataset
4.2. Model Analysis
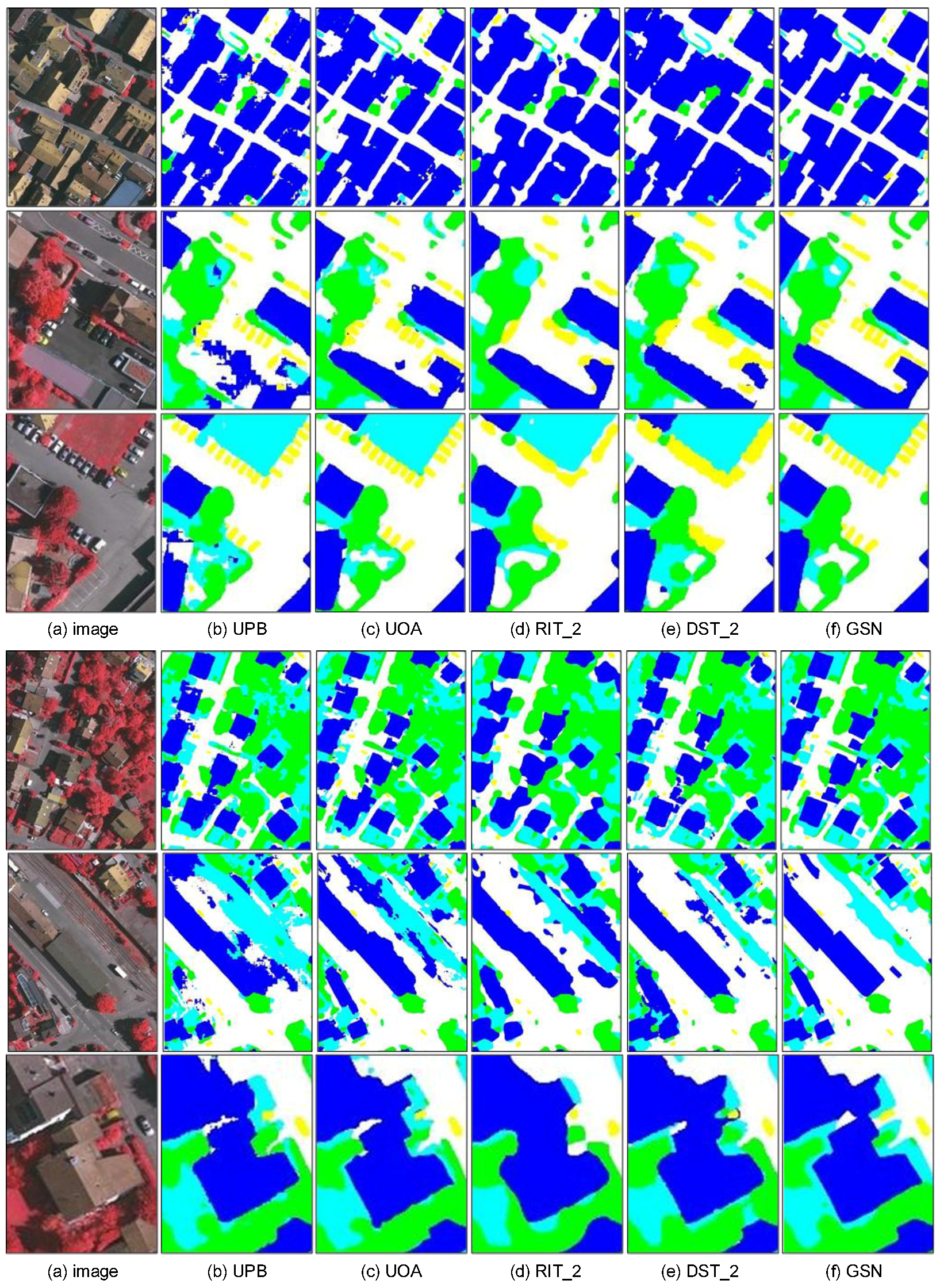
4.3. Comparisons with Related Methods
4.4. Model Visualization
4.5. ISPRS Benchmark Testing Results
4.6. Failed Attempts
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Wang, Q.; Lin, J.; Yuan, Y. Salient band selection for hyperspectral image classification via manifold ranking. IEEE Trans. Neural Netw. Learn. Syst. 2016, 27, 1279–1289. [Google Scholar] [CrossRef] [PubMed]
- Cheng, G.; Zhu, F.; Xiang, S.; Wang, Y.; Pan, C. Accurate urban road centerline extraction from VHR imagery via multiscale segmentation and tensor voting. Neurocomputing 2016, 205, 407–420. [Google Scholar] [CrossRef]
- Yuan, Y.; Lin, J.; Wang, Q. Dual-clustering-based hyperspectral band selection by contextual analysis. IEEE Trans. Geosci. Remote Sens. 2016, 54, 1431–1445. [Google Scholar] [CrossRef]
- Matikainen, L.; Karila, K. egment-based land cover mapping of a suburban area—Comparison of high-resolution remotely sensed datasets using classification trees and test field points. Remote Sens. 2011, 3, 1777–1804. [Google Scholar] [CrossRef]
- Tang, Y.; Zhang, L. Urban change analysis with multi-sensor multispectral imagery. Remote Sens. 2017, 9, 252. [Google Scholar] [CrossRef]
- Yuan, Y.; Lin, J.; Wang, Q. Hyperspectral image classification via multitask joint sparse representation and stepwise MRF optimization. IEEE Trans. Cybern. 2016, 46, 2966–2977. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Q.; Seto, K.C. Mapping urbanization dynamics at regional and global scales using multi-temporal DMSP/OLS nighttime light data. Remote Sens. Environ. 2011, 115, 2320–2329. [Google Scholar] [CrossRef]
- Sherrah, J. Fully convolutional networks for dense semantic labelling of highresolution aerial imagery. arXiv 2016. [Google Scholar]
- Girshick, R. Fast r-cnn. In Proceedings of the IEEE International Conference on Computer Vision, Santiago, Chile, 13–16 December 2015; pp. 1440–1448. [Google Scholar]
- Goodfellow, I.; Pouget-Abadie, J.; Mirza, M.; Xu, B.; Warde-Farley, D.; Ozair, S.; Courville, A.; Bengio, Y. Generative adversarial nets. In Proceedings of the Advances in Neural Information Processing Systems, Montreal, QC, Canada, 8–13 December 2014; pp. 2672–2680. [Google Scholar]
- Yang, S.; Luo, P.; Loy, C.C.; Tang, X. From facial parts responses to face detection: A deep learning approach. In Proceedings of the IEEE International Conference on Computer Vision, Santiago, Chile, 13–16 December 2015; pp. 3676–3684. [Google Scholar]
- Long, J.; Shelhamer, E.; Darrell, T. Fully convolutional networks for semantic segmentation. IEEE Trans. Pattern Anal. Mach. Intell. 2015, 79, 1337–1342. [Google Scholar]
- Ronneberger, O.; Fischer, P.; Brox, T. U-net: Convolutional networks for biomedical image segmentation. In Proceedings of the International Conference on Medical Image Computing and Computer-Assisted Intervention, Munich, Germany, 5–9 October 2015; Springer: Cham, Switzerland, 2015; pp. 234–241. [Google Scholar]
- Badrinarayanan, V.; Kendall, A.; Cipolla, R. Segnet: A deep convolutional encoder-decoder architecture for image segmentation. arXiv 2015. [Google Scholar]
- Lin, G.; Milan, A.; Shen, C.; Reid, I. RefineNet: Multi-path refinement networks with identity mappings for high-resolution semantic segmentation. arXiv 2016. [Google Scholar]
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. Imagenet classification with deep convolutional neural networks. In Proceedings of the Advances in Neural Information Processing Systems, Lake Tahoe, NV, USA, 3–6 December 2012; pp. 1097–1105. [Google Scholar]
- Simonyan, K.; Zisserman, A. Very deep convolutional networks for large-scale image recognition. arXiv 2014. [Google Scholar]
- Szegedy, C.; Liu, W.; Jia, Y.; Sermanet, P.; Reed, S.; Anguelov, D.; Erhan, D.; Vanhoucke, V.; Rabinovich, A. Going deeper with convolutions. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 7–12 June 2015; pp. 1–9. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 27–30 June 2016; pp. 770–778. [Google Scholar]
- Ren, S.; He, K.; Girshick, R.; Sun, J. Faster r-cnn: Towards real-time object detection with region proposal networks. In Proceedings of the Advances in Neural Information Processing Systems, Montreal, QC, Canada, 7–12 December 2015; pp. 91–99. [Google Scholar]
- Chen, L.C.; Papandreou, G.; Kokkinos, I.; Murphy, K.; Yuille, A.L. Deeplab: Semantic image segmentation with deep convolutional nets, atrous convolution, and fully connected crfs. arXiv 2016. [Google Scholar] [CrossRef] [PubMed]
- Zhou, B.; Khosla, A.; Lapedriza, A.; Oliva, A.; Torralba, A. Learning deep features for discriminative localization. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 27–30 June 2016; pp. 2921–2929. [Google Scholar]
- Ghamisi, P.; Dalla Mura, M.; Benediktsson, J.A. A survey on spectral–spatial classification techniques based on attribute profiles. IEEE Trans. Geosci. Remote Sens. 2015, 53, 2335–2353. [Google Scholar] [CrossRef]
- Bruzzone, L.; Demir, B. A review of modern approaches to classification of remote sensing data. In Land Use and Land Cover Mapping in Europe; Springer: Dordrecht, The Netherlands, 2014; pp. 127–143. [Google Scholar]
- Zhang, L.; Zhang, L.; Du, B. Deep learning for remote sensing data: A technical tutorial on the state of the art. IEEE Geosci. Remote Sens. Mag. 2016, 4, 22–40. [Google Scholar] [CrossRef]
- Paisitkriangkrai, S.; Sherrah, J.; Janney, P.; van-Den Hengel, A. Effective semantic pixel labelling with convolutional networks and Conditional Random Fields. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition Workshops, Boston, MA, USA, 7–12 June 2015; pp. 36–43. [Google Scholar]
- Audebert, N.; Le Saux, B.; Lefevre, S. How useful is region-based classification of remote sensing images in a deep learning framework? In Proceedings of the IEEE Conference on Geoscience and Remote Sensing Symposium, Beijing, China, 10–15 July 2016; pp. 5091–5094. [Google Scholar]
- Marmanis, D.; Schindler, K.; Wegner, J.D.; Galliani, S.; Datcu, M.; Stilla, U. Classification with an edge: Improving semantic image segmentation with boundary detection. arXiv 2016. [Google Scholar]
- Kampffmeyer, M.; Salberg, A.B.; Jenssen, R. Semantic segmentation of small objects and modeling of uncertainty in urban remote sensing images using deep convolutional neural networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition Workshops, Seattle, WA, USA, 27–30 June 2016; pp. 1–9. [Google Scholar]
- Arnab, A.; Jayasumana, S.; Zheng, S.; Torr, P.H. Higher order conditional random fields in deep neural networks. In Proceedings of the European Conference on Computer Vision, Amsterdam, The Netherlands, 8–16 October 2016; Springer: Cham, Switzerland, 2016; pp. 524–540. [Google Scholar]
- Zheng, S.; Jayasumana, S.; Romera-Paredes, B.; Vineet, V.; Su, Z.; Du, D.; Huang, C.; Torr, P.H. Conditional random fields as recurrent neural networks. In Proceedings of the IEEE Conference on International Conference on Computer Vision, Los Alamitos, CA, USA, 7–13 December 2015; pp. 1529–1537. [Google Scholar]
- Hochreiter, S.; Schmidhuber, J. Long short-term memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef] [PubMed]
- Dauphin, Y.N.; Fan, A.; Auli, M.; Grangier, D. Language modeling with gated convolutional networks. arXiv 2016. [Google Scholar]
- Zeng, X.; Ouyang, W.; Yan, J.; Li, H.; Xiao, T.; Wang, K.; Liu, Y.; Zhou, Y.; Yang, B.; Wang, Z.; et al. Crafting GBD-Net for Object Detection. arXiv 2016. [Google Scholar]
- Shannon, C.E. A mathematical theory of communication. Bell Syst. Tech. J. 1948, 5, 3–55. [Google Scholar]
- Ioffe, S.; Szegedy, C. Batch normalization: Accelerating deep network training by reducing internal covariate shift. arXiv 2015. [Google Scholar]
- Rumelhart, D.E.; Hinton, G.E.; Williams, R.J. Learning representations by back-propagating errors. Nature 1986, 323, 533–536. [Google Scholar] [CrossRef]
- Russakovsky, O.; Deng, J.; Su, H.; Krause, J.; Satheesh, S.; Ma, S.; Huang, Z.; Karpathy, A.; Khosla, A.; Bernstein, M. ImageNet large scale visual recognition challenge. Int. J. Comput. Vis. 2015, 115, 211–252. [Google Scholar] [CrossRef]
- Hinton, G.E.; Srivastava, N.; Krizhevsky, A.; Sutskever, I.; Salakhutdinov, R.R. Improving neural networks by preventing co-adaptation of feature detectors. Comput. Sci. 2012, 3, 212–223. [Google Scholar]
- Jia, Y.; Shelhamer, E.; Donahue, J.; Karayev, S.; Long, J.; Girshick, R.; Guadarrama, S.; Darrell, T. Caffe: Convolutional architecture for fast feature embedding. arXiv 2014, 675–678. [Google Scholar]
- International Society for Photogrammetry and Remote Sensing (ISPRS). 2D Semantic Labeling Contest. Available online: http://www2.isprs.org/commissions/comm3/wg4/semantic-labeling.html (accessed on 1 April 2015).
- Vedaldi, A.; Lenc, K. Matconvnet: Convolutional neural networks for matlab. In Proceedings of the 23rd ACM international conference on Multimedia, Brisbane, Australia, 26–30 October 2015; 2015; pp. 689–692. [Google Scholar]
- Marcu, A.; Leordeanu, M. Dual local-global contextual pathways for recognition in aerial imagery. arXiv 2016. [Google Scholar]
- Tschannen, M.; Cavigelli, L.; Mentzer, F.; Wiatowski, T.; Benini, L. Deep structured features for semantic segmentation. arXiv 2016. [Google Scholar]
- Lin, G.; Shen, C.; van den Hengel, A.; Reid, I. Efficient piecewise training of deep structured models for semantic segmentation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 27–30 June 2016; pp. 3194–3203. [Google Scholar]
- Piramanayagam, S.; Schwartzkopf, W.; Koehler, F.; Saber, E. Classification of remote sensed images using random forests and deep learning framework. In Proceedings of the SPIE Remote Sensing; International Society for Optics and Photonics: Edinburgh, UK, 2016; p. 100040L. [Google Scholar]
- Audebert, N.; Saux, B.L.; Lefèvre, S. Semantic segmentation of earth observation data using multimodal and multi-scale deep networks. arXiv 2016. [Google Scholar]

| Method | Imp Surf | Building | Low_veg | Tree | Car | Overall Accuracy | Mean Score |
|---|---|---|---|---|---|---|---|
| baseline | 87.6% | 93.2% | 73.3% | 86.9% | 54.1% | 86.1% | 79.0% |
| GSN | 89.2% | 94.5% | 74.9% | 87.5% | 79.8% | 87.9% | 85.2% |
| GSN_noL | 89.1% | 94.3% | 74.7% | 87.4% | 78.7% | 87.8% | 84.8% |
| GSN_w | 89.5% | 94.4% | 75.9% | 87.8% | 80.9% | 88.3% | 85.7% |
| GSN_w_mc | 90.2% | 94.8% | 76.9% | 88.3% | 82.3% | 88.9% | 86.5% |
| Method | Imp Surf | Building | Low_veg | Tree | Car | Overall Accuracy | Mean Score |
|---|---|---|---|---|---|---|---|
| FCN-8s [12] | 87.1% | 91.8% | 75.2% | 86.1% | 63.8% | 85.9% | 80.8% |
| SegNet [14] | 82.7% | 89.1% | 66.3% | 83.9% | 55.7% | 82.1% | 75.5% |
| Deeplab-v2 [21] | 88.5% | 93.5% | 73.9% | 86.9% | 84.7% | 86.9% | 83.5% |
| RefineNet [15] | 88.1% | 93.3% | 74.0% | 87.1% | 65.1% | 86.7% | 81.5% |
| GSN | 89.2% | 94.5% | 74.9% | 87.5% | 79.8% | 87.9% | 85.2% |
| Method | Imp Surf | Building | Low_veg | Tree | Car | Overall Accuracy | Mean Score |
|---|---|---|---|---|---|---|---|
| UPB [43] | 87.5% | 89.3% | 77.3% | 85.8% | 77.1% | 85.1% | 83.4% |
| ETH_C [44] | 87.2% | 92.0% | 77.5% | 87.1% | 54.5% | 85.9% | 79.7% |
| UOA [45] | 89.8% | 92.1% | 80.4% | 88.2% | 82.0% | 87.6% | 86.5% |
| ADL_3 [26] | 89.5% | 93.2% | 82.3% | 88.2% | 63.3% | 88.0% | 83.3% |
| RIT_2 [46] | 90.0% | 92.6% | 81.4% | 88.4% | 61.1% | 88.0% | 82.7% |
| DST_2 [8] | 90.5% | 93.7% | 83.4% | 89.2% | 72.6% | 89.1% | 85.9% |
| ONE_7 [47] | 91.0% | 94.5% | 84.4% | 89.9% | 77.8% | 89.8% | 87.5% |
| DLR_9 [28] | 92.4% | 95.2% | 83.9% | 89.9% | 81.2% | 90.3% | 88.5% |
| GSN | 92.2% | 95.1% | 83.7% | 89.9% | 82.4% | 90.3% | 88.7% |
| Model_1 | Model_2 | Model_3 | GSN | |
|---|---|---|---|---|
| overall accuracy | 83.4% | 60.0% | 82.2% | 86.1% |
| mean score | 75.3% | 57.3% | 74.8% | 79.0% |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, H.; Wang, Y.; Zhang, Q.; Xiang, S.; Pan, C. Gated Convolutional Neural Network for Semantic Segmentation in High-Resolution Images. Remote Sens. 2017, 9, 446. https://doi.org/10.3390/rs9050446
Wang H, Wang Y, Zhang Q, Xiang S, Pan C. Gated Convolutional Neural Network for Semantic Segmentation in High-Resolution Images. Remote Sensing. 2017; 9(5):446. https://doi.org/10.3390/rs9050446
Chicago/Turabian StyleWang, Hongzhen, Ying Wang, Qian Zhang, Shiming Xiang, and Chunhong Pan. 2017. "Gated Convolutional Neural Network for Semantic Segmentation in High-Resolution Images" Remote Sensing 9, no. 5: 446. https://doi.org/10.3390/rs9050446
APA StyleWang, H., Wang, Y., Zhang, Q., Xiang, S., & Pan, C. (2017). Gated Convolutional Neural Network for Semantic Segmentation in High-Resolution Images. Remote Sensing, 9(5), 446. https://doi.org/10.3390/rs9050446






