Image Registration and Fusion of Visible and Infrared Integrated Camera for Medium-Altitude Unmanned Aerial Vehicle Remote Sensing
Abstract
:1. Introduction
1.1. Background
1.1.1. Medium-Altitude UAV and Multi-Sensor-Based Remote Sensing
1.1.2. Utility of Visible and Infrared Image Fusion
1.1.3. Problems of Visible and Infrared Image Registration and Fusion for UAV Applications
1.2. Related Work
1.2.1. Image Registration
1.2.2. Image Fusion
1.3. Present Work
2. Methodology
2.1. UAV System with a Visible Light and Infrared Integrated Camera
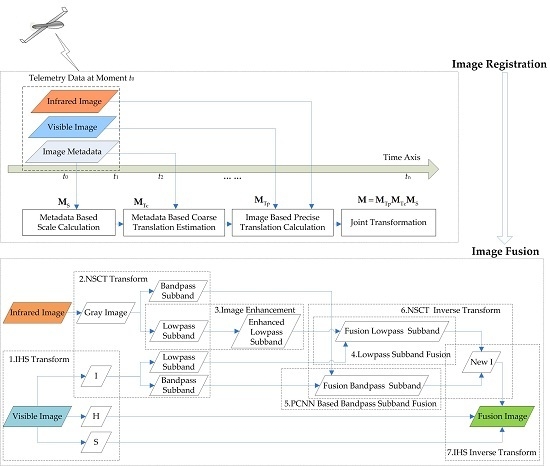
2.2. Scheme of Visibleand Infrared Image Registration and Fusion
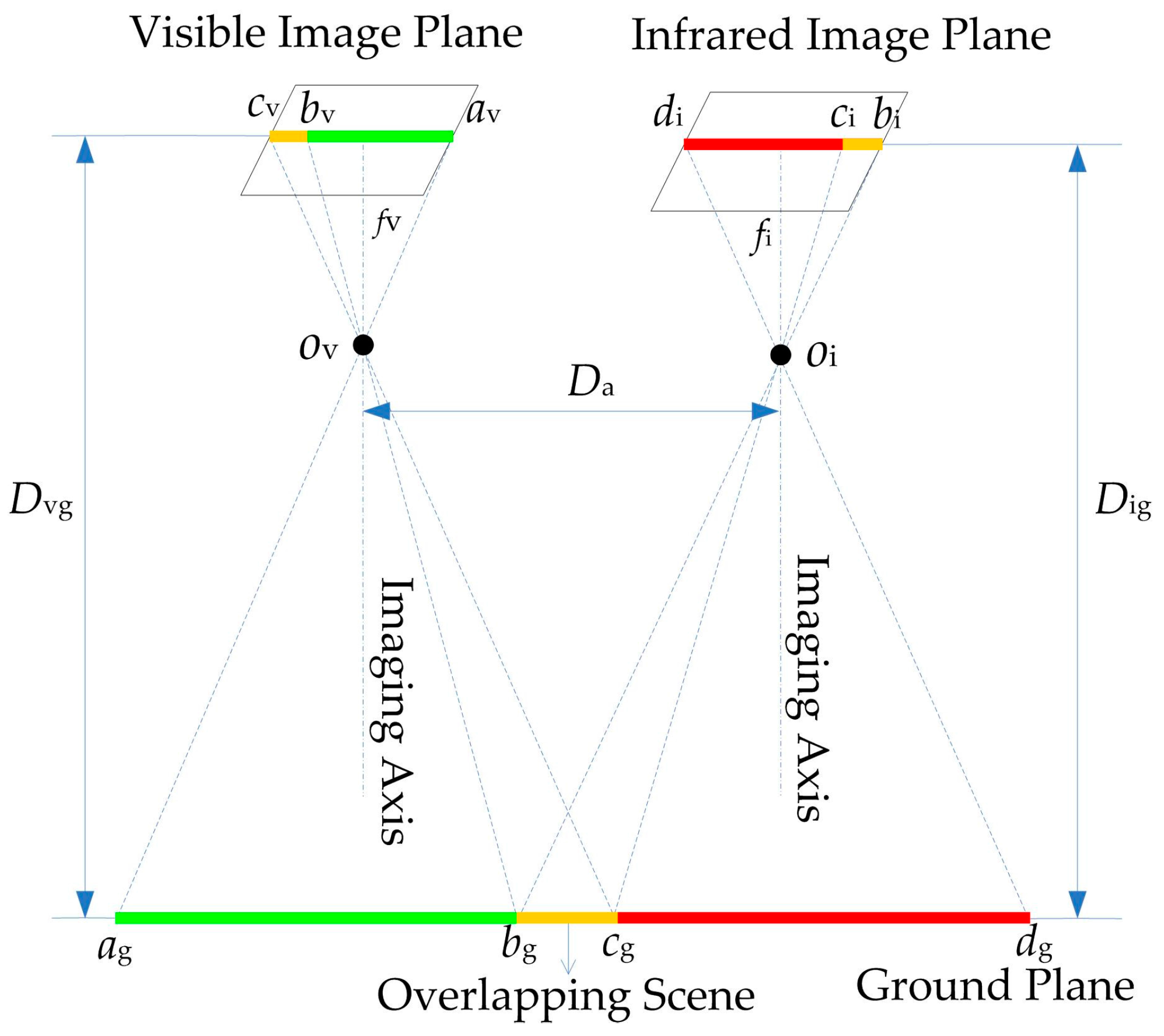
2.2.1. Long-Distance Integrated Parallel Vision
2.2.2. Visibleand Infrared Image Registration
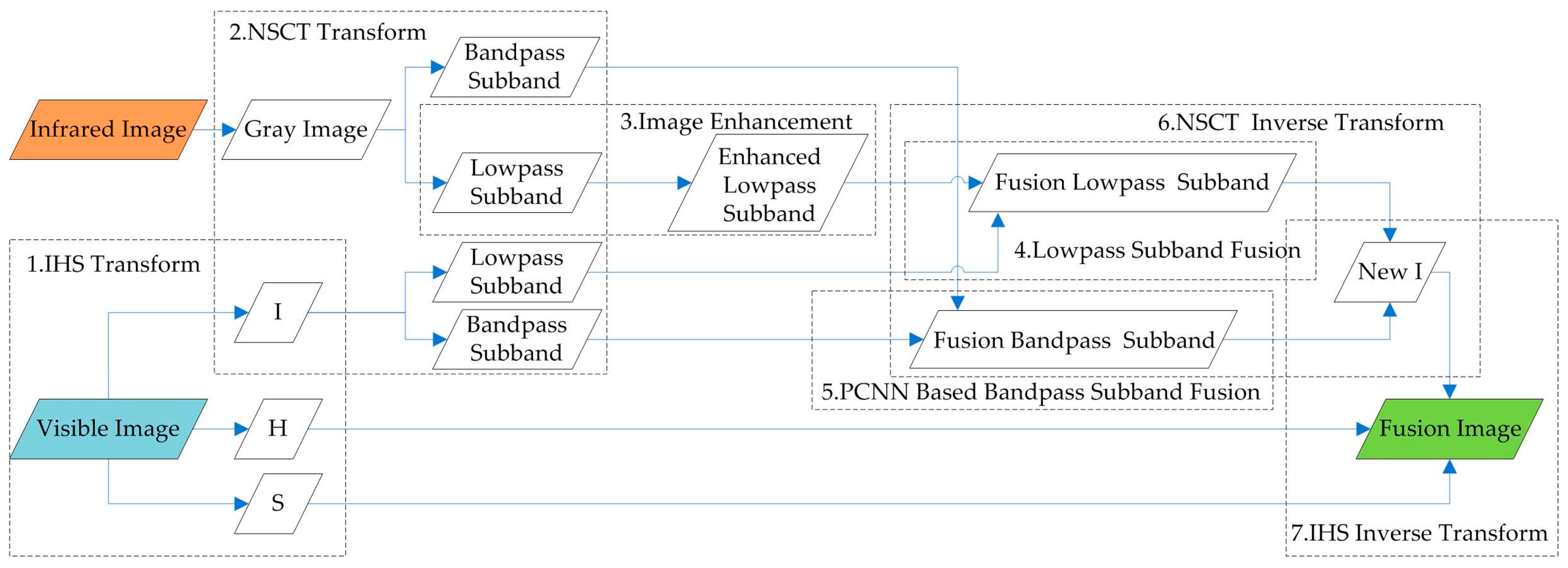
2.2.3. Visible and Infrared Image Fusion
- The IHS transform is used to extract H and S to preserve the color information, and the NSCT multi-scale decomposition is designed to resolve the declining resolution of fusion images caused by the direct substitution of the I channel.
- The lowpass sub-band of the infrared image obtained via NSCT decomposition is processed by gray stretch to enhance the contrast between the target and the background and highlight the interesting areas.
- In view of the PCNN neuron with synchronous pulse and global coupling characteristics, which can realize automatic information transmission and fusion, an algorithm of visible and infrared bandpass sub-band fusion-based PCNN model is proposed.
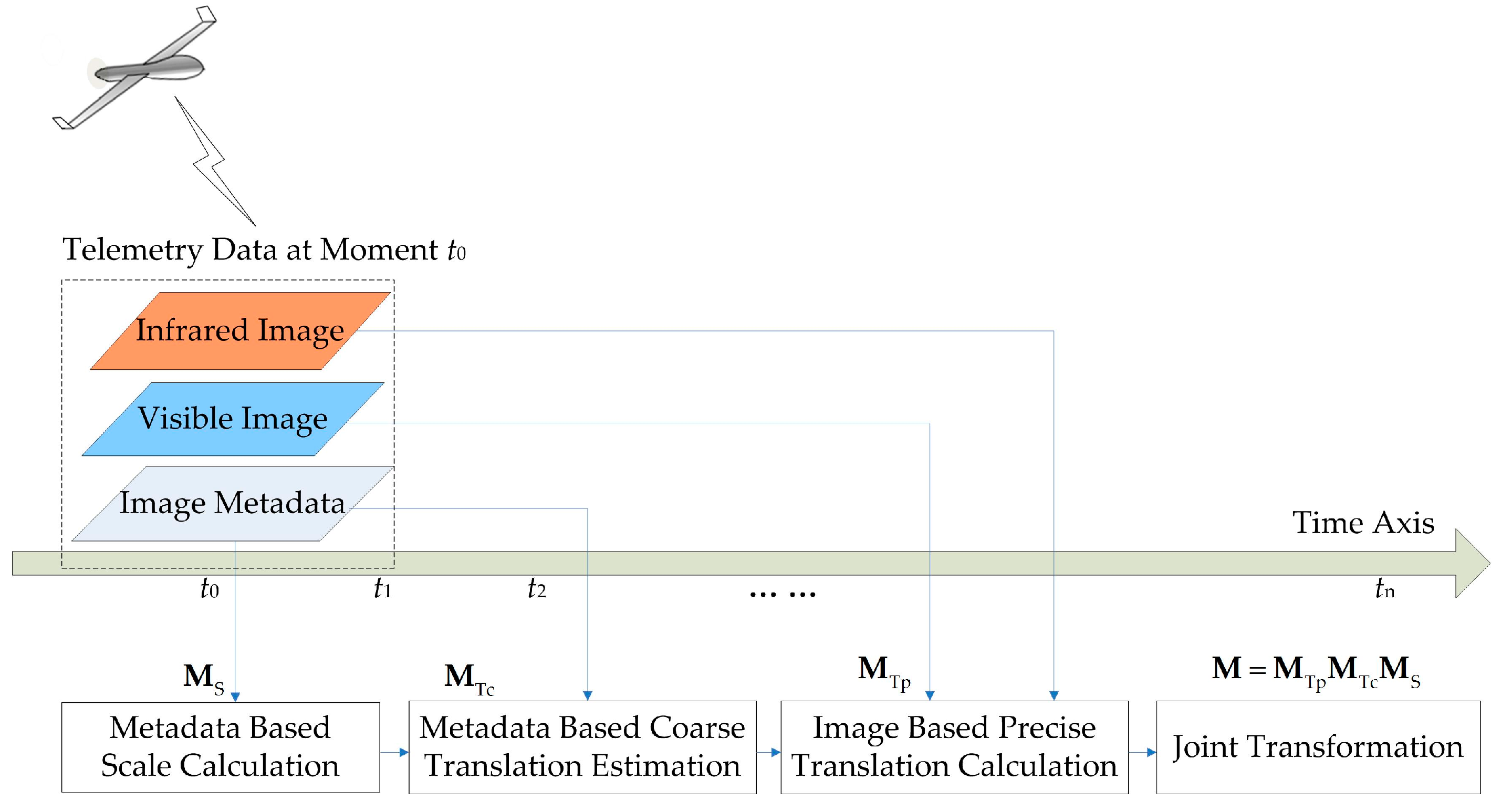
2.3. Metadata-Based Scale Calculation
2.3.1. Metadata
2.3.2. Spatial Geometry-Based Scale Calculation
2.4. Metadata-Based Coarse Translation Estimation
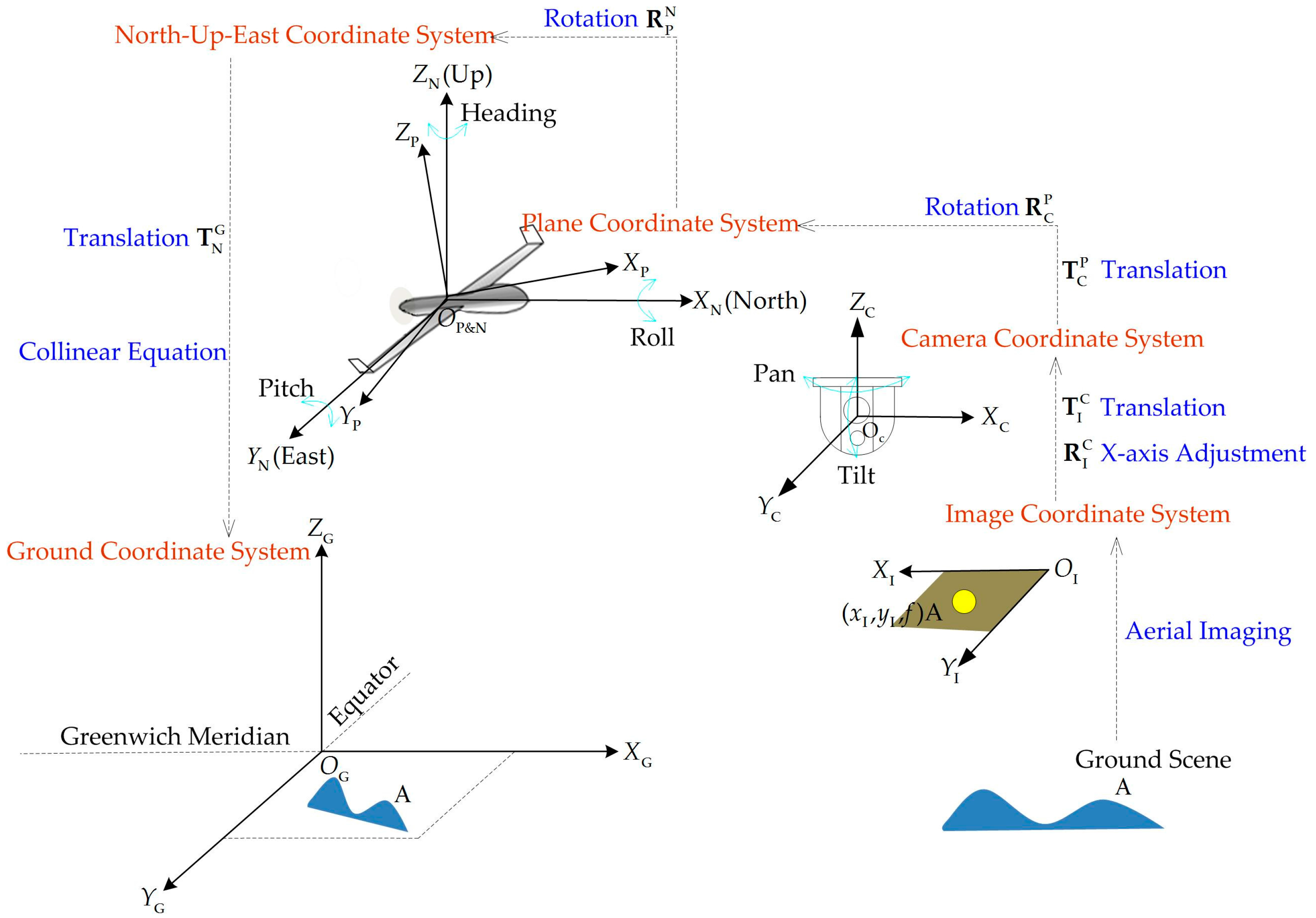
2.4.1. Five Coordinate Systems
2.4.2. Metadata-Based Coordinate Transformation
2.4.3. Coordinate Transformation-Based Coarse Translation Estimation
2.5. Image-Based Precise Translation Estimation
2.5.1. Edge Detection of Visible and Infrared Images
2.5.2. Edge Distance Field Transformation of Visible Image
2.5.3. Non-Strict Registration Based on the Edge Distance Field
Similarity for Registration
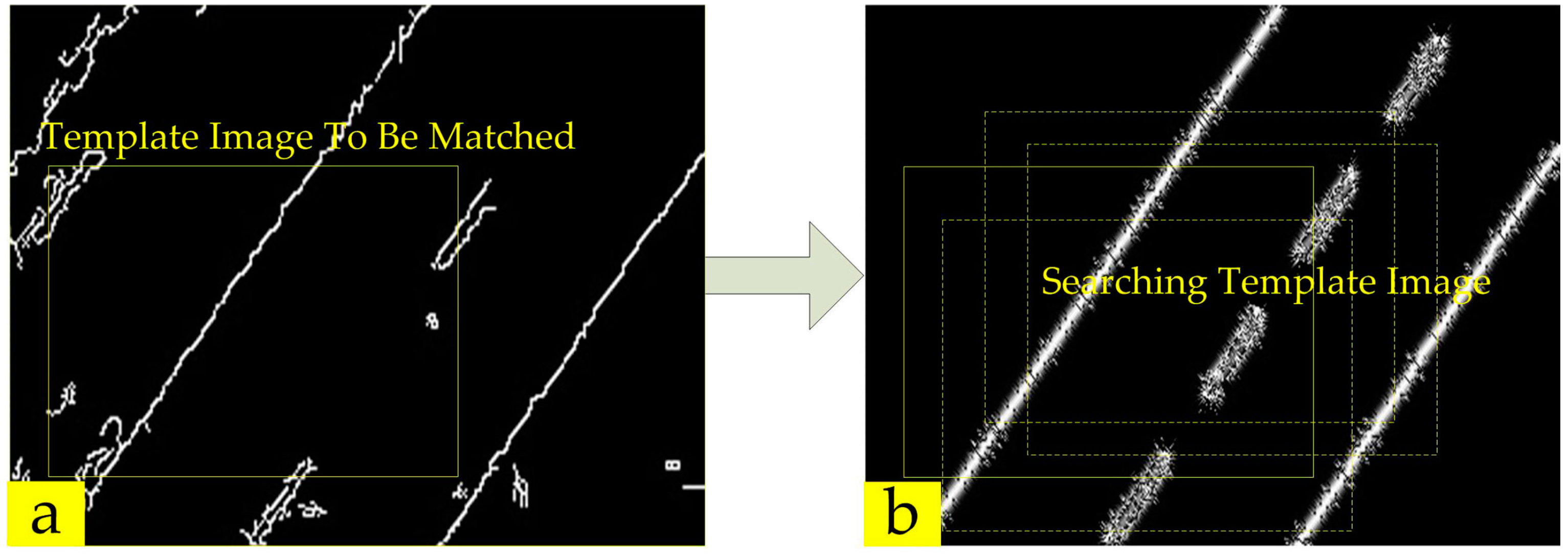
Infrared Template Image Extraction
Searching Algorithm Based on Particle Swarm Optimization
2.6. PCNN- and NSCT-Based Visibleand Infrared Image Fusion
2.6.1. Simplified PCNN Model
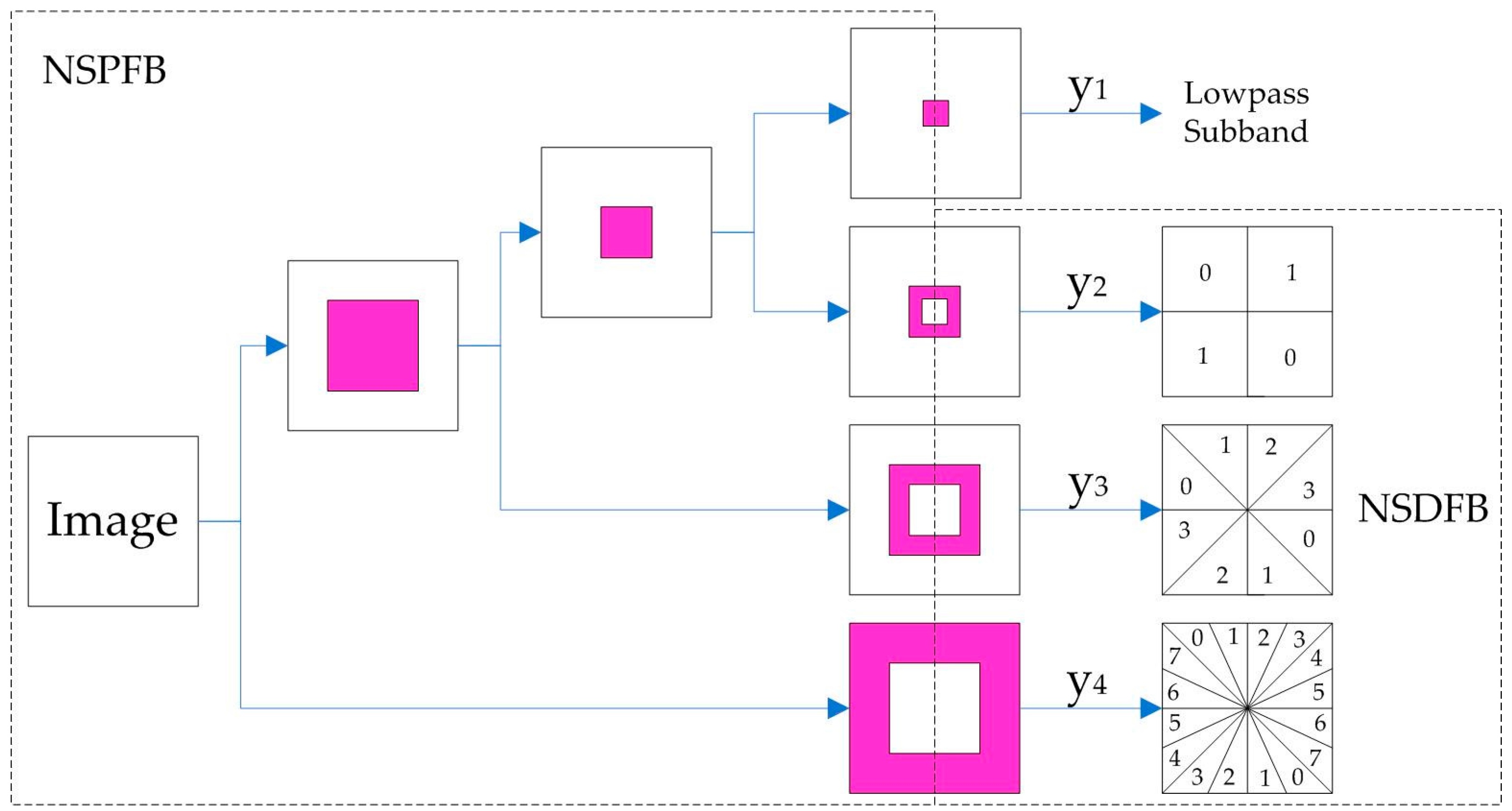
2.6.2. NSCT-Based Image Decomposition
2.6.3. Fusion Algorithm
3. Result and Discussion
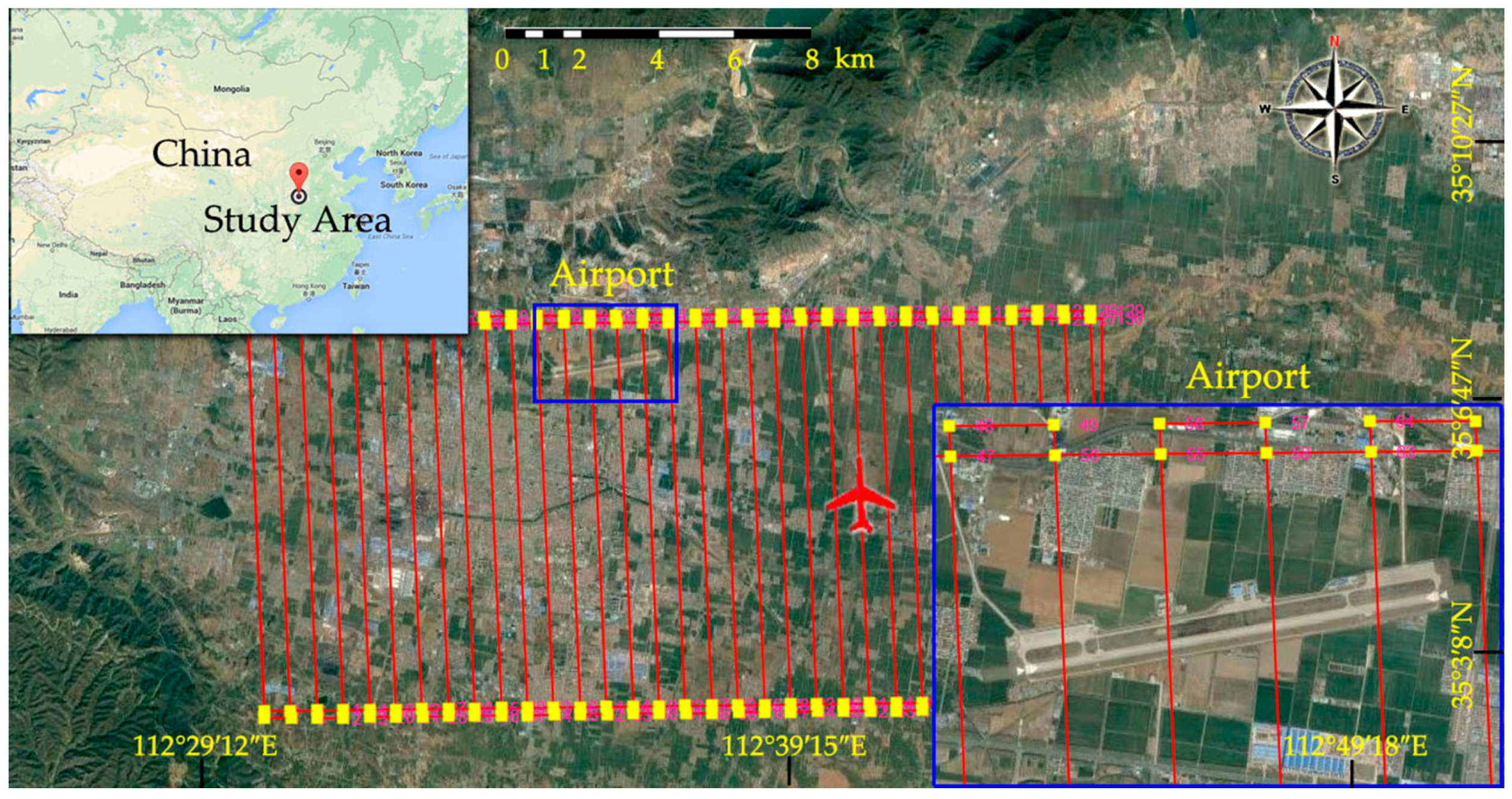
3.1. Study Area and Dataset
3.2. Spatial Geometry-Based Scale Calculation
3.3. Coordinate Transformation-Based Coarse Translation Estimation
3.4. Image Edge-Based Translation Estimation
3.5. PCNN- and NSCT-Based Image Fusion
3.5.1. Fusion of Visible Image and Low Spatial Infrared Image
3.5.2. Fusion of Interesting Areas
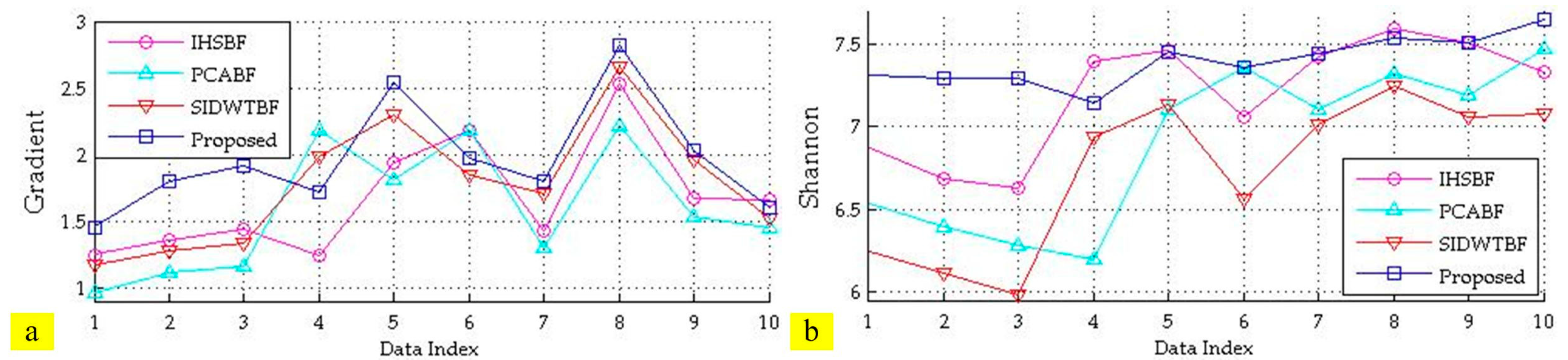
3.6. Performance Analysis
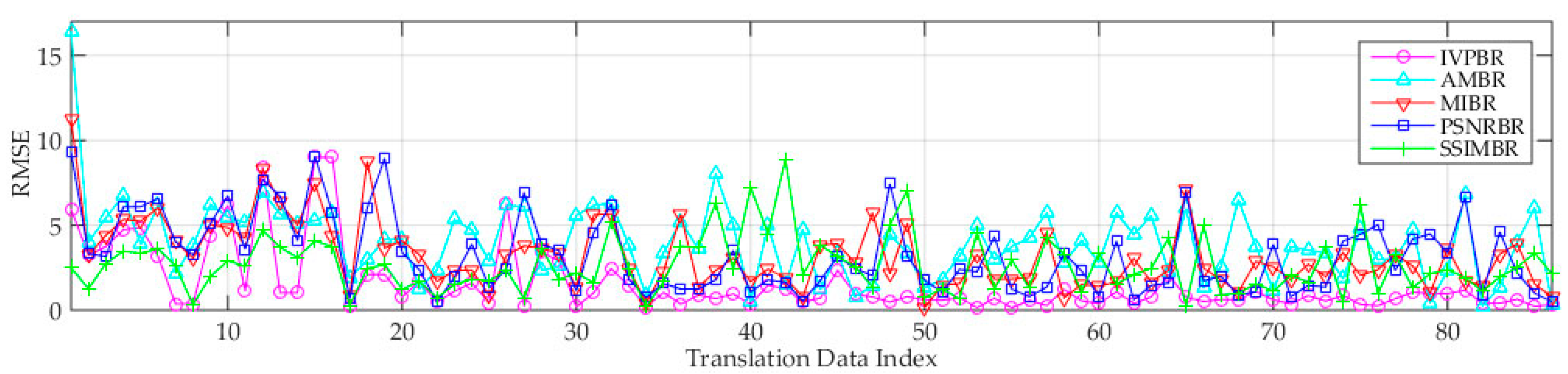
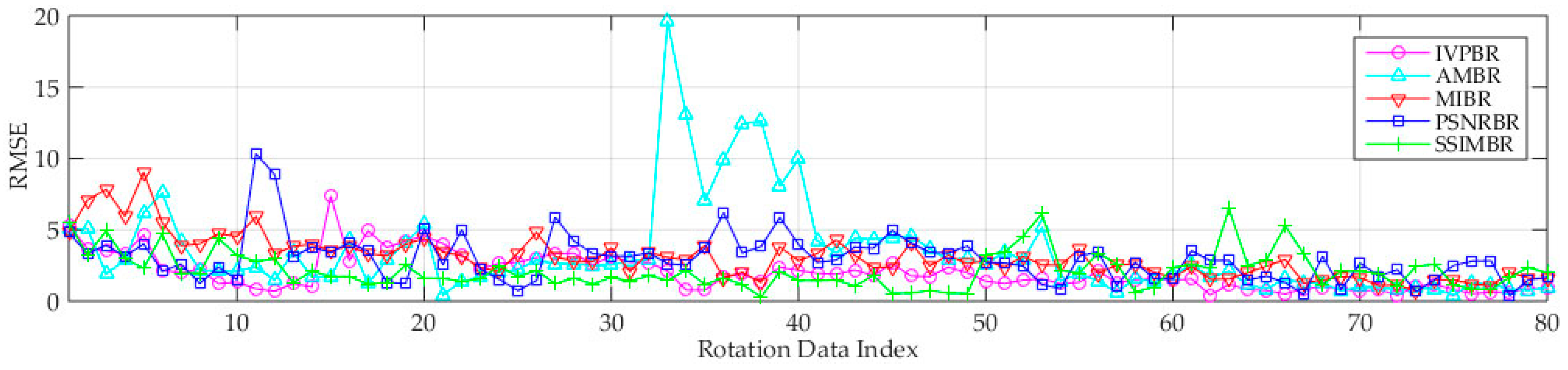
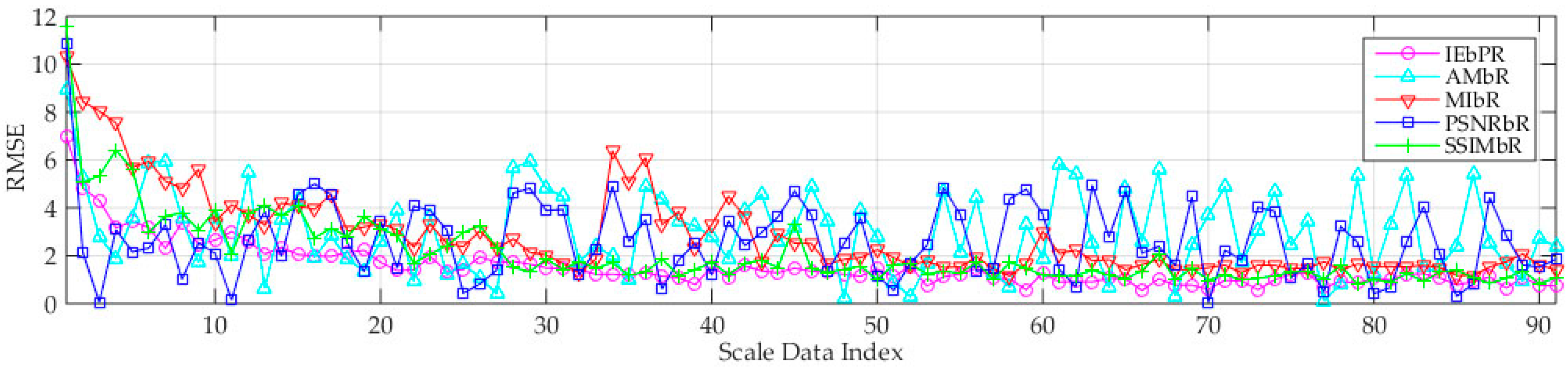
3.6.1. Performance Analysis of Image Registration
- Compared with the four other methods, the proposed IPVBR presents a stable and low MSER. This result shows the high stability and precision of the proposed method.
- SSIMBP is better than PSNRBP, which indicates that structure information is more reliable than pixel information for multimodal image registration.
- The two representative conventional methods of AMBR and MIBR fail to achieve good results under the three motion conditions for medium-altitude UAV applications.
3.6.2. Performance Analysis of Image Fusion
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Deren, L.I. On space-air-ground integrated earth observation network. J. Geo-Inf. Sci. 2012, 14, 419–425. [Google Scholar]
- Zhao, J.; Zhou, Q.; Chen, Y.; Feng, H.; Xu, Z.; Li, Q. Fusion of visible and infrared images using saliency analysis and detail preserving based image decomposition. Infrared Phys. Technol. 2013, 56, 93–99. [Google Scholar] [CrossRef]
- Zhou, D.; Zhong, Z.; Zhang, D.; Shen, L.; Yan, C. Autonomous landing of a helicopter UAV with a ground-based multisensory fusion system. In Proceedings of the International Conference on Machine Vision, Koto-ku, Japan, 18–22 May 2015. [Google Scholar]
- Ulusoy, I.; Yuruk, H. New method for the fusion of complementary information from infrared and visual images for object detection. IET Image Process. 2011, 5, 36–48. [Google Scholar] [CrossRef]
- Niu, Y.F.; Xu, S.T.; Hu, W.D. Fusion of infrared and visible image based on target regions for environment perception. Appl. Mech. Mater. 2011, 128–129, 589–593. [Google Scholar] [CrossRef]
- Pulpea, B.G. Aspects regarding the development of pyrotechnic obscurant systems for visible and infrared protection of military vehicles. In Proceedings of the International Conference Knowledge-Based Organization, Land Forces Academy, Sibiu, Romania, 11–13 June 2015; pp. 731–736. [Google Scholar]
- Teng, H.; Viscarra Rossel, R.A.; Shi, Z.; Behrens, T.; Chappell, A.; Bui, E. Assimilating satellite imagery and visible-near infrared spectroscopy to model and map soil loss by water erosion in australia. Environ. Model. Softw. 2016, 77, 156–167. [Google Scholar] [CrossRef]
- Peña, J.M.; Torres-Sánchez, J.; Serrano-Pérez, A.; de Castro, A.I.; López-Granados, F. Quantifying efficacy and limits of unmanned aerial vehicle (UAV) technology for weed seedling detection as affected by sensor resolution. Sensors 2015, 15, 5609–5626. [Google Scholar] [CrossRef] [PubMed]
- Chrétien, L.P.; Théau, J.; Ménard, P. Visible and thermal infrared remote sensing for the detection of white-tailed deer using an unmanned aerial system. Wildl. Soc. Bull. 2016, 40, 181–191. [Google Scholar] [CrossRef]
- Zhao, B.; Li, Z.; Liu, M.; Cao, W.; Liu, H. Infrared and visible imagery fusion based on region saliency detection for 24-h-surveillance systems. In Proceedings of the IEEE International Conference on Robotics and Biomimetics, Shenzhen, China, 12–14 December 2013; pp. 1083–1088. [Google Scholar]
- Wang, Q.; Yan, P.; Yuan, Y.; Li, X. Multi-spectral saliency detection. Pattern Recognit. Lett. 2013, 34, 34–41. [Google Scholar] [CrossRef]
- Wang, Q.; Zhu, G.; Yuan, Y. Multi-spectral dataset and its application in saliency detection. Comput. Vis. Image Underst. 2013, 117, 1748–1754. [Google Scholar] [CrossRef]
- Berenstein, R.; Hočevar, M.; Godeša, T.; Edan, Y.; Benshahar, O. Distance-dependent multimodal image registration for agriculture tasks. Sensors 2014, 15, 20845–20862. [Google Scholar] [CrossRef] [PubMed]
- Kaneko, S.I.; Murase, I.; Igarashi, S. Robust image registration by increment sign correlation. Pattern Recognit. 2010, 35, 2223–2234. [Google Scholar] [CrossRef]
- Tsin, Y.; Kanade, T. A correlation-based approach to robust point set registration. In Proceedings of the Computer Vision—ECCV 2004, European Conference on Computer Vision, Prague, Czech Republic, 11–14 May 2004; pp. 558–569. [Google Scholar]
- Zhuang, Y.; Gao, K.; Miu, X.; Han, L.; Gong, X. Infrared and visual image registration based on mutual information with a combined particle swarm optimization—Powell search algorithm. Optik—Int. J. Light Electron Opt. 2016, 127, 188–191. [Google Scholar] [CrossRef]
- Zhang, Z.; Yang, G.; Chen, D.; Li, J.; Yang, W. Registration of infrared and visual images based on phase grouping and mutual information of gradient orientation. In Proceedings of the SPIE Photonics Europe, Brussels, Belgium, 4–7 April 2016. [Google Scholar]
- Li, C.; Chen, Q. Ir and visible images registration method based on cross cumulative residual entropy. Proc. SPIE—Int. Soc. Opt. Eng. 2013, 8704, 145–223. [Google Scholar]
- Pohit, M.; Sharma, J. Image registration under translation and rotation in two-dimensional planes using fourier slice theorem. Appl. Opt. 2015, 54, 4514–4519. [Google Scholar] [CrossRef] [PubMed]
- Niu, H.; Chen, E.; Qi, L.; Guo, X. Image registration based on fractional fourier transform. Optik—Int. J. Light Electron Opt. 2015, 126, 3889–3893. [Google Scholar] [CrossRef]
- Li, H.; Zhang, A.; Hu, S. A registration scheme for multispectral systems using phase correlation and scale invariant feature matching. J. Sens. 2016, 2016, 1–9. [Google Scholar] [CrossRef]
- Wang, Q.; Zou, C.; Yuan, Y.; Lu, H.; Yan, P. Image registration by normalized mapping. Neurocomputing 2013, 101, 181–189. [Google Scholar] [CrossRef]
- Lowe, D.G. Object recognition from local scale-invariant features. In Proceedings of the IEEE International Conference on Computer Vision, Kerkyra, Greece, 20–27 September 1999; p. 1150. [Google Scholar]
- Lowe, D.G.; Lowe, D.G. Distinctive image features from scale-invariant keypoints. Int. J. Comput. Vis. 2004, 60, 91–110. [Google Scholar] [CrossRef]
- Huang, Q.; Yang, J.; Wang, C.; Chen, J.; Meng, Y. Improved registration method for infrared and visible remote sensing image using nsct and sift. In Proceedings of the Geoscience and Remote Sensing Symposium, Munich, Germany, 22–27 July 2012; pp. 2360–2363. [Google Scholar]
- Li, D. An Infrared and Visible Image Registration Based on Surf. 2012, 19–25. Available online: https://datahub.io/dataset/an-infrared-and-visible-image-registration-based-on-surf (accessed on 5 May 2017).
- Coiras, E.; Santamaria, J.; Miravet, C. Segment-based registration technique for visual-infrared images. Opt. Eng. 2000, 39, 202–207. [Google Scholar] [CrossRef]
- Han, J.; Pauwels, E.; Zeeuw, P.D. Visible and Infrared Image Registration Employing Line-Based Geometric Analysis; Springer: Berlin/Heidelberg, Germany, 2012; pp. 114–125. [Google Scholar]
- Liu, L.; Tuo, H.Y.; Xu, T.; Jing, Z.L. Multi-spectral image registration and evaluation based on edge-enhanced mser. Imaging Sci. J. 2014, 62, 228–235. [Google Scholar] [CrossRef]
- Qin, H. Visible and infrared image registration based on visual salient features. J. Electron. Imaging 2015, 24, 053017. [Google Scholar]
- Piella, G. Diffusion maps for multimodal registration. Sensors 2014, 14, 10562–10577. [Google Scholar] [CrossRef] [PubMed]
- Xia, Y.J.; Yin, J.Q.; Chen, R. An automatic registration method for multi-modal images based on alignment metric. Appl. Mech. Mater. 2012, 182–183, 1308–1312. [Google Scholar] [CrossRef]
- Han, J.; Pauwels, E.J.; Zeeuw, P.D. Visible and infrared image registration in man-made environments employing hybrid visual features. Pattern Recognit. Lett. 2013, 34, 42–51. [Google Scholar] [CrossRef]
- Huang, Q.; Yang, J.; Chen, J.; Gao, Q.; Song, Z. Visible and infrared image registration algorithm based on nsct and gradient mirroring. Proc. SPIE—Multispectr. Hyperspectr. Ultraspectr. Remote Sens. Technol. Tech. Appl. 2014. [Google Scholar] [CrossRef]
- Wang, R.; Du, L. Infrared and visible image fusion based on random projection and sparse representation. Int. J. Remote Sens. 2014, 35, 1640–1652. [Google Scholar] [CrossRef]
- Pohl, C.; Genderen, J.L.V. Review article multisensor image fusion in remote sensing: Concepts, methods and applications. Int. J. Remote Sens. 1998, 19, 823–854. [Google Scholar] [CrossRef]
- Nawaz, Q.; Bin, X.; Weisheng, L.; Jiao, D.; Hamid, I. Multi-modal medical image fusion using RGB-principal component analysis. J. Med. Imaging Health Inf. 2016, 6, 1349–1356. [Google Scholar] [CrossRef]
- Toet, A.; Walraven, J. New false color mapping for image fusion. Opt. Eng. 1996, 35, 650–658. [Google Scholar] [CrossRef]
- Kadar, I. Quick markov random field image fusion. Proc. SPIE—Int. Soc. Opt. Eng. 1998, 3374, 302–308. [Google Scholar]
- Sharma, R.K.; Leen, T.K.; Pavel, M. Bayesian sensor image fusion using local linear generative models. Opt. Eng. 2002, 40, 1364–1376. [Google Scholar]
- Zhang, Z.L.; Sun, S.H.; Zheng, F.C. Image fusion based on median filters and sofm neural networks: A three-step scheme. Signal Process. 2001, 81, 1325–1330. [Google Scholar] [CrossRef]
- Zhang, Y.X.; Chen, L.; Zhao, Z. A novel pulse coupled neural network based method for multi-focus image fusion. Int. J. Signal Process. Image Process. Pattern Recognit. 2014, 12, 357–366. [Google Scholar] [CrossRef]
- Guan, W.; Li, L.; Jin, W.; Qiu, S.; Zou, Y. Research on hdr image fusion algorithm based on laplace pyramid weight transform with extreme low-light CMOS. In Proceedings of the Applied Optics and Photonics China, Beijing, China, 5–7 May 2015; p. 967524. [Google Scholar]
- Li, H.; Manjunath, B.S.; Mitra, S.K. Multisensor image fusion using the wavelet transform. Graph. Models Image Process. 1995, 57, 235–245. [Google Scholar] [CrossRef]
- Chen, T.; Zhang, J.; Zhang, Y. In Remote sensing image fusion based on ridgelet transform. In Proceedings of the 2005 IEEE International Geoscience and Remote Sensing Symposium, Seoul, South Korea, 25–29 July 2005; pp. 1150–1153. [Google Scholar]
- Lutz, A.; Giansiracusa, M.; Messer, N.; Ezekiel, S.; Blasch, E.; Alford, M. Optimal multi-focus contourlet-based image fusion algorithm selection. In Proceedings of the SPIE Defense + Security, Baltimore, MD, USA, 17–21 April 2016; p. 98410E. [Google Scholar]
- Zhang, Q.; Guo, B.L. Multifocus image fusion using the nonsubsampled contourlet transform. Signal Process. 2009, 89, 1334–1346. [Google Scholar] [CrossRef]
- Han, J.; Loffeld, O.; Hartmann, K.; Wang, R. Multi image fusion based on compressive sensing. In Proceedings of the International Conference on Audio Language and Image Processing, Shanghai, China, 23–25 November 2010; pp. 1463–1469. [Google Scholar]
- Wei, Q.; Bioucas-Dias, J.; Dobigeon, N.; Tourneret, J.Y. Hyperspectral and multispectral image fusion based on a sparse representation. IEEE Trans. Geosci. Remote Sens. 2014, 53, 3658–3668. [Google Scholar] [CrossRef]
- Zhang, Q.; Liu, Y.; Blum, R.S.; Han, J.; Tao, D. Sparse Representation Based Multi-Sensor Image Fusion: A Review. Available online: https://arxiv.org/abs/1702.03515 (accessed on 4 May 2017).
- Han, J.; Pauwels, E.J.; De Zeeuw, P. Fast saliency-aware multi-modality image fusion. Neurocomputing 2013, 111, 70–80. [Google Scholar] [CrossRef]
- Liu, K.; Guo, L.; Li, H.; Chen, J. Fusion of infrared and visible light images based on region segmentation. Chin. J. Aeronaut. 2009, 22, 75–80. [Google Scholar]
- Sturm, P. Pinhole Camera Model; Springer: Washington, DC, USA, 2014; pp. 300–321. [Google Scholar]
- Hartley, R.; Zisserman, A. Multiple view geometry in computer vision. Kybernetes 2001, 30, 1865–1872. [Google Scholar]
- Li, H.; Li, X.; Ding, W.; Huang, Y. Metadata-assisted global motion estimation for medium-altitude unmanned aerial vehicle video applications. Remote Sens. 2015, 7, 12606–12634. [Google Scholar] [CrossRef]
- Han, J.; Farin, D.; De With, P. Broadcast court-net sports video analysis using fast 3-d camera modeling. IEEE Trans. Circuits Syst. Video Technol. 2008, 18, 1628–1638. [Google Scholar]
- Canny, J. A computational approach to edge detection. IEEE Trans. Pattern Anal. Mach. Intell. 1986, 8, 679–698. [Google Scholar] [CrossRef] [PubMed]
- Jie, G.; Ning, L. An improved adaptive threshold canny edge detection algorithm. In Proceedings of the International Conference on Computer Science and Electronics Engineering, Colchester, UK, 28–30 September 2012; pp. 164–168. [Google Scholar]
- Li, Z.; Zhu, X. Matching Multi—Sensor Images Based on Edge Similarity. J. Spacecr. TTC Technol. 2011, 30, 37–41. [Google Scholar]
- Kennedy, J.; Eberhart, R. Particle swarm optimization. In Proceedings of the IEEE International Conference on Neural Networks, Perth, Australia, 27 November–1 December 1995; Volume 1944, pp. 1942–1948. [Google Scholar]
- Song, Y.; Eberhart, R. A modified particle swarm optimizer. In Proceedings of the 1998 IEEE International Conference on Evolutionary Computation Proceedings, Anchorage, AK, USA, 4–9 May 1998. [Google Scholar]
- Arasomwan, M.A.; Adewumi, A.O. On the performance of linear decreasing inertia weight particle swarm optimization for global optimization. Sci. World J. 2013, 78, 1648–1653. [Google Scholar] [CrossRef] [PubMed]
- Kuntimad, G.; Ranganath, H.S. Perfect image segmentation using pulse coupled neural networks. IEEE Trans. Neural Netw. 1999, 10, 591. [Google Scholar] [CrossRef] [PubMed]
- Bamberger, R.H.; Smith, M.J.T. A filter bank for the directional decomposition of images: Theory and design. IEEE Trans. Signal Process. 1992, 40, 882–893. [Google Scholar] [CrossRef]
- Hore, A.; Ziou, D. Image quality metrics: PSNR vs. SSIM. In Proceedings of the 2010 20th International Conference on Pattern Recognition (ICPR), Istanbul, Turkey, 23–26 August 2010; pp. 2366–2369. [Google Scholar]
- He, C.; Liu, Q.; Li, H.; Wang, H. Multimodal medical image fusion based on IHS and PCA. Procedia Eng. 2010, 7, 280–285. [Google Scholar] [CrossRef]
- Xin, W.; Wei, Y.L.; Fu, L. A new multi-source image sequence fusion algorithm based on sidwt. In Proceedings of the Seventh International Conference on Image and Graphics, Qingdao, China, 26–28 July 2013; pp. 568–571. [Google Scholar]

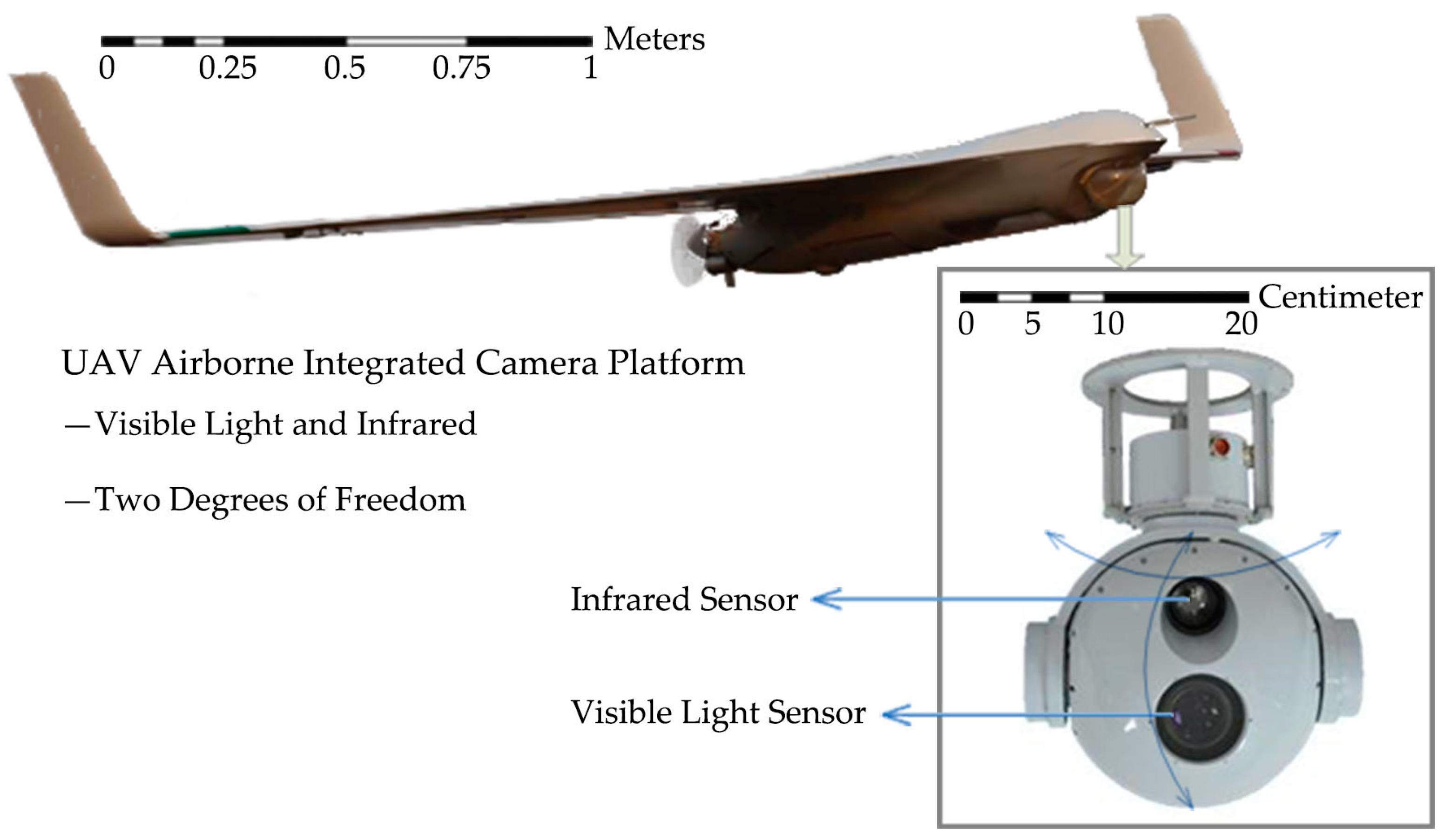









| Item | Description |
|---|---|
| Wing Span | 4.0 m |
| Length | 1.85 m |
| Height | 0.7 m |
| Service Ceiling | 5000 m |
| Maximum Payload | 5 kg |
| Maximum Takeoff Weight | 35 kg |
| Flight Speed | 80–140 km h−1 |
| Control Radius | 60 km |
| Endurance | 5 h |
| ImagingDevice | VisibleLight and Infrared |
| Control Mode | Remote, Program or Autonomous |
| Takeoff Mode | Catapulted Launching |
| Recovery | Parachute |
| Engine | Piston Engine |
| Navigation Mode | BD2/GPS and INS |
| Name | Notation | Source | Description | Accuracy |
|---|---|---|---|---|
| Longitude | GPS | Unit: ° | 2.5 m | |
| Latitude | GPS | Unit: ° | 2.5 m | |
| Altitude | Altimeter | Unit: m | 0.1 m | |
| Terrain Height | GIS | Unit: m | 1.0 m | |
| Vehicle Heading | INS | Unit: ° | 1° | |
| Vehicle Roll | INS | Unit: ° | 0.2° | |
| Vehicle Pitch | INS | Unit: ° | 0.2° | |
| Camera Installation Translation | Measuring Equipment | Unit: m | 0.01 m | |
| Camera Pan | Camera | Unit: ° | 0.2° | |
| Camera Tilt | Camera | Unit: ° | 0.2° | |
| Resolution | Camera | u: Image Row v: Image Column | — | |
| Focal Length | Camera | Unit: m | — | |
| Pixel Size | Camera | Unit: m | — |
| Transformation | Notation | Description | Relevant Metadata |
|---|---|---|---|
| ICS to CCS | Direction rotation of coordinate axis | None | |
| Translation of coordinate system center | |||
| CCS to PCS | Translation of installation error | ||
| Rotation of two angles | , | ||
| PCS to NCS | Rotation of three angles | , , | |
| NCS to GCS | Translation of coordinate system center | , , , |
| Item | Resolution | Focal Length (mm) | Pixel Size (μm) | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Group ID | 1 | 2 | 3 | 1 | 2 | 3 | 1 | 2 | 3 |
| Visible image | 1392 × 1040 | 172 | 65.4 | 50.4 | 4.65 | ||||
| Infrared image | 720 × 576 | 540 | 135 | 135 | 25 | ||||
| Group ID | 1 | 2 | 3 |
|---|---|---|---|
| Result image resolution | 1042 × 834 | 1666 × 1333 | 1284 × 1027 |
| Image Sequence | Translation | ||
|---|---|---|---|
| Group ID | 1 | 2 | 3 |
| Actual Translation | (−31,−29) | (−6,−15) | (−21,11) |
| Translation Estimation | (−36,−37) | (−20,−10) | (−8,2) |
| Error | 9.43 | 14.87 | 15.81 |
| Image Sequence | Translation | ||
|---|---|---|---|
| Group ID | 1 | 2 | 3 |
| Actual Translation | (−31,−29) | (−6,−15) | (−21,11) |
| Translation Estimation | (−30,−27) | (−8,−13) | (−20,9) |
| Error | 2.24 | 2.83 | 2.24 |
| Index | Test Data (Frame Number) | AMBR (RMSE) | MIBR (RMSE) | PSNRBR (RMSE) | SSIMBR (RMSE) | Propose IVPBR (RMSE) |
|---|---|---|---|---|---|---|
| 1 | Translation (86) | 3.98 | 3.19 | 3.24 | 2.63 | 1.55 |
| 2 | Rotation (80) | 3.37 | 3.04 | 2.97 | 2.16 | 2.01 |
| 3 | Scale (91) | 3.00 | 2.61 | 2.94 | 1.90 | 1.54 |
| Average RMSE | 3.45 | 2.95 | 3.05 | 2.23 | 1.70 | |
| Index | Evaluation Index | IHSBF | PCABF | SIDWTBF | Proposed |
|---|---|---|---|---|---|
| 1 | Average Gradient | 1.67 | 1.59 | 1.78 | 1.97 |
| 2 | Shannon | 7.20 | 6.90 | 6.74 | 7.40 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, H.; Ding, W.; Cao, X.; Liu, C. Image Registration and Fusion of Visible and Infrared Integrated Camera for Medium-Altitude Unmanned Aerial Vehicle Remote Sensing. Remote Sens. 2017, 9, 441. https://doi.org/10.3390/rs9050441
Li H, Ding W, Cao X, Liu C. Image Registration and Fusion of Visible and Infrared Integrated Camera for Medium-Altitude Unmanned Aerial Vehicle Remote Sensing. Remote Sensing. 2017; 9(5):441. https://doi.org/10.3390/rs9050441
Chicago/Turabian StyleLi, Hongguang, Wenrui Ding, Xianbin Cao, and Chunlei Liu. 2017. "Image Registration and Fusion of Visible and Infrared Integrated Camera for Medium-Altitude Unmanned Aerial Vehicle Remote Sensing" Remote Sensing 9, no. 5: 441. https://doi.org/10.3390/rs9050441
APA StyleLi, H., Ding, W., Cao, X., & Liu, C. (2017). Image Registration and Fusion of Visible and Infrared Integrated Camera for Medium-Altitude Unmanned Aerial Vehicle Remote Sensing. Remote Sensing, 9(5), 441. https://doi.org/10.3390/rs9050441