2.3. Optimized 3D Flight Path Planning
Calculations that result in the global optimum for view planning are difficult to formulate and lead to very expensive computational loads. The view planning algorithm developed in this paper therefore focuses on identifying a sub-optimal solution capable of producing desirable results with a computational load that permits near real-time calculations. The algorithm includes a high degree of adaptability to different UAV platforms and desired image resolutions by accepting several user-specified parameters that define the capabilities of the camera and the desired resolution. Given these parameters, the algorithm estimates the minimal set of camera locations required for 3D reconstruction, as well as the optimal order in which to visit them. For a typical site of interest (about 900 m), the algorithm finds acceptable image positions and a near optimal route through those points in about 0.65 s on an Intel I7 CPU with 16 GB of RAM.
As it is desirable for the algorithm to eventually run on-board a UAV, the algorithm is also tested on a Raspberry Pi 3. The Pi 3 is a small, single board computer with a 1.2-GHz 64-bit quad-core ARMv8 CPU and 1 GB of RAM. The board measures 85.60 mm × 56.5 mm and weighs 45 g, which makes it feasible for use on-board a UAV. Running on the Raspberry Pi 3, the algorithm took an average of 7.02 s to compute both the image positions and route for the five test areas in the study, placing it within range of in flight re-planning.
The view planning algorithm can be summarized as follows:
Receive detected anomaly location
Obtain a point-cloud
Add dome projection at the point of interest
Convert the point-cloud terrain into a triangle mesh
Place an aerial camera location on the normal line of every triangle
Remove underground and blocked images
Select the best images from the group based on a set of value heuristics
Find the shortest path through all of these points
The following is a description of each of the above steps. Elevation data for the area to be surveyed is downloaded prior to the flight from public data sources, such as the USGS National Elevation Dataset. During an actual UAV flight, points of interest are flagged by anomaly detection; however, for the purposes of this paper, the points of interest are manually tagged before the simulated flight begins. When a point is detected, a geometric area of interest is constructed around the point to define the area to be inspected.
After identifying the area of interest, the full elevation dataset is trimmed down to an area only slightly larger than the area of interest. The slight excess of data is retained to ensure the UAV remains safe from potential obstacles or obstructions. Using only a subset of the original data also greatly helps to minimize computational costs when determining which points are within the view of each camera.
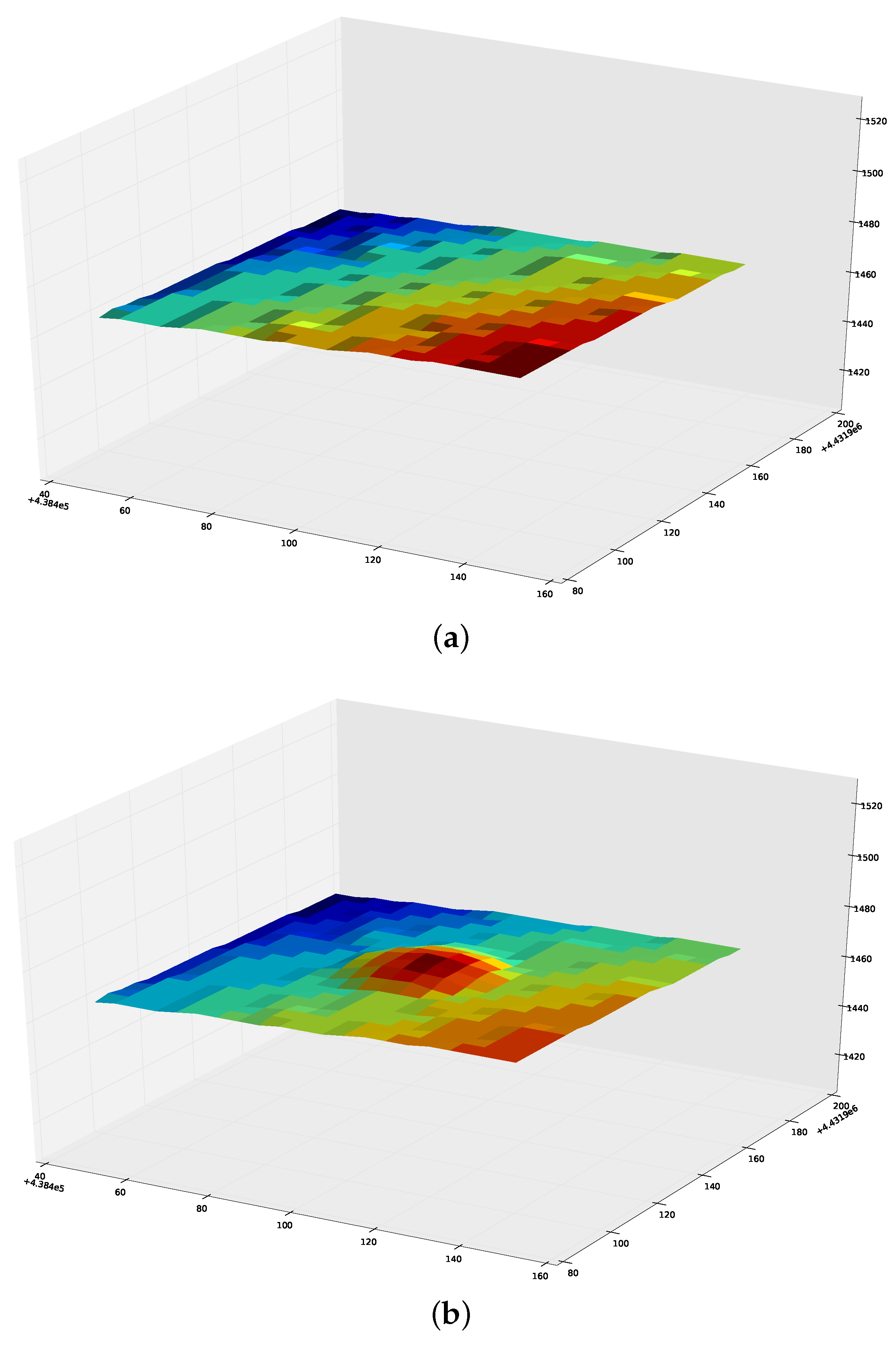
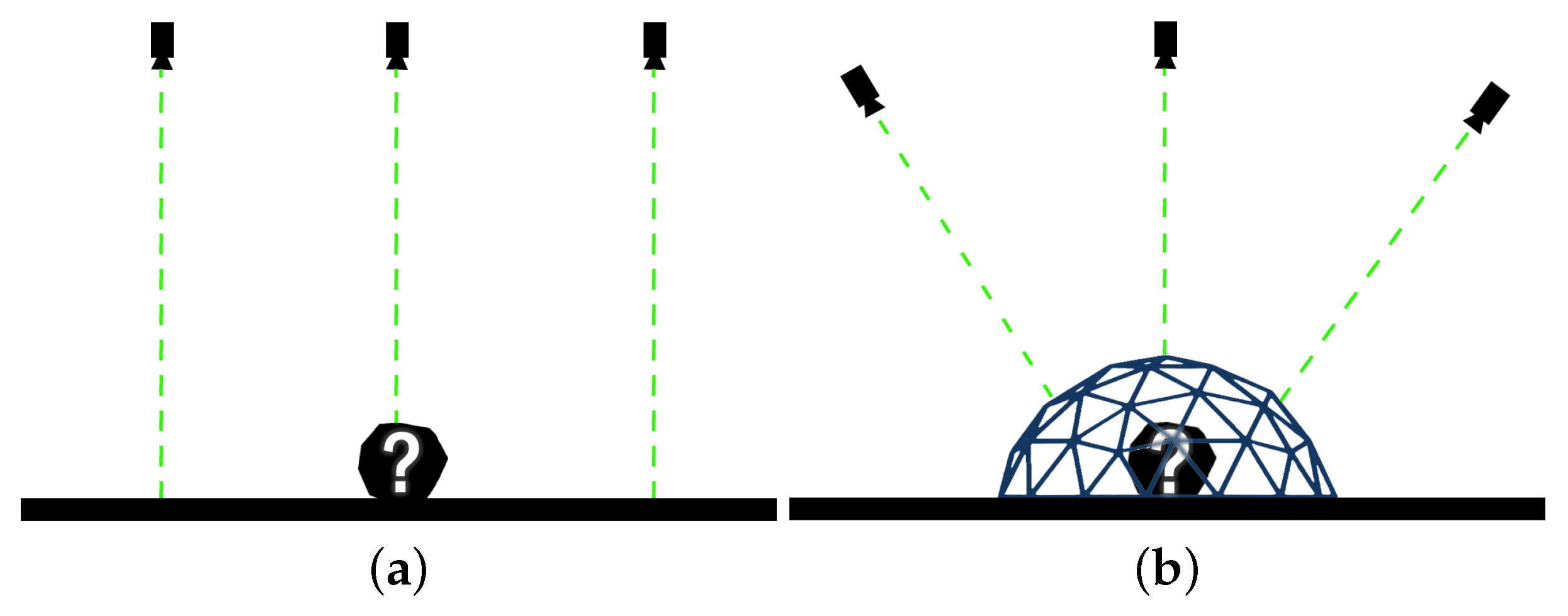
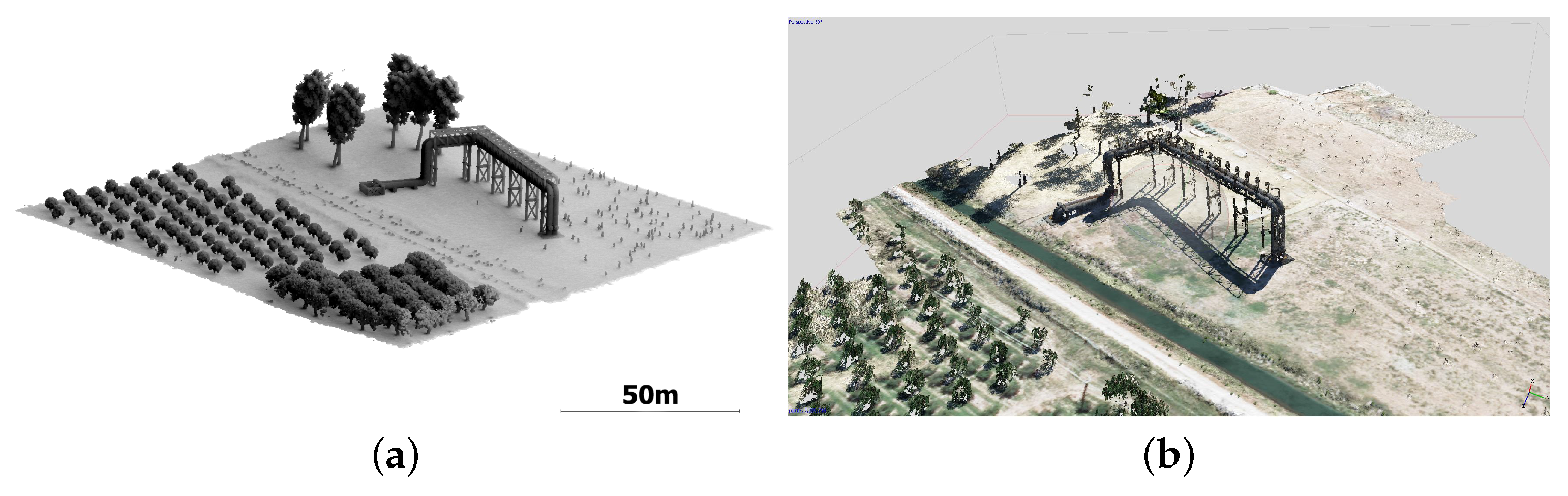
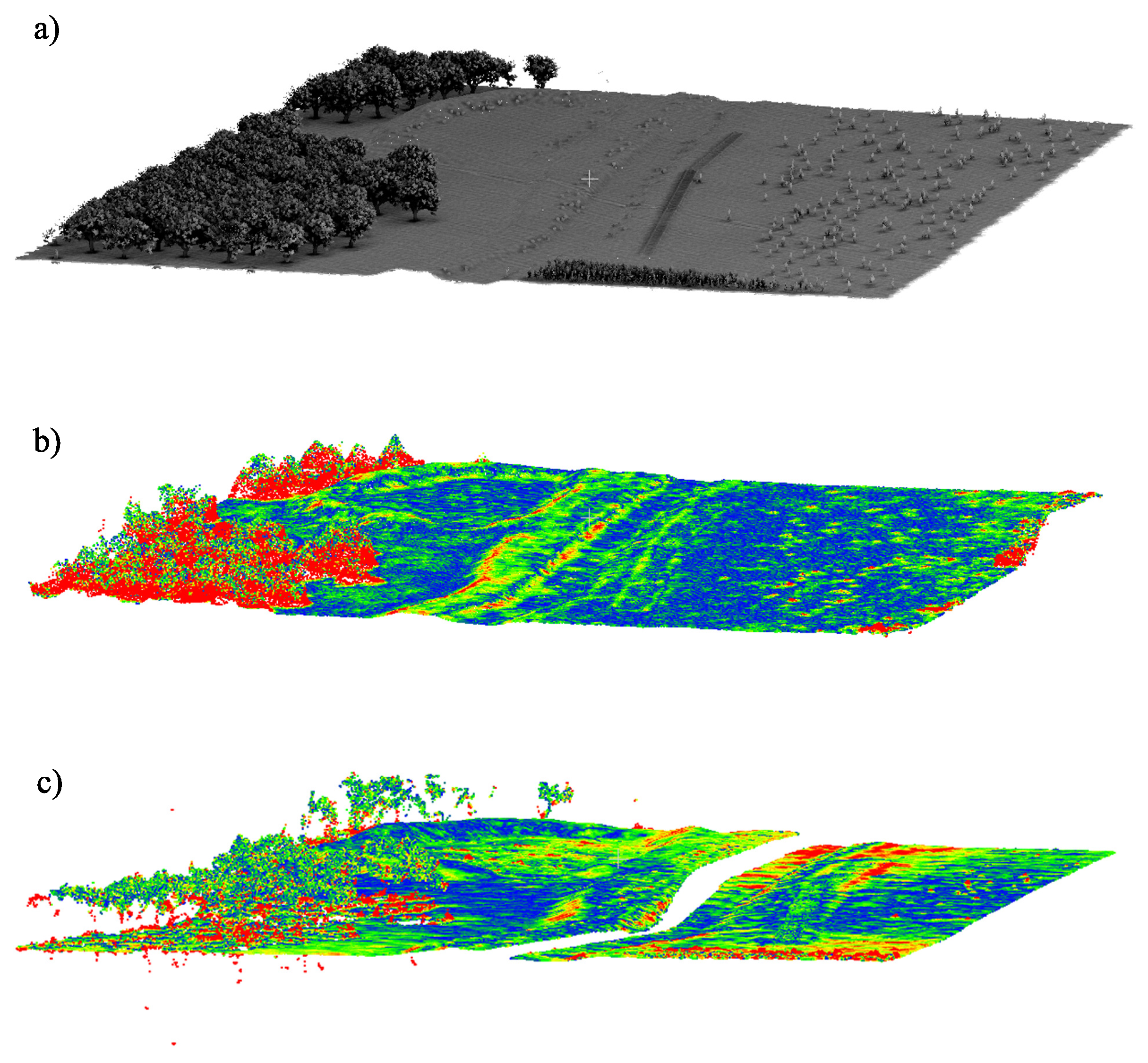
In many cases, the geometry of the detected anomaly is unknown and is not included in the available elevation data. This can lead to insufficient oblique imagery of the anomaly, especially if the shape of the anomaly differs significantly from the underlying terrain. To improve coverage, when an anomaly is detected, the algorithm automatically inserts a dome projection at the point of interest, as demonstrated in
Figure 4 and
Figure 5. The authors have found that the addition of the dome into the dataset aids the algorithm in selecting sufficient oblique imagery to capture the sides of an unknown object, regardless of whether the object is on relatively flat ground or on a steep grade. The dome is created by translating the elevation of each data point upward using a spherical cap, which results in a dome shape that still maintains the underlying geometry of the surface. Without the dome, a flat surface would result in the camera set all pointing directly downwards, and the resulting 3D reconstruction could yield undesirable results. The authors have found that a dome height of 5–10 m and an incident angle with the horizontal of 15
–30
provide an optimal increase in coverage. If the approximate size of the anomaly is known, it is best that the dome is tall and wide enough to completely enclose the anomaly. In the case that additional information is available about the nature of the anomaly, that information should be used in the planning rather than the generic dome projection. To clarify, the dome is not inserted into the Terragen simulation, it is only used in the view planning algorithm to aid in selecting imaging locations.
These resulting elevation data are then converted to a triangle mesh, and the triangle size is normalized by recursive subdivision. This ensures even coverage of vertical features, such as cliffs, hills and canyons, even though the original telemetry data are spaced evenly for latitude and longitude.
After creating the triangle mesh and adjusting the terrain, tentative camera locations are generated at a fixed distance from each triangle midpoint along the normal from each surface. This typically results in several thousand tentative camera locations. Potential camera locations that are generated underground or are otherwise blocked from viewing their original triangle midpoints are removed.
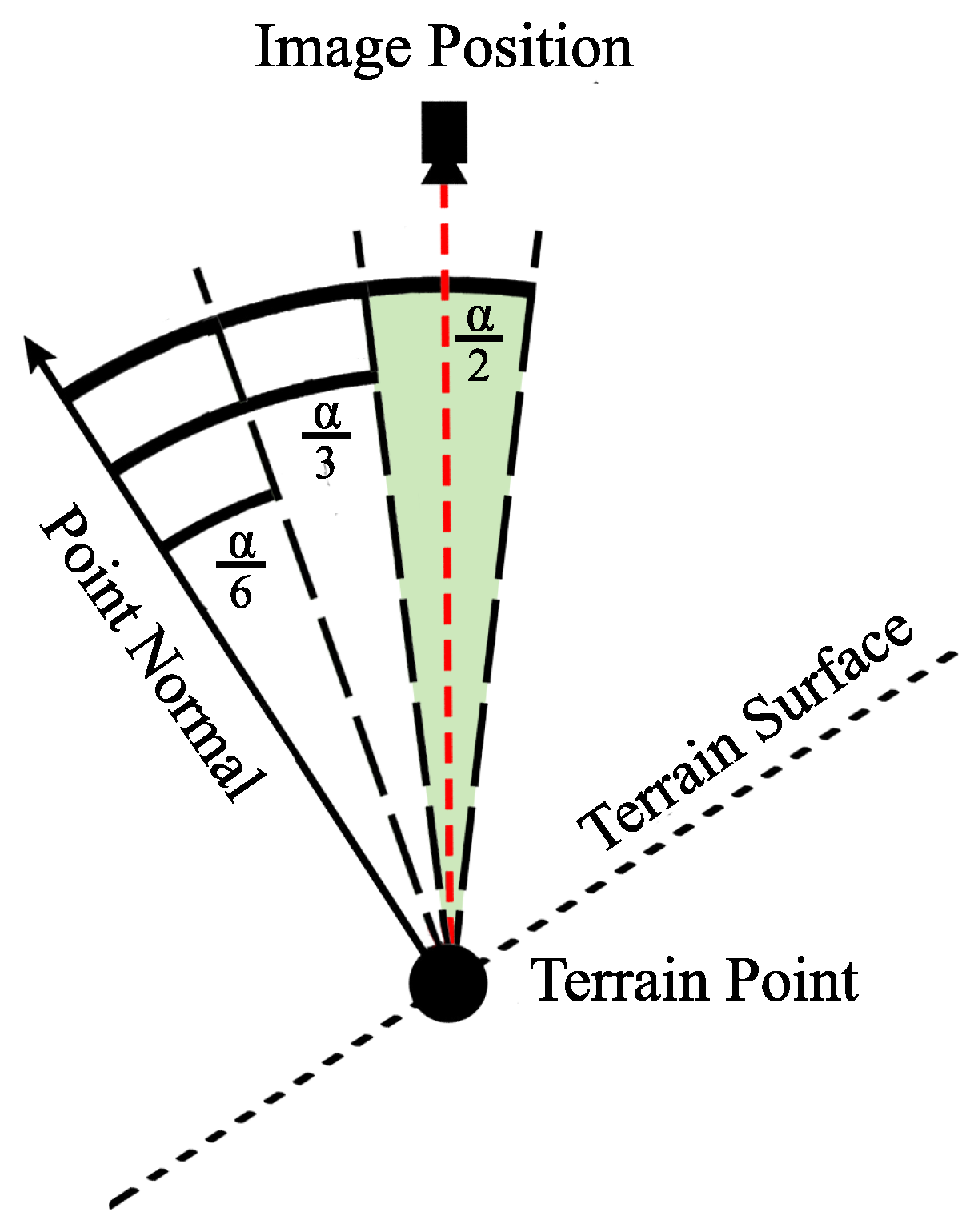
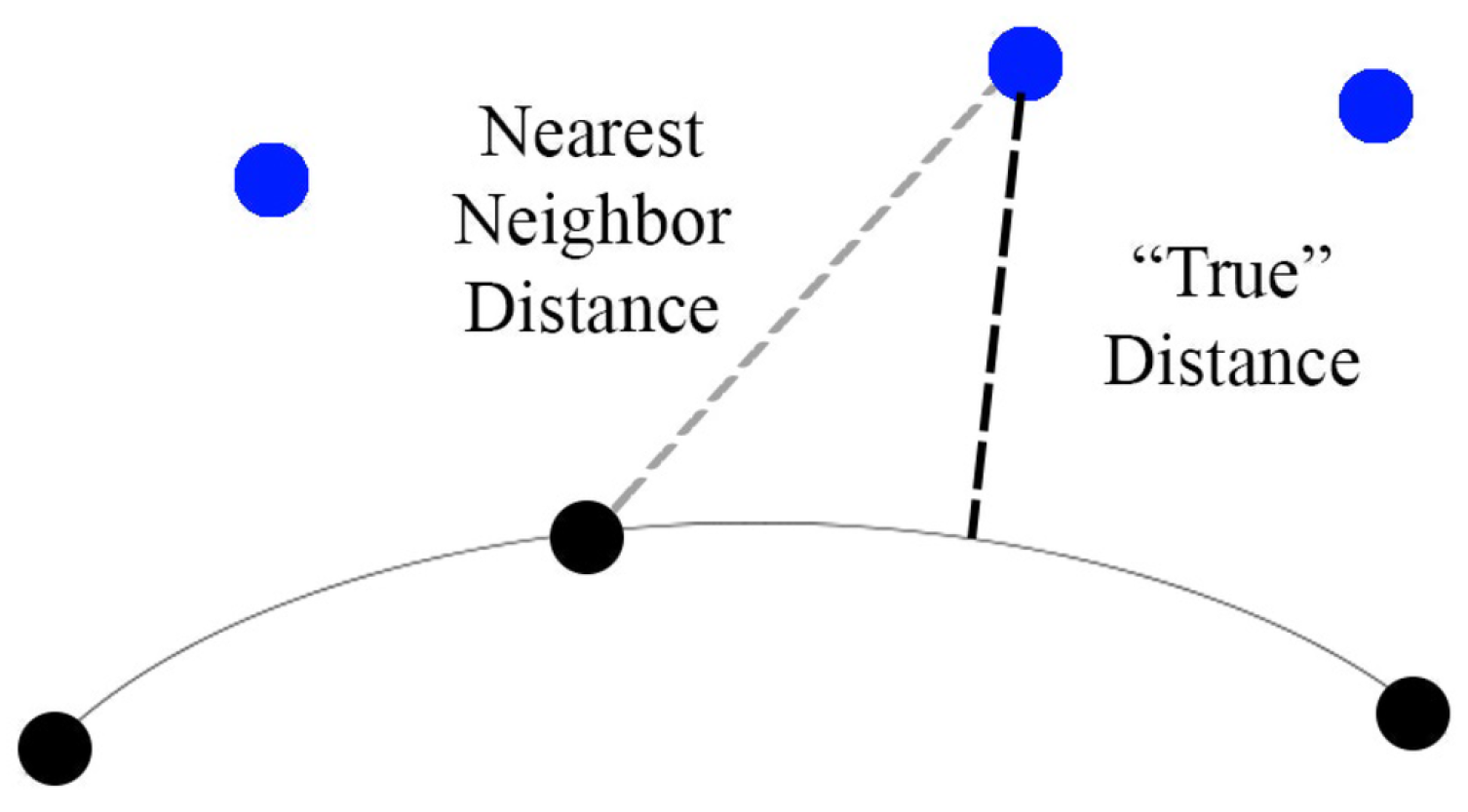
The image selection criteria is based on minimizing the total number of images while maximizing the terrain coverage. A visibility matrix similar to the 3Mmatrix used by [
38] is constructed, containing information on the visibility of each point in the terrain from each camera location and the angles (relative to each surface’s normal) at which each point is viewed. The angles are divided into three ranges (see
Figure 6), and the resulting range is recorded in the histogram. An iterative process then selects camera locations, which maximize the number of triangle midpoints viewed from previously unused angles. That is, once a point is viewed from an angle range, it is considered viewed, and it no longer contributes to the value of other camera locations, which view it from within the same angle range. This results in a sub-optimal heuristic algorithm, which, while not guaranteed to be optimal, can be completed very quickly with satisfactory results. As noted in [
39], this type of heuristic algorithm provides a (1 + ln
n) approximation, where
n is the number of images in the optimal solution.
Once the optimal images are chosen, a short route must be planned for the UAV to visit all of the points; this is an example of a 3D traveling salesman problem. To find a solution, the Christophides algorithm is employed. This algorithm is an approximation, but is guaranteed to find a solution within 1.5-times the length of the optimal solution [
40]. For this application, it was observed that the Christophides algorithm typically generates solutions that are within
of the optimal length as computed by integer linear programming, as shown in Equations (
1)–(
3).
Here, each of the
k waypoints is numbered from 1–
k, and
i and
j represent the waypoints at either end of a selected pathway.
D contains the distance measurements between each of the waypoints. The end solution
x contains integers bounded between 0 and 1. The equality constraints are shown in Equation (
2), and the inequality constraints are shown in Equation (
3).
If a solution is achieved with subtours, Equation (
3) is added as an inequality constraint, and the problem is solved again. The variable
s represents a subtour that occurred in a previous solution.
A sample comparison between the Christophides solution and the optimal solution from linear programming can be found in
Table 4. A completed solution for a generic anomaly, including selected camera locations and the shortest flight path, can be found in
Figure 7. For comparison,
Figure 7 also shows the optimal solution when the dome projection is not used.
For comparison with
Table 2 and
Table 3, the number of images taken by the optimized path planner at each anomaly location, as well as the average elevations of the images are shown in
Table 5.
The number of images required to model the section of industrial piping is significantly larger than the other anomaly areas. This can be explained by the fact that this anomaly location has the largest area of the five due to the fact that it contains the largest structure.
2.6. Simulated System Implementation
Following the collection of simulated images, the physics of each flight is simulated using the ArduCopter Software-in-the-Loop (SITL) package. The main objective of these simulations is to compare the flight time required for each path. The optimized flight planner is implemented in Python and connected to the flight simulation using the 3DR DroneKit library. For these simulations, the desired waypoint navigation speed is set to 60 mph. It is assumed that the UAV platform used has the flight characteristics of a multi-rotor, though for longer endurance, it would be preferable to use a larger single-rotor craft or a UAV capable of transitioning between hovering and forward flight.
The base flight elevation is set to 90 m, which corresponds to a 10-cm Ground Sampling Distance (GSD) for an HD video camera. This is done to simulate a two-camera multi-scale setup in which most of the long linear feature is captured using lower resolution video, while points of interest are imaged using a higher resolution camera.
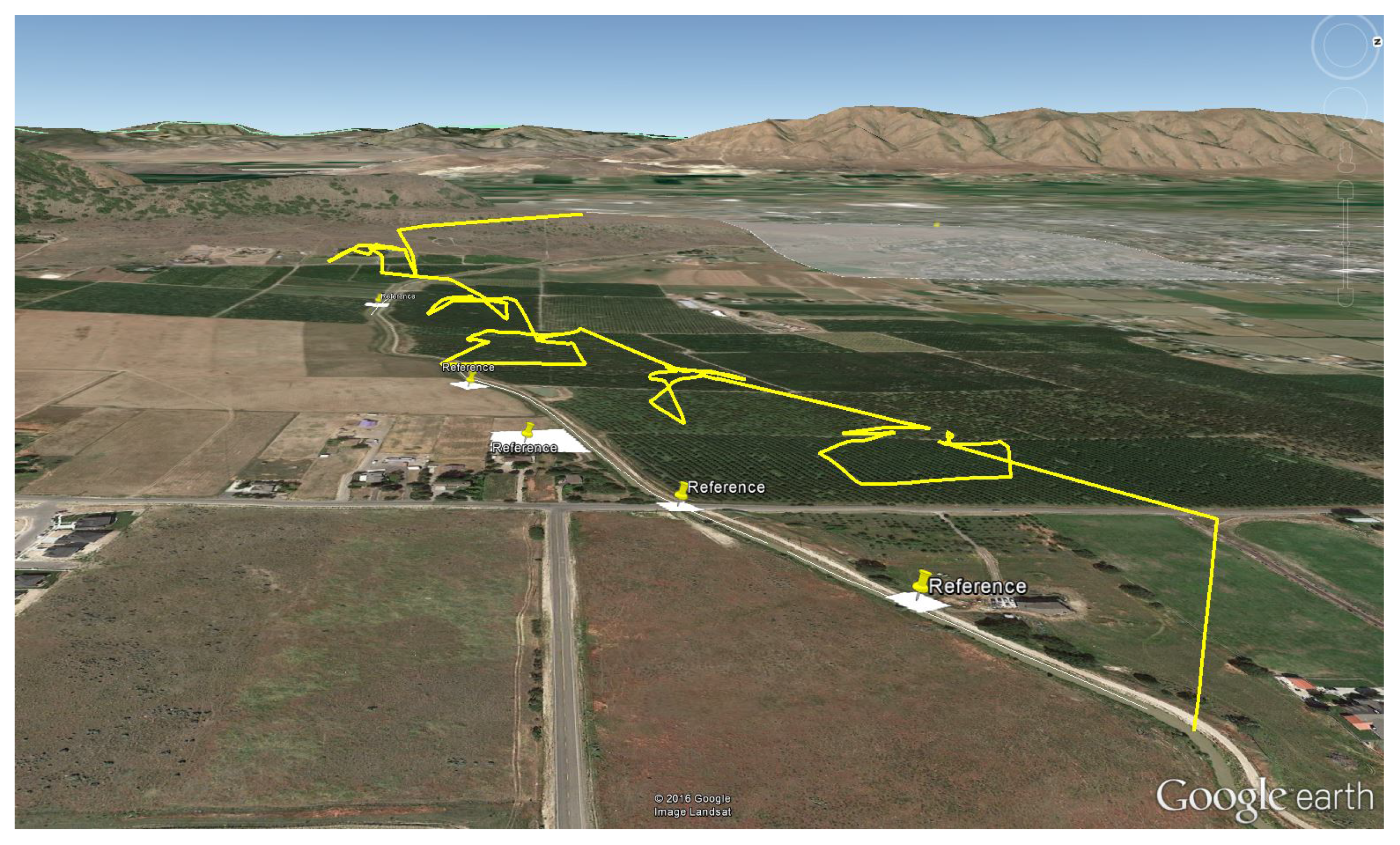
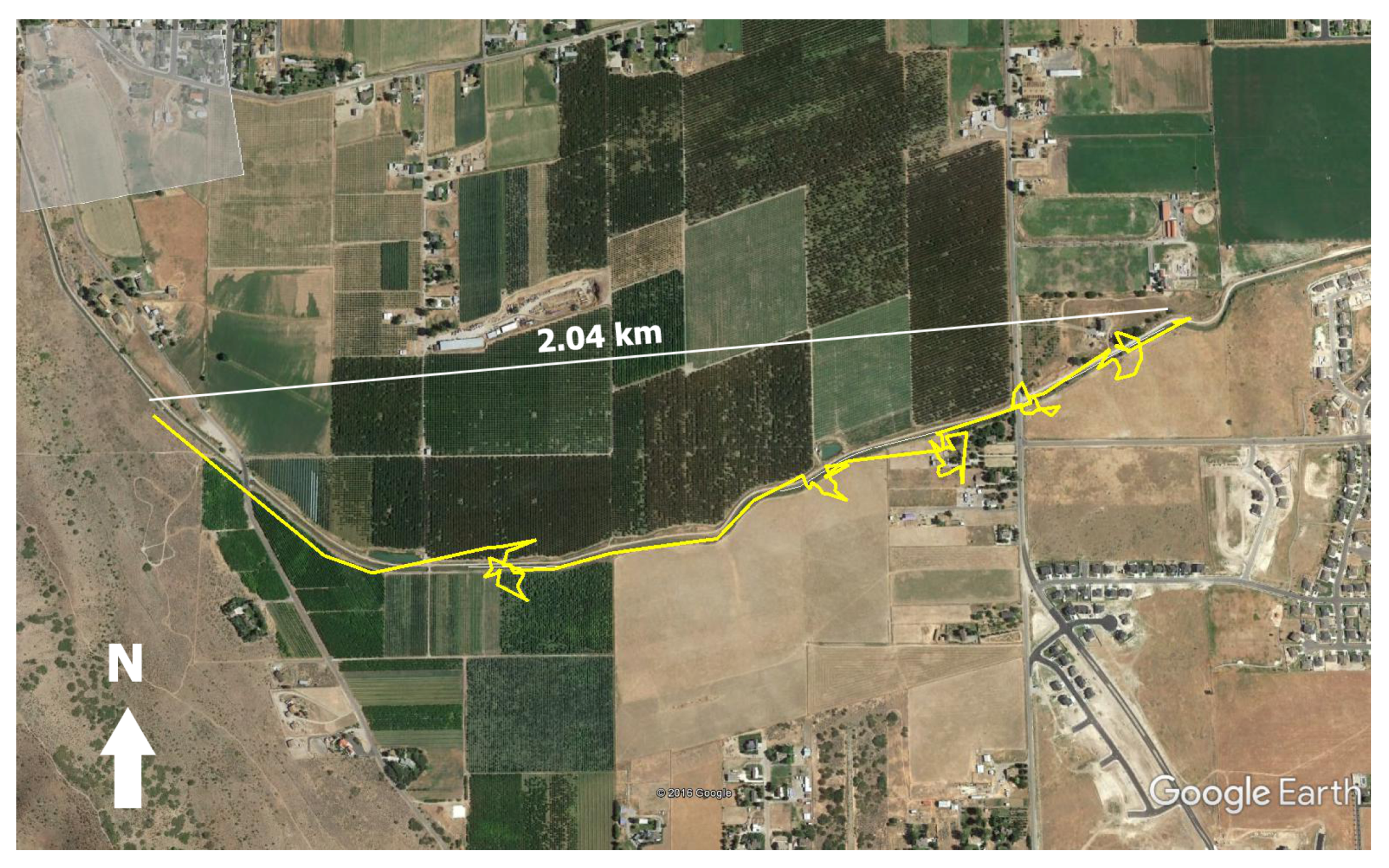
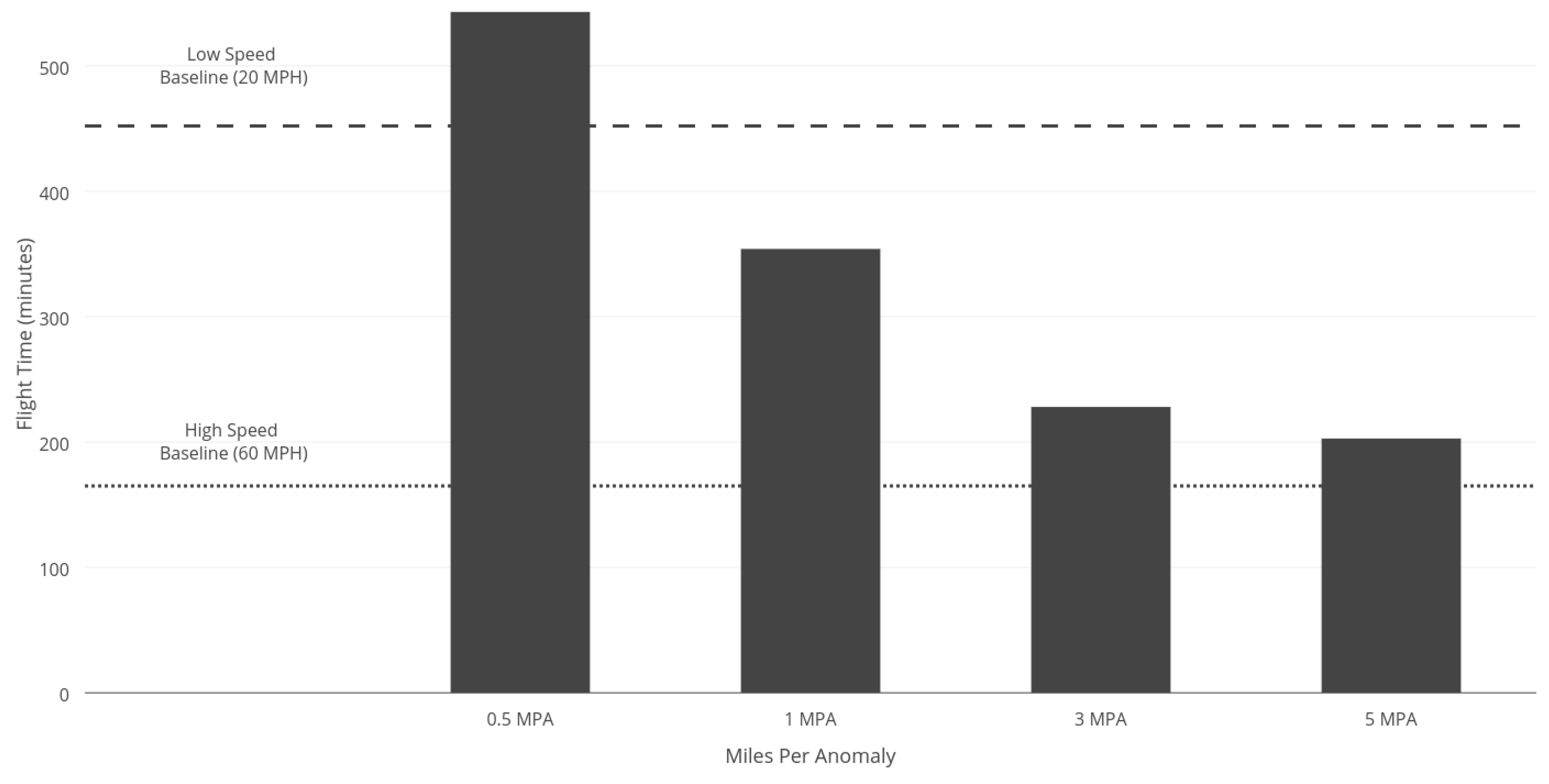
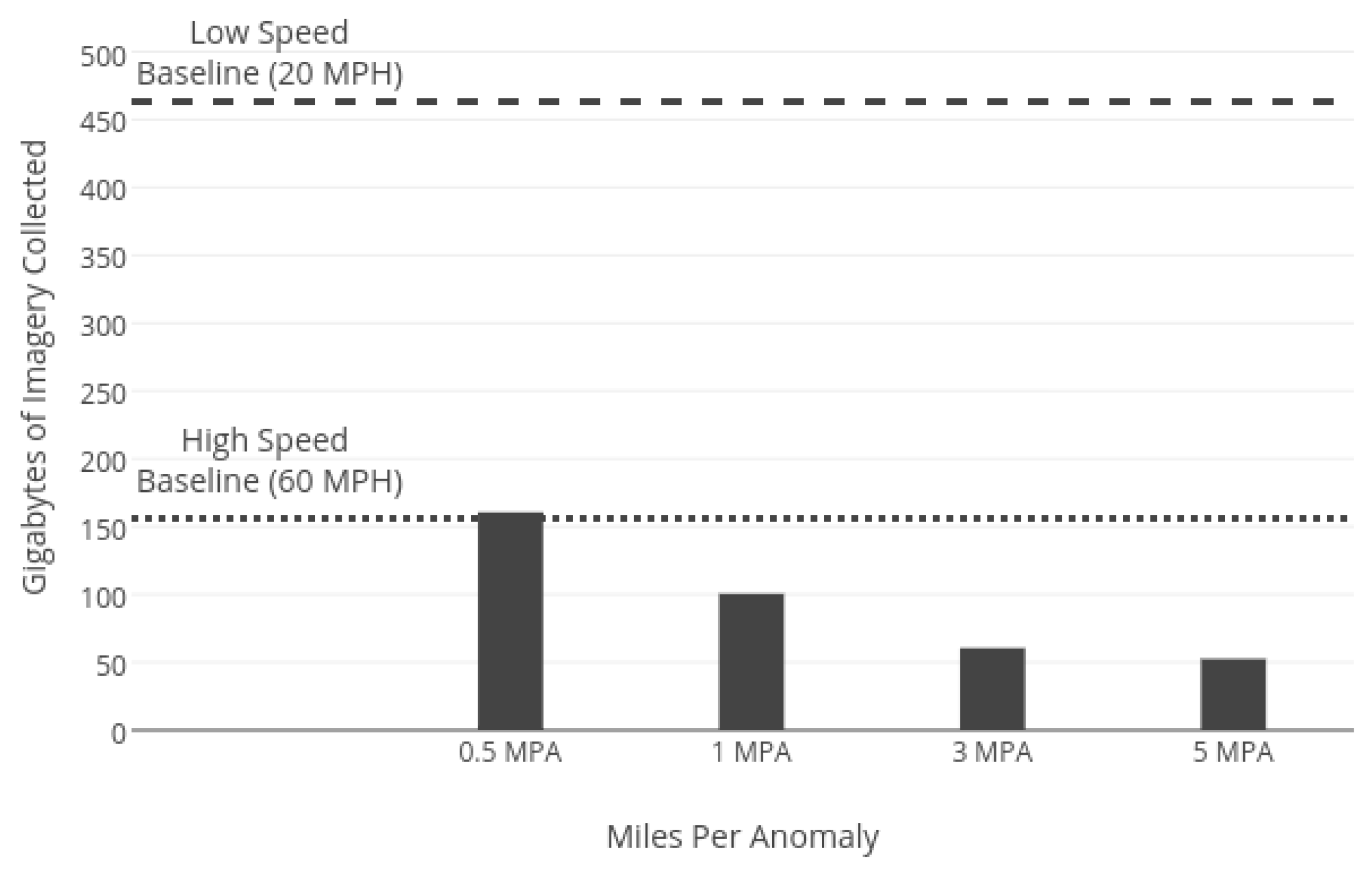
The UAV is set to fly a path along the one mile canal segment simulated in earlier sections. For this study, optimized flight planning is executed in-flight; however, anomaly detection is not performed in real time, and anomaly locations are marked in advance. When the vehicle reaches each of the pre-defined anomaly locations, the location of the anomaly is passed to the optimized flight planner, and an inspection path is generated in real time. The UAV then executes this path before continuing with its original flight route. The flight path taken by the UAV can be seen in
Figure 10 and
Figure 11. The average planning time for each anomaly inspection is approximately 2.3 s.
To create a baseline for comparison, two additional flights are performed with no anomalies present. The first flight is performed at 20 mph and provides an upper bound on flight time. The second, at 60 mph, provides a lower bound on flight time for the conditions tested.