Quantifying Sub-Pixel Surface Water Coverage in Urban Environments Using Low-Albedo Fraction from Landsat Imagery
Abstract
:1. Introduction
- (1)
- The LAF method stands on the H-L-V [23] (i.e., high albedo-low albedo-vegetation) spectral mixture analysis of urban surface reflectances, and investigates the urban surface water extraction problem with the low albedo fraction map. Accordingly, our idea is different from above water extraction methods, especially sub-pixel classifiers and spectral unmixing methods by Zhou [24] and Xie [25].
- (2)
- The LAF method implements a steady initial threshold at 1 and that significantly reduces the work of parameter tuning in LAF. By contrast, current spectral unmixing-based methods by Zhou and Xie could not provide a stable threshold for fraction segmentation. The water index methods also suffer from the unstable initial threshold problem. Therefore, the LAF is easier to implement in real-word applications than other methods, such as spectral unmixing methods and water index methods.
- (3)
- The LAF method obtains high extraction accuracies of urban surface water, and it significantly improves the accuracy of sub-pixel surface water extraction when compared against MNDWI and AWEI.
2. Test Sites and Datasets
3. Methodology
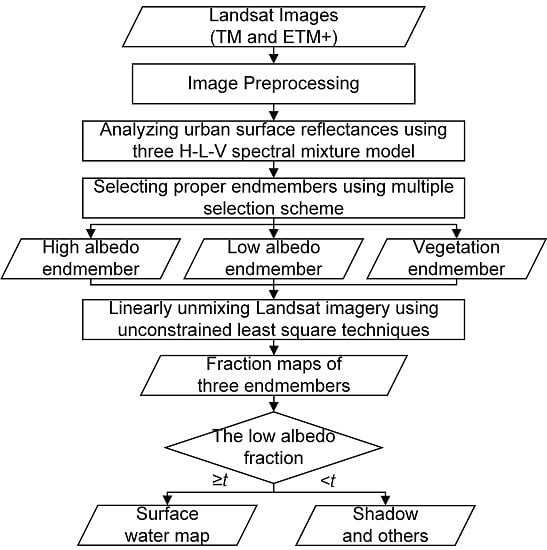
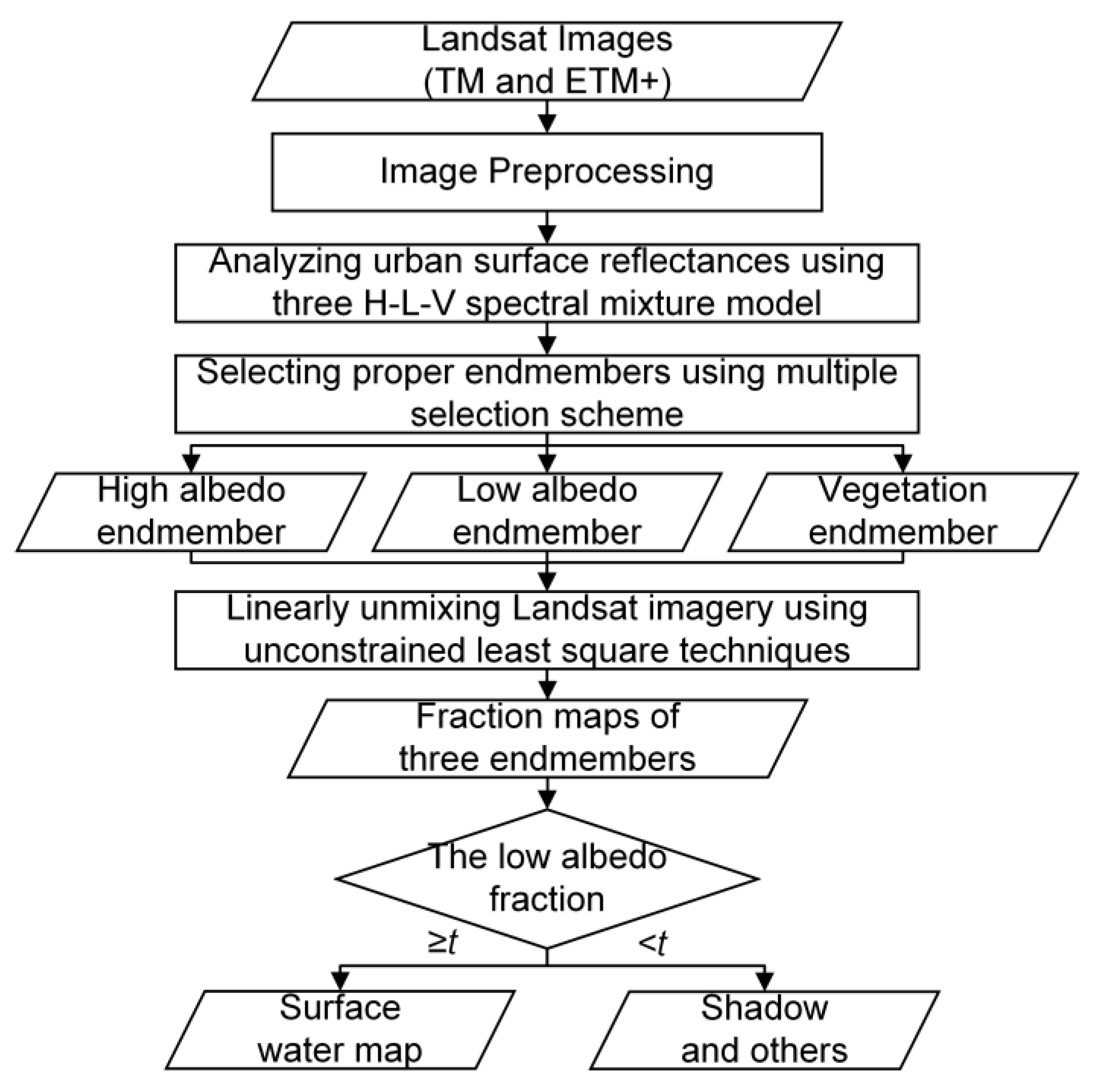
3.1. The Procedure of LAF Method
- (1)
- The Landsat images are preprocessed with radiometric calibration.
- (2)
- The three-endmember H-L-V linear mixture model is implemented to analyze surface reflectances of urban land cover types.
- (3)
- Endmembers covering high albedo, low albedo, and vegetation are carefully selected from Landsat images using our multiple selection scheme.
- (4)
- The unconstrained least square techniques are implemented to unmix Landsat images and to estimate the fractions of all three endmembers at each pixel. Fraction maps of all three endmembers are then obtained.
- (5)
- The binary classification is implemented to segment the fraction map of low albedo endmember, using a given threshold t. The pixels with low albedo fractions no less than t constitute the final surface water map of LAF.
3.1.1. Preprocessing of Landsat Images
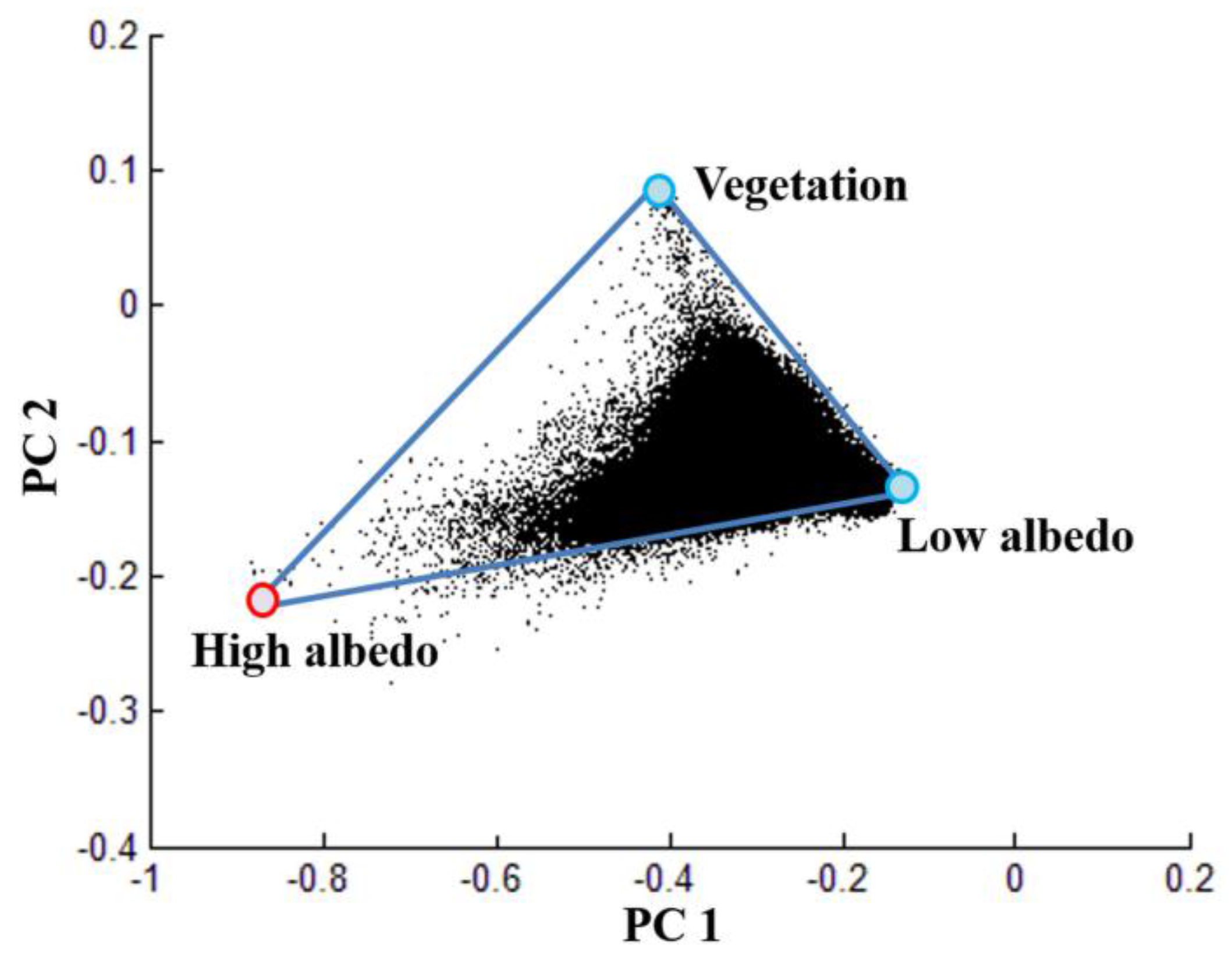
3.1.2. Analyzing Urban Surface Reflectances Using Three-Endmember H-L-V Model
3.1.3. Selecting Proper Endmembers Using a Multiple Selection Scheme
- (1)
- The low albedo endmember: The low-albedo endmembers correspond to deep dark shadow and water [29]. In this study, water is the most important object. Therefore, we chose the low albedo endmember from the deep dark water pixels, and the endmember has minimal brightness values in the image scene via cross-validation. The low albedo endmember is easy to determine from the image.
- (2)
- The vegetation endmember: The vegetation usually corresponds to grass or dense agriculture. The pixel with maximal normalized difference vegetation index (NDVI) values (dense grass and pasture) in the image scene is chosen as the vegetation endmember, using cross-validation. The vegetation endmember is also easily determined in the LAF method.
- (3)
- The high albedo endmember: The high albedo endmember shows much greater sensitivity to the selection method because it varies most greatly in amplitude within the triangular topology [29]. Therefore, we combine Landsat images with HSRI data to optimize the selection of the high albedo endmember via cross-validation. The initial high albedo endmembers are manually selected from building roofs, airport runways, and highway intersections in Landsat images, with reference to corresponding land covers in the HSRI data. Next, these initial endmembers are compared with the high-albedo vertex endmember in the scatter plots of PC1 and PC2. The endmember located closest to the high albedo vertex of the triangular topology is finally selected as the high albedo endmember [35].
3.1.4. Spectral Unmixing and Binary Classification of the Low Albedo Fraction Map
3.2. Accuracy Assessment Schemes on the Per-Pixel and Sub-Pixel Levels
- (1)
- The actual water fractions of testing boundary pixels were manually estimated via the visual overlay analysis of reference data and Landsat images. By overlaying the binary maps of extracted surface water from all three methods (AWEI, MNDWI and LAF) with the HSRI data, the water fraction of each boundary pixel from each method can be calculated. This was equal to the percentages of water pixels in the total number of HSRI pixels that were fully contained within the area of one pixel of Landsat imagery. For example, within the scene of one pixel from Landsat imagery, if the water occupies 20 of the total 50 HSRI pixels, the water fraction of the targeted boundary pixel is 40%. The process is repeated and the actual water fractions of all testing boundary pixels resulting from the three methods were achieved.
- (2)
- The testing boundary pixels were designated into six categories according to their true water fractions. The true water fractions of all testing boundary pixels in the HSRI data can be classified into six categories, 0–10%, 10–30%, 30–50%, 50–70%, 70–90% and 90–100%. For example, Figure 4 shows six categories of true water proportions in the testing boundary pixels of Shahu lake, and the number of testing boundary water pixels is 106.
- (3)
- The estimation errors (EEs) of all three methods on each testing boundary pixel were estimated. The EEs for each testing boundary pixels at the sub-pixel level are the summation of over-estimation error and under-estimation error, defined according to the following two conditions: (a) if a testing boundary pixel in the binary classification map of each method was classified as water, its complement of the true water fraction is regarded as the sub-pixel over-estimation error; (b) in contrast, if the pixel was classified as non-water, its true water fraction is quantified as the under-estimation error at the sub-pixel level.
- (4)
- The average estimation errors (AEEs) in all six categories of testing boundary pixels were calculated and the set of AEEs with six elements for all three methods were obtained to quantify the sub-pixel water extraction accuracy of boundary mixed pixels at different water proportions.
4. Experimental Results and Analysis
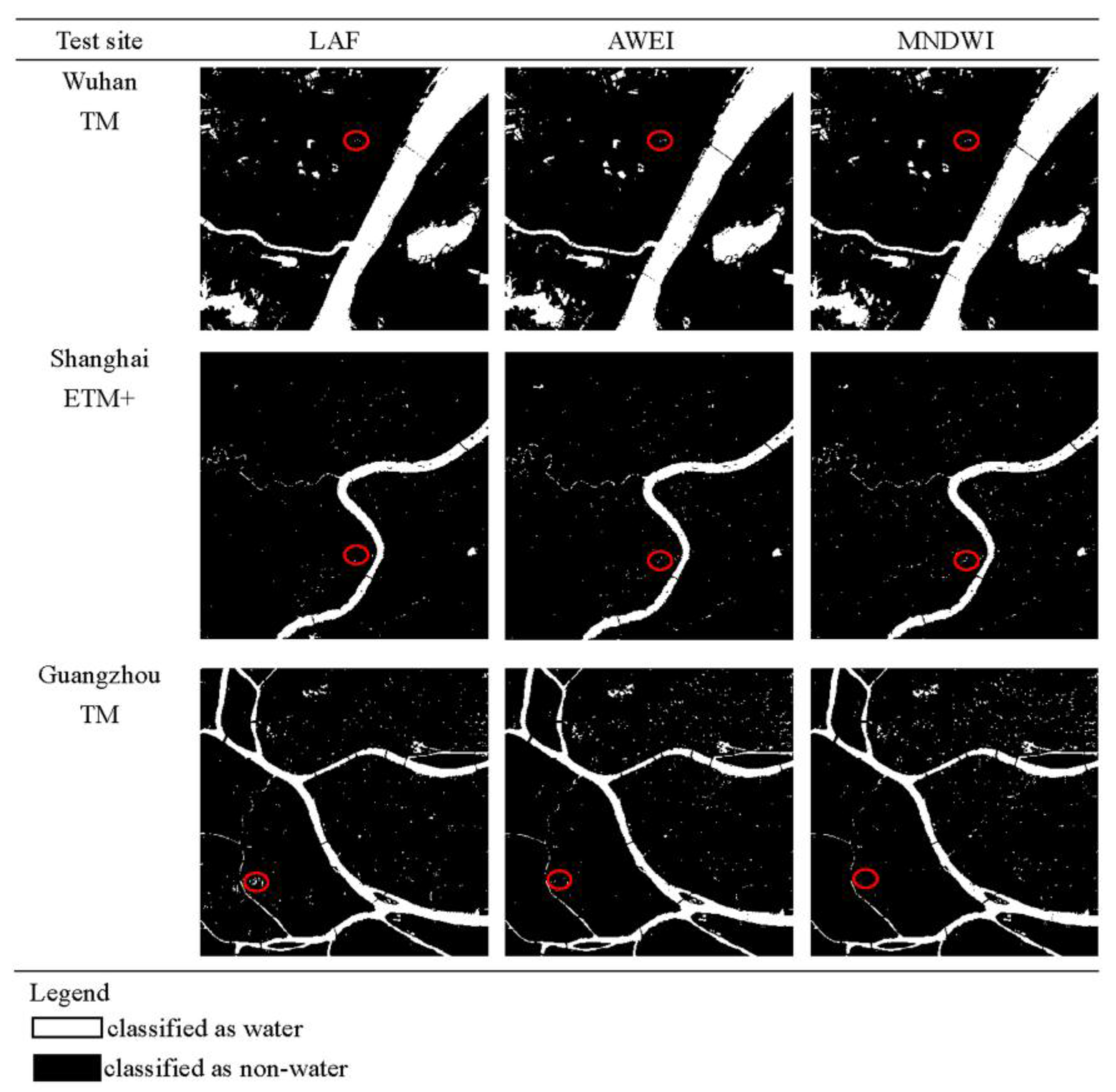
4.1. Water Extraction Maps and Per-Pixel Accuracy Assessment in Overall Result
4.2. Sub-Pixel Accuracy Assessment of LAF in Boundary Mixed Pixels
4.3. Threshold Analysis
5. Discussion
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Liu, Y.; Bai, X.; Shi, P. Realizing China’s urban dream. Nature 2014, 509, 158–160. [Google Scholar]
- United States Geological Survey (USGS). Facing Tomorrow’s Challenges—U.S. Geological Survey Science in the Decade 2007–2017; U.S. Geological Survey: Reston, VA, USA, 2007.
- Giardino, C.; Bresciani, M.; Villa, P.; Martinelli, A. Application of remote sensing in water resource management: The case study of lake trasimeno, Italy. Water Resour. Manag. 2010, 24, 3885–3899. [Google Scholar] [CrossRef]
- Morss, R.E.; Wilhelmi, O.V.; Downton, M.W.; Gruntfest, E. Flood risk, uncertainty, and scientific information for decision making: Lessons from an interdisciplinary project. Bull. Am. Meteorol. Soc. 2005, 86, 1593–1601. [Google Scholar] [CrossRef]
- Wang, Q.; Lin, J.; Yuan, Y. Salient band selection for hyperspectral image classification via manifold ranking. IEEE Trans. Neural Netw. Learn. Syst. 2016, 27, 1279–1289. [Google Scholar] [CrossRef] [PubMed]
- Zhang, P.; Lu, J.Z.; Feng, L.; Chen, X.L.; Zhang, L.; Xiao, X.W.; Liu, H.G. Hydrodynamic and inundation modeling of China’s largest freshwater lake aided by remote sensing data. Remote Sens. 2015, 7, 4858–4879. [Google Scholar] [CrossRef]
- Wang, Q.; Chen, M.; Li, X. Quantifying and Detecting Collective Motion by Manifold Learning. Proceeding of the AAAI Conference on Artificial Intelligence (AAAI), San Francisco, CA, USA, 4–9 February 2017; pp. 4292–4298. [Google Scholar]
- Ji, L.; Zhang, L.; Wylie, B. Analysis of dynamic thresholds for the normalized difference water index. Photogramm. Eng. Remote Sens. 2009, 75, 1307–1317. [Google Scholar] [CrossRef]
- Feyisa, G.L.; Meilby, H.; Fensholt, R.; Proud, S.R. Automated water extraction index: A new technique for surface water mapping using Landsat imagery. Remote Sens. Environ. 2014, 140, 23–35. [Google Scholar] [CrossRef]
- Lira, J. Segmentation and morphology of open water bodies from multispectral images. Int. J. Remote Sens. 2006, 27, 4015–4038. [Google Scholar] [CrossRef]
- Jiang, H.; Feng, M.; Zhu, Y.; Lu, N.; Huang, J.; Xiao, T. An automated method for extracting rivers and lakes from Landsat imagery. Remote Sens. 2014, 6, 5067–5089. [Google Scholar] [CrossRef]
- Yang, Y.; Liu, Y.; Zhou, M.; Zhang, S.; Zhan, W.; Sun, C.; Duan, Y. Landsat 8 OLI image based terrestrial water extraction from heterogeneous backgrounds using a reflectance homogenization approach. Remote Sens. Environ. 2015, 171, 14–32. [Google Scholar] [CrossRef]
- Jain, S.K.; Singh, R.; Jain, M.; Lohani, A. Delineation of flood-prone areas using remote sensing techniques. Water Resour. Manag. 2005, 19, 333–347. [Google Scholar] [CrossRef]
- Jain, S.K.; Saraf, A.K.; Goswami, A.; Ahmad, T. Flood inundation mapping using noaa avhrr data. Water Resour. Manag. 2006, 20, 949–959. [Google Scholar] [CrossRef]
- McFeeters, S. The use of the normalized difference water index (NDWI) in the delineation of open water features. Int. J. Remote Sens. 1996, 17, 1425–1432. [Google Scholar] [CrossRef]
- Xu, H. Modification of normalised difference water index (NDWI) to enhance open water features in remotely sensed imagery. Int. J. Remote Sens. 2006, 27, 3025–3033. [Google Scholar] [CrossRef]
- Rogers, A.; Kearney, M. Reducing signature variability in unmixing coastal marsh thematic mapper scenes using spectral indices. Int. J. Remote Sens. 2004, 25, 2317–2335. [Google Scholar] [CrossRef]
- Verpoorter, C.; Kutser, T.; Tranvik, L. Automated mapping of water bodies using Landsat multispectral data. Limnol. Oceanogr. Methods 2012, 10, 1037–1050. [Google Scholar] [CrossRef]
- Cracknell, A.P. Review article synergy in remote sensing-What’s in a pixel? Int. J. Remote Sens. 1998, 19, 2025–2047. [Google Scholar] [CrossRef]
- Yuan, Y.; Lin, J.; Wang, Q. Dual-clustering-based hyperspectral band selection by contextual analysis. IEEE Trans. Neural Netw. Learn. Syst. 2016, 54, 1431–1445. [Google Scholar] [CrossRef]
- Sethre, P.R.; Rundquist, B.C.; Todhunter, P.E. Remote detection of prairie pothole ponds in the devils lake basin, north dakota. GISci. Remote Sens. 2005, 42, 277–296. [Google Scholar] [CrossRef]
- Sun, X.; Li, L.; Zhang, B.; Chen, D.; Gao, L. Soft urban water cover extraction using mixed training samples and support vector machines. Int. J. Remote Sens. 2015, 36, 3331–3344. [Google Scholar] [CrossRef]
- Keshava, N.; Mustard, J.F. Spectral unmixing. IEEE Signal Process. Mag. 2002, 19, 44–57. [Google Scholar] [CrossRef]
- Zhou, Y.; Luo, J.; Shen, Z.; Hu, X.; Yang, H. Multiscale water body extraction in urban environments from satellite images. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 7, 4301–4312. [Google Scholar] [CrossRef]
- Xie, H.; Luo, X.; Xu, X.; Pan, H.; Tong, X. Automated Subpixel Surface Water Mapping from Heterogeneous Urban Environments Using Landsat 8 OLI Imagery. Remote Sens. 2016, 8, 584. [Google Scholar] [CrossRef]
- United States Geological Survey (USGS). Landsat Data Archive; USGS Global Visualization Viewer (GLOVIS): Reston, VA, USA, 2012.
- EXELIS. Exelis Visual Information Solutions; ENVI v5.0; EXELIS: Boulder, CO, USA, 2013. [Google Scholar]
- Lu, D.; Batistella, M.; Moran, E.; Mausel, P. Application of spectral mixture analysis to amazonian land-use and land-cover classification. Int. J. Remote Sens. 2004, 25, 5345–5358. [Google Scholar] [CrossRef]
- Small, C. The Landsat ETM+ spectral mixing space. Remote Sens. Environ. 2004, 93, 1–17. [Google Scholar] [CrossRef]
- Ridd, M.K. Exploring a VIS (vegetation-impervious surface-soil) model for urban ecosystem analysis through remote sensing: Comparative anatomy for cities. Int. J. Remote Sens. 1995, 16, 2165–2185. [Google Scholar] [CrossRef]
- Small, C. Estimation of urban vegetation abundance by spectral mixture analysis. Int. J. Remote Sens. 2001, 22, 1305–1334. [Google Scholar] [CrossRef]
- Wu, C.; Murray, A.T. Estimating impervious surface distribution by spectral mixture analysis. Remote Sens. Environ. 2003, 84, 493–505. [Google Scholar] [CrossRef]
- Small, C. A global analysis of urban reflectance. Int. J. Remote Sens. 2005, 26, 661–681. [Google Scholar] [CrossRef]
- Smith, M.O.; Johnson, P.E.; Adams, J.B. Quantitative determination of mineral types and abundances from reflectance spectra using principal components analysis. J. Geophys. Res. Solid Earth 1985, 90, C797–C804. [Google Scholar] [CrossRef]
- Weng, Q.; Hu, X. Medium spatial resolution satellite imagery for estimating and mapping urban impervious surfaces using lsma and ann. IEEE Trans. Geosci. Remote Sens. 2008, 46, 2397–2406. [Google Scholar] [CrossRef]
- Roberts, D.A.; Gardner, M.; Church, R.; Ustin, S.; Scheer, G.; Green, R.O. Mapping chaparral in the santa monica mountains using multiple endmember spectral mixture models. Remote Sens. Environ. 1998, 65, 267–279. [Google Scholar] [CrossRef]
- Heinz, D.C.; Chang, C.I. Fully constrained least squares linear spectral mixture analysis method for material quantification in hyperspectral imagery. IEEE Trans. Geosci. Remote Sens. 2001, 39, 529–545. [Google Scholar] [CrossRef]
- Nascimento, J.M.P.; Dias, J.M.B. Vertex component analysis: A fast algorithm to unmix hyperspectral data. IEEE Trans. Geosci. Remote Sens. 2005, 43, 898–910. [Google Scholar] [CrossRef]
- Wang, S.; Baig, M.H.A.; Zhang, L.; Jiang, H.; Ji, Y.; Zhao, H.; Tian, J. A simple enhanced water index (EWI) for percent surface water estimation using Landsat data. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2015, 8, 90–97. [Google Scholar] [CrossRef]
- Jones, J. Efficient wetland surface water detection and monitoring via Landsat: Comparison with in situ data from the everglades depth estimation network. Remote Sens. 2015, 7, 12503–12538. [Google Scholar] [CrossRef]
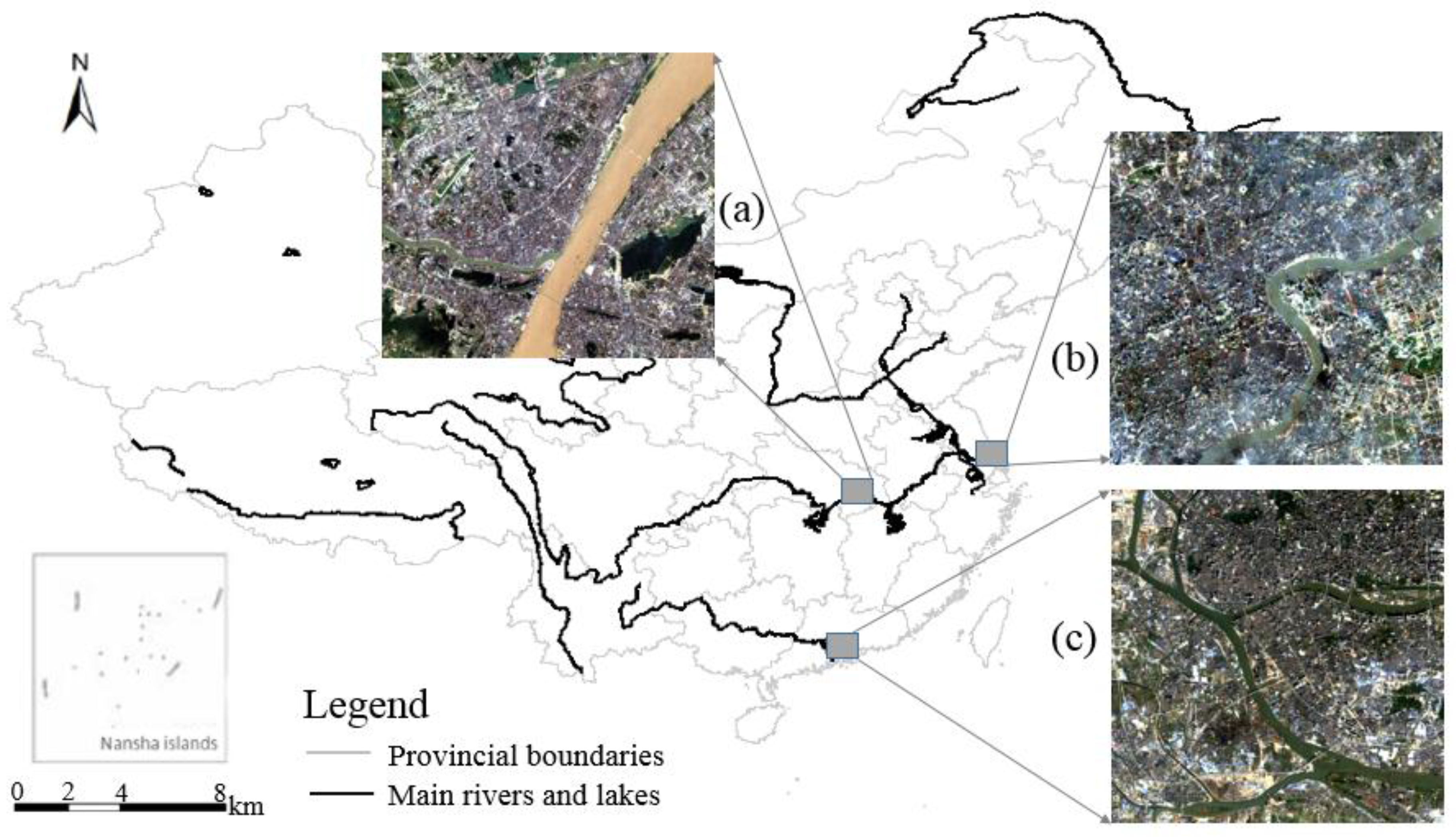

| Test Site | Acquisition Date | Sensors | Path | Row | Source | |
|---|---|---|---|---|---|---|
| Wuhan | Landsat data | 13 September 2000 | TM | 123 | 39 | USGS |
| Reference data | 21 September 2000 | Google Earth ©Digital globe | ||||
| Shanghai | Landsat data | 27 November 2002 | ETM+ | 118 | 38 | USGS |
| Reference data | 28 December 2002 | Google Earth ©Digital globe | ||||
| Guangzhou | Landsat data | 2 January 2009 | TM | 122 | 44 | USGS |
| Reference data | 16 November 2008 | Google Earth ©Digital globe | ||||
| Endmembers | Difficulty Level | Key Words in Operation | Candidate Sources |
|---|---|---|---|
| Low albedo | Easy | minimum brightness | deep dark water |
| Vegetation | Easy | maximal normalized difference vegetation index | grass and pasture |
| High albedo | Difficulty | nearest to the high albedo vertex in the triangular topology | building roofs, airport runway and highway intersections |
| Water Extraction Methods | Kappa Coefficient (KC) | ||
|---|---|---|---|
| Wuhan | Shanghai | Guangzhou | |
| LAF | 0.97 | 0.93 | 0.91 |
| AWEI | 0.95 | 0.92 | 0.93 |
| MNDWI | 0.96 | 0.92 | 0.92 |
| Water Extraction Methods | Extraction Errors of % Water in the Boundary Mixed Pixels | |||||
|---|---|---|---|---|---|---|
| 0–10% | 10–30% | 30–50% | 50–70% | 70–90% | 90–100% | |
| LAF | 0.04 | 0.22 | 0.43 | 0.41 | 0.23 | 0.03 |
| AWEI | 0.04 | 0.30 | 0.49 | 0.47 | 0.34 | 0.03 |
| MNDWI | 0.04 | 0.33 | 0.48 | 0.49 | 0.37 | 0.03 |
| City | Name of Water Bodies | Center Point Coordinate (UTM) | Area (km) | Characteristics of Water Bodies | Topography | Climate |
|---|---|---|---|---|---|---|
| Wuhan | Shahu lake | 30°34′04.30′′N, 114°19′41.76′′E | 3.04 | Clear lake | flat | Subtropical wet |
| Shanghai | Huangpu river | 31°14′33.18′′N, 121°29′21.00″E | 6.79 | Turbid river | flat | Subtropical wet |
| Guangzhou | Zhujiang river | 23°06′19.23′′N, 113°14′17.30′′E | 13.69 | Turbid river | flat | Subtropical wet |
| Water Extraction Methods | Test Site | Threshold Variability | ||
|---|---|---|---|---|
| Wuhan TM | Shanghai ETM+ | Guangzhou TM | Std | |
| LAF | 1.000 | 1.080 | 1.000 | 0.046 |
| AWEI | 0.086 | 0.200 | 0.156 | 0.057 |
| MNDWI | 0.350 | 0.515 | 0.470 | 0.085 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, W.; Du, B.; Xiong, S. Quantifying Sub-Pixel Surface Water Coverage in Urban Environments Using Low-Albedo Fraction from Landsat Imagery. Remote Sens. 2017, 9, 428. https://doi.org/10.3390/rs9050428
Sun W, Du B, Xiong S. Quantifying Sub-Pixel Surface Water Coverage in Urban Environments Using Low-Albedo Fraction from Landsat Imagery. Remote Sensing. 2017; 9(5):428. https://doi.org/10.3390/rs9050428
Chicago/Turabian StyleSun, Weiwei, Bo Du, and Shaolong Xiong. 2017. "Quantifying Sub-Pixel Surface Water Coverage in Urban Environments Using Low-Albedo Fraction from Landsat Imagery" Remote Sensing 9, no. 5: 428. https://doi.org/10.3390/rs9050428
APA StyleSun, W., Du, B., & Xiong, S. (2017). Quantifying Sub-Pixel Surface Water Coverage in Urban Environments Using Low-Albedo Fraction from Landsat Imagery. Remote Sensing, 9(5), 428. https://doi.org/10.3390/rs9050428