Prediction of Species-Specific Volume Using Different Inventory Approaches by Fusing Airborne Laser Scanning and Hyperspectral Data
Abstract
:1. Introduction
2. Materials and Methods
2.1. Data Set Description
2.1.1. Study Area
2.1.2. Field Data
2.1.3. ALS and Hyperspectral Data and Pre-Processing
2.2. Methodology
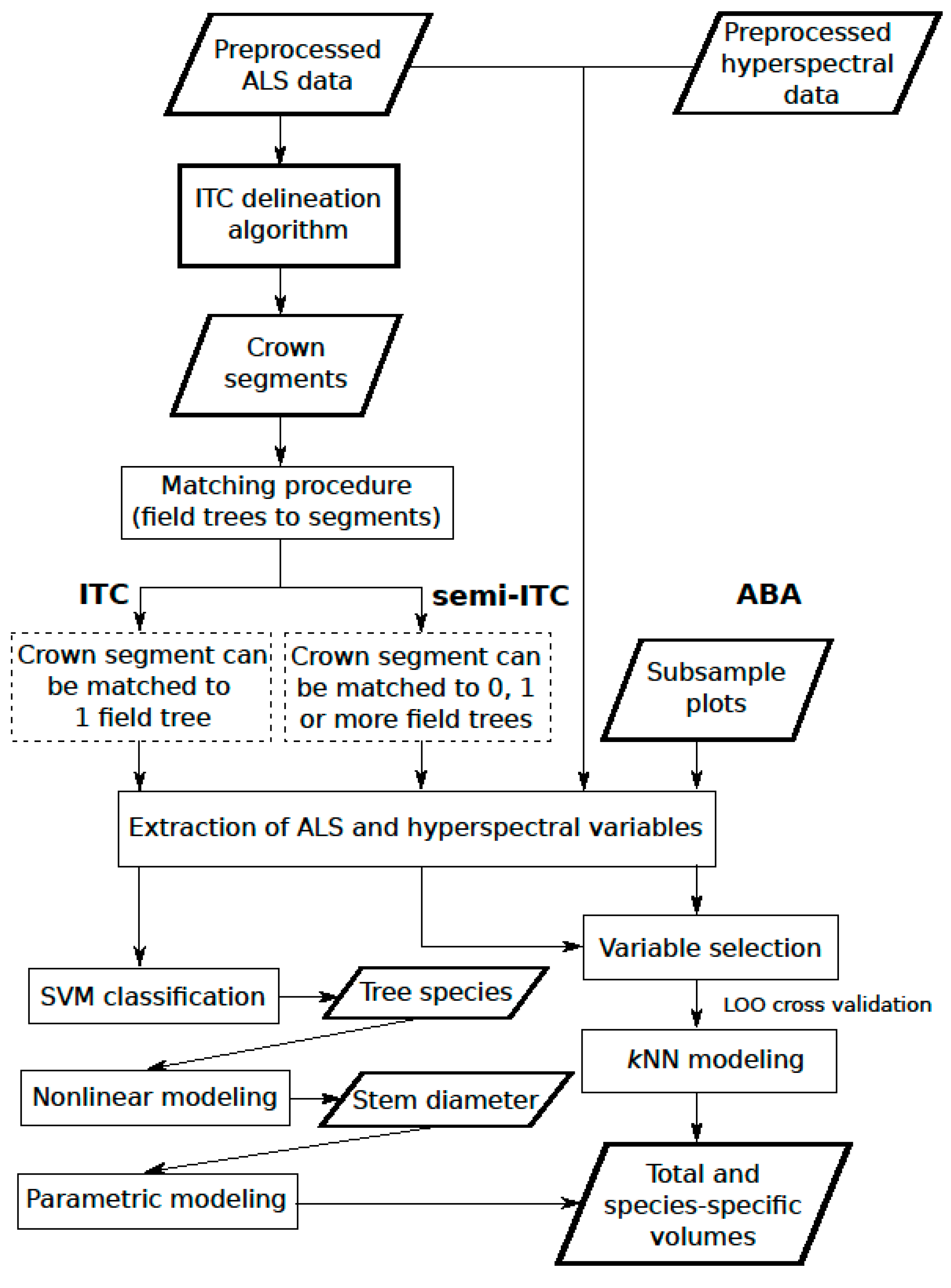
2.2.1. Overview
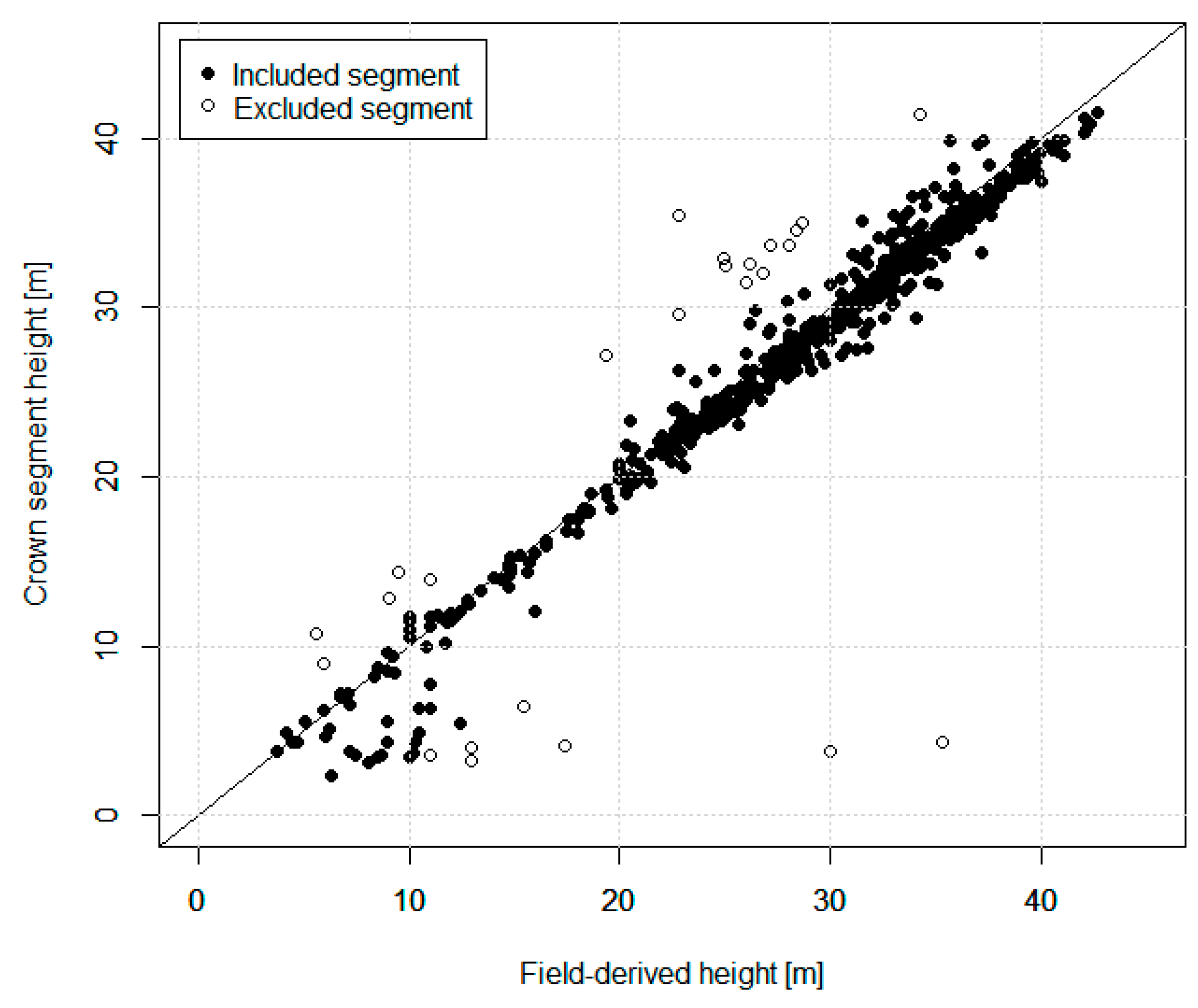
2.2.2. ITC Delineation Method
2.2.3. ITC Approach
2.2.4. Semi-ITC Approach
2.2.5. ABA
2.2.6. Accuracy Assessment
3. Results
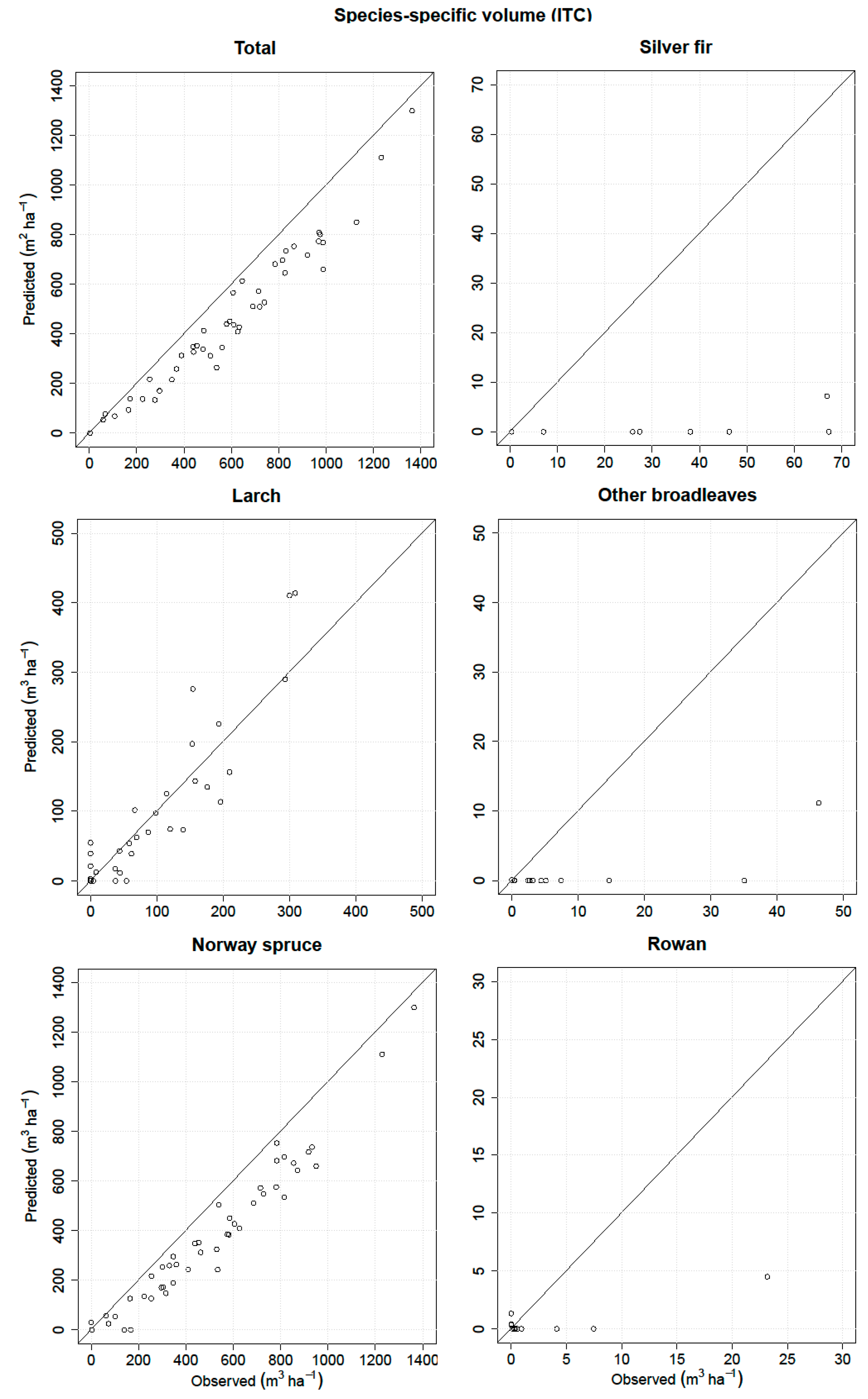
3.1. ITC Approach
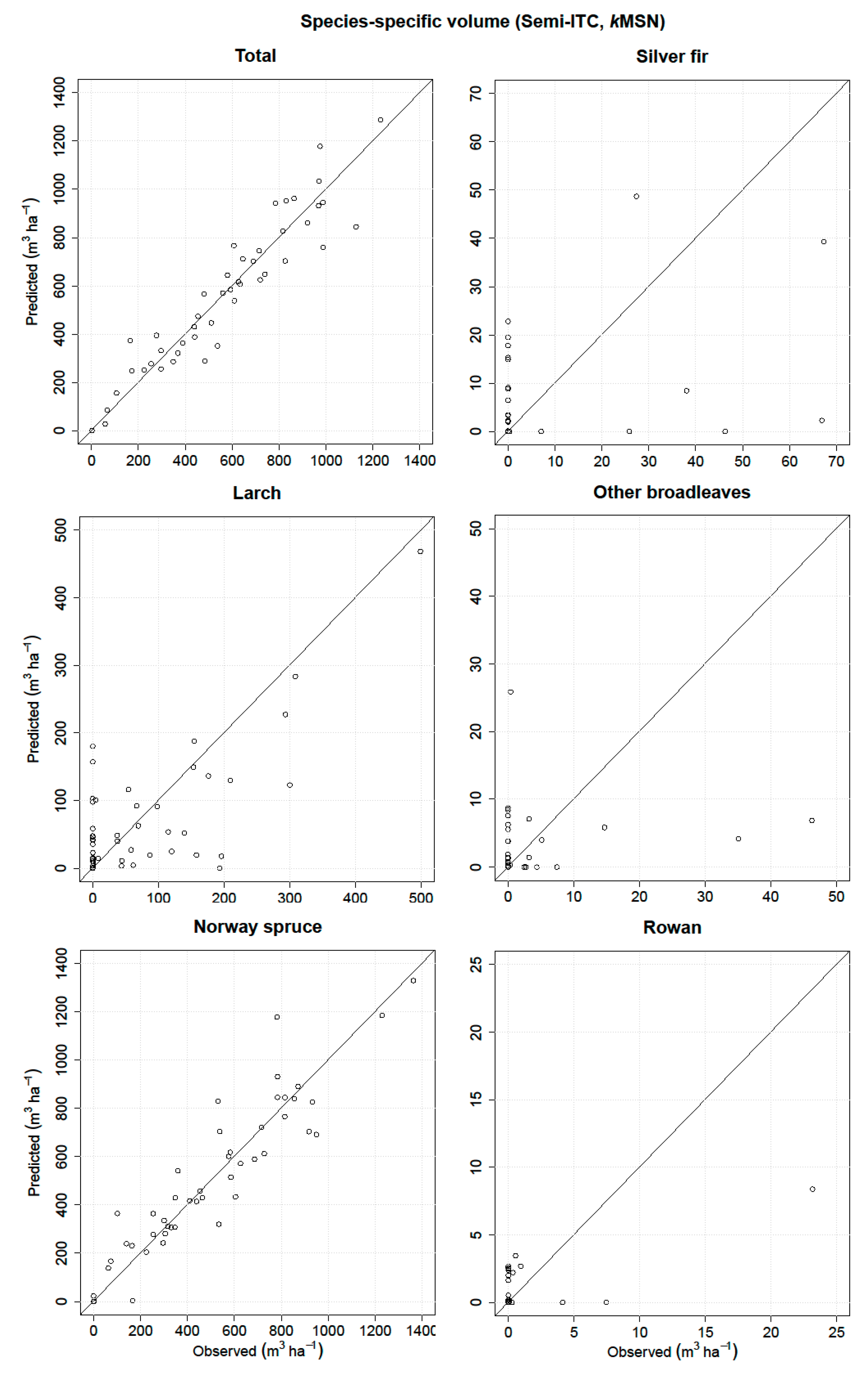
3.2. Semi-ITC Approach
3.3. ABA
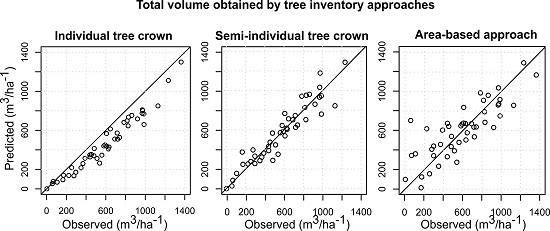
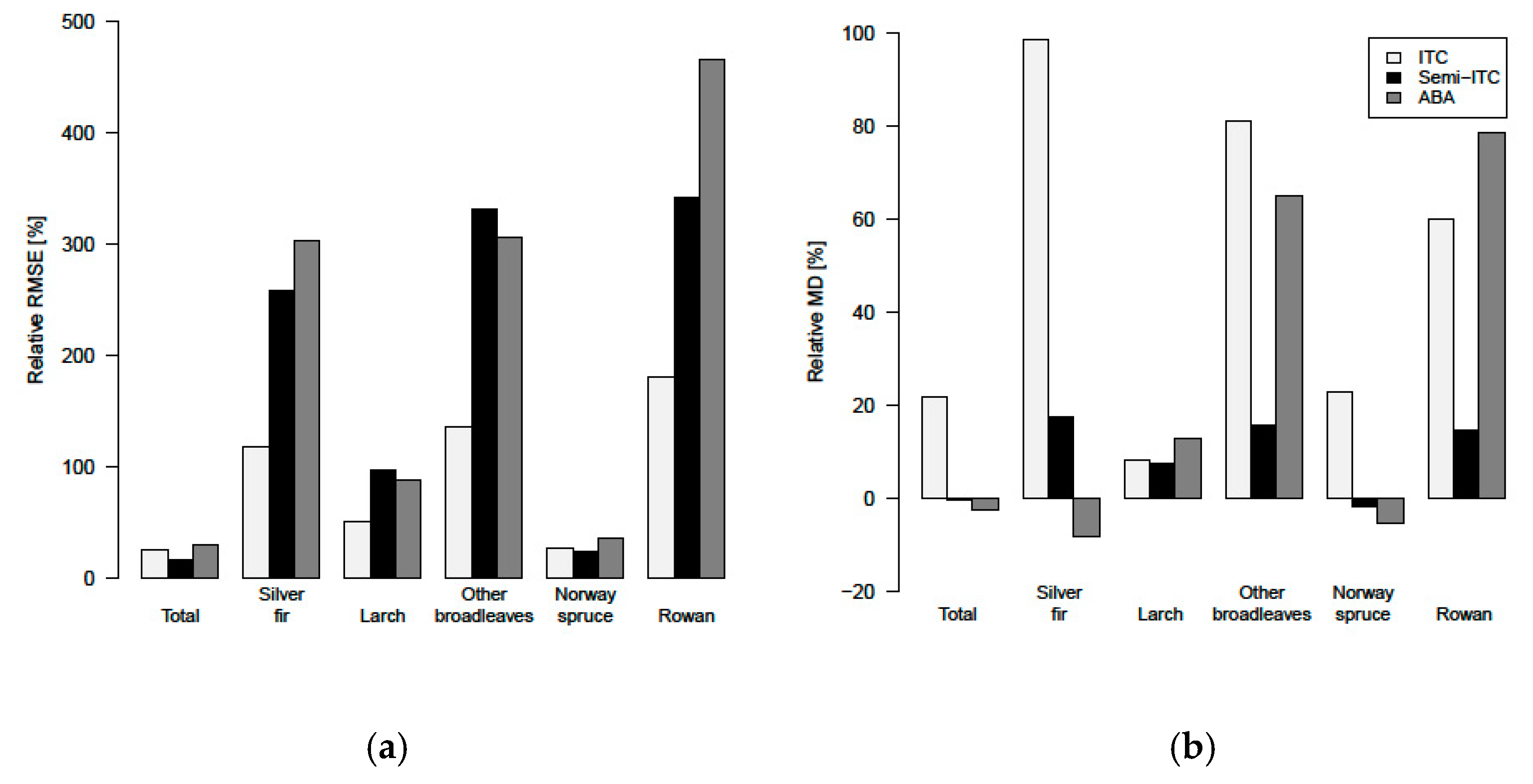
3.4. Comparison of the Different Inventory Approaches
4. Discussion
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Scrinzi, G.; Galvagni, D.; Marzullo, L. I Nuovi Modelli Dendrometrici Per La Stima Delle Masse Assestamentali in Provincia di Trento; Provincia Autonoma di Trento-Servizio Foreste e Fauna: Trento, Italy, 2010. [Google Scholar]
- Næsset, E.; Gobakken, T.; Holmgren, J.; Hyyppä, H.; Hyyppä, J.; Maltamo, M.; Nilsson, M.; Olsson, H.; Persson, Å.; Söderman, U. Laser scanning of forest resources: The nordic experience. Scand. J. For. Res. 2004, 19, 482–499. [Google Scholar] [CrossRef]
- Tomppo, E. The Finish multi-Source National Forest Inventory-Small area estimation and map production. In Forest Inventory: Methodology and Applications; Managing Forest Ecosystems; Kangas, A., Maltamo, M., Eds.; Springer: Dordrecht, The Netherlands, 2006; Volume 10, pp. 195–224. [Google Scholar]
- Eid, T.; Gobakken, T.; Næsset, E. Comparing stand inventories for large areas based on photo-Interpretation and laser scanning by means of cost-Plus-Loss analyses. Scand. J. For. Res. 2004, 19, 512–523. [Google Scholar] [CrossRef]
- Holmgren, J.; Persson, Å. Identifying species of individual trees using airborne laser scanner. Remote Sens. Environ. 2004, 90, 415–423. [Google Scholar] [CrossRef]
- Dalponte, M.; Bruzzone, L.; Gianelle, D. Tree species classification in the southern Alps based on the fusion of very high geometrical resolution multispectral/hyperspectral images and LiDAR data. Remote Sens. Environ. 2012, 123, 258–270. [Google Scholar] [CrossRef]
- Baltsavias, E.P. Airborne laser scanning: Basic relations and formulas. ISPRS J. Photogramm. Remote Sens. 1999, 54, 199–214. [Google Scholar] [CrossRef]
- Wehr, A.; Lohr, U. Airborne laser scanning–An introduction and overview. ISPRS J. Photogramm. Remote Sens. 1999, 54, 68–82. [Google Scholar] [CrossRef]
- Næsset, E. Predicting forest stand characteristics with airborne scanning laser using a practical two-Stage procedure and field data. Remote Sens. Environ. 2002, 80, 88–99. [Google Scholar] [CrossRef]
- Popescu, S.C.; Wynne, R.H.; Nelson, R.F. Estimating plot-Level tree heights with lidar: Local filtering with a canopy-Height based variable window size. Comput. Electron. Agric. 2002, 37, 71–95. [Google Scholar] [CrossRef]
- Maltamo, M.; Suvanto, A.; Packalén, P. Comparison of basal area and stem frequency diameter distribution modelling using airborne laser scanner data and calibration estimation. For. Ecol. Manag. 2007, 247, 26–34. [Google Scholar] [CrossRef]
- Peuhkurinen, J.; Mehtätalo, L.; Maltamo, M. Comparing individual tree detection and the area-based statistical approach for the retrieval of forest stand characteristics using airborne laser scanning in Scots pine stands. Can. J. For. Res. 2011, 41, 583–598. [Google Scholar] [CrossRef]
- Vauhkonen, J.; Ene, L.; Gupta, S.; Heinzel, J.; Holmgren, J.; Pitkanen, J.; Solberg, S.; Wang, Y.; Weinacker, H.; Hauglin, K.M.; et al. Comparative testing of single-tree detection algorithms under different types of forest. Forestry 2011, 85, 27–40. [Google Scholar] [CrossRef]
- Kandare, K.; Ørka, H.O.; Chan, J.C.; Dalponte, M. Effects of forest structure and airborne laser scanning point cloud density on 3D delineation of individual tree crowns. Eur. J. Remote Sens. 2016, 49, 337–359. [Google Scholar] [CrossRef]
- Ørka, H.O.; Næsset, E.; Bollandsås, O.M. Classifying species of individual trees by intensity and structure features derived from airborne laser scanner data. Remote Sens. Environ. 2009, 113, 1163–1174. [Google Scholar] [CrossRef]
- Packalén, P.; Maltamo, M. Predicting the plot volume by tree species using airborne laser scanning and aerial photographs. For. Sci. 2006, 52, 611–622. [Google Scholar]
- Packalén, P.; Maltamo, M. The k-MSN method for the prediction of species-specific stand attributes using airborne laser scanning and aerial photographs. Remote Sens. Environ. 2007, 109, 328–341. [Google Scholar] [CrossRef]
- Niska, H.; Skon, J.-P.; Packalen, P.; Tokola, T.; Maltamo, M.; Kolehmainen, M. Neural networks for the prediction of species-Specific plot volumes using airborne laser scanning and aerial photographs. IEEE Trans. Geosci. Remote Sens. 2010, 48, 1076–1085. [Google Scholar] [CrossRef]
- Popescu, S.C.; Wynne, R.H.; Scrivani, J.A. Fusion of small-Footprint lidar and multispectral data to estimate plot-Level volume and biomass in deciduous and pine forests in Virginia, USA. For. Sci. 2004, 50, 551–565. [Google Scholar]
- Tonolli, S.; Dalponte, M.; Neteler, M.; Rodeghiero, M.; Vescovo, L.; Gianelle, D. Fusion of airborne LiDAR and satellite multispectral data for the estimation of timber volume in the Southern Alps. Remote Sens. Environ. 2011, 115, 2486–2498. [Google Scholar] [CrossRef]
- Dalponte, M.; Ørka, H.O.; Gobakken, T.; Gianelle, D.; Næsset, E. Tree species classification in boreal forests with hyperspectral data. IEEE Trans. Geosci. Remote Sens. 2013, 51, 2632–2645. [Google Scholar] [CrossRef]
- Hill, R.A.; Thomson, A.G. Mapping woodland species composition and structure using airborne spectral and LiDAR data. Int. J. Remote Sens. 2005, 26, 3763–3779. [Google Scholar] [CrossRef]
- Ørka, H.O.; Dalponte, M.; Gobakken, T.; Næsset, E.; Ene, L.T. Characterizing forest species composition using multiple remote sensing data sources and inventory approaches. Scand. J. For. Res. 2013, 28, 677–688. [Google Scholar] [CrossRef]
- Sarrazin, M.J.D.; Van Aardt, J.A.N.; Asner, G.P.; Mcglinchy, J.; Messinger, D.W.; Wu, J. Fusing small-Footprint waveform LiDAR and hyper spectral data for canopy-Level species classification and herbaceous biomass modeling in savanna ecosystems. Can. J. Remote Sens. 2011, 37, 653–665. [Google Scholar] [CrossRef]
- Ahokas, E.; Hyyppä, J.; Yu, X.; Liang, X.; Matikainen, L.; Karila, K.; Litkey, P.; Kukko, A.; Jaakkola, A.; Kaartinen, H.; et al. Towards automatic single-Sensor mapping by multispectral airborne laser scanning. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2016, 41, 155–162. [Google Scholar] [CrossRef]
- Yu, X.; Hyyppä, J.; Litkey, P.; Kaartinen, H.; Vastaranta, M.; Holopainen, M. Single-Sensor Solution to Tree Species Classification Using Multispectral Airborne Laser Scanning. Remote Sens. 2017, 9, 108. [Google Scholar] [CrossRef]
- Junttila, S.; Kaasalainen, S.; Vastaranta, M.; Hakala, T.; Nevalainen, O.; Holopainen, M. Investigating bi-temporal hyperspectral lidar measurements from declined trees-Experiences from laboratory test. Remote Sens. 2015, 7, 13863–13877. [Google Scholar] [CrossRef]
- Clark, M.L.; Roberts, D.A.; Clark, D.B. Hyperspectral discrimination of tropical rain forest tree species at leaf to crown scales. Remote Sens. Environ. 2005, 96, 375–398. [Google Scholar] [CrossRef]
- Ferreira, M.P.; Zortea, M.; Zanotta, D.C.; Shimabukuro, Y.E.; De Souza Filho, C.R. Mapping tree species in tropical seasonal semi-Deciduous forests with hyperspectral and multispectral data. Remote Sens. Environ. 2016, 179, 66–78. [Google Scholar] [CrossRef]
- Asner, G.P.; Knapp, D.E.; Boardman, J.; Green, R.O.; Kennedy-Bowdoin, T.; Eastwood, M.; Martin, R.E.; Anderson, C.; Field, C.B. Carnegie Airborne Observatory-2: Increasing science data dimensionality via high-Fidelity multi-Sensor fusion. Remote Sens. Environ. 2012, 124, 454–465. [Google Scholar] [CrossRef]
- Luo, S.; Wang, C.; Xi, X.; Pan, F.; Peng, D.; Zou, J.; Nie, S.; Qin, H. Fusion of airborne LiDAR data and hyperspectral imagery for aboveground and belowground forest biomass estimation. Ecol. Indic. 2017, 73, 378–387. [Google Scholar] [CrossRef]
- Næsset, E. Estimating timber volume of forest stands using airborne laser scanner data. Remote Sens. Environ. 1997, 61, 246–253. [Google Scholar] [CrossRef]
- Hyyppä, J.; Inkinen, M. Detecting and estimating attributes for single trees using laser scanner. Photogramm. J. Finl. 1999, 16, 27–42. [Google Scholar]
- Wang, Y.; Hyyppä, J.; Liang, X.; Kaartinen, H.; Yu, X.; Lindberg, E.; Holmgren, J.; Qin, Y.; Mallet, C.; Ferraz, A.; et al. International benchmarking of the individual tree detection methods for modeling 3-D canopy structure for silviculture and forest ecology using airborne laser scanning. IEEE Trans. Geosci. Remote Sens. 2016, 54, 5011–5027. [Google Scholar] [CrossRef]
- Hyyppä, J.; Kelle, O.; Lehikoinen, M.; Inkinen, M. A segmentation-Based method to retrieve stem volume estimates from 3-D tree height models produced by laser scanners. IEEE Trans. Geosci. Remote Sens. 2001, 39, 969–975. [Google Scholar] [CrossRef]
- Persson, Å.; Holmgren, J.; Soderman, U. Detecting and measuring individual trees using an airborne laser scanner. Photogramm. Eng. Remote Sens. 2002, 68, 925–932. [Google Scholar]
- Breidenbach, J.; Næsset, E.; Lien, V.; Gobakken, T.; Solberg, S. Prediction of species specific forest inventory attributes using a nonparametric semi-Individual tree crown approach based on fused airborne laser scanning and multispectral data. Remote Sens. Environ. 2010, 114, 911–924. [Google Scholar] [CrossRef]
- Vauhkonen, J.; Seppänen, A.; Packalén, P.; Tokola, T. Improving species-Specific plot volume estimates based on airborne laser scanning and image data using alpha shape metrics and balanced field data. Remote Sens. Environ. 2012, 124, 534–541. [Google Scholar] [CrossRef]
- Moeur, M.; Stage, A.R. Most similar neighbor: An improved sampling inference procedure for natural resource planning. For. Sci. 1995, 41, 337–359. [Google Scholar]
- Ørka, H.O.; Gobakken, T.; Næsset, E.; Ene, L.; Lien, V. Simultaneously acquired airborne laser scanning and multispectral imagery for individual tree species identification. Can. J. Remote Sens. 2012, 38, 125–138. [Google Scholar] [CrossRef]
- McRoberts, R.; Nelson, M.; Wendt, D. Stratified estimation of forest area using satellite imagery, inventory data, and the k-Nearest Neighbors technique. Remote Sens. Environ. 2002, 82, 457–468. [Google Scholar] [CrossRef]
- Yu, B.; Ostland, I.M.; Gong, P.; Pu, R.L. Penalized discriminant analysis of in situ hyperspectral data for conifer species recognition. IEEE Trans. Geosci. Remote Sens. 1999, 37, 2569–2577. [Google Scholar] [CrossRef]
- Falkowski, M.J.; Hudak, A.T.; Crookston, N.L.; Gessler, P.E.; Uebler, E.H.; Smith, A.M.S. Landscape-Scale parameterization of a tree-Level forest growth model: A k-Nearest neighbor imputation approach incorporating LiDAR data. Can. J. For. Res. 2010, 40, 184–199. [Google Scholar] [CrossRef]
- Pippuri, I.; Maltamo, M.; Packalen, P.; Mäkitalo, J. Predicting species-Specific basal areas in urban forests using airborne laser scanning and existing stand register data. Eur. J. For. Res. 2013, 132, 999–1012. [Google Scholar] [CrossRef]
- Räty, J.; Vauhkonen, J.; Maltamo, M.; Tokola, T. On the potential to predetermine dominant tree species based on sparse-Density airborne laser scanning data for improving subsequent predictions of species-Specific timber volumes. For. Ecosyst. 2016, 3, 1–17. [Google Scholar] [CrossRef]
- R Development Core Team R: A Language and Environment for Statistical Computing. Available online: http://www.r-project.org (accessed on 22 September 2016).
- Kaartinen, H.; Hyyppä, J.; Yu, X.; Vastaranta, M.; Hyyppä, H.; Kukko, A.; Holopainen, M.; Heipke, C.; Hirschmugl, M.; Morsdorf, F.; et al. An international comparison of individual tree detection and extraction using airborne laser scanning. Remote Sens. 2012, 4, 950–974. [Google Scholar] [CrossRef]
- Karatzoglou, A.; Smola, A.; Hornik, K. The Kernlab Package. Available online: https://cran.r-project.org/web/packages/kernlab/index.html (accessed on 16 February 2017).
- Dalponte, M.; Coomes, D.A. Tree-Centric mapping of forest carbon density from airborne laser scanning and hyperspectral data. Methods Ecol. Evol. 2016, 7, 1236–1245. [Google Scholar] [CrossRef]
- Crookston, N.L.; Finley, A.O. YaImpute: An R Package for kNN Imputation. J. Stat. Softw. 2008, 23, 1–16. [Google Scholar] [CrossRef]
- McRoberts, R.E.; Gobakken, T.; Næsset, E. Post-Stratified estimation of forest area and growing stock volume using lidar-Based stratifications. Remote Sens. Environ. 2012, 125, 157–166. [Google Scholar] [CrossRef]
- Nilsson, M. Estimation of tree heights and stand volume using an airborne lidar system. Remote Sens. Environ. 1996, 56, 1–7. [Google Scholar] [CrossRef]
- Mohammadi, J.; Joibary, S.S.; Yaghmaee, F.; Mahiny, A.S. Modelling forest stand volume and tree density using Landsat ETM+data. Int. J. Remote Sens. 2010, 31, 2959–2975. [Google Scholar] [CrossRef]
- Mäkelä, H.; Pekkarinen, A. Estimation of forest stand volumes by Landsat TM imagery and stand-Level field-Inventory data. For. Ecol. Manag. 2004, 196, 245–255. [Google Scholar] [CrossRef]
- Packalén, P.; Temesgen, H.; Maltamo, M. Variable selection strategies for nearest neighbor imputation methods used in remote sensing based forest inventory. Can. J. Remote Sens. 2012, 38, 557–569. [Google Scholar] [CrossRef]
- Packalén, P.; Suvanto, A.; Maltamo, M. A two stage method to estimate species-specific growing stock. Photogramm. Eng. Remote Sens. 2009, 75, 1451–1460. [Google Scholar] [CrossRef]
- Puliti, S.; Gobakken, T.; Ørka, H.O.; Næsset, E. Assessing 3D point clouds from aerial photographs for species-Specific forest inventories. Scand. J. For. Res. 2017, 32, 68–79. [Google Scholar] [CrossRef]
- Wikström, P.; Edenius, L.; Elfving, B.; Eriksson, L.O.; LäMåS, T.; Sonesson, J.; ÖHMAN, K.; Wallerman, J.; Waller, C.; Klintebäck, F. The Heureka forestry decision support system: An overview. Math. Comput. For. Nat. Sci. 2011, 3, 87–95. [Google Scholar]
- Latifi, H.; Fassnacht, F.E.; Müller, J.; Tharani, A.; Dech, S.; Heurich, M. Forest inventories by LiDAR data: A comparison of single tree segmentation and metric-Based methods for inventories of a heterogeneous temperate forest. Int. J. Appl. Earth Obs. Geoinf. 2015, 42, 162–174. [Google Scholar] [CrossRef]
- Yu, X.; Hyyppä, J.; Holopainen, M.; Vastaranta, M. Comparison of area-Based and individual tree-Based methods for predicting plot-Level forest attributes. Remote Sens. 2010, 2, 1481–1495. [Google Scholar] [CrossRef]
- Rahlf, J.; Breidenbach, J.; Solberg, S.; Astrup, R. Forest parameter prediction using an image-Based point cloud: A comparison of semi-ITC with ABA. Forests 2015, 6, 4059–4071. [Google Scholar] [CrossRef]
- Bollandsås, O.M.; Maltamo, M.; Gobakken, T.; Næsset, E. Comparing parametric and non-Parametric modelling of diameter distributions on independent data using airborne laser scanning in a boreal conifer forest. Forestry 2013, 86, 493–501. [Google Scholar] [CrossRef]
- Hudak, A.T.; Crookston, N.L.; Evans, J.S.; Hall, D.E.; Falkowski, M.J. Nearest neighbor imputation of species-Level, plot-Scale forest structure attributes from LiDAR data. Remote Sens. Environ. 2008, 112, 2232–2245. [Google Scholar] [CrossRef]
- Penner, M.; Pitt, D.G.; Woods, M.E. Parametric vs. nonparametric LiDAR models for operational forest inventory in boreal Ontario. Can. J. Remote Sens. 2013, 39, 426–443. [Google Scholar]

| Biophysical Attributes | Range (Min-Max) | Mean | SD | |
|---|---|---|---|---|
| Tree level | DBH (cm) | 8.0–89.0 | 33.7 | 19.7 |
| H (m) | 3.50–42.60 | 22.37 | 9.90 | |
| BA (m2) | 0.01–0.62 | 0.08 | 0.12 | |
| V (m3) | 0.01–9.21 | 1.54 | 1.72 | |
| Plot level | Mean DBH (cm) | 13.5–71.8 | 38.0 | 12.8 |
| Mean H (m) | 7.93–37.90 | 23.92 | 7.12 | |
| Stem number (ha) | 14–1132 | 386 | 228 | |
| BA (m2 ha−1) | 0.63–85.73 | 46.26 | 21.22 | |
| V (m3 ha−1) | 2.47–1363.35 | 590.28 | 321.76 |
| Field Volume | Mean (m3 ha−1) | SD (m3 ha−1) | Relative SD (m3 ha−1) |
|---|---|---|---|
| Total | 590.28 | 321.76 | 54.51 |
| Silver fir | 34.88 | 24.85 | 71.25 |
| Larch | 102.37 | 114.16 | 111.51 |
| Other broadleaves | 9.64 | 14.47 | 150.21 |
| Norway spruce | 513.40 | 318.50 | 62.04 |
| Rowan | 3.36 | 6.98 | 207.34 |
| Silver Fir | Larch | Other Broad Leaves | Norway Spruce | Rowan | |
|---|---|---|---|---|---|
| Producer’s accuracy (%) | 16.7 | 71.6 | 14.3 | 90.1 | 75.0 |
| User’s accuracy (%) | 100 | 58.1 | 50.0 | 92.2 | 81.8 |
| Volume | RMSE (m3 ha−1) | Relative RMSE (%) | MD (m3 ha−1) | Relative MD (%) | r2 |
|---|---|---|---|---|---|
| Total | 152.18 | 25.78 | 132.37 | 22.43 * | 0.95 |
| Silver fir | 40.53 | 116.2 | 33.98 | 97.41 * | 0.27 |
| Larch | 48.7 | 47.57 | −5.29 | −5.17 | 0.90 |
| Other broadleaves | 14.71 | 152.67 | 8.77 | 91.02 * | 0.58 |
| Norway spruce | 151.26 | 29.46 | 130.34 | 25.39 * | 0.95 |
| Rowan | 6.21 | 184.71 | 2.77 | 82.25 | 0.76 |
| Volume | RMSE (m3 ha−1) | Relative RMSE (%) | MD (m3 ha−1) | Relative MD (%) | r2 |
|---|---|---|---|---|---|
| Total | 102.78 | 17.41 | –1.59 | –0.27 | 0.90 |
| Silver fir | 15.35 | 258.48 | 1.04 | 17.5 | 0.16 |
| Larch | 76.02 | 96.95 | 5.91 | 7.54 | 0.51 |
| Other broadleaves | 8.82 | 330.74 | 0.41 | 15.57 | 0.03 |
| Norway spruce | 124.25 | 24.73 | –9.07 | –1.81 | 0.85 |
| Rowan | 2.69 | 341.02 | 0.11 | 14.53 | 0.50 |
| Volume | RMSE (m3 ha−1) | Relative RMSE (%) | MD (m3 ha−1) | Relative MD (%) | r2 |
|---|---|---|---|---|---|
| Total | 182.75 | 30.95 | −15.88 | −2.69 | 0.67 |
| Silver fir | 18.01 | 303.25 | −0.49 | −8.26 | 0.01 |
| Larch | 69.36 | 88.44 | 10.00 | 12.76 | 0.60 |
| Other broadleaves | 8.20 | 306.02 | 1.74 | 65.02 | 0.12 |
| Norway spruce | 183.54 | 36.52 | −27.77 | −5.53 | 0.68 |
| Rowan | 3.76 | 465.42 | 0.63 | 78.56 | 0 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kandare, K.; Dalponte, M.; Ørka, H.O.; Frizzera, L.; Næsset, E. Prediction of Species-Specific Volume Using Different Inventory Approaches by Fusing Airborne Laser Scanning and Hyperspectral Data. Remote Sens. 2017, 9, 400. https://doi.org/10.3390/rs9050400
Kandare K, Dalponte M, Ørka HO, Frizzera L, Næsset E. Prediction of Species-Specific Volume Using Different Inventory Approaches by Fusing Airborne Laser Scanning and Hyperspectral Data. Remote Sensing. 2017; 9(5):400. https://doi.org/10.3390/rs9050400
Chicago/Turabian StyleKandare, Kaja, Michele Dalponte, Hans Ole Ørka, Lorenzo Frizzera, and Erik Næsset. 2017. "Prediction of Species-Specific Volume Using Different Inventory Approaches by Fusing Airborne Laser Scanning and Hyperspectral Data" Remote Sensing 9, no. 5: 400. https://doi.org/10.3390/rs9050400
APA StyleKandare, K., Dalponte, M., Ørka, H. O., Frizzera, L., & Næsset, E. (2017). Prediction of Species-Specific Volume Using Different Inventory Approaches by Fusing Airborne Laser Scanning and Hyperspectral Data. Remote Sensing, 9(5), 400. https://doi.org/10.3390/rs9050400