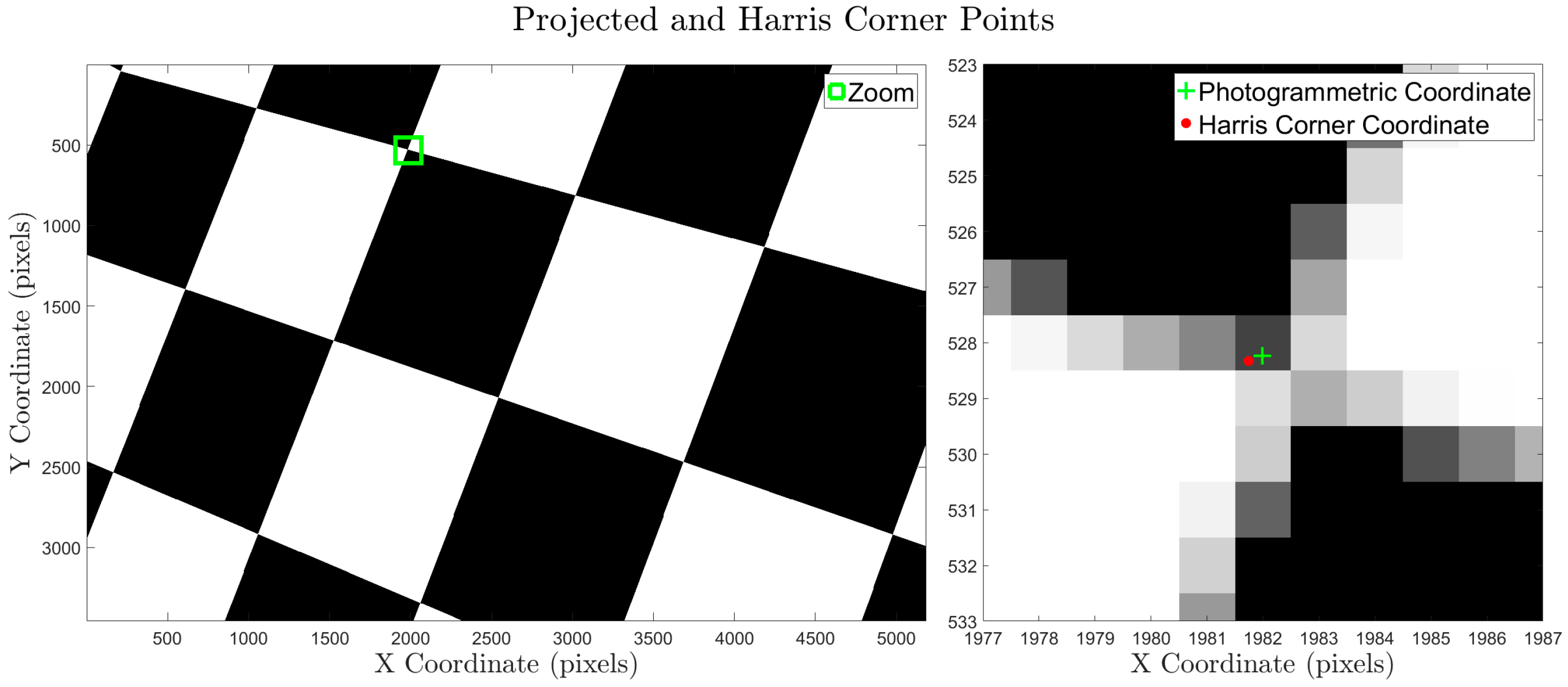
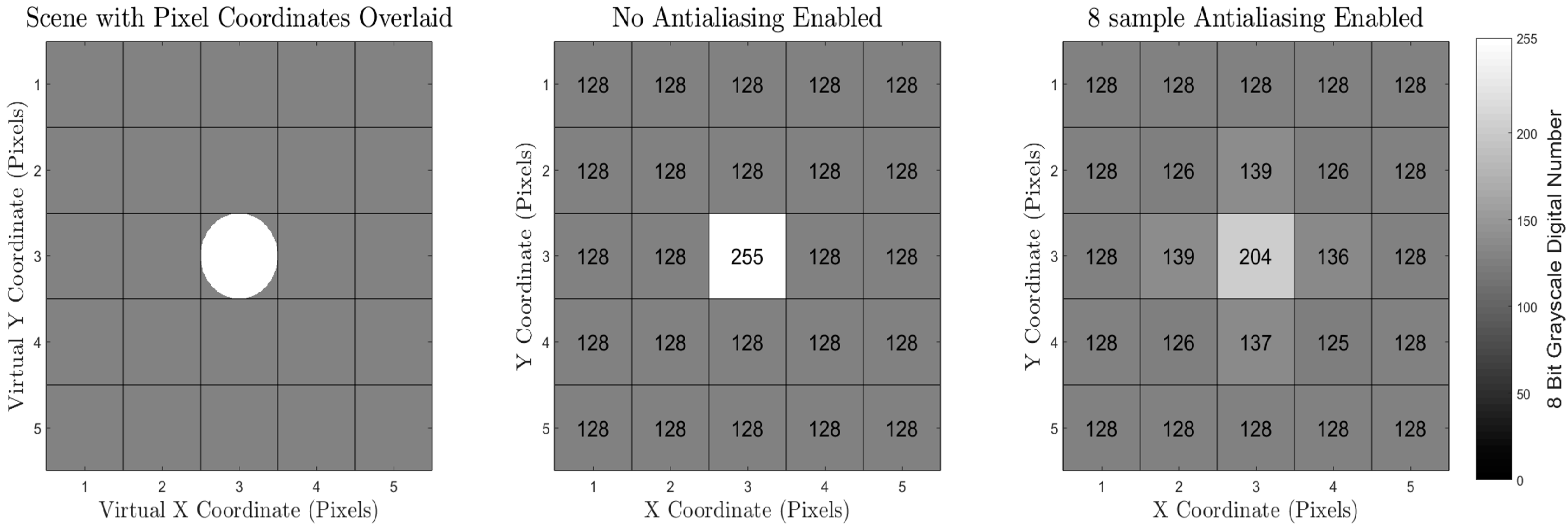
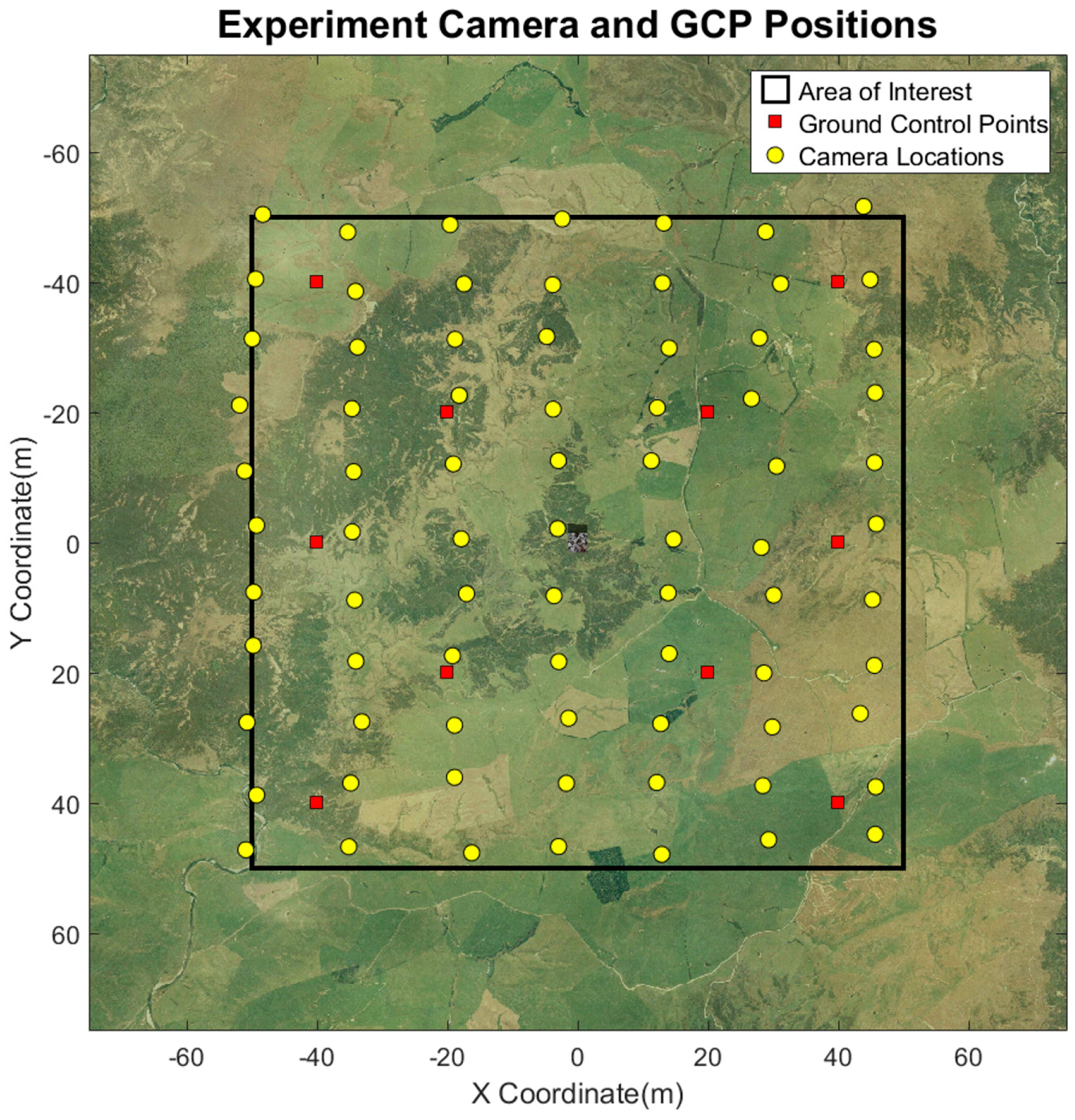
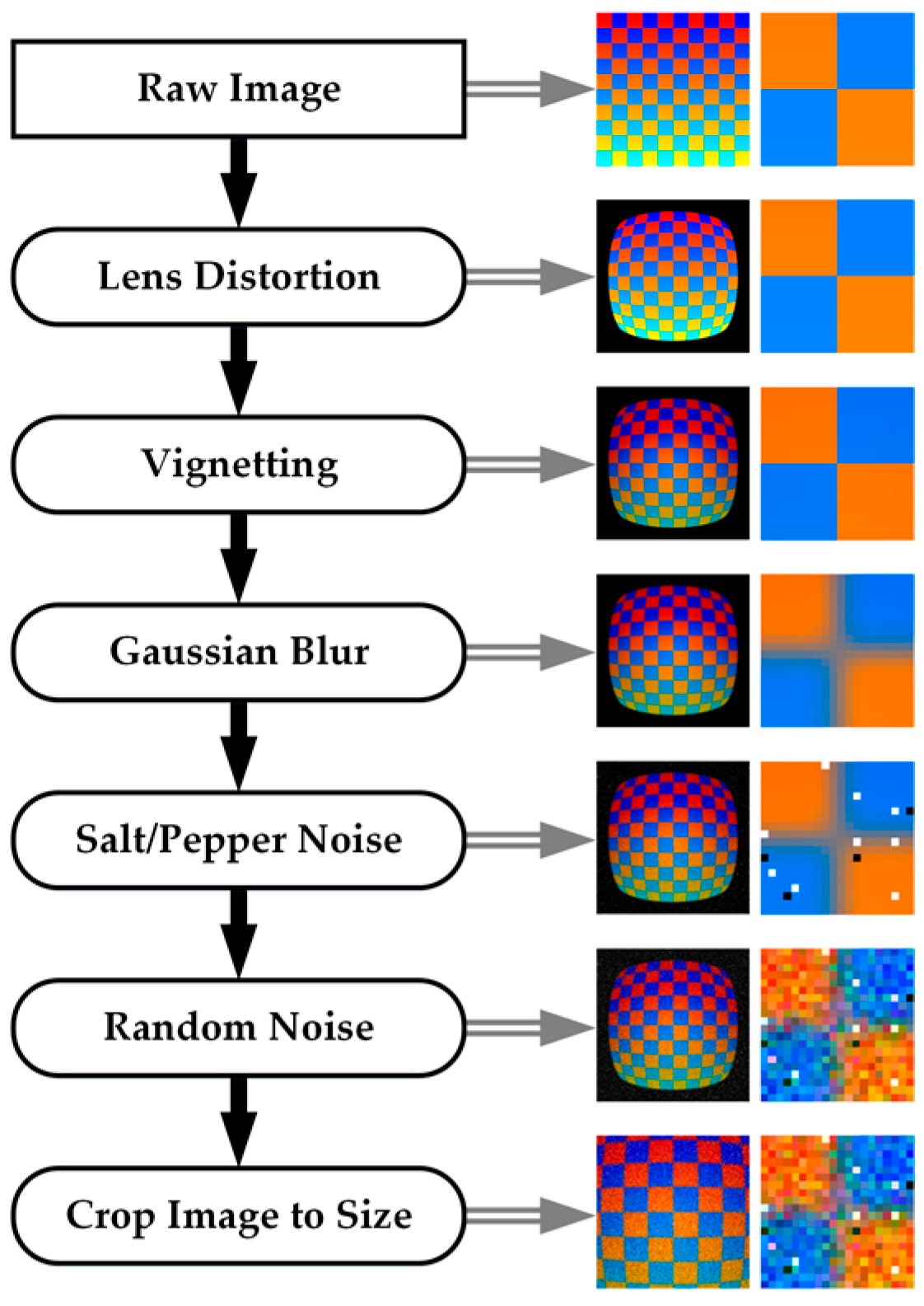
1. Introduction
Efficient acquisition of high-resolution, high-accuracy 3D point clouds has traditionally required either terrestrial, mobile, or airborne LiDAR. However, advances in structure from motion (SfM) and MultiView Stereo (MVS) algorithms have enabled the generation of image-based point cloud products that are often reported to be comparable in density and accuracy to LiDAR data [
1,
2]. Development of SfM algorithms for 3D reconstruction of geometry within the computer vision community began approximately four decades ago [
3,
4], and conventional photogrammetric techniques can be traced back to the mid-1800s or earlier [
5]. However, modern, commercial SfM-MVS software packages have only relatively recently begun to be utilized operationally for surveying applications, leveraging advances in camera hardware, unmanned aircraft systems (UAS), computer processing power, and ongoing algorithm development.
The 3D reconstruction methods used in most commercial software consist of an SfM algorithm first to solve for camera exterior and interior orientations, followed by an MVS algorithm to increase the density of the point cloud. Unordered photographs are input into the software, and a keypoint detection algorithm, such as scale invariant feature transform (SIFT) [
6], is used to detect keypoints and keypoint correspondences between images using a keypoint descriptor. A bundle adjustment is performed to minimize the errors in the correspondences. In addition to solving for camera interior and exterior orientation, the SfM algorithm also generates a sparse point cloud. Without any additional information, the coordinate system is arbitrary in translation and rotation and has inaccurate scale. To further constrain the problem and develop a georectified point cloud, ground control points (GCPs) and/or initial camera positions (e.g., from GNSS) are introduced to constrain the solution. The number of parameters to be solved for can also be reduced by inputting a camera calibration file; however, without camera positions or GCP coordinates, the camera calibration file will only help resolve the scale of the point cloud coordinate system, and not the absolute translation and rotation. The input GCPs can be used to transform the point coordinates to a real-world coordinate system via a Helmert transformation (also known as a seven-parameter or 3D conformal transformation) after the point cloud is generated [
7], or using a commercial software proprietary method to “optimize” rectification. The latter method is vendor-proprietary, and, hence, the mathematical details of the transformation are unknown; however, it is generally reported to produce more accurate results than the Helmert transformation. The interior orientation and exterior orientation for each image are used as the input to the MVS algorithm, which generates a denser point cloud.
Some of the common MVS algorithms generate more correspondences by utilizing a search along the epipolar line between corresponding images, leveraging the known interior and exterior orientations of each camera. For this reason, the accuracy of the MVS algorithm is highly dependent on the accuracy of the parameters calculated with the SfM algorithm. A detailed explanation of the various MVS algorithms can be found in Furukawa and Hernández [
8], who also note that each of these algorithms assumes that the scene is rigid with constant Lambertian surfaces, and that deviations from these assumptions will affect the accuracy.
Research into SfM and MVS in the geomatics community is currently focused on both the accuracy and potential applications of commercial SfM and MVS software packages, such as Agisoft Photoscan Pro and Pix4D [
9]. It has been shown that the accuracy of SfM-MVS can vary greatly depending on a number of factors [
10,
11], which, in turn, vary across different experiments [
7]. In particular, the accuracy of SfM is adversely affected by: poor image overlap, inadequate modeling of lens distortion, poor GCP distribution, inaccurate GCP or camera positions, poor image resolution, blurry imagery, noisy imagery, varying sun shadows, moving objects in the scene, user error in manually selecting image coordinates of GCPs, a low number of images, or a low number of GCPs [
10]. Due to the large number of variables involved, addressing the questions of if/how/when SfM-MVS derived point clouds might replace LiDAR as an alternative surveying tool, without sacrificing accuracy, remains an active area of research [
12,
13,
14].
The most common methodology for assessing the use cases and accuracy of SfM-MVS derived products is to collect imagery in the field using a UAS and, after processing in SfM-MVS software, to compare the point clouds against reference data collected concurrently with terrestrial LiDAR, RTK GNSS, or a total station survey. Numerous studies have been performed to quantify the accuracy of the SfM-MVS algorithms in a variety of environments [
14,
15], including shallow braided rivers [
16], beaches [
17], and forests [
11]. Experimentation utilizing simulated keypoints and assessing the SfM accuracy was used to demonstrate an ambiguity between point cloud “dome” effect and the
K1 coefficient in the Brown distortion model [
18]. A few datasets have been acquired in a lab environment, using a robotic arm to accurately move a camera and a light structure camera to collect reference data for a variety of objects of varying textures [
19,
20]. While this approach works well for testing the underlying algorithms, especially MVS, more application-based experiments performed by the surveying community have demonstrated how on larger scenes with less dense control data the error propagates nonlinearly. Generally, the most common and robust method has been to compare the SfM-MVS derived point cloud to a ground truth terrestrial LiDAR survey [
21,
22].
Despite the widespread use of field surveys for empirically assessing the accuracy of point clouds generated from UAS imagery using SfM-MVS software, there are a number of limitations of this general approach. The extensive field surveys required to gather the reference data are generally expensive and time consuming, and they can also be logistically-challenging and perhaps even dangerous in remote locations or alongside roadways. Additionally, if it is required to test different imagery acquisition parameters (e.g., different cameras, focal lengths, flying heights, exposure settings, etc.), then multiple flights may be needed, increasing the potential for confounding variables (e.g., changing weather conditions and moving objects in the scene) to creep into the experiment.
The use of independent, field-surveyed check points may also lead to an overly-optimistic accuracy assessment when the points used are easily photo-identifiable targets (e.g., checkerboards, or conventional “iron cross” patterns). These targets are generally detected as very accurate keypoints in the SfM processing, and using them as check points will tend to indicate a much better accuracy than if naturally-occurring points in the scene were used instead. In this case, the error reported from independent GCPs may not be indicative of the accuracy of the entire scene. The quality and uniqueness of detected keypoints in an image and on an object is called “texture.” The lack of texture of a scene has been shown to have one of the largest impacts on the accuracy of SfM-MVS point cloud [
13,
14,
17,
20].
We propose an open-source computer graphics based workflow to alleviate the aforementioned issues with assessing the accuracy of point clouds generated from UAS imagery using SfM-MVS software. The basic idea of the approach is to simulate various scenes and maintain full control over the ground-truth and the camera parameters. This workflow, referred to by the project team as the simUAS (simulated UAS) image rendering workflow, allows researchers to perform more robust experiments to assess the feasibility and accuracy of SfM-MVS in various applications. Ground control points, check points and other features are placed virtually in the scene with coordinate accuracies limited only by the numerical precision achievable with the computer hardware and software used. Textures throughout the scene can also be modified, as desired. Camera parameters and other scene properties can also be modified, and new image data sets (with all other independent variables perfectly controlled) can then be generated at the push of a button. The output imagery can then be processed using any desired SfM-MVS software and the resultant point cloud compared to the true surface (where, in this case, “true” and “known” are not misnomers, as they generally are when referring to field-surveyed data with its own uncertainty), and any errors can be attributed to the parameters and parameter uncertainties input by the user.
Computer Graphics for Remote Sensing Analysis
The field of computer graphics emerged in the 1960s and has evolved to encompass numerous fields from medical imaging and scientific visualization, aircraft flight simulators, and movie and video game special effects [
23]. The software that turns a simulated scene with various geometries, material properties, and lighting into an image or sequence of images is called a render engine. While there are numerous render engines available using many different algorithms, they all follow a basic workflow, or computer graphics pipeline.
First, a 3D scene is generated using vertices, faces, and edges. For most photo-realistic rendering, meshes are generated using an array of either triangular surfaces or quadrilateral surfaces to create objects. Material properties are applied to each of the individual surfaces to determine the color of the object. Most software allows for the user to set diffuse, specular, and ambient light coefficients, as well as their associated colors to specify how light will interact with the surface. The coefficient specifies how much diffuse, specular, and ambient light is reflected off the surface of the object, while the color specifies the amount of visible red, green, and blue light that is reflected from the surface. The material color properties are only associated with each plane in the mesh, so for highly-detailed coloring of objects, many small faces can be utilized. The more efficient method of creating detailed colors on an object without increasing the complexity of the surface of the object is to add a “texture” to the object. A texture can consist of geometric patterns or other complex vector based patterns, but in this experimentation a texture is an image which is overlaid on the mesh in a process called u-v mapping. In this process, each vertex is assigned coordinates in image space in units of texels, which are synonymous with pixels but renamed to emphasize the fact that they correspond to a texture and not a rendered image. It is also possible to generate more complex textures by overlaying multiple image textures on the same object and blending them together by setting a transparent “alpha” level for each image. The render engine interpolates the texel coordinates across the surface when the scene is rendered. For interpolated subpixel coordinates, the color value is either interpolated linearly or the nearest pixel value is used. (The computer graphics definition of a “texture” object is not to be confused with the SfM-photogrammetry definition of texture, which relates to the level of detail and unique, photo-identifiable features in an image.)
Once a scene is populated with objects and their associated material and texture properties, light sources and shading algorithms must be applied to the scene. The simplest method is to set an object material as “shadeless,” which eliminates any interaction with light sources and will render each surface based on the material property and texture with the exact RGB values that were input. The more complex and photorealistic method is to place one or more light sources in the scene. Each light source can be set to simulate different patterns and angles of light rays with various levels of intensity and range based intensity falloff. Most render engines also contain shadow algorithms which enable the calculation of occlusions from various light sources. Once a scene is created with light sources and shading parameters set, simulated cameras are placed to create the origin for renders of the scene. The camera translation, rotation, sensor size, focal length, and principal point are input, and a pinhole camera model is used. The rendering algorithm generates a 2D image of the scene using the camera position and all the material properties of the objects. The method, accuracy (especially lighting), and performance of generating this 2D depiction of the scene are where most render engines differ.
There are many different rendering methodologies, but the one chosen for this research is Blender Internal Render Engine, which is a rasterization based engine. The algorithm determines which parts of the scene are visible to the camera, and performs basic light interactions to assign a color to the pixel samples. This algorithm is fast, although it is unable to perform some of the more advanced rendering features such as global illumination and true motion blur. A more detailed description of shader algorithms which are used to generate these detailed scenes can be found in [
24].
The use of synthetic remote sensing datasets to test and validate remote sensing algorithms is not a new concept. A simulated imagery dataset using Terragen 3 was used validate an optimized flight plan methodology for UAS 3D reconstructions [
25]. Numerous studies have been performed using the Rochester Institute of Technology’s Digital Imaging and Remote Sensing Image Generation (DIRSIG) using for various active and passive sensors. DIRSIG has been used to generate an image dataset for SfM-MVS processing to test an algorithm to automate identification of voids in three-dimensional point clouds [
26] and assess SfM accuracy using long range imagery [
27]. While DIRSIG generates radiometrically- and geometrically-accurate imagery, it is currently not available to the public. Considerations in selecting the renderer used in this work included a desire to use publicly-available and open-source software, to the extent possible.
3. Use Case Results
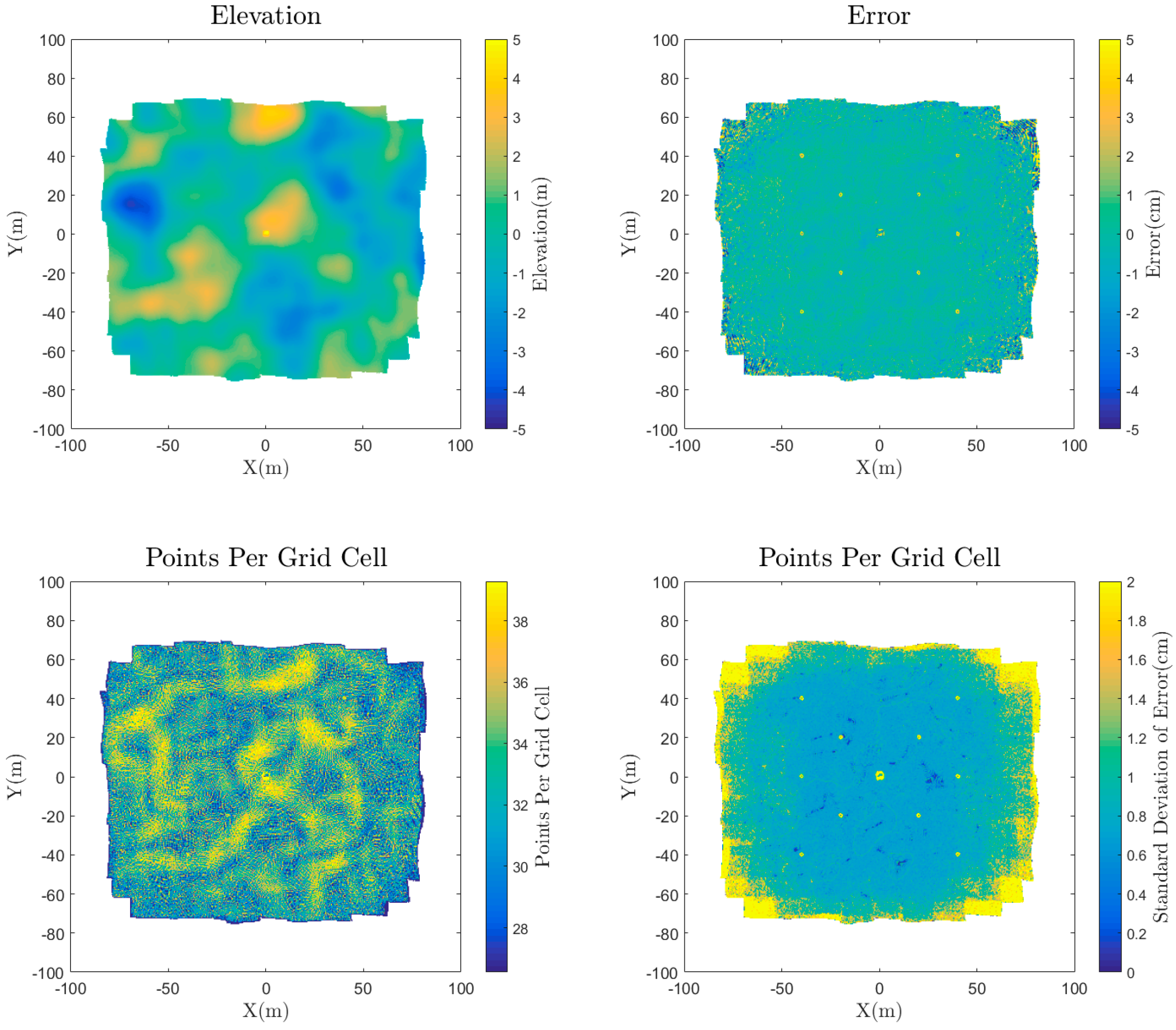
The error was first visualized spatially for each reconstruction by gridding the point cloud elevation and error using a binning gridding algorithm, where the value of each grid cell is calculated as a mean of all the points located horizontally within that grid cell. The number of points and standard deviation of points in each grid cell were also visualized. The results for the medium quality dense reconstruction are shown in
Figure 8. These plots are useful to begin to explore the spatial variability in both the density and the errors in the data. One initial observation for this dataset is that there is a larger standard deviation of error at the edges of the point cloud outside the extents of the AOI. This is due to the poor viewing geometry at the edges of the scene, and suggests that in practice these data points outside of the AOI should be either discarded or used cautiously.
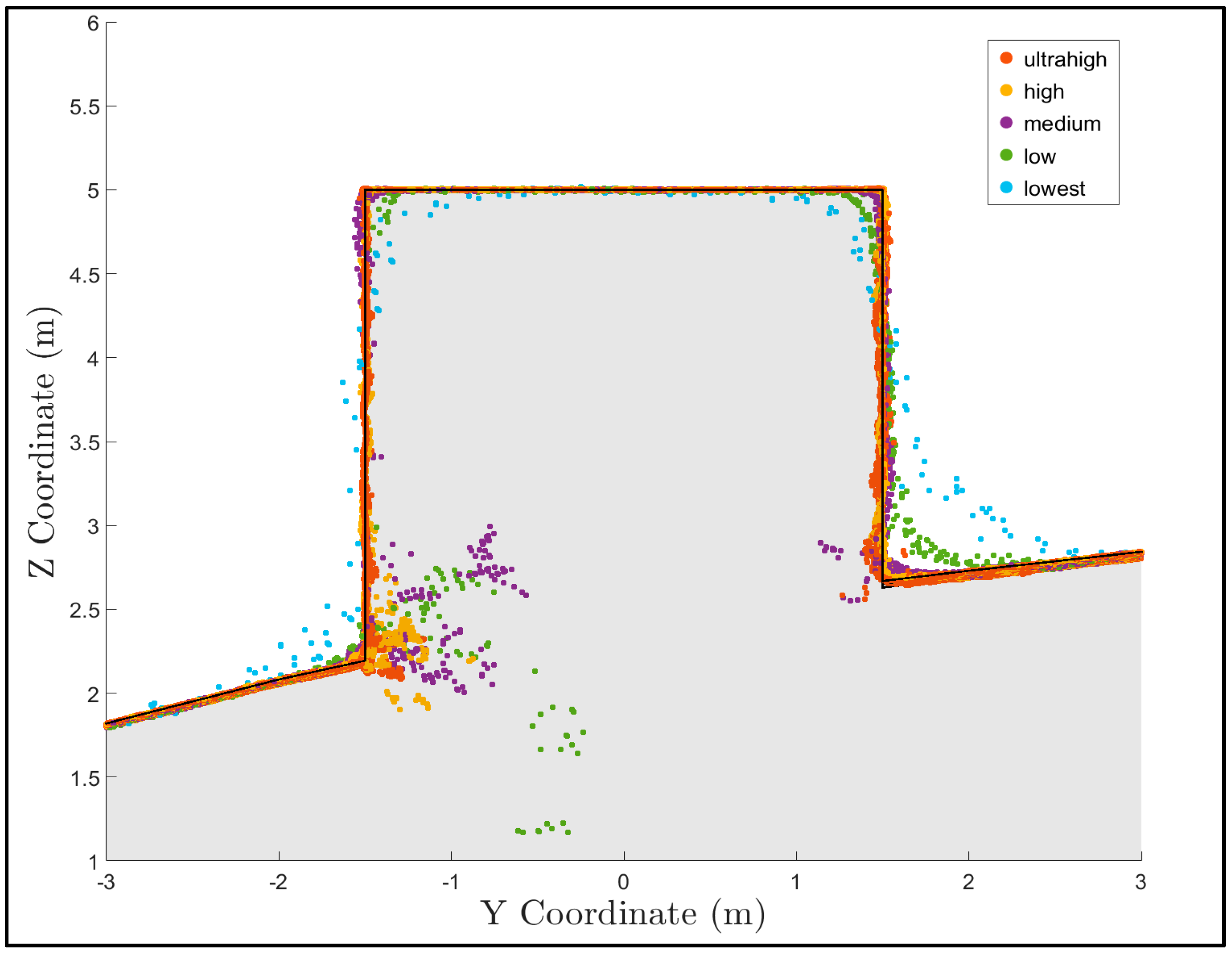
To qualitatively observe the effect of different quality dense reconstructions, a plot showing the true surface and the points from each construction in a 0.5-meter-wide section of the 27 m
3 box is shown in
Figure 9. Notice that the accuracy of each point cloud at the sharp corners of the box improves as the quality of the reconstruction increases, which is consistent with the Agisoft Photoscan Pro manual [
30]. This observation suggests that higher quality dense reconstruction settings will increase accuracy in regions with sharp corners.
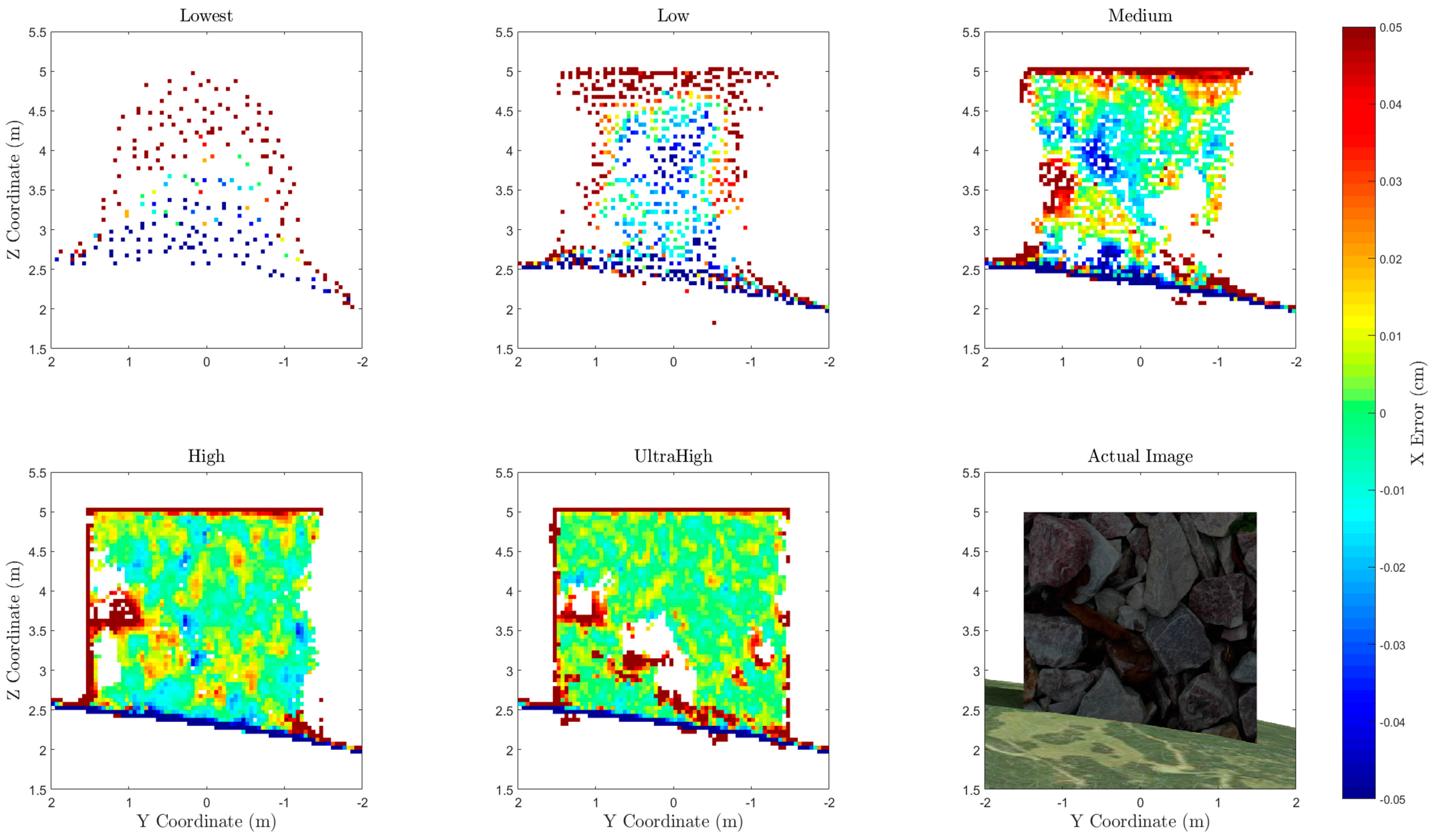
A visualization of the horizontal error of points along one side of the box is shown in
Figure 10. All points within 0.25 m horizontally of the face of the box were compared to the true x coordinate of the box face and gridded at 0.05-m resolution. This 1D error calculation along the x dimension shows how well the face of the box is captured in the point cloud. Note that errors along the edge of the box and along the ground surface should be ignored, as these grid bins on the edge represent areas where the average coordinate will not be equal to the coordinate of the side of the box, even in an ideal case. The regions that are white indicate an absence of data points. The size and location of these data gaps varies between each point cloud. For example, the high-quality setting point cloud contains points in the lower center of the cube, while the ultra-high does not. While the data gap in the ultra-high appears to be correlated to a region of low texture on the actual image, further research is required to definitively determine the cause.
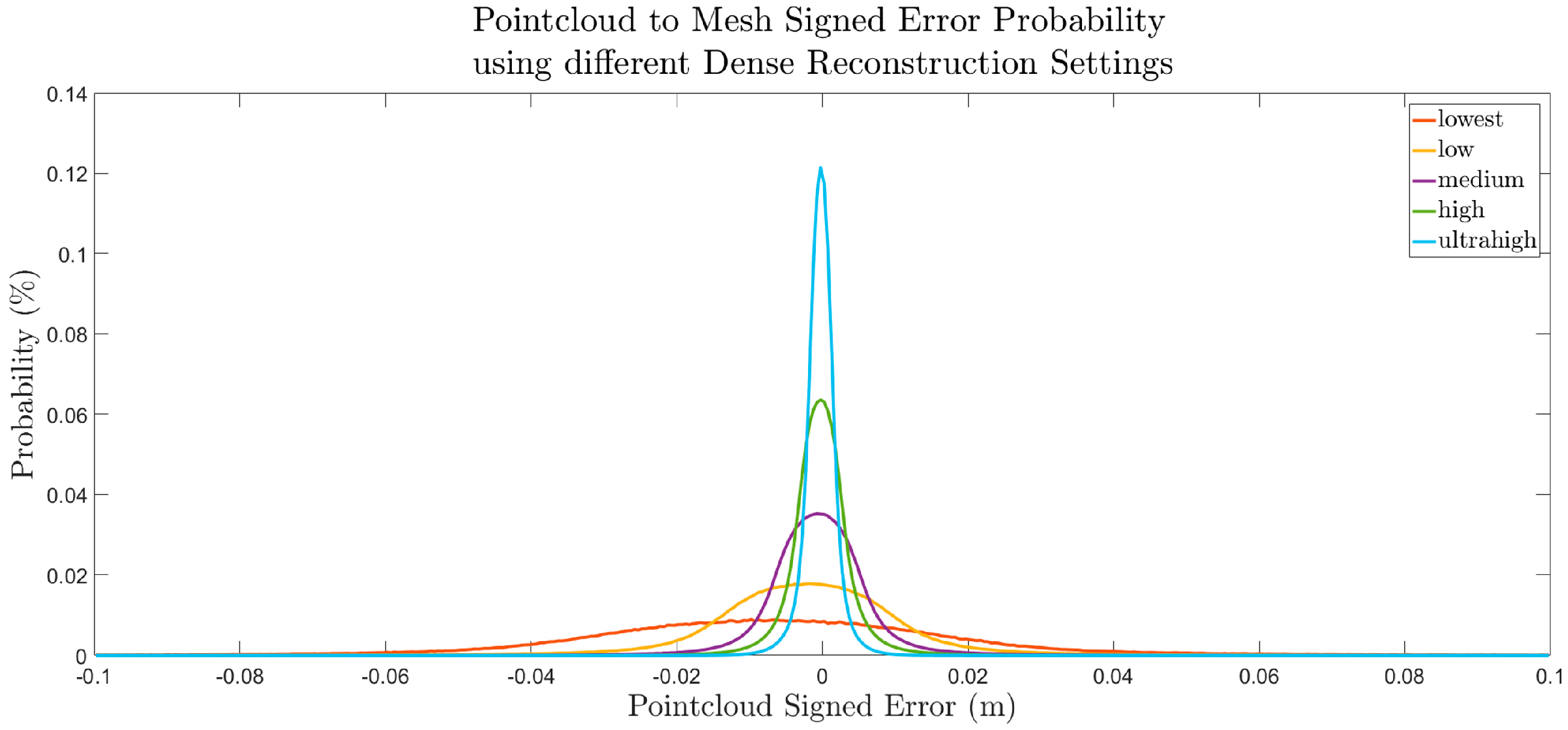
A more quantitative, statistical assessment was performed to assess the error throughout the entire scene by calculating a histogram for the distribution of error in each point cloud, as shown in
Figure 11. These distributions bolster the conclusion derived from the box profile plot, which is that higher quality dense reconstruction settings yield more accurate results than a lower quality reconstruction. While the accuracy of the GCPs, as provided in Agisoft Photoscan, averaged 0.38 mm (RMSE), the standard deviations of the points from the dense reconstruction ranged from 2.6 mm to 32.3 mm, as shown in
Table 6. This observation indicates that the GCP accuracy table is insufficient as a metric to depict the accuracy of the resultant dense point cloud. While these conclusions suggest general trends, further experimentation is required for error distributions to be generalized. The magnitude of the error was likely influenced by the varying sun angle, image noise, image blur, and image vignetting, which were introduced to model the simulated camera more realistically. These variables could be isolated individually in future experimentation.
4. Discussion
The use case demonstration provides just one example of the type of rigorous analysis that can be obtained by utilizing the simUAS image rendering workflow. It is important to note that the results of this experiment are closely coupled to the texture and topography of the scene. Future work will vary these independent variables to assess their effect on point cloud accuracy.
The first conclusion from this example experiment is that the error and standard deviation of error are larger for points outside of the area of interest, which in this experiment was −50 m to 50 m in both the
x and
y directions. This is shown in the spatial error plot in
Figure 8. The cause of this error is the poor viewing geometry for imaging these points, where they are only seen at a few camera stations and, even then, only at oblique angles. In practice, these points should be included in the final data product with caution, as it is shown here that the errors can be significantly greater than those within the AOI.
The second conclusion from this example experiment is that a “higher” quality dense point cloud reconstruction setting results in a more accurate point cloud, as shown qualitatively in
Figure 9 and
Figure 10, and quantitatively in
Figure 11. The quality settings in Photoscan determine the amount of downsampling of the imagery that should occur before performing the reconstruction algorithm. The downsampling of the imagery removes some of the finer texture details in the imagery, and therefore reduces the quality of the keypoint matching. The authors recommend using the “highest” quality dense reconstruction setting that the computer processing the dataset can handle. However, if there are noticeable data gaps in the point cloud, one should consider processing the point cloud on a lower dense reconstruction setting and merging the point clouds. For this experiment, a relatively small number of 20 Mp images (77) were used to create the dense point cloud, which took almost 12 hours for the highest point cloud setting. The resultant point cloud for this setting also contained 186 million points, which caused some point cloud data viewers and processing to fail, due to memory issues. For this reason, ultra-high may not be a viable solution for all experiments.
The third conclusion is that the RMSE of the GCP control network as shown in Agisoft Photoscan Pro is insufficient to characterize the accuracy of the resultant dense point cloud. In this extremely idealized experiment, where the GCP positions, pixel coordinates of GCPs, camera positions, and camera calibration were all input precisely, the GCP control network 3D RMSE reported by Agisoft Photoscan was 0.38 mm. The smallest standard deviation, which occurred using the “ultra-high” quality setting, was 2.6 mm and the largest standard deviation, using the “lowest” setting, was 32.3 mm, as shown in
Table 6. Further experimentation is needed to determine the relationship between the Photoscan reported GCP total RMSE and the computed RMSE of the dense point cloud. The image rendering workflow developed in this research is well suited to perform this experimentation, which is currently being considered as one of a number of planned follow-on studies.
Methodology Implications
This methodology generates photogrammetrically-accurate imagery rendered using a pinhole camera model of a scene with various textures and lighting, which is then processed to assess SfM point cloud accuracy. The rendered imagery can be processed to add noise, blur, nonlinear distortion, and other effects to generate imagery more representative of that from a real-world scenario prior to SfM processing. The accuracy of the camera trajectory, GCP position, camera calibration, and GCP pixel coordinates in each image can also be systematically adjusted to simulate uncertainty in a real-world scenario. The ability to adjust these parameters enables a user to perform a sensitivity analysis with numerous independent variables.
While this methodology enables the user to perform repeatable, accurate experiments without the need for time-consuming fieldwork, there are currently some limitations in the experiment methodology when utilizing the Blender Internal Render Engine. First, the internal render engine does not handle global illumination, and therefore light interactions between objects are not modeled. A second limitation of the lighting schema is that the radiometric accuracy has not been independently validated. There are a few methods within the render engine which effect the “color management” of the resultant imagery. For this experiment, these settings were left at the default settings, providing imagery that was not over- or underexposed. While the lighting in the scene using the Blender Internal Render Engine does not perfectly replicate physics-based lighting, the absolute color of each surface of an object is constant and perfectly Lambertian. The keypoint detection and SfM algorithms utilize gradients in colors and the absolute colors of the scene, and the accuracy of the methodology should not be effected by the imperfect lighting; however, it is recommended that this be rigorously investigated in future research.
Another source of inaccuracy in the Blender Internal Render Engine methodology is that the methodology to convert the scene to pixel values relies on an integration over a finite number of subpixel super-sampling ray calculations. This deviates from a real-world camera where the pixel value is a result of an integration over all available light. The Blender Internal Render Engine uses the term “antialiasing” to describe a super-sampling methodology for each pixel, which can super-sample up to 16 samples per pixel. This small, finite number of samples per pixel can induce a small amount of inaccuracy when mixed pixels are present. These inaccuracies, though, are small enough to be deemed negligible for most experiments which are expected to be undertaken using the workflow presented here.
However, another potential source of uncertainty induced into the system is the use of repeating textures to generate a scene. In the use case provided earlier, the grass texture was repeated 10 times in both the x and y directions. This repeating pattern was overlaid onto another image, to create different image color gradients in an attempt to generate unique texture features without requiring an extremely large image as the texture. Despite this effort, it is possible that keypoint detection and matching algorithms could generate false positives which may bias the result if not removed or detected as outliers. This phenomenon could also occur in a real-world scenario, where manmade structures often exhibit a repeating pattern of similar shapes and colors. In this experiment, this effect was not observed, but if the scene is not generated carefully, these repeating textures could induce a significant amount of inaccuracy in the SfM processing step.
5. Conclusions
This study has demonstrated a new workflow leveraging the Blender Internal Render Engine, an open-source computer graphics render engine, to generate simulated UAS imagery data sets for rendered scenes, suitable for input into SfM-MVS software. The output point clouds can be compared against ground truth (which is truly the “truth,” in this case, as GCPs, check points and other features have been synthetically placed in the scene with exact coordinates) to perform accuracy assessments. By purposefully and systematically varying different input parameters, including modeled camera parameters (e.g., focal length and resolution), modeled acquisition parameters (e.g., flying height and exposure rate), environmental parameters (e.g., solar illumination angle), and processing parameters (e.g., reconstruction settings), sensitivity analyses can be performed by assessing the change in accuracy as a function of change in each of these parameters. In this way, hundreds of experiments on UAS imagery processed in SfM-MVS software can be performed in the office, without the need for extensive, costly field surveys. An additional advantage of the simUAS image rendering approach is that it avoids confounding variables (e.g., variable wind and solar illumination, as well as moving objects in the scene), which can complicate accuracy assessments performed with real-world imagery.
In this paper, one example of a use case was presented, in which we examined the effects of the Agisoft Photoscan reconstruction quality setting (lowest, low, medium, high, and highest) on resultant point cloud accuracy using a simulated UAS imagery data set with a camera model emulating a Sony A5000. It was shown that the RMSE of the resultant point clouds does, in fact, depend strongly on the reconstruction quality setting. An additional finding was that the data points outside of the AOI should be either discarded or used with caution, as the accuracy of those points is higher than that of the point cloud within the AOI. While these results are informative (if, perhaps, not entirely unexpected), it is important to note that this is just one of a virtually limitless number of experiments that can be run using the workflow presented here. The project team is currently planning to use the simUAS workflow to examine point cloud accuracy achievable with new sensor types, and also to conduct accuracy assessments of shallow bathymetric points in SfM-MVS point clouds generated from UAS imagery.
Additional topics for future work include investigating the radiometric fidelity of the simulated imagery, and further assessing the impacts of texture and topography in the simulated scenes. More advanced post-processing effects will be explored, including local random variability from the Brown distortion model and lens aberration (spherical and chromatic). Alternative render engines will also be investigated for feasibility, using the validation methodology described here. As SfM-MVS algorithms are continually being improved, it is also of interest to use this methodology to test new SfM-MVS software packages, both commercial and open source. Another extension of the current work would include using the procedure presented here to simulate imagery acquired not only from UAS, but also vehicles, boats, or handheld cameras. It is anticipated that these procedures will prove increasingly beneficial with the continued expansion of SfM-MVS algorithms into new fields.