Turbidity in Apalachicola Bay, Florida from Landsat 5 TM and Field Data: Seasonal Patterns and Response to Extreme Events
Abstract
:1. Introduction
2. Materials and Methods
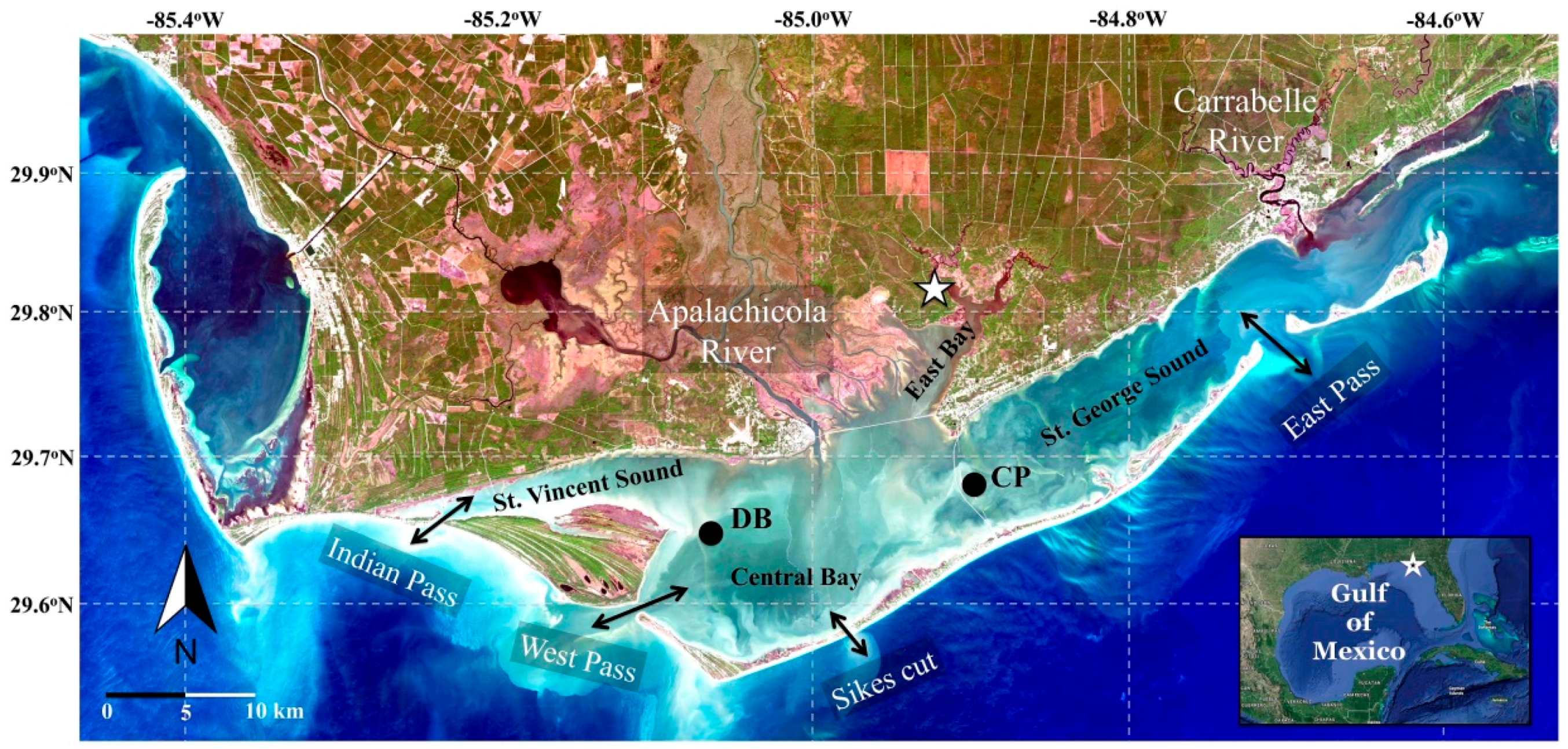
2.1. Study Area
2.2. Data Sources
2.3. Methods
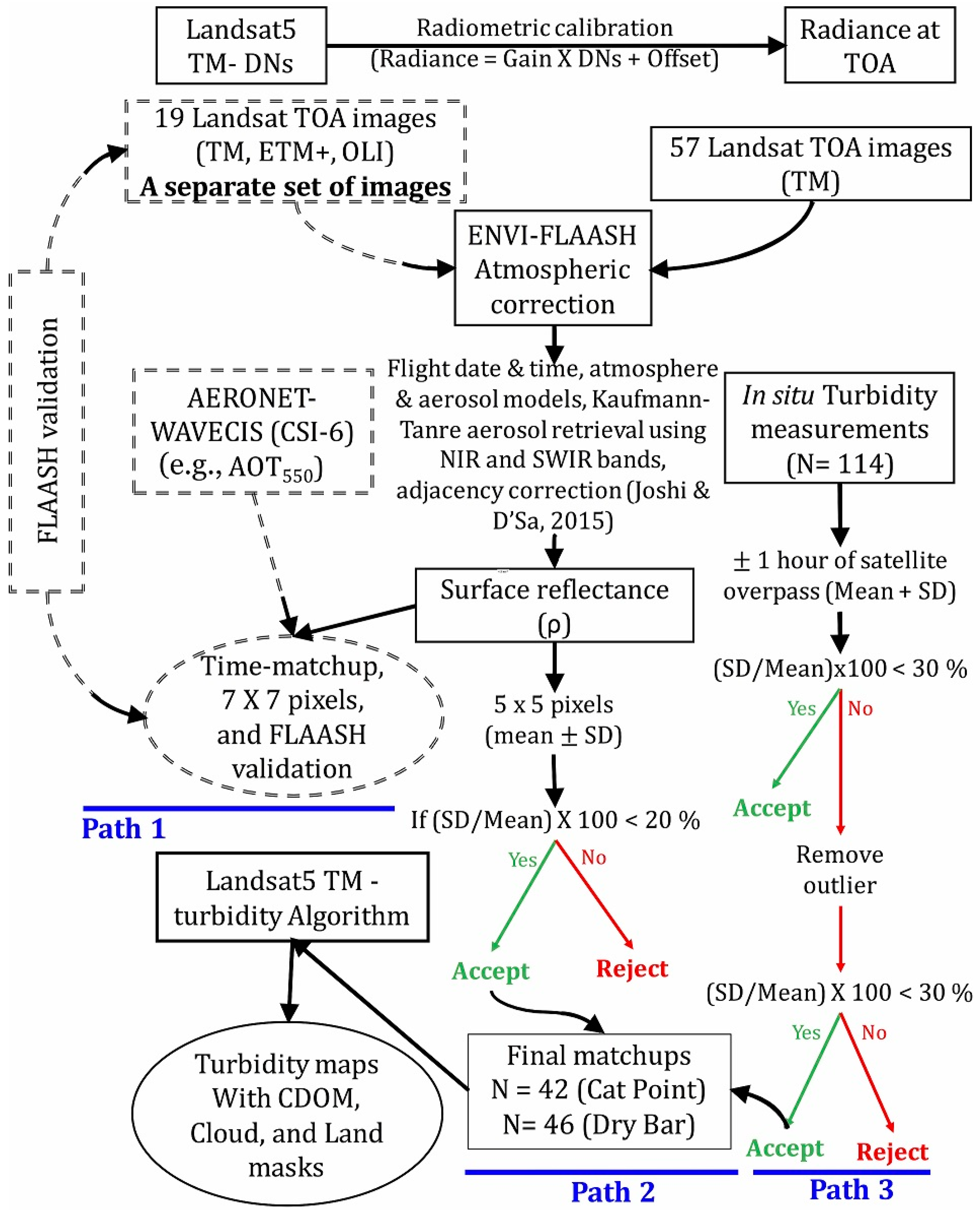
2.3.1. Overview
2.3.2. Landsat Image Processing
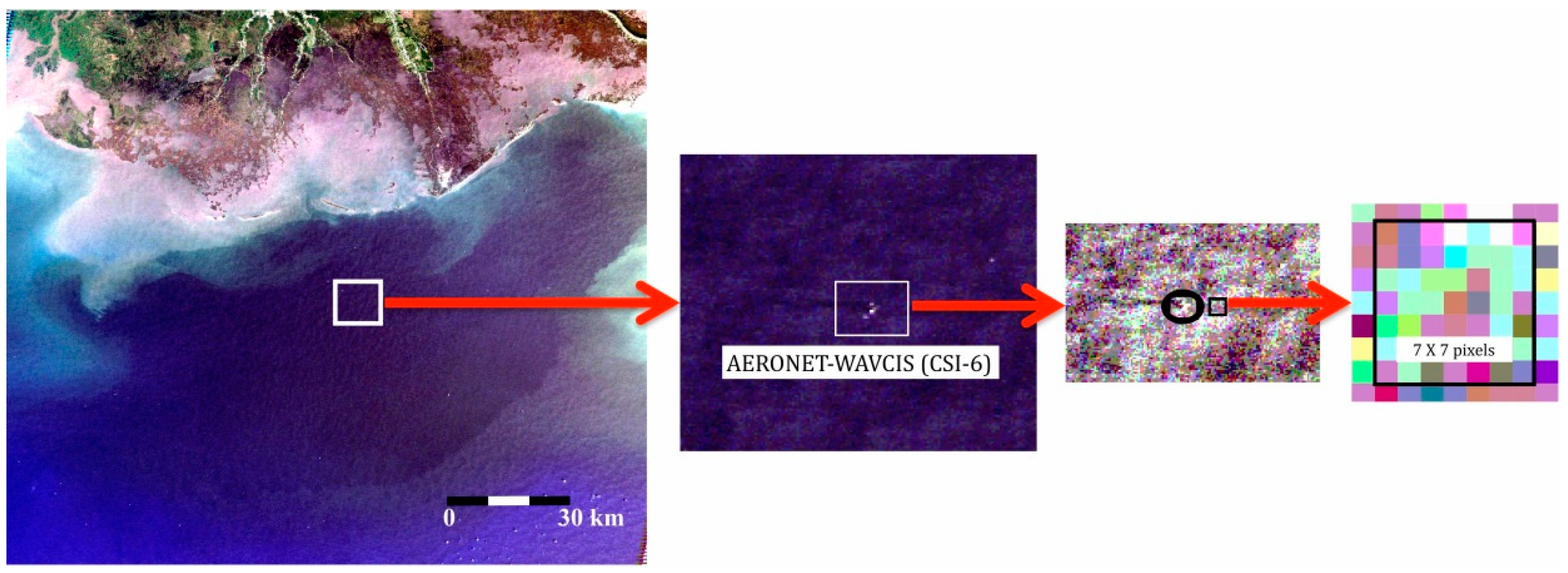
2.3.3. FLAASH vs. AERONET
2.3.4. Statistical Analysis
3. Results and Discussion
3.1. Satellite Assessment of Water Turbidity in Apalachicola Bay
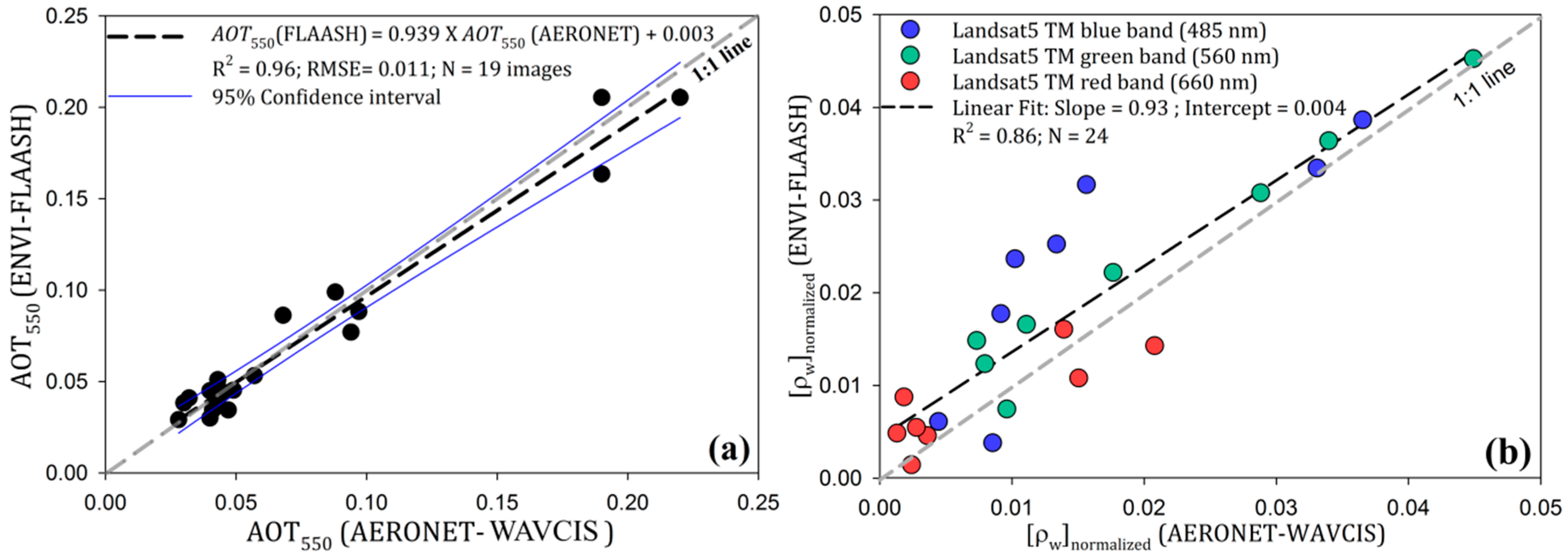
3.1.1. Assessing the Performance of ENVI-FLAASH Based Atmospheric Correction
3.1.2. Band Selection
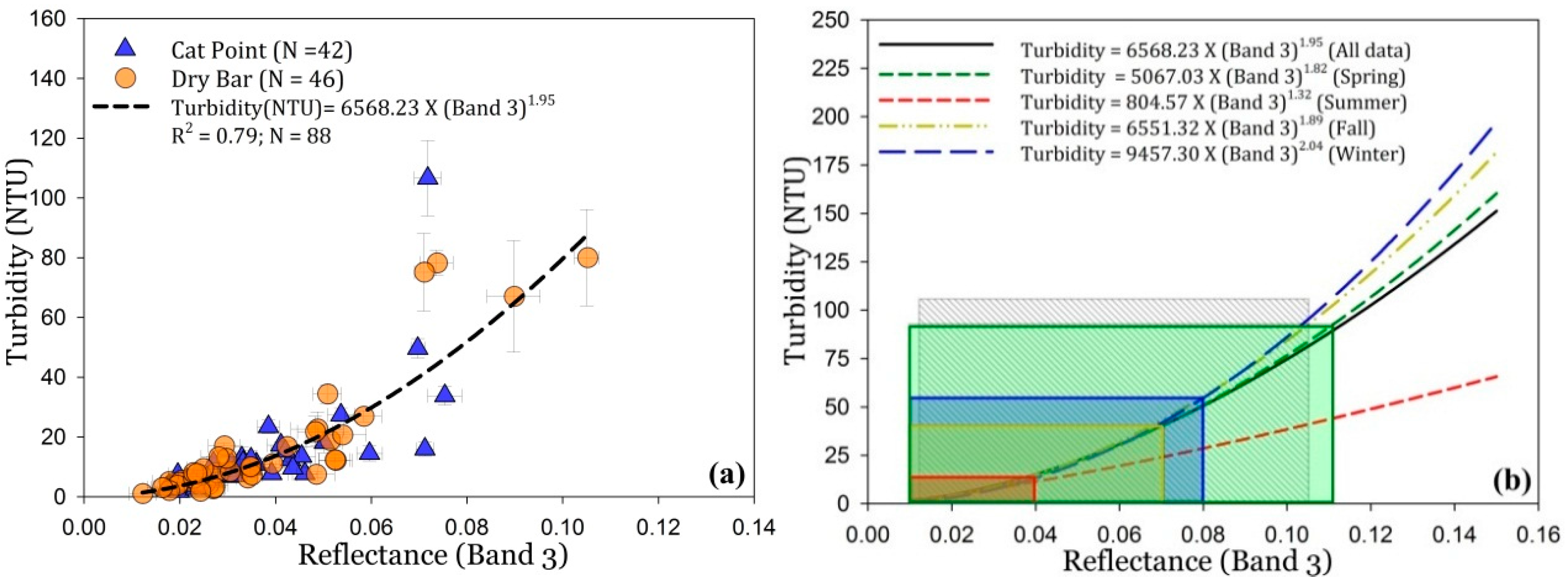
3.1.3. Landsat 5 TM-Turbidity Algorithm and Validation
3.1.4. An Optimization of the General Turbidity Algorithm Based on Seasonal Thresholds
3.2. Temporal Variations in Physical Forcings in Apalachicola Bay
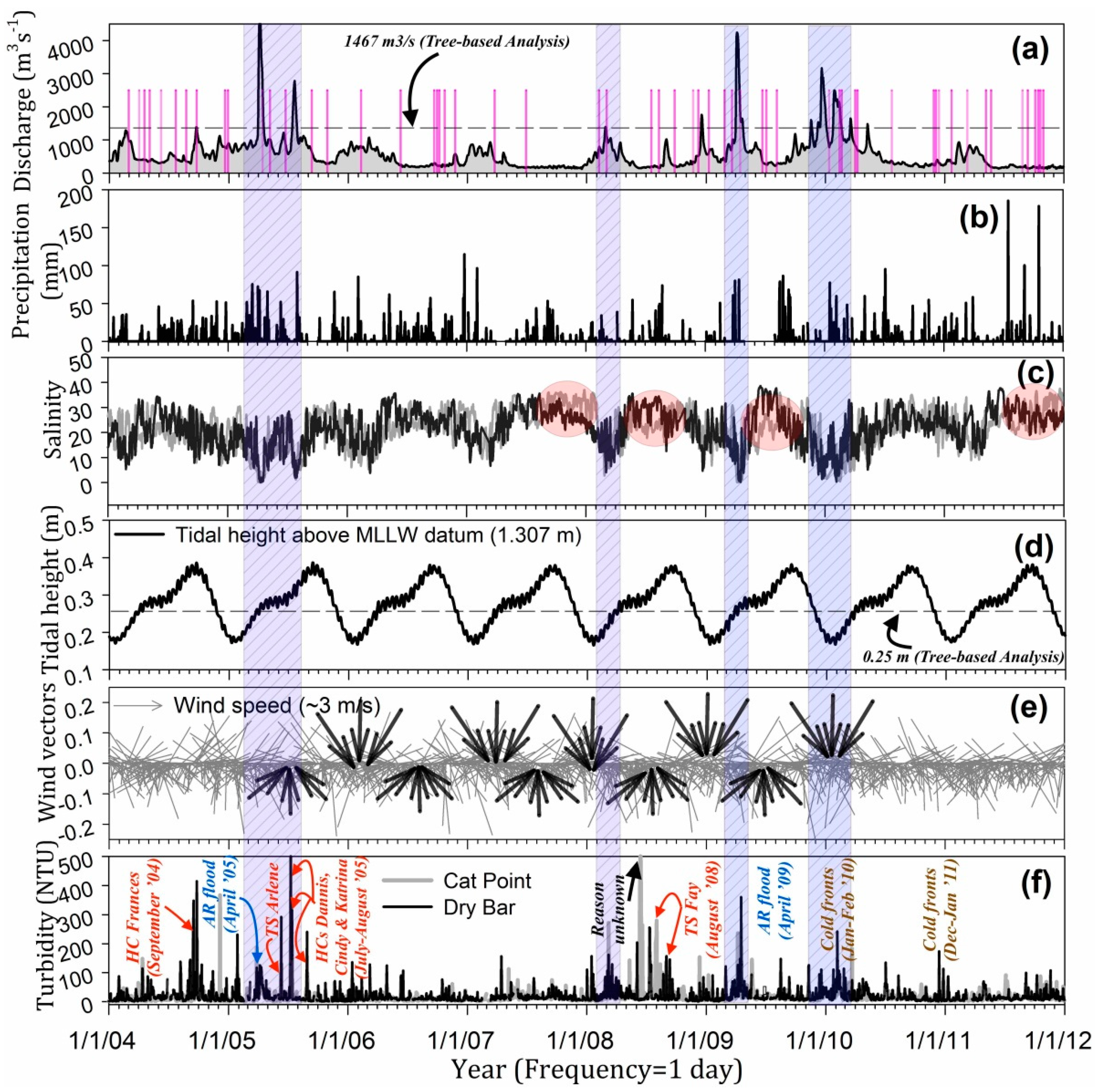
3.2.1. Time-Series Analysis
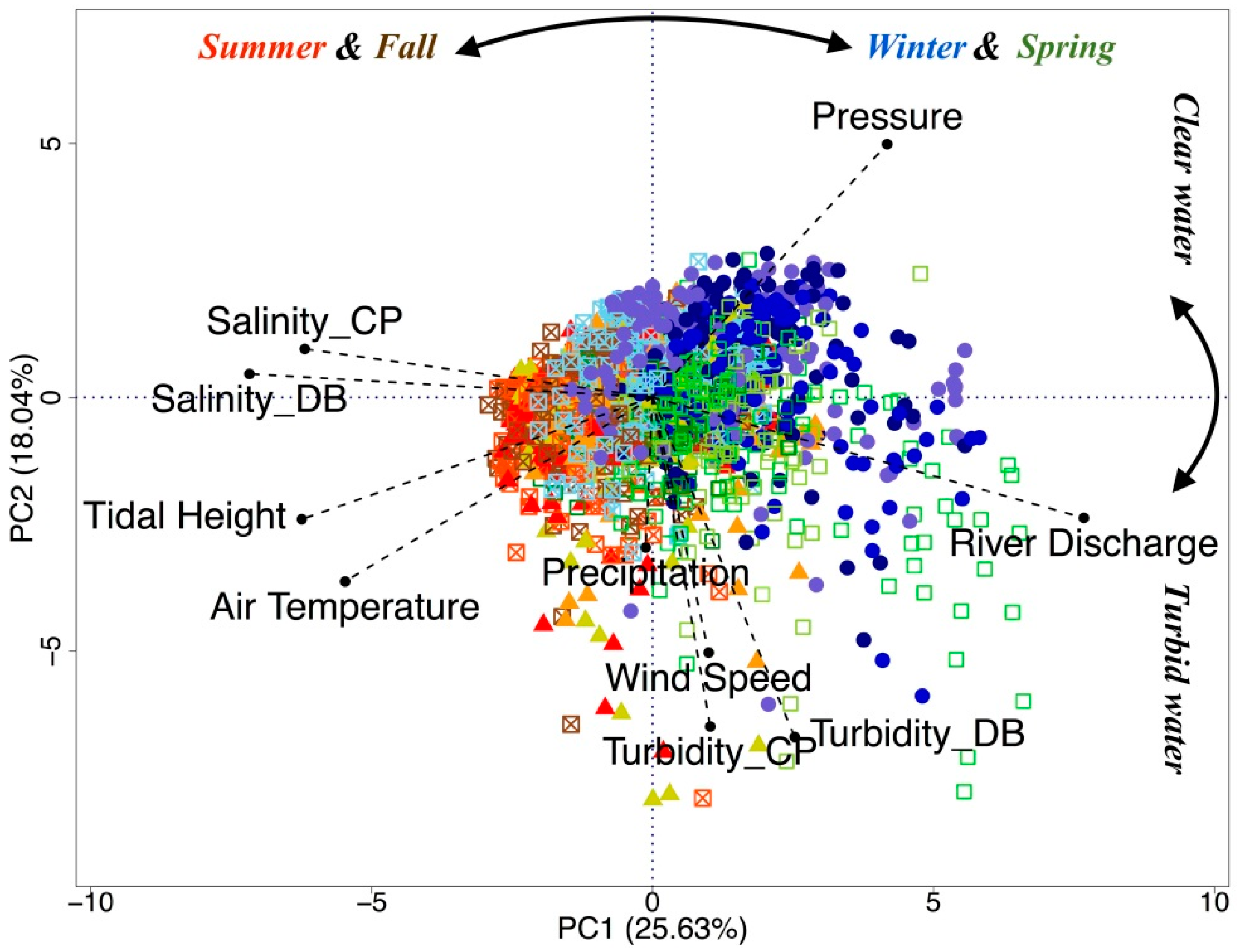
3.2.2. Principal Component Analysis
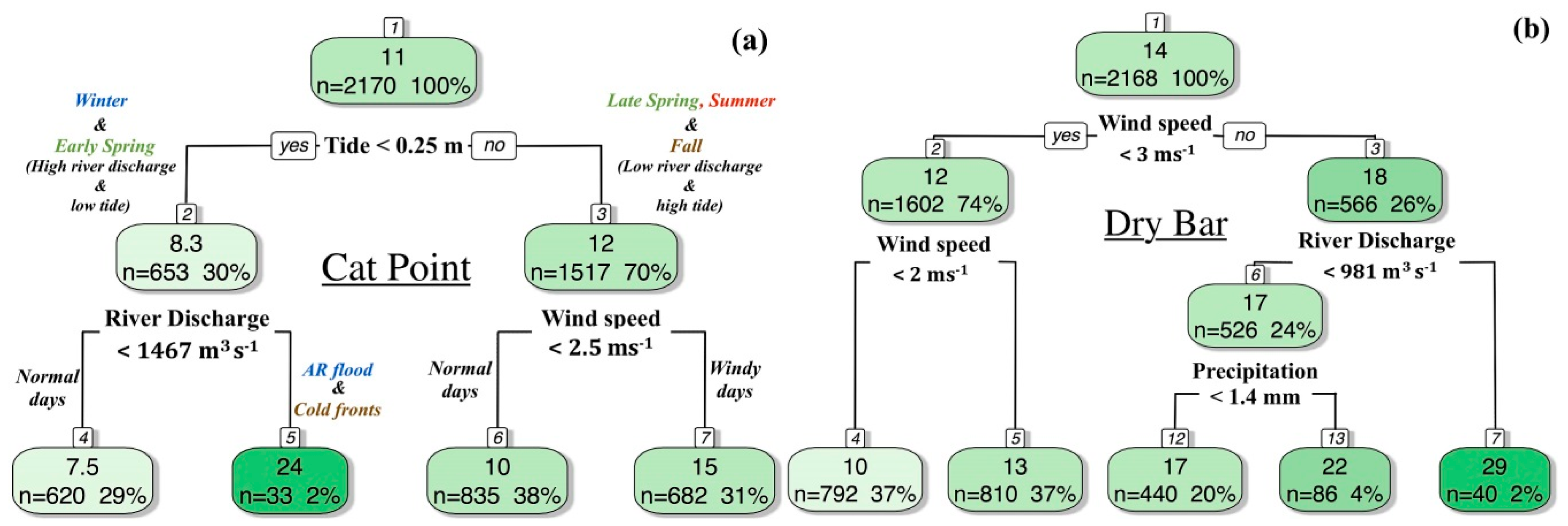
3.2.3. Tree-Based Classification Models
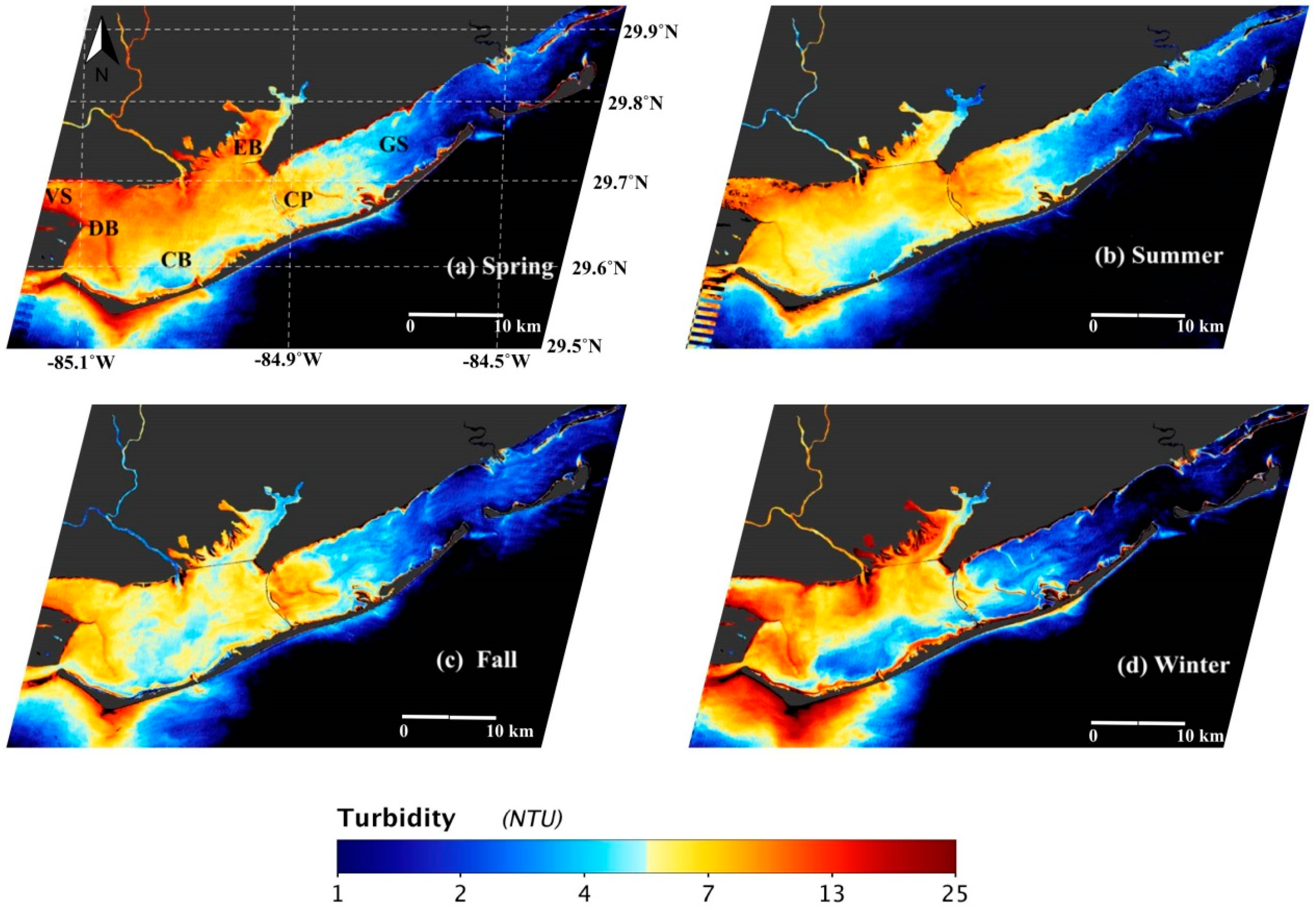
3.2.4. Seasonal Turbidity Patterns in Apalachicola Bay
3.3. Turbidity Maps during Extreme Events in Apalachicola Bay
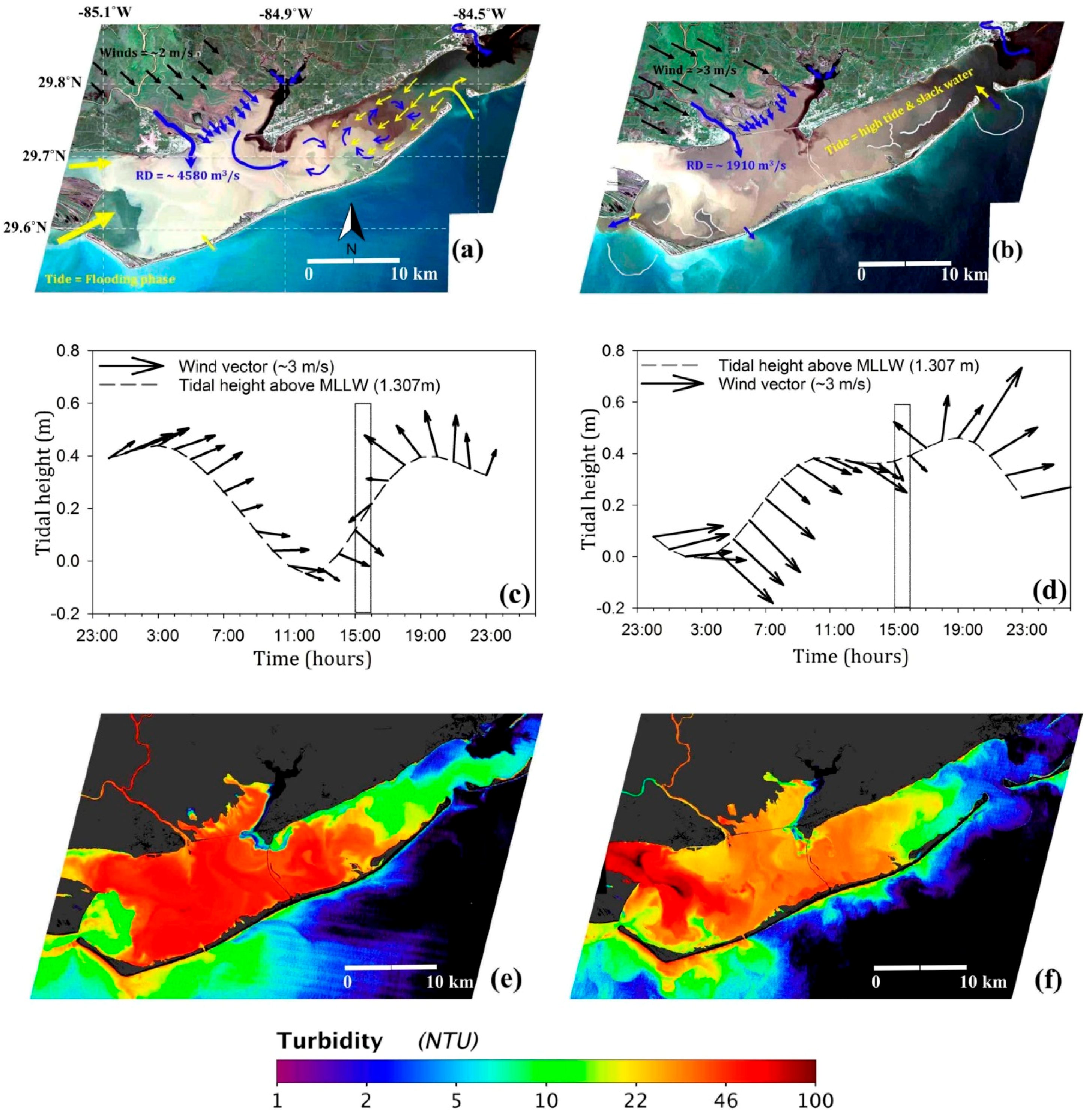
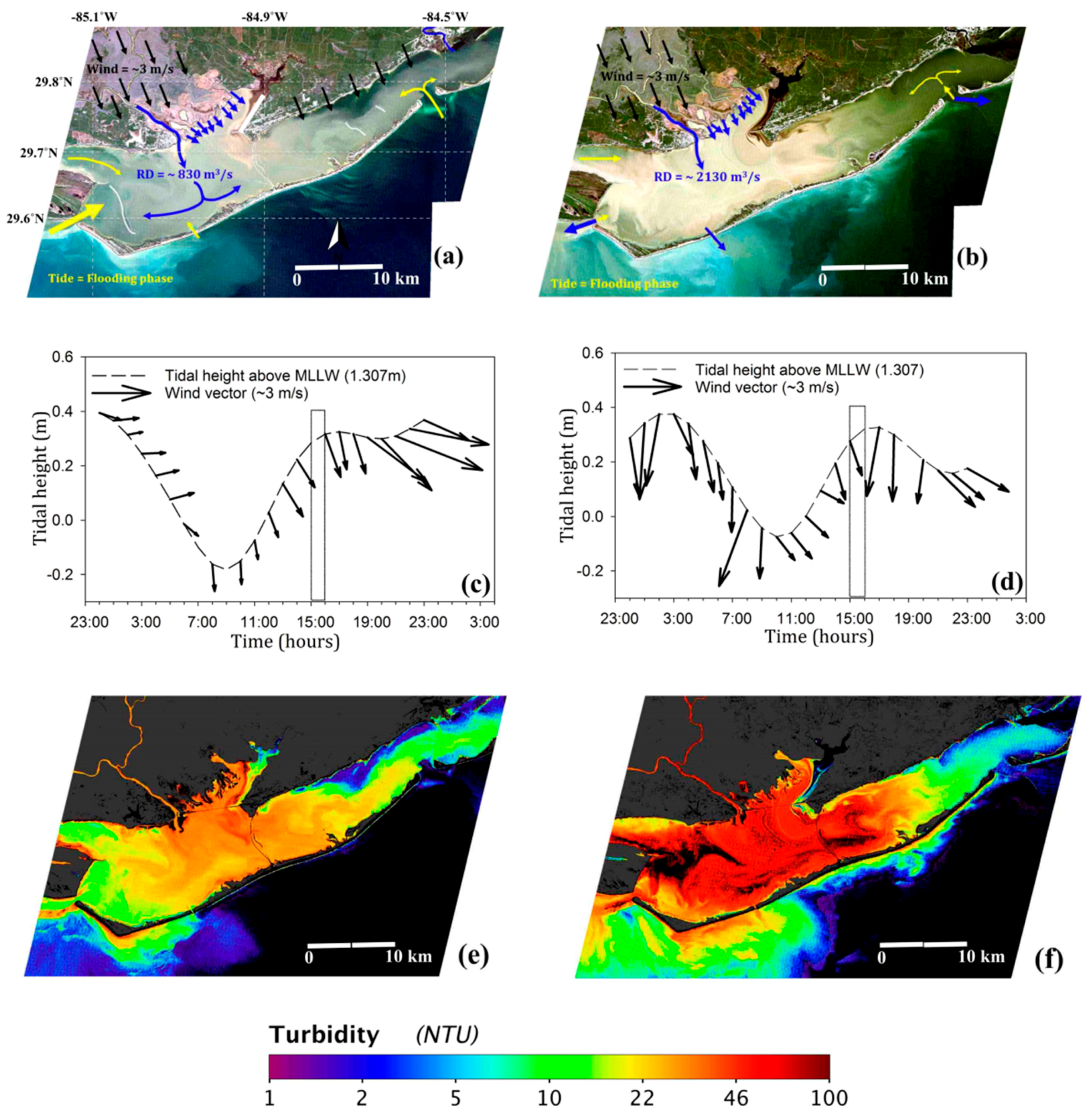
3.3.1. Apalachicola River Flood Conditions (4 April 2005 and 15 April 2009)
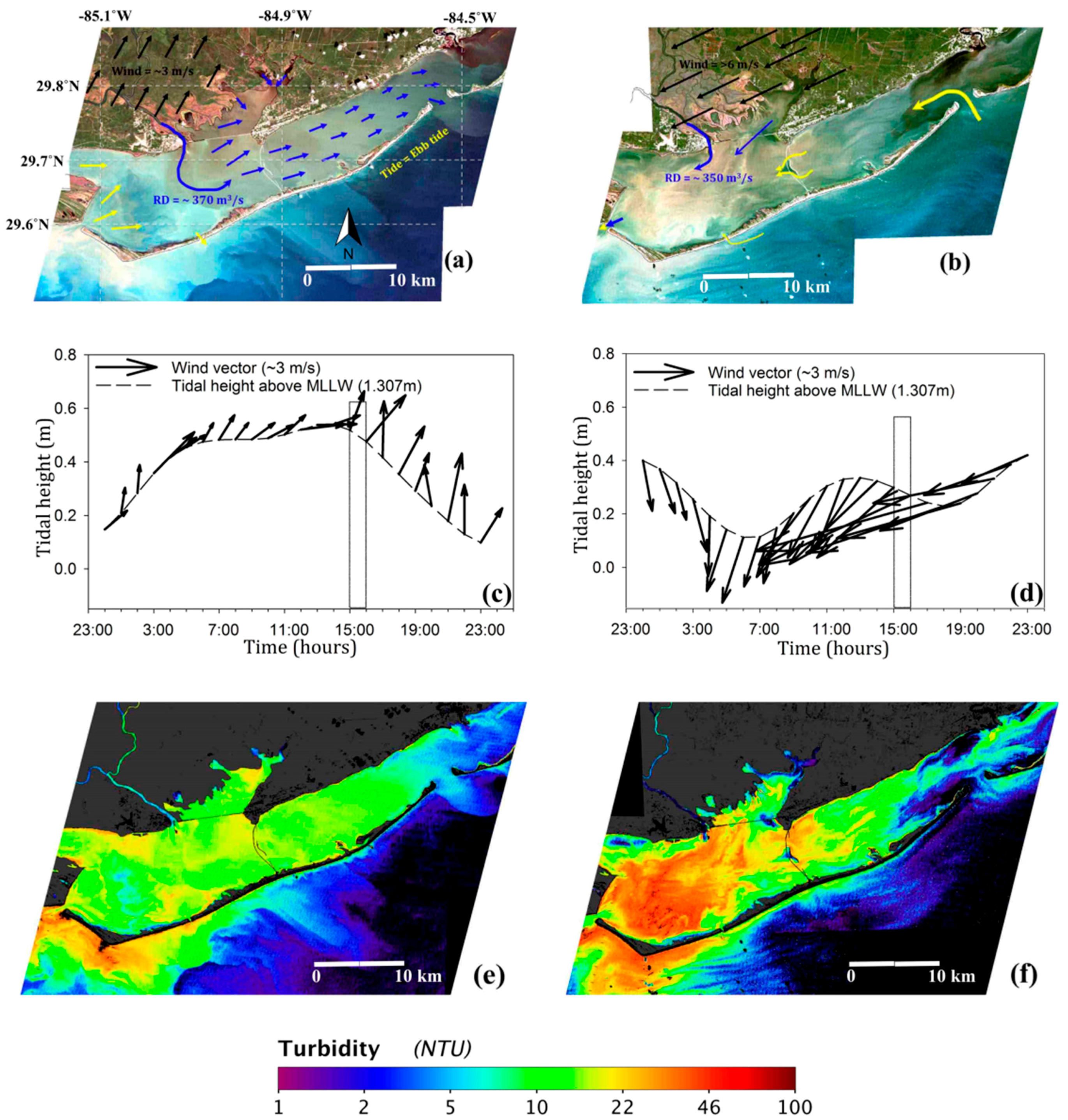
3.3.2. Passages of Strong Cold Fronts over Apalachicola Bay (12 January 2010 and 13 February 2010)
3.3.3. Low Flow Conditions in Apalachicola Bay
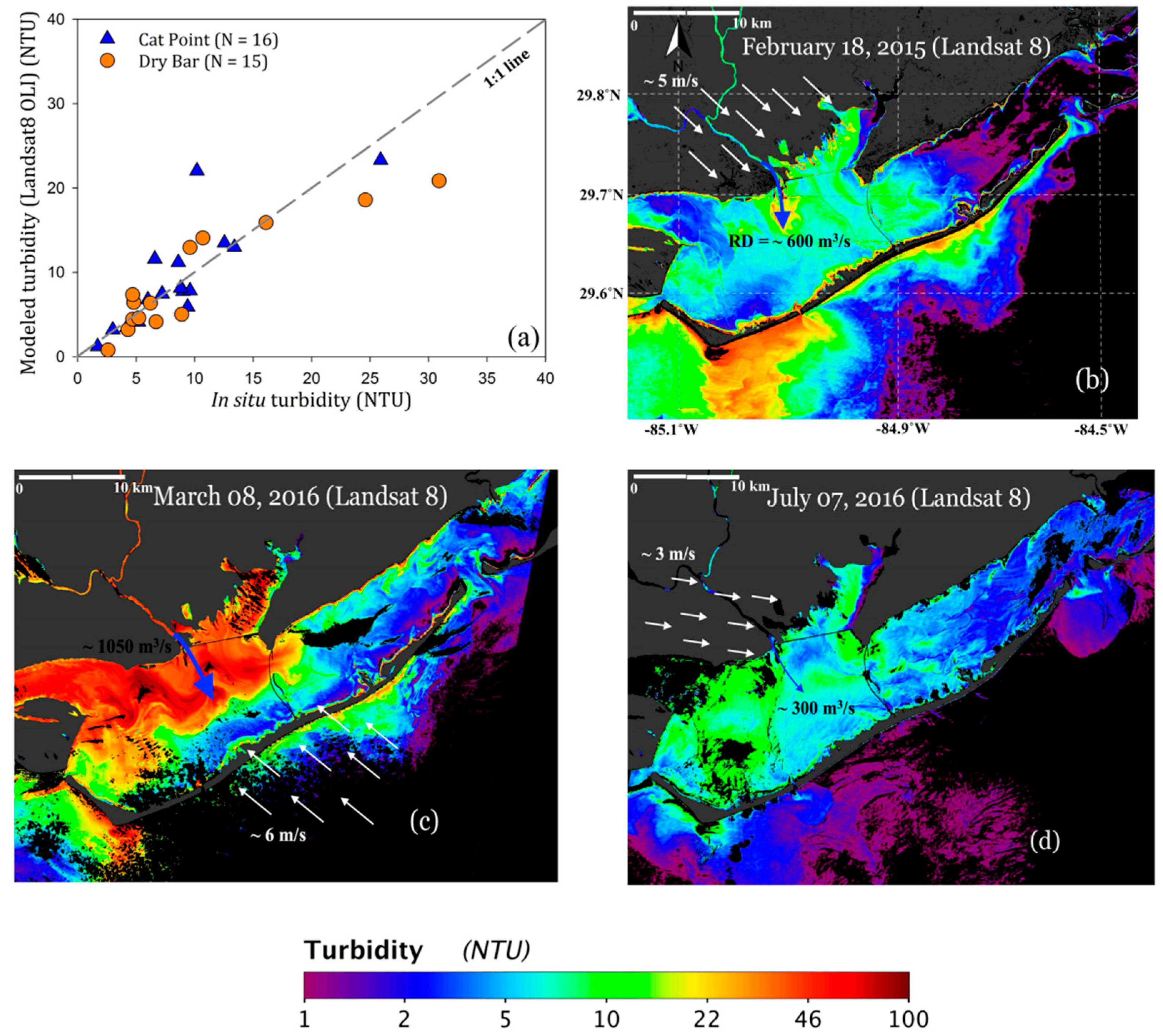
4. Assessing Potential Applicability of Turbidity Algorithm to Landsat 8 OLI
5. Conclusions
Supplementary Materials
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Cloern, J.E.; Foster, S.; Kleckner, A. Phytoplankton primary production in the world’s estuarine-coastal ecosystems. Biogeosciences 2014, 11, 2477–2501. [Google Scholar]
- Chelsea Nagy, R.; Graeme Lockaby, B.; Kalin, L.; Anderson, C. Effects of urbanization on stream hydrology and water quality: The Florida Gulf Coast. Hydrol. Process. 2012, 26, 2019–2030. [Google Scholar]
- Giosan, L.; Syvitski, J.; Constantinescu, S.; Day, J. Climate change: Protect the world’s deltas. Nature 2014, 516, 31–33. [Google Scholar] [CrossRef] [PubMed]
- Fabricius, K.E. Effects of terrestrial runoff on the ecology of corals and coral reefs: Review and synthesis. Mar. Pollut. Bull. 2005, 50, 125–146. [Google Scholar] [PubMed]
- Kenworthy, W.J.; Fonseca, M.S. Light requirements of seagrasses Halodule wrightii and Syringodium filiforme derived from the relationship between diffuse light attenuation and maximum depth distribution. Estuaries 1996, 19, 740–750. [Google Scholar]
- Pedersen, T.M.; Gallegos, C.L.; Nielsen, S.L. Influence of near-bottom re-suspended sediment on benthic light availability. Estuar. Coast. Shelf Sci. 2012, 106, 93–101. [Google Scholar] [CrossRef]
- Thrush, S.F.; Hewitt, J.E.; Cummings, V.J.; Ellis, J.I.; Hatton, C.; Lohrer, A.; Norkko, A. Muddy Waters: Elevating Sediment Input to Coastal and Estuarine Habitats. Front. Ecol. Environ. 2004, 2, 299–306. [Google Scholar]
- Ryan, P.A. Environmental effects of sediment on New Zealand streams: A review. N. Z. J. Mar. Freshw. Res. 1991, 25, 207–221. [Google Scholar]
- Wang, H.; Huang, W.; Harwell, M.A.; Edmiston, L.; Johnson, E.; Hsieh, P.; Milla, K.; Christensen, J.; Stewart, J.; Liu, X. Modeling oyster growth rate by coupling oyster population and hydrodynamic models for Apalachicola Bay, Florida, USA. Ecol. Model. 2008, 211, 77–89. [Google Scholar]
- Robertson, M.J.; Scruton, D.A.; Clarke, K.D. Seasonal effects of suspended sediment on the behavior of juvenile Atlantic salmon. Trans. Am. Fish. Soc. 2007, 136, 822–828. [Google Scholar]
- Pollock, F.J.; Lamb, J.B.; Field, S.N.; Heron, S.F.; Schaffelke, B.; Shedrawi, G.; Bourne, D.G.; Willis, B.L. Sediment and turbidity associated with offshore dredging increase coral disease prevalence on nearby reefs. PLoS ONE 2014, 9, e102498. [Google Scholar] [CrossRef] [PubMed]
- Rügner, H.; Schwientek, M.; Beckingham, B.; Kuch, B.; Grathwohl, P. Turbidity as a proxy for total suspended solids (TSS) and particle facilitated pollutant transport in catchments. Environ. Earth Sci. 2013, 69, 373–380. [Google Scholar] [CrossRef]
- Stubblefield, A.P.; Reuter, J.E.; Goldman, C.R. Sediment budget for subalpine watersheds, Lake Tahoe, California, USA. Catena 2009, 76, 163–172. [Google Scholar] [CrossRef]
- Chen, S.; Huang, W.; Wang, H.; Li, D. Remote sensing assessment of sediment re-suspension during Hurricane Frances in Apalachicola Bay, USA. Remote Sens. Environ. 2009, 113, 2670–2681. [Google Scholar] [CrossRef]
- D’Sa, E.J.; Ko, D.S. Short-term Influences on Suspended Particulate Matter Distribution in the Northern Gulf of Mexico: Satellite and Model Observations. Sensors 2008, 8, 4249–4264. [Google Scholar] [CrossRef] [PubMed]
- Kemker, C. Turbidity, Total Suspended Solids and Water Clarity. In Fundamentals of Environmental Measurements; Fondriest Environmental, Inc.: Fairborn, OH, USA, 2014; Available online: http://www.fondriest.com/environmental-measurements/parameters/water-quality/turbidity-total-suspended-solids-water-clarity/ (accessed on 30 August 2016).
- Mobley, C.; Boss, E.; Roesler, C. Ocean Optics Web Book. 2010. Available online: http://www.oceanopticsbook.info (accessed on15 March 2016).
- Dogliotti, A.; Ruddick, K.; Nechad, B.; Doxaran, D.; Knaeps, E. A single algorithm to retrieve turbidity from remotely-sensed data in all coastal and estuarine waters. Remote Sens. Environ. 2015, 156, 157–168. [Google Scholar] [CrossRef]
- Chen, Z.; Hu, C.; Muller-Karger, F. Monitoring turbidity in Tampa Bay using MODIS/Aqua 250-m imagery. Remote Sens. Environ. 2007, 109, 207–220. [Google Scholar] [CrossRef]
- Choi, J.K.; Park, Y.J.; Ahn, J.H.; Lim, H.S.; Eom, J.; Ryu, J.H. GOCI, the world’s first geostationary ocean color observation satellite, for the monitoring of temporal variability in coastal water turbidity. J. Geophys. Res. Oceans 2012, 117. [Google Scholar] [CrossRef]
- Miller, R.L.; McKee, B.A. Using MODIS Terra 250 m imagery to map concentrations of total suspended matter in coastal waters. Remote Sens. Environ. 2004, 93, 259–266. [Google Scholar] [CrossRef]
- Minella, J.P.; Merten, G.H.; Reichert, J.M.; Clarke, R.T. Estimating suspended sediment concentrations from turbidity measurements and the calibration problem. Hydrol. Process. 2008, 22, 1819–1830. [Google Scholar] [CrossRef]
- Onderka, M.; Pekárová, P. Retrieval of suspended particulate matter concentrations in the Danube River from Landsat ETM data. Sci. Total Environ. 2008, 397, 238–243. [Google Scholar] [CrossRef] [PubMed]
- Zhang, M.; Tang, J.; Dong, Q.; Song, Q.; Ding, J. Retrieval of total suspended matter concentration in the Yellow and East China Seas from MODIS imagery. Remote Sens. Environ. 2010, 114, 392–403. [Google Scholar] [CrossRef]
- Gippel, C.J. Potential of turbidity monitoring for measuring the transport of suspended solids in streams. Hydrol. Process. 1995, 9, 83–97. [Google Scholar] [CrossRef]
- D’Sa, E.J.; Miller, R.L.; McKee, B.A. Suspended particulate matter dynamics in coastal waters from ocean color: Application to the Northern Gulf of Mexico. Geophys. Res. Lett. 2007, 34, L23611. [Google Scholar] [CrossRef]
- Palmer, S.C.J.; Kutser, T.; Hunter, P.D. Remote sensing of inland waters: Challenges, progress and future directions. Remote Sens. Environ. 2015, 157, 1–8. [Google Scholar] [CrossRef]
- D’Sa, E.J.; Roberts, H.H.; Allahdadi, M.N. Suspended particulate matter dynamics along the Louisiana-Texas coast from satellite observation. In Proceedings of the Coastal Sediments 2011, Miami, FL, USA, 2–6 May 2011; Rosati, J.D., Wang, P., Roberts, T.M., Eds.; pp. 2390–2402. [Google Scholar]
- Edmiston, H. A River Meets the Bay—A Characterization of the Apalachicola River and Bay System. Apalachicola National Estuarine Research Reserve; Florida Department of Environmental Protection: Tallahassee, FL, USA, 2008; pp. 1–200. [Google Scholar]
- Leitman, H.M.; Sohm, J.E.; Franklin, M.A. Wetland Hydrology and Tree Distribution of the Apalachicola River Flood Plain, Florida; US Geological Survey: Reston, VA, USA, 1984.
- Whitfield, W.; Beaumariage, D.S. Shellfish management in Apalachicola Bay: Past, Present, Future. In Proceedings of the Conference on the Apalachicola Drainage System, Gainesville, FL, USA, 23–24 April 1977; Florida Department of Natural Resources Marine Research Laboratory: Gainesville, FL, USA, 1977; pp. 130–140. [Google Scholar]
- Havens, K.; Allen, M.; Camp, E.; Irani, T.; Lindsey, A.; Morris, J.; Kane, A.; Kimbro, D.; Otwell, S.; Pine, B. Apalachicola Bay Oyster Situation Report; Florida Sea Grant College Program, Technical Publication TP-200; Florida Sea Grant: Gainesville, FL, USA, 2013; Available online: https://www.flseagrant.org/news/2013/04/apalachicola-oyster-report/ (accessed on 20 May 2016).
- Edmiston, H.L.; Fahrny, S.A.; Lamb, M.S.; Levi, L.K.; Wanat, J.M.; Avant, J.S.; Wren, K.; Selly, N.C. Tropical Storm and Hurricane Impacts on a Gulf Coast Estuary: Apalachicola Bay, Florida. J. Coast. Res. 2008, 38–49. [Google Scholar] [CrossRef]
- Grattan, L.M.; Roberts, S.; Mahan, W.T., Jr.; McLaughlin, P.K.; Otwell, W.S.; Morris, J.G., Jr. The Early Psychological Impacts of the Deepwater Horizon Oil Spill on Florida and Alabama Communities. Environ. Health Perspect. 2011, 119, 838–843. [Google Scholar] [CrossRef] [PubMed]
- Petes, L.E.; Brown, A.J.; Knight, C.R. Impacts of upstream drought and water withdrawals on the health and survival of downstream estuarine oyster populations. Ecol. Evol. 2012, 2, 1712–1724. [Google Scholar] [CrossRef] [PubMed]
- Livingston, R.J. Climate Change and Coastal Ecosystems: Long-Term Effects of Climate and Nutrient Loading on Trophic Organization; CRC Press: Boca Raton, FL, USA, 2014. [Google Scholar]
- Surratt, D.; Cherrier, J.; Robinson, L.; Cable, J. Chronology of sediment nutrient geochemistry in Apalachicola Bay, Florida (U.S.A). J. Coast. Res. 2008, 24, 660–671. [Google Scholar] [CrossRef]
- Koch, M.; Sun, H. Tidal and Non-Tidal Characteristics of water Levels and Flow in the Apalachicola Bay, Florida. WIT Trans. Built Environ. 1970, 43, 357–366. [Google Scholar] [CrossRef]
- Huang, W.; Sun, H.; Nnaji, S.; Jones, W. Tidal Hydrodynamics in a Multiple-Inlet Estuary: Apalachicola Bay, Florida. J. Coast. Res. 2002, 674–684. [Google Scholar]
- Huang, W.; Chen, S.; Yang, X. Remote sensing for water quality monitoring in Apalachicola Bay, USA. In Advances in Earth Observation of Global Change; Chuvieco, E., Li, J., Yang, X., Eds.; Springer: Dordrecht, The Netherlands, 2010; pp. 69–78. [Google Scholar]
- Liu, X.; Huang, W. Modeling sediment resuspension and transport induced by storm wind in Apalachicola Bay, USA. Environ. Model. Softw. 2009, 24, 1302–1313. [Google Scholar] [CrossRef]
- Hu, C.; Chen, Z.; Clayton, T.D.; Swarzenski, P.; Brock, J.C.; Muller–Karger, F.E. Assessment of estuarine water-quality indicators using MODIS medium-resolution bands: Initial results from Tampa Bay, FL. Remote Sens. Environ. 2004, 93, 423–441. [Google Scholar] [CrossRef]
- Gordon, H.R.; Wang, M. Retrieval of water-leaving radiance and aerosol optical thickness over the oceans with SeaWiFS: A preliminary algorithm. Appl. Opt. 1994, 33, 443–452. [Google Scholar] [CrossRef] [PubMed]
- Chavez, P.S. Image- based atmospheric corrections-revisited and improved. Photogramm. Eng. Remote Sens. 1996, 62, 1025–1035. [Google Scholar]
- Hu, C.; Carder, K.L.; Muller-Karger, F.E. Atmospheric correction of SeaWiFS imagery over turbid coastal waters: A practical method. Remote Sens. Environ. 2000, 74, 195–206. [Google Scholar] [CrossRef]
- Ruddick, K.G.; Ovidio, F.; Rijkeboer, M. Atmospheric correction of SeaWiFs imagery for turbid coastal and inland waters. Appl. Opt. 2000, 39, 897–912. [Google Scholar] [CrossRef] [PubMed]
- Siegel, D.A.; Wang, M.; Maritorena, S.; Robinson, W. Atmospheric Correction of Satellite Ocean Color Imagery: The Black Pixel Assumption. Appl. Opt. 2000, 39, 3582–3591. [Google Scholar] [CrossRef] [PubMed]
- Wang, M.; Shi, W. The NIR-SWIR combined atmospheric correction approach for modis ocean color data processing. Opt. Express 2007, 15, 15722–15733. [Google Scholar] [CrossRef] [PubMed]
- Adler-Golden, S.; Berk, A.; Bernstein, L.; Richtsmeier, S.; Acharya, P.; Matthew, M.; Anderson, G.; Allred, C.; Jeong, L.; Chetwynd, J. FLAASH, a MODTRAN4 atmospheric correction package for hyperspectral data retrievals and simulations. In Proceedings of the 7th Ann. JPL Airborne Earth Science Workshop, Pasadena, CA, USA, 12–16 January 1998; pp. 9–14. [Google Scholar]
- Kaufman, Y.; Wald, A.; Remer, L.; Gao, B.-C.; R-R, L.; Flynn, L. The MODIS 2.1-μm channel-correlation with visible reflectance for use in remote sensing of aerosol. IEEE Trans. Geosci. Remote Sens. 1997, 35, 1286–1298. [Google Scholar] [CrossRef]
- Joshi, I.; D’Sa, E.J. Seasonal Variation of Colored Dissolved Organic Matter in Barataria Bay, Louisiana, Using Combined Landsat and Field Data. Remote Sens. 2015, 7, 12478–12502. [Google Scholar] [CrossRef]
- Wilson, R.; Milton, E.; Nield, J. Are visibility-derived aot estimates suitable for parameterizing satellite data atmospheric correction algorithms? Int. J. Remote Sens. 2015, 36, 1675–1688. [Google Scholar] [CrossRef]
- Thuillier, G.; Hersé, M.; Foujols, T.; Peetermans, W.; Gillotay, D.; Simon, P.; Mandel, H. The solar spectral irradiance from 200 to 2400 nm as measured by the SOLSPEC spectrometer from the ATLAS and EURECA missions. Sol. Phys. 2003, 214, 1–22. [Google Scholar] [CrossRef]
- Gordon, H.R. Atmospheric correction of ocean color imagery in the Earth Observing System era. J. Geophys. Res. Atmos. 1997, 102, 17081–17106. [Google Scholar]
- Cleveland, R.B.; Cleveland, W.S.; McRae, J.E.; Terpenning, I. Stl: A Seasonal-Trend Decomposition Procedure Based on Loess. J. Off. Stat. 1990, 6, 3–73. [Google Scholar]
- Breiman, L.; Friedman, J.; Stone, C.J.; Olshen, R.A. Classification and Regression Trees; CRC Press: Boca Raton, FL, USA, 1984. [Google Scholar]
- De’ath, G.; Fabricius, K.E. Classification and Regression Trees: A Powerful Yet Simple Technique for Ecological Data Analysis. Ecology 2000, 81, 3178–3192. [Google Scholar] [CrossRef]
- Zhang, Y.; Liu, X.; Qin, B.; Shi, K.; Deng, J.; Zhou, Y. Aquatic vegetation in response to increased eutrophication and degraded light climate in Eastern Lake Taihu: Implications for lake ecological restoration. Sci. Rep. 2016, 6. [Google Scholar] [CrossRef] [PubMed]
- Efron, B.; Tibshirani, R.J. An Introduction to the Bootstrap; CRC Press: Boca Raton, FL, USA, 1994. [Google Scholar]
- Montgomery, D.C.; Peck, E.A.; Vining, G.G. Introduction to Linear Regression Analysis; John Wiley & Sons: Somerset, NJ, USA, 2015. [Google Scholar]
- Mortazavi, B.; Iverson, R.L.; Landing, W.M.; Lewis, F.G.; Huang, W. Control of phytoplankton production and biomass in a river-dominated estuary: Apalachicola Bay, Florida, USA. Mar. Ecol. Prog. Ser. 2000, 198, 19–31. [Google Scholar] [CrossRef]
- Del Castillo, C.E.; Gilbes, F.; Coble, P.G.; Müller-Karger, F.E. On the dispersal of riverine colored dissolved organic matter over the West Florida Shelf. Limnol. Oceanogr. 2000, 45, 1425–1432. [Google Scholar] [CrossRef]
- Gordon, H.R.; Lewis, M.R.; McLean, S.D.; Twardowski, M.S.; Freeman, S.A.; Voss, K.J.; Boynton, G.C. Spectra of particulate backscattering in natural waters. Opt. Express 2009, 17, 16192–16208. [Google Scholar] [CrossRef] [PubMed]
- Slade, W.H.; Boss, E. Spectral attenuation and backscattering as indicators of average particle size. Appl. Opt. 2015, 54, 7264–7277. [Google Scholar] [CrossRef] [PubMed]
- Fan, C.; Warner, R.A. Characterization of water reflectance spectra variability: Implications for hyperspectral remote sensing in estuarine waters. Mar. Sci. 2014, 4, 1–9. [Google Scholar]
- Joshi, I.D.; D’Sa, E.J.; Osburn, C.L.; Bianchi, T.S.; Ko, D.S.; Oviedo-Vargas, D.; Arellano, A.R.; Ward, N.D. Assessing chromophoric dissolved organic matter (CDOM) distribution, stocks, and fluxes in Apalachicola Bay using combined field, VIIRS ocean color, and model observations. Remote Sens. Environ. 2017, 191, 359–372. [Google Scholar] [CrossRef]
- Doxaran, D.; Froidefond, J.-M.; Castaing, P.; Babin, M. Dynamics of the turbidity maximum zone in a macrotidal estuary (the Gironde, France): Observations from field and MODIS satellite data. Estuar. Coast. Shelf Sci. 2009, 81, 321–332. [Google Scholar] [CrossRef]
- Wang, H.; Hladik, C.M.; Huang, W.; Milla, K.; Edmiston, L.; Harwell, M.; Schalles, J.F. Detecting the spatial and temporal variability of chlorophyll-a concentration and total suspended solids in Apalachicola Bay, Florida using MODIS imagery. Int. J. Remote Sens. 2010, 31, 439–453. [Google Scholar] [CrossRef]
- Bustamante, J.; Pacios, F.; Díaz-Delgado, R.; Aragonés, D. Predictive models of turbidity and water depth in the Doñana marshes using Landsat TM and ETM+ images. J. Environ. Manag. 2009, 90, 2219–2225. [Google Scholar] [CrossRef] [PubMed]
- Pope, R.M.; Fry, E.S. Absorption spectrum (380–700 nm) of pure water. II. Integrating cavity measurements. Appl. Opt. 1997, 36, 8710–8723. [Google Scholar] [CrossRef] [PubMed]
- Novoa, S.; Doxaran, D.; Ody, A.; Vanhellemont, Q.; Lafon, V.; Lubac, B.; Gernez, P. Atmospheric corrections and multi-conditional algorithm for multi-sensor remote sensing of suspended particulate matter in low-to-high turbidity levels coastal waters. Remote Sens. 2017, 9, 61. [Google Scholar] [CrossRef]
- Twichell, D.; Edmiston, L.; Andrews, B.; Stevenson, W.; Donoghue, J.; Poore, R.; Osterman, L. Geologic controls on the recent evolution of oyster reefs in Apalachicola Bay and St. George Sound, Florida. Estuar. Coast. Shelf Sci. 2010, 88, 385–394. [Google Scholar] [CrossRef]
- Reichstetter, M.; Fearns, P.R.; Weeks, S.J.; McKinna, L.I.; Roelfsema, C.; Furnas, M. Bottom Reflectance in Ocean Color Satellite Remote Sensing for Coral Reef Environments. Remote Sens. 2015, 7, 16756–16777. [Google Scholar] [CrossRef]
- Schmidt, N.; Lipp, E.; Rose, J.; Luther, M. ENSO influences on Seasonal Rainfall and River Discharge in Florida. J. Clim. 2001, 14, 615–628. [Google Scholar] [CrossRef]
- Sittel, M.C. Marginal Probabilities of the Extremes of ENSO Events for Temperature and Precipitation in the Southeastern United States; Center for Ocean-Atmosphere Prediction Studies, Florida State University: Tallahassee, FL, USA, 1994. [Google Scholar]
- Wang, M.; Shi, W. Cloud Masking for Ocean Color Data Processing in the Coastal Regions. IEEE Trans. Gesci. Remote Sens. 2006, 44, 3196–3205. [Google Scholar] [CrossRef]
- Roberts, K.; Collins, J.; Paxton, C.H.; Hardy, R.; Downs, J. Weather patterns associated with green turtle hypothermic stunning events in St. Joseph Bay and Mosquito Lagoon, Florida. Phys. Geogr. 2014, 35, 134–150. [Google Scholar] [CrossRef]
| Data | N (Duration) | Location | Source | Purpose |
|---|---|---|---|---|
| Field Measurements | ||||
| Turbidity (NTU) | 2758 (CP) 2745 (DB) (2004–2011) | Cat point (CP) (29.702°N, −84.875°W) Dry Bar (DB) (29.675°N, −85.058°W) | Apalachicola National Estuarine Research Reserve (ANERR) | Temporal and statistical analysis of turbidity, Satellite-based turbidity maps |
| Wind speed (ms−1) and Wind direction | 2842 (2004–2011) | East Bay (EB) (29.791°N, −84.883°W) | ANERR | Effects on turbidity |
| Tidal height (m) | 2922 (2004–2011) | ID-8728690 (29.435°N, −84.90°W) | NOAA Tides and Currents | Effects on turbidity |
| River discharge (m3s−1) | 2922 (2004–2011) | ID-02359170 (near Sumatra, Florida) | USGS Water Data for the Nation | Effects on turbidity |
| Rainfall (mm) | 2439 (2004–2011) | ID-080211 (Apalachicola Airport) | Florida Climate Center | Effects on turbidity |
| Salinity | 2922 (2004–2011) | Cat point (CP) (29.702°N, −84.875°W) Dry Bar (DB) (29.675°N, −85.058°W) | Apalachicola National Estuarine Research Reserve (ANERR) | Effects on turbidity |
| Remote Sensing Measurements | ||||
| Landsat TM, ETM+ & OLI | 19 clear-sky images (2011–2014) | Path 22, Row 40 | Landsat Data Archive (USGS) | Validation of ENVI-FLAASH atmospheric correction |
| Radiance Lw (mWcm−2µm−1sr−1) and AOT | 19 match-ups (2011–2014) | CSI-6 (28.867°N, −90.483°W) | AERONET-OC (WAVCIS) | Validation of ENVI-FLAASH atmospheric correction |
| Landsat 5 TM images | 57 images with clear-sky conditions (2004–2011) | (Path 18/19, Row 39/40) | Landsat Data Archive (USGS) | Landsat based turbidity maps, Analysis of spatiotemporal changes in turbidity |
| Landsat 8 OLI images | 17 images with clear-sky conditions (2014–2016) | (Path 18/19, Row 39/40) | Landsat Data Archive (USGS) | Performance evaluation of turbidity algorithm on Landsat 8 OLI |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Joshi, I.D.; D’Sa, E.J.; Osburn, C.L.; Bianchi, T.S. Turbidity in Apalachicola Bay, Florida from Landsat 5 TM and Field Data: Seasonal Patterns and Response to Extreme Events. Remote Sens. 2017, 9, 367. https://doi.org/10.3390/rs9040367
Joshi ID, D’Sa EJ, Osburn CL, Bianchi TS. Turbidity in Apalachicola Bay, Florida from Landsat 5 TM and Field Data: Seasonal Patterns and Response to Extreme Events. Remote Sensing. 2017; 9(4):367. https://doi.org/10.3390/rs9040367
Chicago/Turabian StyleJoshi, Ishan D., Eurico J. D’Sa, Christopher L. Osburn, and Thomas S. Bianchi. 2017. "Turbidity in Apalachicola Bay, Florida from Landsat 5 TM and Field Data: Seasonal Patterns and Response to Extreme Events" Remote Sensing 9, no. 4: 367. https://doi.org/10.3390/rs9040367
APA StyleJoshi, I. D., D’Sa, E. J., Osburn, C. L., & Bianchi, T. S. (2017). Turbidity in Apalachicola Bay, Florida from Landsat 5 TM and Field Data: Seasonal Patterns and Response to Extreme Events. Remote Sensing, 9(4), 367. https://doi.org/10.3390/rs9040367






