A New Spatial Attraction Model for Improving Subpixel Land Cover Classification
Abstract
:1. Introduction
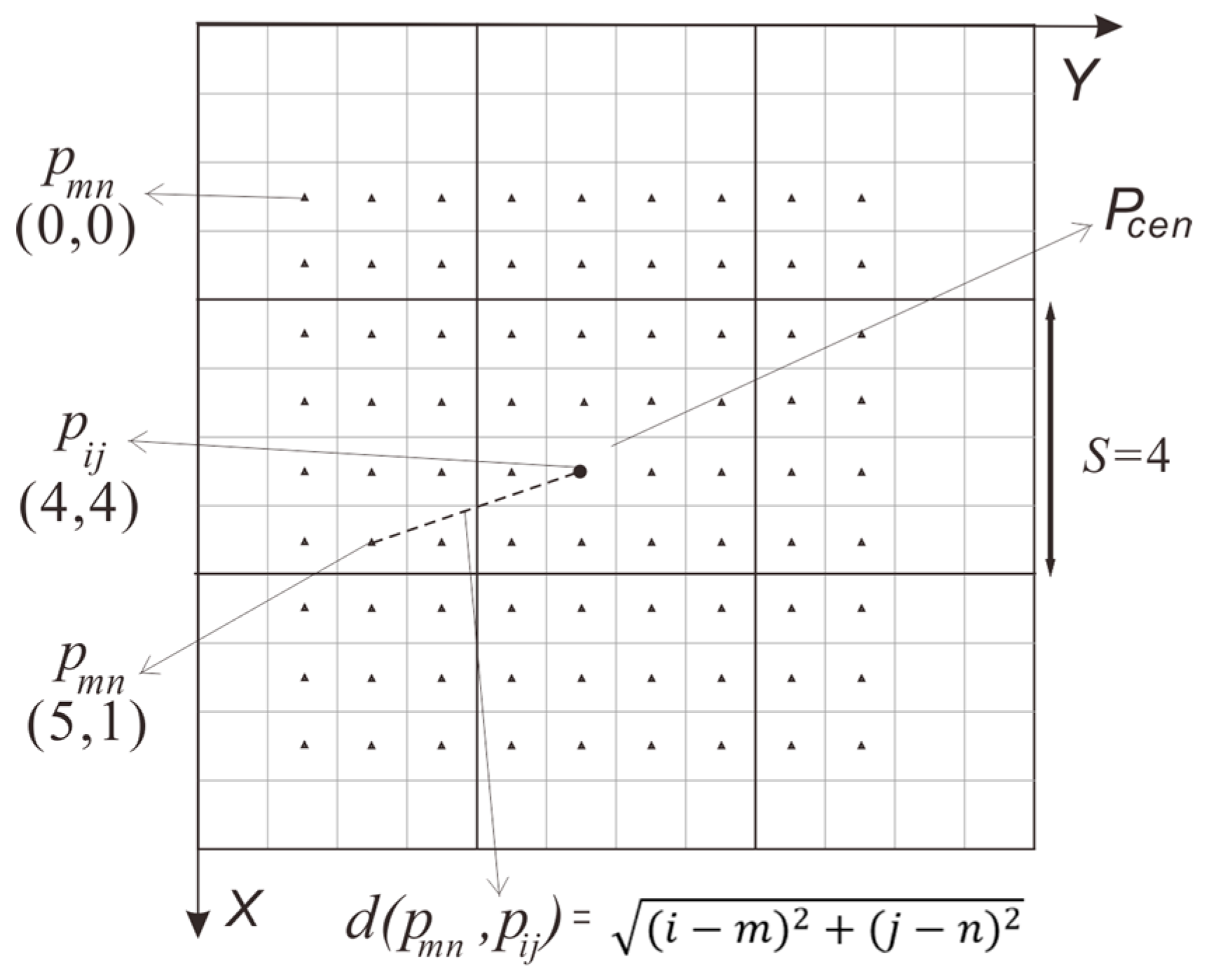
2. Methodology
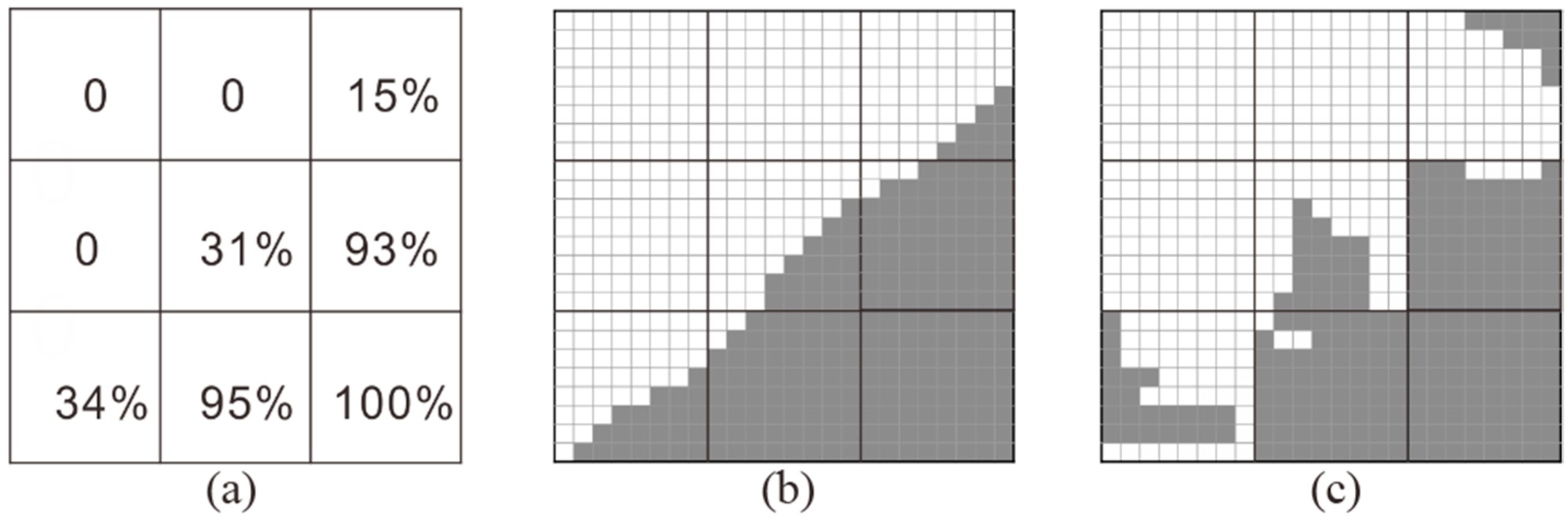
2.1. Subpixel Mapping (SPM): Theory
2.2. SPSAM, MSPSAM, and MSAM
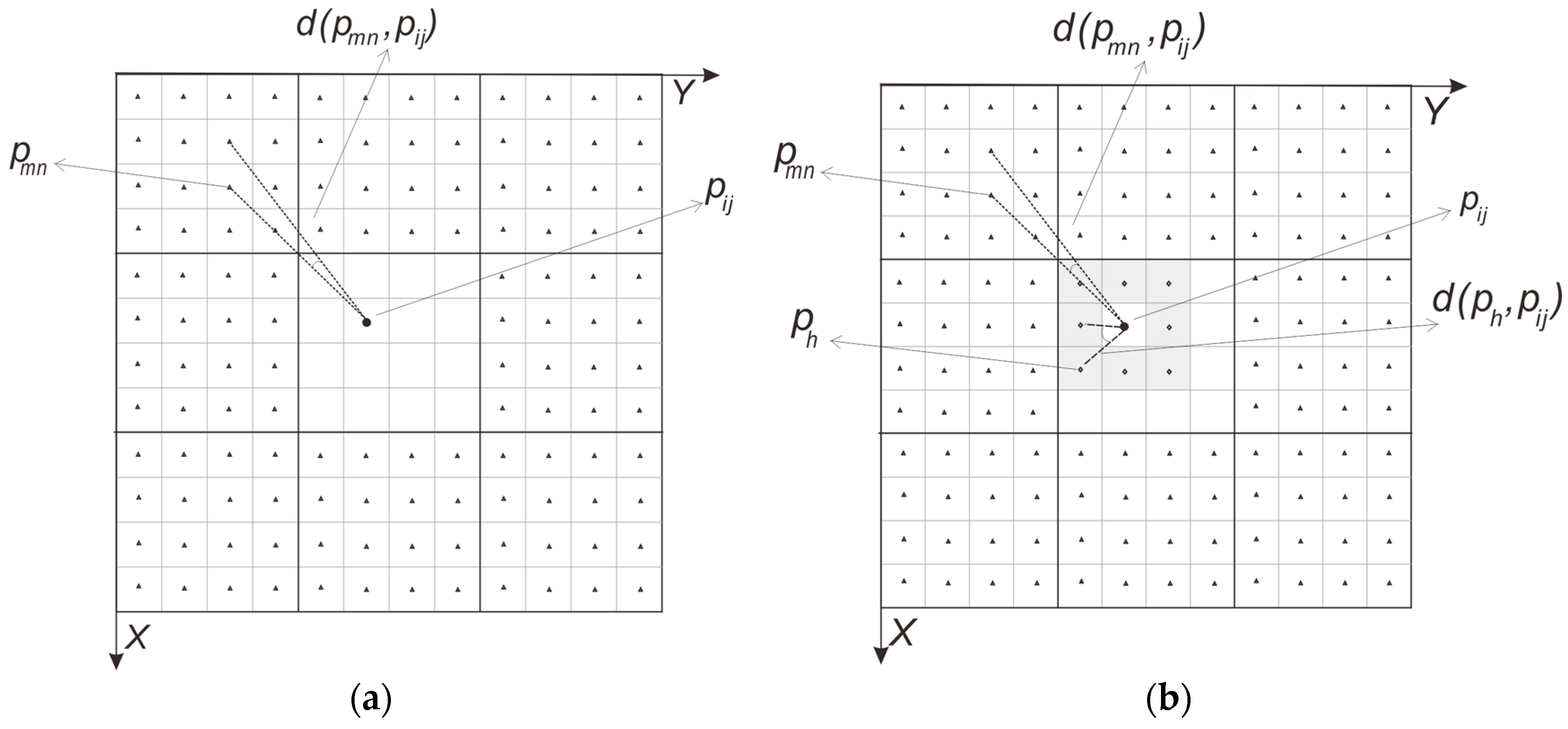
2.2.1. SPSAM
2.2.2. MSPSAM and MSAM
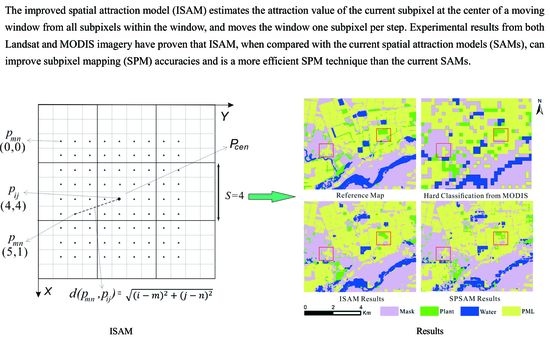
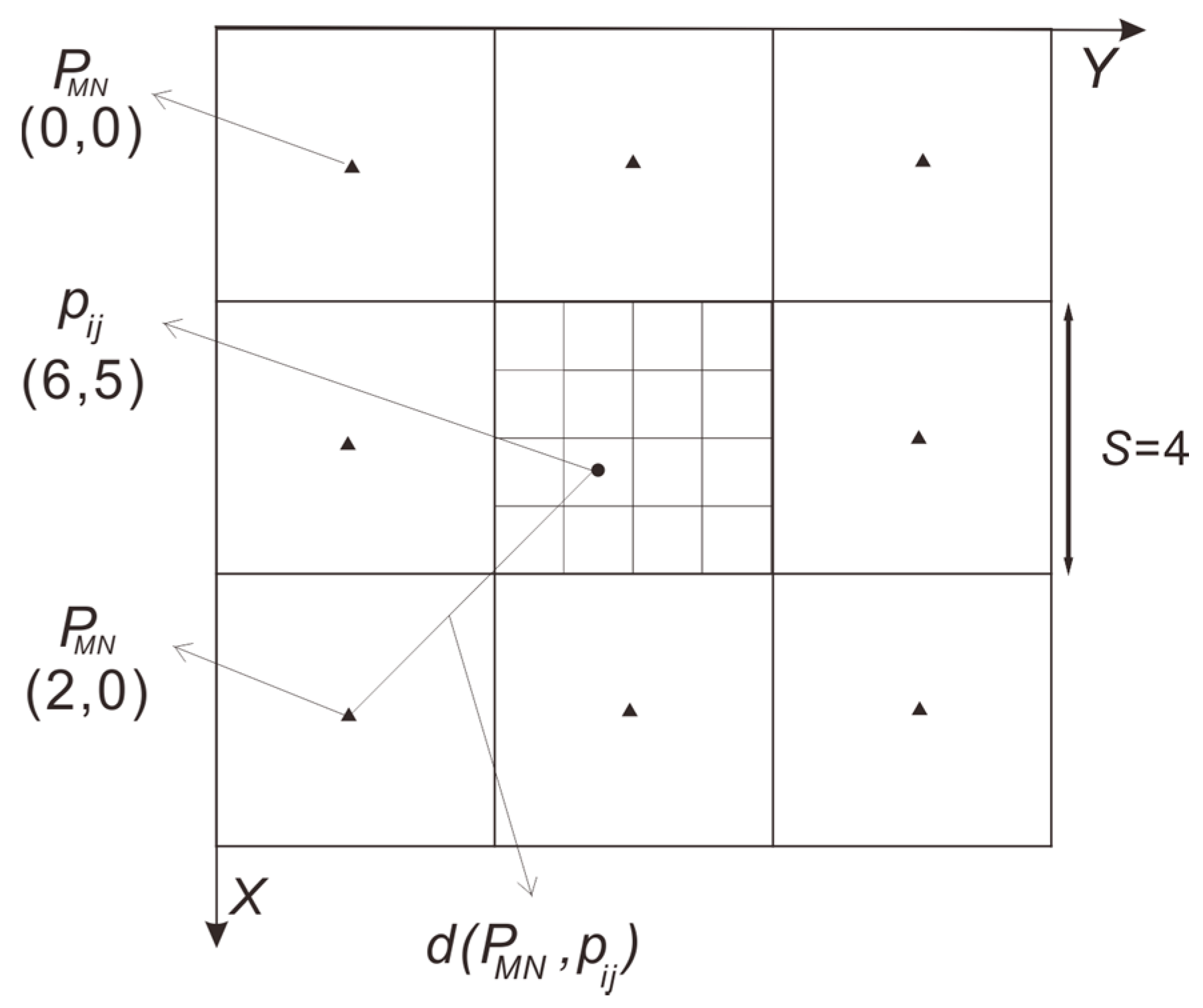
2.3. Improved Spatial Attraction Model (ISAM)
2.4. The Algorithm of ISAM
| Input a soft classification fraction image of C number of classes |
| Set scale factor S Set maximum iteration step Hmax Randomly allocate subpixel to classes based on the pixel-level class fraction Estimate Acc, the accuracies of SPM of previous iteration step Initialize current iteration step H FOR each iteration//H FOR each pixel//Select a pixel as the central pixel Pcen FOR each subpixel within the central pixel Initialize the column and row ranks for subpixels within a moving window around subpixel FOR each class FOR each subpixel within the moving window Calculate the spatial attraction of subpixel exercised by END FOR each subpixel within the moving window Summarize Jc,ij, the spatial attractions of subpixel exercised by subpixels within the moving window END FOR END FOR Sort SLSc (spatial location sequence for class c) by Jc,ij descending order Choose top subpixels and assign them to class c, according to SLSc Reassign the subpixels, which have been assigned to more than one class, to a specific class of which the spatial attractions reach the maximum. Make sure every subpixel is uniquely assigned to a specific class. END FOR Estimate Acc_c, the accuracies of SPM of current iteration step IF Acc ≥ Acc_c or H = Hmax break ELSE Acc = Acc_c ENDIF END FOR |
3. Experiments and Results
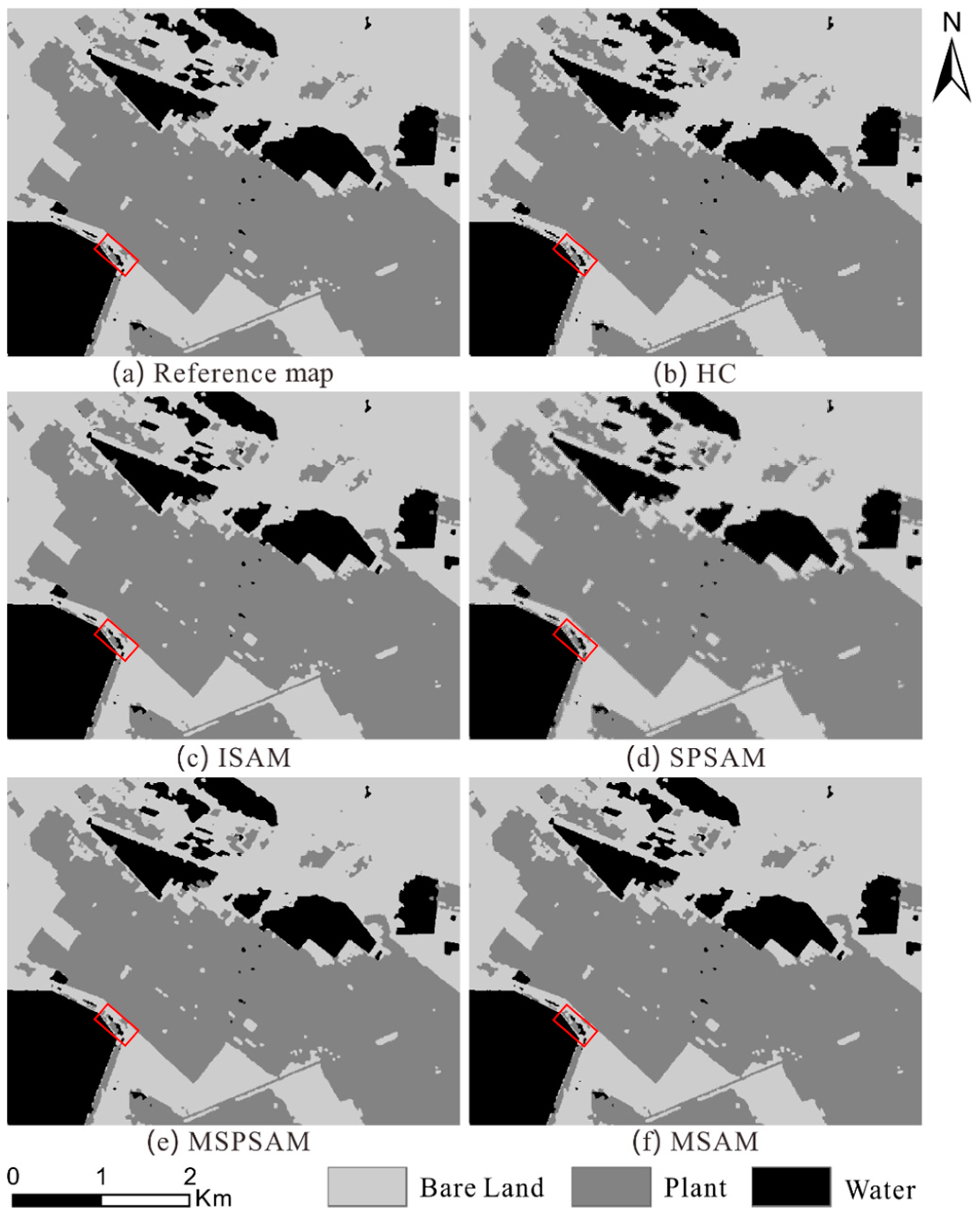
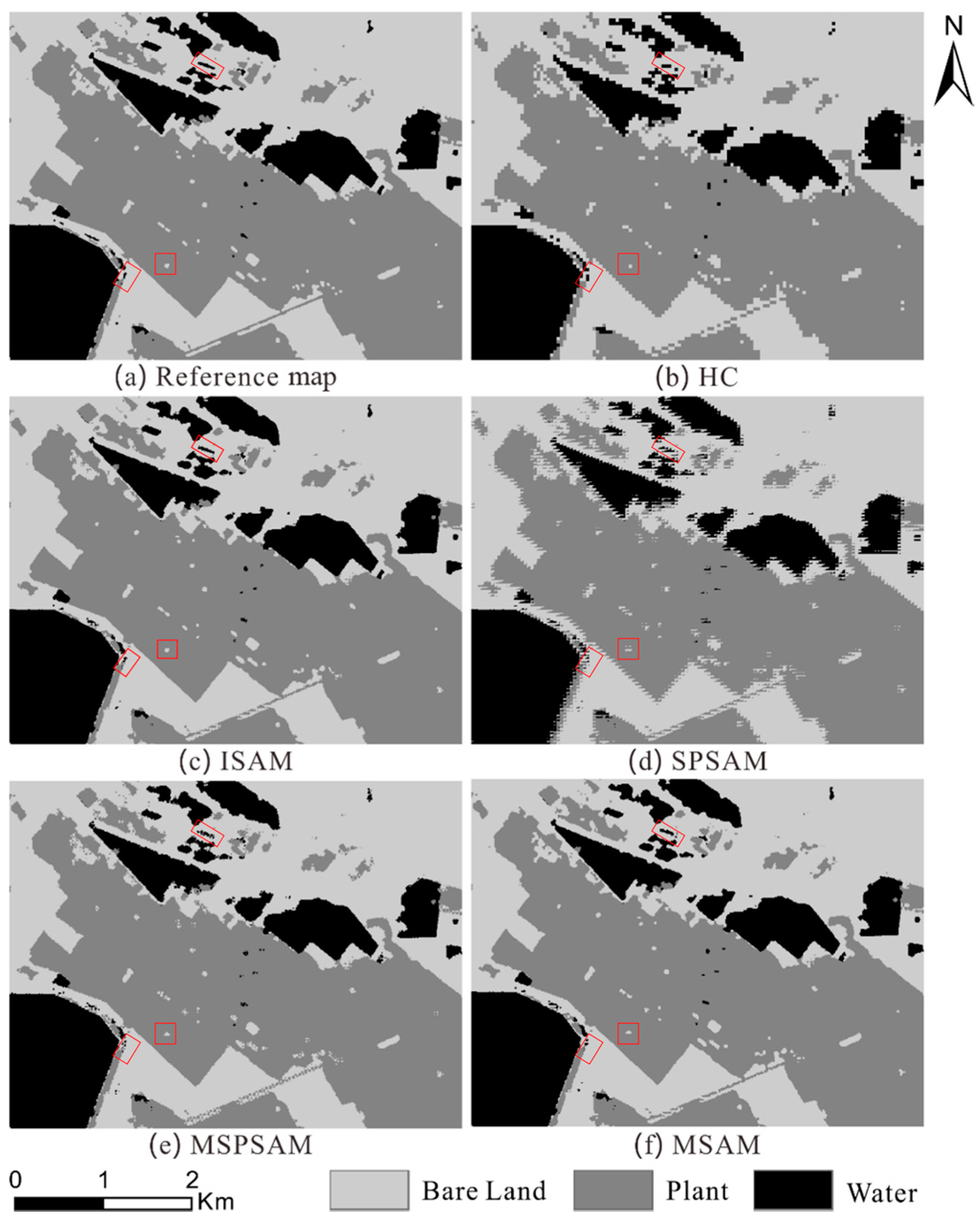
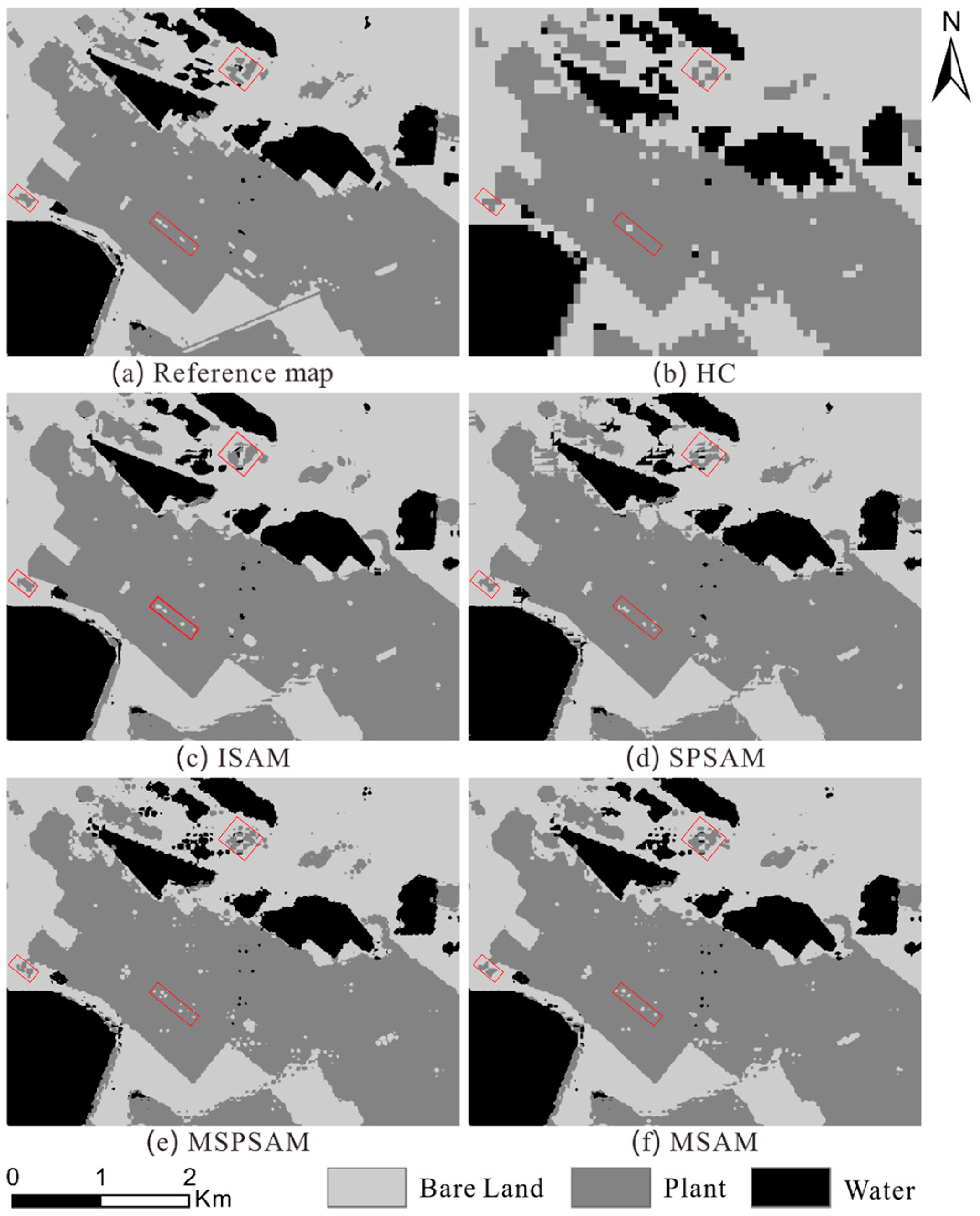
3.1. Experiment with Landsat OLI Imagery
3.1.1. Data Sets
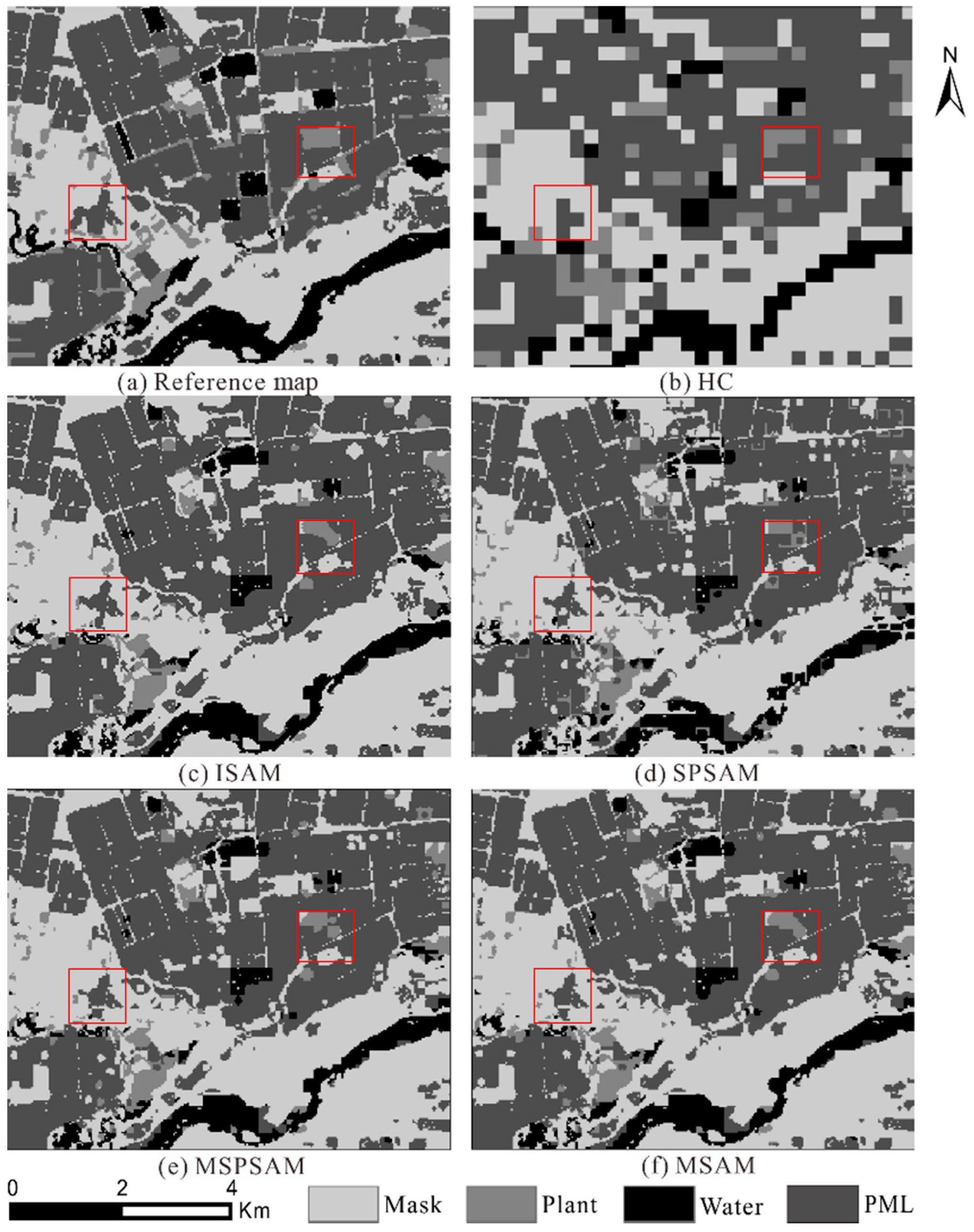
3.1.2. Experiment Results
3.2. Experiment with MODIS Imagery
3.2.1. Data Sets
3.2.2. Experiment Results
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Lu, L.Z.; Di, L.P.; Ye, Y.M. A Decision-tree classifier for extracting transparent plastic-mulched landcover from Landsat-5 TM images. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 7, 4548–4558. [Google Scholar] [CrossRef]
- Lu, L.Z.; Hang, D.W.; Di, L.P. Threshold model for detecting transparent plastic mulched landcover using MODIS time series data: A case study in southern Xinjiang, China. J. Appl. Remote Sens. 2015, 9. [Google Scholar] [CrossRef]
- Wang, Q.; Lin, J.; Yuan, Y. Salient band selection for hyperspectral image classification via manifold ranking. IEEE Trans. Neural Netw. Learn. Syst. 2016, 27, 1–11. [Google Scholar] [CrossRef] [PubMed]
- Yuan, Y.; Lin, J.; Wang, Q. Dual-clustering-based hyperspectral band selection by contextual analysis. IEEE Trans. Geosci. Remote Sens. 2016, 54, 1431–1445. [Google Scholar] [CrossRef]
- Smith, M.O.; Ustin, S.L.; Adams, J.B.; Gillespie, A.R. Vegetation in deserts: I. A regional measure of abundance from multi-spectral images. Remote Sens. Environ. 1990, 31, 1–26. [Google Scholar] [CrossRef]
- Verhoeye, J.; Wulf, R.D. Land cover mapping at sub-pixel scales using linear optimization techniques. Remote Sens. Environ. 2002, 79, 96–104. [Google Scholar] [CrossRef]
- Ling, F.; Wu, S.J.; Xiao, F.; Wu, K. Sub-pixel mapping of remotely sensed imagery: A review. J. Image Graph. 2011, 16, 1335–1345. [Google Scholar]
- Plaza, A.; Martinerz, P.; Perez, R.; Plaza, J. A quantitative and comparative analysis of endmember extraction algortihms from hyperspectral data. IEEE Trans. Geosci. Remote Sens. 2004, 42, 650–663. [Google Scholar] [CrossRef]
- Atkinson, P.M. Sub-pixel target mapping from soft-classified remotely sensed imagery. Photogramm. Eng. Remote Sens. 2005, 71, 839–846. [Google Scholar] [CrossRef]
- Shi, C.; Wang, L. Incorporating spatial information in spectral unmixing: A review. Remote Sens. Environ. 2014, 149, 70–87. [Google Scholar] [CrossRef]
- Bioucas-Dias, J.M.; Plaza, A.; Dobigeon, N.; Pario, P.; Du, Q.; Gader, P. Hyperspectral unmixing overview: Geometrical, statistical, and sparse regression-based approaches. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2012, 5, 354–379. [Google Scholar] [CrossRef]
- Keshava, N.; Mustard, J.F. Spectral unmixing. IEEE Signal Process. Mag. 2002, 19, 44–57. [Google Scholar] [CrossRef]
- Atkinson, P.M. Super-resolution land cover classification using the two-point histogram. In GeoENV VI—Geostatistics for Environmental Applications; Springer: Berlin/Heidelberg, Germany, 2004; pp. 15–28. [Google Scholar]
- Feng, R.Y.; Zhong, Y.F.; Wu, Y.Y.; He, D.; Xu, X.; Zhang, L.P. Nonlocal total variation subpixel mapping for hyperspectral remote sensing imagery. Remote Sens. 2016, 8, 250. [Google Scholar] [CrossRef]
- Ge, Y.; Jiang, Y.; Chen, Y.H.; Stein, A.; Jiang, D.; Jia, Y.X. Designing an experiment to investigate subpixel mapping as an alternative method to obtain land use/land cover maps. Remote Sens. 2016, 8, 360. [Google Scholar] [CrossRef]
- He, D.; Zhong, Y.F.; Feng, R.Y.; Zhang, L.P. Spatial-temporal sub-pixel mapping based on swarm intelligence theory. Remote Sens. 2016, 8, 894. [Google Scholar] [CrossRef]
- Johnson, B.; Tateishi, R.; Kobayashi, T. Remote sensing of fractional green vegetation cover using spatially-interpolated endmembers. Remote Sens. 2012, 4, 2619–2634. [Google Scholar] [CrossRef]
- Ling, F.; Foody, G.M.; Li, X.D.; Zhang, Y.H.; Du, Y. Assessing a temporal change strategy for sub-pixel land cover change mapping from multi-scale remote sensing imagery. Remote Sens. 2016, 8, 642. [Google Scholar] [CrossRef]
- Okujeni, A.; van der Linden, S.; Jakimow, B.; Rabe, A.; Verrelst, J.; Hostert, P. A comparison of advanced regression algorithms for quantifying urban land cover. Remote Sens. 2014, 6, 6324–6346. [Google Scholar] [CrossRef]
- Schneider, W. Land use mapping with subpixel accuracy from Landsat TM image data. In Proceedings of the 25th International Symposium on Remote Sensing and Global Environmental Changes, Graz, Austria, 4–8 April 1993; pp. 155–161. [Google Scholar]
- Atkinson, P.M. Mapping subpixel boundaries from remotely sensed images. In Innovations in GIS 4; Taylor and Francis: London, UK, 1997; pp. 166–180. [Google Scholar]
- Tatem, A.J.; Lewis, H.G.; Atkinson, P.M.; Nixon, M.S. Super-resolution target identification from remotely sensed images using a Hopfield neural network. IEEE Trans. Geosci. Remote Sens. 2001, 39, 781–796. [Google Scholar] [CrossRef]
- Tatem, A.J.; Lewis, H.G.; Atkinson, P.M.; Nixon, M.S. Super-resolution land cover pattern prediction using a Hopfield neural network. Remote Sens. Environ. 2002, 79, 1–14. [Google Scholar] [CrossRef]
- Tatem, A.J.; Lewis, H.G.; Atkinson, P.M.; Nixon, M.S. Increasing the spatial resolution of agricultural land cover maps using a Hopfield neural network. Int. J. Remote Sens. 2003, 24, 4241–4247. [Google Scholar] [CrossRef]
- Wang, Q.M.; Atkinson, P.M.; Shi, W.Z. Fast subpixel mapping algorithms for subpixel resolution change detection. IEEE Trans. Geosci. Remote Sens. 2015, 53, 1692–1706. [Google Scholar] [CrossRef]
- Atkinson, P.M. Super-resolution target mapping from soft-classified remotely sensed imagery. In Proceedings of the 5th International Conference on GeoComputation, London, UK, 23–25 August 2000. [Google Scholar]
- Thornton, M.W.; Atkinson, P.M.; Holland, D.A. Sub-pixel mapping of rural land cover objects from fine spatial resolution satellite sensor imagery using super resolution pixel swapping. Int. J. Remote Sens. 2006, 27, 473–491. [Google Scholar] [CrossRef]
- Makido, Y.; Shortridge, A.; Messina, J.P. Assessing alternatives for modeling the spatial distribution of multiple land-cover classes at sub-pixel scales. Photogramm. Eng. Remote Sens. 2007, 73, 935–943. [Google Scholar] [CrossRef]
- Shen, Z.Q.; Qi, J.G.; Wang, K. Modification of pixel-swapping algorithm with initialization from a sub-pixel/pixel spatial model. Photogramm. Eng. Remote Sens. 2009, 75, 557–567. [Google Scholar] [CrossRef]
- Mertens, K.C.; Baets, B.D.; Verbeke, L.P.C.; Wulf, R.R.D. A sub-pixel mapping algorithm based on sub-pixel/ pixel spatial attraction model. Int. J. Remote Sens. 2006, 27, 3293–3310. [Google Scholar] [CrossRef]
- Kasetkasem, T.; Arora, M.K.; Varshney, P.K. Super-resolution land-cover mapping using a Markov random field based approach. Remote Sens. Environ. 2005, 96, 302–314. [Google Scholar] [CrossRef]
- Wang, L.G.; Wang, Q.M. Subpixel mapping using Markov random field with multiple spectral constraints from subpixel shifted remote sensing images. IEEE Trans. Geosci. Remote Sens. 2013, 10, 598–602. [Google Scholar] [CrossRef]
- Mertens, K.C.; Verbeke, L.P.C.; Ducheyne, E.I.; Wulf, R.R.D. Using genetic algorithms in sub-pixel mapping. Int. J. Remote Sens. 2003, 24, 4241–4247. [Google Scholar] [CrossRef]
- Wang, Q.M.; Wang, L.G.; Liu, D.F. Particle swarm optimization-based sub-pixel mapping for remote-sensing imagery. Int. J. Remote Sens. 2012, 33, 6480–6496. [Google Scholar] [CrossRef]
- Boucher, A.; Kyriakidis, P.C.; Cronkite-Ratcliff, C. Geostatistical solutions for super-resolution land cover mapping. IEEE Trans. Geosci. Remote Sens. 2008, 46, 272–283. [Google Scholar] [CrossRef]
- Wang, Q.M.; Shi, W.Z.; Wang, L.G. Indicator cokriging-based subpixel land cover mapping with shifted images. IEEE Trans. Geosci. Remote Sens. 2014, 7, 327–339. [Google Scholar]
- Wang, Q.M.; Wang, L.G.; Liu, D.F. Integration of spatial attractions between and within pixels for sub-pixel mapping. J. Syst. Eng. Electron. 2012, 23, 293–303. [Google Scholar] [CrossRef]
- Woodcock, C.E.; Strahler, A.H. The factor of scale in remote sensing. Remote Sens. Environ. 1987, 21, 311–332. [Google Scholar] [CrossRef]
- Atkinson, P.M. Issues of uncertainty in super-resolution mapping and their implications for the design of an inter-comparison study. Int. J. Remote Sens. 2009, 30, 5293–5308. [Google Scholar] [CrossRef]
- USGS Official Website. Available online: http://earthexplorer.usgs.gov/ (accessed on 8 August 2015).
- NASA Official Website. Available online: http://reverb.echo.nasa.gov/reverb/ (accessed on 10 August 2015).
- Liu, J.G. Smoothing filter-based intensity modulation: A spectral preserve image fusion technique for improving spatial details. Int. J. Remote Sens. 2000, 21, 3461–3472. [Google Scholar] [CrossRef]

| SAM Type | Accuracies (Scale Factor S = 2) | |
|---|---|---|
| Overall Accuracy (OA, %) | Kappa Coefficient (κ) | |
| ISAM | 99.806 | 0.996 |
| SPSAM | 97.970 | 0.967 |
| MSPSAM | 99.629 | 0.994 |
| MSAM | 99.781 | 0.996 |
| SAM Type | Accuracies (Scale Factor S = 4) | |
|---|---|---|
| Overall Accuracy (OA, %) | Kappa Coefficient (κ) | |
| ISAM | 98.776 | 0.980 |
| SPSAM | 95.852 | 0.933 |
| MSPSAM | 98.116 | 0.969 |
| MSAM | 98.734 | 0.979 |
| SAM Type | Accuracies (Scale Factor S = 8) | |
|---|---|---|
| Overall Accuracy (OA, %) | Kappa Coefficient (κ) | |
| ISAM | 96.671 | 0.947 |
| SPSAM | 96.154 | 0.938 |
| MSPSAM | 95.594 | 0.929 |
| MSAM | 96.001 | 0.936 |
| Iterations | ISAM | SPSAM | MSPSAM | MSAM |
|---|---|---|---|---|
| Steps | 4 | 1 | 5 | 9 |
| Optimization time per step (s) | ≈4000 | 240 | ≈4890 | ≈4890 |
| Accuracies | ISAM | SPSAM | MSPSAM | MSAM |
|---|---|---|---|---|
| Overall accuracy (OA, %) | 82.44 | 70.22 | 82.13 | 82.25 |
| Kappa coefficient (κ) | 0.66 | 0.46 | 0.66 | 0.66 |
| SAM Type | Scale Factor S = 2 | Scale Factor S = 4 | Scale Factor S = 8 | |||
|---|---|---|---|---|---|---|
| Optimization Time per Step (s) | Steps | Optimization Time per Step (s) | Steps | Optimization Time per Step (s) | Steps | |
| ISAM | 1.18 | 3 | 5.20 | 4 | 35.30 | 5 |
| SPSAM | 0.90 | 1 | 1.10 | 1 | 2.6 | 1 |
| MSPSAM | 1.20 | 3 | 5.60 | 4 | 40.25 | 6 |
| MSAM | 1.25 | 3 | 6.80 | 7 | 47.10 | 11 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lu, L.; Huang, Y.; Di, L.; Hang, D. A New Spatial Attraction Model for Improving Subpixel Land Cover Classification. Remote Sens. 2017, 9, 360. https://doi.org/10.3390/rs9040360
Lu L, Huang Y, Di L, Hang D. A New Spatial Attraction Model for Improving Subpixel Land Cover Classification. Remote Sensing. 2017; 9(4):360. https://doi.org/10.3390/rs9040360
Chicago/Turabian StyleLu, Lizhen, Yanlin Huang, Liping Di, and Danwei Hang. 2017. "A New Spatial Attraction Model for Improving Subpixel Land Cover Classification" Remote Sensing 9, no. 4: 360. https://doi.org/10.3390/rs9040360
APA StyleLu, L., Huang, Y., Di, L., & Hang, D. (2017). A New Spatial Attraction Model for Improving Subpixel Land Cover Classification. Remote Sensing, 9(4), 360. https://doi.org/10.3390/rs9040360