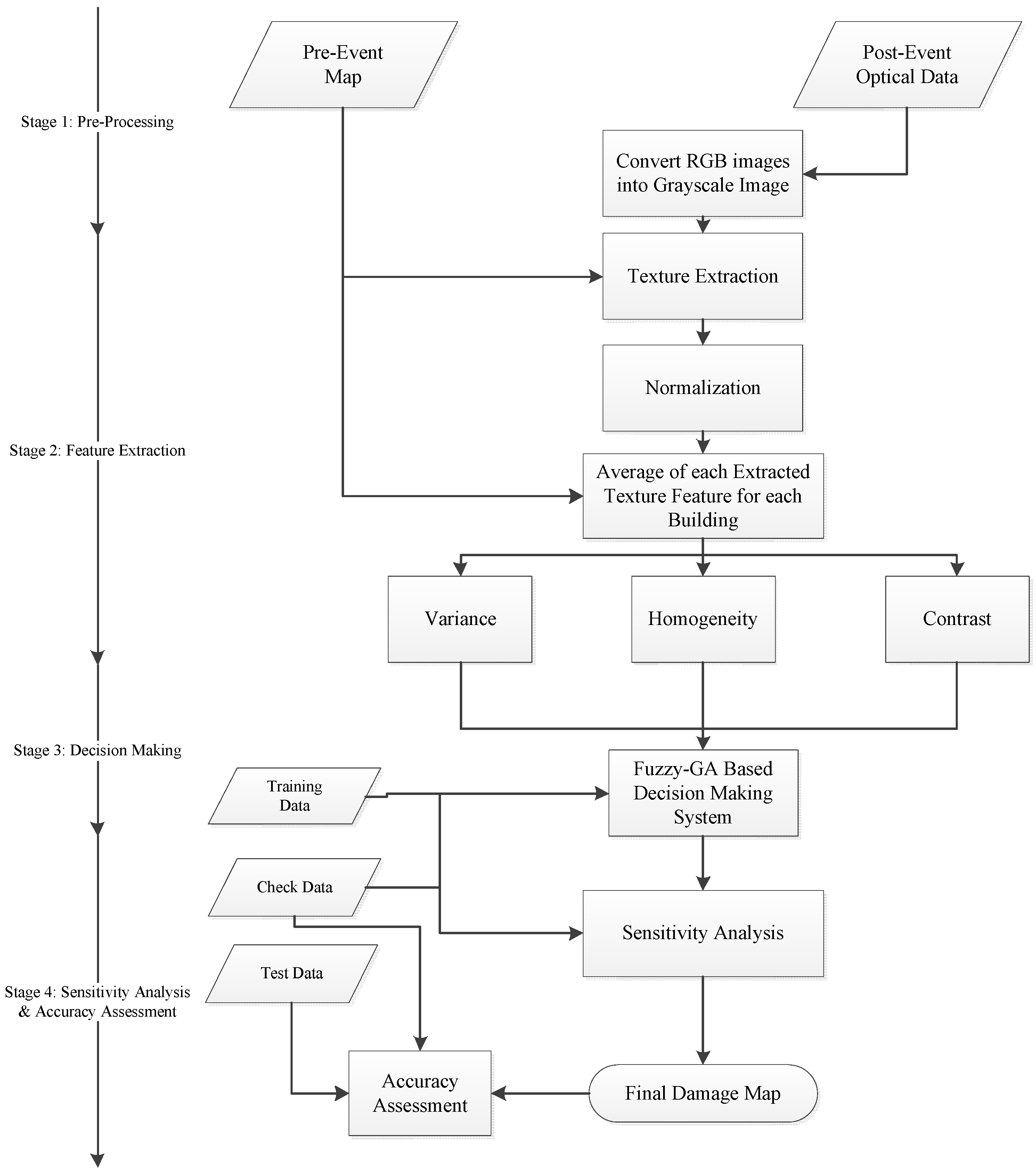
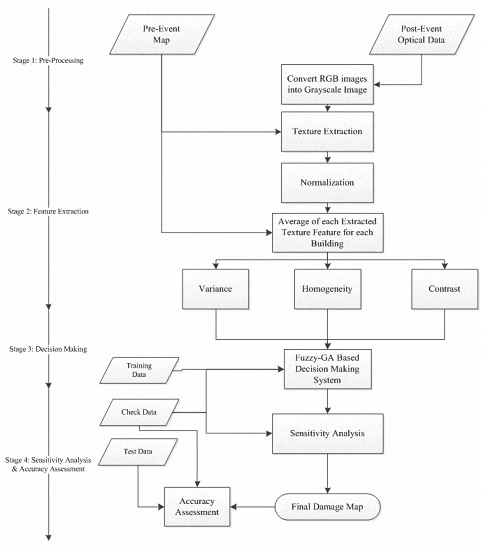
2.3.2. Stage 2: Feature Extraction
Extracting textural features is the main process of the feature extraction stage. The potential of textural features in measuring variations of digital numbers in the spatial domain enables us to use them in satellite image processing, especially after natural hazards. Natural hazards suddenly cause damage of objects of the earth’s surface leading to reflectance changes in the spatial domain. Therefore, the textural features extracted from remotely sensed optical data are widely used for detecting damaged areas. Based on previous works presented in the literature review section, different texture extraction methods have been used in damage detection applications. In most of the previous works [
20,
23], Haralick features were widely chosen for extracting textural features. For this reason, these features are also used in our study. For further study on the Haralick texture extraction method, please see [
41,
42].
In this study, in order to detect damaged buildings from textural features, variance, homogeneity, and contrast features were chosen, which can be calculated from Equation (2), Equation (3), and Equation (4), respectively. The selection of these features was based on three reasons. First of all, three texture features with three linguistic terms and Gaussian membership functions (MFs) generate 24 unknown parameters regarding MFs in a Mamdani fuzzy inference system which should be simultaneously set. It seems that the number of unknown parameters is sufficient to test an optimization algorithm and the selection of them by an expert is a difficult task. For the second reason, based on equations of the mentioned features, it appears that correlation among the selected features is low. Finally, the performance of our decision making system and advanced machine learning techniques would be investigated in similar conditions (i.e., with three texture features). Hence, the selection of the mentioned texture features is within the path of objectives of this study.
where,
is the mean value of gray-levels in an area selected for producing texture features. Moreover,
P and
G are the probability matrix and the number of image gray-levels, respectively.
There are two important points about extracting textural features in this study. For the first point, for preserving the negative effects of non-building pixels on extracted textural features, building pixels are specified by the pre-event map and are only used to extract textural features. For the second point, to compare the three mentioned texture features, they should be standardized. Hence, Equation (5) is employed to standardize the extracted textural features.
where,
is the
th standardized texture feature;
and
are the minimum and maximum values of the
th texture feature; and
is an arbitrary value of the
th texture feature.
2.3.3. Stage 3: Decision Making
After extracting textural features, it is necessary to employ a decision making system [
43] or a machine learning technique to provide a relation between the extracted features and the damage extent of buildings. In this study, a decision making system based on MFIS and GA is used to provide the mentioned relation. MFIS was firstly proposed by Zadeh [
44]. In a MFIS, initially, crisp input values are converted into fuzzy values by input MFs. This is called “fuzzification”. In fact, fuzzification is a mapping process that is performed using membership functions. In this process, membership functions act as connectors among crisp and fuzzy spaces. Then, using fuzzy values, the inference system and existing rules in the fuzzy rule base, fuzzy output values are generated. Finally, the fuzzy output values are transformed into crisp output values by a defuzzification method [
31].
In general, a MFIS is a function of three main parameters according to Equation (6) including: parameters of membership functions (), rules (), and parameters of the inference system (). Therefore, in designing a MFIS, two essential tasks must be performed by an expert: (1) designing rules of the fuzzy rule base and parameters of the inference system, and (2) designing and selecting type and parameters of input and output MFs. In this study, we focus on the second task, because the number of rules in our study is minor and can be easily selected and also an expert could select the small parameters of the inference system.
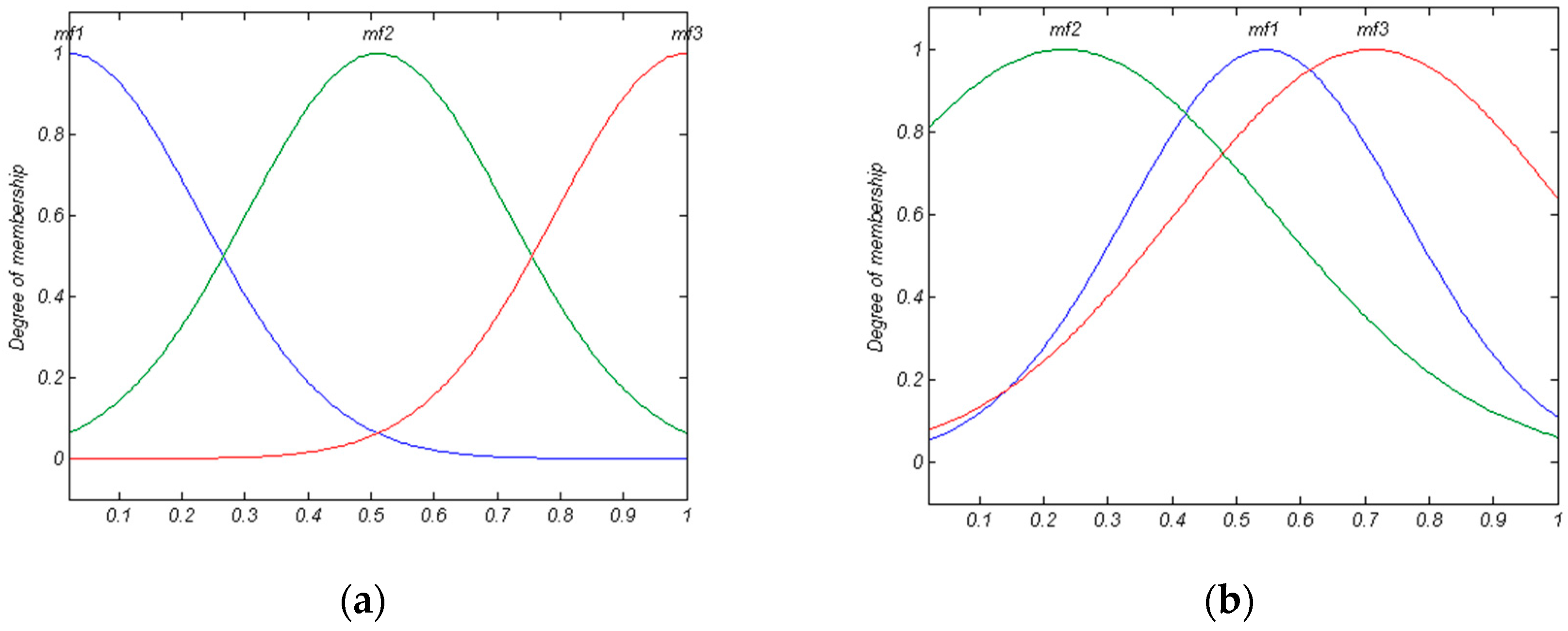
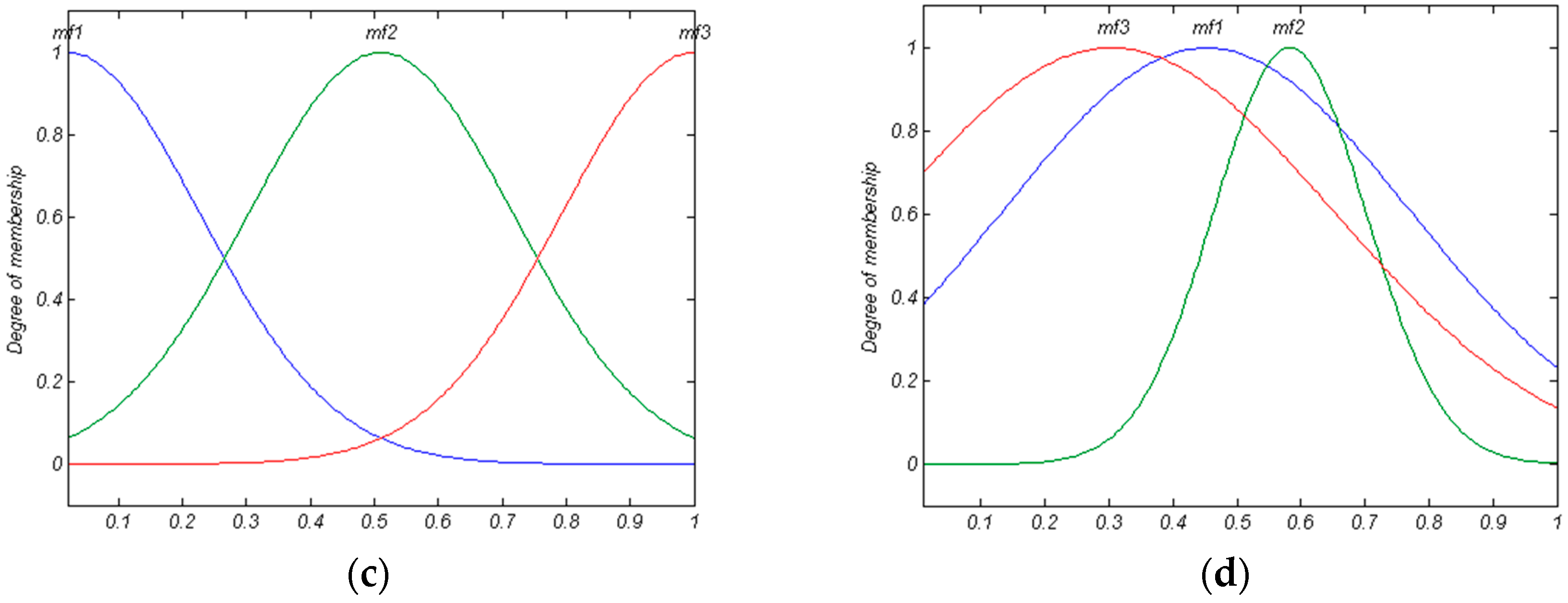
For expressing the importance of the second mentioned task, an example is employed here. Please note that this example is also used as a MFIS in our damage detection method. A MFIS with three inputs and one output (its MF type is Gaussian) is presented in
Figure 2. Suppose three rules similar to Equations (7) to (9) have been designed by an expert. Based on these equations, we can express that
is a function of some unknown parameters (Equation (10)).
where,
,
and
are input linguistic variables 1 to 3, respectively and
is the output linguistic variable. Moreover,
and
are the mean and standard deviation of a Gaussian membership function.
According to
Figure 2 and the designed rules, 24 unknown parameters of MFs (Equation (11)) must be set by an expert. From our viewpoint, the procedure of selection of 24 unknown parameters in a continuous-space is an optimization problem. For this reason, in this study, Genetic Algorithm (GA), as an optimization algorithm, is employed to select unknown parameters [
45,
46]. The ability of GA in selecting optimum answers was the main reason for the selection of this algorithm. In fact, in this research, MFIS and GA are integrated to select appropriate parameters of MFs leading to the best result. In the following, concepts of GA and its integration with the MFIS are presented.
Genetic Algorithm (GA) is based on the mechanism exhibited by nature incorporating the robustness of biological systems as presented by Charles Darwin [
47]. This algorithm is one of the powerful artificial intelligence algorithms, which selects the optimal answer using a random searching method in the search-space.
To find the optimal unknown parameters regarding MFs of a fuzzy inference system using GA, five main steps are employed in GA. The employed steps are presented below:
The first step: initial parameters regarding MFs of the fuzzy system are generated in a random manner. Suppose the number of the population is equal to
k and the generated parameters are:
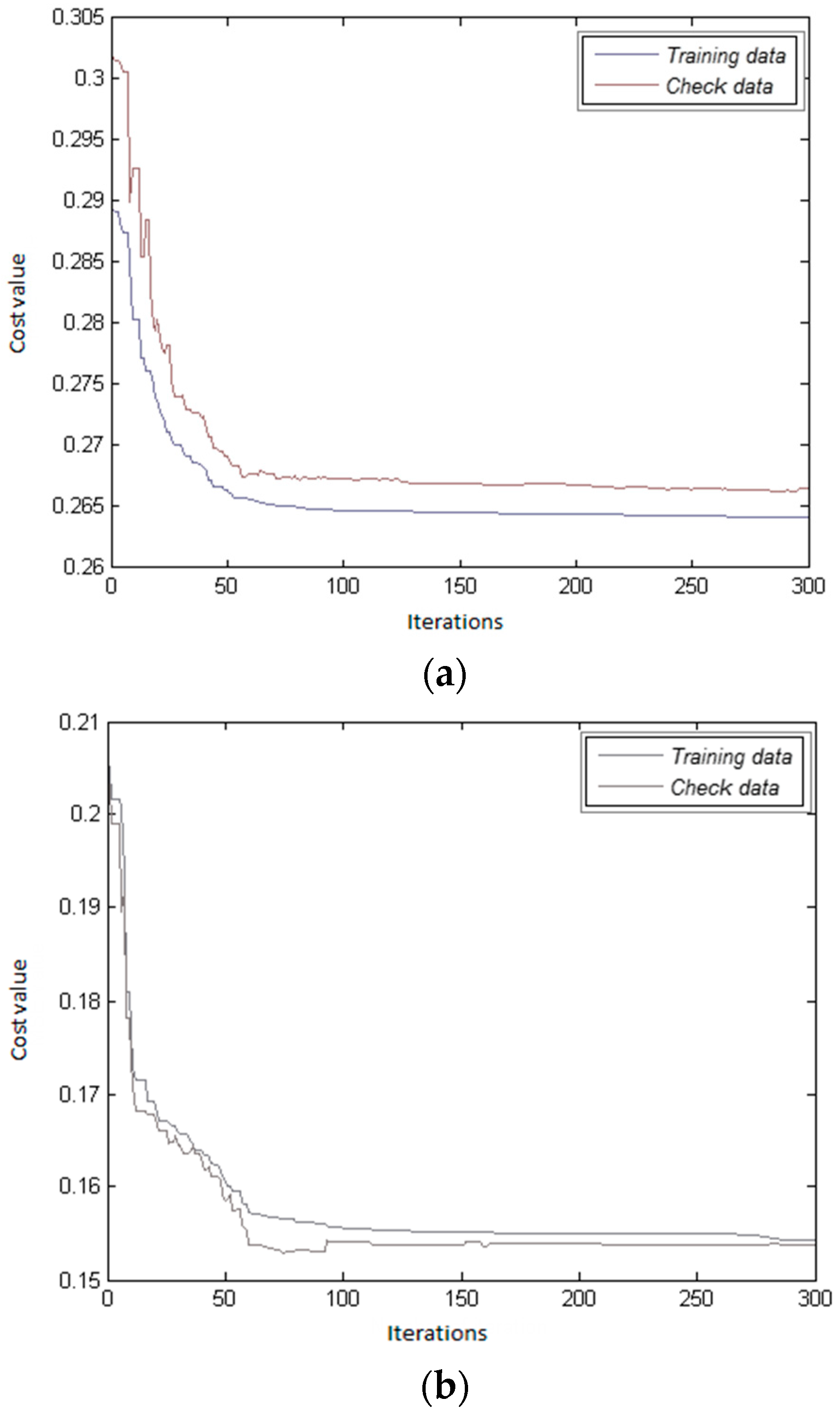
After generating the initial parameters, it is necessary to use a cost function to calculate the efficiency of each population. It should be considered that the fitness function and objective function terms are also used instead of the cost function one. The cost function is at the heart of our proposed system. The integration of the fuzzy system and GA is the main task of this function. Moreover, the cost function is responsible for assessing population. In this study, to obtain the cost of population, some training and check samples according to Equations (13) and (14) are considered. The duty of training samples is to learn the fuzzy-GA system. Furthermore, check samples are employed to prevent an over-learning problem.
where,
,
,
are values of textural features regarding the
training sample. Moreover,
is the damage extent of the
training sample.
,
,
are values of textural features regarding the
check sample. Moreover,
is the damage extent of the
check sample. Furthermore,
and
are the number of training samples and the number of check samples, respectively.
To estimate the cost of each population for training samples (Equation (15)), at first, the parameters of the MFs are updated using the population (Equation (16)). For population r, the updated MFIS is represented by Equation (17). Then, using the updated MFIS and Equation (18), the damage extent of training samples is obtained from Equation (19). Finally, the cost of population r () obtained from the training samples is calculated from Equation (20). The cost of check samples is also estimated in the same way.
where,
and
are parameters of MFs obtained from population
r and the fuzzy inference system updated from
, respectively.
The second step: In this step, new MF parameters are obtained from crossover function and population generated by the previous step. Crossover is one of the important functions in GA, which is responsible for generating new children (parameters of fuzzy systems) from their parents. To generate new children, the number of uses of crossover function (
) should be specified. To this end, at first, parameter
is calculated from the crossover rate and the number of population (
) using Equation (21). Then, the number of uses of crossover function is obtained from Equation (22). For generating new MF parameters from the crossover function, first, two random parents (like
and
) are chosen. Afterwards, new children are achieved from Equation (23). Since unknown parameters were defined in specific ranges, there are two conditions according to Equations (24) and (25) for undefined values. Finally, by using Equations (15) to (20), costs of the new children are calculated and inserted into Equation (26) [
47].
where,
is a random number between −0.1 and 1.1.
and
are the variance and mean of the
variable achieved from the crossover function, respectively.
The third step: In this step, one of the parameters of a population is changed using the mutation function. The mutation is another important function in GA. The mutation function has an undeniable role in solving the local minimum problem in GA. To generate new children by the mutation function, the number of uses of the mutation function () should be specified. To this end, at first, parameter is calculated from the mutation rate and the number of population using Equation (27). Then, the number of uses of the mutation function is obtained from Equation (28). For each use of the mutation function, one random population is selected. Afterwards, a new child is achieved. Equation (29) depicts all new children achieved from the mutation function. Undefined values of variables are corrected using Equations (24) and (25). Finally, using Equations (15) to (20), costs of the new children are calculated and inserted into Equation (30).
where,
is a random number. Moreover,
is calculated from Equation (31). Variables
and
are defined respectively in a range of [0.01–0.5] and [0–1]. Because the range of the variable
is lower than the variable
, sigma values of Equation (31) regarding these variables are different:
The fourth step: In this step, using elitism operator, GA is able to preserve the best answer of iterations. To this end, at first, all population and costs obtained from the previous steps are inserted in two pools according to Equations (32) and (33). Afterwards, they are sorted in descending order by Equation (34) (i.e., a population with the minimum cost value is the best answer). Finally, we select population with minimum cost values as the best answers from the sorted population (Equation (35)). With the elitism operator, it is possible to preserve the best solutions and GA can be converged on the best solution. In fact, with deep insight into this step, we can conclude that the artificial intelligence of GA exists in the fourth step.
The fifth step: The second, third and fourth steps should be repeated to obtain the best solution. The first row of Equation (35) is the best solution with the minimum cost value.