Object-Based Detection of Lakes Prone to Seasonal Ice Cover on the Tibetan Plateau
Abstract
:1. Introduction
2. Previous Work
2.1. Thresholding Methods
2.2. Classification Methods
2.3. Classification Methods and Monitoring
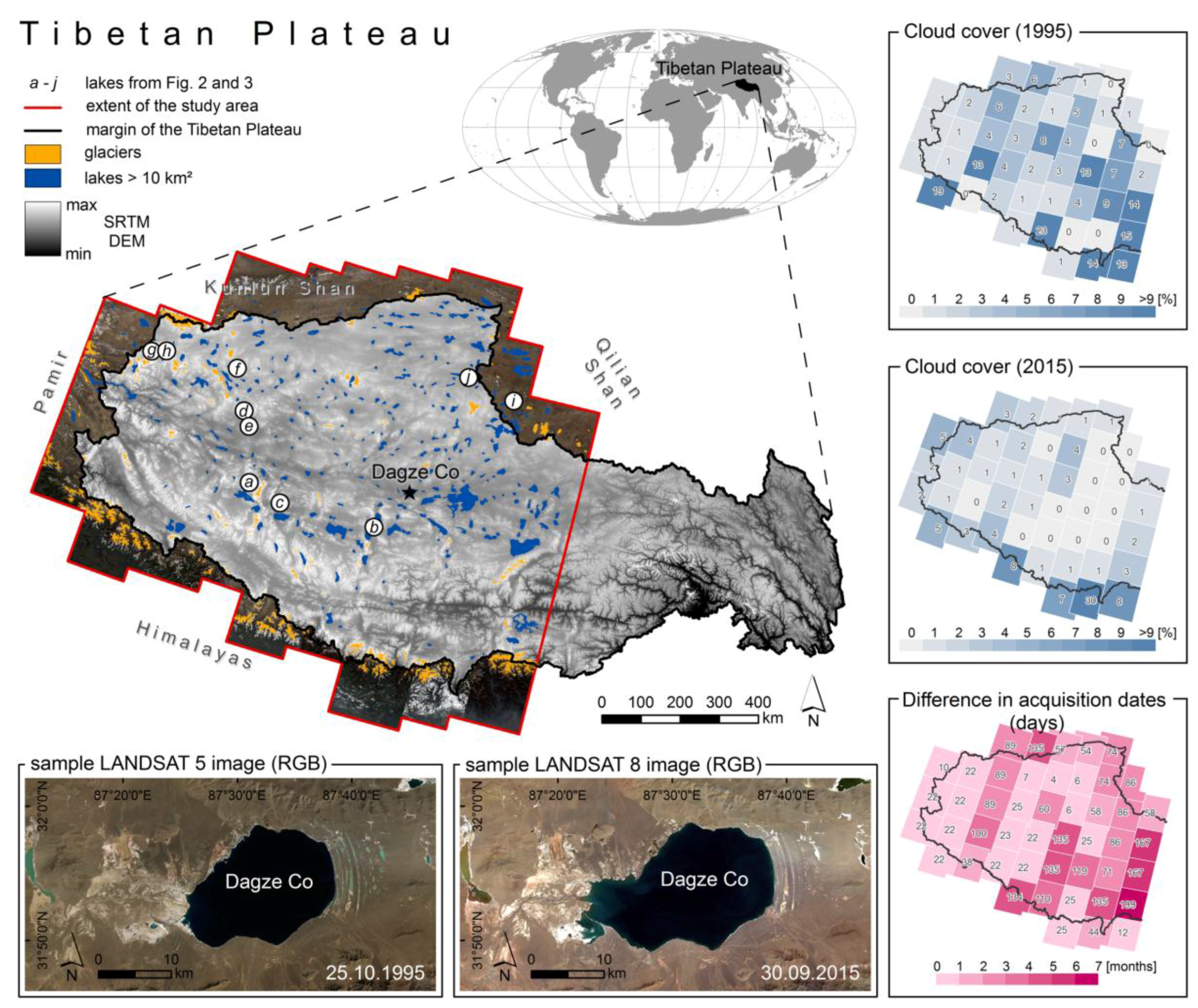
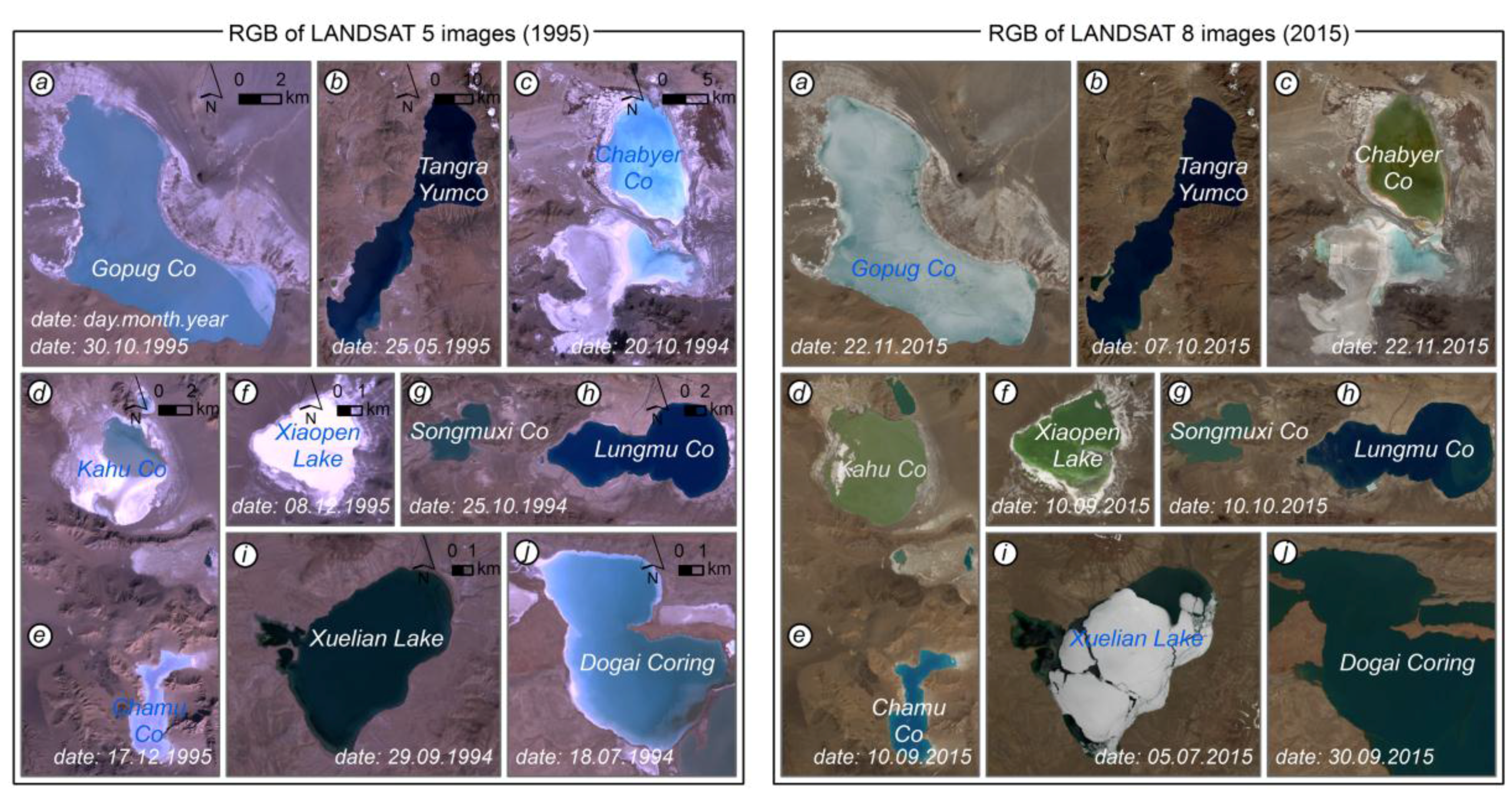
3. Study Area and Data
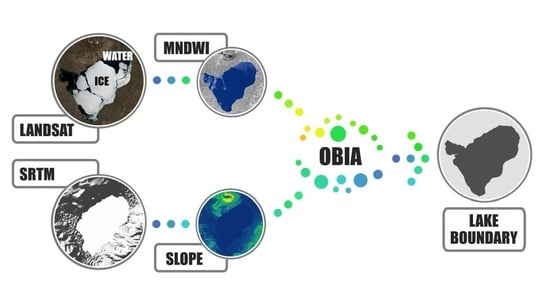
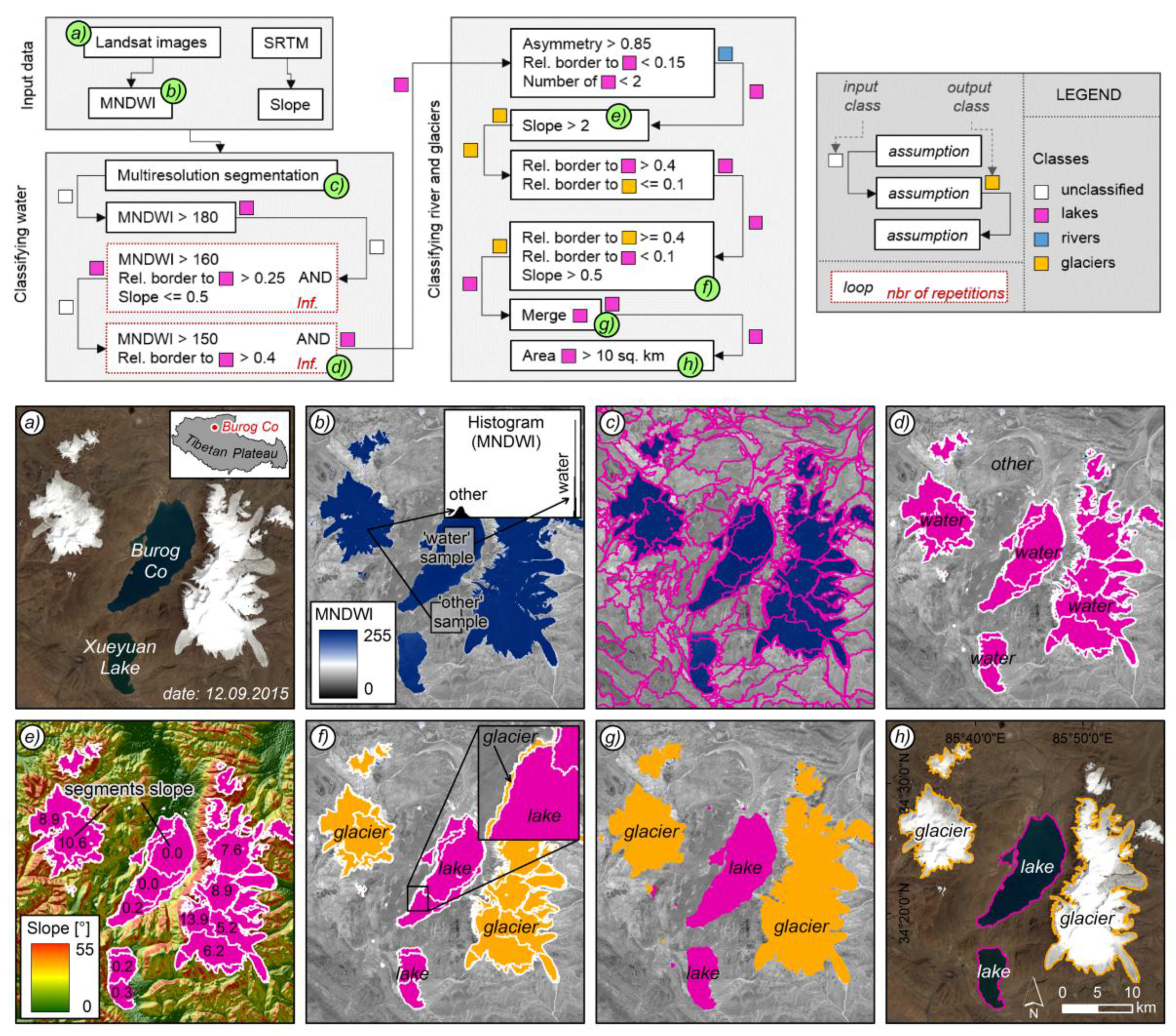
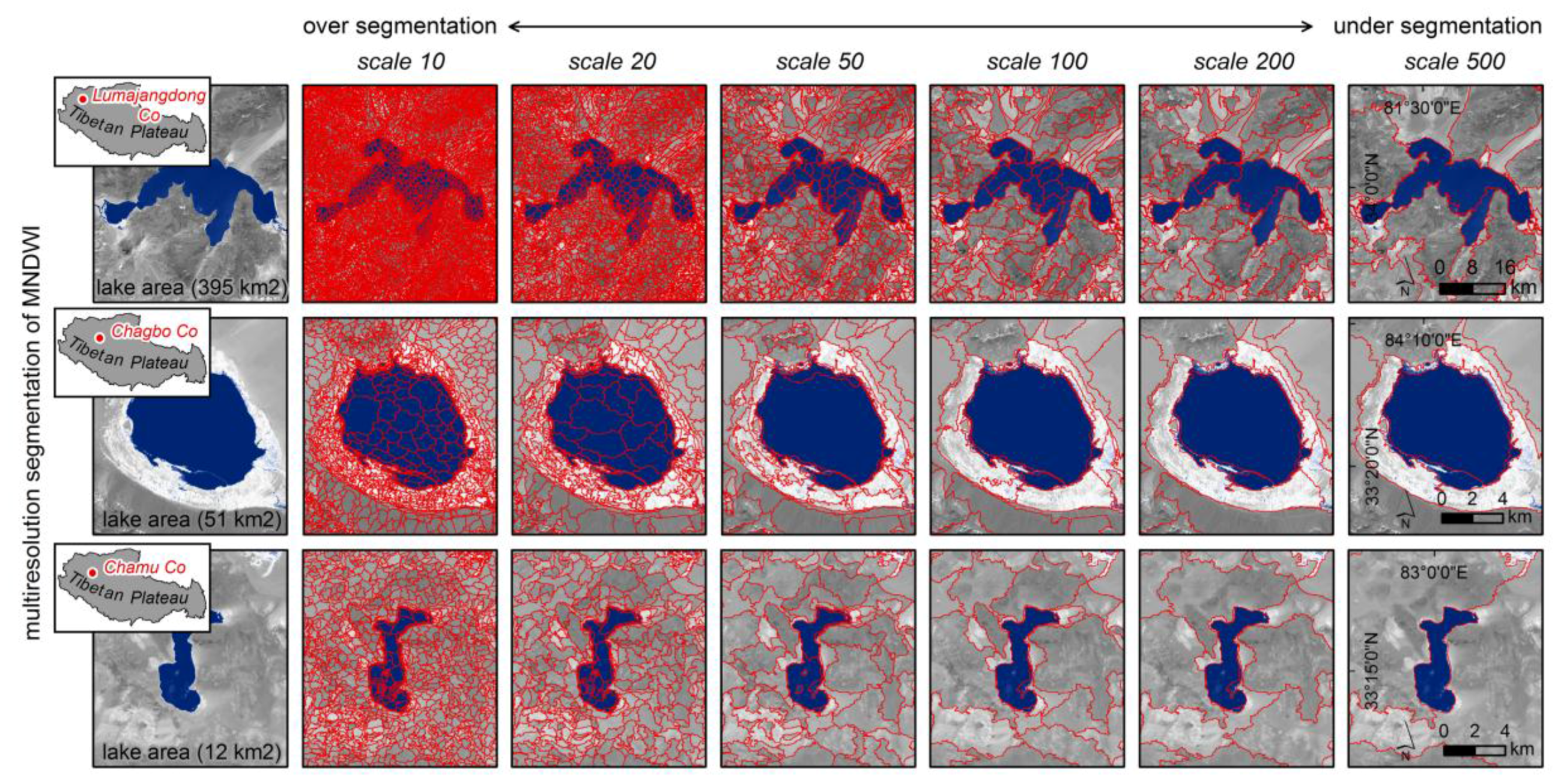
4. Methods
5. Results
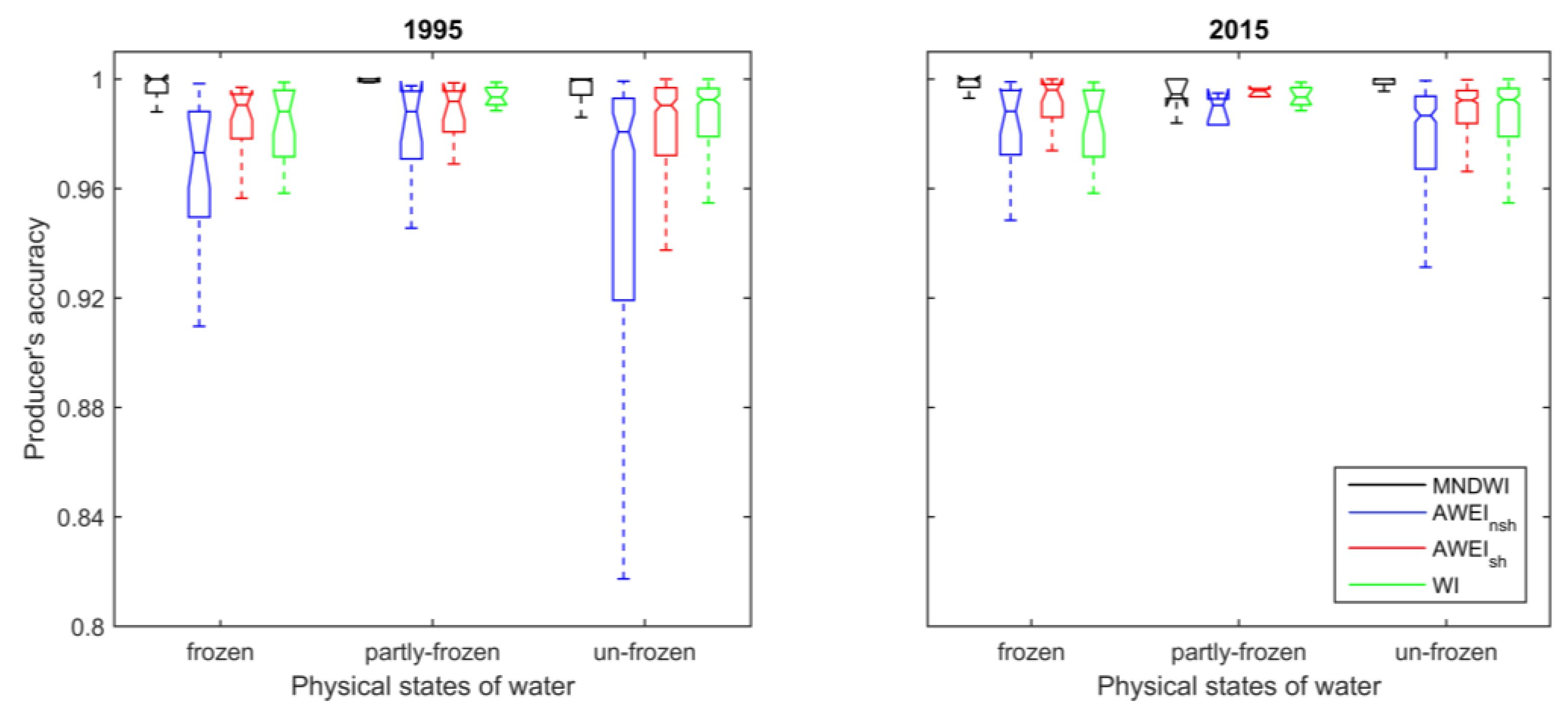
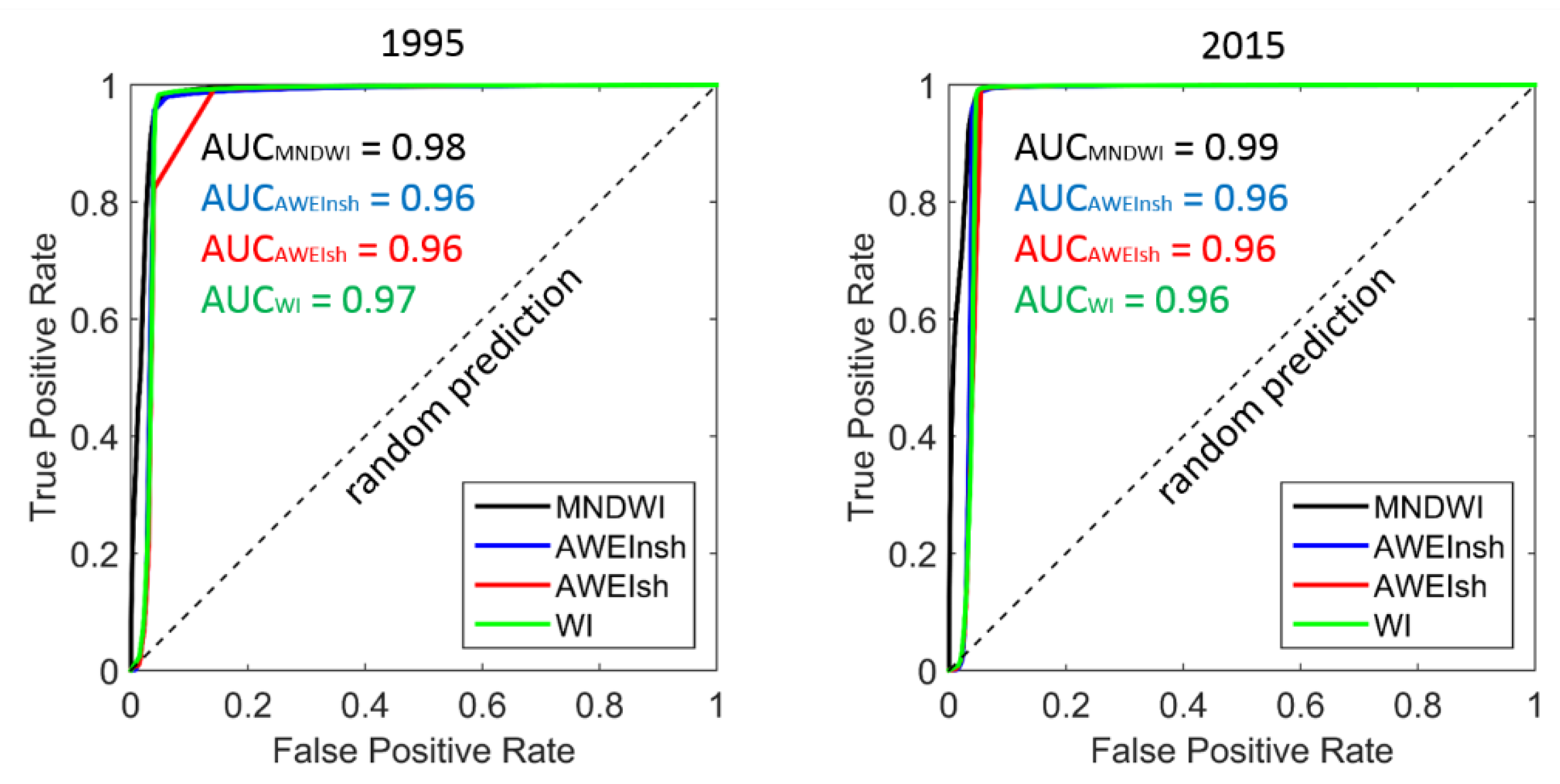
5.1. Accuracy of Extracted Lakes
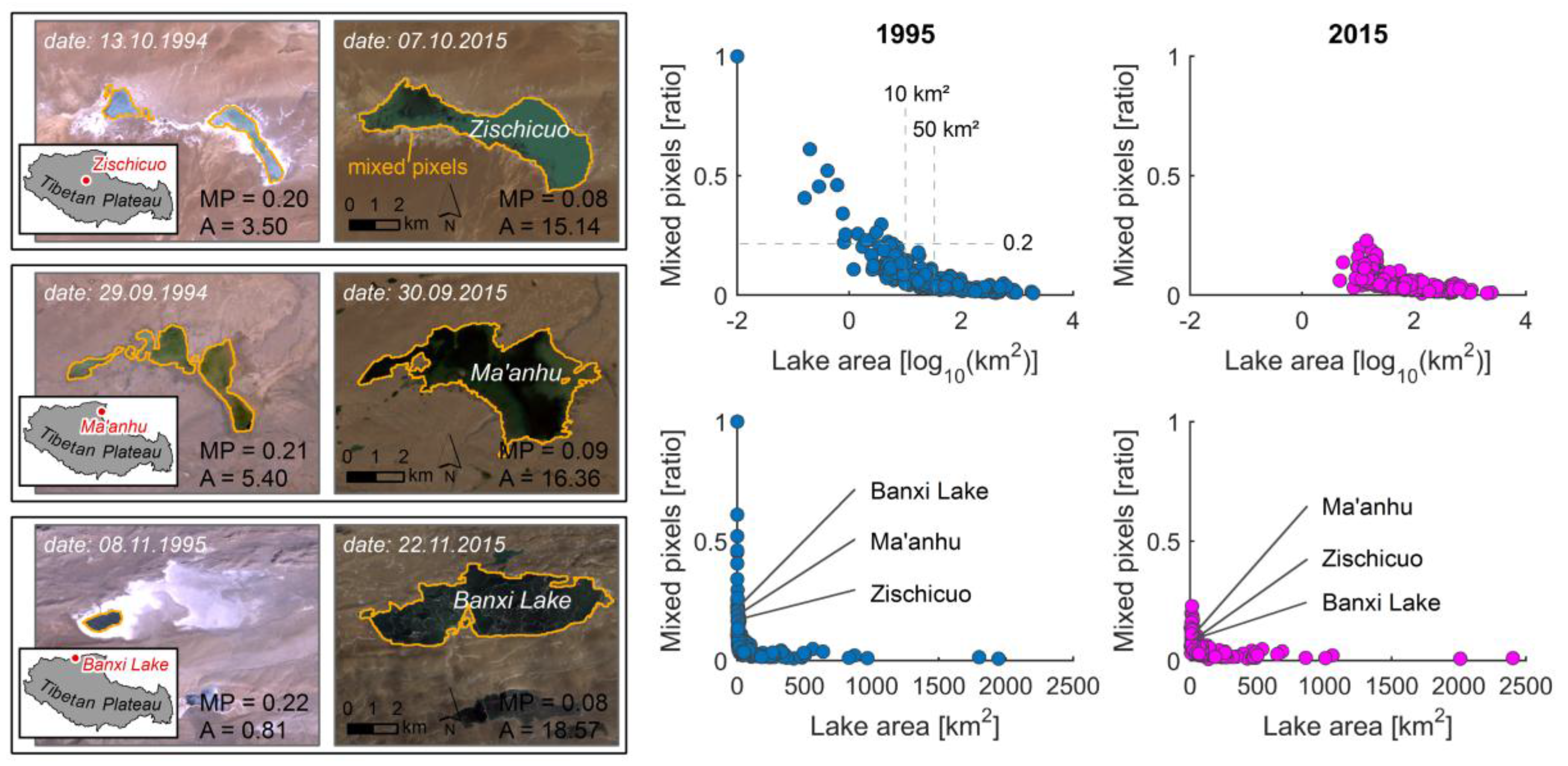
5.2. Sources of Error in the Analyses
5.3. Lake-Area Changes (1995–2015)
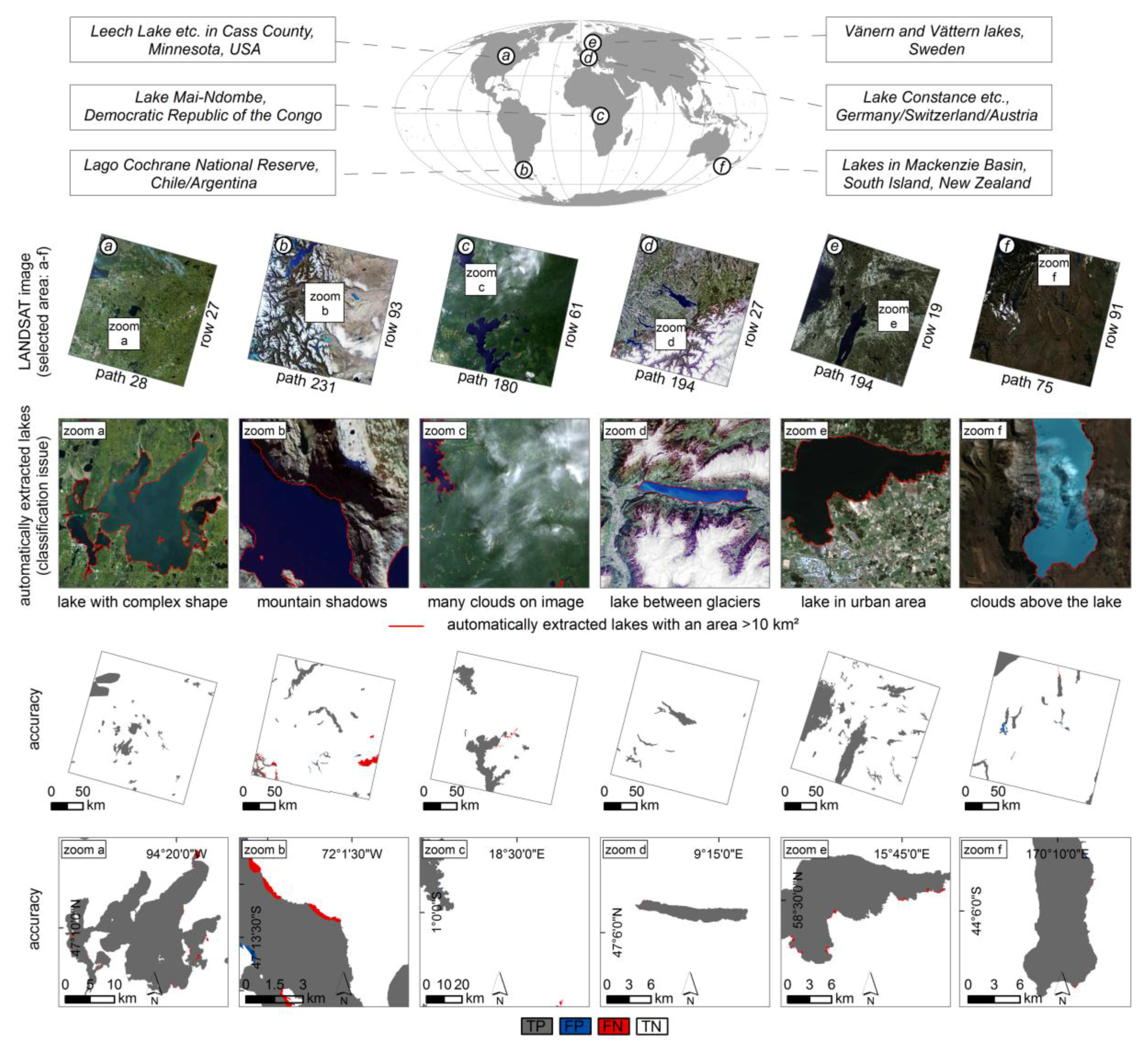
5.4. Transferability of OBIA Approach
6. Discussion
7. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Qiu, J. The Third Pole. Nature 2008, 454, 393–396. [Google Scholar] [CrossRef] [PubMed]
- Song, C.; Huang, B.; Ke, L.; Richards, K.S. Remote sensing of alpine lake water environment changes on the Tibetan Plateau and surroundings: A review. ISPRS J. Photogramm. Remote Sens. 2014, 92, 26–37. [Google Scholar] [CrossRef]
- Wang, C. A remote sensing perspective of alpine grasslands on the Tibetan Plateau: Better or worse under ‘Tibet Warming’? Remote Sens. Appl. Soc. Environ. 2016, 3, 36–44. [Google Scholar] [CrossRef]
- Liu, X.; Chen, B. Climatic warming in the Tibetan Plateau during recent decades. Int. J. Climatol. 2000, 20, 1729–1742. [Google Scholar] [CrossRef]
- Immerzeel, W.W.; van Beek, L.P.H.; Bierkens, M.F.P. Climate change will affect the Asian Water Towers. Science 2010, 328, 1382–1385. [Google Scholar] [CrossRef] [PubMed]
- Song, C.; Huang, B.; Ke, L. Modeling and analysis of lake water storage changes on the Tibetan Plateau using multi-mission satellite data. Remote Sens. Environ. 2013, 135, 25–35. [Google Scholar] [CrossRef]
- Immerzeel, W.W.; Kraaijenbrink, P.D.A.; Shea, J.M.; Shrestha, A.B.; Pellicciotti, F.; Bierkens, M.F.P.; De Jong, S.M. High-resolution monitoring of Himalayan glacier dynamics using unmanned aerial vehicles. Remote Sens. Environ. 2014, 150, 93–103. [Google Scholar] [CrossRef]
- Yao, T.; Thompson, L.; Yang, W.; Yu, W.; Gao, Y.; Guo, X.; Yang, X.; Duan, K.; Zhao, H.; Xu, B.; et al. Different glacier status with atmospheric circulations in Tibetan Plateau and surroundings. Nat. Clim. Chang. 2012, 2, 663–667. [Google Scholar] [CrossRef]
- Zhang, Y.; Yao, T.; Ma, Y. Climatic changes have led to significant expansion of endorheic lakes in Xizang (Tibet) since 1995. Sci. Cold Arid Reg. 2011, 3, 463–467. [Google Scholar]
- Yao, T.; Thompson, L.G.; Mosbrugger, V.; Zhang, F.; Ma, Y.; Luo, T.; Xu, B.; Yang, X.; Tayal, S.; Jilani, R.; et al. Third Pole Environment (TPE). Environ. Dev. 2012, 3, 52–64. [Google Scholar] [CrossRef]
- Yang, W.; Yao, T.; Xu, B.; Wu, G.; Ma, L.; Xin, X. Quick ice mass loss and abrupt retreat of the maritime glaciers in the Kangri Karpo Mountains, southeast Tibetan Plateau. Chin. Sci. Bull. 2008, 53, 2547–2551. [Google Scholar] [CrossRef]
- Yang, M.; Nelson, F.E.; Shiklomanov, N.I.; Guo, D.; Wan, G. Permafrost degradation and its environmental effects on the Tibetan Plateau: A review of recent research. Earth-Sci. Rev. 2010, 103, 31–44. [Google Scholar] [CrossRef]
- Yang, X.; Lu, X. Drastic change in China’s lakes and reservoirs over the past decades. Sci. Rep. 2014, 4, 1–10. [Google Scholar] [CrossRef] [PubMed]
- Shao, Z.G.; Zhu, D.G.; Meng, X.G.; Zheng, D.X.; Qiao, Z.J.; Bin Yang, C.; Han, J.E.; Yu, J.; Meng, Q.W.; Lü, R.P. Characteristics of the change of major lakes on the Qinghai-Tibet Plateau in the last 25 years. Geol. Bull. China 2007, 26, 1633–1645. [Google Scholar] [CrossRef]
- Zhu, L.P.; Xie, M.P.; Wu, Y.H. Quantitative analysis of lake area variations and the influence factors from 1971 to 2004 in the Nam Co basin of the Tibetan Plateau. Chin. Sci. Bull. 2010, 55, 1294–1303. [Google Scholar] [CrossRef]
- Zhang, G.; Xie, H.; Kang, S.; Yi, D.; Ackley, S.F. Monitoring lake level changes on the Tibetan Plateau using ICESat altimetry data (2003–2009). Remote Sens. Environ. 2011, 115, 1733–1742. [Google Scholar] [CrossRef]
- Phan, V.H.; Lindenbergh, R.; Menenti, M. ICESat derived elevation changes of Tibetan lakes between 2003 and 2009. Int. J. Appl. Earth Obs. Geoinf. 2012, 17, 12–22. [Google Scholar] [CrossRef]
- Ouma, Y.O.; Tateishi, R. A water index for rapid mapping of shoreline changes of five East African Rift Valley lakes: An empirical analysis using Landsat TM and ETM+ data. Int. J. Remote Sens. 2006, 27, 3153–3181. [Google Scholar] [CrossRef]
- Song, C.; Huang, B.; Ke, L.; Richards, K.S. Seasonal and abrupt changes in the water level of closed lakes on the Tibetan Plateau and implications for climate impacts. J. Hydrol. 2014, 514, 131–144. [Google Scholar] [CrossRef]
- Ma, R.; Duan, H.; Hu, C.; Feng, X.; Li, A.; Ju, W.; Jiang, J.; Yang, G. A half-century of changes in China’s lakes: Global warming or human influence? Geophys. Res. Lett. 2010, 37, 2–7. [Google Scholar] [CrossRef]
- Fang, Y.; Cheng, W.; Zhang, Y.; Wang, N.; Zhao, S.; Zhou, C.; Chen, X.; Bao, A. Changes in inland lakes on the Tibetan Plateau over the past 40 years. J. Geogr. Sci. 2016, 26, 415–438. [Google Scholar] [CrossRef]
- Liu, J.; Kang, S.; Gong, T.; Lu, A. Growth of a high-elevation large inland lake, associated with climate change and permafrost degradation in Tibet. Hydrol. Earth Syst. Sci. 2010, 14, 481–489. [Google Scholar] [CrossRef]
- Lei, Y.; Yao, T.; Bird, B.W.; Yang, K.; Zhai, J.; Sheng, Y. Coherent lake growth on the central Tibetan Plateau since the 1970s: Characterization and attribution. J. Hydrol. 2013, 483, 61–67. [Google Scholar] [CrossRef]
- Li, J.; Sheng, Y.; Luo, J. Automatic extraction of Himalayan glacial lakes with remote sensing. J. Remote Sens. 2011, 15, 29–43. [Google Scholar]
- Wang, X.; Gong, P.; Zhao, Y.; Xu, Y.; Cheng, X.; Niu, Z.; Luo, Z.; Huang, H.; Sun, F.; Li, X. Water-level changes in China’s large lakes determined from ICESat/GLAS data. Remote Sens. Environ. 2013, 132, 131–144. [Google Scholar] [CrossRef]
- Blaschke, T. Object based image analysis for remote sensing. ISPRS J. Photogramm. Remote Sens. 2010, 65, 2–16. [Google Scholar] [CrossRef]
- Xu, H. Modification of normalised difference water index (NDWI) to enhance open water features in remotely sensed imagery. Int. J. Remote Sens. 2006, 27, 3025–3033. [Google Scholar] [CrossRef]
- Singh, A. Review Article Digital change detection techniques using remotely-sensed data. Int. J. Remote Sens. 1989, 10, 989–1003. [Google Scholar] [CrossRef]
- Melesse, A.M.; Weng, Q.; Thenkabail, P.S.; Seney, G.B. Remote sensing sensors and applications in environmental resources mapping and modelling. Sensors 2007, 7, 3209–3241. [Google Scholar] [CrossRef]
- Arp, C.D.; Jones, B.M.; Lu, Z.; Whitman, M.S. Shifting balance of thermokarst lake ice regimes across the Arctic Coastal Plain of northern Alaska. Geophys. Res. Lett. 2012, 39, 1–5. [Google Scholar] [CrossRef]
- Chander, G.; Markham, B.L.; Helder, D.L. Summary of current radiometric calibration coefficients for Landsat MSS, TM, ETM+, and EO-1 ALI sensors. Remote Sens. Environ. 2009, 113, 893–903. [Google Scholar] [CrossRef]
- Frazier, P.S.; Page, K.J. Water body detection and delineation with Landsat TM data. Photogramm. Eng. Remote Sens. 2000, 66, 1461–1467. [Google Scholar]
- McFeeters, S.K. Using the normalized difference water index (NDWI) within a geographic information system to detect swimming pools for mosquito abatement: A practical approach. Remote Sens. 2013, 5, 3544–3561. [Google Scholar] [CrossRef]
- Mueller, N.; Lewis, A.; Roberts, D.; Ring, S.; Melrose, R.; Sixsmith, J.; Lymburner, L.; McIntyre, A.; Tan, P.; Curnow, S.; et al. Water observations from space: Mapping surface water from 25 years of Landsat imagery across Australia. Remote Sens. Environ. 2016, 174, 341–352. [Google Scholar] [CrossRef]
- Yang, K.; Smith, L.C. Supraglacial streams on the Greenland ice sheet delineated from combined spectral-shape information in high-resolution satellite imagery. IEEE Geosci. Remote Sens. Lett. 2013, 10, 801–805. [Google Scholar] [CrossRef]
- Fitzpatrick, A.A.W.; Hubbard, A.L.; Box, J.E.; Quincey, D.J.; Van As, D.; Mikkelsen, A.P.B.; Doyle, S.H.; Dow, C.F.; Hasholt, B.; Jones, G.A. A decade (2002–2012) of supraglacial lake volume estimates across Russell Glacier, West Greenland. Cryosphere 2014, 8, 107–121. [Google Scholar] [CrossRef]
- Zhu, W.; Jia, S.; Lv, A. Monitoring the fluctuation of Lake Qinghai using multi-source remote sensing data. Remote Sens. 2014, 6, 10457–10482. [Google Scholar] [CrossRef]
- Nath, R.K.; Deb, S.K. Water-body area extraction from high resolution satellite images-An Introduction, review, and comparison. Int. J. Image Process. 2010, 3, 353–372. [Google Scholar]
- Ryu, J.H.; Won, J.S.; Min, K.D. Waterline extraction from Landsat TM data in a tidal flat a case study in Gomso Bay, Korea. Remote Sens. Environ. 2002, 83, 442–456. [Google Scholar] [CrossRef]
- McFeeters, S.K. The use of the Normalized Difference Water Index (NDWI) in the delineation of open water features. Int. J. Remote Sens. 1996, 17, 1425–1432. [Google Scholar] [CrossRef]
- Townshend, J.R.G.; Justice, C.O. Analysis of the dynamics of African vegetation using the normalized difference vegetation index. Int. J. Remote Sens. 1986, 7, 1435–1445. [Google Scholar] [CrossRef]
- Rogers, A.S.; Kearney, M.S. Reducing signature variability in unmixing coastal marsh Thematic Mapper scenes using spectral indices. Int. J. Remote Sens. 2004, 25, 2317–2335. [Google Scholar] [CrossRef]
- Ji, L.; Zhang, L.; Wylie, B. Analysis of dynamic thresholds for the Normalized Difference Water Index. Photogramm. Eng. Remote Sens. 2009, 75, 1307–1317. [Google Scholar] [CrossRef]
- Feyisa, G.L.; Meilby, H.; Fensholt, R.; Proud, S.R. Automated Water Extraction Index: A new technique for surface water mapping using Landsat imagery. Remote Sens. Environ. 2014, 140, 23–35. [Google Scholar] [CrossRef]
- Fisher, A.; Flood, N.; Danaher, T. Comparing Landsat water index methods for automated water classification in eastern Australia. Remote Sens. Environ. 2016, 175, 167–182. [Google Scholar] [CrossRef]
- Jawak, S.D.; Kulkarni, K.; Luis, A.J. A review on extraction of lakes from remotely sensed optical satellite data with a special focus on cryospheric lakes. Adv. Remote Sens. 2015, 4, 196–213. [Google Scholar] [CrossRef]
- Habib, T.; Gay, M.; Chanussot, J.; Bertolino, P. Segmentation of high resolution satellite images SPOT applied to lake detection. In Proceedings of the IEEE International Conference on Geoscience and Remote Sensing Symposium, Denver, CO, USA, 31 July–4 August 2006; pp. 3680–3683. [Google Scholar]
- Verpoorter, C.; Kutser, T.; Tranvik, L.J. Automated mapping of water bodies using Landsat multispectral data. Limnol. Oceanogr. Methods 2012, 10, 1037–1050. [Google Scholar] [CrossRef]
- Jiang, H.; Feng, M.; Zhu, Y.; Lu, N.; Huang, J.; Xiao, T. An automated method for extracting rivers and lakes from Landsat imagery. Remote Sens. 2014, 6, 5067–5089. [Google Scholar] [CrossRef]
- Yamazaki, D.; Trigg, M.A.; Ikeshima, D. Development of a global ~90 m water body map using multi-temporal Landsat images. Remote Sens. Environ. 2015, 171, 337–351. [Google Scholar] [CrossRef]
- Sheng, Y.; Song, C.; Wang, J.; Lyons, E.A.; Knox, B.R.; Cox, J.S.; Gao, F. Representative lake water extent mapping at continental scales using multi-temporal Landsat-8 imagery. Remote Sens. Environ. 2016, 185, 129–141. [Google Scholar] [CrossRef]
- Gao, H.; Birkett, C.; Lettenmaier, D.P. Global monitoring of large reservoir storage from satellite remote sensing. Water Resour. Res. 2012, 48, 1–12. [Google Scholar] [CrossRef]
- Deus, D.; Gloaguen, R. Remote sensing analysis of lake dynamics in semi-arid regions: Implication for water resource management. Lake Manyara, East African Rift, Northern Tanzania. Water 2013, 5, 698–727. [Google Scholar] [CrossRef]
- Bai, J.; Chen, X.; Li, J.; Yang, L.; Fang, H. Changes in the area of inland lakes in arid regions of central Asia during the past 30 years. Environ. Monit. Assess. 2011, 178, 247–256. [Google Scholar] [CrossRef] [PubMed]
- Rokni, K.; Ahmad, A.; Selamat, A.; Hazini, S. Water feature extraction and change detection using multitemporal landsat imagery. Remote Sens. 2014, 6, 4173–4189. [Google Scholar] [CrossRef]
- Reuter, H.I.; Nelson, A.; Jarvis, A. An evaluation of void-filling interpolation methods for SRTM data. Int. J. Geogr. Inf. Sci. 2007, 21, 983–1008. [Google Scholar] [CrossRef]
- Baatz, M.; Schäpe, A. Multiresolution Segmentation: An Optimization Approach for High Quality Multi-Scale Image Segmentation; Strobl, J., Blaschke, T., Griesebner, G., Eds.; Angew. Geogr. Informationsverarbeitung XII. Beiträge zum Agit. Salzbg; Herbert Wichmann Verlag: Karlsruhe, Germany, 2000; pp. 12–23. [Google Scholar]
- Drǎguţ, L.; Tiede, D.; Levick, S.R. ESP: A tool to estimate scale parameter for multiresolution image segmentation of remotely sensed data. Int. J. Geogr. Inf. Sci. 2010, 24, 859–871. [Google Scholar] [CrossRef]
- Martha, T.R.; Kerle, N.; Van Westen, C.J.; Jetten, V.; Kumar, K.V. Segment optimization and data-driven thresholding for knowledge-based landslide detection by object-based image analysis. IEEE Trans. Geosci. Remote Sens. 2011, 49, 4928–4943. [Google Scholar] [CrossRef]
- Sithole, G.; Vosselman, G. Experimental comparison of filter algorithms for bare-Earth extraction from airborne laser scanning point clouds. ISPRS J. Photogramm. Remote Sens. 2004, 59, 85–101. [Google Scholar] [CrossRef]
- Congalton, R.G. A review of assessing the accuracy of classifications of remotely sensed data. Remote Sens. Environ. 1991, 37, 35–46. [Google Scholar] [CrossRef]
- Cohen, J. A coefficient of agreement for nominal scales. Educ. Psychol. Meas. 1960, 20, 37–46. [Google Scholar] [CrossRef]
- Jawak, S.D.; Luis, A.J. A semiautomatic extraction of Antarctic lake features using Worldview-2 imagery. Photogramm. Eng. Remote Sens. 2014, 80, 33–46. [Google Scholar] [CrossRef]


| Index | Equation | Author |
|---|---|---|
| Normalised Difference Vegetation Index | NDVI = ( − )/( + ) | Townshend and Justice [41] |
| Normalised Difference Water Index | NDWI = ( − )/( + ) | McFeeters [40] |
| Normalised Difference Water Index | NDWI = ( − )/( + ) | Rogers and Kearny [42] |
| Modified Normalised Difference Water Index | MNDWI = ( − )/( + ) | Xu [27] |
| Automated Water Extraction Index (for non-shadow areas) | Feyisa et al. [44] | |
| Automated Water Extraction Index (for shadow areas) | Feyisa et al. [44] | |
| Water Index | Fisher et al. [45] |
| Performance Metrics | ||
|---|---|---|
| Type I error | FP/(TP + FP) |  |
| Type II error | FN/(FN + TN) | |
| Total error | (FP + FN)/(TP + FP + FN + TN) | |
| Overall accuracy | (TP + TN)/(TP + FP + FN + TN) | |
| Producer’s accuracy | TP/(TP + FP) | |
| User’s accuracy | TP/(TP + FN) | |
| Cohen’s kappa | (po − pe)/(1 − pe) | |
| F-score | 2TP/(2TP + FP + FN) | |
| Root mean square error | ||
| Mean absolute error | ||
| Bias (Mean error) | ||
| Performance Metric | 1995 | 2015 | ||||||
|---|---|---|---|---|---|---|---|---|
| MNDWI | WI | AWEInsh | AWEIsh | MNDWI | WI | AWEInsh | AWEIsh | |
| Type I | 0.0134 | 0.0089 | 0.0234 | 0.0140 | 0.0169 | 0.0081 | 0.0337 | 0.0143 |
| Type II | 0.0003 | 0.0016 | 0.0005 | 0.0022 | 0.0005 | 0.0018 | 0.0007 | 0.0016 |
| Total | 0.0006 | 0.0018 | 0.0010 | 0.0024 | 0.0010 | 0.0020 | 0.0016 | 0.0020 |
| O. Acc. | 0.9994 | 0.9982 | 0.9990 | 0.9976 | 0.9990 | 0.9980 | 0.9984 | 0.9980 |
| P. Acc. | 0.9866 | 0.9911 | 0.9766 | 0.9860 | 0.9831 | 0.9919 | 0.9663 | 0.9857 |
| U. Acc. | 0.9850 | 0.9292 | 0.9778 | 0.9073 | 0.9808 | 0.9376 | 0.9732 | 0.9428 |
| Kappa | 0.9855 | 0.9583 | 0.9767 | 0.9438 | 0.9815 | 0.9630 | 0.9690 | 0.9628 |
| F-score | 0.9858 | 0.9592 | 0.9772 | 0.9450 | 0.9819 | 0.9640 | 0.9698 | 0.9638 |
| RMSE | 0.0244 | 0.0420 | 0.0309 | 0.0490 | 0.0309 | 0.0442 | 0.0398 | 0.0442 |
| MAE | 0.0005 | 0.0018 | 0.0010 | 0.0024 | 0.0010 | 0.0020 | 0.0016 | 0.0020 |
| ME | −0.0003 | −0.0014 | 0.0003 | −0.0018 | −0.0001 | −0.0015 | 0.0002 | −0.0012 |
| TS | Continent (Country) | Landscape Type | Extracted Lakes | Date | TA |
|---|---|---|---|---|---|
| a | North America (USA) | Flat area | Leech Lake, etc. in Cass County, Minnesota | 29.09.2015 | 2156.28 |
| b | South America (Chile/Argentina) | Mountains | Lakes in Lago Cochrane National Reserve | 01.04.2014 | 1518.87 |
| c | Africa (Democratic Republic of the Congo) | Flat forested area | Mai-Ndombe Lake, etc. | 12.01.2016 | 2812.52 |
| d | Europe (Germany/Switzerland/Austria) | Mountains with glaciers | Constance Lake, etc. | 22.05.2016 | 802.76 |
| e | Europe (Sweden) | Lakeland—flat postglacial area | Vänern and Vättern Lakes, etc. | 09.05.2016 | 5848.82 |
| f | Australia (New Zealand) | Hilly region | Lakes in Mackenzie Basin | 17.03.2016 | 1696.70 |
| Performance Metrics | Test Area | |||||
|---|---|---|---|---|---|---|
| a | b | c | d | e | f | |
| Type I error | 0.0022 | 0.0216 | 0.0021 | 0.0050 | 0.0025 | 0.0471 |
| Type II error | 0.0004 | 0.0120 | 0.0014 | 0.0001 | 0.0012 | 0.0005 |
| Total error | 0.0005 | 0.0124 | 0.0014 | 0.0002 | 0.0014 | 0.0027 |
| Overall accuracy | 0.9995 | 0.9876 | 0.9986 | 0.9998 | 0.9986 | 0.9973 |
| Producer’s accuracy | 0.9978 | 0.9784 | 0.9979 | 0.9950 | 0.9975 | 0.9529 |
| User’s accuracy | 0.9940 | 0.7825 | 0.9835 | 0.9948 | 0.9939 | 0.9899 |
| Cohen’s kappa | 0.9956 | 0.8631 | 0.9898 | 0.9948 | 0.9949 | 0.9697 |
| F-score | 0.9959 | 0.8695 | 0.9906 | 0.9949 | 0.9957 | 0.9711 |
| Root mean square error | 0.0220 | 0.1113 | 0.0381 | 0.0149 | 0.0369 | 0.0515 |
| Mean absolute error | 0.0005 | 0.0124 | 0.0014 | 0.0002 | 0.0014 | 0.0027 |
| Mean error | −0.0002 | −0.0106 | −0.0011 | −0.0001 | −0.0006 | 0.0017 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Korzeniowska, K.; Korup, O. Object-Based Detection of Lakes Prone to Seasonal Ice Cover on the Tibetan Plateau. Remote Sens. 2017, 9, 339. https://doi.org/10.3390/rs9040339
Korzeniowska K, Korup O. Object-Based Detection of Lakes Prone to Seasonal Ice Cover on the Tibetan Plateau. Remote Sensing. 2017; 9(4):339. https://doi.org/10.3390/rs9040339
Chicago/Turabian StyleKorzeniowska, Karolina, and Oliver Korup. 2017. "Object-Based Detection of Lakes Prone to Seasonal Ice Cover on the Tibetan Plateau" Remote Sensing 9, no. 4: 339. https://doi.org/10.3390/rs9040339
APA StyleKorzeniowska, K., & Korup, O. (2017). Object-Based Detection of Lakes Prone to Seasonal Ice Cover on the Tibetan Plateau. Remote Sensing, 9(4), 339. https://doi.org/10.3390/rs9040339