Texture-Guided Multisensor Superresolution for Remotely Sensed Images
Abstract
:1. Introduction
- Versatile methodology: This paper proposes a versatile methodology for multisensor superresolution in remote sensing.
- Comprehensive evaluation: This paper demonstrates six different types of multisensor superresolution, which fuse the following image pairs: MS-PAN images (MS pan-sharpening), HS-PAN images (HS pan-sharpening), HS-MS images, optical-SAR images, long-wavelength infrared (LWIR) HS and RGB images, and DEM-MS images. The performance of TGMS is evaluated both quantitatively and qualitatively.
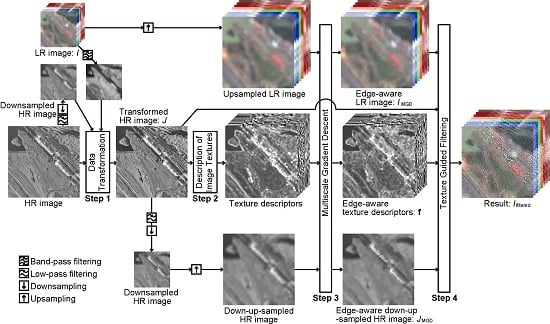
2. Texture-Guided Multisensor Superresolution
2.1. Data Transformation
2.2. Texture Descriptors
2.3. Multiscale Gradient Descent
2.4. Texture-Guided Filtering
3. Evaluation Methodology
3.1. Three Evaluation Scenarios
3.1.1. Synthetic Data Evaluation
3.1.2. Semi-Real Data Evaluation
3.1.3. Real Data Evaluation
3.2. Quality Indices
3.2.1. PSNR
3.2.2. SAM
3.2.3. ERGAS
3.2.4.
4. Experiments on Optical Data Fusion
4.1. Data Sets
4.1.1. MS Pan-Sharpening
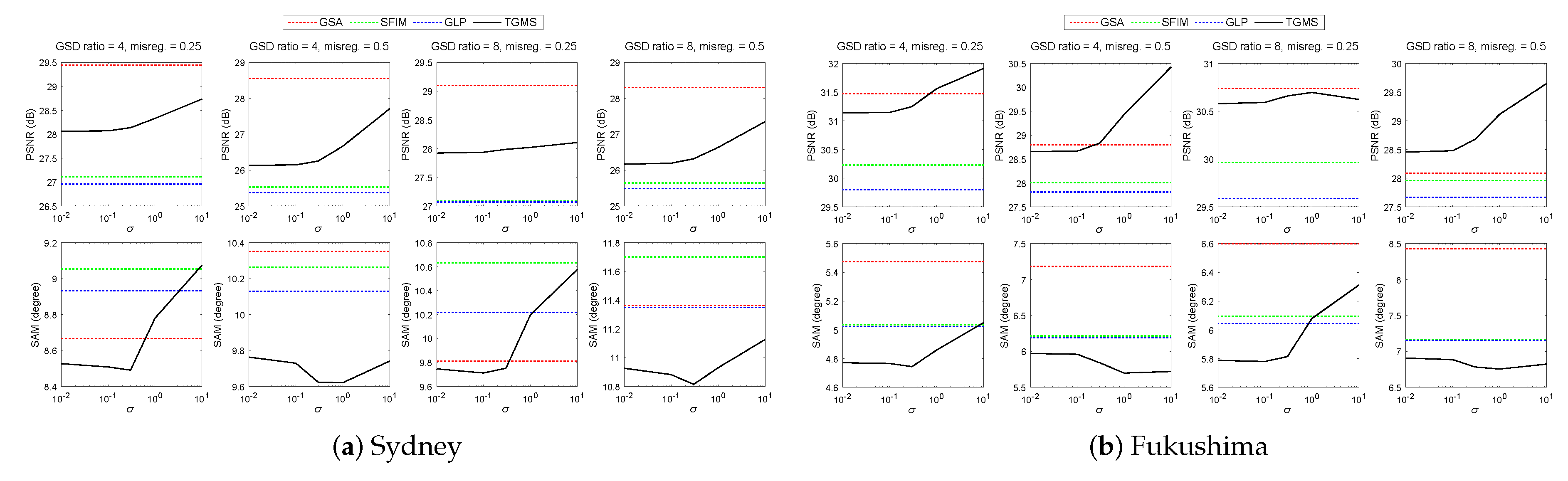
- WorldView-3 Sydney: This data set was acquired by the visible and near-infrared (VNIR) and PAN sensors of WorldView-3 over Sydney, Australia, on 15 October 2014. (Available Online: https://www.digitalglobe.com/resources/imagery-product-samples/standard-satellite-imagery). The MS image has eight spectral bands in the VNIR range. The GSDs of the MS-PAN images are 1.6 m and 0.4 m, respectively. The study area is a 1000 × 1000 pixel size image at the resolution of the MS image, which includes parks and urban areas.
- WorldView-3 Fukushima: This data set was acquired by the VNIR and PAN sensors of WorldView-3 over Fukushima, Japan, on 10 August 2015. The MS image has eight spectral bands in the VNIR range. The GSDs of the MS-PAN images are 1.2 m and 0.3 m, respectively. The study area is a 1000×1000 pixel size image at the resolution of the MS image taken over a town named Futaba.
4.1.2. HS Pan-Sharpening
- ROSIS-3 University of Pavia: This data was acquired by the reflective optics spectrographic imaging system (ROSIS-3) optical airborne sensor over the University of Pavia, Italy, in 2003. A total of 103 bands covering the spectral range from 0.430 to 0.838 m are used in the experiment after removing 12 noisy bands. The study scene is a 560 × 320 pixel size image with a GSD of 1.3 m.
- Hyperspec-VNIR Chikusei: The airborne HS data set was taken by Headwall’s Hyperspec-VNIR-C imaging sensor over agricultural and urban areas in Chikusei, Ibaraki, Japan, on 19 July 2014. The data set comprises 128 bands in the spectral range from 0.363 to 1.018 m. The study scene is a 540 × 420 pixel size image with a GSD of 2.5 m. More detailed descriptions regarding the data acquisition and processing are given in [48].
4.1.3. HS-MS Data Fusion
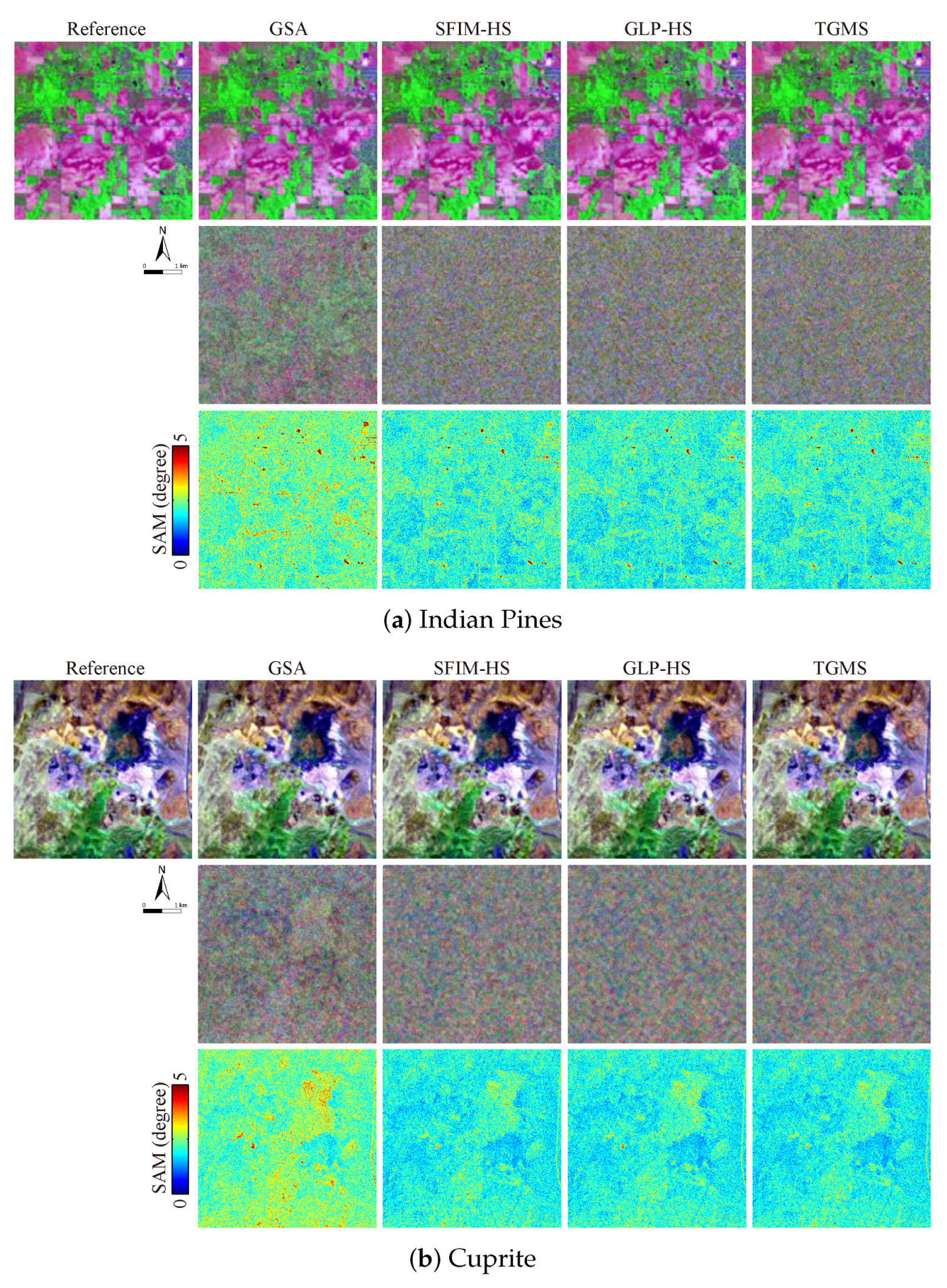
- AVIRIS Indian Pines: This HS image was acquired by the AVIRIS sensor over the Indian Pines test site in northwestern Indiana, USA, in 1992 [49]. The AVIRIS sensor acquired 224 spectral bands in the wavelength range from 0.4 to 2.5 m with an FWHM of 10 nm. The image consists of 512 × 614 pixels at a GSD of 20 m. The study area is a 360 × 360 pixel size image with 192 bands after removing bands of strong water vapor absorption and low SNRs.
- AVIRIS Cuprite: This data set was acquired by the AVIRIS sensor over the Cuprite mining district in Nevada, USA, in 1995. (Available Online: http://aviris.jpl.nasa.gov/data/free_data.html). The entire data set comprises five reflectance images and this study used one of them saved in the file named f970619t01p02_r02_sc03.a.rfl. The full image consists of 512 × 614 pixels at a GSD of 20 m. The study area is a 420 × 360 pixel size image with 185 bands after removing noisy bands.
4.2. Results
4.2.1. MS Pan-Sharpening
4.2.2. HS Pan-Sharpening
4.2.3. HS-MS Fusion
4.2.4. Parameter Sensitivity Analysis
5. Experiments on Multimodal Data Fusion
5.1. Data Sets
- Optical-SAR fusion: This data set is composed of Landsat-8 and TerraSAR-X images taken over the Panama Canal, Panama. The Landsat-8 image was acquired on 5 March 2015. Bands 1–7 at a GSD of 30 m are used for the LR image of multisensor superresolution. The TerraSAR-X image was acquired with the sparing spotlight mode on 12 December 2013, and distributed as the enhanced ellipsoid corrected product at a pixel spacing of 0.24 m. (Available Online: http://www.intelligence-airbusds.com/en/23-sample-imagery). To reduce the speckle noise, the TerraSAR-X image was downsampled using a Gaussian filter for low-pass filtering so that the pixel spacing is equal to 3 m. The study area is a 1000 × 1000 pixel size image at the higher resolution. The backscattering coefficient is used for the experiment.
- LWIR-HS-RGB fusion: This data set comprises LWIR-HS and RGB images taken over an urban area near Thetford Mines in Québec, Canada, simultaneously on 21 May 2013. The data set was provided for the IEEE 2014 Geoscience and Remote Sensing Society (GRSS) Data Fusion Contest by Telops Inc. (Québec, QC, Canada) [50]. The LWIR-HS image was acquired by the Hyper-Cam, which is an airborne LWIR-HS imaging sensor based on a Fourier-transform spectrometer, with 84 bands covering the wavelengths from 7.8 to 11.5 m at a GSD of 1 m. The RGB image was acquired by a digital color camera at a GSD of 0.2 m. The study area is a 600 × 600 pixel size image at the higher resolution. There is a large degree of local misregistration (more than one pixel in the lower resolution) between the two images. The LWIR-HS image was registered to the RGB image by a projective transformation with manually selected control points.
- DEM-MS fusion: The DEM-MS data set was simulated using LiDAR-derived DEM and HS data taken over the University of Houston and its surrounding urban areas. The original data set was provided for the IEEE 2013 GRSS Data Fusion Contest [51]. The HS image has 144 spectral bands in the wavelength range from 0.4 to 1.0 m with an FWHM of 5 nm. Both images consist of 349 × 1905 pixels at a GSD of 2.5 m. The study area is a 344 × 500 pixel size image mainly over the campus of the University of Houston. To set a realistic problem, only four bands in the wavelengths of 0.46, 0.56, 0.66, and 0.82 m of the HS image are used as the HR-MS image. The DEM is degraded spatially using filtering and downsampling. Filtering was performed using an isotropic Gaussian PSF with an FWHM of the Gaussian function equal to the GSD ratio, which was set to four.
5.2. Results
6. Discussion
7. Conclusions and Future Lines
Acknowledgments
Conflicts of Interest
References
- Alparone, L.; Wald, L.; Chanussot, J.; Thomas, C.; Gamba, P.; Bruce, L.M. Comparison of pan sharpening algorithms: Outcome of the 2006 GRS-S data fusion contest. IEEE Trans. Geosci. Remote Sens. 2007, 45, 3012–3021. [Google Scholar] [CrossRef]
- Aiazzi, B.; Alparone, L.; Baronti, S.; Garzelli, A.; Selva, M. 25 years of pansharpening: A critical review and new developments. In Signal Image Processing for Remote Sensing, 2nd ed.; Chen, C.H., Ed.; CRC Press: Boca Raton, FL, USA, 2011; Chapter 28; pp. 533–548. [Google Scholar]
- Vivone, G.; Alparone, L.; Chanussot, J.; Mura, M.D.; Garzelli, A.; Licciardi, G.; Restaino, R.; Wald, L. A critical comparison among pansharpening algorithms. IEEE Trans. Geosci. Remote Sens. 2015, 53, 2565–2586. [Google Scholar] [CrossRef]
- Carper, W.; Lillesand, T.M.; Kiefer, P.W. The use of Intensity-Hue-Saturation transformations for merging SPOT panchromatic and multispectral image data. Photogramm. Eng. Remote Sens. 1990, 56, 459–467. [Google Scholar]
- Laben, C.A.; Brower, B.V. Process for Enhancing the Spatial Resolution of Multispectral Imagery Using Pan-Sharpening. U.S. Patent 6,011,875 A, 4 January 2000. [Google Scholar]
- Aiazzi, B.; Baronti, S.; Selva, M. Improving component substitution pansharpening through multivariate regression of MS + Pan data. IEEE Trans. Geosci. Remote Sens. 2007, 45, 3230–3239. [Google Scholar] [CrossRef]
- Liu, J.G. Smoothing Filter-based Intensity Modulation: A spectral preserve image fusion technique for improving spatial details. Int. J. Remote Sens. 2000, 21, 3461–3472. [Google Scholar] [CrossRef]
- Aiazzi, B.; Alparone, L.; Baronti, S.; Garzelli, A.; Selva, M. MTF-tailored multiscale fusion of high-resolution MS and Pan imagery. Photogramm. Eng. Remote Sens. 2006, 72, 591–596. [Google Scholar] [CrossRef]
- Pardo-Igúzquiza, E.; Chica-Olmo, M.; Atkinson, P.M. Downscaling cokriging for image sharpening. Remote Sens. Environ. 2006, 102, 86–98. [Google Scholar] [CrossRef]
- Sales, M.H.R.; Souza, C.M.; Kyriakidis, P.C. Fusion of MODIS images using kriging with external drift. IEEE Trans. Geosci. Remote Sens. 2013, 51, 2250–2259. [Google Scholar] [CrossRef]
- Wang, Q.; Shi, W.; Atkinson, P.M.; Zhao, Y. Downscaling MODIS images with area-to-point regression kriging. Remote Sens. Environ. 2015, 166, 191–204. [Google Scholar] [CrossRef]
- Wang, Q.; Shi, W.; Li, Z.; Atkinson, P.M. Fusion of Sentinel-2 images. Remote Sens. Environ. 2016, 187, 241–252. [Google Scholar] [CrossRef]
- Li, S.; Yang, B. A New Pan-Sharpening Method Using a Compressed Sensing Technique. IEEE Trans. Geosci. Remote Sens. 2011, 49, 738–746. [Google Scholar] [CrossRef]
- Zhu, X.X.; Bamler, R. A sparse image fusion algorithm With application to pan-sharpening. IEEE Trans. Geosci. Remote Sens. 2013, 51, 2827–2836. [Google Scholar] [CrossRef]
- He, X.; Condat, L.; Bioucas-Dias, J.M.; Chanussot, J.; Xia, J. A new pansharpening method based on spatial and spectral sparsity priors. IEEE Trans. Image Process. 2014, 23, 4160–4174. [Google Scholar] [CrossRef] [PubMed]
- Guanter, L.; Kaufmann, H.; Segl, K.; Förster, S.; Rogaß, C.; Chabrillat, S.; Küster, T.; Hollstein, A.; Rossner, G.; Chlebek, C.; et al. The EnMAP spaceborne imaging spectroscopy mission for earth observation. Remote Sens. 2015, 7, 8830–8857. [Google Scholar] [CrossRef]
- Iwasaki, A.; Ohgi, N.; Tanii, J.; Kawashima, T.; Inada, H. Hyperspectral imager suite (HISUI)—Japanese hyper-multi spectral radiometer. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium, Vancouver, BC, Canada, 24–29 July 2011; pp. 1025–1028. [Google Scholar]
- Stefano, P.; Angelo, P.; Simone, P.; Filomena, R.; Federico, S.; Tiziana, S.; Umberto, A.; Vincenzo, C.; Acito, N.; Marco, D.; et al. The PRISMA hyperspectral mission: Science activities and opportunities for agriculture and land monitoring. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium, Melbourne, VIC, Australia, 21–26 July 2013; pp. 4558–4561. [Google Scholar]
- Green, R.; Asner, G.; Ungar, S.; Knox, R. NASA mission to measure global plant physiology and functional types. In Proceedings of the IEEE Aerospace Conference, Big Sky, MT, USA, 1–8 March 2008; pp. 1–7. [Google Scholar]
- Michel, S.; Gamet, P.; Lefevre-Fonollosa, M.J. HYPXIM—A hyperspectral satellite defined for science, security and defense users. In Proceedings of the IEEE Hyperspectral Image and Signal Processing: Evolution in Remote Sensing (WHISPERS), Lisbon, Portugal, 6–9 June 2011; pp. 1–4. [Google Scholar]
- Eckardt, A.; Horack, J.; Lehmann, F.; Krutz, D.; Drescher, J.; Whorton, M.; Soutullo, M. DESIS (DLR Earth sensing imaging spectrometer for the ISS-MUSES platform. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium, Milan, Italy, 26–31 July 2015; pp. 1457–1459. [Google Scholar]
- Feingersh, T.; Dor, E.B. SHALOM—A Commercial Hyperspectral Space Mission. In Optical Payloads for Space Missions; Qian, S.E., Ed.; John Wiley & Sons, Ltd.: Chichester, UK, 2015; Chapter 11; pp. 247–263. [Google Scholar]
- Chan, J.C.W.; Ma, J.; Kempeneers, P.; Canters, F. Superresolution enhancement of hyperspectral CHRIS/ Proba images with a thin-plate spline nonrigid transform model. IEEE Trans. Geosci. Remote Sens. 2010, 48, 2569–2579. [Google Scholar] [CrossRef]
- Yokoya, N.; Mayumi, N.; Iwasaki, A. Cross-calibration for data fusion of EO-1/Hyperion and Terra/ASTER. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2013, 6, 419–426. [Google Scholar] [CrossRef]
- Loncan, L.; Almeida, L.B.; Dias, J.B.; Briottet, X.; Chanussot, J.; Dobigeon, N.; Fabre, S.; Liao, W.; Licciardi, G.A.; Simões, M.; et al. Hyperspectral pansharpening: A review. IEEE Geosci. Remote Sens. Mag. 2015, 3, 27–46. [Google Scholar] [CrossRef]
- Yokoya, N.; Grohnfeldt, C.; Chanussot, J. Hyperspectral and multispectral data fusion: A comparative review. IEEE Geosci. Remote Sens. Mag. 2017, in press. [Google Scholar]
- Eismann, M.T.; Hardie, R.C. Application of the stochastic mixing model to hyperspectral resolution enhancement. IEEE Trans. Geosci. Remote Sens. 2004, 42, 1924–1933. [Google Scholar] [CrossRef]
- Yokoya, N.; Yairi, T.; Iwasaki, A. Coupled nonnegative matrix factorization unmixing for hyperspectral and multispectral data fusion. IEEE Trans. Geosci. Remote Sens. 2012, 50, 528–537. [Google Scholar] [CrossRef]
- Simões, M.; Dias, J.B.; Almeida, L.; Chanussot, J. A convex formulation for hyperspectral image superresolution via subspace-based regularization. IEEE Trans. Geosci. Remote Sens. 2015, 53, 3373–3388. [Google Scholar] [CrossRef]
- Chen, Z.; Pu, H.; Wang, B.; Jiang, G.M. Fusion of hyperspectral and multispectral images: A novel framework based on generalization of pan-sharpening methods. IEEE Geosci. Remote Sens. Lett. 2014, 11, 1418–1422. [Google Scholar] [CrossRef]
- Selva, M.; Aiazzi, B.; Butera, F.; Chiarantini, L.; Baronti, S. Hyper-sharpening: A first approach on SIM-GA data. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2015, 8, 3008–3024. [Google Scholar] [CrossRef]
- Moran, M.S. A Window-based technique for combining Landsat Thematic Mapper thermal data with higher-resolution multispectral data over agricultural land. Photogramm. Eng. Remote Sens. 1990, 56, 337–342. [Google Scholar]
- Haala, N.; Brenner, C. Extraction of buildings and trees in urban environments. ISPRS J. Photogramm. Remote Sens. 1999, 54, 130–137. [Google Scholar] [CrossRef]
- Sirmacek, B.; d’Angelo, P.; Krauss, T.; Reinartz, P. Enhancing urban digital elevation models using automated computer vision techniques. In Proceedings of the ISPRS Commission VII Symposium, Vienna, Austria, 5–7 July 2010. [Google Scholar]
- Alparone, L.; Baronti, S.; Garzelli, A.; Nencini, F. A global quality measurement of pan-sharpened multispectral imagery. IEEE Geosci. Remote Sens. Lett. 2004, 1, 313–317. [Google Scholar] [CrossRef]
- Arbelot, B.; Vergne, R.; Hurtut, T.; Thollot, J. Automatic texture guided color transfer and colorization. In Proceedings of the Expressive, Lisbon, Portugal, 7–9 May 2016. [Google Scholar]
- Tuzel, O.; Porikli, F.; Meer, P. A fast descriptor for detection and classification. In Proceedings of the 9th European Conference on Computer Vision, Graz, Austria, 7–13 May 2006; pp. 589–600. [Google Scholar]
- Karacan, L.; Erdem, E.; Erdem, A. Structure-preserving image smoothing via region covariances. ACM Trans. Graph. 2013, 32, 176:1–176:11. [Google Scholar] [CrossRef]
- Wald, L.; Ranchin, T.; Mangolini, M. Fusion of satellite images of different spatial resolutions: Assessing the quality of resulting images. Photogramm. Eng. Remote Sens. 1997, 63, 691–699. [Google Scholar]
- Yokoya, N.; Chan, J.C.W.; Segl, K. Potential of resolution-enhanced hyperspectral data for mineral mapping using simulated EnMAP and Sentinel-2 images. Remote Sens. 2016, 8, 172. [Google Scholar] [CrossRef]
- Veganzones, M.; Simões, M.; Licciardi, G.; Yokoya, N.; Bioucas-Dias, J.; Chanussot, J. Hyperspectral super-resolution of locally low rank images from complementary multisource data. IEEE Trans. Image Process. 2016, 25, 274–288. [Google Scholar] [CrossRef] [PubMed]
- Palsson, F.; Sveinsson, J.R.; Ulfarsson, M.O.; Benediktsson, J.A. Quantitative Quality Evaluation of Pansharpened Imagery: Consistency Versus Synthesis. IEEE Trans. Geosci. Remote Sens. 2016, 54, 1247–1259. [Google Scholar] [CrossRef]
- Alparone, L.; Aiazzi, B.; Baronti, S.; Garzelli, A.; Nencini, F.; Selva, M. Multispectral and panchromatic data fusion assessment without reference. Photogramm. Eng. Remote Sens. 2008, 74, 193–200. [Google Scholar] [CrossRef]
- Kruse, F.A.; Lefkoff, A.B.; Boardman, J.W.; Heidebrecht, K.B.; Shapiro, A.T.; Barloon, J.P.; Goetz, A.F.H. The spectral image processing system (SIPS)—Interactive visualization and analysis of imaging spectrometer data. Remote Sens. Environ. 1993, 44, 145–163. [Google Scholar] [CrossRef]
- Wald, L. Quality of High Resolution Synthesised Images: Is There a Simple Criterion? In Proceedings of the Fusion of Earth Data: Merging Point Measurements, Raster Maps and Remotely Sensed Images, Sophia Antipolis, France, 26 January 2000; pp. 99–103. [Google Scholar]
- Garzelli, A.; Nencini, F. Hypercomplex quality assessment of multi/hyperspectral images. IEEE Geosci. Remote Sens. Lett. 2009, 6, 662–665. [Google Scholar] [CrossRef]
- Wang, Z.; Bovik, A.C. A universal image quality index. IEEE Signal Process. Lett. 2002, 9, 81–84. [Google Scholar] [CrossRef]
- Yokoya, N.; Iwasaki, A. Airborne Hyperspectral Data over Chikusei; Technical Report SAL-2016-05-27; Space Application Laboratory, The University of Tokyo: Tokyo, Japan, 2016. [Google Scholar]
- Baumgardner, M.F.; Biehl, L.L.; Landgrebe, D.A. 220 Band AVIRIS Hyperspectral Image Data Set: June 12, 1992 Indian Pine Test Site 3. Purdue Univ. Res. Repos. 2015. [Google Scholar] [CrossRef]
- Liao, W.; Huang, X.; Van Coillie, F.; Gautama, S.; Pižurica, A.; Philips, W.; Liu, H.; Zhu, T.; Shimoni, M.; Moser, G.; et al. Processing of multiresolution thermal hyperspectral and digital color data: Outcome of the 2014 IEEE GRSS data fusion contest. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2015, 8, 2984–2996. [Google Scholar] [CrossRef]
- Debes, C.; Merentitis, A.; Heremans, R.; Hahn, J.; Frangiadakis, N.; van Kasteren, T.; Liao, W.; Bellens, R.; Piz̆urica, A.; Gautama, S.; et al. Hyperspectral and LiDAR Data Fusion: Outcome of the 2013 GRSS Data Fusion Contest. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 7, 2405–2418. [Google Scholar] [CrossRef]
- Tomasi, C.; Manduchi, R. Bilateral filtering for gray and color images. In Proceedings of the IEEE International Conference on Computer Vision, Bombay, India, 4–7 Jaunary 1998; pp. 839–846. [Google Scholar]
- Suri, S.; Reinartz, P. Mutual-information-based registration of TerraSAR-X and Ikonos imagery in urban areas. IEEE Trans. Geosci. Remote Sens. 2010, 48, 939–949. [Google Scholar] [CrossRef]
- Garzelli, A.; Capobianco, L.; Alparone, L.; Aiazzi, B.; Baronti, S.; Selva, M. Hyperspectral pansharpening based on modulation of pixel spectra. In Proceedings of the IEEE 2nd Workshop on Hyperspectral Image and Signal Processing: Evolution in Remote Sensing (WHISPERS), Reykjavìk, Iceland, 14–16 June 2010; pp. 1–4. [Google Scholar]




| Type of Fusion | Num. of Bands | Data Transform of HR Data | |
|---|---|---|---|
| LR | HR | ||
| MS-PAN | Multiple | One | Histogram matching |
| HS-PAN | Multiple | One | Histogram matching |
| Optical-SAR | Multiple | One | Histogram matching |
| HS-MS | Multiple | Multiple | Linear regression |
| DEM-MS | One | Multiple | Local linear regression |
| LWIR-HS-RGB | Multiple | Multiple | Linear regression |
| Coarse Category | Optical Data Fusion | Multimodal Data Fusion | ||||
|---|---|---|---|---|---|---|
| Fusion problem | MS-PAN | HS-PAN | HS-MS | Optical-SAR | LWIR-HS-RGB | DEM-MS |
| Evaluation scenario | Semi-real | Synthetic | Synthetic | Real | Real | Semi-real |
| Quality indices | PSNR, SAM, ERGAS, | — | — | Q index | ||
| Data Set | WorldView-3 Sydney | |||||||
| GSD Ratio | 4 | 8 | ||||||
| Method | PSNR | SAM | ERGAS | PSNR | SAM | ERGAS | ||
| GSA | 30.5889 | 7.0639 | 4.8816 | 0.84731 | 29.5442 | 8.9376 | 2.7818 | 0.80189 |
| SFIM | 30.284 | 7.4459 | 4.9078 | 0.80717 | 29.0397 | 9.3161 | 2.8346 | 0.75794 |
| GLP | 30.0165 | 7.5339 | 5.0067 | 0.819 | 28.634 | 9.7685 | 2.9399 | 0.76188 |
| TGMS | 30.5383 | 7.061 | 4.8447 | 0.84063 | 29.3084 | 8.8521 | 2.7895 | 0.79366 |
| Data Set | WorldView-3 Fukushima | |||||||
| GSD Ratio | 4 | 8 | ||||||
| Method | PSNR | SAM | ERGAS | PSNR | SAM | ERGAS | ||
| GSA | 35.2828 | 3.5409 | 2.1947 | 0.86497 | 32.6051 | 5.3814 | 1.5341 | 0.7814 |
| SFIM | 34.4099 | 3.5878 | 2.2865 | 0.82623 | 31.9744 | 5.1626 | 1.5426 | 0.7534 |
| GLP | 34.9059 | 3.4938 | 2.162 | 0.84492 | 32.1053 | 5.2448 | 1.5273 | 0.76752 |
| TGMS | 35.2873 | 3.2785 | 2.0986 | 0.86442 | 32.5916 | 4.9253 | 1.4623 | 0.78618 |
| ROSIS University of Pavia | Hyperspec-VNIR Chikusei | |||||||
|---|---|---|---|---|---|---|---|---|
| Method | PSNR | SAM | ERGAS | Q | PSNR | SAM | ERGAS | Q |
| GSA | 31.085 | 6.8886 | 3.6877 | 0.63454 | 33.8284 | 6.9878 | 4.7225 | 0.81024 |
| SFIM | 31.0686 | 6.7181 | 3.6715 | 0.60115 | 34.5728 | 6.409 | 4.3559 | 0.84793 |
| GLP | 31.6378 | 6.5862 | 3.4586 | 0.6462 | 33.9539 | 7.201 | 4.6249 | 0.81834 |
| TGMS | 31.8983 | 6.2592 | 3.3583 | 0.6541 | 35.3262 | 6.1197 | 4.0381 | 0.86051 |
| AVIRIS Indian Pines | AVIRIS Cuprite | |||||||
|---|---|---|---|---|---|---|---|---|
| Method | PSNR | SAM | ERGAS | Q | PSNR | SAM | ERGAS | Q |
| GSA | 40.0997 | 0.96775 | 0.44781 | 0.95950 | 39.2154 | 0.98265 | 0.37458 | 0.98254 |
| SFIM-HS | 40.7415 | 0.84069 | 0.40043 | 0.91297 | 40.8674 | 0.79776 | 0.31375 | 0.97017 |
| GLP-HS | 41.2962 | 0.82635 | 0.37533 | 0.95236 | 40.8240 | 0.80250 | 0.31570 | 0.97838 |
| TGMS | 40.8867 | 0.83001 | 0.39279 | 0.9187 | 40.9704 | 0.78922 | 0.30984 | 0.97852 |
© 2017 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yokoya, N. Texture-Guided Multisensor Superresolution for Remotely Sensed Images. Remote Sens. 2017, 9, 316. https://doi.org/10.3390/rs9040316
Yokoya N. Texture-Guided Multisensor Superresolution for Remotely Sensed Images. Remote Sensing. 2017; 9(4):316. https://doi.org/10.3390/rs9040316
Chicago/Turabian StyleYokoya, Naoto. 2017. "Texture-Guided Multisensor Superresolution for Remotely Sensed Images" Remote Sensing 9, no. 4: 316. https://doi.org/10.3390/rs9040316
APA StyleYokoya, N. (2017). Texture-Guided Multisensor Superresolution for Remotely Sensed Images. Remote Sensing, 9(4), 316. https://doi.org/10.3390/rs9040316