Glacier Mass Loss during the 1960s and 1970s in the Ak-Shirak Range (Kyrgyzstan) from Multiple Stereoscopic Corona and Hexagon Imagery
Abstract
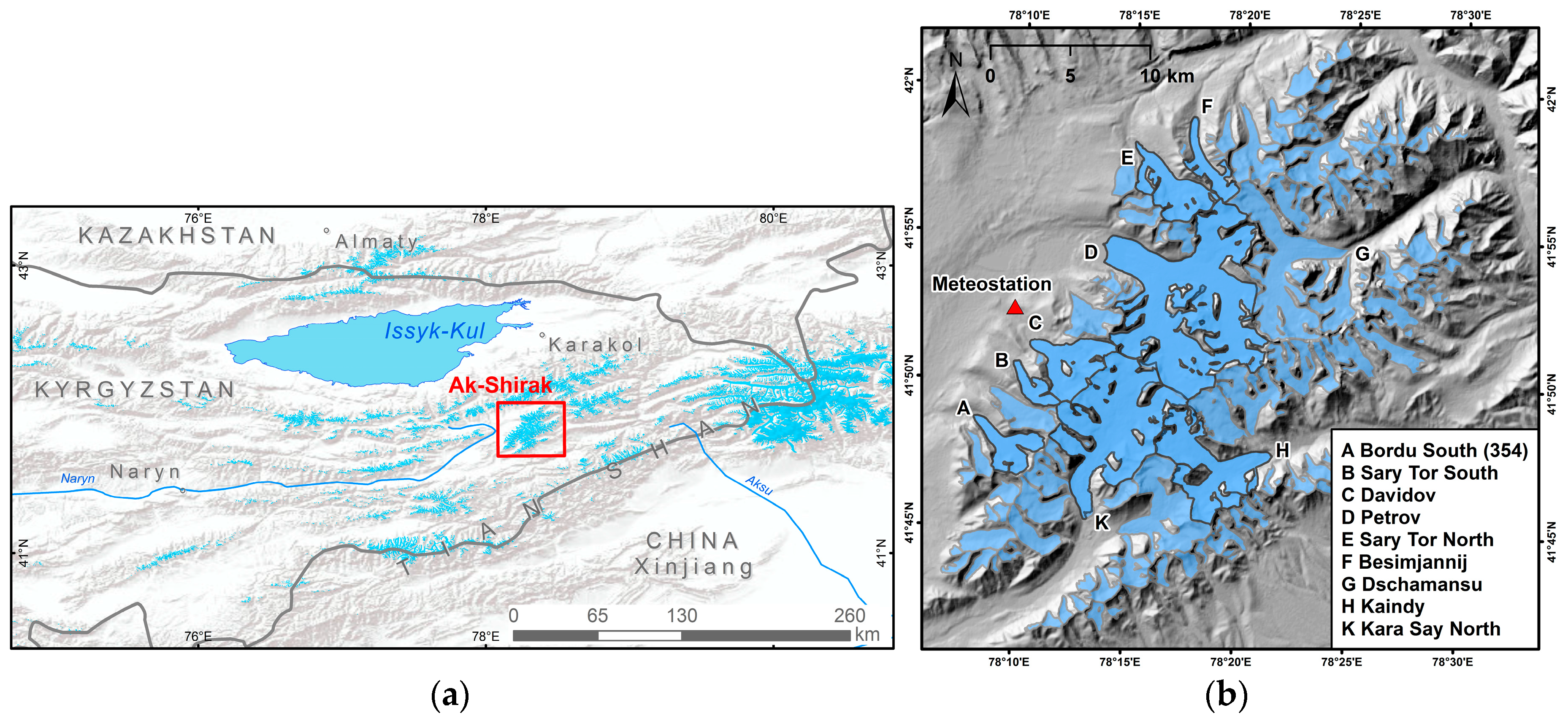
:1. Introduction
2. Materials and Methods
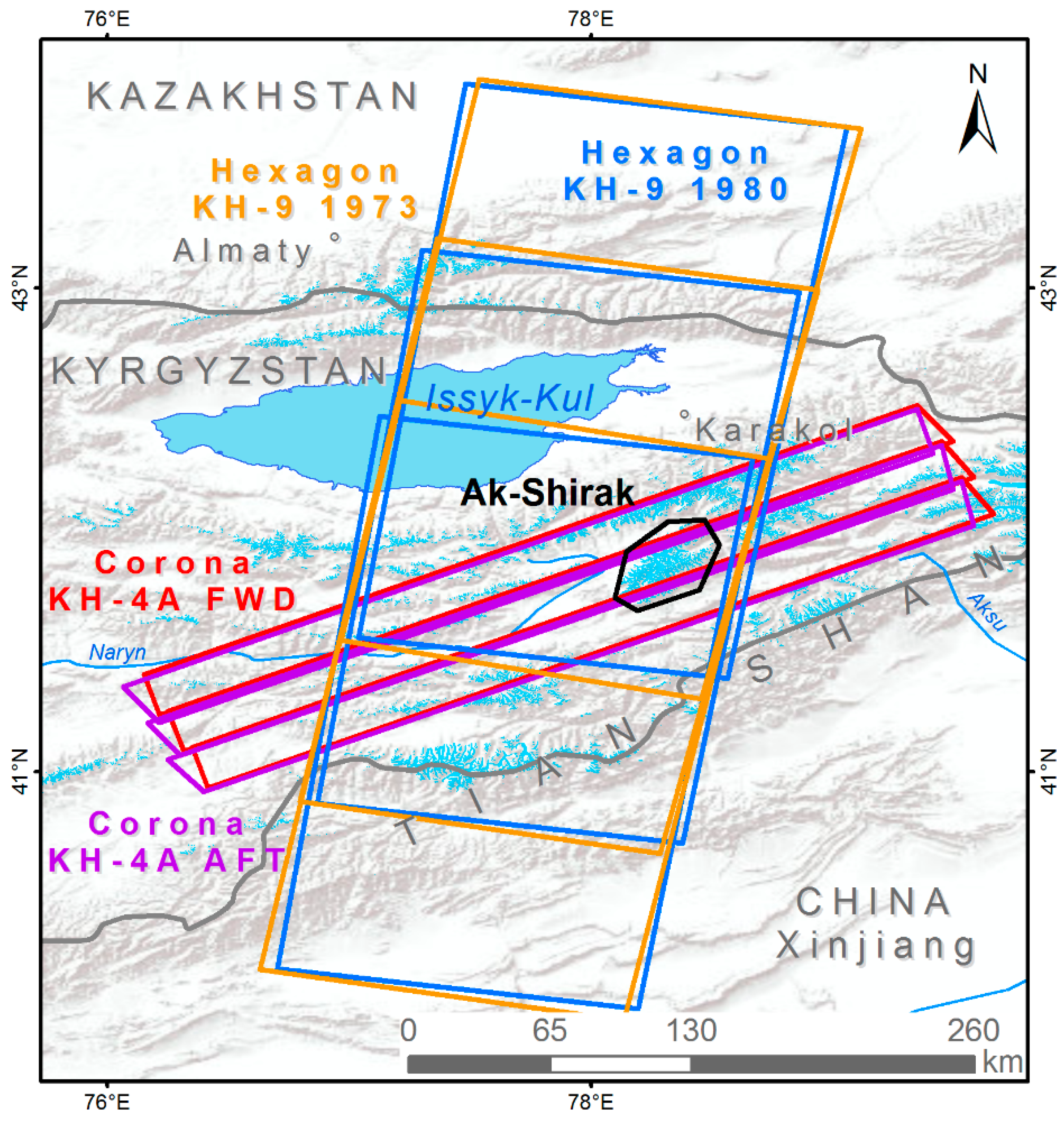
2.1. Data
2.1.1. Corona and Hexagon Imagery
2.1.2. Reference Data
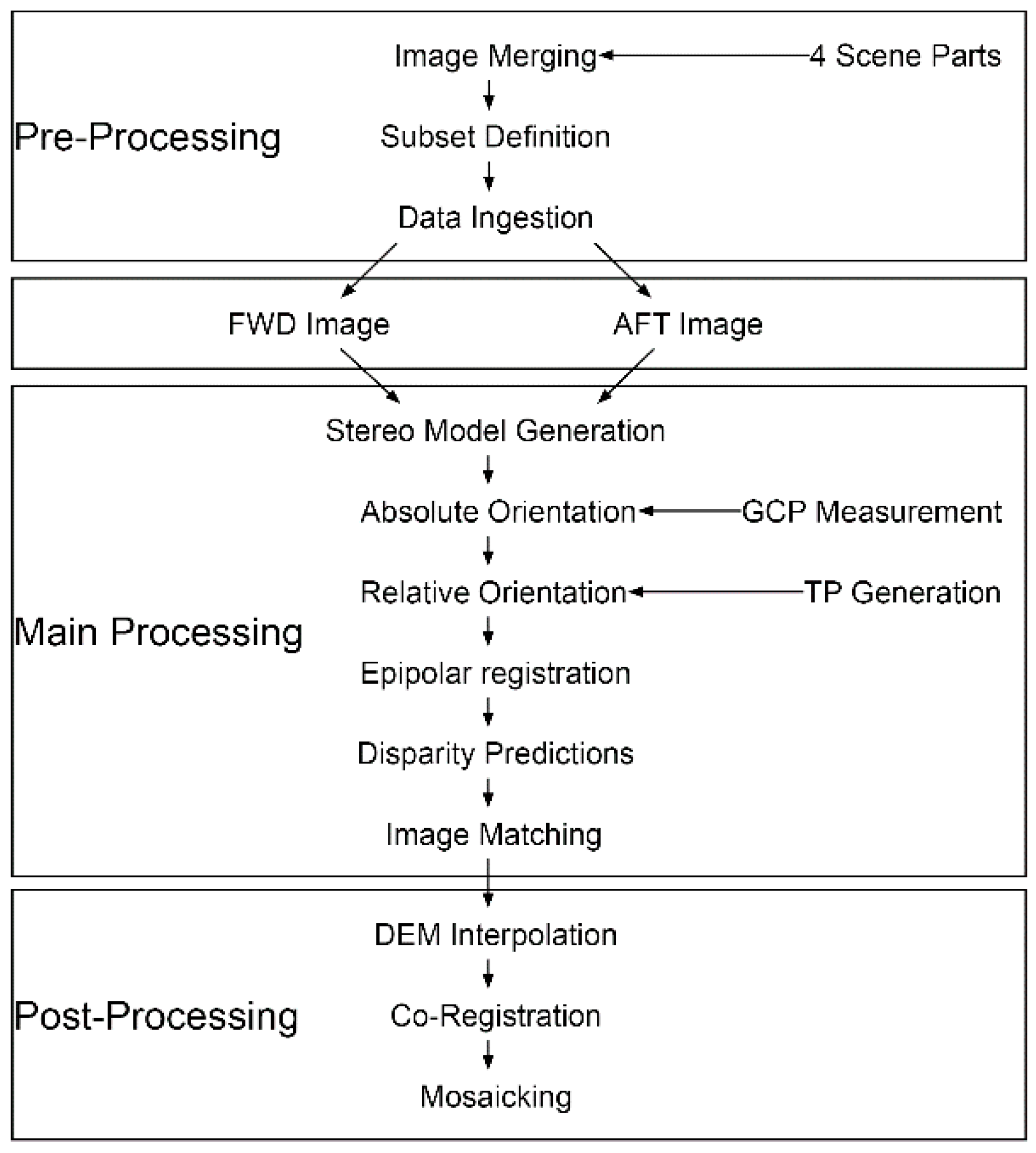
2.2. Methods
2.2.1. DTM Generation
2.2.2. Glacier Mapping and Length Changes
2.2.3. Data Gap/Outlier Handling
2.2.4. Accuracy Assessment
3. Results
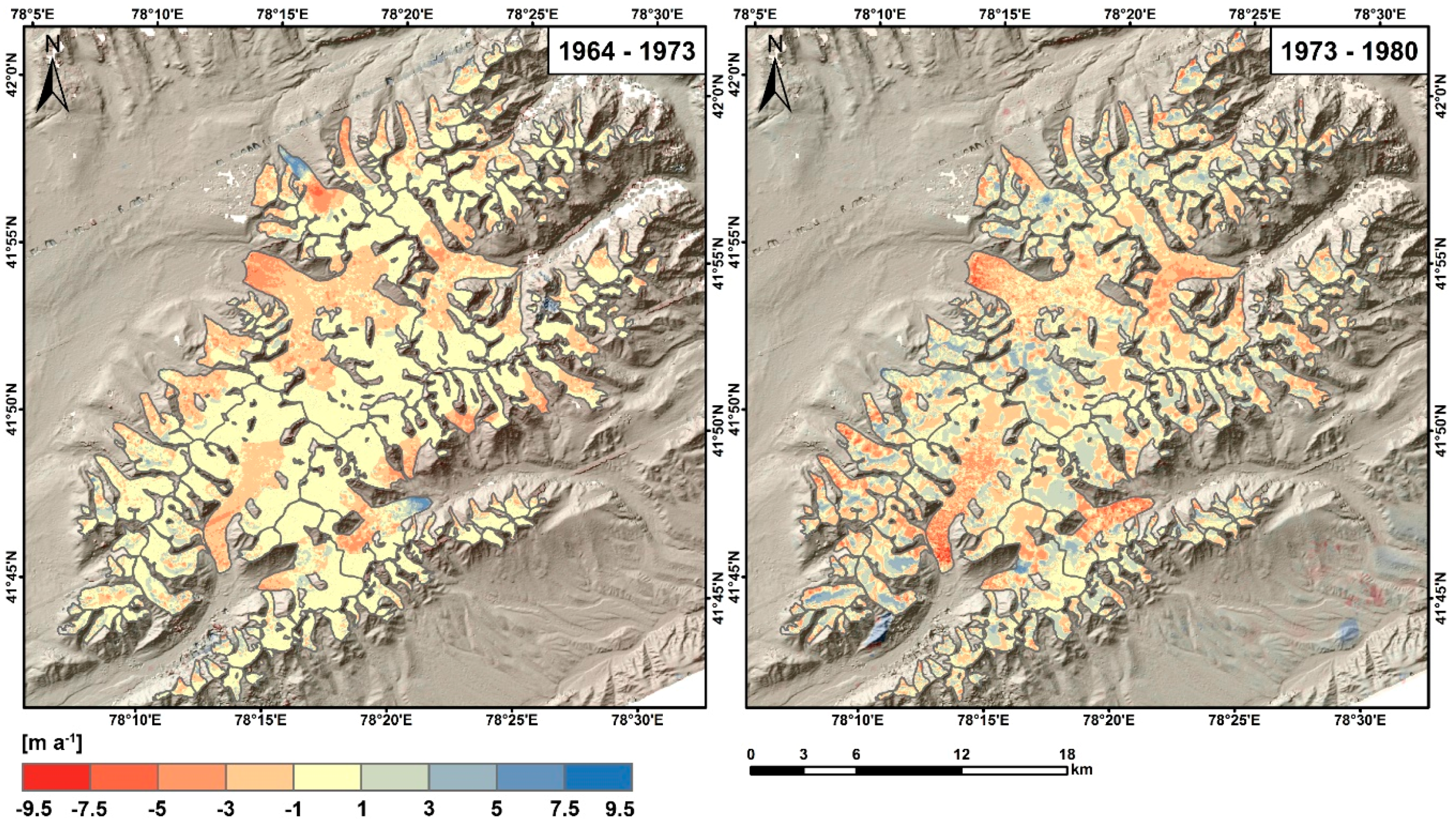
3.1. Glacier Length Changes
3.2. Mass Budgets
4. Discussion
4.1. Data limitations
4.2. Mass Budget
5. Conclusions
Supplementary Materials
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Sorg, A.; Bolch, T.; Stoffel, M.; Solomina, O.; Beniston, M. Climate change impacts on glaciers and runoff in Tien Shan (Central Asia). Nat. Clim. Chang. 2012, 2, 725–731. [Google Scholar] [CrossRef]
- Unger-Shayesteh, K.; Vorogushyn, S.; Farinotti, D.; Gafurov, A.; Duethmann, D.; Mandychev, A.; Merz, B. What do we know about past changes in the water cycle of Central Asian headwaters? A review. Glob. Planet. Chang. 2013, 110, 4–25. [Google Scholar] [CrossRef]
- Farinotti, D.; Longuevergne, L.; Moholdt, G.; Duethmann, D.; Mölg, T.; Bolch, T.; Vorogushyn, S.; Güntner, A. Substantial glacier mass loss in the Tien Shan over the past 50 years. Nat. Geosci. 2015, 8, 716–722. [Google Scholar] [CrossRef]
- Kriegel, D.; Mayer, C.; Hagg, W.; Vorogushyn, S.; Duethmann, D.; Gafurov, A.; Farinotti, D. Changes in glacierisation, climate and runoff in the second half of the 20th century in the Naryn basin, Central Asia. Glob. Planet. Chang. 2013, 110, 51–61. [Google Scholar] [CrossRef]
- Pieczonka, T.; Bolch, T. Region-wide glacier mass budgets and area changes for the Central Tien Shan between ~1975 and 1999 using Hexagon KH-9 imagery. Glob. Planet. Chang. 2015, 128, 1–13. [Google Scholar] [CrossRef]
- Dolgoushin, L.D.; Osipova, G.B. Glacier surges and the problem of their forecasting. IAHS Publ. 1975, 104, 292–304. [Google Scholar]
- Mukherjee, K.; Bolch, T.; Goerlich, F.; Kutuzov, S.; Osmonov, A.; Pieczonka, T.; Shesterova, I. Surge-type glaciers in the Tien Shan (Central Asia). Arct. Antarct. Alp. Res. 2017, 49, 147–171. [Google Scholar] [CrossRef]
- Ozmonov, A.; Bolch, T.; Xi, C.; Wei, J.; Kurban, A. Glaciers characteristics and changes in the Sary-Jaz River Basin (Central Tien Shan) 1990–2010 Remote Sensing Letters. Remote Sens. Lett. 2013, 4, 725–734. [Google Scholar] [CrossRef]
- Koscielny-Bunde, E.; Bunde, A.; Havlin, S.; Roman, H.E.; Goldreich, Y.; Schellnhuber, H.J. Indication of a universal persistence law governing atmospheric variability. Phys. Rev. Lett. 1998, 81, 729. [Google Scholar] [CrossRef]
- Aizen, V.B.; Kuzmichenok, V.A.; Surazakov, A.B.; Aizen, E.M. Glacier changes in the Tien Shan as determined from topographic and remotely sensed data. Glob. Planet. Chang. 2007, 56, 328–340. [Google Scholar] [CrossRef]
- Kuzmichenok, V.A. Fluctuations in the condition of Davydov and Sary-Tor glaciers according to the topographic survey data. Mater. Glyaciol. Issled. 1988, 62, 193–198. (In Russian) [Google Scholar]
- Maurer, J.M.; Rupper, S.B.; Schaefer, J.M. Quantifying ice loss in the eastern Himalayas since 1974 using declassified spy satellite imagery. Cryosphere 2016, 10, 2203. [Google Scholar] [CrossRef]
- Bolch, T.; Pieczonka, T.; Mukherjee, K.; Shea, J. Brief Communications: Glaciers in the Hunza Catchment (Karakoram) have been almost in balance since the 1970s. Cryosphere 2017, 11. [Google Scholar] [CrossRef]
- Pieczonka, T.; Bolch, T.; Junfeng, W.; Shiyin, L. Heterogeneous mass loss of glaciers in the Aksu-Tarim Catchment (Central Tien Shan) revealed by 1976 KH-9 Hexagon and 2009 SPOT-5 stereo imagery. Remote Sens. Environ. 2013, 130, 233–244. [Google Scholar] [CrossRef]
- U.S. Geological Survey. Declassified Intelligence Satellite Photographs: U.S. Geological Survey Fact Sheet 2008–3054; U.S. Geological Survey: Reston, VA, USA, 2008.
- Beck, A.; Philip, G.; Abdulkarim, M.; Donoghue, D. Evaluation of Corona and Ikonos high resolution satellite imagery for archaeological prospection in western Syria. Antiquity 2007, 81, 161–175. [Google Scholar] [CrossRef]
- Altmaier, A.; Kany, C. Digital surface model generation from CORONA satellite images. ISPRS J. Photogram. Remote Sens. 2002, 56, 221–235. [Google Scholar] [CrossRef]
- Schmidt, S.; Nüsser, M. Changes of high altitude glaciers from 1969 to 2010 in the trans-Himalayan Kang Yatze Massif, Ladakh, northwest India. Arct. Antarct. Alp. Res. 2012, 44, 107–121. [Google Scholar] [CrossRef]
- Narama, C.; Kääb, A.; Duishonakunov, M.; Abdrakhmatov, K. Spatial variability of recent glacier area changes in the Tien Shan Mountains, Central Asia, using Corona (~1970), Landsat (~2000), and ALOS (~2007) satellite data. Glob. Planet. Chang. 2010, 71, 42–54. [Google Scholar] [CrossRef]
- Bhambri, R.; Bolch, T.; Chaujar, R.K. Frontal recession of Gangotri Glacier, Garhwal Himalayas, from 1965 to 2006, measured through highresolution remote sensing data. Curr. Sci. 2012, 102, 489–494. [Google Scholar]
- Bolch, T.; Buchroithner, M.; Pieczonka, T.; Kunert, A. Planimetric and volumetric glacier changes in the Khumbu Himal, Nepal, since 1962 using Corona, Landsat TM and ASTER data. J. Glaciol. 2008, 54, 592–600. [Google Scholar] [CrossRef]
- Bolch, T.; Pieczonka, T.; Benn, D.I. Multi-decadal mass loss of glaciers in the Everest area (Nepal Himalaya) derived from stereo imagery. Cryosphere 2011, 5, 349–358. [Google Scholar] [CrossRef]
- Bolch, T. Glacier area and mass changes since 1964 in the Ala Archa Valley, Kyrgyz Ala-Too, northern Tien Shan. Лёд и Снег (Ice and Snow) 2015, 1, 28–39. [Google Scholar] [CrossRef]
- Lamsal, D.; Sawagaki, T.; Watanabe, T. Digital terrain modelling using Corona and ALOS PRISM data to investigate the distal part of Imja Glacier, Khumbu Himal, Nepal. J. Mount. Sci. 2011, 8, 390–402. [Google Scholar] [CrossRef]
- Maurer, J.; Rupper, S. Tapping into the Hexagon spy imagery database: A new automated pipeline for geomorphic change detection. ISPRS J. Photogramm. Remote Sens. 2015, 108, 113–127. [Google Scholar] [CrossRef]
- Kronenberg, M.; Brandun, M.; Hoelzle, M.; Huss, M.; Farinotti, D.; Azisov, E.; Usubaliev, R.; Gafurov, A.; Petrakov, D.; Kääb, A. Mass-balance reconstruction for Glacier No. 354, Tien Shan, from 2003 to 2014. Ann. Glaciol. 2015, 57, 92–102. [Google Scholar] [CrossRef]
- Dashora, A.; Lohani, B.; Malik, J.N. A repository of earth resource information-CORONA satellite programme. Curr. Sci. 2007, 92, 926–932. [Google Scholar]
- Galiatsatos, N. The shift from film to digital product: Focus on CORONA imagery. Photogramm. Fernerkund. Geoinf. 2009, 2009, 251–260. [Google Scholar] [CrossRef] [PubMed]
- Kaufmann, V.; Sulzer, W. Über die Nutzungsmöglichkeit hochauflösender amerikanischer Spionage-Satellitenbilder (1960–1972). Vermess. Geoinf. 1997, 3, 97. [Google Scholar]
- Schneider, T.; Jacobsen, K.; Seitz, R.; Förster, B. Remote sensing based parameter extraction for erosion control purposes in the Loess plateau of China. In Proceedings of ISPRS/EARSeL Joint Workshop on High-Resolution Mapping from Space, Hannover, Germany, 19–21 September 2001.
- Burnett, M. Hexagon (KH-9) Mapping Program and Evolution; National Reconnaissance Office: Chantilly, Virginia, 2012.
- Surazakov, A.; Aizen, V. Positional accuracy evaluation of declassified Hexagon KH-9 mapping camera imagery. Photogramm. Eng. Remote Sens. 2010, 76, 603–608. [Google Scholar] [CrossRef]
- Rabus, B.; Eineder, M.; Roth, A.; Bamler, R. The shuttle radar topography mission—A new class of digital elevation models acquired by spaceborne radar. ISPRS J. Photogramm. Remote Sens. 2003, 57, 241–262. [Google Scholar] [CrossRef]
- Berthier, E.; Arnaud, Y.; Vincent, C.; Remy, F. Biases of SRTM in high-mountain areas: Implications for the monitoring of glacier volume changes. Geophys. Res. Lett. 2006, 33. [Google Scholar] [CrossRef]
- EarthExplorer. Available online: http://earthexplorer.usgs.gov/ (accessed on 21 March 2016).
- Förstner, W.; Gülch, E. A fast operator for detection and precise location of distinct points, corners and centres of circular features. In Proceedings of the ISPRS Intercommission Conference on Fast Processing of Photogrammetric Data, Interlaken, Switzerland, 2–4 June 1987; pp. 281–305.
- Pieczonka, T.; Bolch, T.; Buchroithner, M. Generation and evaluation of multitemporal digital terrain models of the Mt. Everest area from different optical sensors. ISPRS J. Photogramm. Remote Sens. 2011, 66, 927–940. [Google Scholar] [CrossRef]
- Nuth, C.; Kääb, A. Co-registration and bias corrections of satellite elevation data sets for quantifying glacier thickness change. Cryosphere 2011, 5, 271. [Google Scholar] [CrossRef]
- Koblet, T.; Gärtner-Roer, I.; Zemp, M.; Jansson, P.; Thee, P.; Haeberli, W.; Holmlund, P. Reanalysis of multi-temporal aerial images of Storglaciären, Sweden (1959–99)–Part 1: Determination of length, area, and volume changes. Cryosphere 2010, 4, 333–343. [Google Scholar] [CrossRef]
- Huss, M.; Jouvet, G.; Farinotti, D.; Bauder, A. Future high-mountain hydrology: A new parameterization of glacier retreat. Hydrol. Earth Syst. Sci. 2010, 14, 815–829. [Google Scholar] [CrossRef]
- Sapiano, J.J.; Harrison, W.T.; Echelmeyer, K.A. Elevation, volume and terminus changes of nine glaciers in North America. J. Glaciol. 1998, 44, 119–135. [Google Scholar] [CrossRef]
- Gardelle, J.; Berthier, E.; Arnaud, Y.; Kääb, A. Region-wide glacier mass balances over the Pamir-Karakoram-Himalaya during 1999–2011. Cryosphere 2013, 7, 1885–1886. [Google Scholar] [CrossRef]
- Huss, M. Density assumptions for converting geodetic glacier volume change to mass change. Cryosphere 2013, 7, 877–887. [Google Scholar] [CrossRef]
- Bolch, T.; Menounos, B.; Wheate, R. Landsat-based inventory of glaciers in western Canada, 1985–2005. Remote Sens. Environ. 2010, 114, 127–137. [Google Scholar] [CrossRef]
- Hall, D.K.; Bayr, K.J.; Schöner, W.; Bindschadler, R.A.; Chien, J.Y. Consideration of the errors inherent in mapping historical glacier positions in Austria from the ground and space (1893–2001). Remote Sens. Environ. 2003, 86, 566–577. [Google Scholar] [CrossRef]
- Pieczonka, T.; Bolch, T.; Buchroithner, M. Volumetric glacier changes in the Khumbu Himal since 1962 using space imagery. Grazer Schriften der Geographie und Raumforschung 2010, 45, 295–302. [Google Scholar]
- Höhle, J.; Höhle, M. Accuracy assessment of digital elevation models by means of robust statistical methods. ISPRS J. Photogramm. Remote Sens. 2009, 64, 398–406. [Google Scholar] [CrossRef]
- Magnússon, E.; Muñoz-Cobo Belart, J.; Pálsson, F.; Ágústsson, H.; Crochet, P. Geodetic mass balance record with rigorous uncertainty estimates deduced from aerial photographs and lidar data—Case study from Drangajökull ice cap, NW Iceland. Cryosphere 2016, 10, 159–177. [Google Scholar] [CrossRef]
- Goossens, R.; De Wulf, A.; Bourgeois, J.; Gheyle, W.; Willems, T. Satellite imagery and archaeology: The example of CORONA in the Altai Mountains. J. Archaeol. Sci. 2006, 33, 745–755. [Google Scholar] [CrossRef]
- Meszaros, M.; Szatmari, J.; Tobal, Z.; Mucsi, L. Extraction of digital surface models from Corona satellite stereo images. J. Environ. Geogr. 2008, 1, 5–10. [Google Scholar]
- Sorg, A.; Kääb, A.; Roesch, A.; Bigler, C.; Stoffel, M. Contrasting responses of Central Asian rock glaciers to global warming. Sci. Rep. 2015, 5, 8228. [Google Scholar] [CrossRef]
- Khromova, T.E.; Dyurgerov, M.B.; Barry, R.G. Late-twentieth century changes in glacier extent in the Ak-shirak Range, Central Asia, determined from historical data and ASTER imagery. Geophys. Res. Lett. 2003, 30. [Google Scholar] [CrossRef]
- Gardner, A.S.; Moholdt, G.; Cogley, J.G.; Wouters, B.; Arendt, A.A.; Wahr, J.; Berthier, E.; Hock, R.; Pfeffer, W.T.; Kaser, G.; et al. A reconciled estimate of glacier contributions to sea level rise: 2003 to 2009. Science 2013, 340, 852–857. [Google Scholar] [CrossRef] [PubMed]
- Engel, Z.; Sobr, M.; Yerokhin, S.A. Changes of Petrov glacier and its proglacial lake in the Akshiirak massif, central Tien Shan, since 1977. J. Glaciol. 2012, 58, 388–398. [Google Scholar] [CrossRef]
- Kuzmichenok, V.A. Statistical studies of the geometry of the valley glaciers of Kyrgyzstan. Mater. Glyaciol. Issled. 2006, 12, 80–86. (In Russian) [Google Scholar]
- Petrakov, D.A.; Lavrientiev, I.I.; Kovalenko, N.V.; Usubaliev, R.A. Snow Cover and Glaciers Ice Thickness, Volume and Current Changes of the Sary-Tor Glacier Area (Ak-Shyirak Massif, Inner Tian Shan). Earth’s Cryosphere 2014, 18, 83–91. [Google Scholar]
- World Glacier Monitoring Service (WGMS). Global Glacier Change Bulletin No. 1 (2012–2013). ICSU(WDS)/IUGG(IACS)/UNEP/UNESCO WMO; Zemp, M., Gärtner-Roer, I., Nussbaumer, S.U., Hüsler, F., Machguth, H., Mölg, N., Paul, F., Hoelzle, M., Eds.; World Glacier Monitoring Service: Zurich, Switzerland, 2015; p. 230. [Google Scholar]
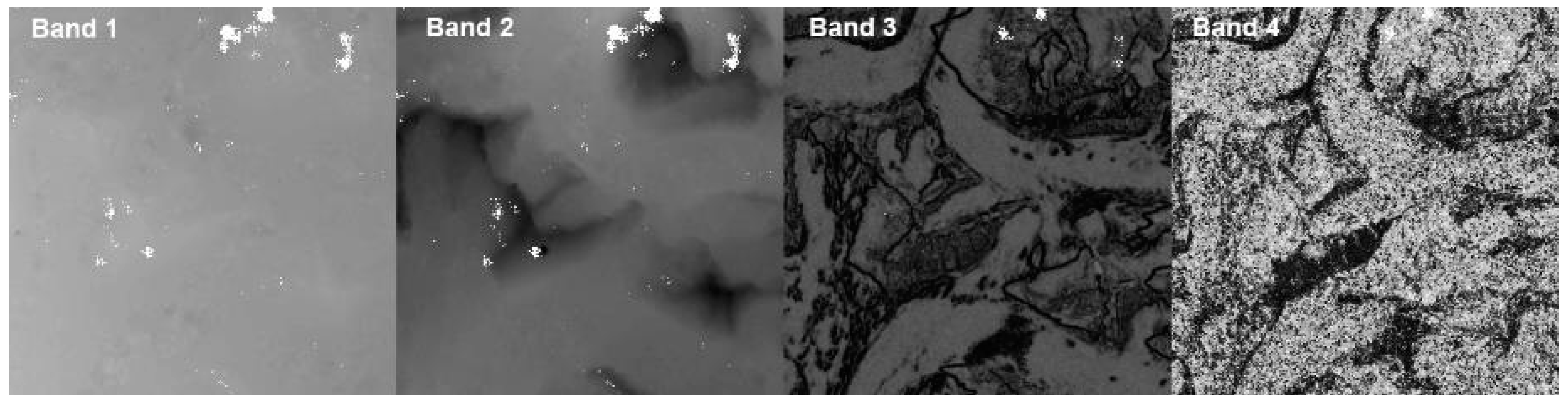
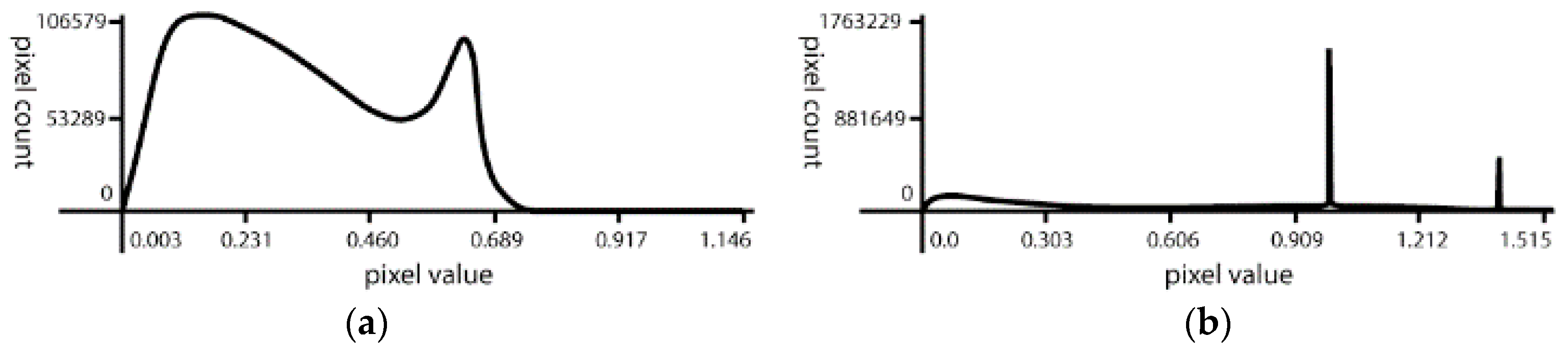
| Sensor | Date | Scene ID/Path-Row | Spatial Resolution | Usage |
|---|---|---|---|---|
| Corona KH-4A | 18/11/1964 | DS1014-2134DA088 | 7.6 m | DTM generation; Mass budget; Glacier mapping |
| DS1014-2134DA089 | ||||
| DS1014-2134DA090 | ||||
| DS1014-2134DF084 | ||||
| DS1014-2134DF085 | ||||
| DS1014-2134DF086 | ||||
| Hexagon KH-9 DTM | 31/07/1973 | DZB1206-500069L010001 | 7.6 m (DTM 25 m) | Mass budget; Co-registration |
| DZB1206-500069L011001 | ||||
| DZB1206-500069L012001 | ||||
| Hexagon KH-9 | 21/08/1980 | DZB1216-500277L021001 | 7.6 m | DTM generation; Mass budget; Glacier mapping |
| DZB1216-500277L022001 | ||||
| DZB1216-500277L023001 | ||||
| SRTM | 11/02/2000 | n41_e076 | ~30 m | Vertical reference |
| n41_e077 | ||||
| Landsat 7 ETM+ | 17/08/1999 | LE71480301999229EDC00 | 15 m | Geocoding |
| 19/08/2000 | LE71480312000232SGS00 | |||
| 09/09/1999 | LE71490311999252SGS00 | |||
| 29/10/2000 | LE71490302000303SGS00 | |||
| Landsat 8 OLI | 02/10/2013 | lc81480312013275lgn00 | 15 m | Geocoding |
| Image | No. of GCPs | RMS Res X | RMS Res Y |
|---|---|---|---|
| DA88 | 24 | 2.94 | 2.80 |
| DA89 | 35 | 2.82 | 2.88 |
| DA90 | 36 | 2.86 | 2.04 |
| DF84 | 20 | 2.35 | 3.14 |
| DF85 | 24 | 2.56 | 2.65 |
| DF86 | 40 | 2.99 | 2.78 |
| Scene | Omega (ω) | Phi (φ) | Kappa (κ) | Flying Height (m) | Focal Length (mm) | Size (px) |
|---|---|---|---|---|---|---|
| FWD | 0° | 15° | 61° | 200,000 | 609.602 | 18,001 × 3801 |
| AFT | −15° |
| Stereo Pair | Tie Points | RMS Res (px) | MIN Res (px) | MAX Res (px) | |||
|---|---|---|---|---|---|---|---|
| x | y | x | y | x | y | ||
| DA88_DF84 | 131 | 14.81 | 1.44 | −34.76 | −3.11 | 32.44 | 3.02 |
| DA88_DF85 | 75 | 5.16 | 0.31 | −8.40 | −0.86 | 12.21 | 0.65 |
| DA89_DF85 | 139 | 24.68 | 2.18 | −54.84 | −4.87 | 51.56 | 4.79 |
| DA89_DF86 | 108 | 31.25 | 1.31 | −74.55 | −2.85 | 76.14 | 2.90 |
| DA90_DF86 | 149 | 25.25 | 1.92 | −55.60 | −4.31 | 62.53 | 4.63 |
| Name | Length 1964 (m) | 1964–1973 (m·a−1) | 1973–1980 (m·a−1) | 1964–1980 (m·a−1) |
|---|---|---|---|---|
| Besimjannij | 6549 | −11.2 ± 2.0 | −38.2 ± 2.0 | −49.4 ± 1.1 |
| Bordu South (No. 354) | 5282 | −3.9 ± 2.0 | −6.8 ± 2.0 | −10.7 ± 1.1 |
| Davidov | 5728 | 12.1 ± 2.0 | 8.4 ± 2.0 | 20.5 ± 1.1 |
| Dschamansu | 11,517 | −2.1 ± 2.0 | 0.0 ± 2.0 | −2.1 ± 1.1 |
| Kaindy | 9205 | 36.1 ± 2.0 | 2.9 ± 2.0 | 39.0 ± 1.1 |
| Kara-Say North | 12,415 | −24.3 ± 2.0 | 0.0 ± 2.0 | −24.3 ± 1.1 |
| Petrov | 15,309 | −24.2 ± 2.0 | −33.5 ± 2.0 | −57.7 ± 1.1 |
| Sary-Tor North | 6668 | 0.0 ± 2.0 | −24.3 ± 2.0 | −24.3 ± 1.1 |
| Sary-Tor South | 4395 | 0.4 ± 2.0 | −8.8 ± 2.0 | −8.4 ± 1.1 |
| Glacier | Mass Budget (m w.e.) | |||||
|---|---|---|---|---|---|---|
| 1964–1973 | 1973–1980 | 1964–1980 | ||||
| Overall | Annual (a−1) | Overall | Annual (a−1) | Overall | Annual (a−1) | |
| All Glaciers | −4.0 ± 1.6 | −0.4 ± 0.2 | −1.9 ± 1.5 | −0.3 ± 0.2 | −5.8 ± 1.5 | −0.4 ± 0.1 |
| Bordu South (354) | −0.4 ± 2.8 | 0.0 ± 0.3 | −6.0 ± 3.1 | −0.9 ± 0.4 | −4.4 ± 2.3 | −0.3 ± 0.1 |
| Besimjannij | −8.4 ± 5.0 | −0.9 ± 0.6 | −1.1 ± 2.0 | −0.2 ± 0.3 | −8.4 ± 3.4 | −0.5 ± 0.2 |
| Davidov | −6.7 ± 2.7 | −0.7 ± 0.3 | +1.1 ± 2.4 | +0.2 ± 0.3 | −5.9 ± 3.6 | −0.4 ± 0.2 |
| Dschamansu | −5.2 ± 4.5 | −0.6 ± 0.5 | −5.8 ± 3.3 | −0.8 ± 0.5 | −11.4 ± 3.9 | −0.7 ± 0.2 |
| Kaindy | −2.0 ± 5.0 | −0.2 ± 0.6 | −3.5 ± 4.1 | −0.5 ± 0.6 | −4.8 ± 4.7 | −0.3 ± 0.3 |
| Kara-Say North | −4.6 ± 5.3 | −0.5 ± 0.6 | −4.6 ± 3.3 | −0.7 ± 0.5 | −9.1 ± 4.9 | −0.6 ± 0.3 |
| Petrov | −6.7 ± 2.2 | −0.7 ± 0.2 | −2.4 ± 2.8 | −0.3 ± 0.4 | −9.1 ± 2.2 | −0.6 ± 0.1 |
| Sary-Tor North | −4.3 ± 2.9 | −0.5 ± 0.3 | −0.7 ± 2.2 | −0.1 ± 0.3 | −6.5 ± 2.9 | −0.4 ± 0.2 |
| Sary-Tor South | −5.2 ± 6.0 | −0.6 ± 0.7 | −0.6 ± 2.4 | −0.1 ± 0.3 | −4.2 ± 6.0 | −0.3 ± 0.4 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license ( http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Goerlich, F.; Bolch, T.; Mukherjee, K.; Pieczonka, T. Glacier Mass Loss during the 1960s and 1970s in the Ak-Shirak Range (Kyrgyzstan) from Multiple Stereoscopic Corona and Hexagon Imagery. Remote Sens. 2017, 9, 275. https://doi.org/10.3390/rs9030275
Goerlich F, Bolch T, Mukherjee K, Pieczonka T. Glacier Mass Loss during the 1960s and 1970s in the Ak-Shirak Range (Kyrgyzstan) from Multiple Stereoscopic Corona and Hexagon Imagery. Remote Sensing. 2017; 9(3):275. https://doi.org/10.3390/rs9030275
Chicago/Turabian StyleGoerlich, Franz, Tobias Bolch, Kriti Mukherjee, and Tino Pieczonka. 2017. "Glacier Mass Loss during the 1960s and 1970s in the Ak-Shirak Range (Kyrgyzstan) from Multiple Stereoscopic Corona and Hexagon Imagery" Remote Sensing 9, no. 3: 275. https://doi.org/10.3390/rs9030275
APA StyleGoerlich, F., Bolch, T., Mukherjee, K., & Pieczonka, T. (2017). Glacier Mass Loss during the 1960s and 1970s in the Ak-Shirak Range (Kyrgyzstan) from Multiple Stereoscopic Corona and Hexagon Imagery. Remote Sensing, 9(3), 275. https://doi.org/10.3390/rs9030275







