Geostatistical Integration of Coarse Resolution Satellite Precipitation Products and Rain Gauge Data to Map Precipitation at Fine Spatial Resolutions
Abstract
:1. Introduction
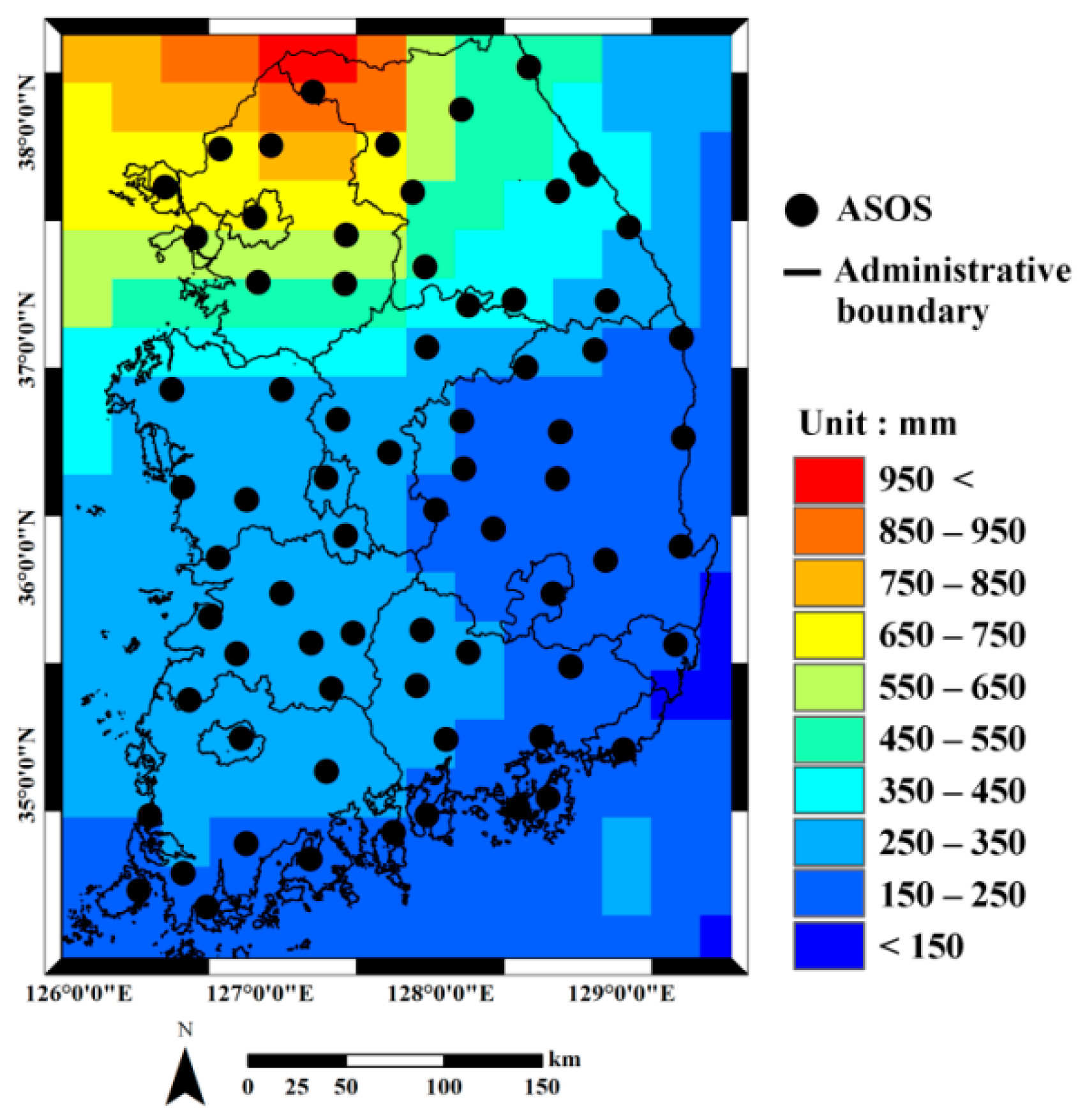
2. Study Area and Data
3. Methodology
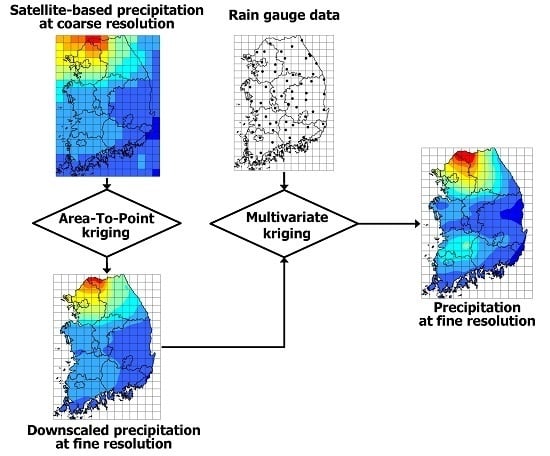
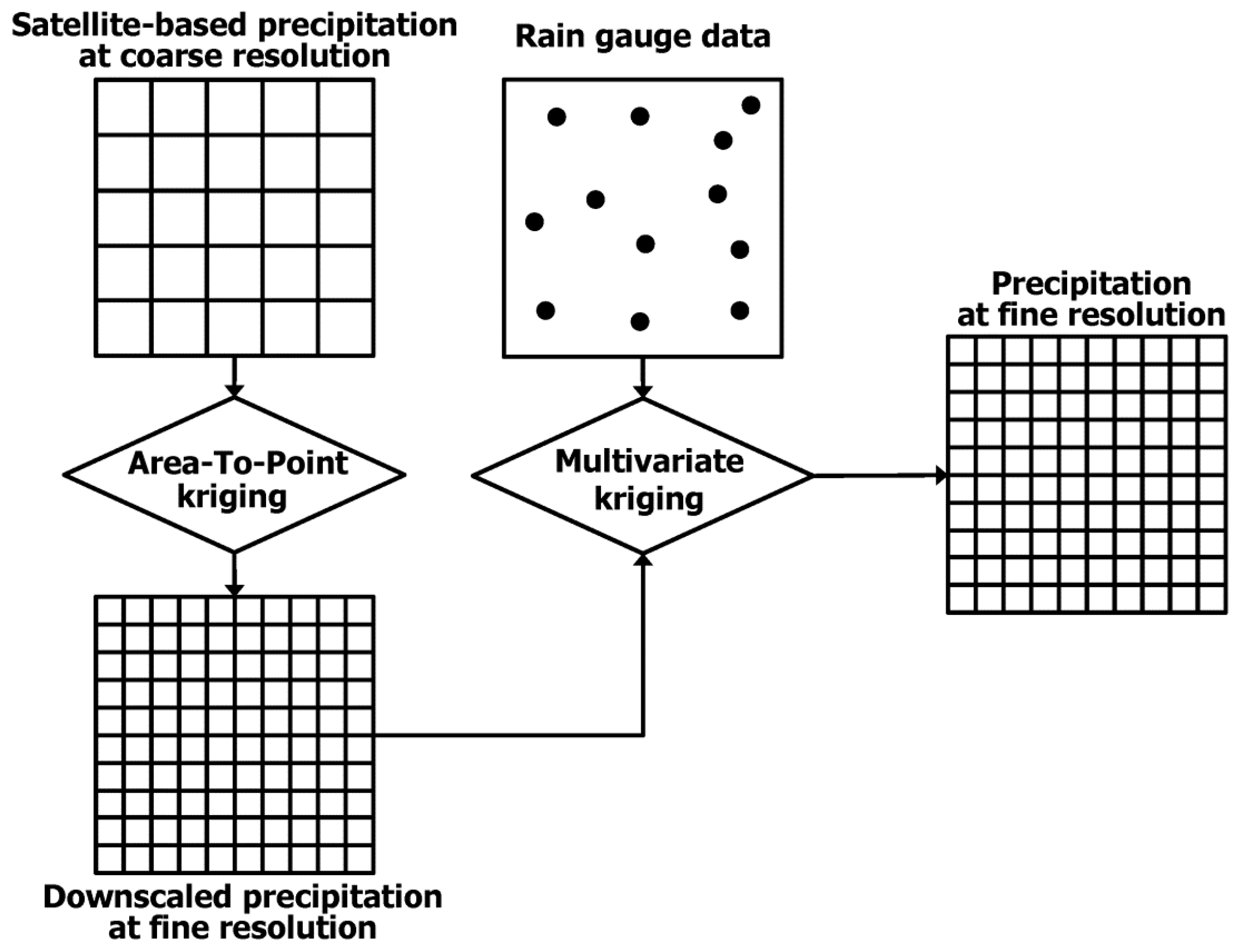
3.1. Geostatistical Downscaling
3.2. Geostatistical Integration
3.2.1. Simple Kriging with Local Means
3.2.2. Kriging with an External Drift
3.2.3. Conditional Merging
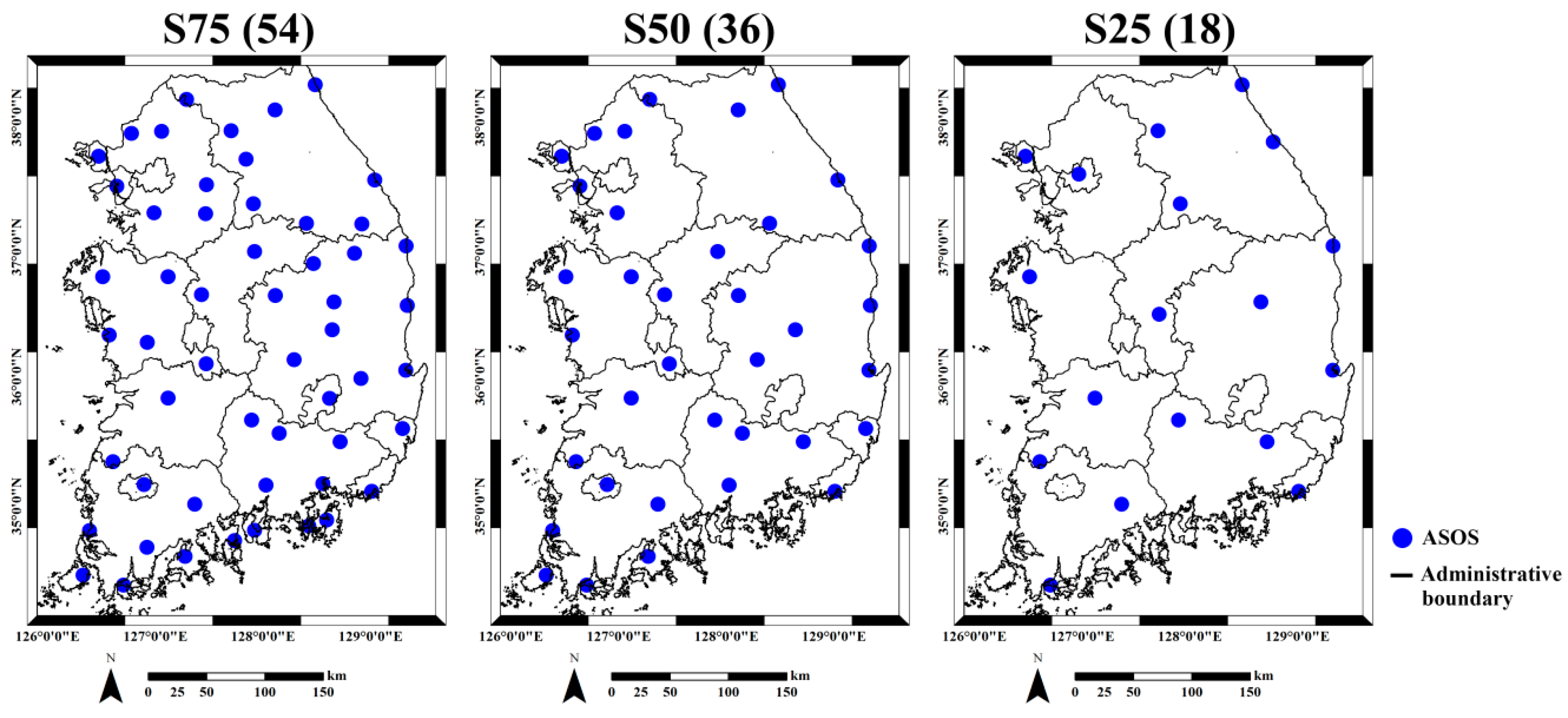
3.3. Performance Evaluation
4. Results
4.1. Downscaling of TRMM Precipitation Products
4.2. Prediction Results
4.3. Performance Evaluation Results
5. Discussion
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Kyriakidis, P.C.; Miller, N.L.; Kim, J. Uncertainty propagation of regional climate model precipitation forecasts to hydrologic impact assessment. J. Hydrometeorol. 2001, 2, 140–160. [Google Scholar] [CrossRef]
- Kyriakidis, P.C.; Kim, J.; Miller, N.L. Geostatistical mapping of precipitation from rain gauge data using atmospheric and terrain characteristics. J. Appl. Meteor. 2001, 40, 1855–1877. [Google Scholar] [CrossRef]
- Goovaerts, P. Geostatistical approaches for incorporating elevation into the spatial interpolation of rainfall. J. Hydrol. 2000, 228, 113–129. [Google Scholar] [CrossRef]
- Park, N.-W. Spatial downscaling of TRMM precipitation using geostatistics and fine scale environmental variables. Adv. Meteorol. 2013, 2013, 237126. [Google Scholar] [CrossRef]
- Atlas, D. Radar in Meteorology; Springer: New York, NY, USA, 1990. [Google Scholar]
- Hong, Y.; Gourley, J.J. Radar Hydrology: Principles, Models, and Applications; CRC Press: Boca Raton, FL, USA, 2014. [Google Scholar]
- Seo, D.-J.; Breidenbach, J.P.; Johnson, E.R. Real-time estimation of mean field bias in radar rainfall data. J. Hydrol. 1999, 3–4, 131–147. [Google Scholar] [CrossRef]
- Ciach, G.J.; Krajewski, W.F.; Villarini, G. Product-error-driven uncertainty model for probabilistic precipitation estimation with NEXRAD data. J. Hydrometeorol. 2007, 8, 1325–1347. [Google Scholar] [CrossRef]
- Kummerow, C.D.; Barnes, W.; Kozu, T.; Shiue, J.; Simpson. The tropical rainfall measuring mission (TRMM) sensor package. J. Atmos. Ocean. Tech. 1998, 15, 809–817. [Google Scholar] [CrossRef]
- Imaoka, K.; Kachi, M.; Fujii, H.; Murakami, H.; Hori, M.; Ono, A.; Igarashi, T.; Nakagawa, K.; Oki, T.; Honda, Y.; et al. Global change observation mission (GCOM) for monitoring carbon, water cycles, and climate change. Proc. IEEE 2010, 98, 717–734. [Google Scholar] [CrossRef]
- Hou, A.Y.; Kakar, R.K.; Neeck, S.; Azarbarzin, A.A.; Kummerow, C.D.; Kojima, M.; Oki, R.; Nakamura, K.; Iguchi, T. The global precipitation measurement mission. Bull. Am. Meteorol. Soc. 2014, 95, 701–722. [Google Scholar] [CrossRef]
- Atkinson, P.M. Downscaling in remote sensing. Int. J. Appl. Earth Obs. Geoinf. 2013, 22, 106–114. [Google Scholar] [CrossRef]
- Immerzeel, W.W.; Rutten, M.M.; Droogers, P. Spatial downscaling of TRMM precipitation using vegetative response on the Iberian Peninsula. Remote Sens. Environ. 2009, 113, 362–370. [Google Scholar] [CrossRef]
- Jia, S.; Zhu, W.; Lü, A.; Yan, T. A statistical spatial downscaling algorithm of TRMM precipitation based on NDVI and DEM in the Qaidam basin of China. Remote Sens. Environ. 2011, 115, 3069–3079. [Google Scholar] [CrossRef]
- Chen, F.; Liu, Y.; Liu, Q.; Li, X. Spatial downscaling of TRMM 3B43 precipitation considering spatial heterogeneity. Int. J. Remote Sens. 2014, 35, 3074–3093. [Google Scholar] [CrossRef]
- Shi, Y.; Song, L.; Xia, Z.; Lin, Y.; Myneni, R.B.; Choi, S.; Wang, L.; Ni, X.; Lao, C.; Yang, F. Mapping annual precipitation across mainland China in the period 2001–2010 from TRMM 3B43 product using spatial downscaling approach. Remote Sens. 2015, 7, 5849–5878. [Google Scholar] [CrossRef]
- Park, N.-W.; Hong, S.; Kyriakidis, P.C.; Lee, W.; Lyu, S.-J. Geostatistical downscaling of AMSR2 precipitation with COMS infrared observations. Int. J. Remote Sens. 2016, 37, 3858–3869. [Google Scholar] [CrossRef]
- Jing, W.; Yang, Y.; Yue, X.; Zhao, X. A spatial downscaling algorithm for satellite-based precipitation over the Tibetan plateau based on NDVI, DEM, and land surface temperature. Remote Sens. 2016, 8, 655. [Google Scholar] [CrossRef]
- Chen, C.; Zhao, S.H.; Duan, Z.; Qin, Z.H. An improved spatial downscaling procedure for TRMM 3B43 precipitation product using geographically weighted regression. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2015, 8, 4592–4604. [Google Scholar] [CrossRef]
- Xu, S.; Wu, C.; Wang, L.; Gonsamo, A.; Shen, Y.; Niu, Z. A new satellite-based monthly precipitation downscaling algorithm with non-stationary relationship between precipitation and land surface characteristics. Remote Sens. Environ. 2015, 162, 119–140. [Google Scholar] [CrossRef]
- Huffman, G.J.; Bolvin, D.T.; Nelkin, E.J.; Wolff, D.B.; Adler, R.F.; Gu, G.; Hong, Y.; Bowman, K.P.; Stocker, E.F. The TRMM multisatellite precipitation analysis (TMPA): Quasi-global, multiyear, combined-sensor precipitation estimates at fine scale. J. Hydrometeorol. 2007, 8, 38–55. [Google Scholar] [CrossRef]
- Nerini, D.; Zulkafli, Z.; Wang, L.-P.; Onof, C.; Buytaert, W.; Lavado-Casimiro, W.; Guyot, J.-L. A comparative analysis of TRMM-rain gauge data merging techniques at the daily time scale for distributed rainfall-runoff modeling applications. J. Hydrometeorol. 2015, 16, 2153–2168. [Google Scholar] [CrossRef]
- Porcù, F.; Milani, L.; Petracca, M. On the uncertainties in validating satellite instantaneous rainfall estimates with raingauge operational network. Atmos. Res. 2014, 144, 73–81. [Google Scholar] [CrossRef]
- Li, M.; Shao, Q. An improved statistical approach to merge satellite rainfall estimates and raingauge data. J. Hydrol. 2010, 385, 51–64. [Google Scholar] [CrossRef]
- Todini, E. A Bayesian technique for conditioning radar precipitation estimates to rain-gauge measurements. Hydrol. Earth Syst. Sci. 2001, 5, 187–199. [Google Scholar] [CrossRef]
- Baik, J.; Park, J.; Ryu, D.; Choi, M. Geospatial blending to improve spatial mapping of precipitation with high spatial resolution by merging satellite-based and ground-based data. Hydrol. Process. 2016, 30, 2789–2803. [Google Scholar]
- Chappell, A.; Renzullo, L.J.; Raupach, T.H.; Haylock, M. Evaluating geostatistical methods of blending satellite and gauge data to estimate near real-time daily rainfall for Australia. J. Hydrol. 2013, 493, 105–114. [Google Scholar] [CrossRef]
- Berndt, C.; Rabiei, E.; Haberlandt, U. Geostatistical merging of rain gauge and radar data for high temporal resolutions and various station density scenarios. J. Hydrol. 2014, 508, 88–101. [Google Scholar] [CrossRef]
- Erdin, R.; Frei, C.; Küsch, H.R. Data transformation and uncertainty in geostatistical combination of radar and rain gauges. J. Hydrometeorol. 2012, 13, 1332–1346. [Google Scholar] [CrossRef]
- Goudenhoofdt, E.; Delobbe, L. Evaluation of radar-gauge merging methods for quantitative precipitation estimates. Hydrol. Earth Syst. Sci. 2009, 13, 195–203. [Google Scholar] [CrossRef]
- Hunink, J.E.; Immerzeel, W.W.; Droogers, P. A high-resolution precipitation 2-step mapping procedure (HiP2P): development and application to a tropical mountainous area. Remote Sens. Environ. 2014, 140, 179–188. [Google Scholar] [CrossRef]
- Duan, Z.; Bastiaanssen, W.G.M. First results from version 7 TRMM 3B43 precipitation product in combination with a new downscaling-calibration procedure. Remote Sens. Environ. 2013, 131, 1–13. [Google Scholar] [CrossRef]
- Kyriakidis, P.C. A geostatistical framework for area-to-point spatial interpolation. Geogr. Anal. 2004, 36, 259–289. [Google Scholar] [CrossRef]
- Korea Meteorological Administration. Available online: http://web.kma.go.kr/eng/biz/climate_01.jsp (accessed on 31 January 2017).
- Oh, H.-J.; Sohn, B.-J.; Smith, E.A.; Turk, F.J.; Seo, A.-S.; Chung, H.-S. Validating infrared-based rainfall retrieval algorithms with 1-minute spatially dense raingage measurements over Korean peninsula. Meteorol. Atmos. Phys. 2002, 81, 273–287. [Google Scholar] [CrossRef]
- Kyriakidis, P.C.; Yoo, E.H. Geostatistical prediction and simulation of point values from areal data. Geogr. Anal. 2005, 37, 124–151. [Google Scholar] [CrossRef]
- Goovaerts, P. Kriging and semivariogram deconvolution in the presence of irregular geographical units. Math. Geosci. 2008, 40, 101–128. [Google Scholar] [CrossRef]
- Hengl, T.; Heuvelink, G.B.M.; Stein, A. A generic framework for spatial prediction of soil variables based on regression-kriging. Geoderma 2004, 120, 75–93. [Google Scholar] [CrossRef]
- Goovaerts, P. Geostatistics for Natural Resources Evaluation; Oxford University Press: New York, NY, USA, 1997. [Google Scholar]
- Patriarche, D.; Castro, M.C.; Goovaerts, P. Estimating regional hydraulic conductivity fields-a comparative study of geostatistical methods. Math. Geol. 2005, 37, 587–613. [Google Scholar] [CrossRef]
- Sales, M.H.; Souza, C.M., Jr.; Kyriakidis, P.C. Fusion of MODIS images using kriging with external drift. IEEE Trans. Geosci. Remote Sens. 2013, 51, 2250–2259. [Google Scholar] [CrossRef]
- Ehret, U. Rainfall and Flood Nowcasting in Small Catchments Using Weather Radar. Ph.D. Thesis, University of Stuttgart, Stuttgart, Germany, 2002. [Google Scholar]
- Sinclair, S.; Pegram, G. Combining radar and rain gauge rainfall estimates using conditional merging. Atmos. Sci. Lett. 2005, 6, 19–22. [Google Scholar] [CrossRef]
- Deutsch, C.V.; Journel, A.G. GSLIB: Geostatistical Software Library and User’s Guide, 2nd ed.; Oxford University Press: New York, NY, USA, 1998. [Google Scholar]
- Liu, Y.; Journel, A.G. A package for geostatistical integration of coarse and fine scale data. Comput. Geosci. 2009, 35, 527–547. [Google Scholar] [CrossRef]
- Goovaerts, P. Combining areal and point data in geostatistical interpolation: Applications to soil science and medical geography. Math. Geosci. 2010, 42, 535–554. [Google Scholar] [CrossRef] [PubMed]
- Remy, N.; Boucher, A.; Wu, J. Applied Geostatistics with SGeMS: A User’s Guide; Cambridge University Press: Cambridge, UK, 2009. [Google Scholar]
- Park, N.-W. Spatial downscaling of coarse scale satellite products: State-of-the-arts and issues. In Proceedings of the Fall Meeting of Korean Society of Remote Sensing, Chungjoo, Korea, 4 November 2016; pp. 310–311. (In Korean)
- Gires, A.; Tchiguirinskaia, I.; Schertzer, D.; Schellart, A.; Berne, A.; Lovejoy, S. Influence of small scale rainfall variability on standard comparison tools between radar and rain gauge data. Atmos. Res. 2014, 138, 125–138. [Google Scholar] [CrossRef]
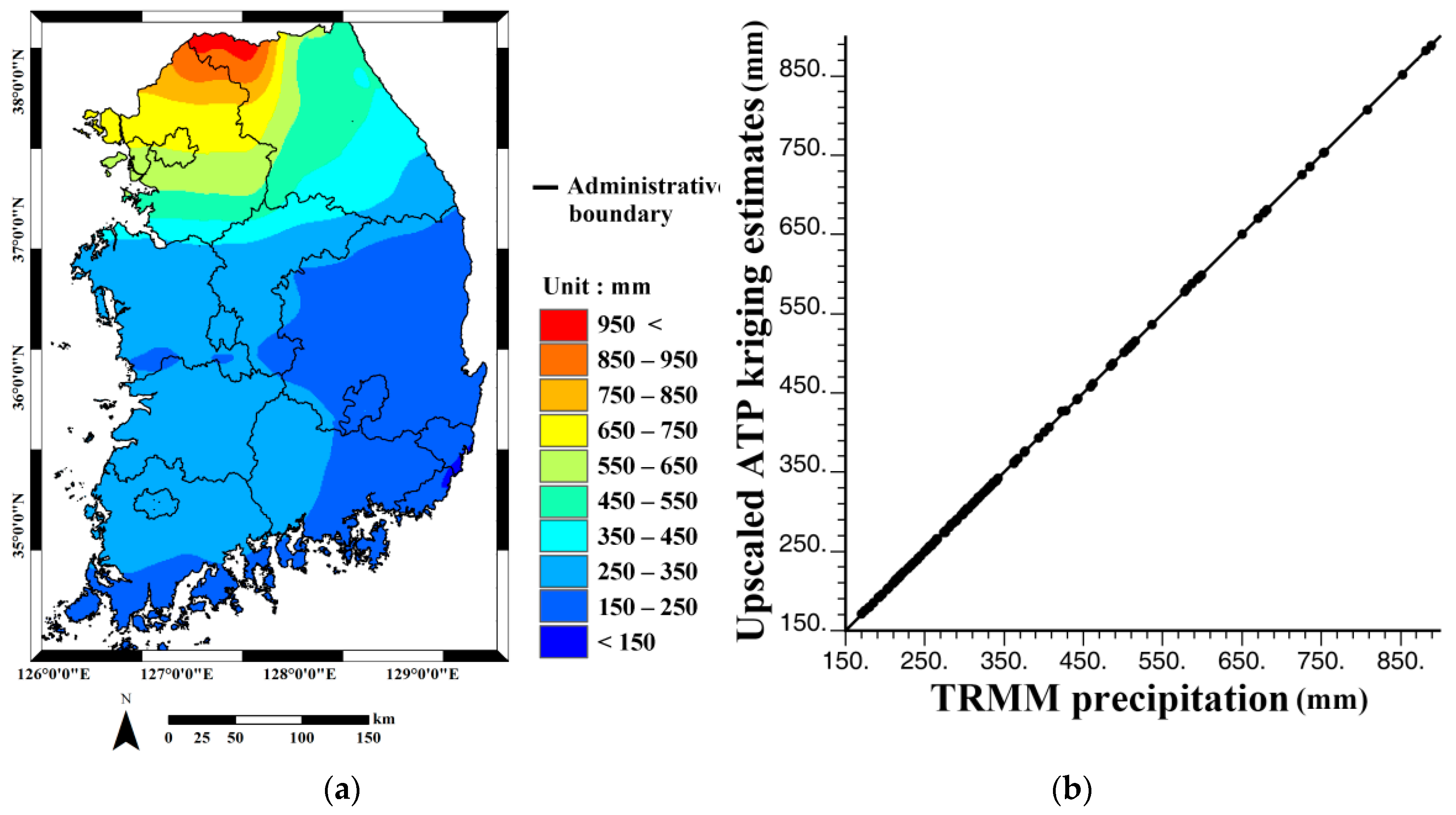
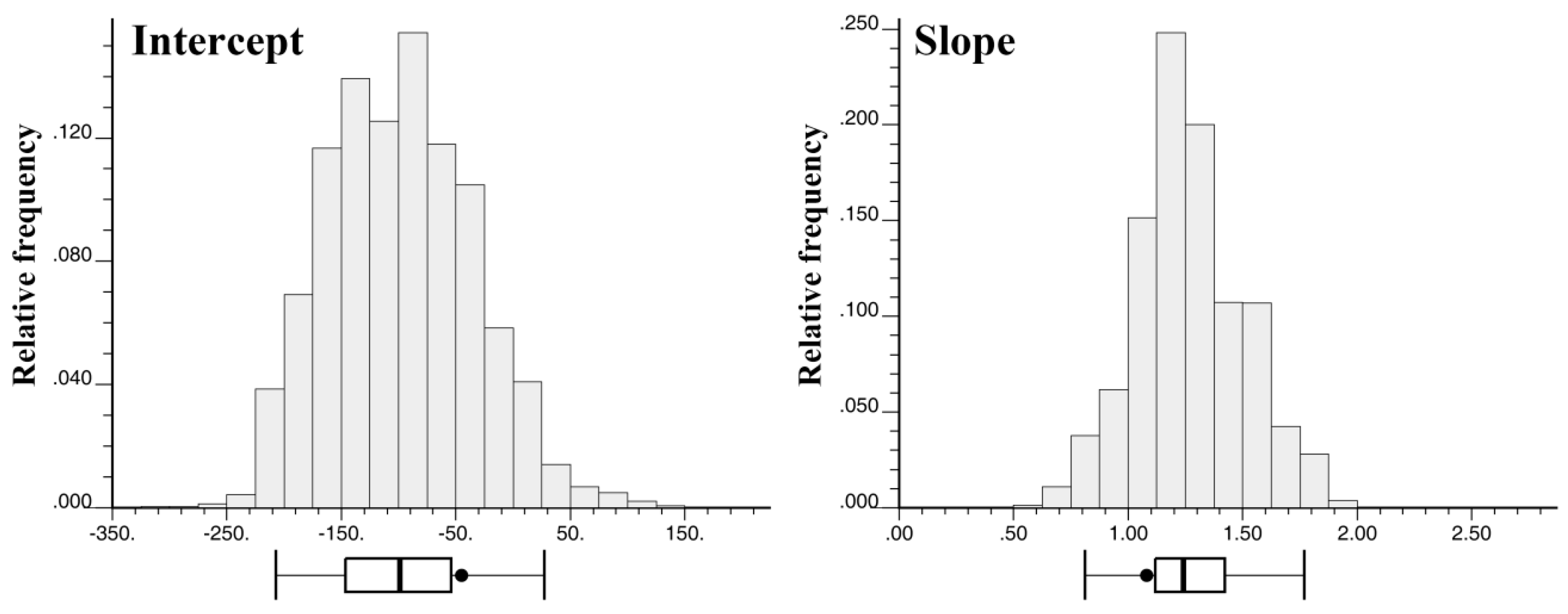
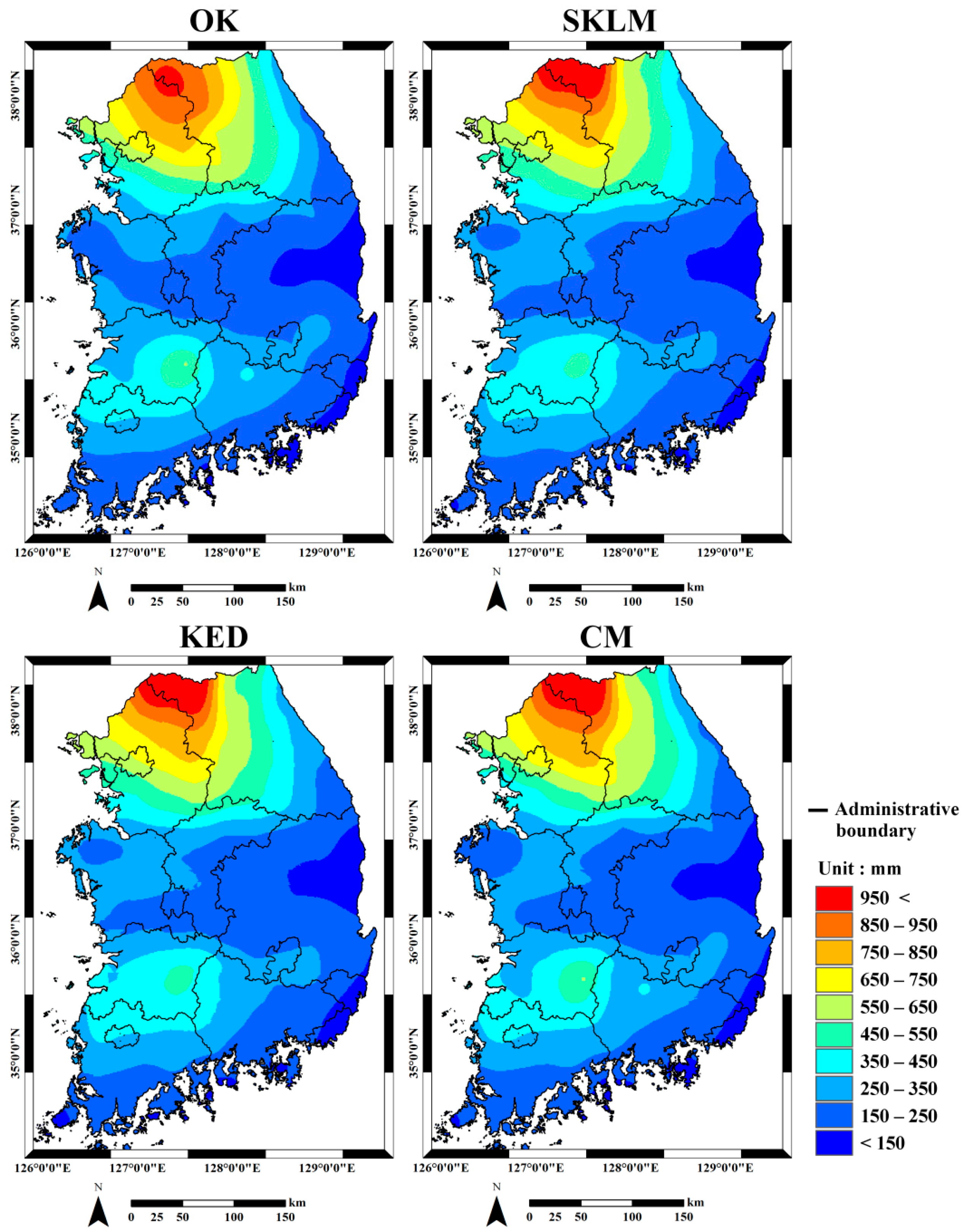
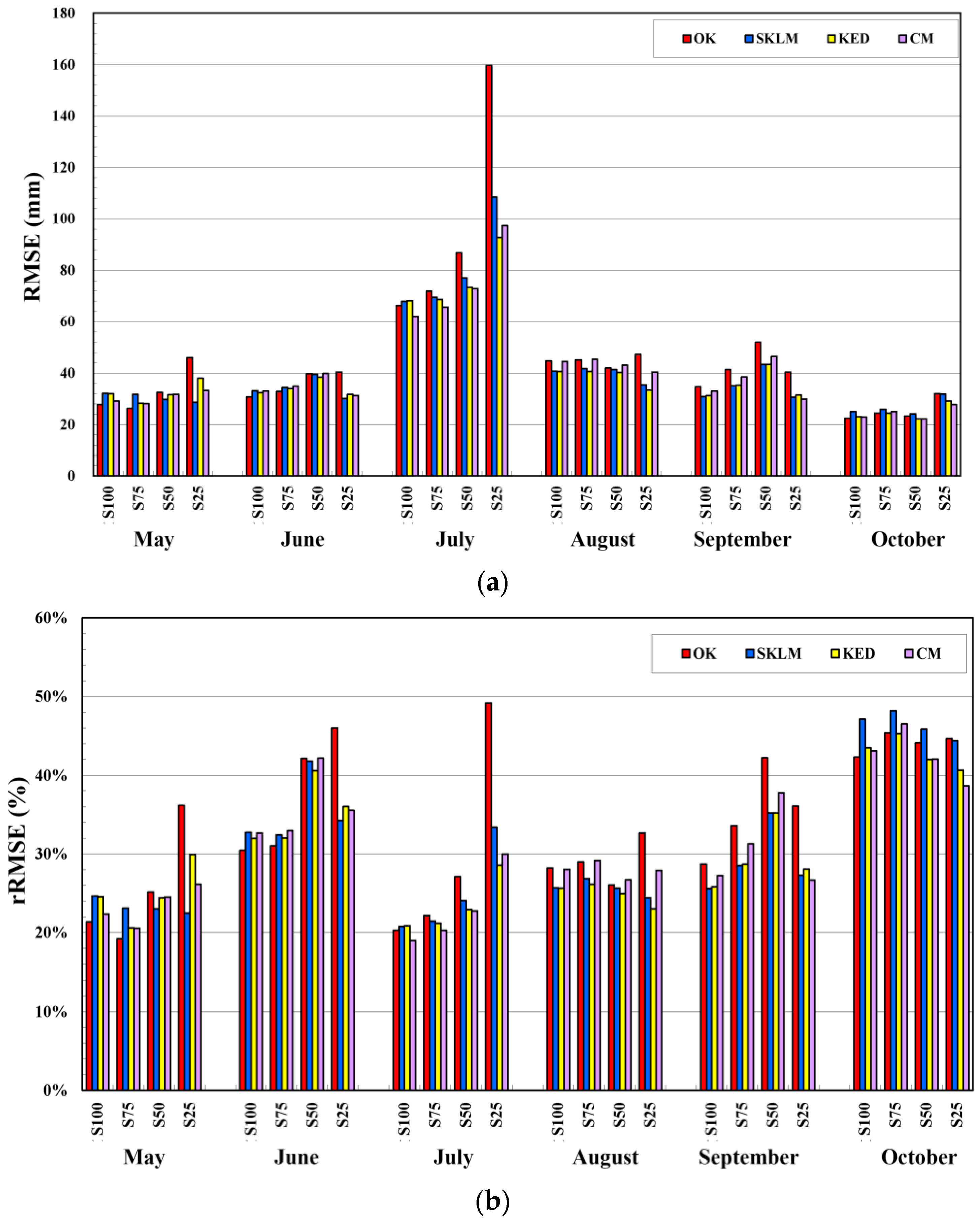
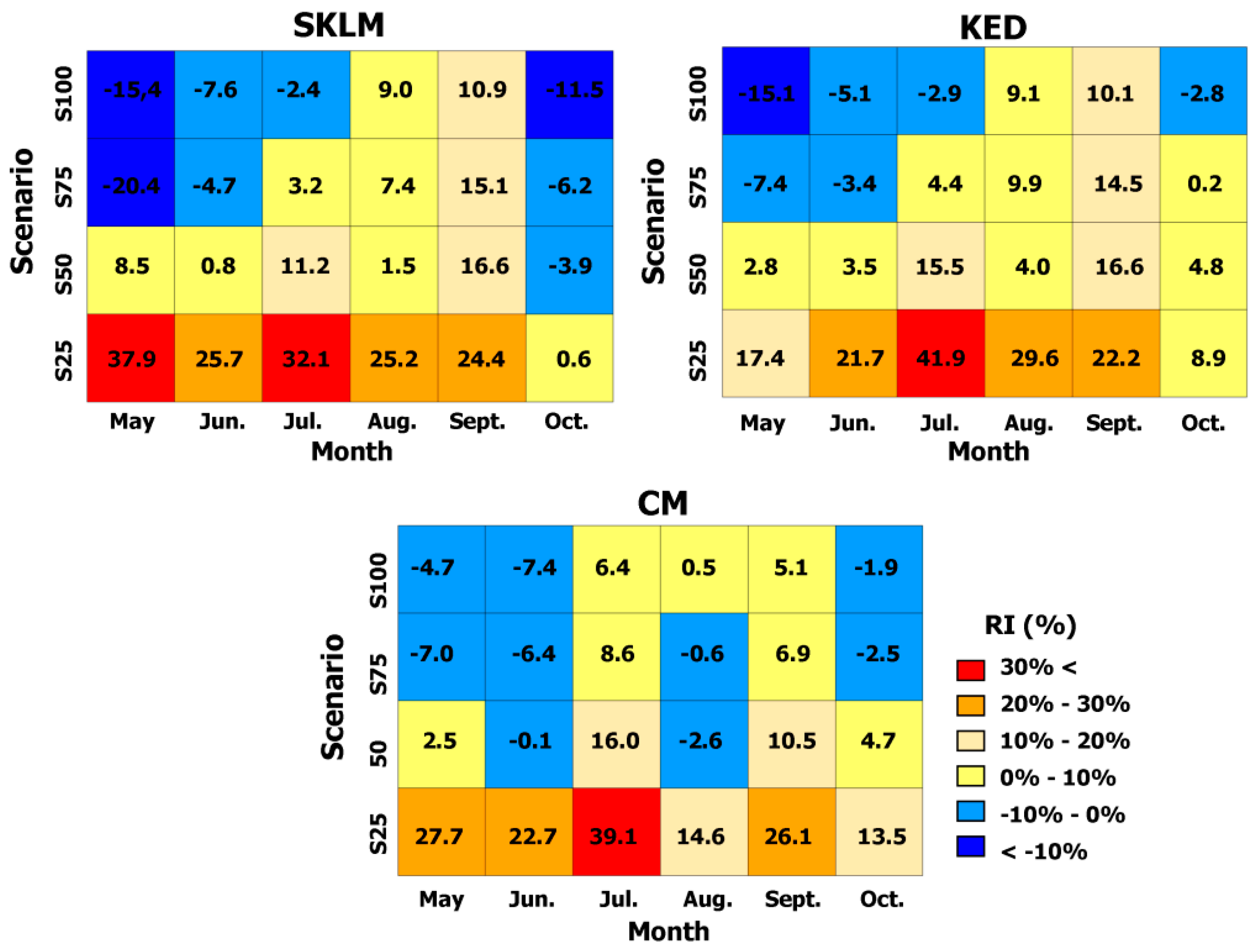
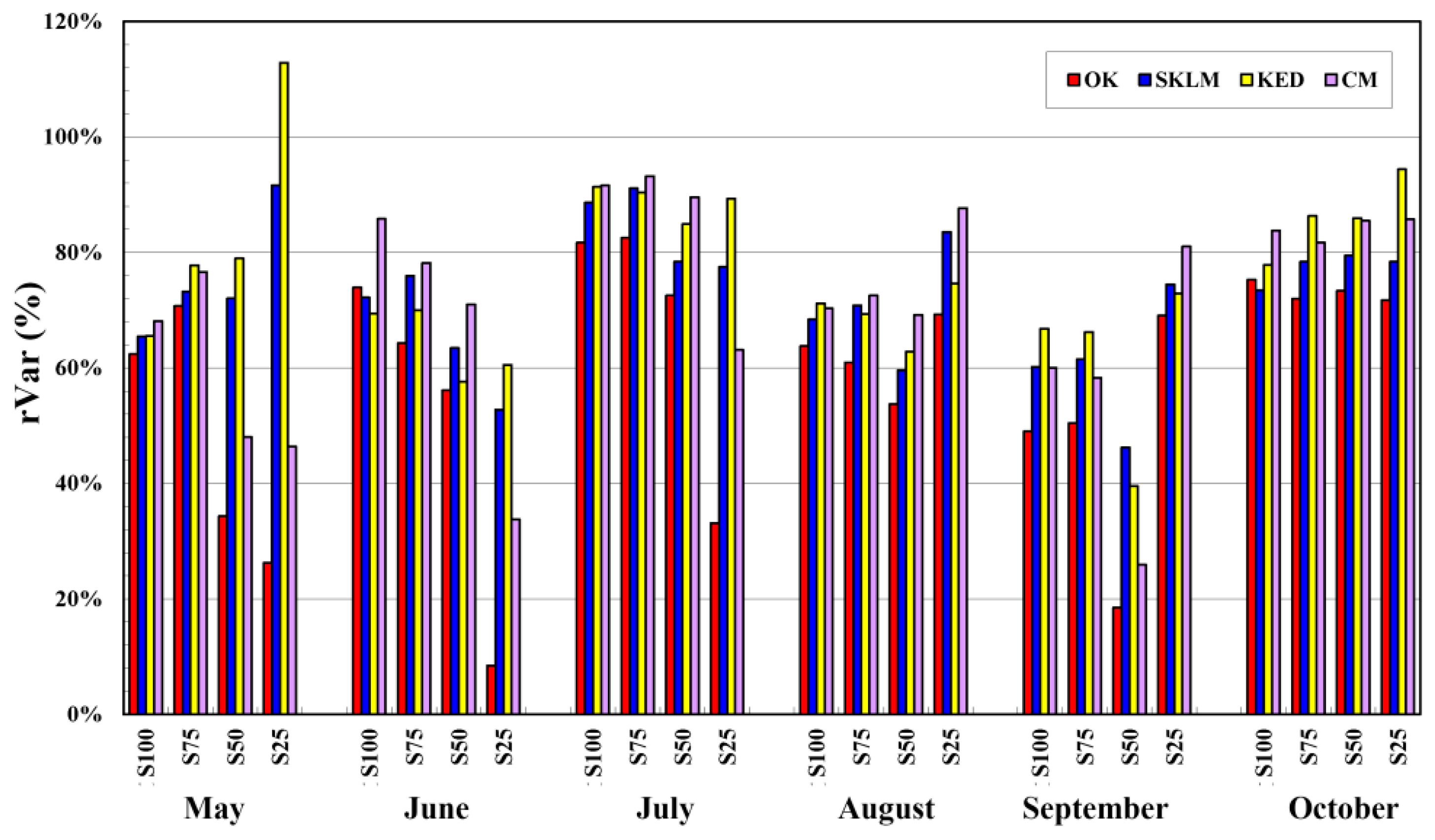
| Month | rME (%) | RMSE (mm) | rRMSE (%) | rVar (%) | Correlation |
|---|---|---|---|---|---|
| May | 1.42 | 31.61 | 24.28 | 44.46 | 0.81 |
| June | 12.44 | 36.51 | 36.13 | 36.75 | 0.75 |
| July | 5.19 | 82.56 | 25.28 | 71.45 | 0.91 |
| August | 7.53 | 42.80 | 27.00 | 58.23 | 0.79 |
| September | 10.11 | 35.53 | 29.41 | 56.47 | 0.73 |
| October | 5.30 | 24.26 | 45.71 | 67.12 | 0.87 |
| Average | 7.00 | 42.21 | 31.30 | 55.75 | 0.81 |
| Statistics | Scenario | OK | SKLM | KED | CM |
|---|---|---|---|---|---|
| rME (%) | S100 | 0.14 | 0.08 | 0.66 | 0.06 |
| S75 | 0.39 | 0.43 | 0.27 | 0.18 | |
| S50 | 0.33 | 0.09 | −0.01 | 0.23 | |
| S25 | −0.39 | −0.40 | −0.13 | −0.03 | |
| rRMSE (%) | S100 | 28.55 | 29.43 | 28.73 | 28.74 |
| S75 | 30.05 | 30.09 | 28.99 | 30.12 | |
| S50 | 34.45 | 32.59 | 31.69 | 32.66 | |
| S25 | 40.80 | 31.03 | 31.04 | 30.81 | |
| rVar (%) | S100 | 67.69 | 71.39 | 73.68 | 76.62 |
| S75 | 66.81 | 75.17 | 76.67 | 76.76 | |
| S50 | 51.45 | 66.55 | 68.30 | 64.87 | |
| S25 | 46.32 | 76.39 | 84.11 | 66.29 | |
| RI of RMSE (%) | S100 | - | −2.84 | −1.11 | −0.33 |
| S75 | - | −0.92 | 3.04 | −0.17 | |
| S50 | - | 5.78 | 7.87 | 5.18 | |
| S25 | - | 24.30 | 23.62 | 23.95 |
| Case | SKLM | KED | CM |
|---|---|---|---|
| (a) Comparison with TRMM error statistics and predictions | |||
| rRMSE for TRMM precipitation versus rRMSE for kriging predictions | 0.96 | 0.95 | 0.92 |
| Average of correlation of TRMM precipitation versus kriging predictions | 0.97 | 0.95 | 0.92 |
| (b) Comparison with OK error statistics and predictions | |||
| rRMSE for OK predictions versus rRMSE for kriging predictions | 0.80 | 0.81 | 0.85 |
| Average of correlation for OK predictions versus kriging predictions | 0.90 | 0.90 | 0.93 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license ( http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Park, N.-W.; Kyriakidis, P.C.; Hong, S. Geostatistical Integration of Coarse Resolution Satellite Precipitation Products and Rain Gauge Data to Map Precipitation at Fine Spatial Resolutions. Remote Sens. 2017, 9, 255. https://doi.org/10.3390/rs9030255
Park N-W, Kyriakidis PC, Hong S. Geostatistical Integration of Coarse Resolution Satellite Precipitation Products and Rain Gauge Data to Map Precipitation at Fine Spatial Resolutions. Remote Sensing. 2017; 9(3):255. https://doi.org/10.3390/rs9030255
Chicago/Turabian StylePark, No-Wook, Phaedon C. Kyriakidis, and Sungwook Hong. 2017. "Geostatistical Integration of Coarse Resolution Satellite Precipitation Products and Rain Gauge Data to Map Precipitation at Fine Spatial Resolutions" Remote Sensing 9, no. 3: 255. https://doi.org/10.3390/rs9030255
APA StylePark, N.-W., Kyriakidis, P. C., & Hong, S. (2017). Geostatistical Integration of Coarse Resolution Satellite Precipitation Products and Rain Gauge Data to Map Precipitation at Fine Spatial Resolutions. Remote Sensing, 9(3), 255. https://doi.org/10.3390/rs9030255