Reconstruction of Daily Sea Surface Temperature Based on Radial Basis Function Networks
Abstract
:1. Introduction
2. Data Description
3. Methodology
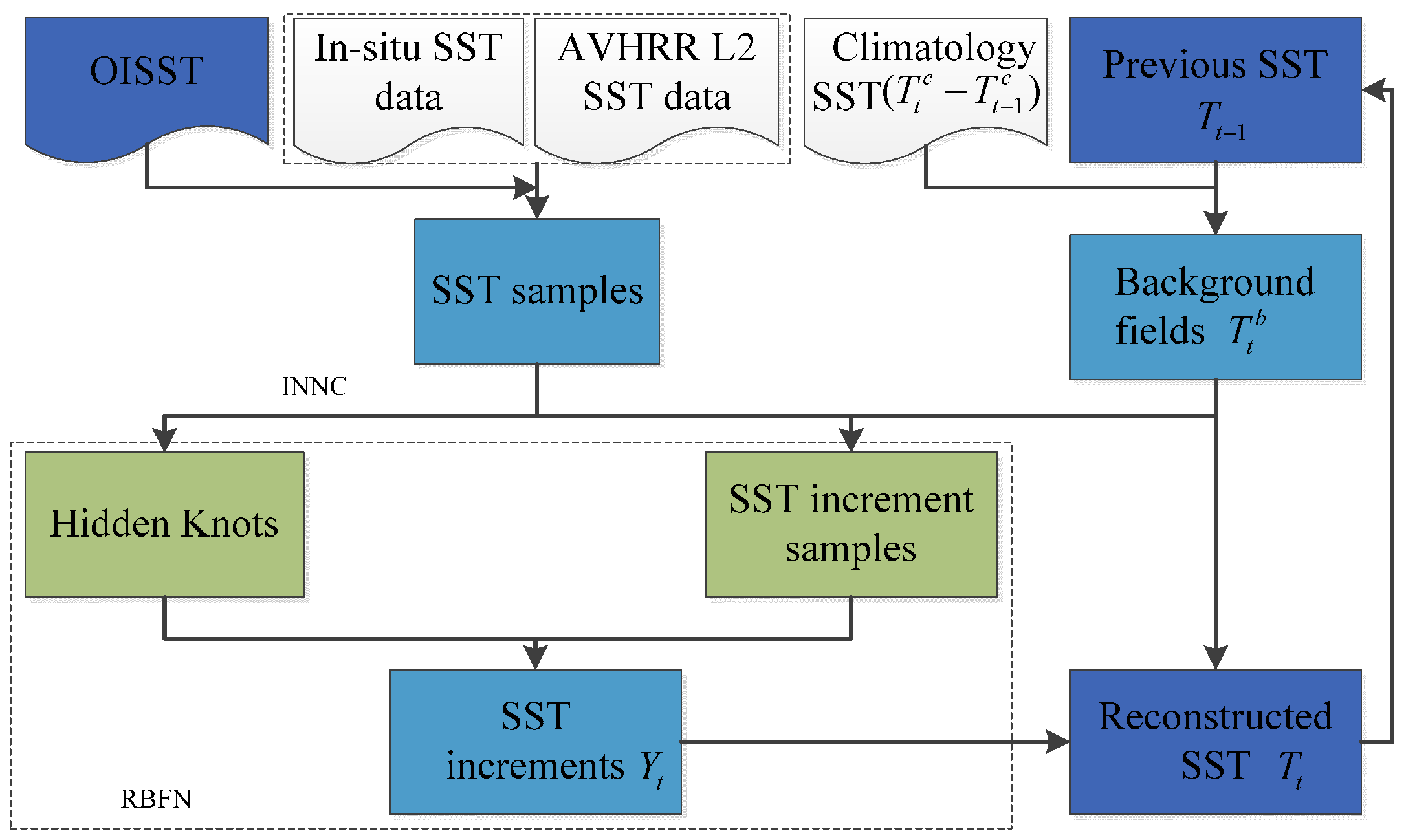
3.1. RBFN Method
3.2. INNC Algorithm
- (1)
- Standardizing the original SST data, and make sure each variable of in the SST matrix, with the mean of 0 and standard deviation of 1, where z is the value of the SST at the position of in the SST matrix.
- (2)
- Define a minimal distance D and set the first SST sample as the first center .
- (3)
- For the second SST sample , the Euclidean distance s to the center is calculated. If s > D, then the position is the next center , otherwise the algorithm searches for the next SST sample .
- (4)
- For the i-th SST sample , the Euclidean distance to each center is calculated, k = 1,…,K. K is the number of center. If the minimal distance , then the position is the next center , otherwise the algorithm searches for the next SST sample, until the last one is found.
- (5)
- The values from the background field are used to fill the positions without SST samples, before repeating step (3) for each position to select the centers from the background field. This continues until all of the positions are processed in the SST matrix, and the hidden knots are obtained by using the positions of centers in the SST matrix.
3.3. Evaluating the Performance of the RBFN Method
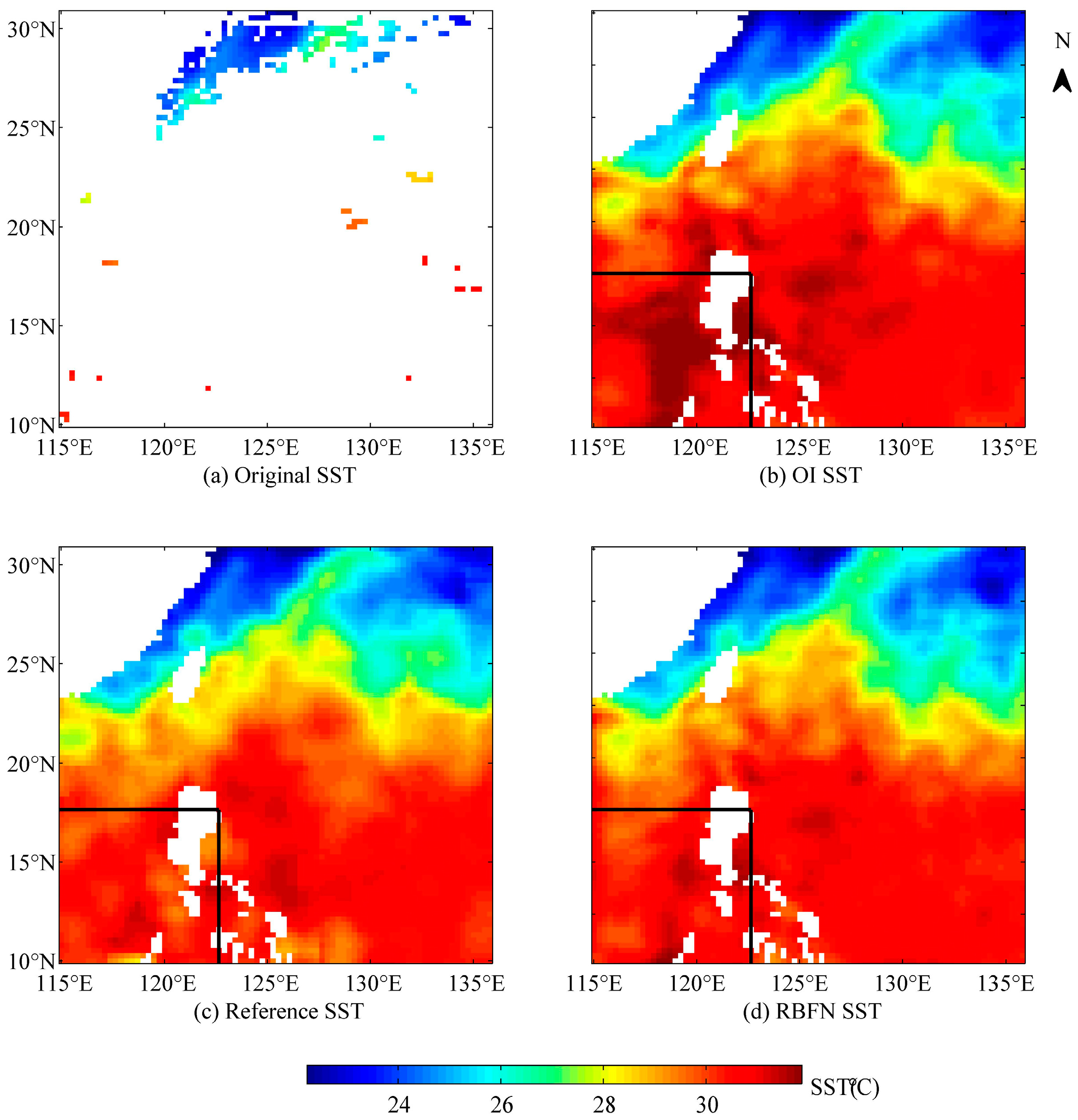
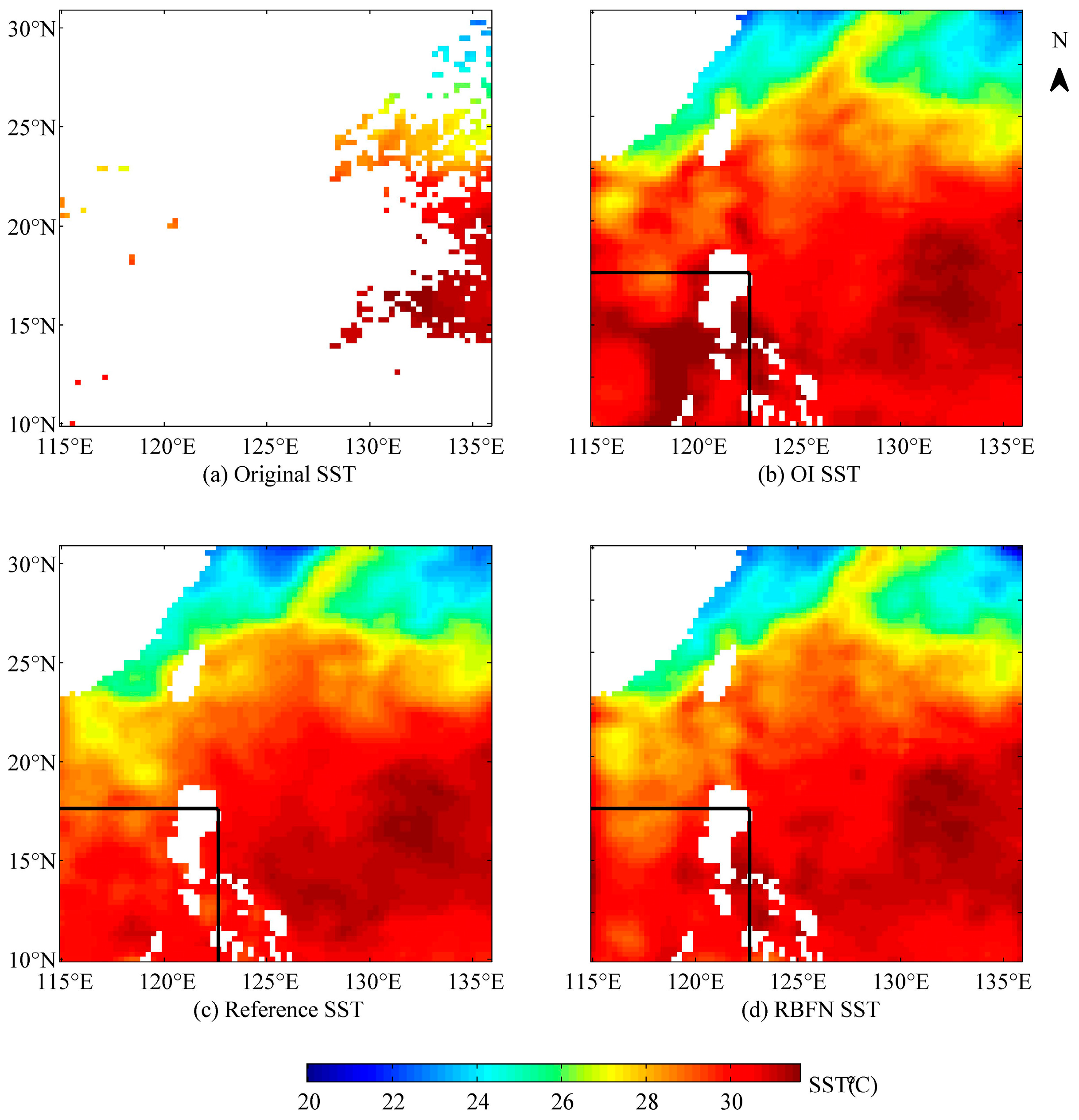
4. Results
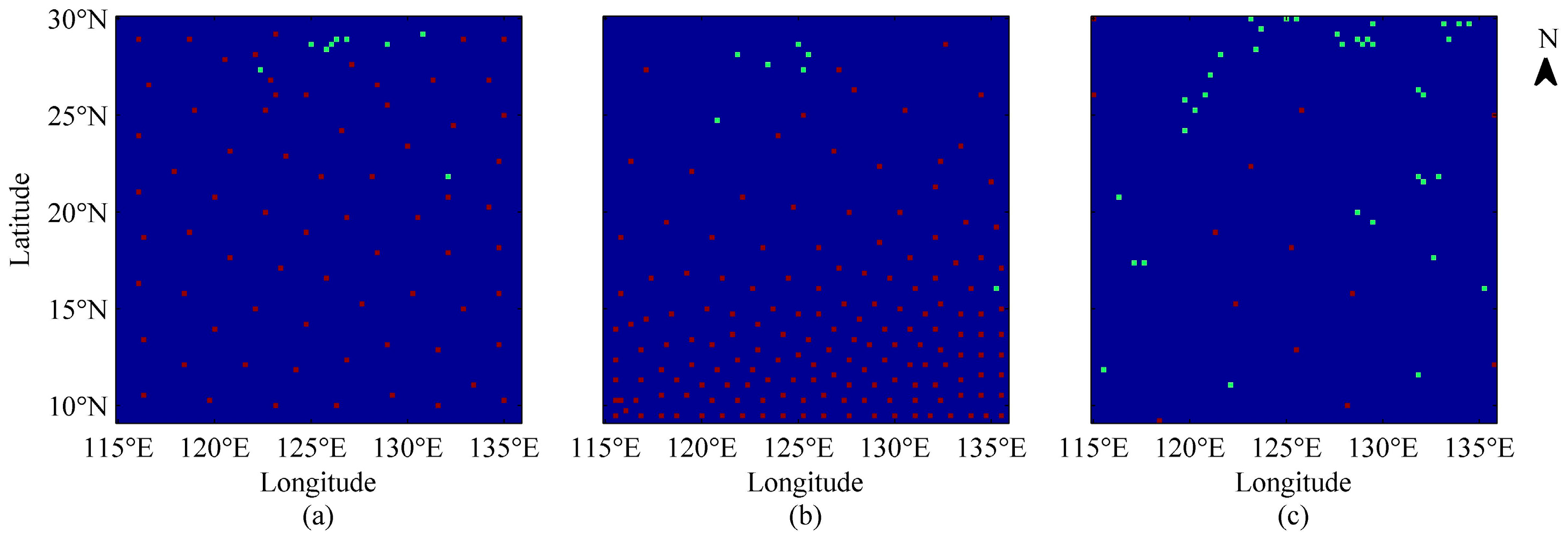
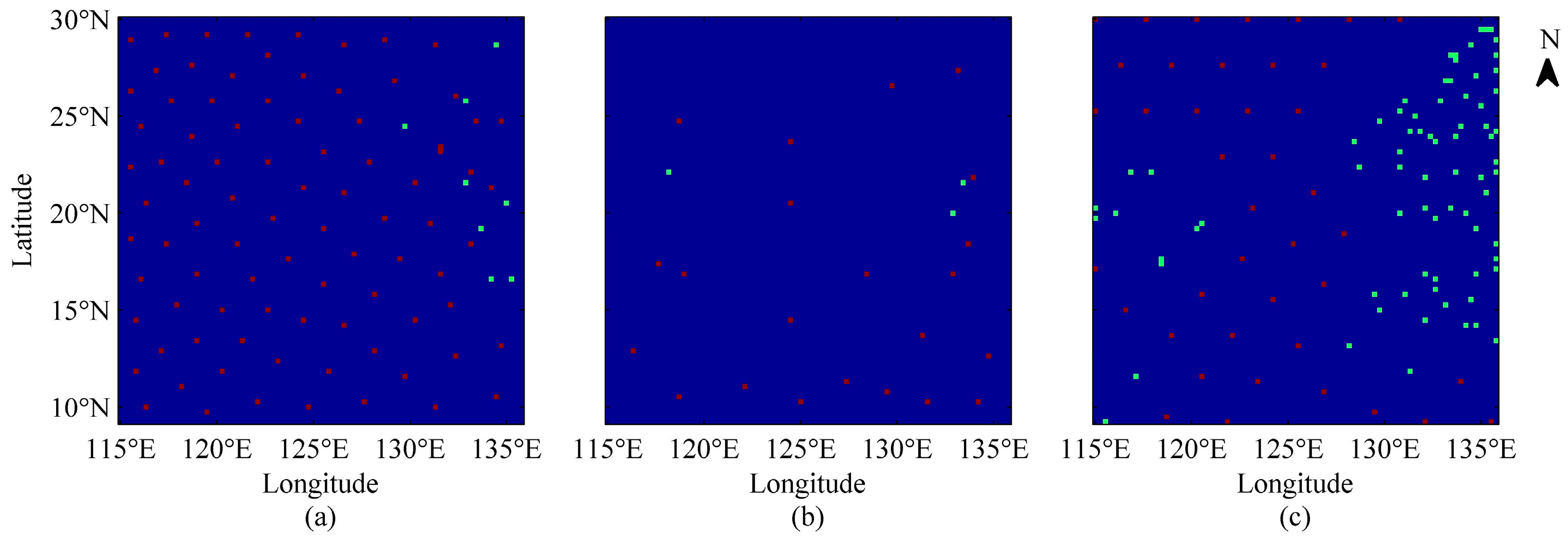
4.1. Results from Different Basis Functions
4.2. Results from Different Clustering Algorithms
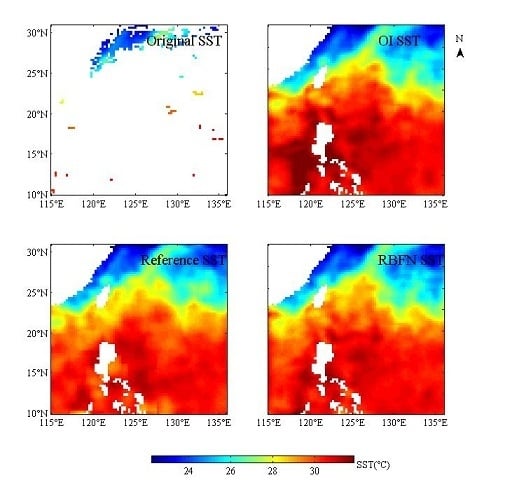
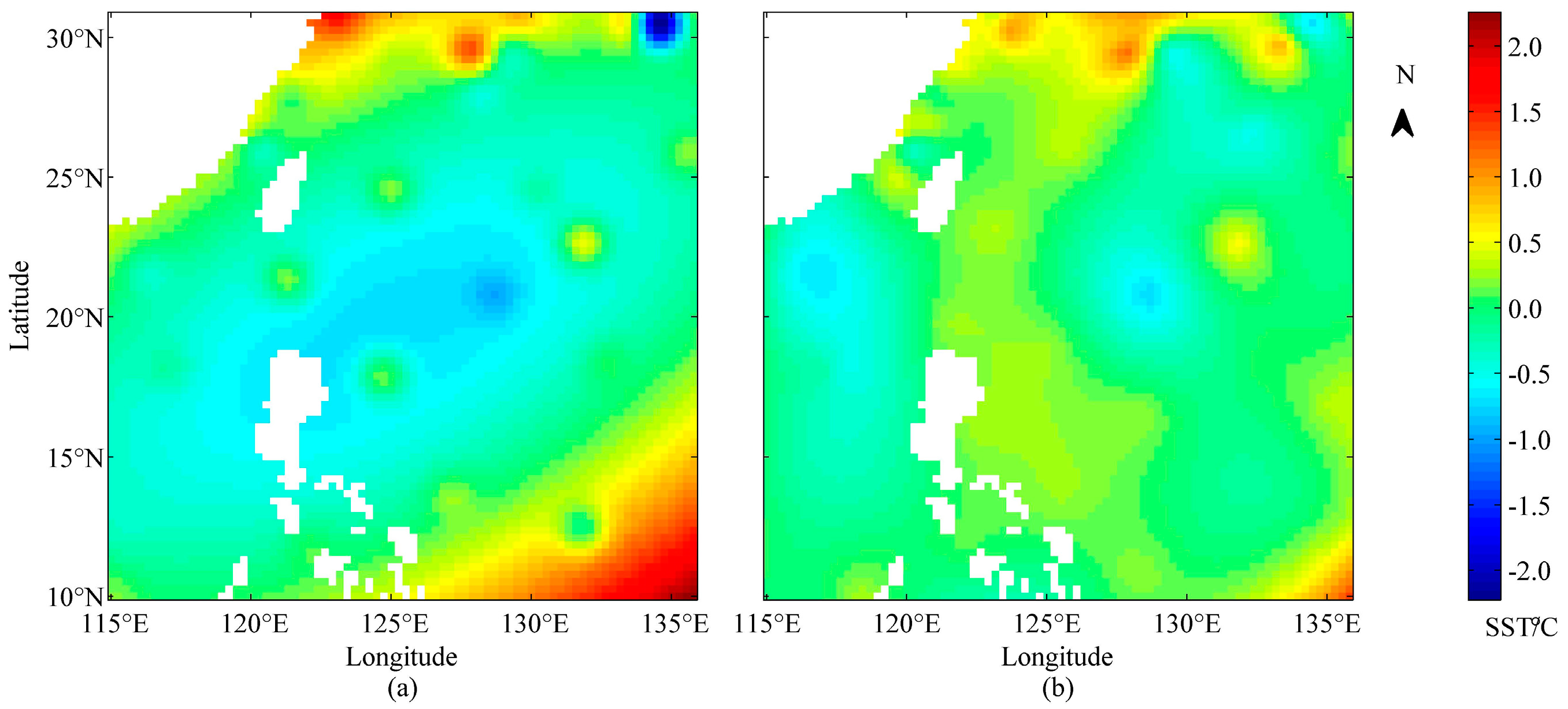
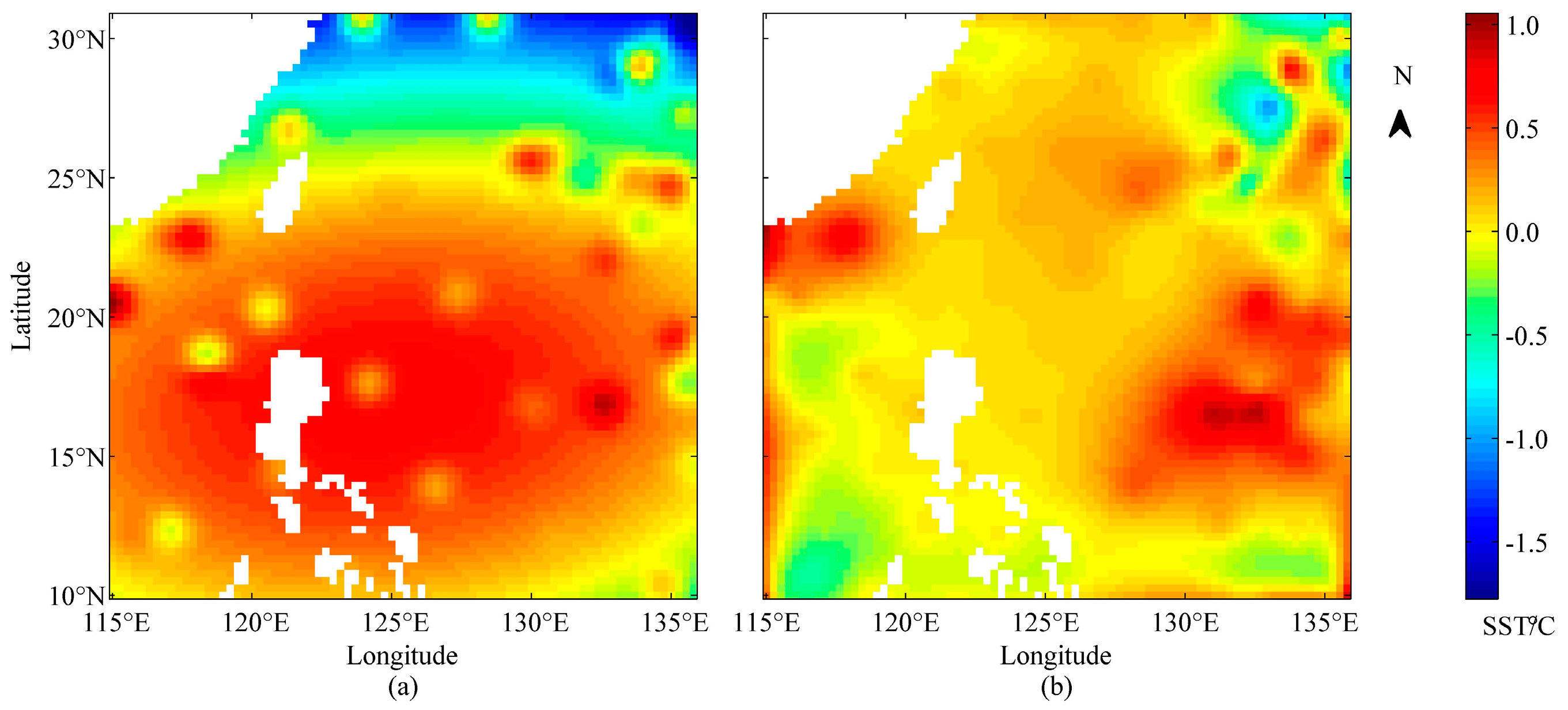
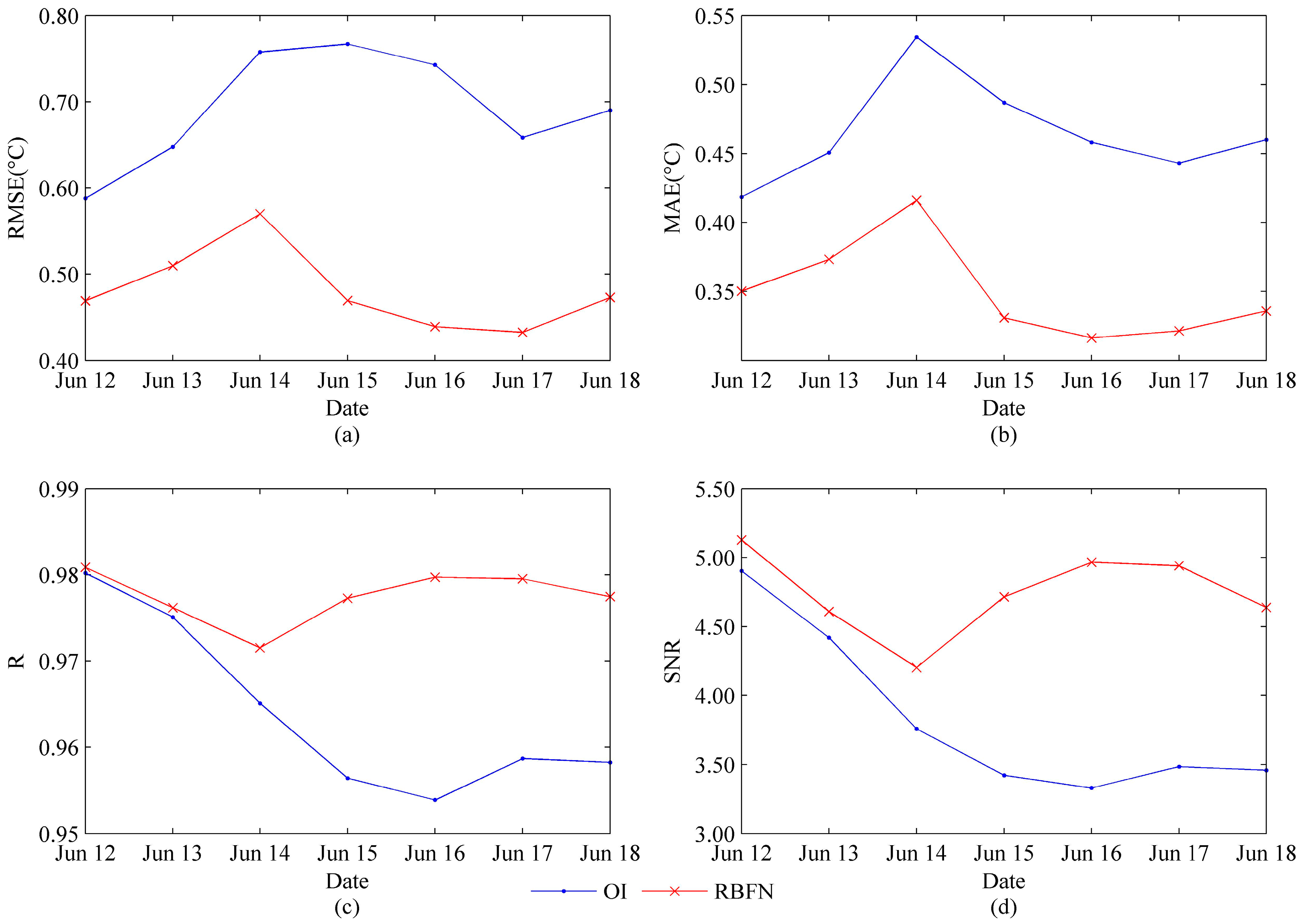
4.3. Comparison with the OI Method
5. Discussion
5.1. The INCC Algorithm for RBFNs
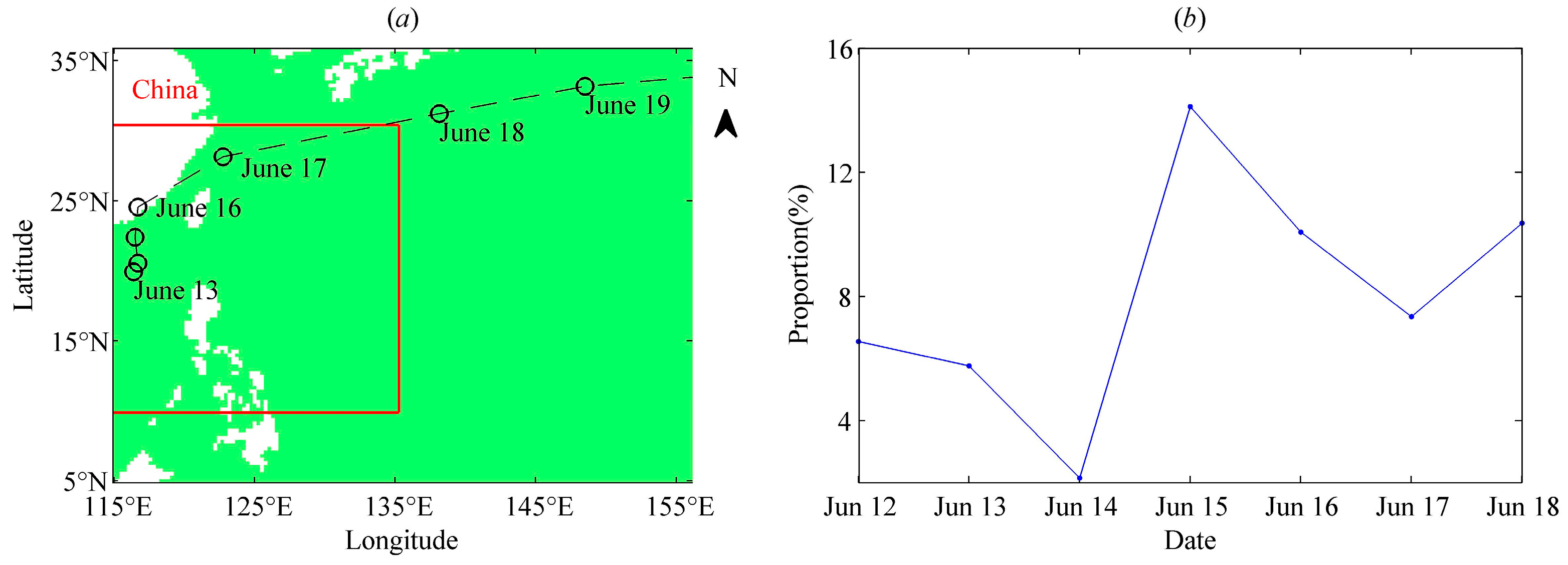
5.2. SST Samples
5.3. The Performance of the RBFN Method
6. Conclusions
Supplementary Materials
Supplementary File 1Acknowledgments
Author Contributions
Conflicts of Interest
References
- Saha, S.; Moorthi, S.; Wu, X.; Wang, J.; Nadiga, S.; Tripp, P.; Behringer, D.; Hou, Y.T.; Chuang, H.Y.; Iredell, M.; et al. The NCEP climate forecast system version 2. J. Clim. 2014, 27, 2185–2208. [Google Scholar] [CrossRef]
- Shirvani, A.; Nazemosadat, S.; Kahya, E. Analyses of the Persian Gulf sea surface temperature: Prediction and detection of climate change signals. Arabian J. Geosci. 2015, 8, 2121–2130. [Google Scholar] [CrossRef]
- Knutson, T.R.; McBride, J.L.; Chan, J.; Emanuel, K.; Holland, G.; Landsea, C.; Held, I.; Kossin, J.P.; Srivastava, A.K.; Sugi, M. Tropical cyclones and climate change. Nat. Geosci. 2010, 3, 157–163. [Google Scholar] [CrossRef] [Green Version]
- Donlon, C.; Rayner, N.; Robinson, I.; Poulter, D.J.S.; Casey, K.S.; Vazquez-Cuervo, J.; Armstrong, E.; Bingham, A.; Arino, O.; Gentemann, C.; et al. The global ocean data assimilation experiment high-resolution sea surface temperature pilot project. Bull. Am. Meteorol. Soc. 2007, 88, 1197–1213. [Google Scholar] [CrossRef]
- Martin, M.; Dash, P.; Ignatov, A.; Banzon, V.; Beggs, H.; Brasnett, B.; Cayula, J.F.; Cummings, J.; Donlon, C.; Gentemann, C.; et al. Group for High Resolution Sea Surface temperature (GHRSST) analysis fields inter-comparisons. Part 1: A GHRSST multi-product ensemble (GMPE). Deep Sea Res. Part II 2012, 77, 21–30. [Google Scholar] [CrossRef]
- Reynolds, R.W.; Smith, T.M.; Liu, C.; Chelton, D.B.; Casey, K.S.; Schlax, M.G. Daily high-resolution-blended analyses for sea surface temperature. J. Clim. 2007, 20, 5473–5496. [Google Scholar] [CrossRef]
- Reynolds, R.W. A real-time global sea surface temperature analysis. J. Clim. 1988, 1, 75–87. [Google Scholar] [CrossRef]
- Smith, T.M.; Reynolds, R.W.; Livezey, R.E.; Stokes, D.C. Reconstruction of historical sea surface temperatures using empirical orthogonal functions. J. Clim. 1996, 9, 1403–1420. [Google Scholar] [CrossRef]
- Smith, T.M.; Livezey, R.E.; Shen, S.S. An improved method for analyzing sparse and irregularly distributed SST data on a regular grid: The tropical Pacific Ocean. J. Clim. 1998, 11, 1717–1729. [Google Scholar] [CrossRef]
- Ping, B.; Su, F.; Meng, Y. Reconstruction of satellite-derived sea surface temperature data based on an improved DINEOF algorithm. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2015, 8, 4181–4188. [Google Scholar] [CrossRef]
- Beckers, J.-M.; Rixen, M. EOF calculations and data filling from incomplete oceanographic datasets. J. Atmos. Ocean. Technol. 2003, 20, 1839–1856. [Google Scholar] [CrossRef]
- Beggs, H.; Zhong, A.; Warren, G.; Alves, O.; Brassington, G.; Pugh, T. RAMSSA—An operational, high-resolution, Regional Australian Multi-Sensor Sea surface temperature Analysis over the Australian region. Aust. Meteorol. Oceanogr. J. 2011, 61, 1. [Google Scholar] [CrossRef]
- Brasnett, B. The impact of satellite retrievals in a global sea-surface-temperature analysis. Q. J. R. Meteorol. Soc. 2008, 134, 1745–1760. [Google Scholar] [CrossRef]
- Cummings, J.A. Operational multivariate ocean data assimilation. Q. J. R. Meteorol. Soc. 2005, 131, 3583–3604. [Google Scholar] [CrossRef]
- Donlon, C.J.; Martin, M.; Stark, J.; Roberts-Jones, J.; Fiedler, E.; Wimmer, W. The operational sea surface temperature and sea ice analysis (OSTIA) system. Remote Sens. Environ. 2012, 116, 140–158. [Google Scholar] [CrossRef]
- Gemmill, W.; Katz, B.; Li, X. Daily Real-Time Global Sea Surface Temperature—High-Resolution Analysis: RTG_SST_HR; NCEP No. 260; EMC Office Note: Maryland City, MD, USA, 2007.
- Gentemann, C.L.; Wentz, F.J.; DeMaria, M. Near real time global optimum interpolated microwave SSTs: Applications to hurricane intensity forecasting. In Proceedings of the 27th Conference on Hurricanes and Tropical Meteorology, Monterey, CA, USA, 23–28 April 2006. [Google Scholar]
- Park, J.; Sandberg, I.W. Universal approximation using radial-basis-function networks. Neural Comput. 1991, 3, 246–257. [Google Scholar] [CrossRef]
- Holmes, C.; Mallick, B. Bayesian radial basis functions of variable dimension. Neural Comput. 1998, 10, 1217–1233. [Google Scholar] [CrossRef]
- Powell, J. Radial basis function approximations to polynomials. In Numerical Analysis 1987; Longman Publishing Group: White Plains, NY, USA, 1987; pp. 223–241. [Google Scholar]
- Liu, L.; Chua, L.; Ghista, D. Mesh-free radial basis function method for static, free vibration and buckling analysis of shear deformable composite laminates. Compos. Struct. 2007, 78, 58–69. [Google Scholar] [CrossRef]
- Miazhynskaia, T.; Frühwirth-Schnatter, S.; Dorffner, G. Neural network models for conditional distribution under bayesian analysis. Neural Comput. 2008, 20, 504–522. [Google Scholar] [CrossRef] [PubMed]
- Konishi, S.; Ando, T.; Imoto, S. Bayesian information criteria and smoothing parameter selection in radial basis function networks. Biometrika 2004, 91, 27–43. [Google Scholar] [CrossRef]
- Ryu, D.; Liang, F.; Mallick, B.K. Sea surface temperature modeling using radial basis function networks with a dynamically weighted particle filter. J. Am. Stat. Assoc. 2013, 108, 111–123. [Google Scholar] [CrossRef]
- Xu, F.; Ignatov, A. In Situ SST quality monitor (i Quam). J. Atmos. Ocean. Technol. 2014, 31, 164–180. [Google Scholar] [CrossRef]
- Reynolds, R.W.; Smith, T.M. Improved global sea surface temperature analyses using optimum interpolation. J. Clim. 1994, 7, 929–948. [Google Scholar] [CrossRef]
- Banzon, V.F.; Reynolds, R.W.; Stokes, D.; Xue, Y. A 1/4°-spatial-resolution daily sea surface temperature climatology based on a blended satellite and In Situ analysis. J. Clim. 2014, 27, 8221–8228. [Google Scholar] [CrossRef]
- Diao, X.H. Study on regional financial risk early warning system based on uniform design method and Nearest Neighbo-Clustering RBFNN. In Proceedings of the 2011 IEEE International Conference on Intelligent Computing and Integrated Systems (ICISS), Guilin, China, 24–26 October 2011. [Google Scholar]
- Zhu, M.; Zhang, D. Study on the algorithms of selecting the radial basis function center. J. Anhui Univ. 2000, 3, 72–78. [Google Scholar]
- Lowe, D. Adaptive radial basis function nonlinearities, and the problem of generalisation. In Proceedings of the 1989 First IEE International Conference on Artificial Neural Networks, London, UK, 16–18 October 1989. No. 313. [Google Scholar]
- Kanungo, T.; Mount, D.M.; Netanyahu, N.S.; Piatko, C.D.; Silverman, R.; Wu, A.Y. An efficient k-means clustering algorithm: Analysis and implementation. IEEE Trans. Pattern Anal. Mach. Intell. 2002, 24, 881–892. [Google Scholar] [CrossRef]
- Latif, B.A.; Lecerf, R.; Mercier, G.; Hubert-Moy, L. Preprocessing of low-resolution time series contaminated by clouds and shadows. IEEE Trans. Geosci. Remote Sens. 2008, 46, 2083–2096. [Google Scholar] [CrossRef]
- Kohonen, T. The self-organizing map. Proc. IEEE 1990, 78, 1464–1480. [Google Scholar] [CrossRef]
- Zhang, H.; Qin, S.; Ma, J.; You, H. Using residual resampling and sensitivity analysis to improve particle filter data assimilation accuracy. IEEE Geosci. Remote Sens. Lett. 2013, 10, 1404–1408. [Google Scholar] [CrossRef]
- Haykin, S. Neural Networks and Learning Machines, 3rd ed.; McMaster University: Hamilton, ON, Canada, 2009. [Google Scholar]

| RMSE (°C) | MAE (°C) | R | SNR | |
|---|---|---|---|---|
| 0.66 | 0.96 | 0.49 | 3.43 | |
| 0.51 | 0.98 | 0.37 | 4.61 | |
| 0.66 | 0.97 | 0.49 | 4.02 | |
| 0.55 | 0.97 | 0.43 | 4.18 |
| RMSE (°C) | MAE (°C) | R | SNR | |
|---|---|---|---|---|
| 0.73 | 0.97 | 0.52 | 3.60 | |
| 0.47 | 0.98 | 0.34 | 4.64 | |
| 0.59 | 0.97 | 0.43 | 4.06 | |
| 0.69 | 0.96 | 0.51 | 3.39 |
| RMSE (°C) | MAE (°C) | R | SNR | |
|---|---|---|---|---|
| OI | 0.69 | 0.46 | 0.96 | 3.82 |
| RBFN | 0.48 | 0.35 | 0.98 | 4.94 |
| RMSE (°C) | MAE (°C) | R | SNR | |
|---|---|---|---|---|
| OI | 0.18 | 0.08 | 0.99 | 65.38 |
| RBFN | 0.19 | 0.10 | 0.99 | 62.21 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liao, Z.; Dong, Q.; Xue, C.; Bi, J.; Wan, G. Reconstruction of Daily Sea Surface Temperature Based on Radial Basis Function Networks. Remote Sens. 2017, 9, 1204. https://doi.org/10.3390/rs9111204
Liao Z, Dong Q, Xue C, Bi J, Wan G. Reconstruction of Daily Sea Surface Temperature Based on Radial Basis Function Networks. Remote Sensing. 2017; 9(11):1204. https://doi.org/10.3390/rs9111204
Chicago/Turabian StyleLiao, Zhihong, Qing Dong, Cunjin Xue, Jingwu Bi, and Guangtong Wan. 2017. "Reconstruction of Daily Sea Surface Temperature Based on Radial Basis Function Networks" Remote Sensing 9, no. 11: 1204. https://doi.org/10.3390/rs9111204
APA StyleLiao, Z., Dong, Q., Xue, C., Bi, J., & Wan, G. (2017). Reconstruction of Daily Sea Surface Temperature Based on Radial Basis Function Networks. Remote Sensing, 9(11), 1204. https://doi.org/10.3390/rs9111204