Mechanisms of SAR Imaging of Shallow Water Topography of the Subei Bank
Abstract
1. Introduction
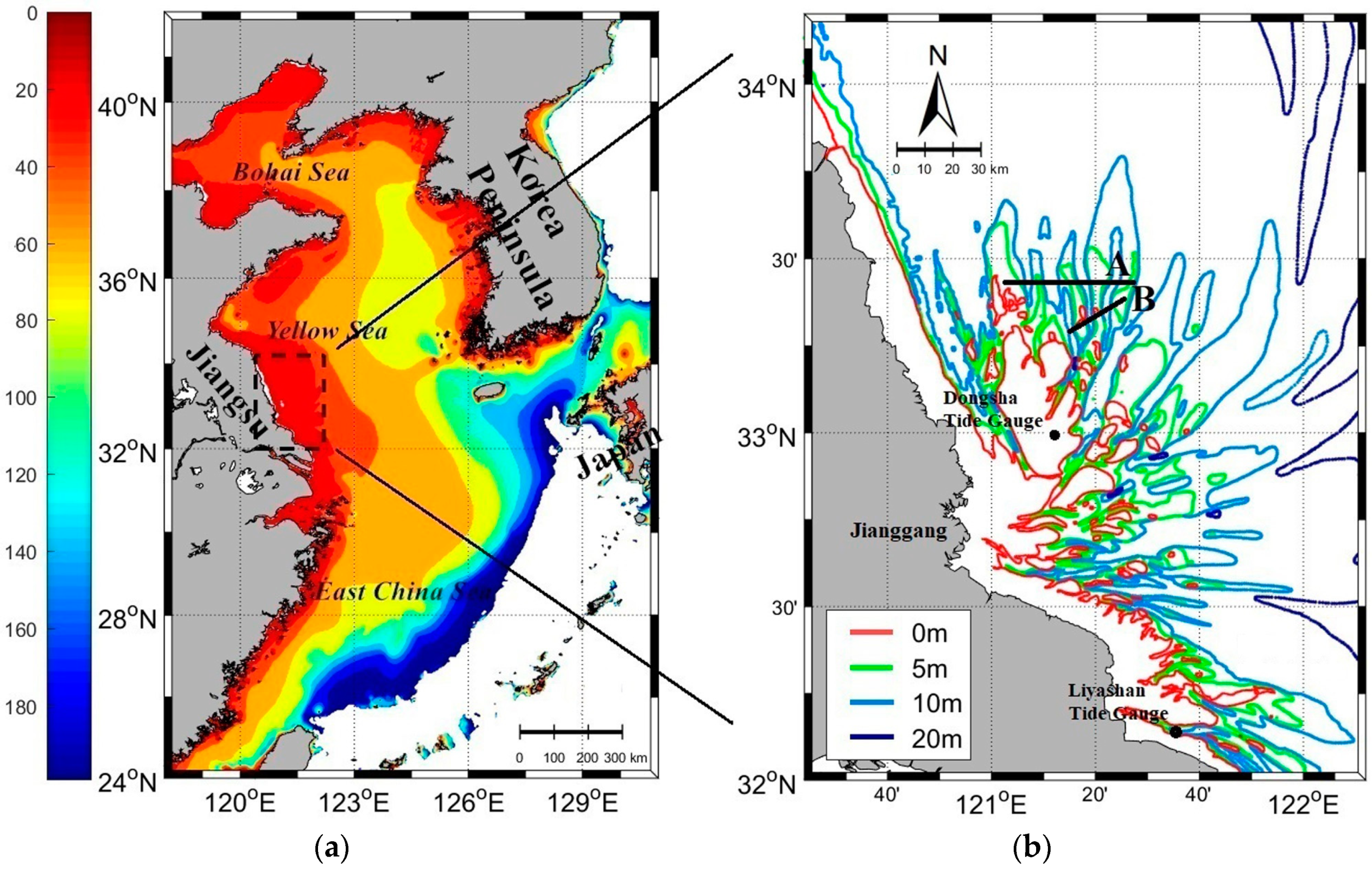
2. Data and Methods
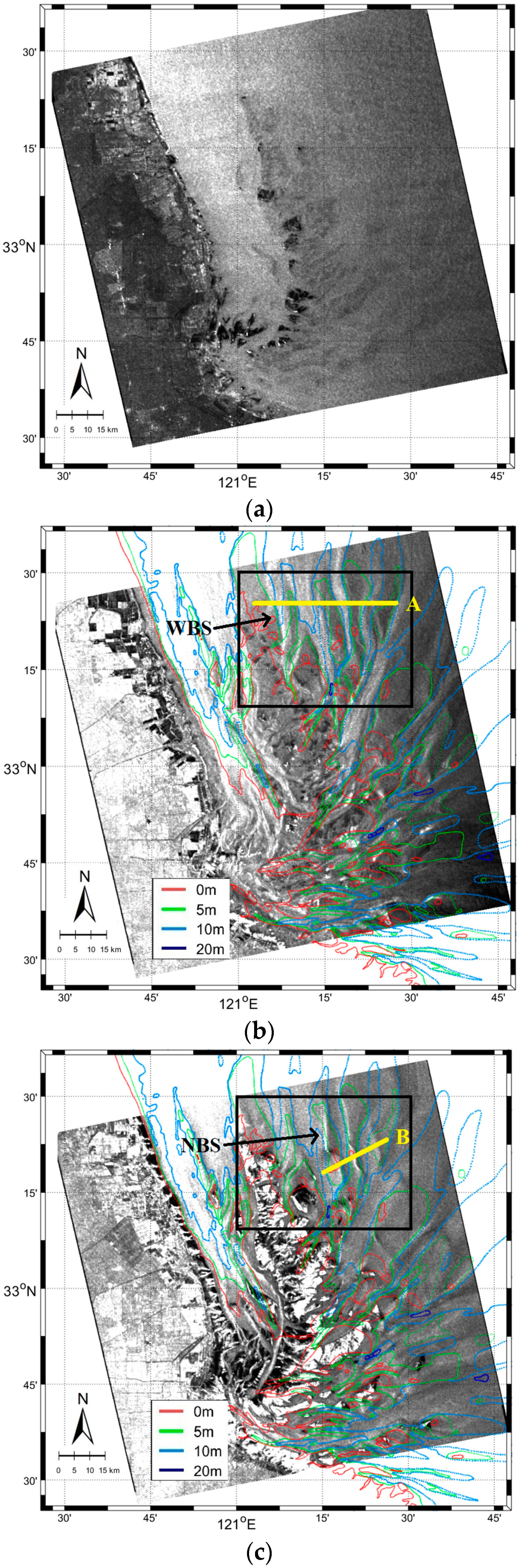
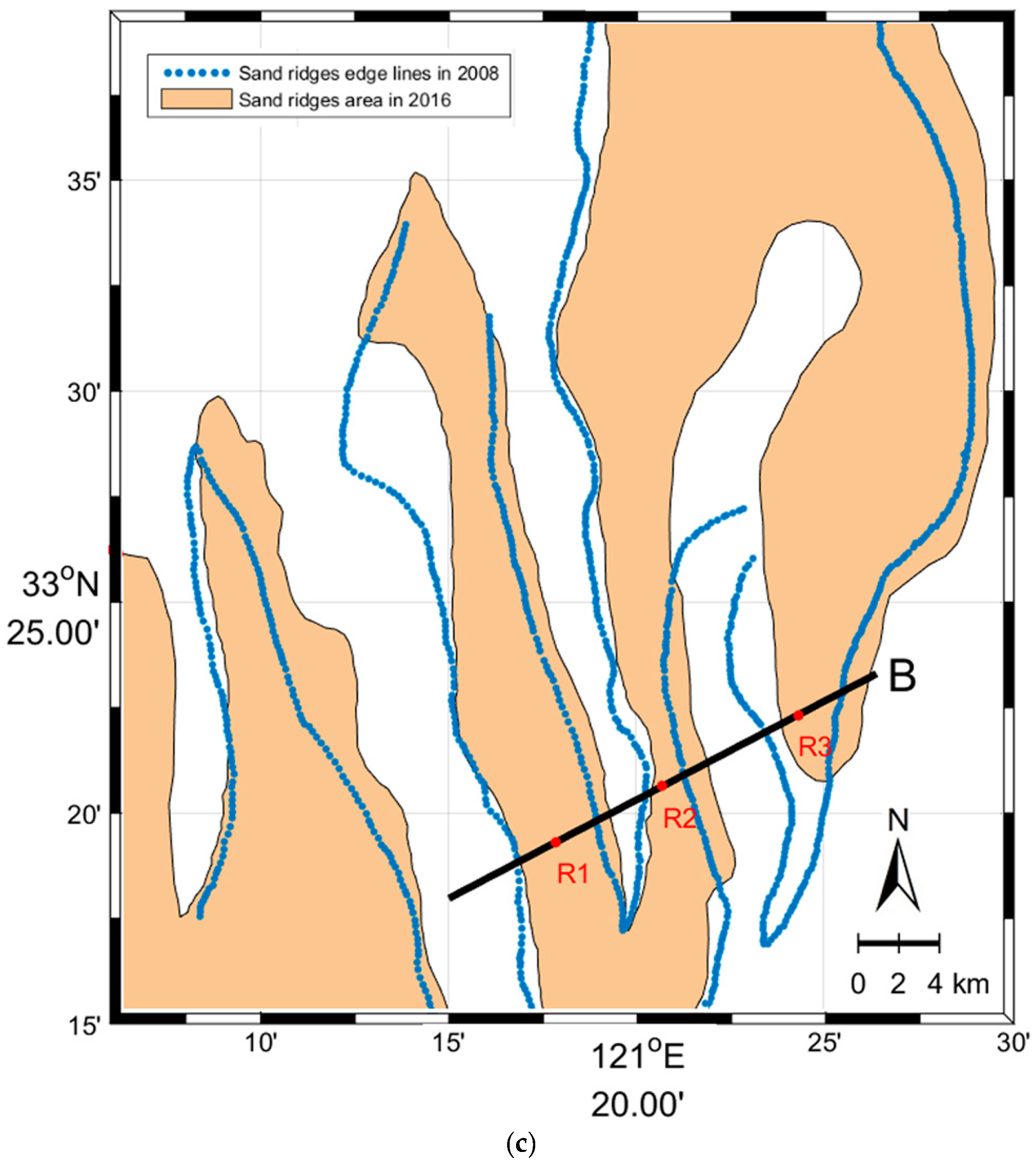
3. Bathymetric Features of Subei Bank on SAR Imagery
4. SAR Imaging Mechanisms
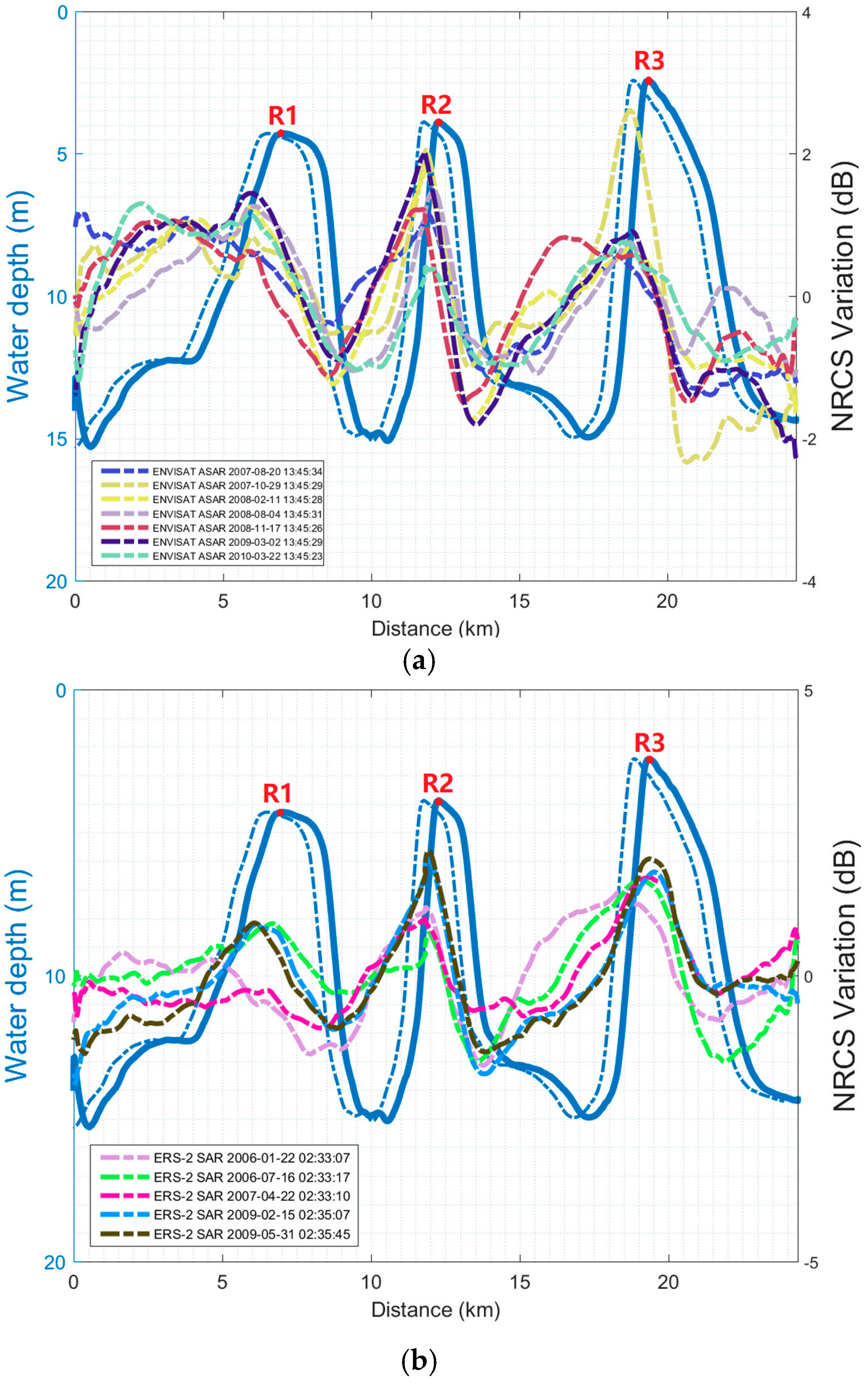
4.1. SAR Imaging of Tidal Channels
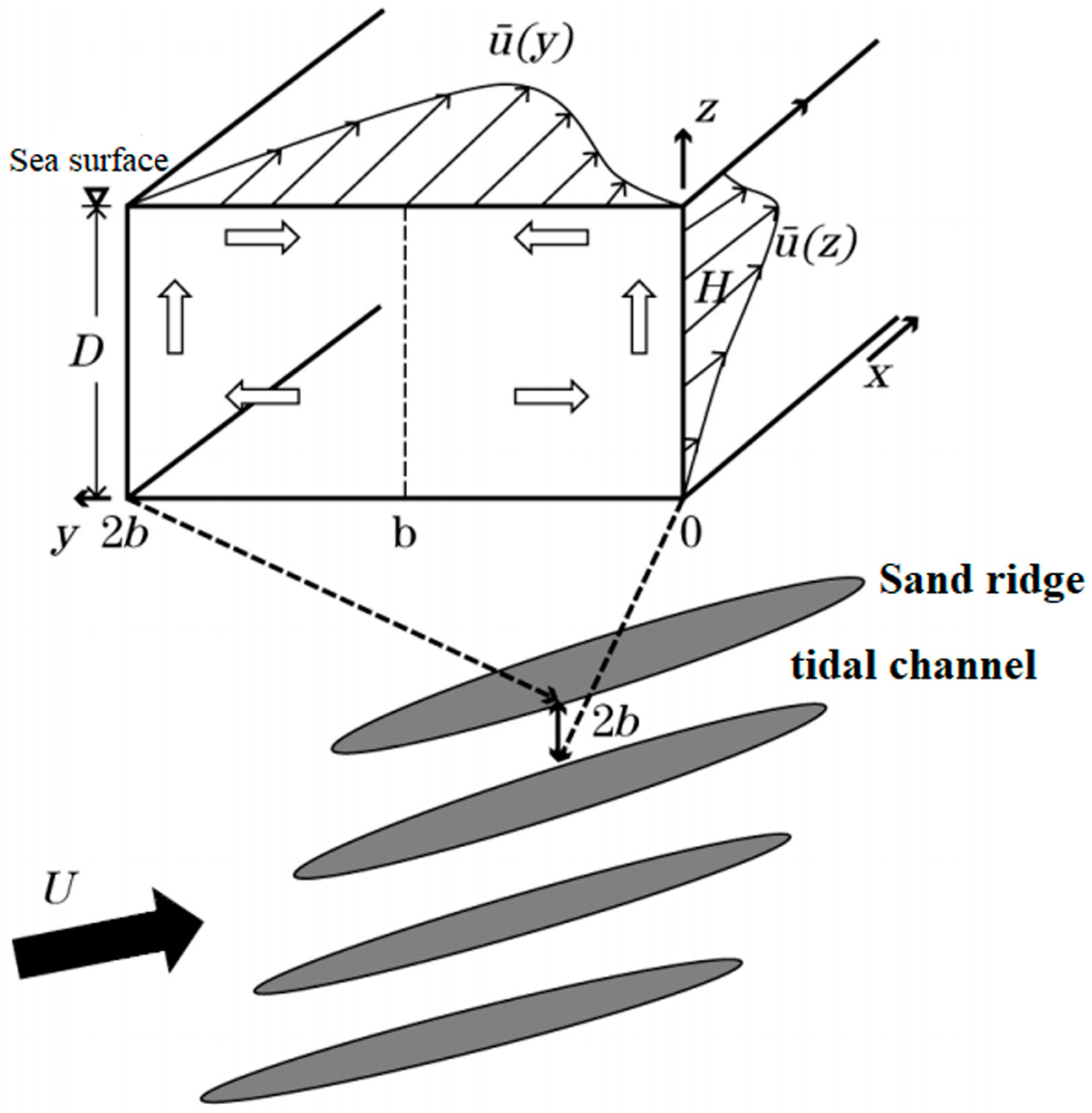
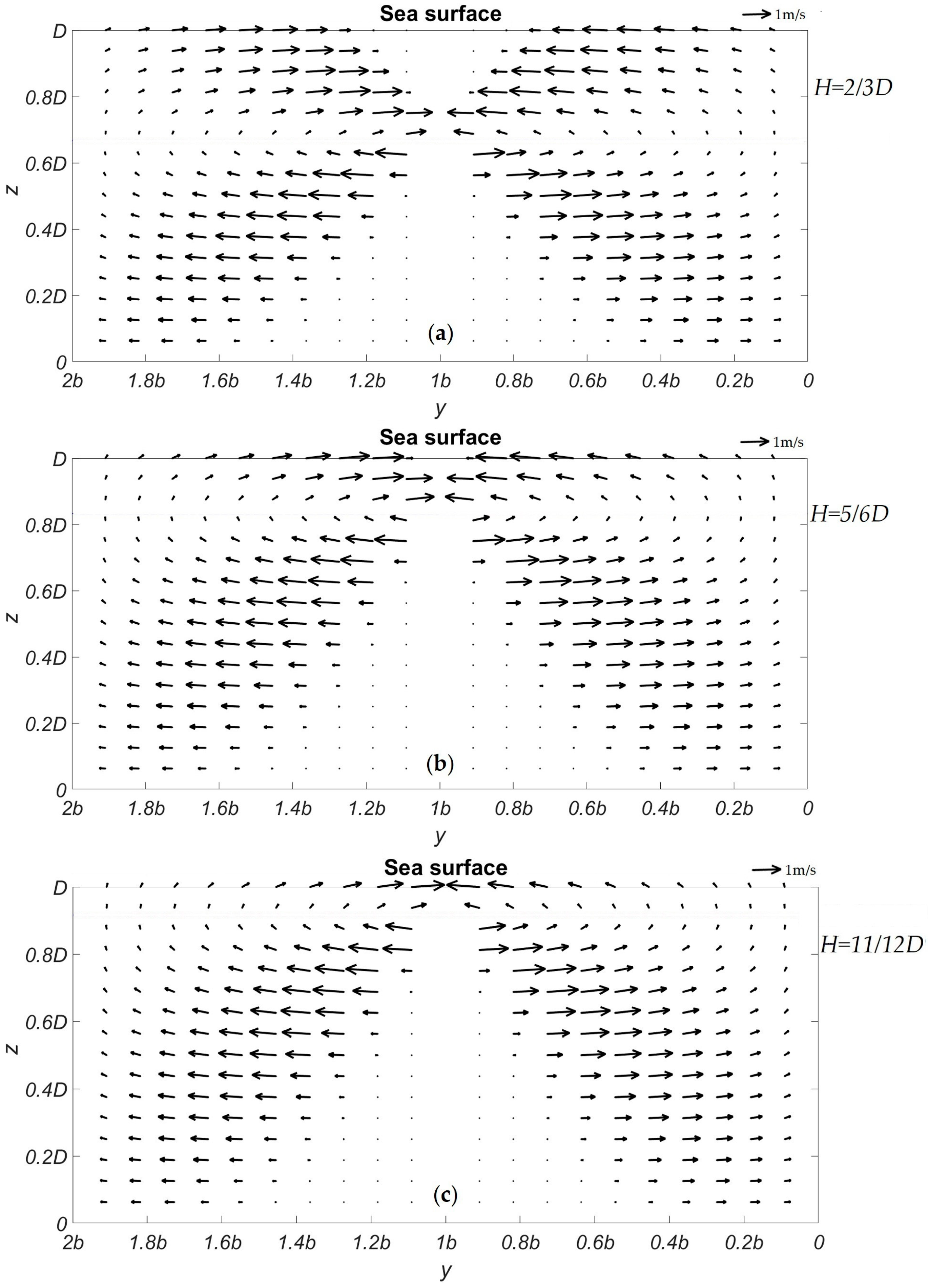
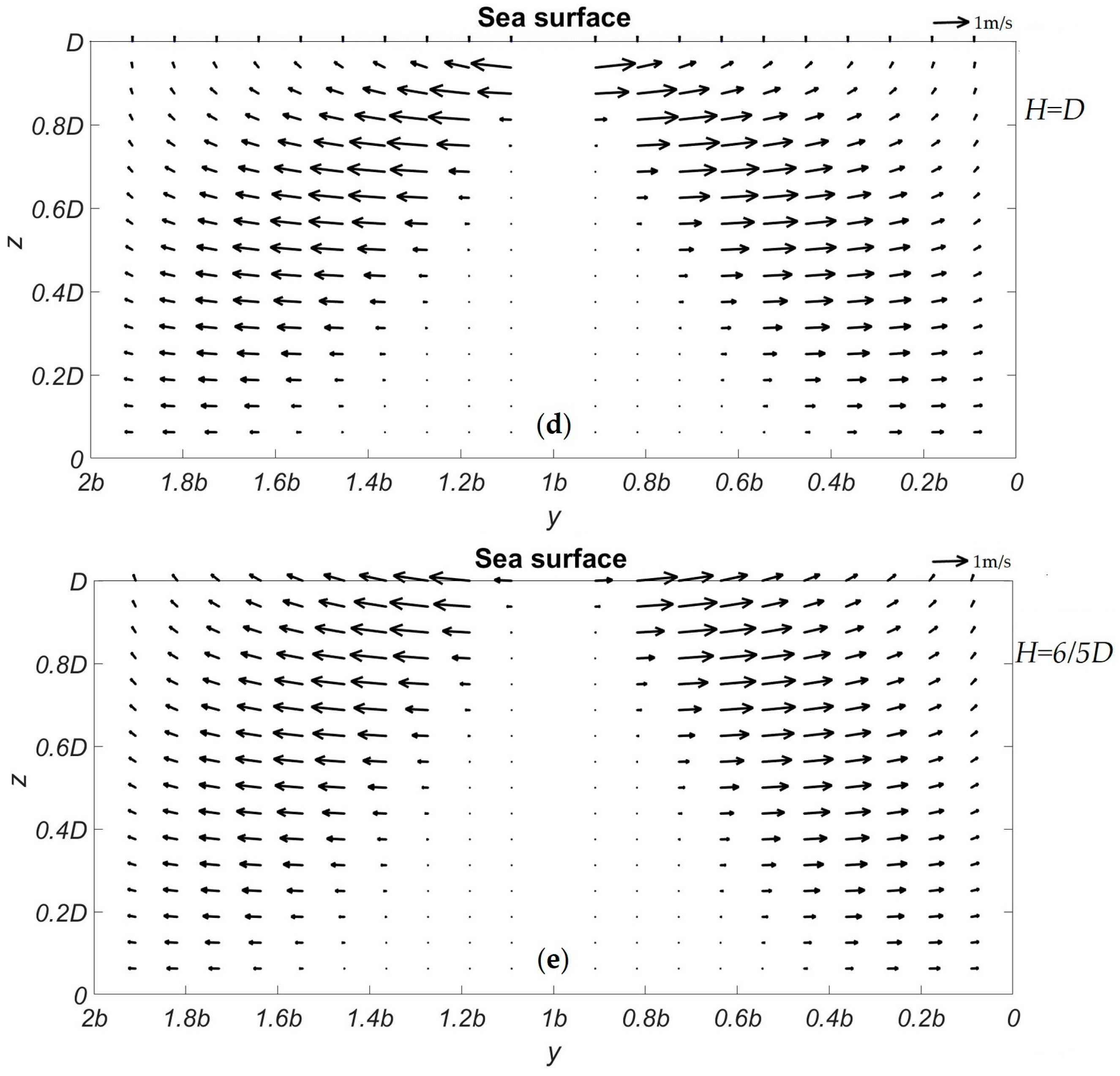
4.2. SAR Imaging of Sand Ridges
4.3. Discussion
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Appendix A. Derivation of Secondary Circulation Solutions
References
- He, X.; Chen, N.; Zhang, H.; Fu, B.; Wang, X. Reconstruction of sand wave bathymetry using both satellite imagery and multi-beam bathymetric data: A case study of the Taiwan Banks. Int. J. Remote Sens. 2014, 35, 3286–3299. [Google Scholar] [CrossRef]
- Ma, S.; Tao, Z.; Yang, X.; Yu, Y.; Zhou, X.; Li, Z. Bathymetry retrieval from hyperspectral remote sensing data in optical-shallow water. IEEE Trans. Geosci. Remote Sens. 2014, 52, 1205–1212. [Google Scholar] [CrossRef]
- Pacheco, A.; Horta, J.; Loureiro, C.; Ferreira, Ó. Retrieval of nearshore bathymetry from Landsat 8 images: A tool for coastal monitoring in shallow waters. Remote Sens. Environ. 2015, 159, 102–116. [Google Scholar] [CrossRef]
- Wozencraft, J.M.; Millar, D. Airborne LIDAR and integrated technologies for coastal mapping and nautical charting. Mar. Technol. Soc. J. 2005, 39, 27–35. [Google Scholar] [CrossRef]
- Shi, W.; Wang, M.; Li, X.; Pichel, W.G. Ocean sand ridge signatures in the Bohai Sea observed by satellite ocean color and synthetic aperture radar measurements. Remote Sens. Environ. 2011, 115, 1926–1934. [Google Scholar] [CrossRef]
- De Loor, G.P. The observation of tidal patterns, currents, and bathymetry with SLAR imagery of the sea. IEEE J. Ocean. Eng. 1981, 6, 124–129. [Google Scholar] [CrossRef]
- Alpers, W.; Hennings, I. A theory of the imaging mechanism of underwater bottom topography by real and synthetic aperture radar. J. Geophys. Res. 1984, 89, 1029–1054. [Google Scholar] [CrossRef]
- Zheng, Q.; Li, L.; Guo, X.; Ge, Y.; Zhu, D.; Li, C. SAR Imaging and hydrodynamic analysis of ocean bottom topographic waves. J. Geophys. Res. 2006, 111. [Google Scholar] [CrossRef]
- Li, X.; Li, C.; Xu, Q.; Pichel, W.G. Sea surface manifestation of along-tidal-channel underwater ridges imaged by SAR. IEEE Trans. Geosci. Remote Sens. 2009, 47, 2467–2477. [Google Scholar] [CrossRef]
- Li, X.; Yang, X.; Zheng, Q.; Pietrafesa, L.J.; Pichel, W.G.; Li, Z.; Li, X. Deep-water bathymetry feature imaged by spaceborne SAR in the Gulf Stream region. Geophys. Res. Lett. 2010, 37. [Google Scholar] [CrossRef]
- Hennings, I. An historical overview of radar imagery of sea bottom topography. Int. J. Remote Sens. 1998, 19, 1447–1454. [Google Scholar] [CrossRef]
- Zheng, Q.; Holt, B.; Li, X.; Liu, X.; Zhao, Q.; Yuan, Y.; Yang, X. Deep-water seamount wakes on SEASAT SAR image in the Gulf Stream region. Geophys. Res. Lett. 2012, 39. [Google Scholar] [CrossRef]
- De Loor, G.P.; Hulten, B.V. Microwave Measurements over the North Sea. Bound. Layer Meteorol. 1978, 13, 119–131. [Google Scholar] [CrossRef]
- Van der Kooij, M.W.A.; Vogelzang, J.; Calkoen, C.J. A simple analytical model for brightness modulations caused by submarine sand waves in radar imagery. J. Geophys. Res. 1995, 100, 7069–7082. [Google Scholar] [CrossRef]
- Vogelzang, J.; Wensink, G.J.; Calkoen, C.J.; Van der Kooij, M.W.A. Mapping Submarine Sand Waves with Multiband Imaging Radar: Experimental Results and Model Comparison. J. Geophys. Res. 1997, 102, 1183–1192. [Google Scholar] [CrossRef]
- Romeiser, R.; Alpers, W. An improved composite surface model for the radar backscattering cross section of the ocean surface, 2, Model response to surface roughness variations and the radar imaging of underwater bottom topography. J. Geophys. Res. 1997, 102, 25251–25267. [Google Scholar] [CrossRef]
- Zheng, Q.; Zhao, Q.; Yuan, Y.; Xian, L.; Hu, J.; Liu, X.; Yin, L.; Ye, Y. Shear-flow induced secondary circulation in parallel underwater topographic corrugation and its application to satellite image interpretation. J. Ocean. Univ. China 2012, 11, 427–435. [Google Scholar] [CrossRef]
- Wang, X.; Zhang, H.; Li, X.; Fu, B.; Guan, W. SAR imaging of a topography-induced current front in a tidal channel. Int. J. Remote Sens. 2015, 36, 3563–3574. [Google Scholar] [CrossRef]
- Zhang, S.; Xu, Q.; Cheng, Y.; Li, Y.; Huang, Q. Bathymetric features of Subei Bank on ENVISAT ASAR images. In Proceedings of the IEEE Progress in Electromagnetic Research Symposium (PIERS), Shanghai, China, 8–11 August 2016. [Google Scholar]
- Liu, Y.; Li, M.; Cheng, L.; Li, F.; Chen, K. Topographic mapping of offshore sandbank tidal flats using the waterline detection method: A case study on the Dongsha Sandbank of Jiangsu Radial Tidal Sand Ridges, China. Mar. Geod. 2012, 35, 362–378. [Google Scholar] [CrossRef]
- Iwenfei, N.; Wang, Y.; Zou, X.; Zhang, J.; Gao, J. Sediment dynamics in an offshore tidal channel in the southern Yellow Sea. Int. J. Remote Sens. 2014, 29, 246–259. [Google Scholar] [CrossRef]
- Song, Y.; Zhang, J. Study on Evolutions of Jiangsu Radiating Sandbanks Based on SAR Images. In Advances in SAR Oceanography from Envisat and ERS Missions, Proceedings of the SEASAR 2006, Frascati, Italy, 23–26 January 2006; Lacoste, H., Ouwehand, L., Eds.; ESA Publications Division: Noordwijk, The Netherlands, 2006; Available online: https://earth.esa.int/workshops/seasar2006/proceedings/papers/p11_song.pdf (accessed on 1 November 2017).
- Desnos, Y.L.; Buck, C.; Guijarro, J.; Suchail, J.L.; Torres, R.; Attema, E. ASAR-ENVISAT’s advanced synthetic aperture radar. ESA Bull. 2000, 102, 91–100. [Google Scholar]
- Moreira, A.; Prats-Iraola, P.; Younis, M.; Krieger, G.; Hajnsek, I.; Papathanassiou, K.P. A tutorial on synthetic aperture radar. IEEE Geosci. Remote Sens. Mag. 2013, 1, 6–43. [Google Scholar] [CrossRef]
- Lin, H.; Xu, Q.; Zheng, Q. An overview on SAR measurements of sea surface wind. Prog. Nat. Sci. 2008, 18, 913–919. [Google Scholar] [CrossRef]
- Xu, Q.; Lin, H.; Li, X.; Zuo, J.; Zheng, Q.; Pichel, W.G.; Liu, Y. Assessment of an analytical model for sea surface wind speed retrieval from spaceborne SAR. Int. J. Remote Sens. 2010, 31, 993–1008. [Google Scholar] [CrossRef]
- Yang, X.; Li, X.; Zheng, Q.; Gu, X.; Pichel, W.G.; Li, Z. Comparison of ocean surface winds retrieved from QuikSCAT scatterometer and Radarsat-1 SAR in offshore waters of the U.S. West Coast. IEEE Geosci. Remote Sens. Lett. 2010, 8, 163–167. [Google Scholar] [CrossRef]
- Yang, X.; Li, X.; Pichel, W.G.; Li, Z. Comparison of ocean surface winds from ENVISAT ASAR, MetOp ASCAT scatterometer, buoy measurements, and NOGAPS model. IEEE Trans. Geosci. Remote Sens. 2011, 49, 4743–4750. [Google Scholar] [CrossRef]
- Hersbach, H.; Stoffelen, A.; De, S.H. An improved c-band scatterometer ocean geophysical model function: CMOD5. J. Geophys. Res. 2007, 112, 225–237. [Google Scholar] [CrossRef]
- Zhang, H.; Bates, J.J.; Reynolds, R.W. Assessment of composite global sampling: Sea surface wind speed. Geophys. Res. Lett. 2006, 33, L17714. [Google Scholar] [CrossRef]
- Egbert, G.D.; Erofeeva, S.Y. Efficient inverse modeling of barotropic ocean tides. J. Atmos. Ocean. Technol. 2002, 19, 183–204. [Google Scholar] [CrossRef]
- Padman, L.; Erofeeva, S. Tide Model Driver (TMD) Manual; Earth & Space Research: Seattle, WA, USA, 2005. [Google Scholar]
- The Navigation Guarantee Department of the Chinese Navy Headquarters. Sea Chart of Yellow Sea: Sheyanghe Kou to Lvsi Gang; China Navigation Publications Press: Tianjin, China, 2013. [Google Scholar]
- Chen, J.; Wang, Y.; Zhang, R.; Lin, X. Stability study on the Dongsha Sandbanks in submarine radial sand ridges field off Jiangsu coast. Ocean Eng. 2007, 25, 105–113. [Google Scholar]
- Kundu, P.K. Fluid Mechanics; Academic Press: New York, NY, USA, 1990; pp. 263–298. [Google Scholar]
- Alpers, W. Theory of radar imaging of internal waves. Nature 1985, 314, 245–247. [Google Scholar] [CrossRef]
- Zhang, C.; Zhang, D.; Zhang, J.; Wang, Z. Tidal current-induced formation—Storm-induced change—Tidal current-induced recovery. Sci. China Ser. D Earth Sci. 1999, 42, 1–12. [Google Scholar] [CrossRef]
- Ekman, V.W. On the influence of the earth’s rotation on ocean currents. Matem. Astr. Fysik. 1905, 2, 1–52. [Google Scholar]
- Yang, Y.; Feng, W. Numerical simulation of wave fields in radial sand ridge filed of southern yellow sea. J. Hohai Univ. 2010, 38, 457–461. [Google Scholar]
- Evander, L. Breaking Wave; Alphascript Publishing: Beau Bassin, Mauritius, 2010. [Google Scholar]
- Nelson, R.C.; Gonsalves, J. Surf zone transformation of wave height to water depth ratios. Coast. Eng. 1992, 17, 49–70. [Google Scholar] [CrossRef]
- Hubert, W.E. A preliminary report on numerical sea condition forecasts. Mon. Weather Rev. 1957, 85, 200–204. [Google Scholar] [CrossRef]




| Satellite | Date | Bathymetric Features 1 | Tidal Phase | Wind Direction 2 | Tidal Height (m) | Wind Speed (m/s) | Wave Height (m) | Wave Breaking Depth (m) | Instantaneous Water Depth (m) | |
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | ENVISAT | 2008-04-21 | WBS | flood | 105 | 0.29 | 6.30 | 1.22 | 1.90 | 4.61 |
| 2 | ENVISAT | 2008-10-13 | WBS | flood | 174 | 1.61 | 4.80 | 0.71 | 1.10 | 5.93 |
| 3 | ENVISAT | 2009-04-06 | WBS | flood | 172 | 1.83 | 3.10 | 0.29 | 0.46 | 6.15 |
| 4 | ERS-2 | 2009-10-18 | WBS | flood | 195 | 1.90 | 5.60 | 0.96 | 1.50 | 6.22 |
| 5 | ENVISAT | 2010-04-26 | WBS | flood | 210 | 1.76 | 4.60 | 0.65 | 1.01 | 6.08 |
| 6 | ERS-2 | 2006-01-22 | NBS | ebb | 351 | −1.61 | 6.10 | 1.14 | 1.90 | 1.86 |
| 7 | ERS-2 | 2006-07-16 | NBS | flood | 158 | −1.75 | 10.50 | 3.38 | 5.63 | 1.72 |
| 8 | ERS-2 | 2007-04-22 | NBS | flood | 20 | −1.46 | 9.80 | 2.94 | 4.90 | 2.01 |
| 9 | ENVISAT | 2007-08-20 | NBS | ebb | 125 | −1.75 | 10.10 | 3.12 | 5.20 | 1.72 |
| 10 | ENVISAT | 2007-10-29 | NBS | flood | 24 | −1.46 | 6.60 | 1.33 | 2.22 | 2.01 |
| 11 | ENVISAT | 2008-02-11 | NBS | flood | 355 | −2.34 | 9.20 | 2.59 | 4.32 | 1.13 |
| 12 | ENVISAT | 2008-08-04 | NBS | flood | 132 | −1.46 | 6.30 | 1.22 | 2.03 | 2.01 |
| 13 | ENVISAT | 2008-11-17 | NBS | flood | 351 | −2.34 | 13.90 | 5.91 | 9.86 | 1.13 |
| 14 | ERS-2 | 2009-02-15 | NBS | flood | 17 | −1.46 | 6.50 | 1.29 | 2.16 | 2.01 |
| 15 | ENVISAT | 2009-03-02 | NBS | flood | 28 | −1.90 | 5.80 | 1.03 | 1.72 | 1.57 |
| 16 | ERS-2 | 2009-05-31 | NBS | ebb | 200 | −2.04 | 5.40 | 0.89 | 1.49 | 1.43 |
| 17 | ENVISAT | 2010-03-22 | NBS | ebb | 149 | −1.31 | 6.60 | 1.33 | 2.22 | 2.16 |
| 18 | ERS-2 | 2006-02-26 | none | flood | 355 | 1.61 | 8.62 | 2.27 | 3.67 | 5.51 |
| 19 | ENVISAT | 2006-09-04 | none | ebb | 45 | 1.02 | 8.00 | 1.96 | 3.16 | 4.92 |
| 20 | ENVISAT | 2008-03-17 | none | ebb | 124 | 1.32 | 5.90 | 1.07 | 1.72 | 5.22 |
| 21 | ENVISAT | 2008-12-22 | none | ebb | 300 | 0.59 | 7.60 | 1.77 | 2.85 | 4.49 |
| 22 | ERS-2 | 2009-03-22 | none | ebb | 342 | 0.44 | 9.20 | 2.59 | 4.18 | 4.34 |
| 23 | ERS-2 | 2009-09-13 | none | ebb | 162 | −0.58 | 3.30 | 0.33 | 0.54 | 3.32 |
| 24 | ENVISAT | 2009-09-28 | none | ebb | 156 | −0.29 | 6.70 | 1.37 | 2.22 | 3.61 |
| 25 | ENVISAT | 2010-01-11 | none | ebb | 346 | 1.32 | 10.20 | 3.18 | 5.14 | 5.22 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, S.; Xu, Q.; Zheng, Q.; Li, X. Mechanisms of SAR Imaging of Shallow Water Topography of the Subei Bank. Remote Sens. 2017, 9, 1203. https://doi.org/10.3390/rs9111203
Zhang S, Xu Q, Zheng Q, Li X. Mechanisms of SAR Imaging of Shallow Water Topography of the Subei Bank. Remote Sensing. 2017; 9(11):1203. https://doi.org/10.3390/rs9111203
Chicago/Turabian StyleZhang, Shuangshang, Qing Xu, Quanan Zheng, and Xiaofeng Li. 2017. "Mechanisms of SAR Imaging of Shallow Water Topography of the Subei Bank" Remote Sensing 9, no. 11: 1203. https://doi.org/10.3390/rs9111203
APA StyleZhang, S., Xu, Q., Zheng, Q., & Li, X. (2017). Mechanisms of SAR Imaging of Shallow Water Topography of the Subei Bank. Remote Sensing, 9(11), 1203. https://doi.org/10.3390/rs9111203







