Estimating Leaf Area Density of Individual Trees Using the Point Cloud Segmentation of Terrestrial LiDAR Data and a Voxel-Based Model
Abstract
:1. Introduction
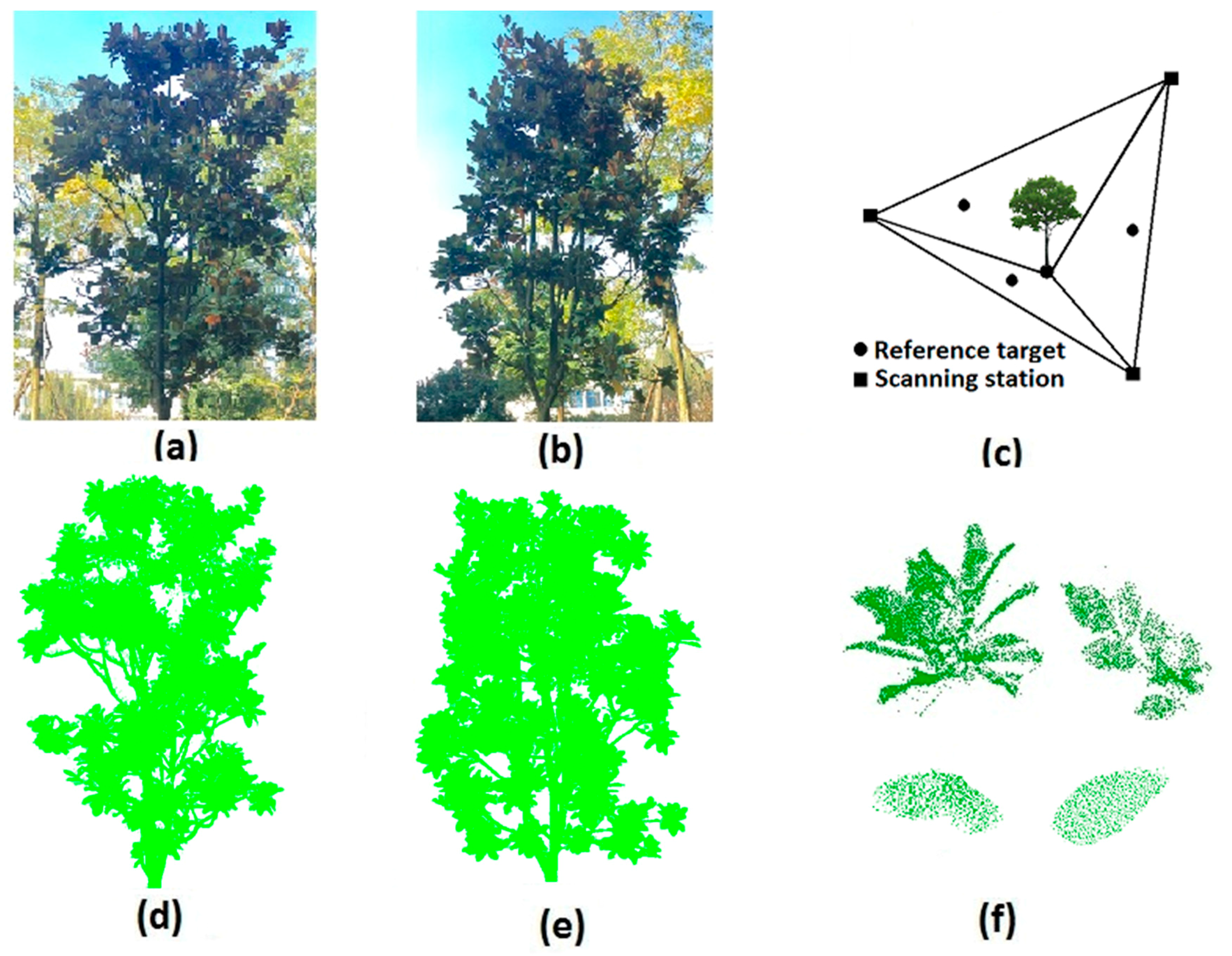
2. Study Site and Field Measurements
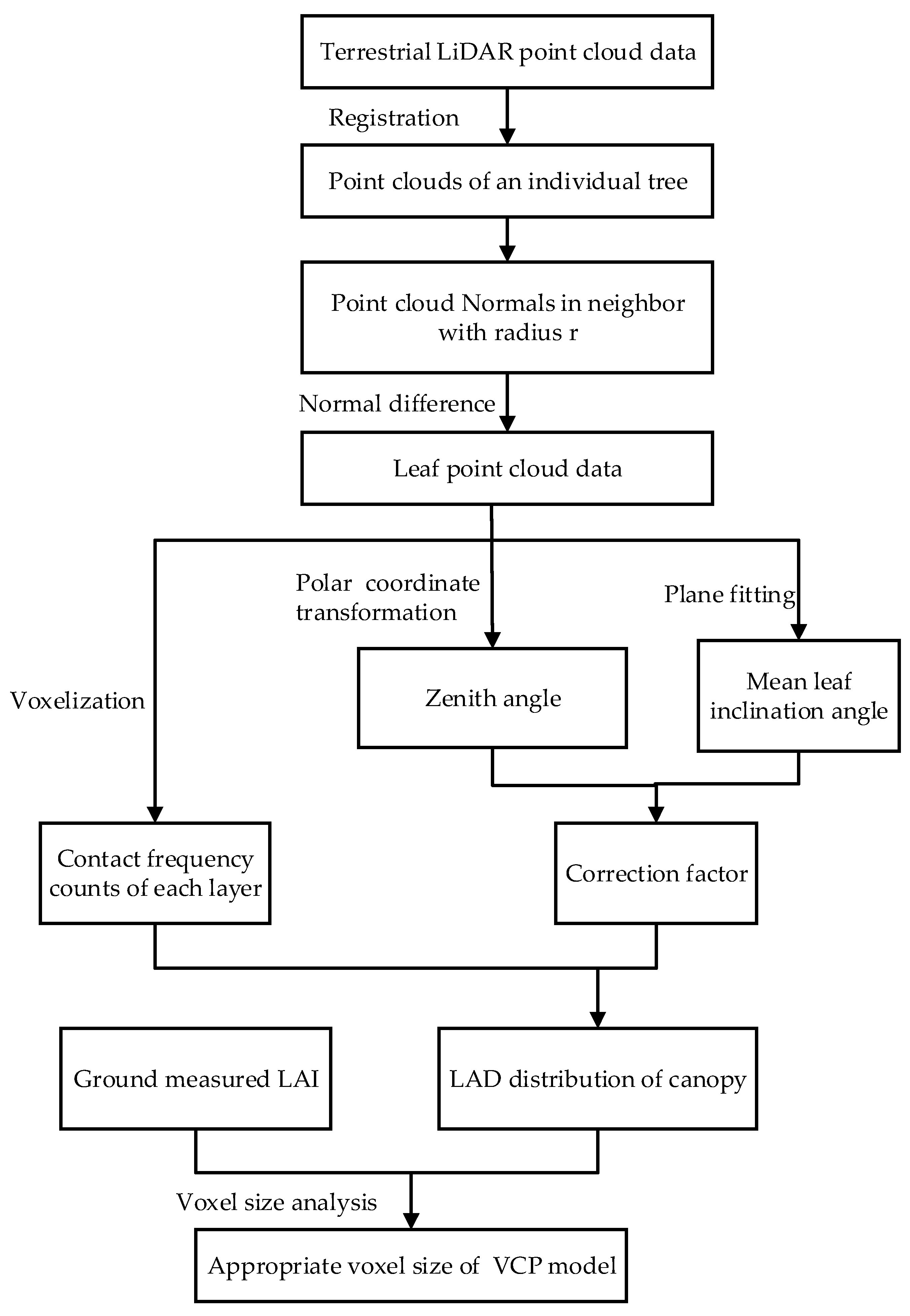
3. Materials and Methods
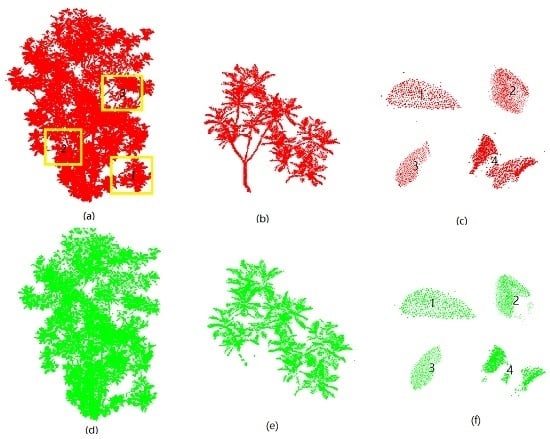
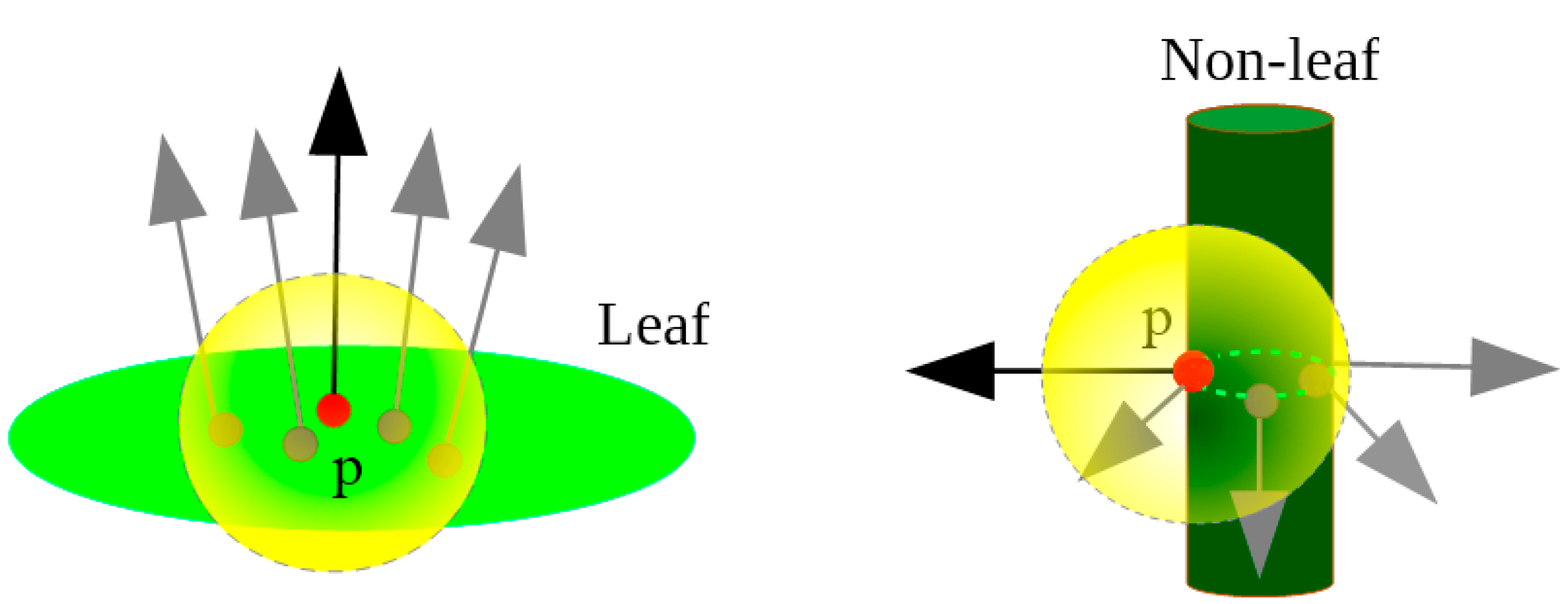
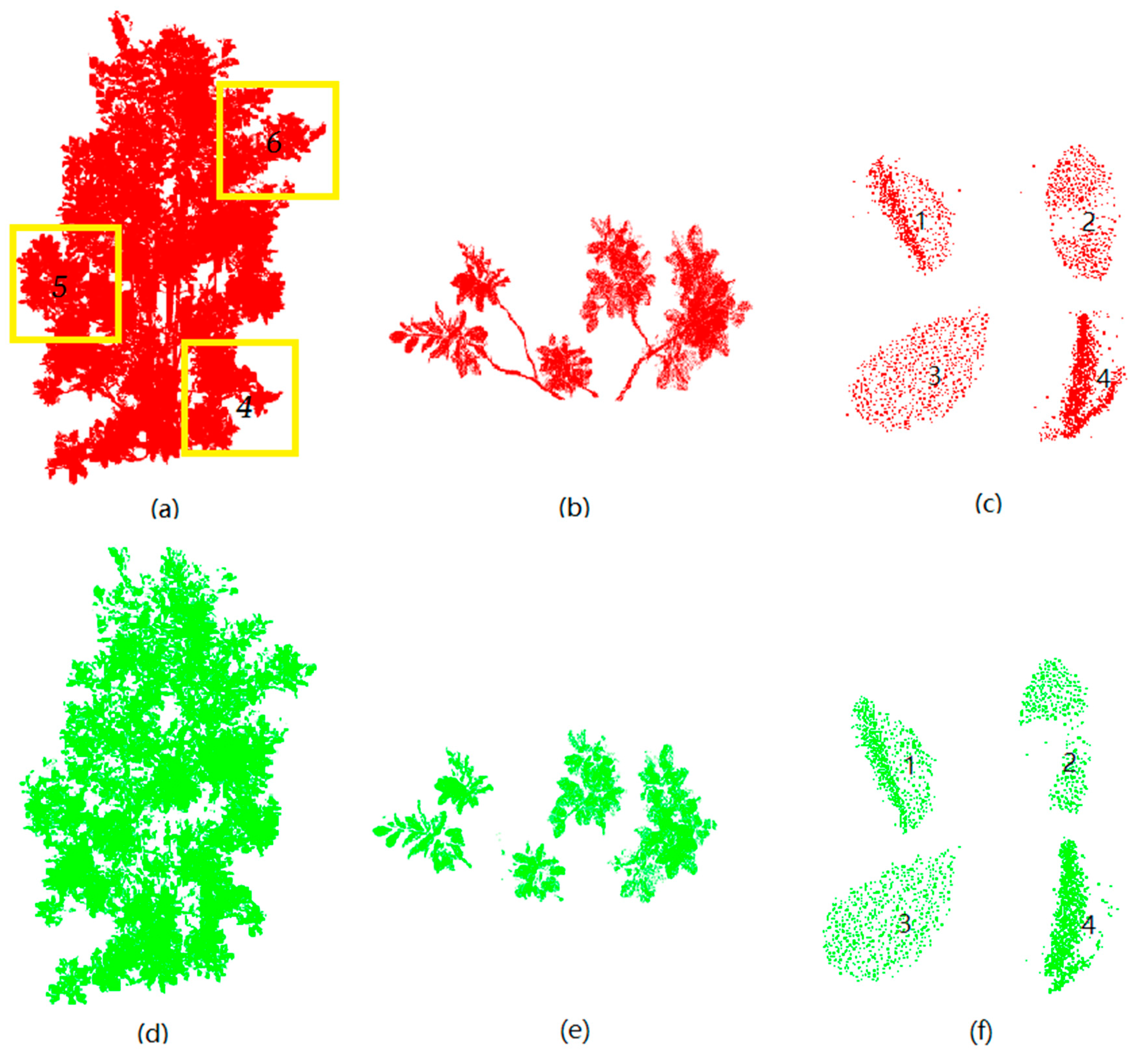
3.1. Extraction of Leaf Point Cloud
3.2. Voxel-Based LAD Estimation Method
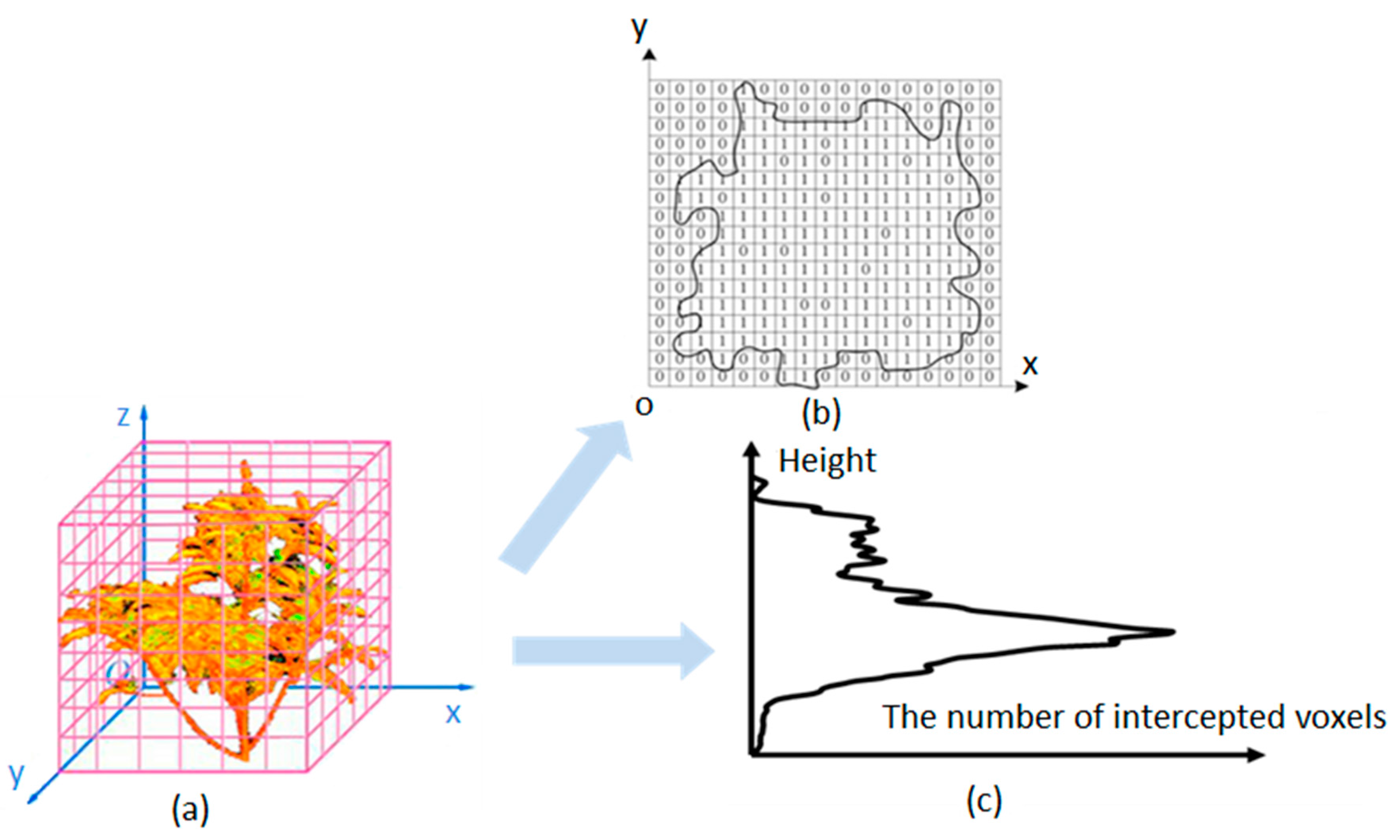
3.2.1. Voxelization
3.2.2. LAD Estimation Model Description
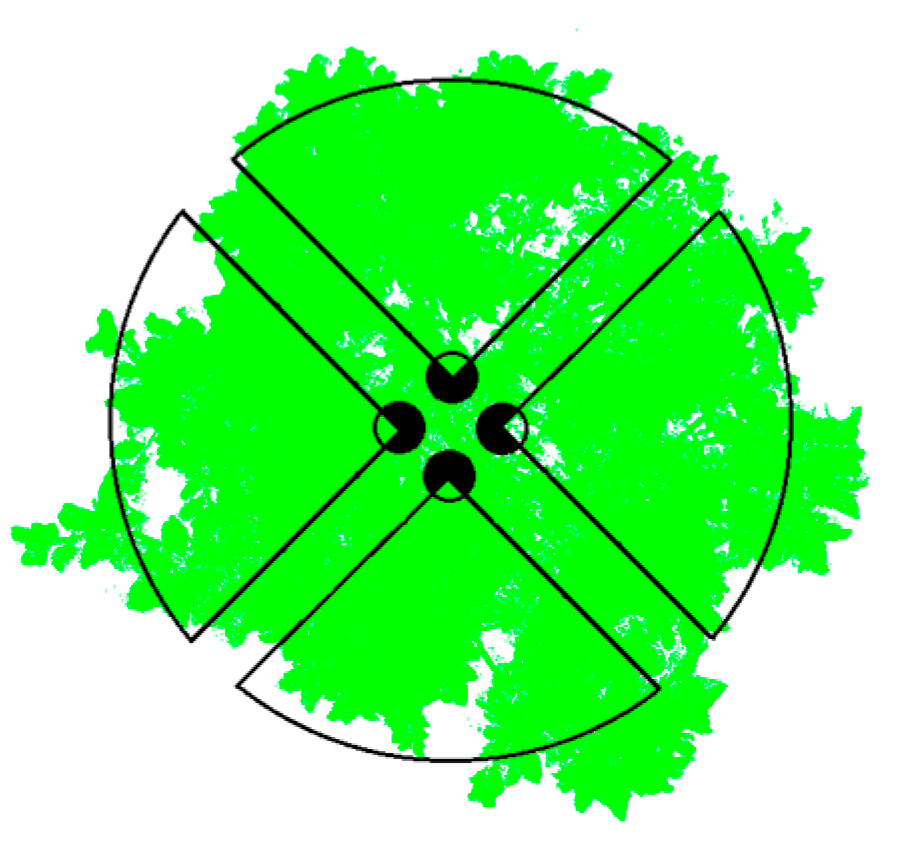
3.3. Validation
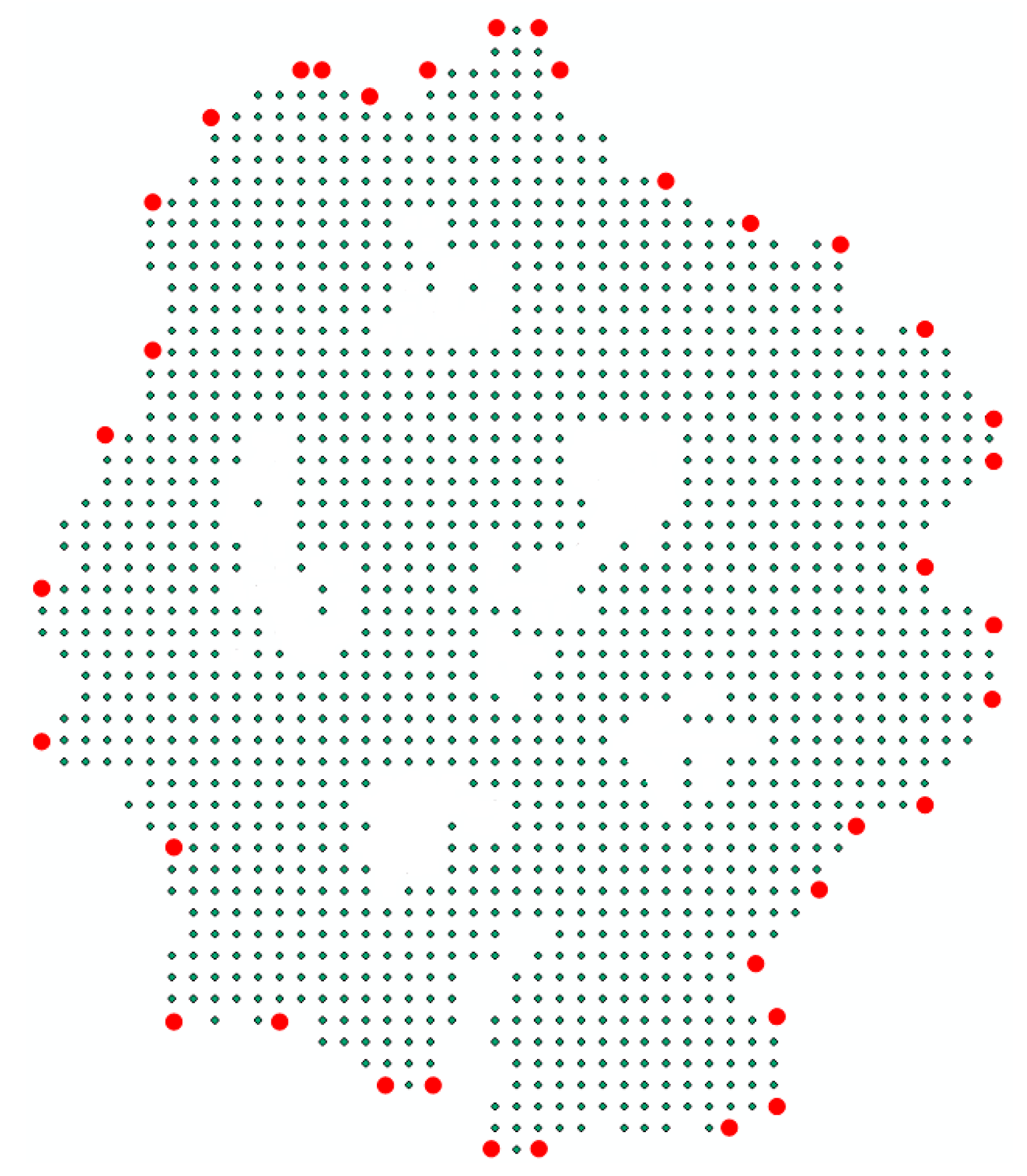
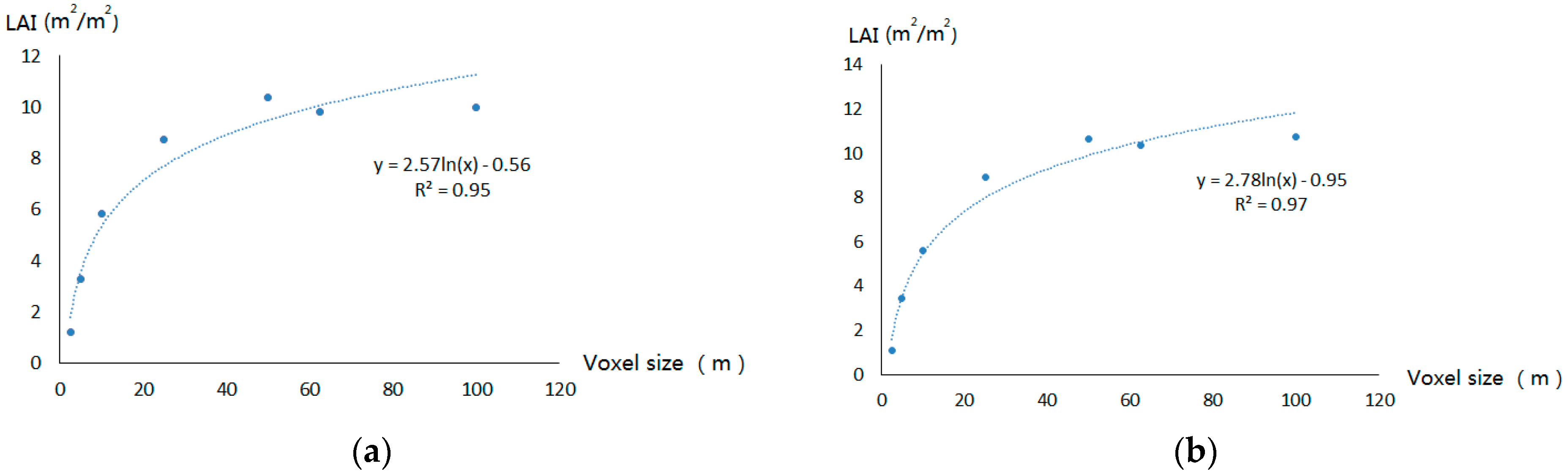
3.4. Voxel Size Effects Analysis
4. Results and Discussion
4.1. Extraction of Leaf Point Cloud Data for Two Magnolia Trees
4.2. LAD Estimation
4.2.1. LAD Estimation in the Voxel Size of 2.5 mm
4.2.2. Voxel Size Effects
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Hosoi, F.; Omasa, K. Voxel-based 3-D modeling of individual trees for estimating leaf area density using high-resolution portable scanning LiDAR. IEEE Trans. Geosci. Remote Sens. 2006, 44, 3610–3618. [Google Scholar] [CrossRef]
- Béland, M.; Baldocchi, D.D.; Widlowski, J.L.; Fournier, R.A.; Verstraete, M.M. On seeing the wood from the leaves and the role of voxel size in determining leaf area distribution of forests with terrestrial LiDAR. Agric. For. Meteorol. 2014, 184, 82–97. [Google Scholar] [CrossRef]
- Zheng, G.; Moskal, L.M. Computational-geometry-based retrieval of effective leaf area index using terrestrial laser scanning. IEEE Trans. Geosci. Remote Sens. 2012, 50, 3958–3969. [Google Scholar] [CrossRef]
- Huang, P.; Pretzsch, H. Using terrestrial laser scanner for estimating leaf areas of individual trees in a conifer forest. Trees 2010, 24, 609–619. [Google Scholar] [CrossRef]
- Weiss, M.; Baret, F.; Smith, G.J.; Jonckheere, I.; Coppin, P. Review of methods for in situ leaf area index (LAI) determination: Part II. Estimation of LAI, errors and sampling. Agric. For. Meteorol. 2004, 121, 37–53. [Google Scholar] [CrossRef]
- Hosoi, F.; Omasa, K. Factors contributing to accuracy in the estimation of the woody canopy leaf area density profile using 3D portable LiDAR imaging. J. Exp. Bot. 2007, 58, 3463–3473. [Google Scholar] [CrossRef] [PubMed]
- Wilson, J.W. Estimation of foliage denseness and foliage angle by inclined point quadrats. Aust. J. Bot. 1963, 11, 95–105. [Google Scholar] [CrossRef]
- Monsi, M.; Saeki, T. On the factor light in plant communities and its importance for matter production. Ann. Bot. 2005, 95, 549–567. [Google Scholar] [CrossRef] [PubMed]
- Qin, Y.; Vu, T.T.; Ban, Y. Toward an optimal algorithm for LiDAR waveform decomposition. IEEE Geosci. Remote Sens. Lett. 2012, 9, 482–486. [Google Scholar] [CrossRef]
- Qin, Y.; Li, S.; Vu, T.T.; Niu, Z.; Ban, Y. Synergistic application of geometric and radiometric features of LiDAR data for urban land cover mapping. Opt. Express 2015, 23, 13761–13775. [Google Scholar] [CrossRef] [PubMed]
- Hosoi, F.; Nakai, Y.; Omasa, K. 3-D voxel-based solid modeling of a broad-leaved tree for accurate volume estimation using portable scanning LiDAR. ISPRS J. Photogramm. Remote Sens. 2013, 82, 41–48. [Google Scholar] [CrossRef]
- Li, W.; Niu, Z.; Li, J.; Chen, H.; Gao, S.; Wu, M.; Li, D. Generating pseudo large footprint waveforms from small footprint full-waveform airborne LiDAR data for the layered retrieval of LAI in orchards. Opt. Express 2016, 24, 10142–10156. [Google Scholar] [CrossRef] [PubMed]
- Béland, M.; Widlowski, J.L.; Fournier, R.A. A model for deriving voxel-level tree leaf area density estimates from ground-based LiDAR. Environ. Model. Softw. 2014, 51, 184–189. [Google Scholar] [CrossRef]
- Ma, L.; Zheng, G.; Eitel, J.U.H.; Moskal, L.M.; He, W.; Huang, H. Improved salient feature-based approach for automatically separating photosynthetic and nonphotosynthetic components within terrestrial LiDAR point cloud data of forest canopies. IEEE Trans. Geosci. Remote Sens. 2016, 54, 679–696. [Google Scholar] [CrossRef]
- Béland, M.; Widlowski, J.L.; Fournier, R.A.; Côté, J.F.; Verstraete, M.M. Estimating leaf area distribution in savanna trees from terrestrial LiDAR measurements. Agric. For. Meteorol. 2011, 151, 1252–1266. [Google Scholar] [CrossRef]
- Tao, S.; Guo, Q.; Su, Y.; Xu, S.; Li, Y.; Wu, F. A geometric method for wood-leaf separation using terrestrial and simulated LiDAR data. Photogramm. Eng. Remote Sen. 2015, 81, 767–776. [Google Scholar] [CrossRef]
- Wang, H.; Li, S.; Guo, J.; Liang, Z. Retrieval of the leaf area density of Magnolia woody canopy with terrestrial Laser-scanning data. J. Remote Sens. 2016, 20, 570–578. [Google Scholar] [CrossRef]
- Ioannou, Y.; Taati, B.; Harrap, R.; Greenspan, M. Difference of normals as a multi-scale operator in unorganized point clouds. In Proceedings of the IEEE Second International Conference on 3D Imaging, Modeling, Processing, Visualization and Transmission, Zurich, Switzerland, 13–15 October 2012. [Google Scholar]
- Awrangjeb, M.; Fraser, C.S. Automatic segmentation of raw LiDAR data for extraction of building roofs. Remote Sens. 2014, 6, 3716–3751. [Google Scholar] [CrossRef]
- Li, W.; Guo, Q.; Jakubowski, M.K.; Kelly, M. A new method for segmenting individual trees from the LiDAR point cloud. Eng. Remote Sens. 2012, 78, 75–84. [Google Scholar] [CrossRef]
- Li, Z.; Zhang, L.; Tong, X.; Du, B.; Wang, Y.; Zhang, L.; Zhang, Z.; Liu, H.; Mei, J.; Xing, X.; et al. A three-step approach for TLS point cloud classification. IEEE Trans. Geosci. Remote Sens. 2016, 54, 5412–5424. [Google Scholar] [CrossRef]
- Radtke, P.J.; Bolstad, P.V. Laser point-quadrat sampling for estimating foliage-height profiles in broad-leaved forests. Can. J. For. Res. 2001, 31, 410–418. [Google Scholar] [CrossRef]
- Parker, G.G.; Harding, D.J.; Berger, M.L. A portable LIDAR system for rapid determination of forest canopy structure. J. Appl. Ecol. 2004, 41, 755–767. [Google Scholar] [CrossRef]
- Sumida, A.; Nakai, T.; Yamada, M.; Ono, K.; Uemura, S.; Hara, T. Ground-based estimation of leaf area index and vertical distribution of leaf area density in a Betula ermanii forest. Silva Fenn. 2009, 43, 799–816. [Google Scholar] [CrossRef]
- Grau, E.; Durrieu, S.; Fournier, R.; Gastellu-Etchegorry, J.P.; Yin, T. Estimation of 3D vegetation density with Terrestrial Laser Scanning data using voxels. A sensitivity analysis of influencing parameters. Remote Sens. Environ. 2017, 191, 373–388. [Google Scholar] [CrossRef]
- Hosoi, F.; Nakai, Y.; Omasa, K. Estimation and error analysis of woody canopy leaf area density profiles using 3-D airborne and ground-based scanning LiDAR remote-sensing techniques. IEEE Trans. Geosci. Remote Sens. 2010, 48, 2215–2223. [Google Scholar] [CrossRef]
- Van der Zande, D.; Stuckens, J.; Verstraeten, W.W.; Mereu, S.; Muys, B.; Coppin, P. 3D modeling of light interception in heterogeneous forest canopies using ground-based LiDAR data. Int. J. Appl. Earth Obs. Geoinf. 2011, 13, 792–800. [Google Scholar] [CrossRef]
- Iio, A.; Kakubari, Y.; Mizunaga, H. A three-dimensional light transfer model based on the vertical point-quadrant method and Monte-Carlo simulation in a Fagus crenata forest canopy on Mount Naeba in Japan. Agric. For. Meteorol. 2011, 151, 461–479. [Google Scholar] [CrossRef]
- Leica Cyclone 3D Point Cloud Processing Software. Available online: http://hds.leica-geosystems.com/en/Leica-Cyclone_6515.htm (accessed on 16 September 2017).
- Li, S.; Wang, J.; Liang, Z.; Su, L. Tree point cloud registration using an improved ICP algorithm based on KD-tree. In Proceedings of the IGARSS 2016—2016 IEEE International Geoscience and Remote Sensing Symposium, Beijing, China, 10–15 July 2016. [Google Scholar]
- Woo, H.; Kang, E.; Wang, S.; Kelly, M. A new segmentation method for point cloud data. Int. J. Mach. Tools Manuf. 2002, 42, 167–178. [Google Scholar] [CrossRef]
- Yao, C.; Chen, H. Automated retinal blood vessels segmentation based on simplified PCNN and fast 2D-Otsu algorithm. J. Cent. South Univ. Technol. 2009, 16, 640–646. [Google Scholar] [CrossRef]
- Graham, R.L. An efficient algorith for determining the convex hull of a finite planar set. Inf. Process. Lett. 1972, 1, 132–133. [Google Scholar] [CrossRef]
- Alsuwaiyel, M.H. Algorithms: Design Techniques and Analysis; World Scientific Publishing Company: Singapore, 1998; pp. 471–474. [Google Scholar]
- Zhao, J.; Li, J.; Liu, Q. Review of forest vertical structure parameter inversion based on remote sensing technology. J. Remote Sens. 2013, 17, 697–716. [Google Scholar] [CrossRef]
- LI-COR. LAI-2200 Plant Canopy Analyzer Instruction Manual; LI-COR: Lincoln, NE, USA, 2010. [Google Scholar]

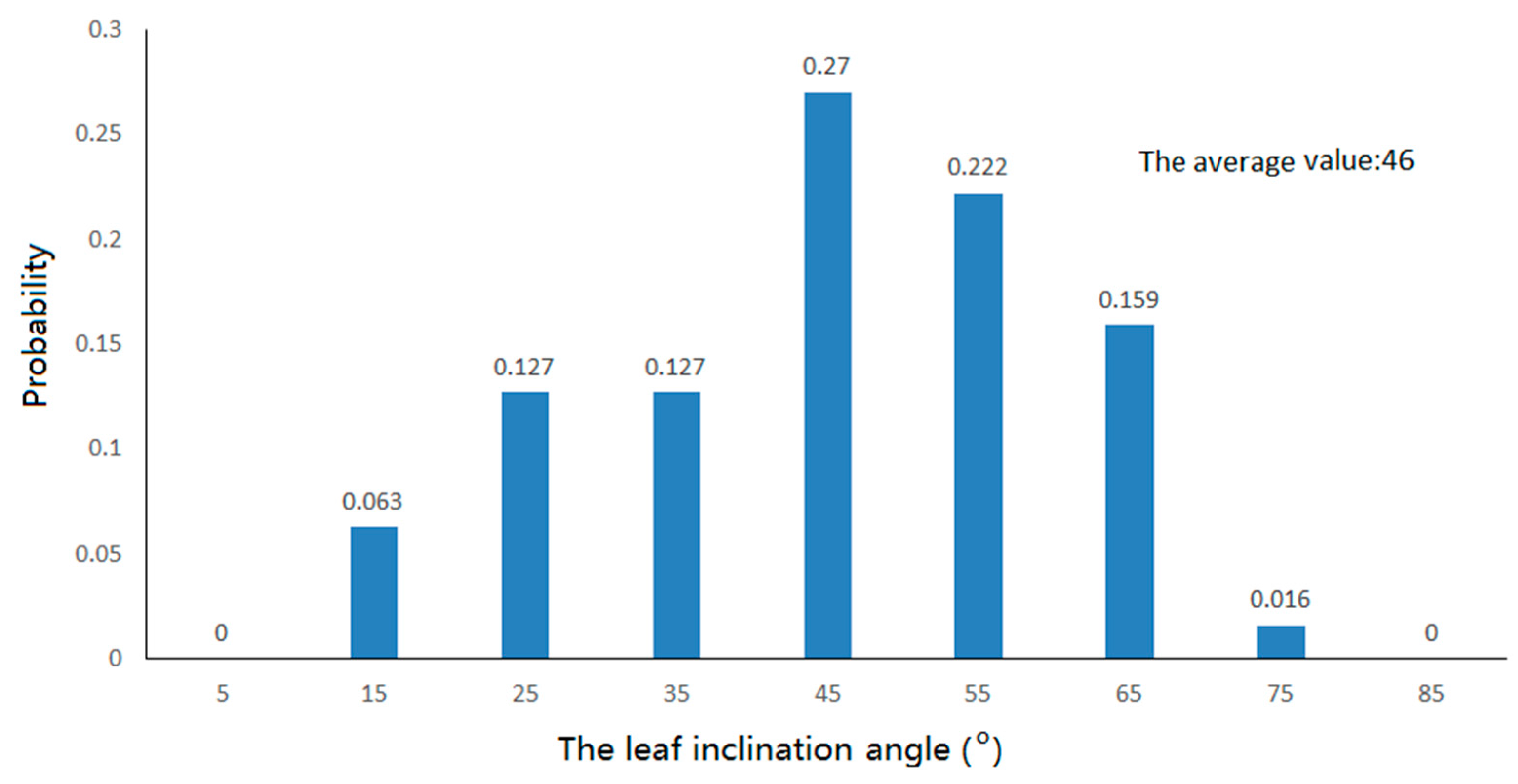
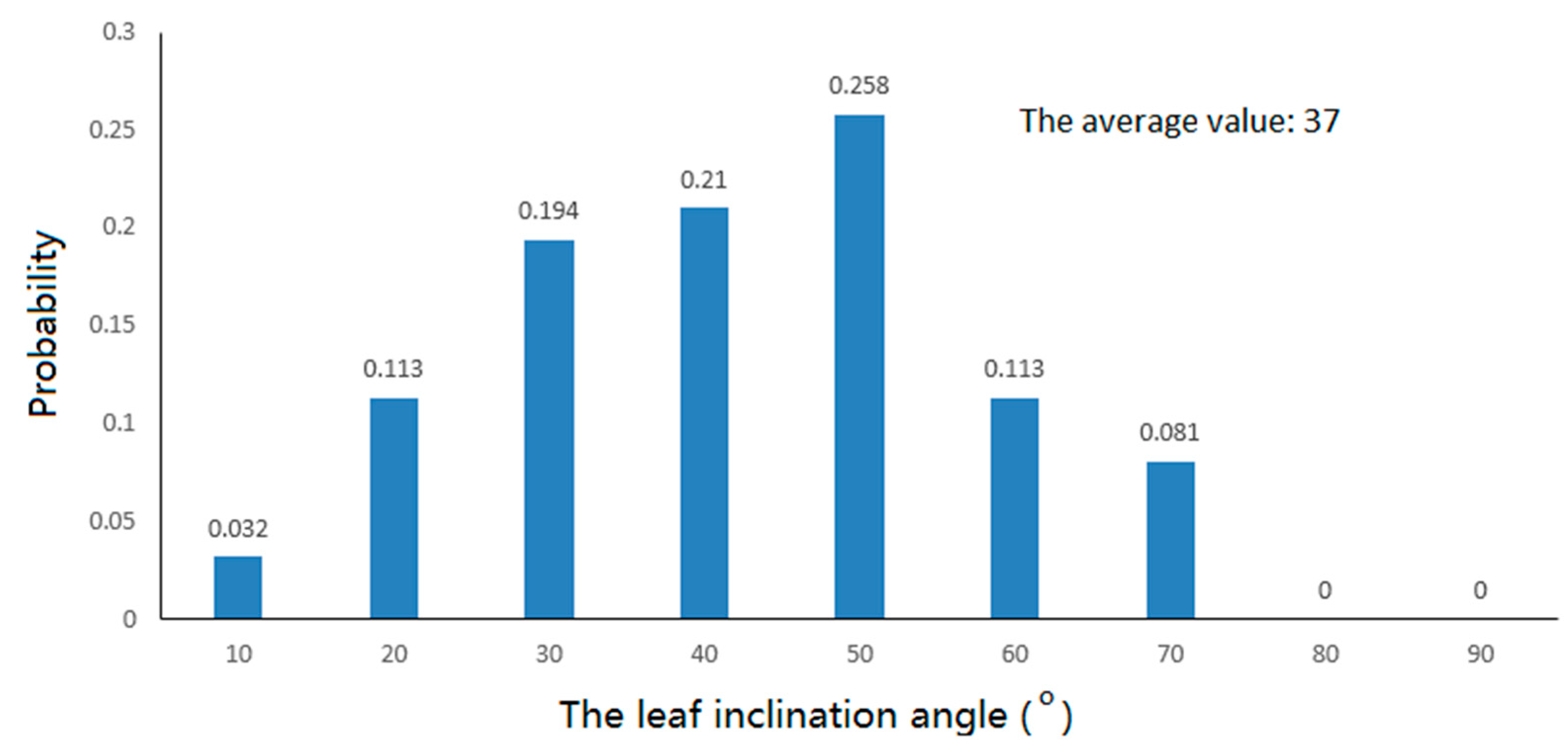
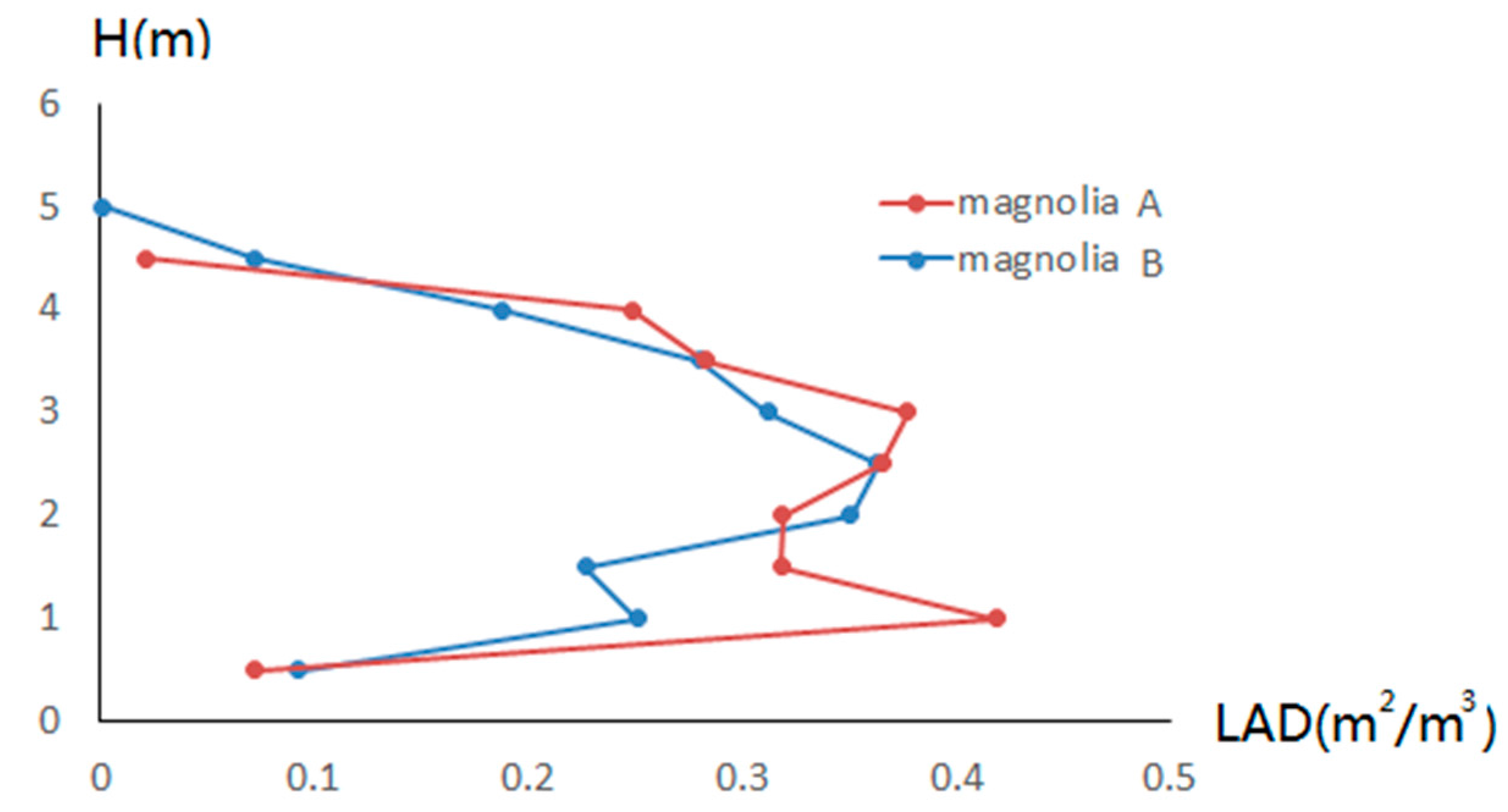
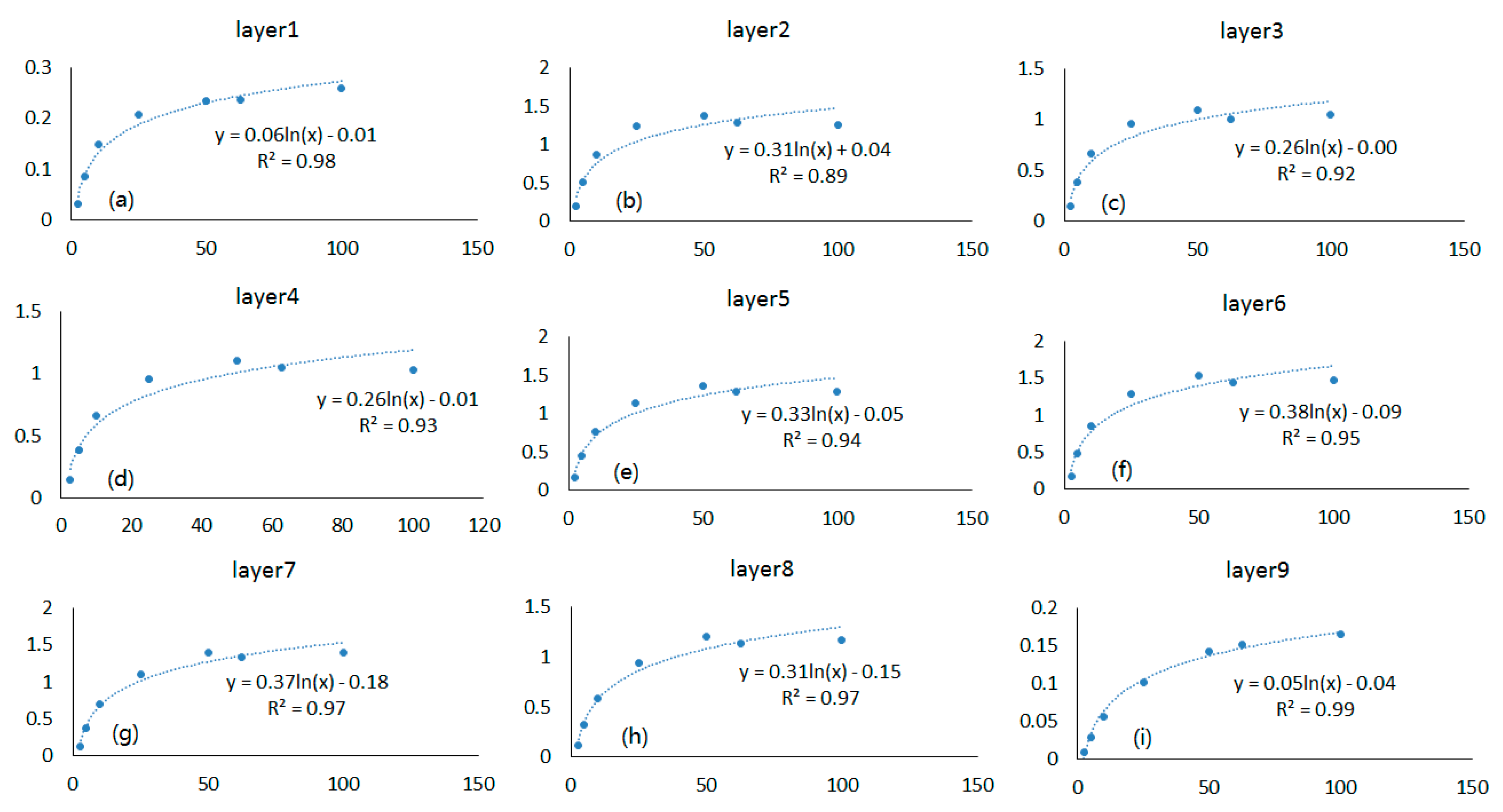
| Tree | Height | Canopy Depth | Crown Size | Average Leaf Length | Average Leaf Width |
|---|---|---|---|---|---|
| Magnolia A | 6.1 | 4.1 | 2.80 × 2.83 | 0.144 | 0.075 |
| Magnolia B | 6.4 | 4.5 | 2.81 × 3.29 | 0.156 | 0.078 |
| Magnolia A | Magnolia B | |
|---|---|---|
| Estimated LAI | 1.21 | 1.07 |
| LAI2200 Measured LAI | 1.20 | 1.18 |
| Accuracy | 99.9% | 90.7% |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, S.; Dai, L.; Wang, H.; Wang, Y.; He, Z.; Lin, S. Estimating Leaf Area Density of Individual Trees Using the Point Cloud Segmentation of Terrestrial LiDAR Data and a Voxel-Based Model. Remote Sens. 2017, 9, 1202. https://doi.org/10.3390/rs9111202
Li S, Dai L, Wang H, Wang Y, He Z, Lin S. Estimating Leaf Area Density of Individual Trees Using the Point Cloud Segmentation of Terrestrial LiDAR Data and a Voxel-Based Model. Remote Sensing. 2017; 9(11):1202. https://doi.org/10.3390/rs9111202
Chicago/Turabian StyleLi, Shihua, Leiyu Dai, Hongshu Wang, Yong Wang, Ze He, and Sen Lin. 2017. "Estimating Leaf Area Density of Individual Trees Using the Point Cloud Segmentation of Terrestrial LiDAR Data and a Voxel-Based Model" Remote Sensing 9, no. 11: 1202. https://doi.org/10.3390/rs9111202
APA StyleLi, S., Dai, L., Wang, H., Wang, Y., He, Z., & Lin, S. (2017). Estimating Leaf Area Density of Individual Trees Using the Point Cloud Segmentation of Terrestrial LiDAR Data and a Voxel-Based Model. Remote Sensing, 9(11), 1202. https://doi.org/10.3390/rs9111202