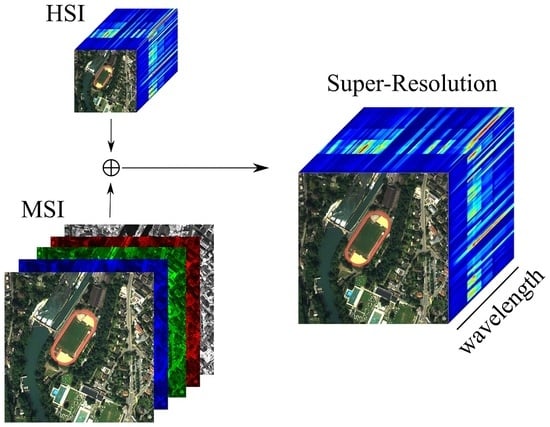
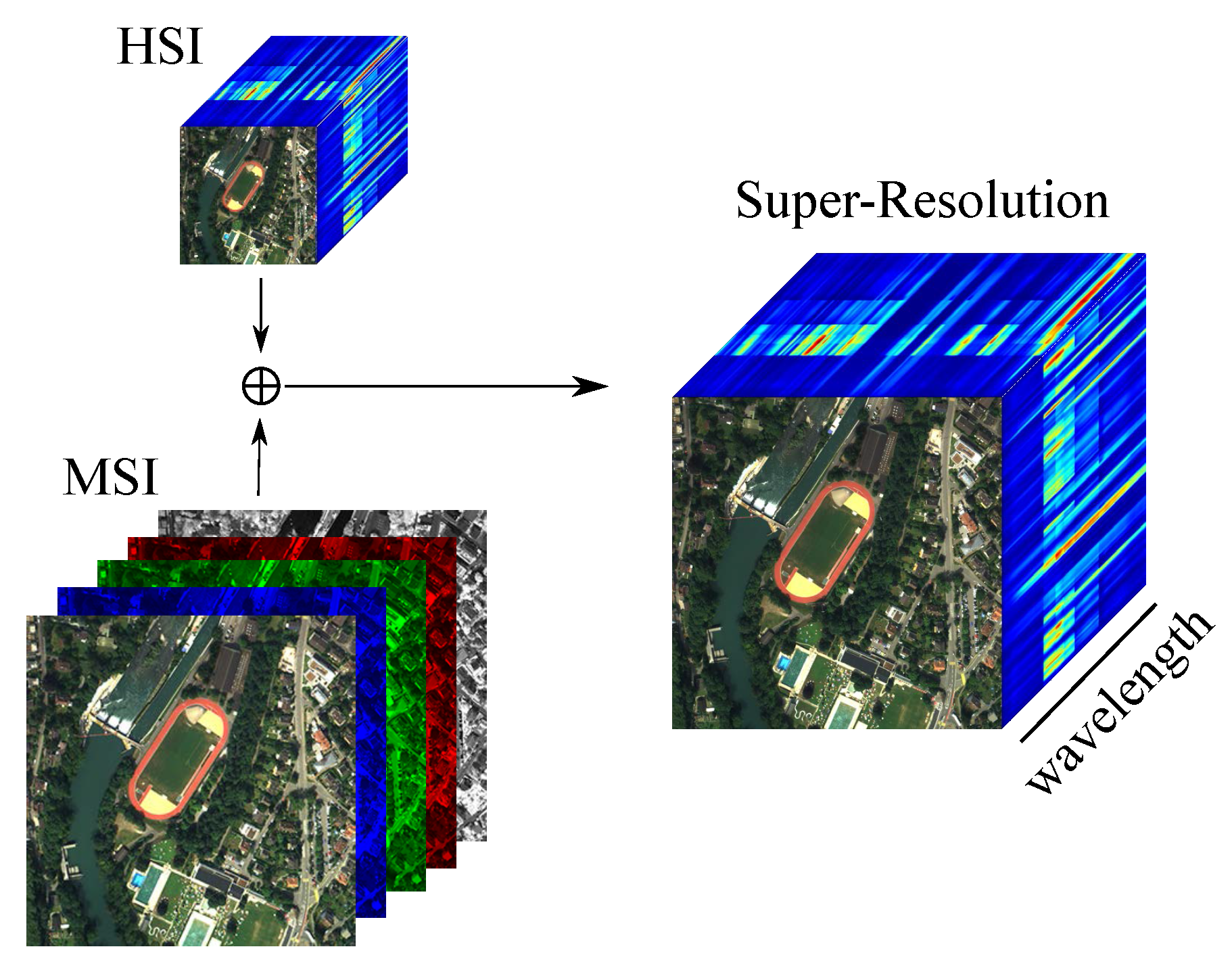
Hyperspectral Super-Resolution with Spectral Unmixing Constraints
Abstract
1. Introduction
2. Related Work
3. Problem Formulation
3.1. Constraints
4. Proposed Solution
4.1. Super Resolution
4.1.1. Optimization Scheme
| Algorithm 1 Solution of minimization problem Equation (6a). |
| Require: |
| Initialize with SISAL and with SUnSAL |
| Initialize by upsampling |
| while do |
| // low-resolution step: |
| Estimate with (10a) and (10b) |
| // high-resolution step: |
| Estimate with (11a) and (11b) |
| end while |
| return |
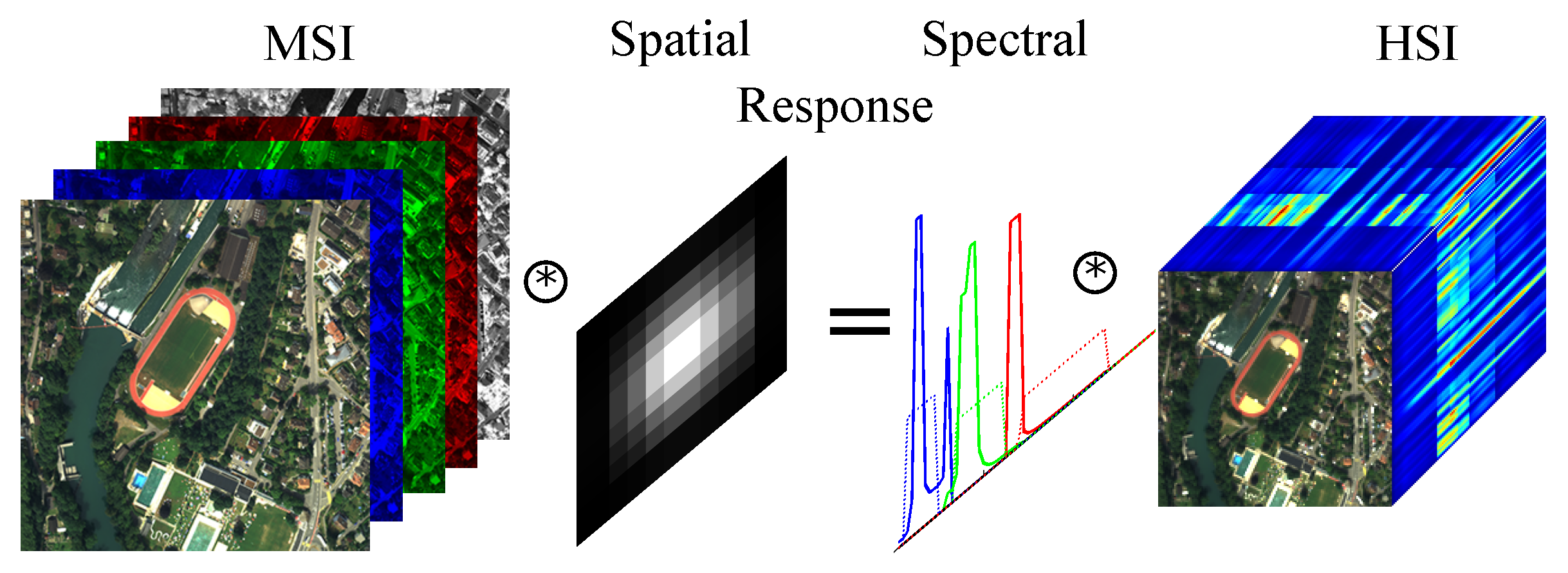
4.2. Relative Spatial Response
4.3. Relative Spectral Response
5. Experiments
5.1. Datasets
5.1.1. APEX and Pavia University
5.1.2. CAVE and Harvard
5.1.3. Real EO-1 Data
5.2. Error Metrics and Baselines
5.3. Implementation Details
6. Experimental Results and Discussion
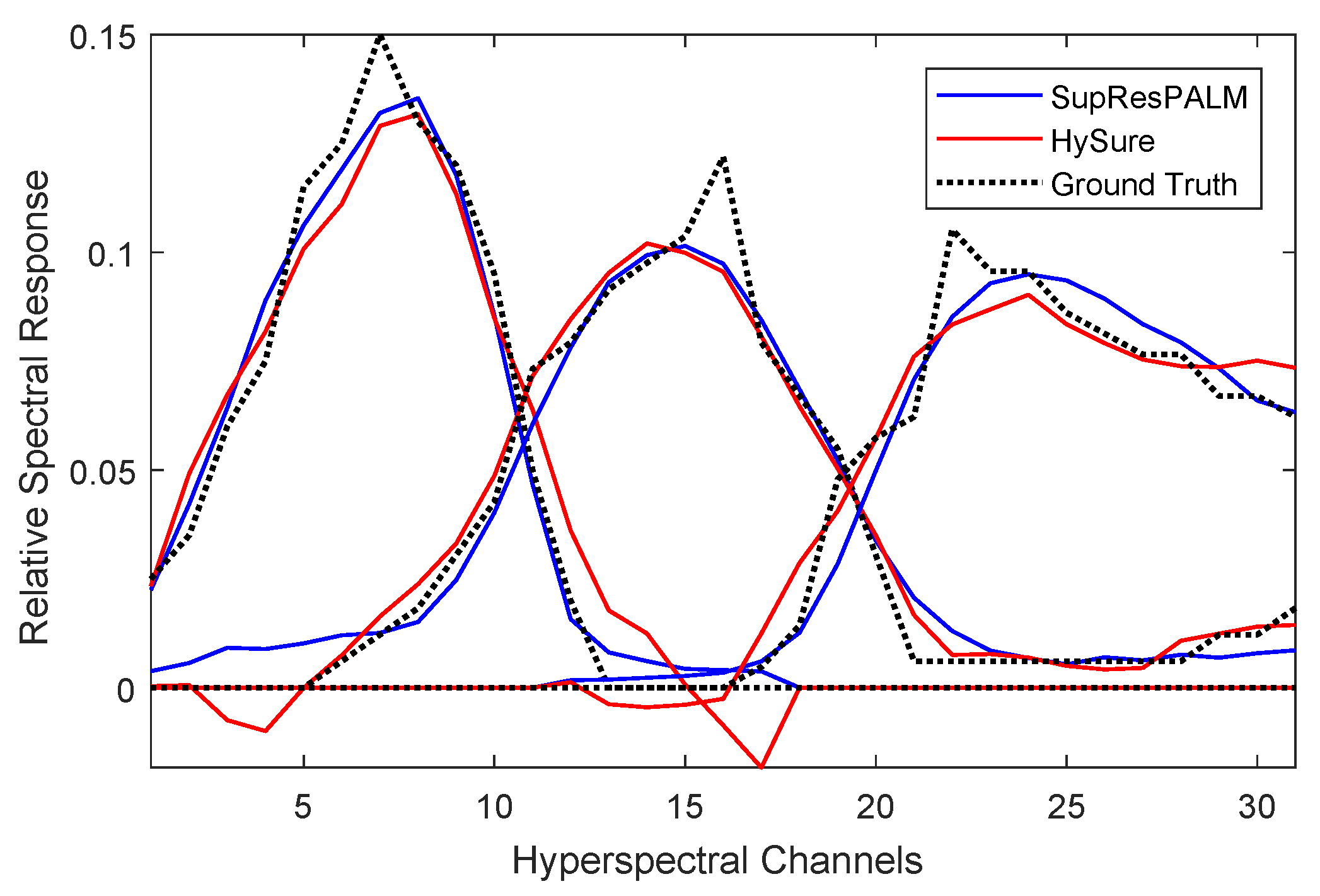
6.1. Relative Responses
6.1.1. CAVE Database
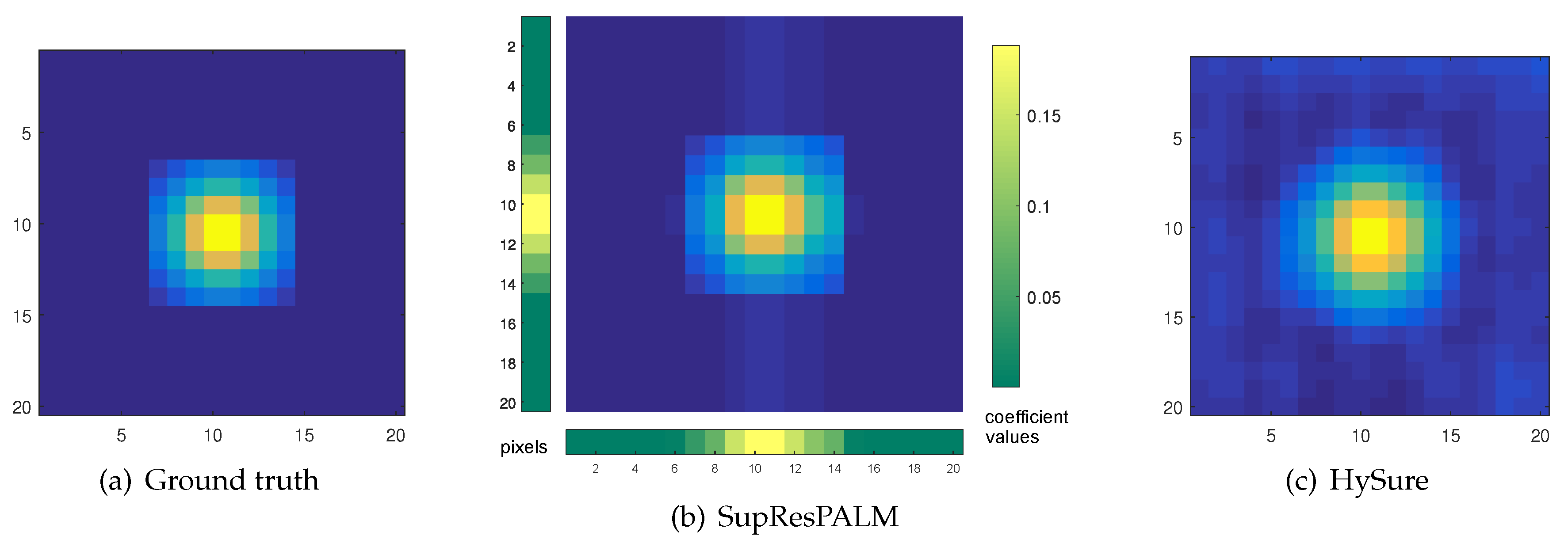
6.1.2. Real EO-1 Data
6.2. Super-Resolution
6.2.1. APEX and Pavia University
6.2.2. CAVE and Harvard
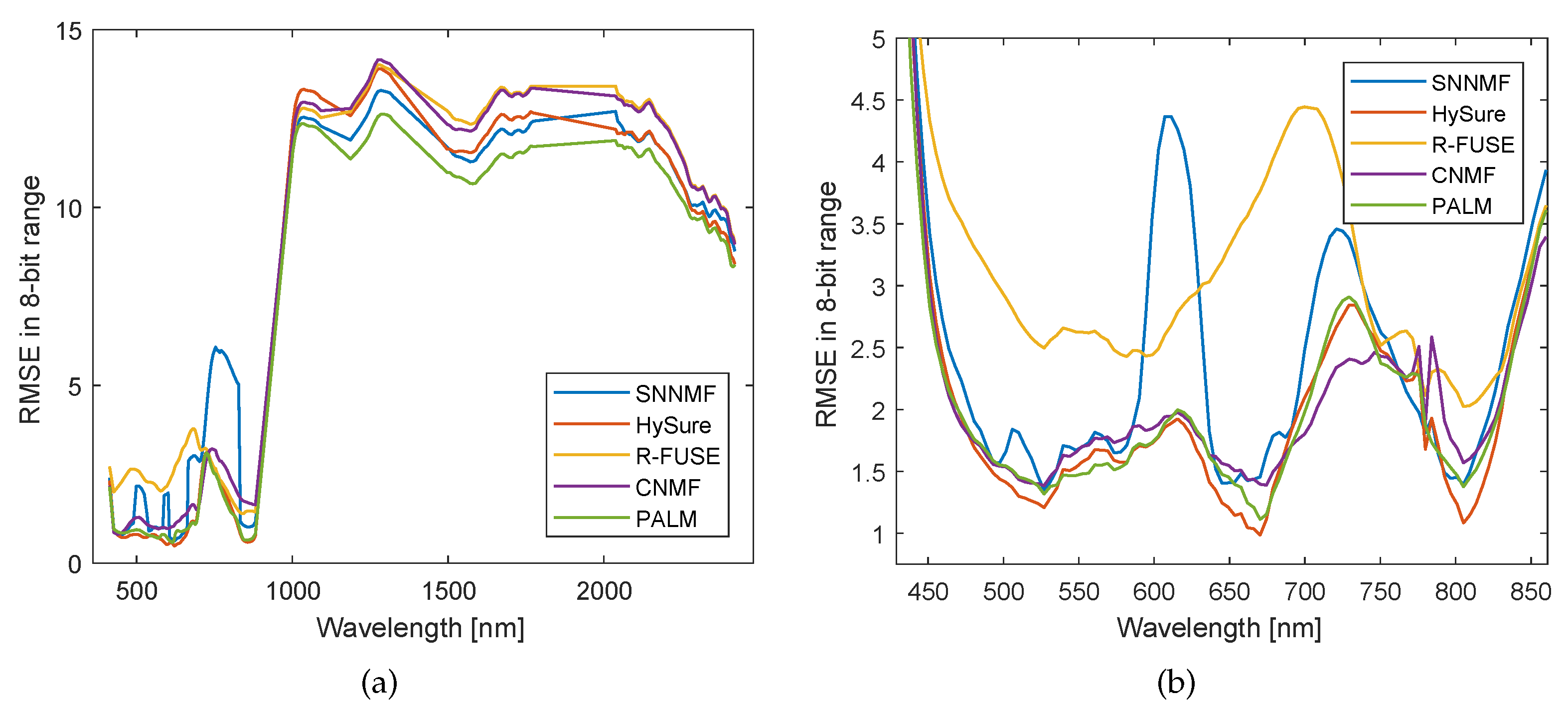
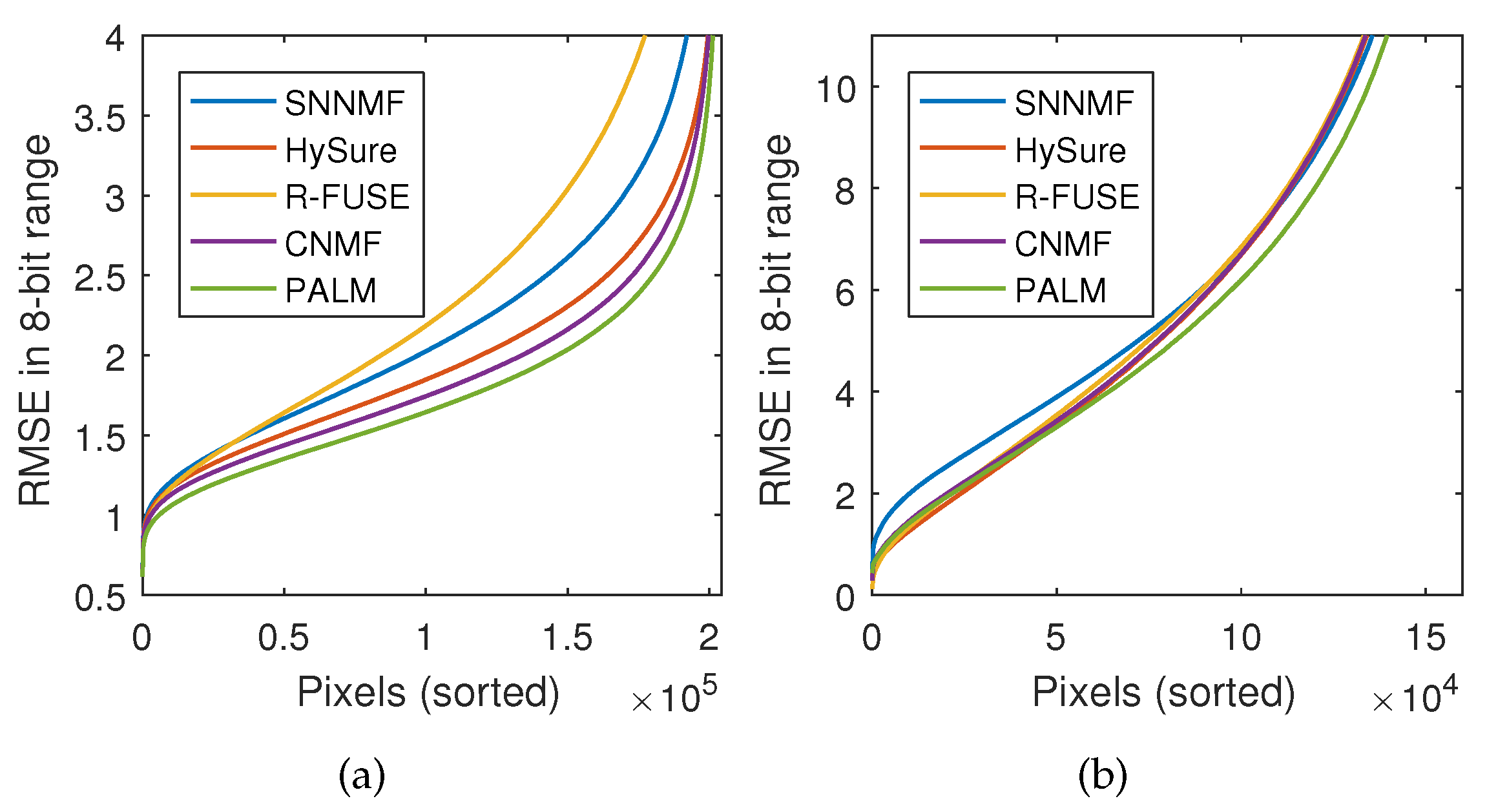
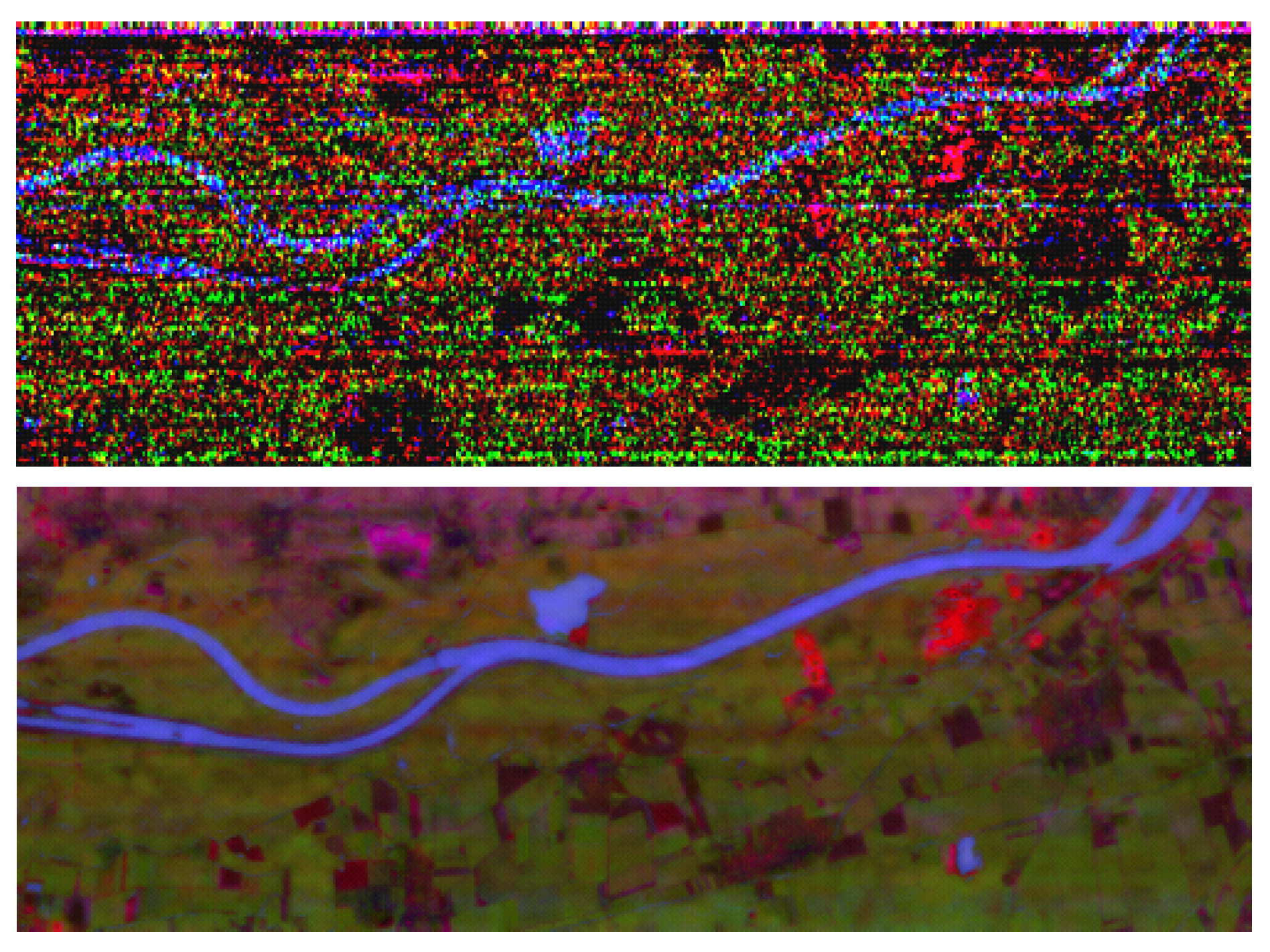
6.2.3. Real EO-1 Data
6.3. Discussion
6.3.1. Spectral Unmixing
6.3.2. Effect of the Sparsity Term
6.3.3. Effect of the Spatial Regularization
6.3.4. Denoising
7. Conclusions
Supplementary Materials
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Varshney, P.K.; Arora, M.K. Advanced Image Processing Techniques for Remotely Sensed Hyperspectral Data; Springer: Berlin, Germany, 2004. [Google Scholar]
- Yokoya, N.; Grohnfeldt, C.; Chanussot, J. Hyperspectral and Multispectral Data Fusion: A comparative review of the recent literature. IEEE Geosci. Remote Sens. Mag. 2017, 5, 29–56. [Google Scholar] [CrossRef]
- Keshava, N.; Mustard, J.F. Spectral unmixing. IEEE Signal Process. Mag. 2002, 19, 44–57. [Google Scholar] [CrossRef]
- Wang, T.; Yan, G.; Ren, H.; Mu, X. Improved methods for spectral calibration of on-orbit imaging spectrometers. IEEE Trans. Geosci. Remote Sens. 2010, 48, 3924–3931. [Google Scholar] [CrossRef]
- Lanaras, C.; Baltsavias, E.; Schindler, K. Hyperspectral Super-Resolution by Coupled Spectral Unmixing. In Proceedings of the IEEE International Conference on Computer Vision (ICCV), Santiago, Chile, 11–18 December 2015; pp. 3586–3594. [Google Scholar]
- Wang, Z.; Ziou, D.; Armenakis, C.; Li, D.; Li, Q. A comparative analysis of image fusion methods. IEEE Trans. Geosci. Remote Sens. 2005, 43, 1391–1402. [Google Scholar] [CrossRef]
- Loncan, L.; de Almeida, L.B.; Bioucas-Dias, J.M.; Briottet, X.; Chanussot, J.; Dobigeon, N.; Fabre, S.; Liao, W.; Licciardi, G.A.; Simoes, M.; et al. Hyperspectral Pansharpening: A Review. IEEE Geosci. Remote Sens. Mag. 2015, 3, 27–46. [Google Scholar] [CrossRef]
- Kawakami, R.; Wright, J.; Tai, Y.W.; Matsushita, Y.; Ben-Ezra, M.; Ikeuchi, K. High-resolution hyperspectral imaging via matrix factorization. In Proceedings of the IEEE Computer Vision and Pattern Recognition (CVPR), Colorado Springs, CO, USA, 20–25 June 2011; pp. 2329–2336. [Google Scholar]
- Huang, B.; Song, H.; Cui, H.; Peng, J.; Xu, Z. Spatial and spectral image fusion using sparse matrix factorization. IEEE Trans. Geosci. Remote Sens. 2014, 52, 1693–1704. [Google Scholar] [CrossRef]
- Akhtar, N.; Shafait, F.; Mian, A. Sparse Spatio-spectral Representation for Hyperspectral Image Super-Resolution. In Proceedings of the European Conference on Computer Vision, Zurich, Switzerland, 6–12 September 2014; pp. 63–78. [Google Scholar]
- Simoes, M.; Bioucas-Dias, J.; Almeida, L.; Chanussot, J. A Convex Formulation for Hyperspectral Image Superresolution via Subspace-Based Regularization. IEEE Trans. Geosci. Remote Sens. 2015, 53, 3373–3388. [Google Scholar] [CrossRef]
- Yokoya, N.; Yairi, T.; Iwasaki, A. Coupled nonnegative matrix factorization unmixing for hyperspectral and multispectral data fusion. IEEE Trans. Geosci. Remote Sens. 2012, 50, 528–537. [Google Scholar] [CrossRef]
- Wycoff, E.; Chan, T.H.; Jia, K.; Ma, W.K.; Ma, Y. A non-negative sparse promoting algorithm for high resolution hyperspectral imaging. In Proceedings of the IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Vancouver, BC, Canada, 26–31 May 2013; pp. 1409–1413. [Google Scholar]
- Veganzones, M.A.; Simoes, M.; Licciardi, G.; Yokoya, N.; Bioucas-Dias, J.M.; Chanussot, J. Hyperspectral super-resolution of locally low rank images from complementary multisource data. IEEE Trans. Image Process. 2016, 25, 274–288. [Google Scholar] [CrossRef] [PubMed]
- Hardie, R.C.; Eismann, M.T.; Wilson, G.L. MAP estimation for hyperspectral image resolution enhancement using an auxiliary sensor. IEEE Trans. Image Process. 2004, 13, 1174–1184. [Google Scholar] [CrossRef] [PubMed]
- Wei, Q.; Dobigeon, N.; Tourneret, J.Y. Bayesian fusion of multi-band images. IEEE J. Sel. Top. Signal Process. 2015, 9, 1117–1127. [Google Scholar] [CrossRef]
- Wei, Q.; Dobigeon, N.; Tourneret, J.Y. Fast fusion of multi-band images based on solving a Sylvester equation. IEEE Trans. Image Process. 2015, 24, 4109–4121. [Google Scholar] [CrossRef] [PubMed]
- Wei, Q.; Dobigeon, N.; Tourneret, J.Y.; Bioucas-Dias, J.; Godsill, S. R-FUSE: Robust Fast Fusion of Multiband Images Based on Solving a Sylvester Equation. IEEE Signal Process. Lett. 2016, 23, 1632–1636. [Google Scholar] [CrossRef]
- Zou, C.; Xia, Y. Hyperspectral Image Superresolution Based on Double Regularization Unmixing. IEEE Geosci. Remote Sens. Lett. 2017, 14, 1022–1026. [Google Scholar] [CrossRef]
- Wei, Q.; Bioucas-Dias, J.; Dobigeon, N.; Tourneret, J.Y.; Chen, M.; Godsill, S. Multiband Image Fusion Based on Spectral Unmixing. IEEE Trans. Geosci. Remote Sens. 2016, 54, 7236–7249. [Google Scholar] [CrossRef]
- Akhtar, N.; Shafait, F.; Mian, A. Bayesian Sparse Representation for Hyperspectral Image Super Resolution. In Proceedings of the IEEE Computer Vision and Pattern Recognition (CVPR), Boston, MA, USA, 7–12 June 2015; pp. 3631–3640. [Google Scholar]
- Yokoya, N.; Mayumi, N.; Iwasaki, A. Cross-Calibration for Data Fusion of EO-1/Hyperion and Terra/ASTER. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2013, 6, 419–426. [Google Scholar] [CrossRef]
- Bioucas-Dias, J.M.; Plaza, A.; Dobigeon, N.; Parente, M.; Du, Q.; Gader, P.; Chanussot, J. Hyperspectral unmixing overview: Geometrical, statistical, and sparse regression-based approaches. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2012, 5, 354–379. [Google Scholar] [CrossRef]
- Bolte, J.; Sabach, S.; Teboulle, M. Proximal alternating linearized minimization for nonconvex and nonsmooth problems. Math. Programm. 2014, 146, 459–494. [Google Scholar] [CrossRef]
- Condat, L. Fast projection onto the simplex and the l1 ball. Math. Programm. 2016, 158, 575–585. [Google Scholar] [CrossRef]
- Bioucas-Dias, J.M. A variable splitting augmented Lagrangian approach to linear spectral unmixing. In Proceedings of the Workshop on Hyperspectral Image and Signal Processing: Evolution in Remote Sensing (WHISPERS), Grenoble, France, 26–28 August 2009; pp. 1–4. [Google Scholar]
- Bioucas-Dias, J.M.; Nascimento, J.M. Hyperspectral subspace identification. IEEE Trans. Geosci. Remote Sens. 2008, 46, 2435–2445. [Google Scholar] [CrossRef]
- Boyd, S.; Vandenberghe, L. Convex Optimization; Cambridge University Press: Cambridge, UK, 2004. [Google Scholar]
- Lanaras, C.; Baltsavias, E.; Schindler, K. Estimating the relative spatial and spectral sensor response for hyperspectral and multispectral image fusion. In Proceedings of the Asian Conference on Remote Sensing (ACRS), Colombo, Sri Lanka, 17–21 October 2016. [Google Scholar]
- Knight, E.J.; Kvaran, G. Landsat-8 operational land imager design, characterization and performance. Remote Sens. 2014, 6, 10286–10305. [Google Scholar] [CrossRef]
- Schaepman, M.E.; Jehle, M.; Hueni, A.; D’Odorico, P.; Damm, A.; Weyermann, J.; Schneider, F.D.; Laurent, V.; Popp, C.; Seidel, F.C.; et al. Advanced radiometry measurements and Earth science applications with the Airborne Prism Experiment (APEX). Remote Sens. Environ. 2015, 158, 207–219. [Google Scholar] [CrossRef]
- Lanaras, C.; Baltsavias, E.; Schindler, K. Advances in Hyperspectral and Multispectral Image Fusion and Spectral Unmixing. ISPRS Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2015, XL-3/W3, 451–458. [Google Scholar] [CrossRef]
- Yasuma, F.; Mitsunaga, T.; Iso, D.; Nayar, S. Generalized Assorted Pixel Camera: Post-Capture Control of Resolution, Dynamic Range and Spectrum; Technical Report; Department of Computer Science, Columbia University: New York, NY, USA, 2008. [Google Scholar]
- Chakrabarti, A.; Zickler, T. Statistics of Real-World Hyperspectral Images. In Proceedings of the IEEE Computer Vision and Pattern Recognition (CVPR), Colorado Springs, CO, USA, 20–25 June 2011; pp. 193–200. [Google Scholar]
- Wald, L. Quality of high resolution synthesised images: Is there a simple criterion? In Proceedings of the International Conference on Fusion of Earth Data, Sophia Antipolis, France, 26–28 January 2000; Volume 1, pp. 99–105. [Google Scholar]
- Yuhas, R.H.; Goetz, A.F.; Boardman, J.W. Discrimination among semi-arid landscape endmembers using the spectral angle mapper (SAM) algorithm. In Proceedings of the Summaries of the Third Annual JPL Airborne Geoscience Workshop, Pasadena, CA, USA, 1–5 June 1992; pp. 147–149. [Google Scholar]
- Garzelli, A.; Nencini, F. Hypercomplex quality assessment of multi/hyperspectral images. IEEE Geosci. Remote Sens. Lett. 2009, 6, 662–665. [Google Scholar] [CrossRef]
- Cerra, D.; Muller, R.; Reinartz, P. Noise reduction in hyperspectral images through spectral unmixing. IEEE Geosci. Remote Sens. Lett. 2014, 11, 109–113. [Google Scholar] [CrossRef]





| Method | APEX | Pavia University | ||||||
|---|---|---|---|---|---|---|---|---|
| RMSE | ERGAS | SAM | Q2n | RMSE | ERGAS | SAM | Q2n | |
| SNNMF | 8.82 | 3.23 | 8.53 | 0.812 | 2.76 | 0.97 | 3.10 | 0.918 |
| HySure | 8.75 | 3.15 | 7.44 | 0.756 | 2.33 | 0.83 | 2.76 | 0.928 |
| R-FUSE | 9.29 | 3.53 | 7.70 | 0.757 | 3.36 | 1.22 | 3.50 | 0.854 |
| CNMF | 9.17 | 3.35 | 7.41 | 0.757 | 2.33 | 0.85 | 2.48 | 0.892 |
| SupResPALM | 8.23 | 3.02 | 7.27 | 0.821 | 2.28 | 0.79 | 2.41 | 0.935 |
| Method | CAVE Database | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| RMSE | ERGAS | SAM | Q2n | |||||||||
| Aver. | Med. | 1st | Aver. | Med. | 1st | Aver. | Med. | 1st | Aver. | Med. | 1st | |
| Bic. upsampling | 24.14 | 22.03 | 0 | 3.191 | 3.157 | 0 | 16.01 | 15.83 | 0 | 0.810 | 0.837 | 0 |
| SNNMF | 4.47 | 4.29 | 0 | 0.590 | 0.570 | 0 | 18.13 | 19.60 | 0 | 0.909 | 0.935 | 2 |
| HySure | 4.50 | 3.94 | 0 | 0.563 | 0.536 | 1 | 19.27 | 19.05 | 0 | 0.913 | 0.938 | 4 |
| R-FUSE | 4.16 | 3.74 | 1 | 0.644 | 0.526 | 1 | 8.61 | 8.28 | 2 | 0.912 | 0.933 | 5 |
| CNMF | 3.54 | 2.92 | 8 | 0.490 | 0.420 | 8 | 7.16 | 7.05 | 7 | 0.913 | 0.940 | 2 |
| SupResPALM | 3.15 | 2.88 | 23 | 0.430 | 0.351 | 22 | 6.46 | 6.54 | 23 | 0.927 | 0.948 | 19 |
| Method | Harvard Database | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| RMSE | ERGAS | SAM | Q2n | |||||||||
| Aver. | Med. | 1st | Aver. | Med. | 1st | Aver. | Med. | 1st | Aver. | Med. | 1st | |
| Bic. upsampling | 12.97 | 12.30 | 0 | 1.481 | 1.437 | 0 | 5.50 | 5.22 | 0 | 0.863 | 0.921 | 0 |
| SNNMF | 2.47 | 2.04 | 2 | 0.411 | 0.354 | 2 | 5.25 | 4.47 | 0 | 0.925 | 0.965 | 11 |
| HySure | 2.18 | 1.86 | 0 | 0.390 | 0.335 | 1 | 4.75 | 4.10 | 1 | 0.929 | 0.966 | 7 |
| R-FUSE | 2.28 | 2.01 | 0 | 0.398 | 0.372 | 0 | 3.87 | 3.71 | 1 | 0.927 | 0.960 | 3 |
| CNMF | 1.91 | 1.61 | 20 | 0.299 | 0.286 | 24 | 3.15 | 2.99 | 36 | 0.926 | 0.964 | 7 |
| SupResPALM | 1.81 | 1.53 | 55 | 0.318 | 0.278 | 50 | 3.16 | 3.04 | 39 | 0.934 | 0.969 | 49 |
| EO-1 Real Data | ||||
|---|---|---|---|---|
| Method | RMSE | ERGAS | SAM | Q2n |
| Bicubic upsampling | 5.99 | 12.58 | 4.06 | 0.547 |
| SupResPALM = 0, | 3.63 | 13.49 | 3.01 | 0.765 |
| SupResPALM = 0.01, | 3.61 | 13.52 | 3.10 | 0.764 |
| SupResPALM = 0 | 3.48 | 13.50 | 2.85 | 0.774 |
| SupResPALM = 0.01 | 3.39 | 13.58 | 2.80 | 0.776 |
| Relative Responses | |||
|---|---|---|---|
| HySure | SupResPALM | ||
| R-FUSE | RMSE | 3.89 | 3.91 |
| ERGAS | 13.81 | 13.80 | |
| SAM | 3.40 | 3.52 | |
| Q2n | 0.747 | 0.752 | |
| HySure | RMSE | 4.77 | 4.76 |
| ERGAS | 14.18 | 14.19 | |
| SAM | 3.97 | 3.97 | |
| Q2n | 0.698 | 0.698 | |
| SupResPALM | RMSE | 3.34 | 3.39 |
| ERGAS | 13.73 | 13.58 | |
| SAM | 2.75 | 2.80 | |
| Q2n | 0.775 | 0.776 | |
| APEX | Pavia University | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| s/Nm | – | 6 | 5 | 4 | 3 | 2 | – | 6 | 5 | 4 | 3 | 2 |
| RMSE | 8.23 | 8.29 | 8.46 | 8.68 | 9.07 | 10.31 | 2.28 | 2.61 | 2.79 | 3.18 | 4.29 | 7.87 |
| ERGAS | 3.02 | 3.06 | 3.14 | 3.24 | 3.42 | 4.01 | 0.79 | 0.93 | 0.98 | 1.09 | 1.36 | 2.26 |
| SAM | 7.27 | 6.96 | 7.02 | 7.18 | 7.57 | 9.17 | 2.41 | 2.72 | 2.88 | 3.22 | 4.00 | 6.08 |
| Q2n | 0.821 | 0.811 | 0.810 | 0.808 | 0.790 | 0.696 | 0.935 | 0.925 | 0.914 | 0.883 | 0.793 | 0.664 |
| CAVE Database | ||||||
|---|---|---|---|---|---|---|
| s/Nm | – | 6 | 5 | 4 | 3 | 2 |
| RMSE | 3.15 | 3.18 | 3.23 | 3.32 | 3.77 | 5.18 |
| ERGAS | 0.430 | 0.436 | 0.443 | 0.457 | 0.531 | 0.700 |
| SAM | 6.46 | 6.41 | 6.56 | 6.75 | 7.46 | 8.56 |
| Q2n | 0.927 | 0.927 | 0.926 | 0.923 | 0.920 | 0.904 |
| Method SupResPALM | APEX | Pavia University | ||||||
|---|---|---|---|---|---|---|---|---|
| RMSE | ERGAS | SAM | Q2n | RMSE | ERGAS | SAM | Q2n | |
| 8.23 | 3.02 | 7.27 | 0.821 | 2.28 | 0.791 | 2.41 | 0.935 | |
| 8.19 | 2.98 | 6.98 | 0.822 | 2.34 | 0.817 | 2.42 | 0.935 | |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lanaras, C.; Baltsavias, E.; Schindler, K. Hyperspectral Super-Resolution with Spectral Unmixing Constraints. Remote Sens. 2017, 9, 1196. https://doi.org/10.3390/rs9111196
Lanaras C, Baltsavias E, Schindler K. Hyperspectral Super-Resolution with Spectral Unmixing Constraints. Remote Sensing. 2017; 9(11):1196. https://doi.org/10.3390/rs9111196
Chicago/Turabian StyleLanaras, Charis, Emmanuel Baltsavias, and Konrad Schindler. 2017. "Hyperspectral Super-Resolution with Spectral Unmixing Constraints" Remote Sensing 9, no. 11: 1196. https://doi.org/10.3390/rs9111196
APA StyleLanaras, C., Baltsavias, E., & Schindler, K. (2017). Hyperspectral Super-Resolution with Spectral Unmixing Constraints. Remote Sensing, 9(11), 1196. https://doi.org/10.3390/rs9111196