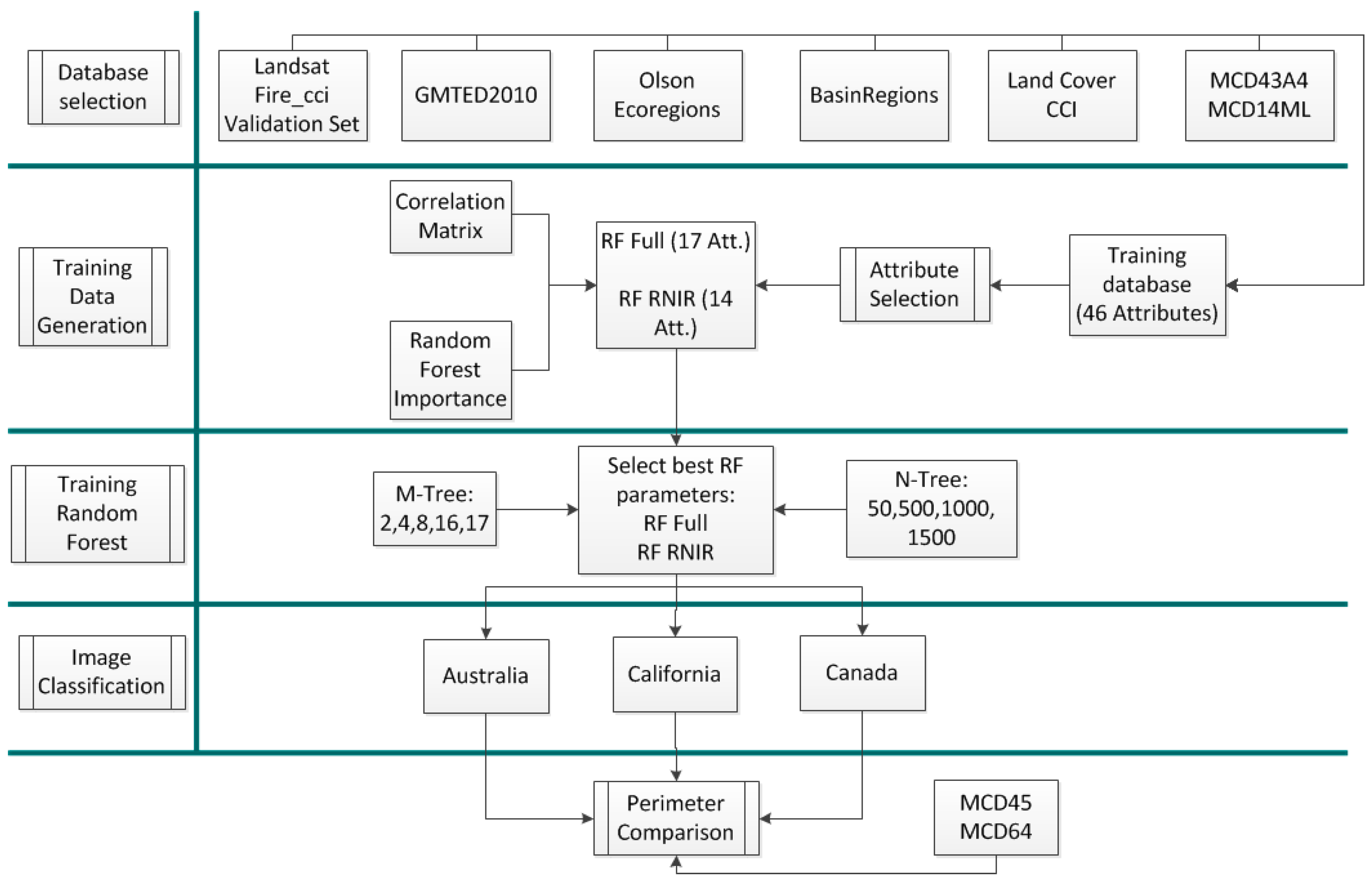
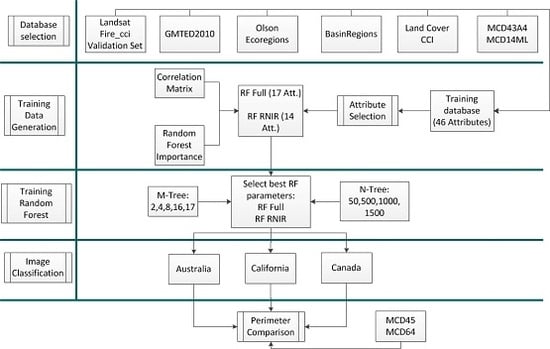
2.2. Input Data
Input data for the RF algorithm was the last available version of the MCD43A4 product (v6) (
https://lpdaac.usgs.gov/dataset_discovery/MODIS/MODIS_products_table/mcd43a4_v006, last access on August 2017), based on the Schaaf [
42] BRDF inversion algorithm. This product combines the observations from Terra and Aqua satellites and daily provides 500 m MODIS BRDF corrected reflectances in bands 1 to 7 (covering the visible to the SWIR spectrum:
Table 1). The current version of the product includes daily images, where the corrected reflectance corresponds to the BRDF inversion of a moving 16-day period, including only cloud-free observations. The date of the product is centered upon the retrieval period. We used full inversion and magnitude inversion pixel values (the latter when there are at least seven observations in the moving 16-day window), which correspond to quality values 0, 1, and 2. We followed a conservative approach to avoid losing too many observations in cloudy or poorly observed areas [
43].
In addition to the reflectance bands, the following spectral indices were computed as inputs to the training phase.
Soil Adjusted Vegetation Index (SAVI): Designed to improve the sensitivity of the vegetation index to the contribution of soil reflectance [
44], and computed as:
where
is band 2 and
is band 1 from MODIS. L is 0.5 [
45]. SAVI has been used in burned land mapping by several authors, as it improves the discriminability of BA in sparsely vegetated areas [
46,
47,
48].
Global Environmental Monitoring Index (GEMI): This index was developed by Pinty and Verstraete [
49] as a more global index of vegetation activity than NDVI. Being a non-linear index, several studies have found it more sensitive to low reflectances in the R/NIR space. For this reason, it has also proven more appropriate than NDVI for burned area detection [
47,
50]:
With the same meaning as (1).
Normalized Burn Ratio (NBR): First proposed by Lopez and Caselles [
51], and widely used for analyzing burn severity [
52,
53]:
For our analysis, and are MODIS bands 2 and 7.
Normalized difference water index (NDWI): This has the following structure:
It was originally designed for water content estimation [
54], and it has been shown to be closely related to fuel moisture content [
55], and is therefore associated with short-term fire impacts (reduction of leaf water caused by fire heat [
56]). The index variables have the same meaning as NBR, but using the MODIS bands 5 and 6 for the SWIR channels.
Visible Atmospherically Resistant Index (VARI): Designed by Gitelson [
57] for agricultural purposes, but has since been used in several fire-related studies, particularly to improve detection of chlorophyll changes as a result of fire [
58]:
where
is band 4,
is band 3 and
is band 1 from MODIS.
Enhanced vegetation index (EVI): this has proven more sensitive than NDVI for monitoring densely vegetated areas and reducing atmospheric effects [
45]:
where
is band 2,
is band 3, and
is band 1 from MODIS. This index was included as a more sensitive and robust estimation of pre-fire vegetation conditions than the standard NDVI, but it has also been successfully tested in post-fire regeneration analysis [
59].
Mid-Infrared Burnt Index (MIRBI): Designed by Trigg [
41] to estimate burning impacts in South Africa, and later successfully used for BA classification in other ecosystems [
60].
where
and
are reflectances of band 6 and band 7, respectively.
In addition to reflectance and spectral indices, we also used the MODIS thermal anomalies product (MCD14ML version 5.1), which provides daily and global information on hotspots (HS). Most of these are active fires, and therefore are very useful for discriminating burned patches from other land-cover changes. Since the thermal contrast of fires with the background is much higher than the reflectance change caused by the burned signal, HS information has been widely used in BA algorithms [
61,
62], particularly at a global scale [
19,
21]. For this research, we created an auxiliary variable with the distances from each pixel to the closest HS. To compute this distance, we also considered HS located in the surrounding margins of the Landsat sampled scenes (up to 50 km outside), to avoid artifacts created by border effects.
We included auxiliary data in the training phase that could help to adapt the RF models to regional BA conditions, and had been related to fire occurrence in previous studies: elevation, biomes and continental regions [
63,
64]. We imported elevation data from the Global multi-resolution terrain elevation data 2010 (GMTED2010) [
65]. Slopes and aspect were calculated using formulas proposed by Burrough [
66]. Land cover information was obtained from the Land Cover CCI project, which provides global LC information at 300 m resolution in three different epochs: 2000, 2005, 2010 [
67]. This variable was produced from ENVISAT-MERIS images, and follows the standard FAO classification system [
68]. We used only the 2005 epoch, as it was the closest pre-fire period to the training and test series used in this research. Ecosystem variation was considered through the Olson biomes map [
69], which divides the world into 16 regions on the basis of their geology, climate and evolutionary history. We also incorporated the continental regions defined for the Global Fire Emission Database (GFED), which have previously been used to quantify fire effects, into the input database [
18].
2.3. Training Phase
The RF models are built from iterative generations of decision trees, using a random sub-dataset of the input data for each one [
23]. Those trees are later used to classify the target area, where each pixel is generally assigned to the category with maximum number of single-tree assignments. The user, depending on data complexity, decides the number of trees. A similar amount of input data is sampled in each random selection. Each of these samples is divided into two groups: a training set, composed by two-thirds of the sampled data; and a validation set (named Out of bag, OOB), which is used to validate the decision tree generated in each step (OOB error). Each decision tree is built with a randomly selected group of attributes (M parameter). To create a decision tree, the algorithm looks for the best data partition [
70] using the randomly selected attributes. The quality of the training phase is estimated from the average OOB error [
71]. When the training phase is over, every case in the training set is classified from the ensemble of all decision trees previously generated, assigning it to the category with the majority of assignments.
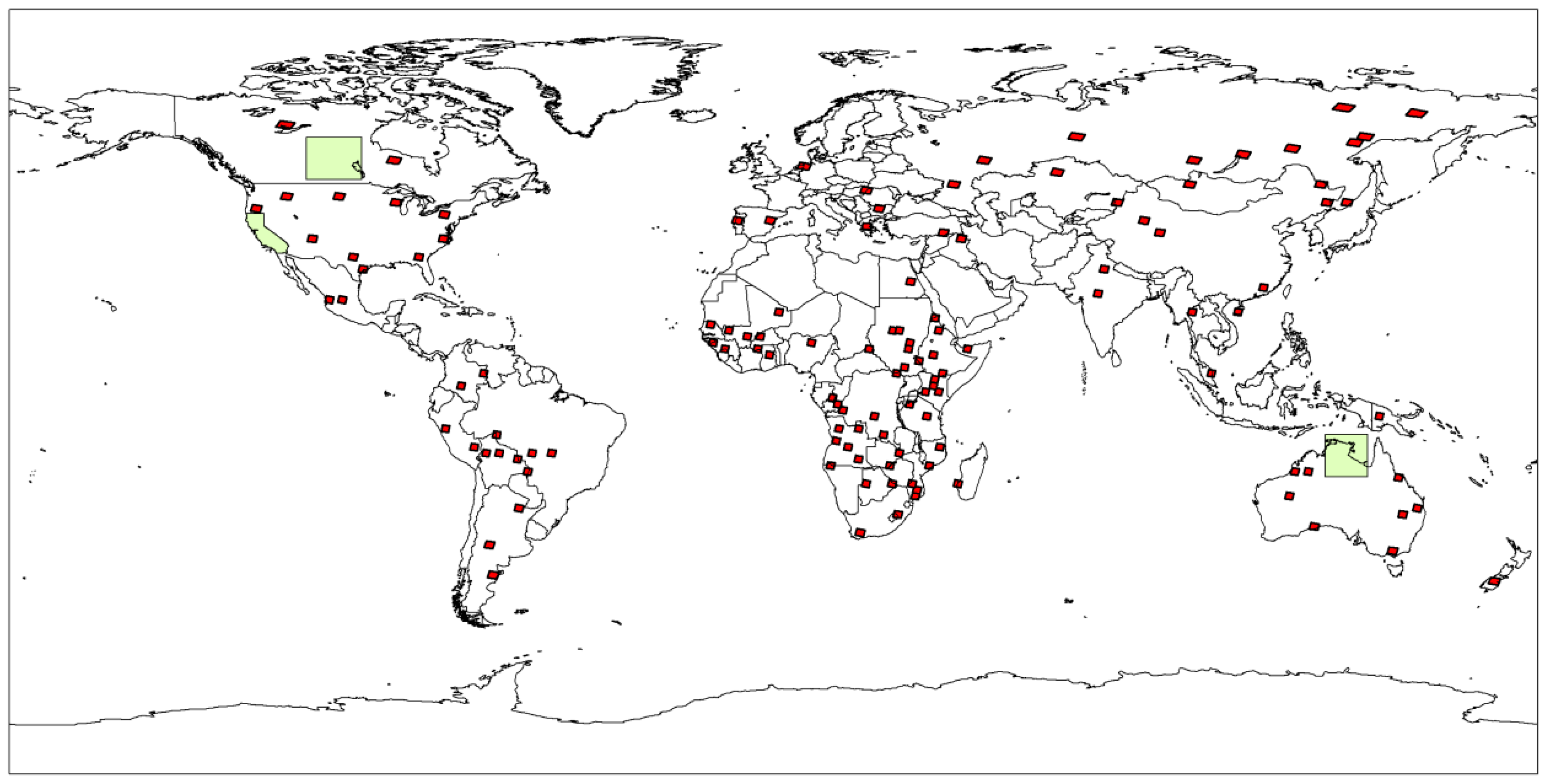
In order to take into account a great variety of burning conditions, the training phase was based on a statistically designed global sample of BA perimeters. This sample was originally generated within the Fire_cci project to validate a global BA product [
72]. More specifically, 130 sites were selected using two-stage stratified random sampling. The first stratification level was based on the Olson biomes (seven classes), and the second one on the BA extent in 2008 (high and low), provided by the Global Fire Emissions Database (GFED) version 3 [
18,
19]. The global distribution of the sampled sites is illustrated in
Figure 2. Each site covers approximately the area of a Landsat scene.
Reference burned perimeters were extracted from Landsat multitemporal images using a semi-automatic algorithm [
60], and were visually inspected by two independent interpreters to assure data quality [
72]. Unburned islands within fire perimeters were discriminated as well. All Landsat images were acquired in 2008. Derived perimeters were restricted to those burned areas occurring in between the two Landsat dates for each scene following standard CEOS Cal-Val approaches. Each burned pixel was dated with the date of the closest HS. The 130 sampled scenes included a total of 66,717 burned patches. Being developed from a statistically designed sample, the training sites can be considered a reliable estimation of fire conditions worldwide, at least for 2008; and therefore, the derived RF models should be globally applicable. The sample includes 1.58 million km
2, of which 31,578 km
2 were burned. The most extended land covers in the sample were: Rainfed cropland (10.10%); Tree cover, broadleaved, evergreen, closed to open >15% cover proportion (10.63%); Tree cover, broadleaved, deciduous, open 15–40% (5.45%); Tree cover, needleleaved, evergreen, closed to open >15% (8.54%); Shrubland (14.42%); Grassland (16.16%); Sparse vegetation (tree, shrub, herbaceous cover <15%) (6.95%); and Water bodies (5.13%).
The RF training database was created by overlapping a 500 × 500 m grid size (MODIS pixel resolution) to the Landsat scenes, computing the proportion of burned area in each cell (from 0 to 100%). Pixel size was homogenized to the 500 × 500 m spatial resolution of the MCD43A4 product. A total of 15,000 images were necessary to generate this training dataset for two reasons: (1) MODIS tiles had to be selected from all regions covered by the Landsat scenes; and (2) all MODIS daily images covering the two Landsat observations had to be processed, as the burning date of each pixel may occur anytime in between those dates. In addition, the temporal series included images acquired from at least 10 days before and 10 days after the Landsat acquisition dates, to avoid problems caused by cloud obscuration or BRDF inversion issues.
For each cell of the training dataset, the MODIS reflectances were obtained based on the most probable date of the burned perimeters. For doing so, we had first to date every burned patch. Since the Landsat images in each site were separated from 16 to 144 days, depending on the image availability (although most scenes had less than 32 days of separation between Landsat pairs [
72]), we used the date of the active fires (extracted from the MCD14 product) to label each pixel within the Landsat burned perimeters. Once the date was assigned to each 500 × 500 m cell, we extracted MODIS reflectances from the day prior to the fire (t1) and two days after the fire (t2). We did not select as t2 the day just after the fire in order to avoid the potential contamination caused by the smoke plumes. Whenever the target dates didn’t have good observations, due to either image gaps, noise, or clouds (which are removed in the MCD43A4 product), we selected alternative days within a 10-day temporal window before t1 and after t2. For non-burned pixels, the t1 reflectance was taken from the MODIS image of the first date of the Landsat multitemporal pair. The t2 reflectance was extracted from the MODIS image dated in the median day between the two Landsat images.
To reduce potential noises caused by errors in dating or the impact of previous burnings (those occurring before the first date of the Landsat pair), we introduced three filters in the training dataset. Firstly, we removed pixels labelled as burned when the NIR reflectance of the t2 image was higher than t1, as it is extremely unlikely that a burned pixel exhibits an increase in comparison to the pre-fire NIR reflectance [
73]. We tested this issue in many images, and found that all these situations corresponded to false detections. We also removed those pixels within a 3000 m radius of any HS in all images acquired 90 days before t1. This decision was intended to avoid the inclusion of pixels that were burned in previous periods as unburned pixels. Finally, those pixels with less than 80% burned area were removed as well. We applied this criterion in order for training to take place only with those pixels that were more clearly burned, avoiding pixels with a mixed signal.
Applying these rules, our final training database had a total of 6,341,570 pixels (500 × 500 m spatial resolution), including 48,365 burned pixels (0.76%) and 6,293,205 unburned. This sample size is considerably larger than most previous studies based on RF classification models [
24,
26,
28,
38,
74].
The attributes of the training database included t1 and t2 reflectances for all 7 bands of the MODIS MCD43 product, plus the spectral indices and their temporal differences (
Table 2). In addition to these, seven auxiliary variables were considered (Land Cover, Olson Biomes, GFED Regions, HS distance, Elevation, Slope, and Aspect), totaling 46 attributes for the training dataset.
2.5. Parameter Selection
Once the input attributes were selected, the next step was finding the best parameters to build the RF models. Several trainings were conducted after modifying two factors: number of trees and number of input variables [
76]. In both cases, the final selection was driven by both the accuracy and performance of the output models. In all cases, the training dataset was divided in two groups: calibration (80% of the data) and test (the remaining 20%). We selected this threshold instead of the standard 2/3 and 1/3 proportion in order to increase the number of burned pixels in the calibration, as they were a small proportion of the training sample. However, we also tested the standard proportions, with very similar accuracy values. Finally, considering the high imbalance of the training dataset, with burned areas only covering less than 1% of all training data, we performed a stratified training [
77,
78,
79], forcing to introduce in each tree at least 10% of randomly selected burned pixels. Doing this ensured that all burned pixels were included in the RF model [
80].
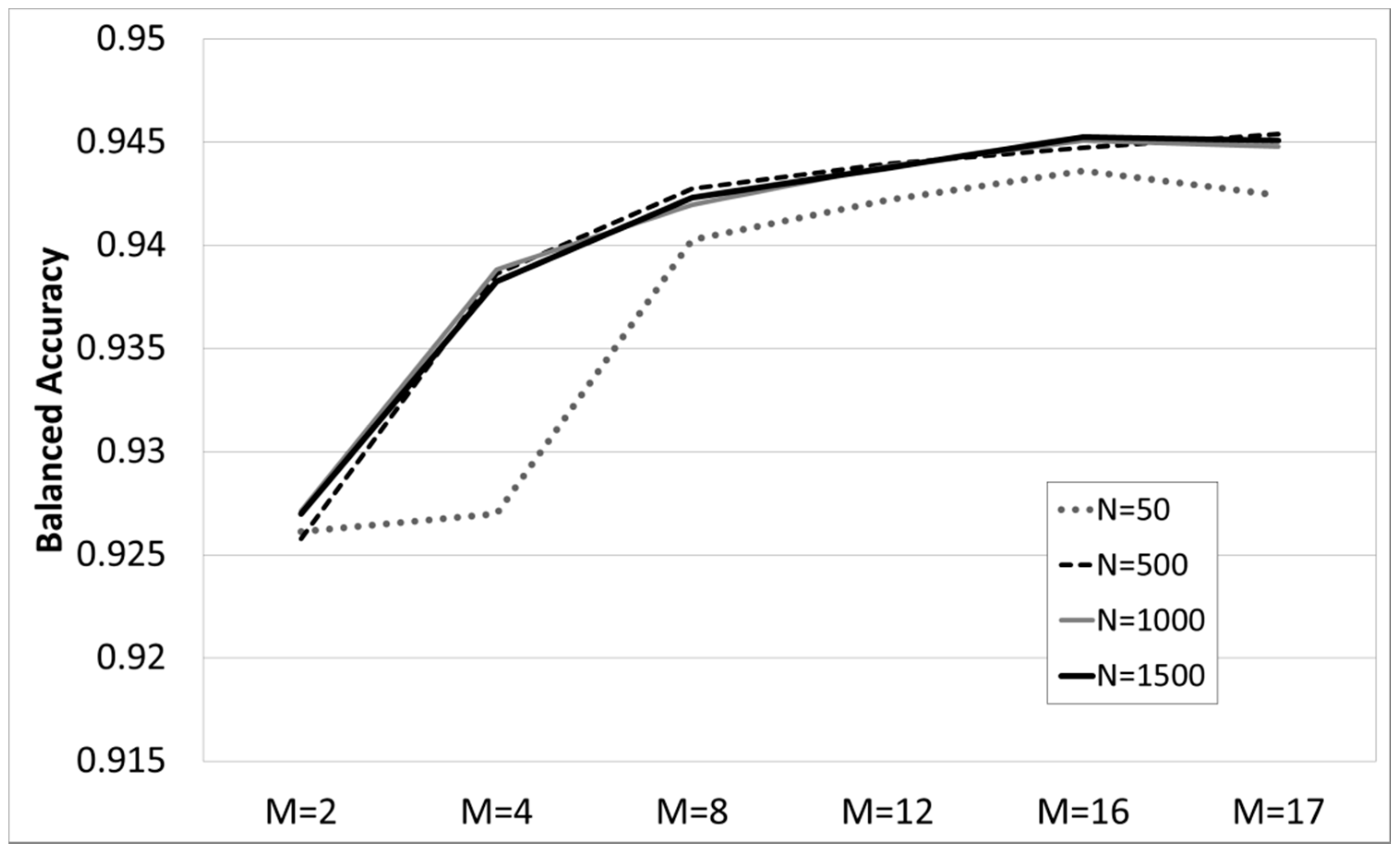
A total of 24 RF models were built. We tested combinations of four numbers of trees (N = 50, 500, 1000, 1500) and six numbers of attributes (M = 2, 4, 8, 12, 16, 17). The models were assessed by the Balanced Accuracy [
81] metric defined in (
Table 3):
In terms of performance, the literature suggests using the simplest model (less #trees and #parameters) if they provide similar accuracy to more complex ones [
28,
81].
2.8. Comparison with Existing BA Information
As a first assessment of the accuracy of the RF models, the outputs were compared with national fire perimeters and existing global BA MODIS products. Three sites were selected for comparison, as they had available reference perimeters and were representative sites of three different fire regimes (Boreal, Temperature and Tropical).
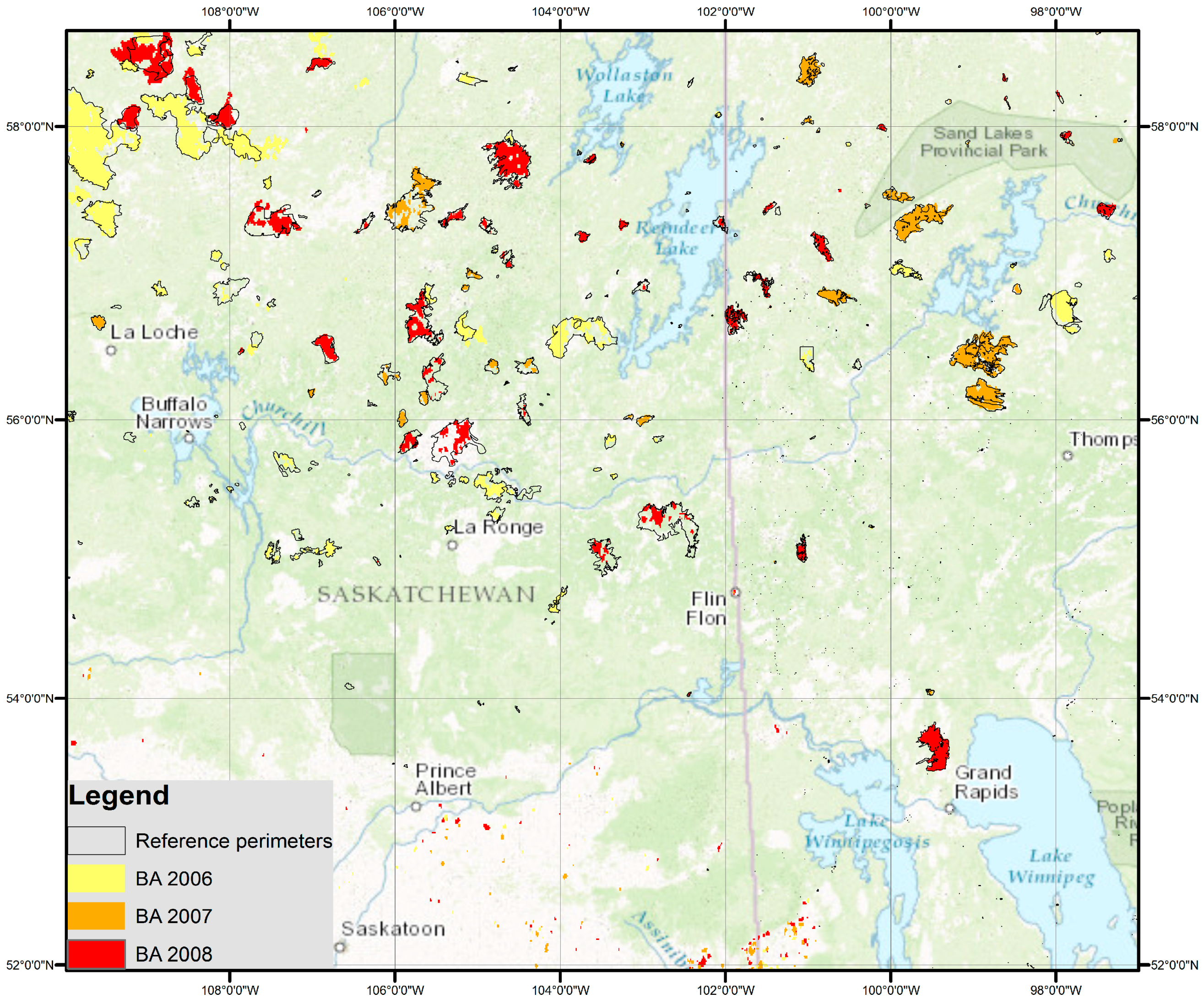
As an example of Boreal fire conditions, we selected a region of 926,167 km
2 in Canada, covering the provinces of Manitoba and Saskatchewan. Fire perimeters were downloaded from the Canadian Wildland Fire Information System (cwfis.cfs.nrcan.gc.ca/ha/nfdb/, last accessed August 2017). This system is part of the Canadian National Fire Database (CNFDB), which is a collection of fire data provided by different fire management agencies (provinces, territories, and Parks Canada), and generated by different means. The CNFDB has been extensively used for fire regime characterization studies [
82,
83,
84,
85]. Fire perimeters were reprojected to WGS84 to facilitate cross-tabulation analysis with our results.
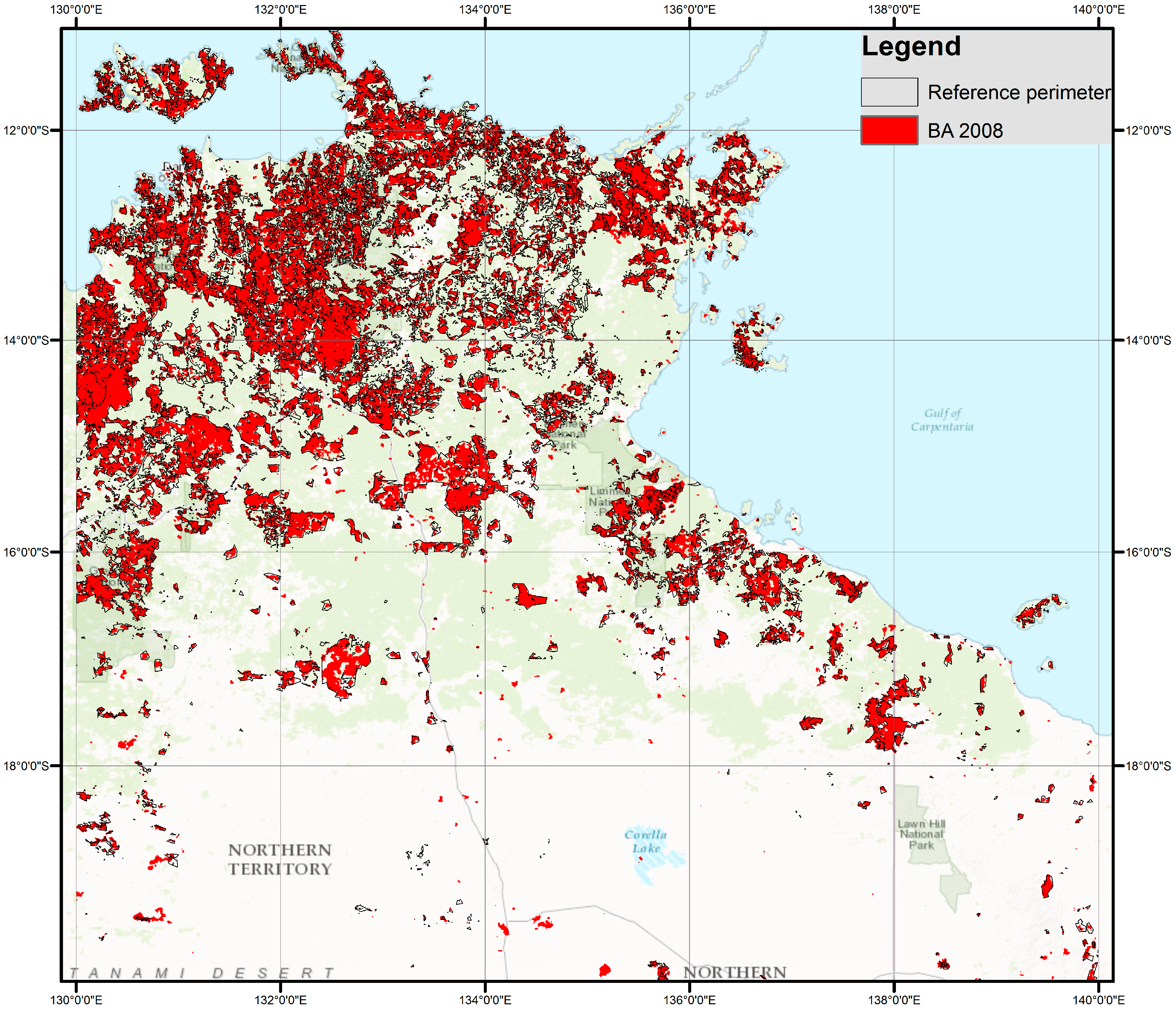
For Tropical fires, we selected a region in Northern Australia. The area embraces a region of 1,192,585 km
2 mainly covered by Savannah and Tropical forest. Fire perimeters were downloaded from the North Australian Fire Information database (
www.firenorth.org.au/nafi2/, last accessed August, 2017). Burned patches were processed by the Darwin Centre for bushfires research at Charles Darwin University (for Northern Territory fire scars) and Cape York Peninsula sustainable futures (for Queensland). They were obtained from multitemporal comparison of 250 m MODIS imagery, using segmentation and visual interpretation.
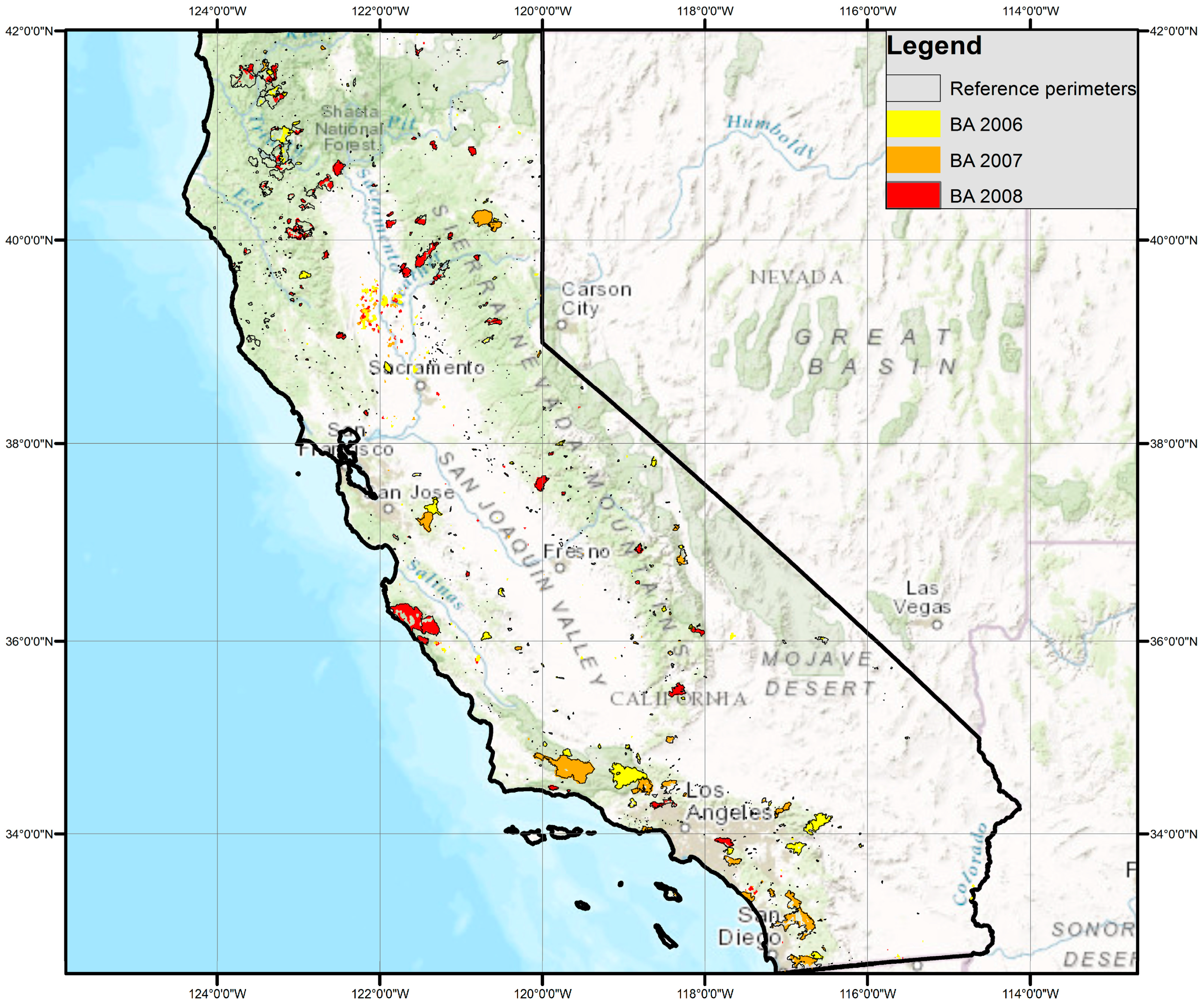
Finally, as an example of temperate fires, we selected the whole state of California (409,719 km
2). These fire perimeters were downloaded from the Fire and Resource Assessment program (FRAP) webpage (
frap.fire.ca.gov, last accessed August 2017). These were obtained by several agencies: CAL FIRE/FRAP, the USDA Forest Service Region 5 Remote Sensing Lab, the Bureau of Land Management, and the National Park Service.
The three test sites included a total area of 2,528,471km2, with the main land covers comprising Rainfed cropland (8.22%), Tree cover, needleleaved evergreen, closed to open >15% (23.84%); Shrubland (28.33%); Grassland (8.93%); Sparse vegetation <15% (tree shrub herbaceous cover, 13.96%); and Water bodies (6.87%).
In addition to comparing the RF results with these national fire perimeters, we also cross-tabulated them with the two existing MODIS BA products: the MCD45 and the MCD64 (both v5.1), to check consistency with existing BA products. It is important to emphasize that we did not run this comparison to assess the RF models, but just to check their performance and accuracy for selected areas and periods where reliable fire information was available. Comparison with fire perimeters and global BA products cannot be properly considered as a validation exercise, but it provides a first evaluation on the potential usability of our RF models for global BA mapping.
Comparison between both MODIS and RF products with reference fire perimeters was based on the generation of standard confusion matrices (same as
Table 3). Burned perimeters from the national fire services were rasterized to 500 × 500 m to facilitate comparison with BA products. Omission and commission errors, overall accuracy and error balance were computed from the confusion matrices as follows:
And error balance was computed from Relative Bias (RB) following Padilla [
86] as:
All with the same meanings as in
Table 3. RB indicates whether the BA product has a proper balance between omission and commission errors.