Sparse Weighted Constrained Energy Minimization for Accurate Remote Sensing Image Target Detection
Abstract
:1. Introduction
2. The Proposed Method
2.1. CEM Algorithm
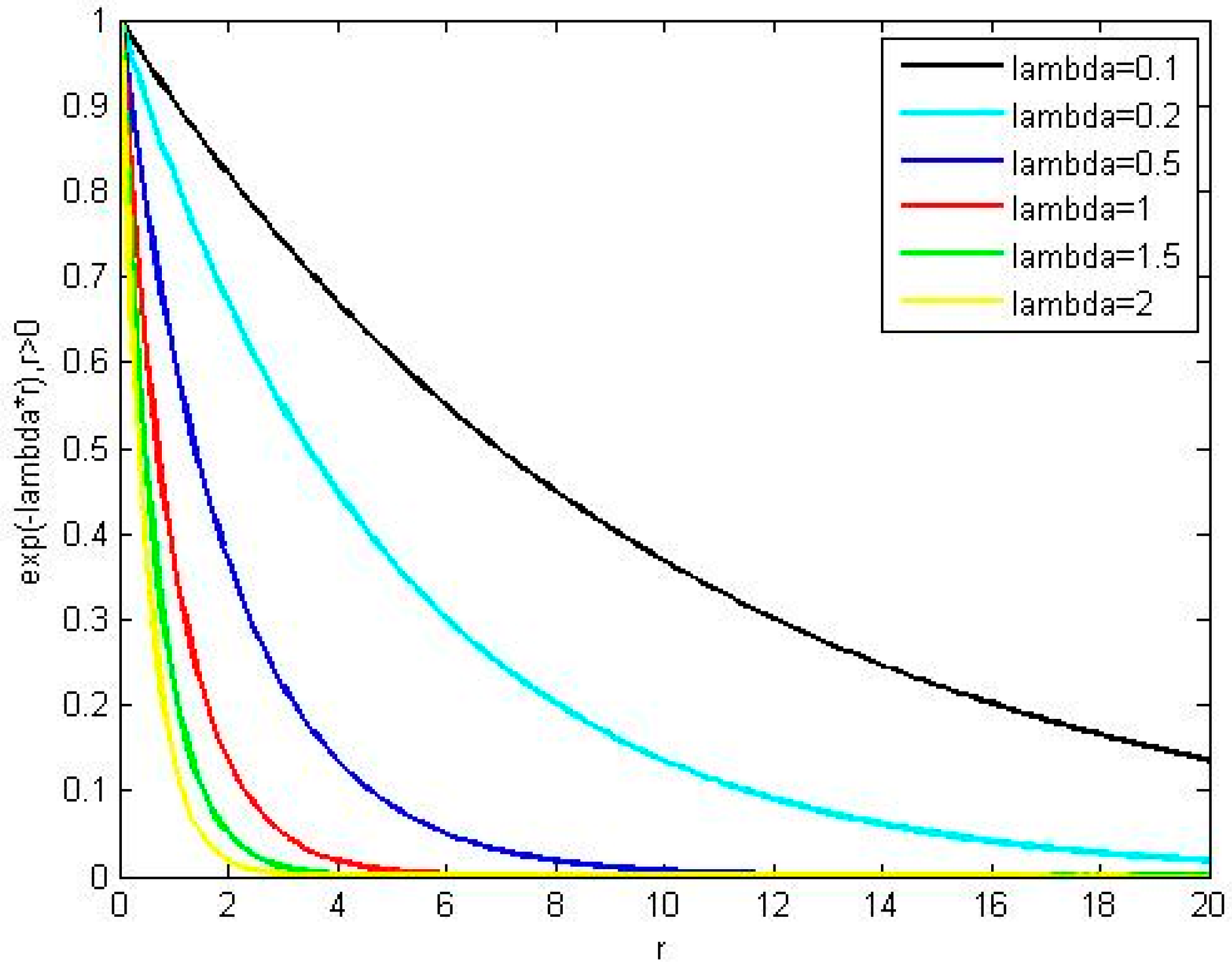
2.2. Sparse Representation Algorithm
2.3. SWCEM Algorithm
| Algorithm 1 SWCEM Algorithm | |
| Input: | |
| spectral matrix , target spectrum , target dictionary , parameter λ, sparse level δ. | |
| Sparse weighted: | |
| 1. Target dictionary : | |
| 2. Recovery residual and the weight | |
| 3. | |
| Constrained Energy Minimization: | |
| 4. Get the autocorrelation matrix: | |
| 5. | |
| 6. Solve the optimization problem: | |
| Output: | |
| 7. final output: | |
3. Results
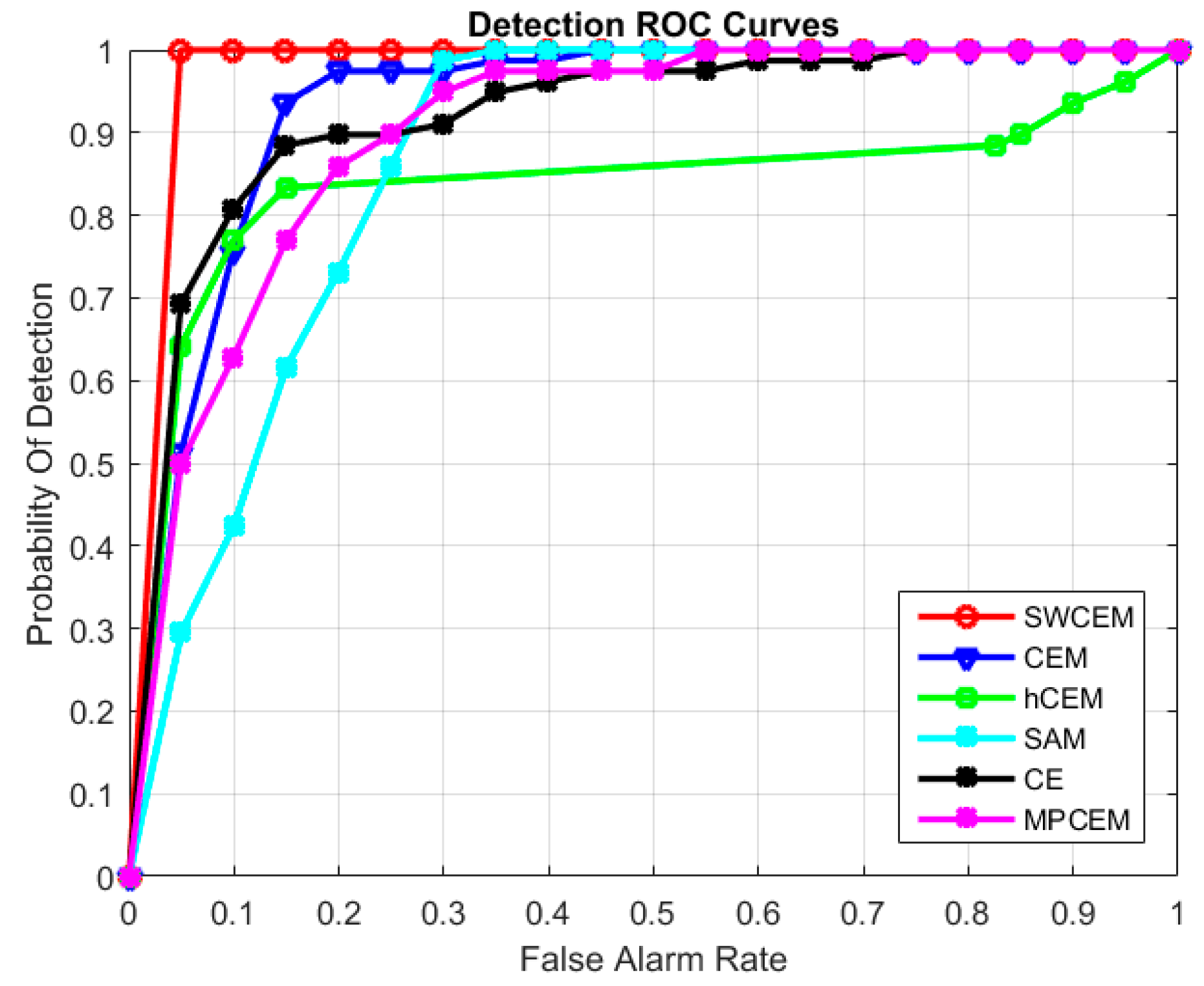
3.1. Experiment on the First Dataset
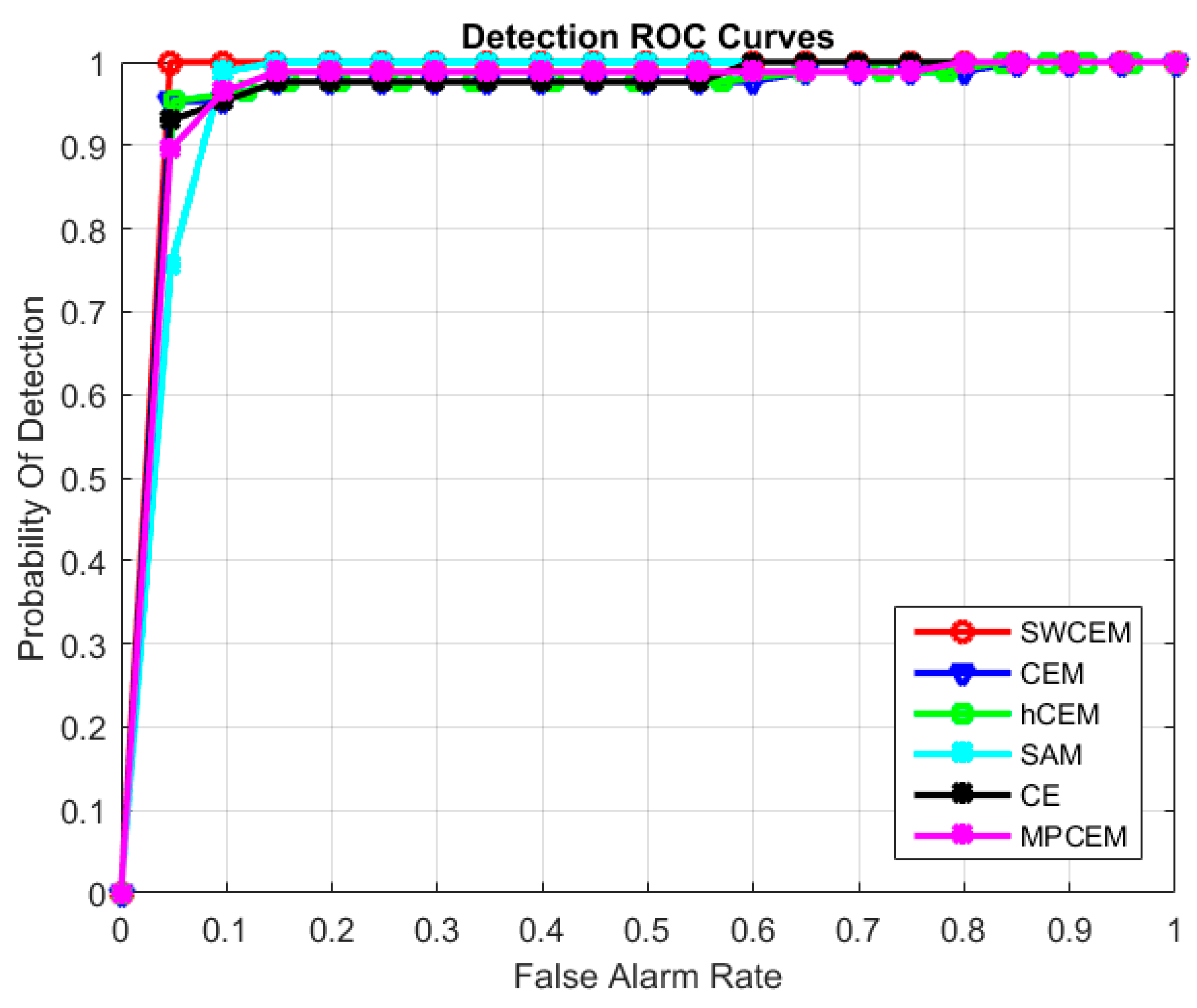
3.2. Experiment on the Second Dataset
3.3. Experiment on the Third Dataset
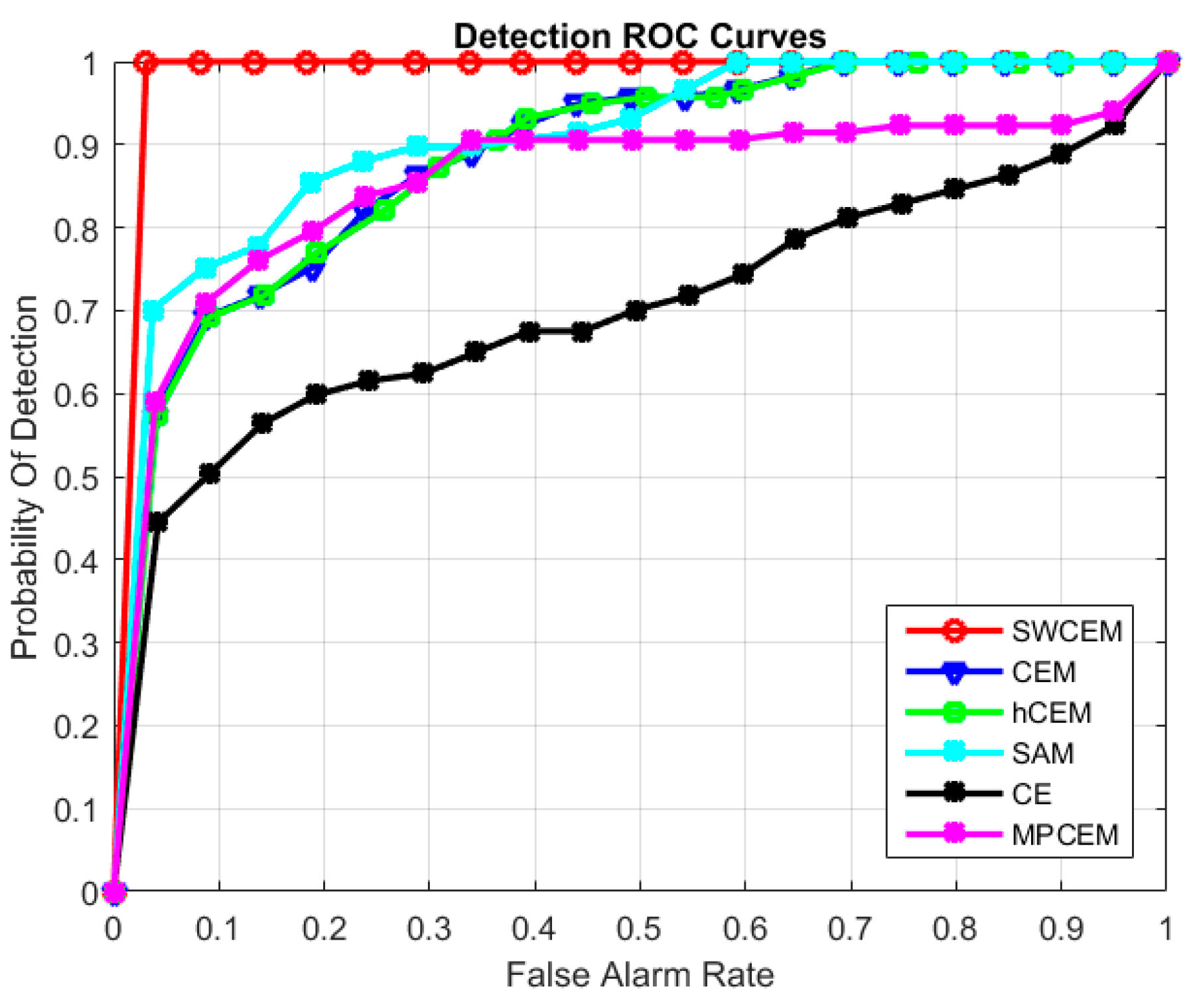
3.4. Experiment on the Fourth Dataset
4. Discussion
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Han, J.; Zhang, D.; Cheng, G. Object detection in optical remote sensing images based on weakly supervised learning and high-level feature learning. IEEE Trans. Geosci. Remote Sens. 2015, 53, 3325–3337. [Google Scholar] [CrossRef]
- Wang, Q.; Meng, Z.; Li, X. Locality Adaptive Discriminant Analysis for Spectral-Spatial Classification of Hyperspectral Images. IEEE Geosci. Remote Sens. Lett. 2017, 14, 2077–2081. [Google Scholar] [CrossRef]
- Gao, J.; Wang, Q.; Yuan, Y. Embedding structured contour and location prior in siamesed fully convolutional networks for road detection. In Proceedings of the IEEE International Conference on Robotics and Automation, Singapore, 29 May–3 June 2017; pp. 1–12. [Google Scholar]
- Wang, Q.; Gao, J.; Yuan, Y. A Joint Convolutional Neural Networks and Context Transfer for Street Scenes Labeling. IEEE Trans. Intell. Trans. Syst. 2017. [CrossRef]
- Han, J.; Zhou, P.; Zhang, D. Efficient, simultaneous detection of multi-class geospatial targets based on visual saliency modeling and discriminative learning of sparse coding. ISPRS J. Photogramm. Remote Sens. 2014, 89, 37–48. [Google Scholar] [CrossRef]
- Li, X.; Zhang, S.; Pan, X. Straight road edge detection from high-resolution remote sensing images based on the ridgelet transform with the revised parallel-beam Radon transform. Int. J. Remote Sens. 2010, 31, 5041–5059. [Google Scholar] [CrossRef]
- Liu, W.; Yamazaki, F.; Vu, T.T. Automated vehicle extraction and speed determination from QuickBird satellite images. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2011, 4, 75–82. [Google Scholar] [CrossRef]
- Karakaya, A.; Yüksel, S.E. Target detection in hyperspectral images. In Proceedings of the IEEE International Conference on Signal Processing and Communication Application, Zonguldak, Turkey, 16–19 May 2016; pp. 1501–1504. [Google Scholar]
- Manolakis, D.; Marden, D.; Shaw, G.A. Hyperspectral image processing for automatic target detection applications. Linc. Lab. J. 2003, 14, 79–116. [Google Scholar]
- Manolakis, D.; Siracusa, C.; Shaw, G. Hyperspectral subpixel target detection using the linear mixing model. IEEE Trans. Geosci. Remote Sens. 2001, 39, 1392–1409. [Google Scholar] [CrossRef]
- Kerekes, J.P.; Baum, J.E. Spectral imaging system analytical model for subpixel object detection. IEEE Trans. Geosci. Remote Sens. 2002, 40, 1088–1101. [Google Scholar] [CrossRef]
- Stefanou, M.S.; Kerekes, J.P. Image-derived prediction of spectral image utility for target detection applications. IEEE Trans. Geosci. Remote Sens. 2010, 48, 1827–1833. [Google Scholar] [CrossRef]
- Manolakis, D.; Shaw, G. Detection algorithms for hyperspectral imaging applications. IEEE Signal Process. Mag. 2002, 19, 29–43. [Google Scholar] [CrossRef]
- Manolakis, D.; Lockwood, R.; Cooley, T.; Jacobson, J. Is there a best hyperspectral detection algorithm? In Proceedings of the SPIE Defense, Security, and Sensing, Orlando, FL, USA, 13–17 March 2009. [Google Scholar]
- Robey, F.C.; Fuhrmann, D.R.; Kelly, E.J. A CFAR adaptive matched filter detector. IEEE Trans. Aerosp. Electron. Syst. 1992, 28, 208–216. [Google Scholar] [CrossRef]
- Chen, W.S.; Reed, I.S. A new CFAR detection test for radar. Digit. Signal Process. 1991, 1, 198–214. [Google Scholar] [CrossRef]
- Kruse, F.A.; Lefkoff, A.B.; Boardman, J.W. The spectral image processing system (SIPS)-interactive visualization and analysis of imaging spectrometer data. Remote Sens. Environ. 1993, 44, 145–163. [Google Scholar] [CrossRef]
- Fakiris, E.; Papatheodorou, G.; Geraga, M.; Ferentinos, G. An Automatic Target Detection Algorithm for Swath Sonar Backscatter Imagery, Using Image Texture and Independent Component Analysis. Remote Sens. 2016, 8, 373. [Google Scholar] [CrossRef]
- Wang, J.; Chang, C.I. Independent component analysis-based dimensionality reduction with applications in hyperspectral image analysis. IEEE Trans. Geosci. Remote Sens. 2006, 44, 1586–1600. [Google Scholar] [CrossRef]
- Farrand, W.H.; Harsanyi, J.C. Mapping the distribution of mine tailings in the Coeur d′Alene River Valley, Idaho, through the use of a constrained energy minimization technique. Remote Sens. Environ. 1997, 59, 64–76. [Google Scholar] [CrossRef]
- Harsanyi, J.C. Detection and Classification of Subpixel Spectral Signatures in Hyperspectral Image Sequences. Ph.D. Thesis, University of Maryland Baltimore County, Baltimore, MD, USA, 1993. [Google Scholar]
- Bidon, S.; Besson, O.; Tourneret, J.Y. The adaptive coherence estimator is the generalized likelihood ratio test for a class of heterogeneous environments. IEEE Signal Process. Lett. 2008, 15, 281–284. [Google Scholar] [CrossRef] [Green Version]
- Yang, S.; Shi, Z.; Tang, W. Robust hyperspectral image target detection using an inequality constraint. IEEE Trans. Geosci. Remote Sens. 2015, 53, 3389–3404. [Google Scholar] [CrossRef]
- Geng, X.; Yang, W.; Ji, L.; Wang, F.; Zhao, Y. The match filter (MF) is always superior to constrained energy minimization (CEM). Remote Sens. Lett. 2017, 8, 696–702. [Google Scholar] [CrossRef]
- Yang, S.; Shi, Z. SparseCEM and SparseACE for hyperspectral image target detection. IEEE Geosci. Remote Sens. Lett. 2014, 11, 2135–2139. [Google Scholar] [CrossRef]
- Zou, Z.; Shi, Z. Hierarchical suppression method for hyperspectral target detection. IEEE Trans. Geosci. Remote Sens. 2016, 54, 330–342. [Google Scholar] [CrossRef]
- Geng, X.; Ji, L.; Sun, K. Clever eye algorithm for target detection of remote sensing imagery. Isprs J. Photogramm. Remote Sens. 2016, 114, 32–39. [Google Scholar] [CrossRef]
- Wang, Y.; Huang, S.; Liu, D.; Wang, H. A Target Detection Method for Hyperspectral Imagery Based on Two-Time Detection. J. Indian Soc. Remote Sens. 2017, 45, 239–246. [Google Scholar] [CrossRef]
- Ren, H.; Du, Q.; Chang, C.I. Comparing between constrained energy minimization based approaches for hyperspectral imagery. In Proceedings of the IEEE Workshop on Advances in Techniques for Analysis of Remotely Sensed Data, Greenbelt, MD, USA, 27–28 October 2003; pp. 244–248. [Google Scholar]
- Du, Q.; Ren, H.; Chang, C.I. A study between orthogonal subspace projection and generalized likelihood ratio test in hyperspectral image analysis. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium, Toronto, ON, Canada, 24–28 June 2002. [Google Scholar]
- Harsanyi, J.C.; Chang, C.I. Hyperspectral image classification and dimensionality reduction: An orthogonal subspace projection approach. IEEE Trans. Geosci. Remote Sens. 1994, 32, 779–785. [Google Scholar] [CrossRef]
- Scharf, L.L.; Friedlander, B. Matched subspace detectors. IEEE Trans. Signal Process. 1994, 42, 2146–2157. [Google Scholar] [CrossRef]
- Sun, W.; Jiang, M.; Li, W.; Liu, Y. A Symmetric Sparse Representation Based Band Selection Method for Hyperspectral Imagery Classification. Remote Sens. 2016, 8, 238. [Google Scholar] [CrossRef]
- Zhang, Y.; Du, B.; Zhang, L. A sparse representation-based binary hypothesis model for target detection in hyperspectral images. IEEE Trans. Geosci. Remote Sens. 2015, 53, 1346–1354. [Google Scholar] [CrossRef]
- Chen, Y.; Nasrabadi, N.M.; Tran, T.D. Hyperspectral image classification using dictionary-based sparse representation. IEEE Trans. Geosci. Remote Sens. 2011, 49, 3973–3985. [Google Scholar] [CrossRef]
- Chen, Y.; Nasrabadi, N.M.; Tran, T.D. Hyperspectral image classification via kernel sparse representation. IEEE Trans. Geosci. Remote Sens. 2013, 51, 217–231. [Google Scholar] [CrossRef]
- Chen, Y.; Nasrabadi, N.M.; Tran, T.D. Simultaneous joint sparsity model for target detection in hyperspectral imagery. IEEE Geosci. Remote Sens. Lett. 2011, 8, 676–680. [Google Scholar] [CrossRef]
- Chang, C.I. Multiparameter receiver operating characteristic analysis for signal detection and classification. IEEE Sens. J. 2010, 10, 423–442. [Google Scholar] [CrossRef]
- Chen, Y.; Nasrabadi, N.M.; Tran, T.D. Sparse representation for target detection in hyperspectral imagery. IEEE J. Sel. Top. Signal Process. 2011, 5, 629–640. [Google Scholar] [CrossRef]
- Niu, Y.; Wang, B. Hyperspectral target detection using learned dictionary. IEEE Geosci. Remote Sens. Lett. 2015, 12, 1531–1535. [Google Scholar]
- Tropp, J.A.; Gilbert, A.C. Signal recovery from random measurements via orthogonal matching pursuit. IEEE Trans. Inf. Theory 2007, 53, 4655–4666. [Google Scholar] [CrossRef]
- Nocedat, J.; Wright, S.J. Numerical Optimization; Springer: New York, NY, USA, 2000. [Google Scholar]
- Peng, X.; Lu, C.; Yi, Z.; Tang, H. Connections between Nuclear-Norm and Frobenius-Norm-Based Representations. IEEE Trans. Neural Netw. Learn. Syst. 2016, PP, 1–7. [Google Scholar] [CrossRef] [PubMed]
- Peng, X.; Lu, J.; Yi, Z.; Yan, R. Automatic Subspace Learning via Principal Coefficients Embedding. IEEE Trans. Cybern. 2017, 47, 3583–3596. [Google Scholar] [CrossRef] [PubMed]
- Peng, X.; Yu, Z.; Yi, Z.; Tang, H. Constructing the L2-Graph for Robust Subspace Learning and Subspace Clustering. IEEE Trans. Cybern. 2017, 47, 1053–1066. [Google Scholar] [CrossRef] [PubMed]











| CEM | hCEM | SAM | CE | MPCEM | SWCEM | |
|---|---|---|---|---|---|---|
| AUC | 0.7937 | 0.7534 | 0.7063 | 0.8174 | 0.7741 | 0.8492 |
| CEM | hCEM | SAM | CE | MPCEM | SWCEM | |
|---|---|---|---|---|---|---|
| AUC | 0.7937 | 0.7534 | 0.7063 | 0.7957 | 0.7105 | 0.8474 |
| CEM | hCEM | SAM | CE | MPCEM | SWCEM | |
|---|---|---|---|---|---|---|
| AUC | 0.9306 | 0.8361 | 0.8709 | 0.9197 | 0.9005 | 0.9756 |
| CEM | hCEM | SAM | CE | MPCEM | SWCEM | |
|---|---|---|---|---|---|---|
| AUC | 0.9578 | 0.9571 | 0.9637 | 0.9578 | 0.9619 | 0.9765 |
| CEM | hCEM | SAM | CE | MPCEM | SWCEM | |
|---|---|---|---|---|---|---|
| AUC | 0.8847 | 0.8832 | 0.9069 | 0.7020 | 0.8541 | 0.9845 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Y.; Fan, M.; Li, J.; Cui, Z. Sparse Weighted Constrained Energy Minimization for Accurate Remote Sensing Image Target Detection. Remote Sens. 2017, 9, 1190. https://doi.org/10.3390/rs9111190
Wang Y, Fan M, Li J, Cui Z. Sparse Weighted Constrained Energy Minimization for Accurate Remote Sensing Image Target Detection. Remote Sensing. 2017; 9(11):1190. https://doi.org/10.3390/rs9111190
Chicago/Turabian StyleWang, Ying, Miao Fan, Jie Li, and Zhaobin Cui. 2017. "Sparse Weighted Constrained Energy Minimization for Accurate Remote Sensing Image Target Detection" Remote Sensing 9, no. 11: 1190. https://doi.org/10.3390/rs9111190
APA StyleWang, Y., Fan, M., Li, J., & Cui, Z. (2017). Sparse Weighted Constrained Energy Minimization for Accurate Remote Sensing Image Target Detection. Remote Sensing, 9(11), 1190. https://doi.org/10.3390/rs9111190




