Source Parameters of the 2016–2017 Central Italy Earthquake Sequence from the Sentinel-1, ALOS-2 and GPS Data
Abstract
:1. Introduction
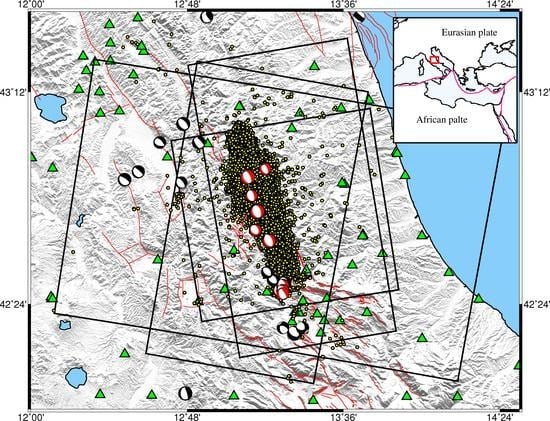
2. Tectonic Background
3. Data Overview
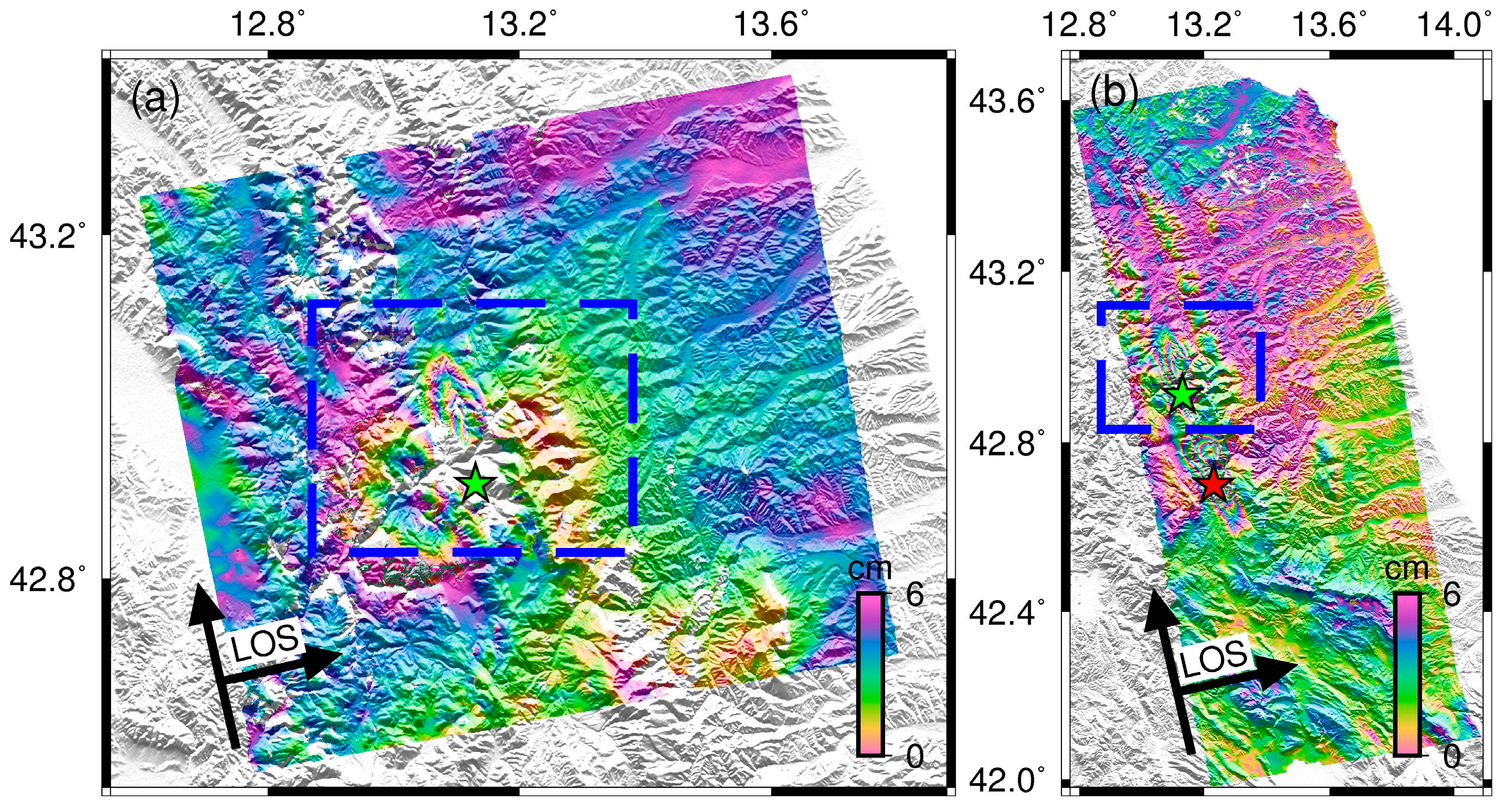
3.1. Sentinel-1 TOPS, ALOS-2 Interferograms, and GPS Data
3.2. Data Reduction and Weighting
4. Inversion
4.1. Method
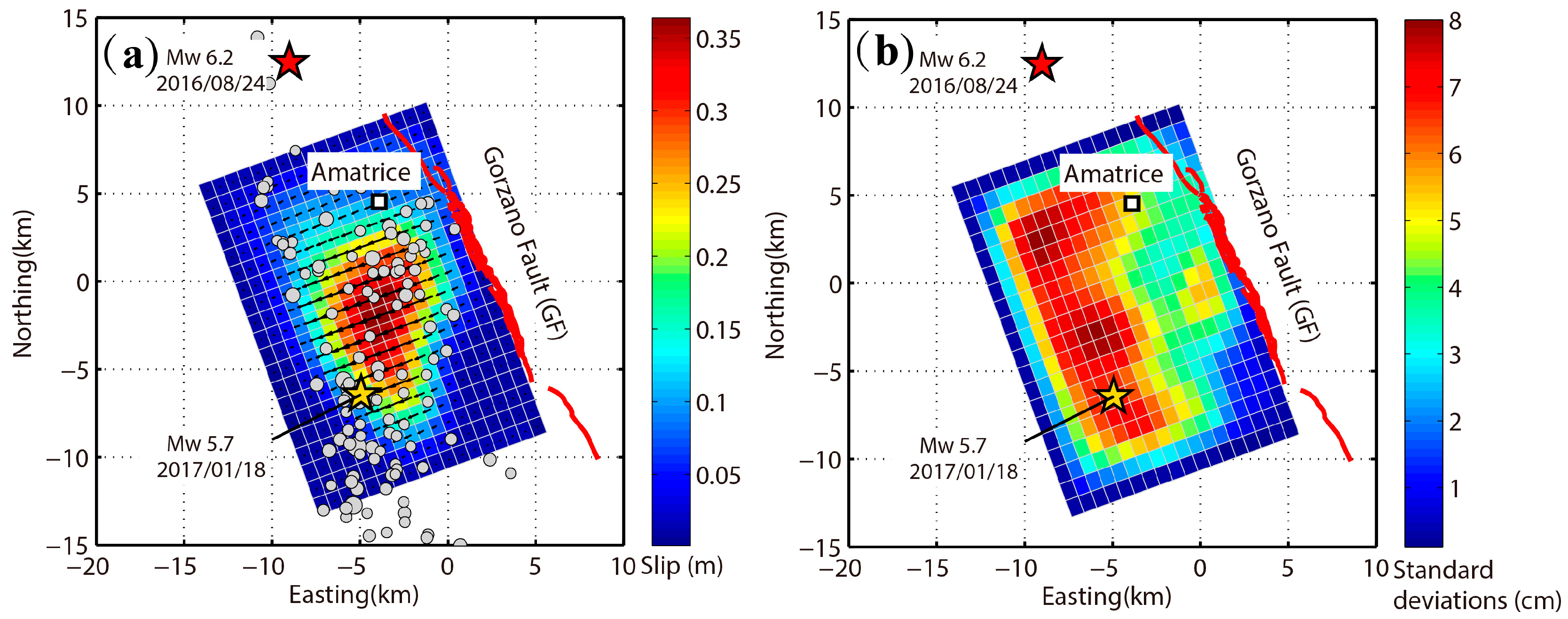
4.2. The 2016 Amatrice Earthquake
4.3. The 2016 Visso Earthquake
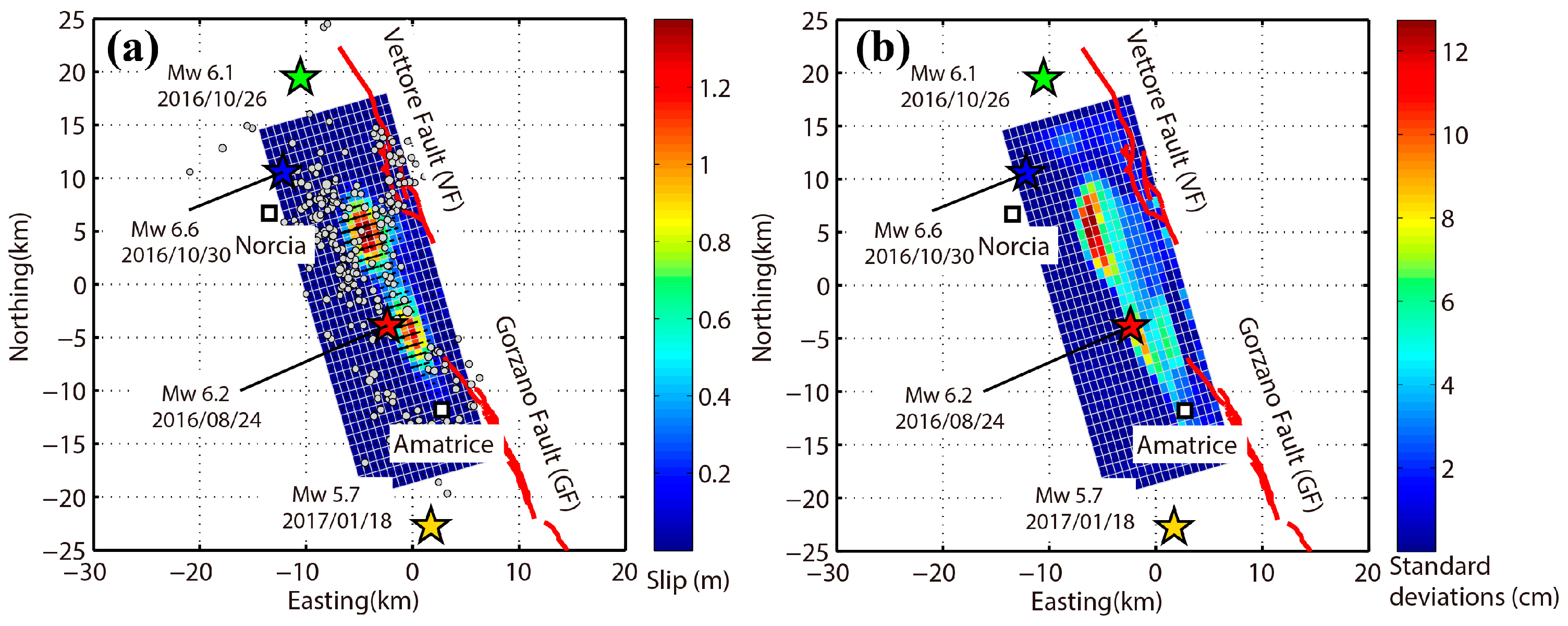
4.4. The 2016 Norcia Earthquake
4.5. The 2017 Campotosto Earthquake
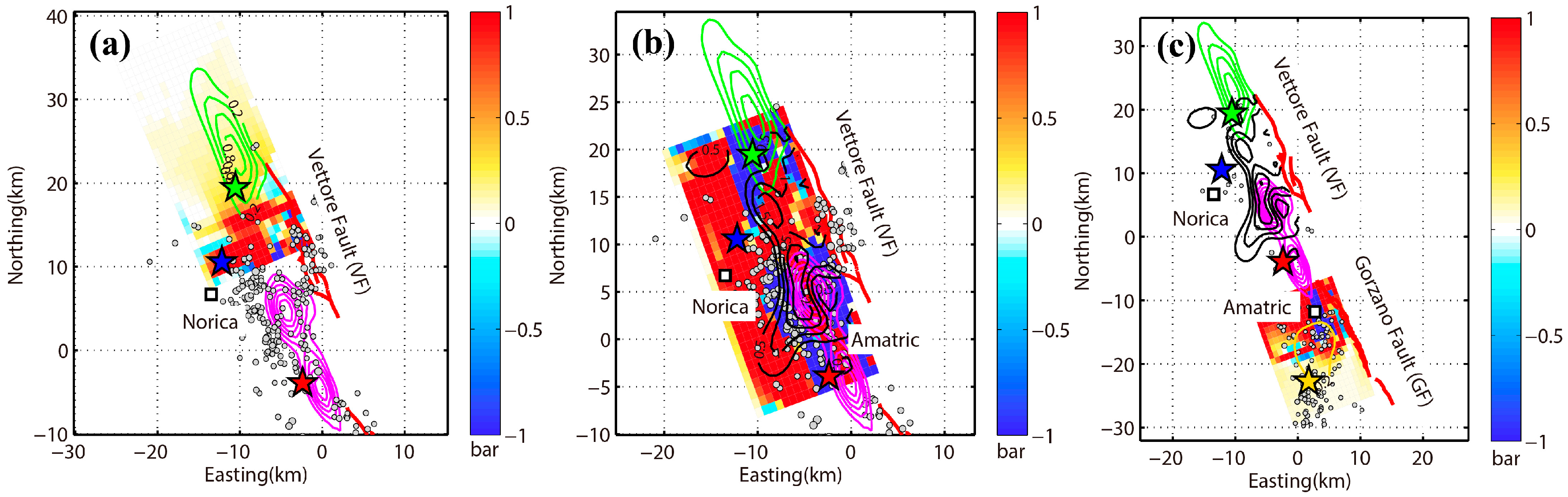
5. Static Coulomb Stress Change
6. Discussion
7. Conclusions and Outlook
Supplementary Materials
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Global Centroid Moment Tensor. Available online: http://www.globalcmt.org/CMTsearch.html (accessed on 30 June 2017).
- Tinti, E.; Scognamiglio, L.; Michelini, A.; Cocco, M. Slip heterogeneity and directivity of the ML 6.0, 2016, Amatrice earthquake estimated with rapid finite-fault inversion. Geophys. Res. Lett. 2016, 43, 10745–10752. [Google Scholar] [CrossRef]
- Liu, C.; Zheng, Y.; Xie, Z.; Xiong, X. Rupture features of the 2016 Mw 6.2 Norcia earthquake and its possible relationship with strong seismic hazards. Geophys. Res. Lett. 2017, 44, 1320–1328. [Google Scholar] [CrossRef]
- Huang, M.-H.; Fielding, E.J.; Liang, C.; Milillo, P.; Bekaert, D.; Dreger, D.; Salzer, J. Coseismic deformation and triggered landslides of the 2016 Mw 6.2 Amatrice earthquake in Italy. Geophys. Res. Lett. 2017, 44, 1266–1274. [Google Scholar] [CrossRef]
- Lavecchia, G.; Castaldo, R.; De Nardis, R.; De Novellis, V.; Ferrarini, F.; Pepe, S.; Brozzetti, F.; Solaro, G.; Cirillo, D.; Bonano, M.; et al. Ground deformation and source geometry of the 24 August 2016 Amatrice earthquake (Central Italy) investigated through analytical and numerical modeling of DInSAR measurements and structural-geological data. Geophys. Res. Lett. 2016, 43, 12389–12398. [Google Scholar] [CrossRef]
- Chiaraluce, L.; Di Stefano, R.; Tinti, E.; Scognamiglio, L.; Michele, M.; Casarotti, M.; Cattaneo, M.; De Gori, P.; Chiarabba, C.; et al. The 2016 Central Italy Seismic Sequence: A First Look at the Mainshocks, Aftershocks, and Source Models. Seismol. Res. Lett. 2017, 88, 757–771. [Google Scholar] [CrossRef]
- Cheloni, D.; De Novellis, V.; Albano, M.; Antonioli, A.; Anzidei, M.; Atzori, S.; Castaldo, R.; Casu, F.; Cecere, G.; De Luca, C.; et al. Geodetic model of the 2016 Central Italy earthquake sequence inferred from InSAR and GPS data. Geophys. Res. Lett. 2017, 44. [Google Scholar] [CrossRef]
- Xu, C.J.; Ding, K.H.; Cai, J.Q.; Grafarend, E.W. Methods of determining weight scaling factors for geodetic-geophysical joint inversion. J. Geodyn. 2009, 47, 39–46. [Google Scholar] [CrossRef]
- United States Geological Survey. Available online: https://earthquake.usgs.gov/earthquakes/eventpage/ (accessed on 30 June 2017).
- D’Agostino, N. Complete seismic release of tectonic strain and earthquake recurrence in the Apennines (Italy). Geophys. Res. Lett. 2014, 41, 1155–1162. [Google Scholar] [CrossRef]
- Galli, P.; Galadini, F.; Pantosti, D. Twenty years of paleoseismology in Italy. Earth Sci. Rev. 2008, 88, 89–117. [Google Scholar] [CrossRef]
- Institute of Geophysics and Volcanology. Available online: http://info.terremoti.ingv.it/ (accessed on 30 June 2017).
- Utsu, T. A statistical study on the occurrence of the aftershocks. Geophys. Mag. 1961, 30, 521–605. [Google Scholar]
- Wen, Y.; Xu, C.; Liu, Y.; Jiang, G. Deformation and source parameters of the 2015 Mw 6.5 earthquake in Pishan, Western China, from Sentinel-1A and ALOS-2 data. Remote Sens. 2016, 8, 134. [Google Scholar] [CrossRef]
- Torres, R.; Snoeij, P.; Geudtner, D.; Bibby, D.; Davidson, M.; Attema, E.; Potin, P.; Rommen, B.; Floury, N.; Brown, M.; et al. GMES Sentinel-1 mission. Remote Sens. Environ. 2012, 120, 9–24. [Google Scholar] [CrossRef]
- De Zan, F.; Guarnieri, A.M. TOPSAR: Terrain Observation by Progressive Scans. IEEE Trans. Geosci. Remote Sens. 2006, 44, 2352–2360. [Google Scholar] [CrossRef]
- Sandwell, D.T.; Myer, D.; Mellors, R.; Shimada, M.; Brooks, B.; Foster, J. Accuracy and resolution of ALOS interferometry: Vector deformation maps of the Father’s Day intrusion at Kilauea. IEEE Trans. Geosci. Remote Sens. 2008, 46, 3524–3534. [Google Scholar] [CrossRef]
- Werner, C.; Wegmüller, U.; Strozzi, T.; Wiesmann, A. GAMMA SAR and interferometric processing software. In Proceedings of the ERS ENVISAT Symposium, Gothenburg, Sweden, 16–20 October 2001. [Google Scholar]
- González, P.J.; Bagnardi, M.; Hooper, A.J.; Larsen, Y.; Marinkovic, P.; Samsonov, S.V.; Wright, T.J. The 2014–2015 eruption of Fogo volcano: Geodetic modeling of Sentinel-1 TOPS interferometry. Geophys. Res. Lett. 2015, 42, 9239–9246. [Google Scholar] [CrossRef]
- Scheiber, R.; Moreira, A. Coregistration of interferometric SAR images using spectral diversity. IEEE Trans. Geosci. Remote Sens. 2000, 38, 2179–2191. [Google Scholar] [CrossRef]
- Farr, T.; Rosen, P.; Caro, E. The shuttle radar topography mission. Rev. Geophys. 2000, 45, 37–55. [Google Scholar] [CrossRef]
- Goldstein, R.; Werner, C. Radar interferogram filtering for geophysical applications. Geophys. Res. Lett. 1998, 25, 4035–4038. [Google Scholar] [CrossRef]
- Goldstein, R.; Zebker, H.; Werner, C. Satellite radar interferometry: Two-dimensional phase unwrapping. Radio Sci. 1988, 23, 713–720. [Google Scholar] [CrossRef]
- INGV Ring Working Group, Rete Integrata Nazionale GPS. Available online: http://ring.gm.ingv.it (accessed on 30 June 2017).
- Nevada Geodetic Laboratory. Available online: http://geodesy.unr.edu (accessed on 30 June 2017).
- Lohman, R.B.; Simons, M. Some thoughts on the use of InSAR data to constrain models of surface deformation: Noise structure and data downsampling. Geochem. Geophys. Geosyst. 2005, 6, 359–361. [Google Scholar] [CrossRef]
- Okada, Y. Surface deformation due to shear and tensile faults in a half-space. Bull. Seismol. Soc. Am. 1985, 75, 1135–1154. [Google Scholar]
- Feng, W.; Li, Z.; Elliott, J.R.; Fukushima, Y.; Hoey, T.; Singleton, A.; Cook, R.; Xu, Z. The 2011 MW 6.8 Burma earthquake: Fault constraints provided by multiple SAR techniques. Geophys. J. Int. 2013, 195, 650–660. [Google Scholar] [CrossRef]
- Toda, S.; Stein, R.S.; Richards-Dinger, K.; Bozkurt, S. Forecasting the evolution of seismicity in southern California: Animations built on earthquake stress transfer. J. Geophys. Res. 2005, 110, 361–368. [Google Scholar] [CrossRef]
- King, G.C.P.; Stein, R.S.; Lin, J. Static stress changes and the triggering of earthquakes. Bull. Seismol. Soc. Am. 1994, 84, 935–953. [Google Scholar]
- Stein, R.S. The role of stress transfer in earthquake occurrence. Nature 1999, 402, 605–609. [Google Scholar] [CrossRef]
- Ziv, A.; Rubin, A.M. Static stress transfer and earthquake triggering: No lower threshold in sight? J. Geophys. Res. 2000, 105, 13631–13642. [Google Scholar] [CrossRef]
- Papadopoulos, G.A.; Ganas, A.; Agalos, A.; Papageorgiou, A.; Triantafyllou, I.; Kontoes, C.; Papoutsis, I.; Diakogianni, G. Earthquake Triggering Inferred from Rupture Histories, DInSAR Ground Deformation and Stress-Transfer Modelling: The Case of Central Italy During August 2016–January 2017. Pure Appl. Geophys. 2017, 174, 3689–3711. [Google Scholar] [CrossRef]
- Jiang, G.; Wen, Y.; Liu, Y.; Xu, X.; Fang, L.; Chen, G.; Gong, M.; Xu, C. Joint analysis of the 2014 Kangding, southwest China, earthquake sequence with seismicity relocation and InSAR inversion. Geophys. Res. Lett. 2015, 42, 3273–3281. [Google Scholar] [CrossRef]
- Wang, S.; Xu, C.J.; Wen, Y.M.; Yin, Z.; Jiang, G.Y.; Fang, L.H. Slip model for the 25 November 2016 Mw 6.6 Aketao earthquake, Western Chine, revealed by Sentinel-1 and ALOS-2 observations. Remote Sens. 2017, 9, 325. [Google Scholar] [CrossRef]
- Yang, Z.F.; Li, Z.W.; Zhu, J.J.; Yi, H.W.; Hu, J.; Feng, G.C. Deriving Dynamic Subsidence of Coal Mining Areas Using InSAR and Logistic Model. Remote Sens. 2017, 9, 125. [Google Scholar] [CrossRef]
- Wessel, P.; Smith, W.H.F. New, improved version of generic mapping tools released. Eos Trans. Am. Geophys. Union 1998, 79, 579. [Google Scholar] [CrossRef]
- Wessel, P.; Smith, W.H.F.; Scharroo, R.; Luis, J.; Wobbe, F. Generic Mapping Tools: Improved version released. Eos Trans. Am. Geophys. Union 2013, 94, 409–410. [Google Scholar] [CrossRef]

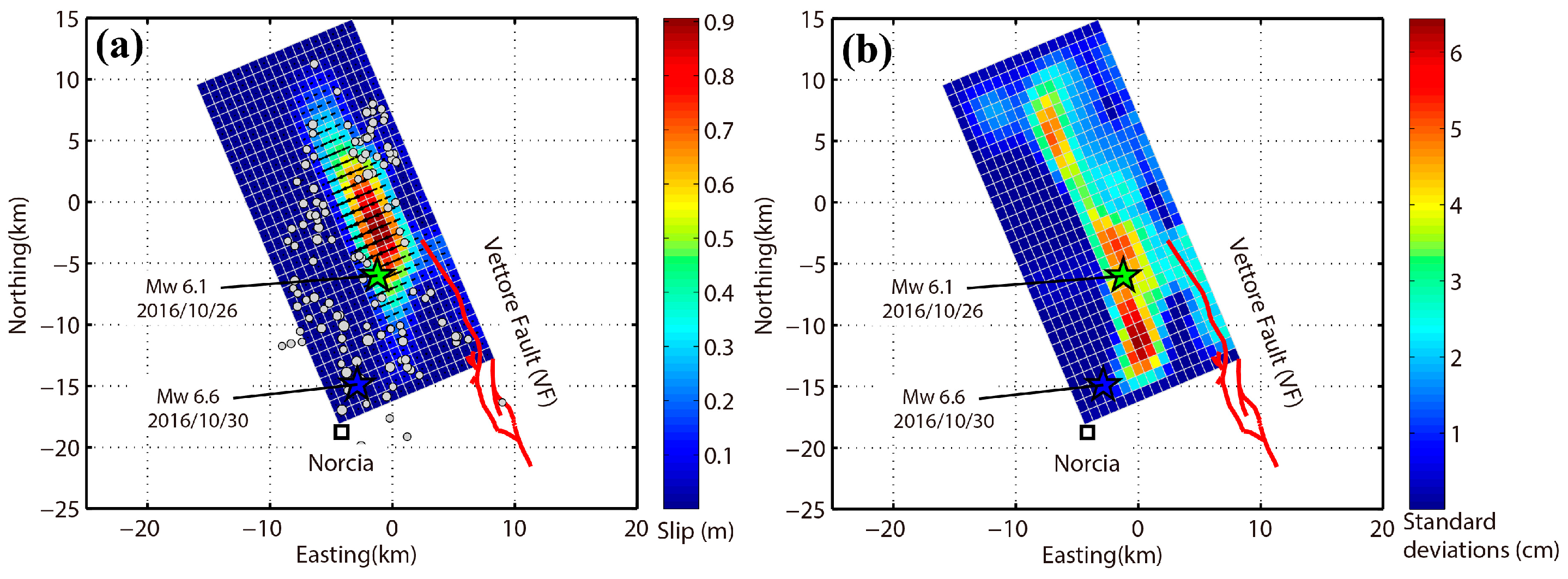
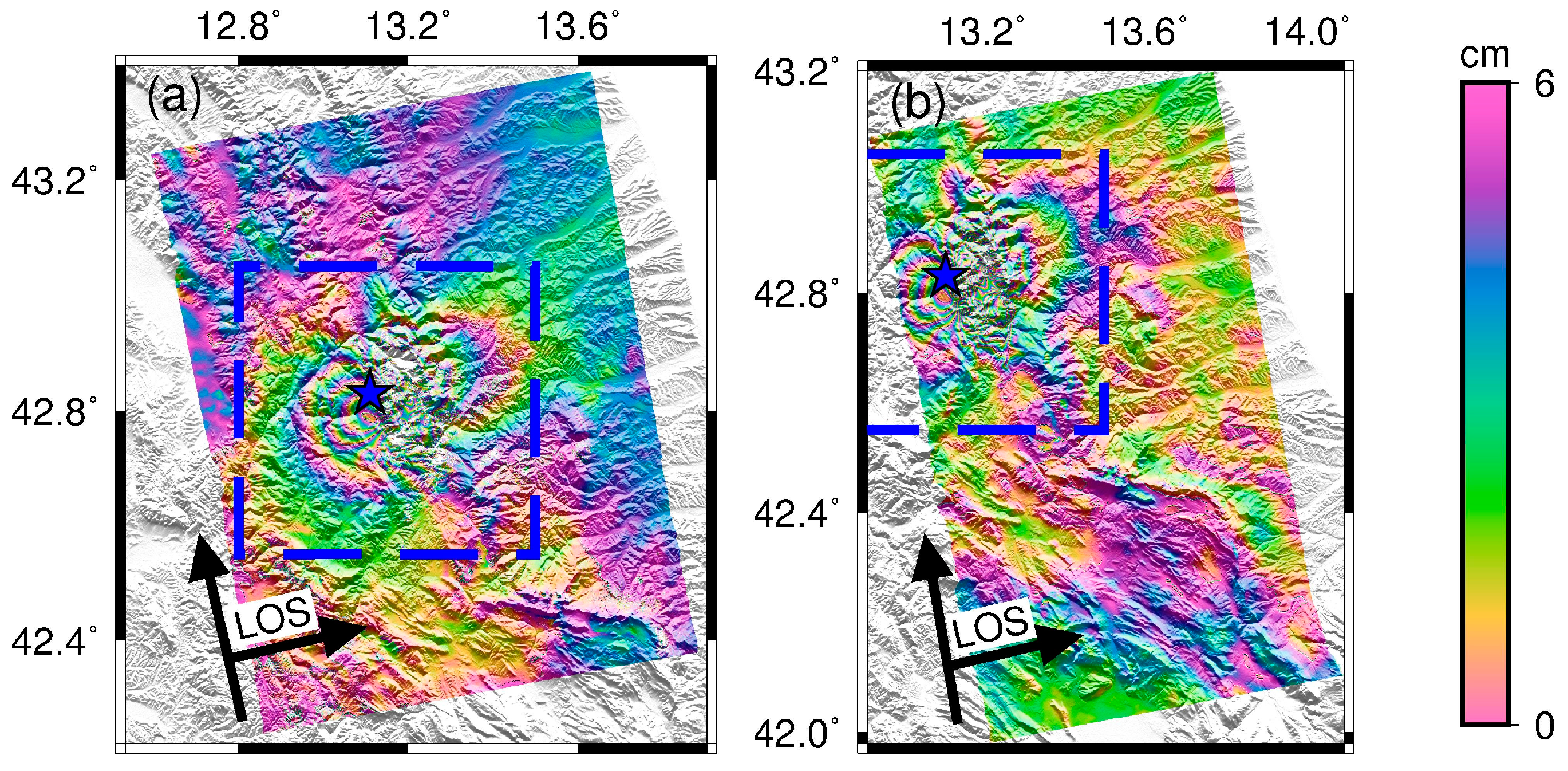
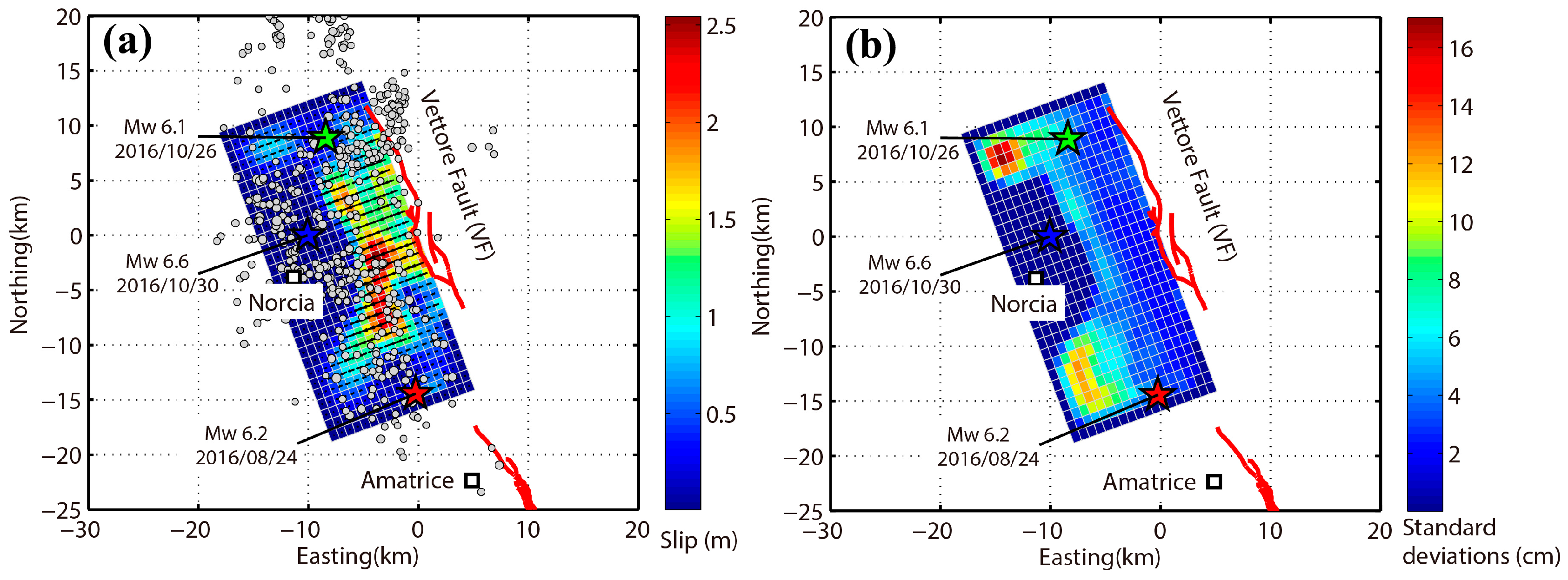
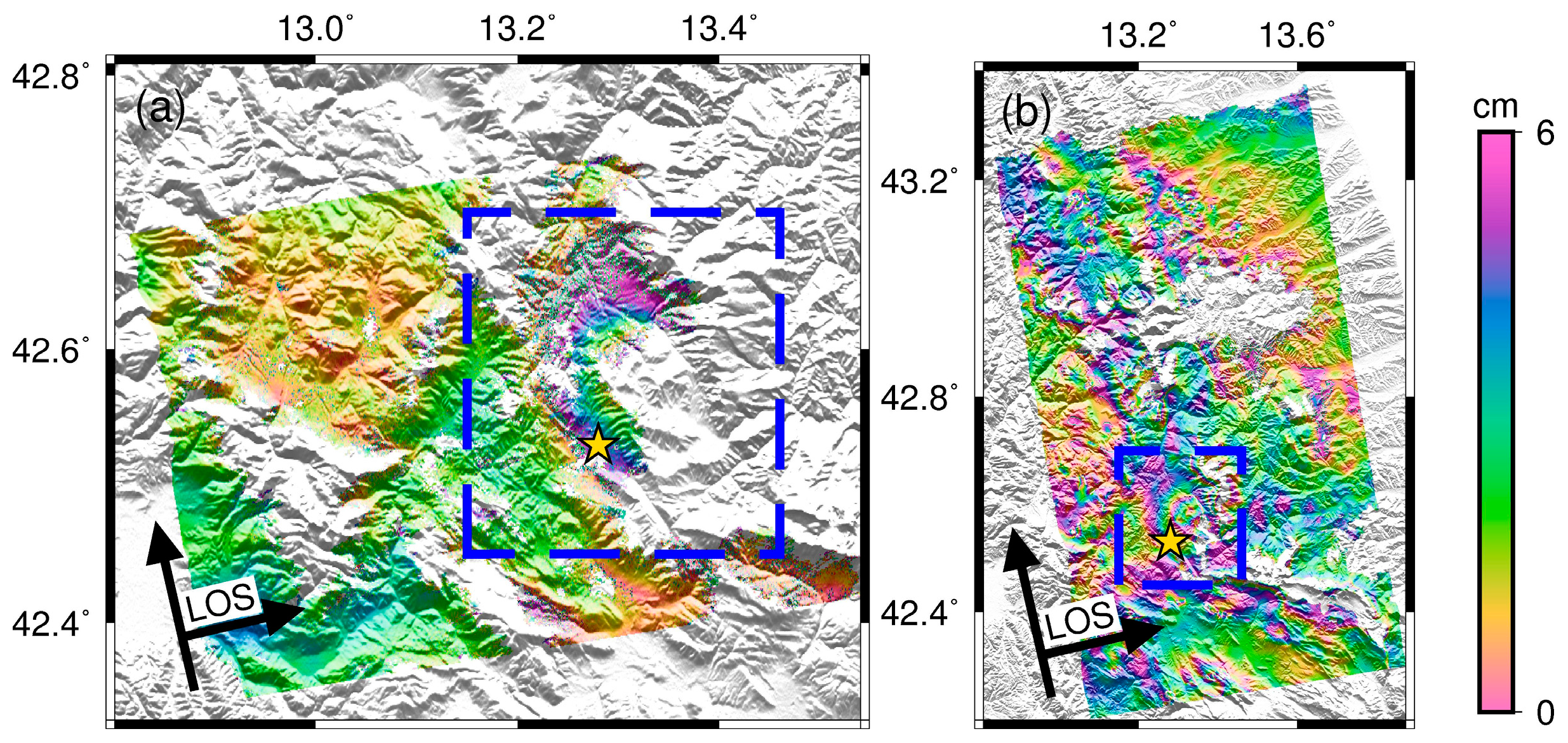

| Event * | Date | Time (GMT) | Latitude ° | Longitude ° | Magnitude Mw | Depth km |
|---|---|---|---|---|---|---|
| 2016 Amatrice earthquake (A) | 2016/08/24 | 1:36:36.2 | 42.64 | 13.22 | 6.2 | 12.0 |
| 2016/08/24 | 2:33:32.3 | 42.68 | 13.15 | 5.6 | 12.0 | |
| 2016 Visso earthquake (B) | 2016/10/26 | 17:10:39 | 42.81 | 13.13 | 5.5 | 12.0 |
| 2016/10/26 | 19:18:11 | 42.88 | 13.11 | 6.1 | 12.0 | |
| 2016 Norcia earthquake (C) | 2016/10/30 | 6:40:24.1 | 42.75 | 13.16 | 6.6 | 12.0 |
| 2016/11/01 | 7:56:43.5 | 42.91 | 13.20 | 5.0 | 12.0 | |
| 2017 Campotosto earthquake (D) | 2017/01/18 | 9:25:42.5 | 42.45 | 13.27 | 5.4 | 12.0 |
| 2017/01/18 | 10:14:12.8 | 42.47 | 13.29 | 5.7 | 12.0 | |
| 2017/01/18 | 10:25:28.4 | 42.45 | 13.29 | 5.6 | 13.1 | |
| 2017/01/18 | 13:33:39.8 | 42.44 | 13.29 | 5.3 | 18.1 |
| Satellite | Track | Pass | Master | Slave | Perp.B | Inc.Angle | Azi.Angle | † | ‡ | Events * |
|---|---|---|---|---|---|---|---|---|---|---|
| m | ° | ° | mm | km | ||||||
| Sentinel-1 | 117 | ASC | 2016/08/15 | 2016/08/27 | 32 | 43.8 | −9.3 | 9.4 | 15.3 | A |
| Sentinel-1 | 022 | DESC | 2016/08/21 | 2016/08/27 | 79 | 41.2 | −170.3 | 11.3 | 12.8 | A |
| ALOS-2 | 197 | ASC | 2015/09/09 | 2016/08/24 | −198 | 40.5 | −9.7 | 9.9 | 13.5 | A |
| ALOS-2 | 092 | DESC | 2016/05/25 | 2016/09/31 | 88 | 36.2 | −169.7 | 16.0 | 8.7 | A |
| ALOS-2 | 197 | ASC | 2016/02/05 | 2016/10/28 | −87 | 31.4 | −10.9 | 7.3 | 4.7 | A,B |
| Sentinel-1 | 044 | ASC | 2016/10/21 | 2016/10/27 | 72 | 33.7 | −10.7 | 8.2 | 32.5 | B |
| Sentinel-1 | 044 | ASC | 2016/10/27 | 2016/11/02 | 18 | 33.5 | −10.7 | 7.2 | 3.3 | C |
| ALOS-2 | 196 | ASC | 2016/01/28 | 2016/11/11 | 55 | 31.5 | −10.8 | 8.9 | 6.6 | C |
| Sentinel-1 | 117 | ASC | 2017/01/12 | 2017/01/24 | 16 | 43.7 | −9.3 | 7.4 | 3.2 | D |
| ALOS-2 | 197 | ASC | 2016/11/02 | 2017/01/25 | 55 | 40.5 | −9.7 | 18 | 8.4 | D |
| Source | Lon | Lat | Strike | Dip | Rake | Depth | Length | Width | Slip | Mw | Seismic Moment | Data |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| ° | ° | ° | ° | ° | km | km | km | m | 1018 Nm | |||
| USGS [9] | 13.188 | 42.723 | 165.0 | 49.0 | −78.0 | 4.4 | - | - | - | 6.2 | 2.45 | - |
| GCMT [1] | 13.220 | 42.640 | 145.0 | 38.0 | −101.0 | 12.0 | - | - | - | 6.2 | 2.48 | - |
| INGV [12] | 13.220 | 42.710 | 155.0 | 41.0 | −93.0 | 5.0 | - | - | - | 6.0 | 1.07 | - |
| Tinti et al. [2] | 13.230 | 42.700 | 156.0 | 50.0 | −120.0~−70.0 | 7.3 | 26.0 | 12.0 | - | 6.1 | 1.60 | strong motion accelerometers |
| Lavecchia et al. [5] | 13.250/13.220 | 42.700/42.780 | 161.0/161.0 | 52.0/42.0 | −85.0/−85.0 | 0.5/0.6 | 15.0/13.0 | 10.0/10.0 | 0.6/0.5 | 6.2 | 2.50 | SAR (S1,ALOS-2) |
| Huang et al. [4] | - | - | 167.0 | 46.0 | −73.0 | - | 39.0 | 15.0 | - | 6.2 | 1.88 | SAR (S1, ALOS-2) GPS (105 stations) |
| Liu et al. [3] | 13.234 | 42.698 | 155.0 | 46.0 | - | 4.4 | 28.8 | 16.0 | - | 6.2 | 2.30 | GPS (106 stations), strong-motion records, Teleseismic waveforms |
| Cheloni et al. [7] | - | - | - | 50.0/40.0 | - | - | - | - | - | 6.2 | 2.12 | SAR (S1, ALOS-2, CSK) GPS (58 stations) |
| Uniform slip model | 13.259 0.001 | 42.735 0.001 | 164.0 0.4 | 43.6 1.8 | −68.2 3.0 | 2.7 0.1 | 18.6 0.3 | 5.9 0.4 | 0.63 0.1 | 6.2 | 2.07 | SAR (S1, ALOS-2) GPS (128 stations) |
| Distributed slip model | 13.259 | 42.735 | 164.0 | 43.6 | −89.7 | 2.7 | 36.0 | 18.0 | 0.1 | 6.2 | 2.16 | SAR (S1, ALOS-2) GPS (128 stations) |
| Source | Lon | Lat | Strike | Dip | Rake | Depth | Length | Width | Slip | Mw | Seismic Moment | Data |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| ° | ° | ° | ° | ° | km | km | km | m | 1018 Nm | |||
| USGS [9] | 13.067 | 42.956 | 155 | 50 | −89 | 10.0 | - | - | - | 6.10 | 1.84 | - |
| GCMT [1] | 13.11 | 42.88 | 152 | 35 | −94 | 12.0 | - | - | - | 6.10 | 1.61 | - |
| INGV [12] | 13.13 | 42.91 | 159 | 47 | −93 | 8.0 | - | - | - | 5.90 | 0.738 | - |
| Chiaraluce et al. [6] | 13.14/13.10 | 42.91/42.92 | 159/159 | 47/47 | −81/−80 | 4.5/7.4 | 8.0/8.0 | 5.5/5.5 | 0.12/0.24 | 6.00 | 1.13 | strong-motion data |
| Cheloni et al. [7] | - | - | 160 | 40 | - | - | 20 | 4 | - | 6.16 | 1.97 | SAR (S1, ALOS-2) GPS |
| Uniform slip model | 13.145 0.001 | 42.964 0.001 | 157.2 1.3 | 40 fixed | −90.8 3.9 | 2.3 0.2 | 13.9 0.4 | 5.3 0.2 | 0.63 0.03 | 6.08 | 1.39 | SAR (S1) GPS (127 stations) |
| Distributed slip model | 13.145 | 42.964 | 157.2 | 40 | −89.7 | 2.3 | 30 | 18 | 0.11 | 6.14 | 1.81 | SAR (S1) GPS (127 stations) |
| Source | Lon | Lat | Strike | Dip | Rake | Depth | Length | Width | Slip | Mw | Seismic Moment | Data |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| ° | ° | ° | ° | ° | km | km | km | m | 1018 Nm | |||
| USGS [9] | 13.096 | 42.862 | 162.0 | 27.0 | −84.0 | 8.0 | - | - | - | 6.6 | 10.7 | - |
| GCMT [1] | 13.160 | 42.750 | 154.0 | 37.0 | −96.0 | 12.0 | - | - | - | 6.6 | 9.58 | - |
| INGV [12] | 13.110 | 42.830 | 151.0 | 47.0 | −89.0 | 5.0 | - | - | - | 6.5 | 7.07 | - |
| Liu et al. [3] | 13.110 | 42.840 | 155.0 | 46.0 | - | 8.0 | 32.0 | 24.0 | - | 6.6 | 10.5 | GPS (40 stations), strong-motion records |
| Chiaraluce et al. [6] | 13.110 | 42.900 | 151.0 | 47.0 | −90.0 | 9.5 | 24.0 | 8.2 | 0.42 | 6.4 | 4.43 | strong-motion data |
| Cheloni et al. [7] | - | - | 160.0 | 40.0 | - | - | 20.0 | 4.0 | - | 6.59 | 8.46 | SAR (S1, ALOS-2) GPS |
| Uniform slip model | 13.233 0.001 | 42.830 0.001 | 160.0 fixed | 39.7 0.3 | −99.4 0.8 | 0.0 7 × 10−5 | 19.9 0.4 | 10.2 0.4 | 1.29 0.02 | 6.6 | 7.85 | SAR (S1, ALOS-2) GPS (114 stations) |
| Distributed slip model | 13.233 | 42.830 | 160.0 | 39.7 | −88.8 | −0.0 | 30.0 | 18.0 | 0.55 | 6.6 | 8.97 | SAR (S1, ALOS-2) GPS (114 stations) |
| Source | Lon | Lat | Strike | Dip | Rake | Depth | Length | Width | Slip | Mw | Seismic Moment | Data |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| ° | ° | ° | ° | ° | km | km | km | m | 1018 Nm | |||
| USGS [9] | 13.227 | 42.601 | 163.0 | 55.0 | −80.0 | 7.0 | - | - | - | 5.70 | 0.509 | - |
| GCMT [1] | 13.290 | 42.470 | 152.0 | 37.0 | −100.0 | 12.0 | - | - | - | 5.70 | 0.481 | - |
| INGV [12] | 13.280 | 42.530 | 161.0 | 51.0 | −86.0 | 5.0 | - | - | - | 5.50 | 0.215 | - |
| Uniform slip model | 13.340 0.001 | 42.588 0.001 | 160.0 fixed | 40.0 fixed | −93.2 5.7 | 2.0 0.5 | 6.5 1.0 | 8.4 1.0 | 0.36 0.10 | 5.80 | 0.590 | SAR (S1, ALOS-2) GPS (4 stations) |
| Distributed slip model | 13.340 | 42.588 | 160.0 | 40.0 | −76 | 2.0 | 20.0 | 18.0 | 0.10 | 5.97 | 1.04 | SAR (S1, ALOS-2) GPS (4 stations) |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, G.; Xu, C.; Wen, Y.; Jiang, G. Source Parameters of the 2016–2017 Central Italy Earthquake Sequence from the Sentinel-1, ALOS-2 and GPS Data. Remote Sens. 2017, 9, 1182. https://doi.org/10.3390/rs9111182
Xu G, Xu C, Wen Y, Jiang G. Source Parameters of the 2016–2017 Central Italy Earthquake Sequence from the Sentinel-1, ALOS-2 and GPS Data. Remote Sensing. 2017; 9(11):1182. https://doi.org/10.3390/rs9111182
Chicago/Turabian StyleXu, Guangyu, Caijun Xu, Yangmao Wen, and Guoyan Jiang. 2017. "Source Parameters of the 2016–2017 Central Italy Earthquake Sequence from the Sentinel-1, ALOS-2 and GPS Data" Remote Sensing 9, no. 11: 1182. https://doi.org/10.3390/rs9111182
APA StyleXu, G., Xu, C., Wen, Y., & Jiang, G. (2017). Source Parameters of the 2016–2017 Central Italy Earthquake Sequence from the Sentinel-1, ALOS-2 and GPS Data. Remote Sensing, 9(11), 1182. https://doi.org/10.3390/rs9111182