1. Introduction
The Earth Radiation Budget (ERB) at the top of the atmosphere describes how the Earth gains energy from the sun, and loses energy to space through reflection of solar radiation and the emission of thermal radiation. The ERB is of fundamental importance for climate since:
- (1)
The global climate, as quantified e.g., by the global average temperature, is determined by this energy exchange.
- (2)
The solar insolation is stronger at the equator than at the poles, therefore the net ERB at the equator is positive, while it is negative at the poles. The equator to pole gradient of the ERB is the driver of the general circulation in the atmosphere and the oceans, which transports heat from the equator to the poles.
- (3)
In a climate at equilibrium the ERB terms are in balance. Climate change, as we are currently experiencing, is provoked by an ERB imbalance.
In this paper we review the efforts that have been made to measure the ERB from space, and we summarise the resultating state of our knowledge of the ERB. In
Section 2 we review the measurements of the Total Solar Irradiance (TSI). In
Section 3 we review the broadband space instruments used for the measurements of the outgoing terms of the ERB. In
Section 4 we review the ERB instuments calibration results and the state of our knowledge of the ERB imbalance. In
Section 5 we review the annual mean spatial distribution of the ERB. In
Section 6 we review the interannual variability and long-term changes of the Outgoing Longwave Radiation (OLR). In
Section 7 we discuss what has been achieved.
2. Total Solar Irradiance
The Total Solar Irradiance (TSI) quantifies the amount of solar energy that is received by the Earth. TSI is defined as the amount of solar power that reaches the Earth per unit surface perpendicular to the Sun–Earth direction at the mean Sun–Earth distance.
The first TSI measurement from space was made with the Temperature Control Flux Monitor (TCFM) on Mariner 6 and 7 by Plamondon [
1]. Continuous measurement of the TSI started with the Earth Radiation Budget (ERB) instrument on Nimbus 7 by Hickey et al. [
2]. Continuous monitoring with an ageing corrected TSI instrument started with the Active Cavity Radiomer Irradiance Monitor (ACRIM) 1 instrument on the Solar Maximum Mission (SMM) by Willson et al. [
3]. A summary of TSI space instruments is given in
Table 1.
The instruments used for the TSI measurement are electrical substitution cavity radiometers. Their core detector consists of a blackened cavity in which nearly all incident radiation flowing through a precision aperture is absorbed. The thermal effect of the absorbed optical power is measured by comparison with the thermal effect of known electrical power.
A TSI radiometer ages by exposure to solar UV radiation. For ageing correction, a backup channel is used, for which the total solar UV exposure is kept low such that the ageing of the backup channel is negligible.
Relative variations of the TSI in phase with the 11-year solar cycle of the order of 1 W/m
are now well established, as summarised by Dewitte and Nevens [
21]. Apart from these true TSI variations, differences in the absolute level above 1 W/m
are measured by different instruments indicating limitations of the absolute accuracy.
As the Sun is nearly a point source, TSI radiometers use a view-limiting mechanism to eliminate the entrance of all except direct solar radiation into the cavity.
Classical radiometers place a large view-limiting aperture in front of a small precision aperture. In this geometry, scattering and diffraction around the edges of the view-limiting aperture increase the amount of solar power flowing through the precision aperture. When this effect is underestimated it may lead to a too-high measurement of the TSI.
The Total Irradiance Monitoring (TIM) radiometers use an alternative geometry where the small precision aperture is put in front of the larger view-limiting aperture. In this geometry, scattering and diffraction around the edges of the precision aperture decrease the amount of solar power flowing through the view limiting aperture. When this effect is underestimated it may lead to a too-low measurement of the TSI.
Table 2 summarises the equivalent TSI at a solar minimum measured by three independent instruments: TIM on the Solar Radiation and Climate Experiment (SORCE) in 2003, the Differential Absolute Radiometer (DIARAD) as part of the Solar Variability Irradiance Monitor (SOVIM) in 2008 and TIM on the Total Solar Irradiance Transfer Experiment (TCTE) in 2013. We consider TIM/TCTE as more reliable than TIM/SORCE, since TIM/TCTE went through additional pre-flight characterisations as compared to TIM/SORCE. A TSI level at a solar minimum of 1362 +/− 0.9 W/m
can be derived from the combination of DIARAD/SOVIM and TIM/TCTE.
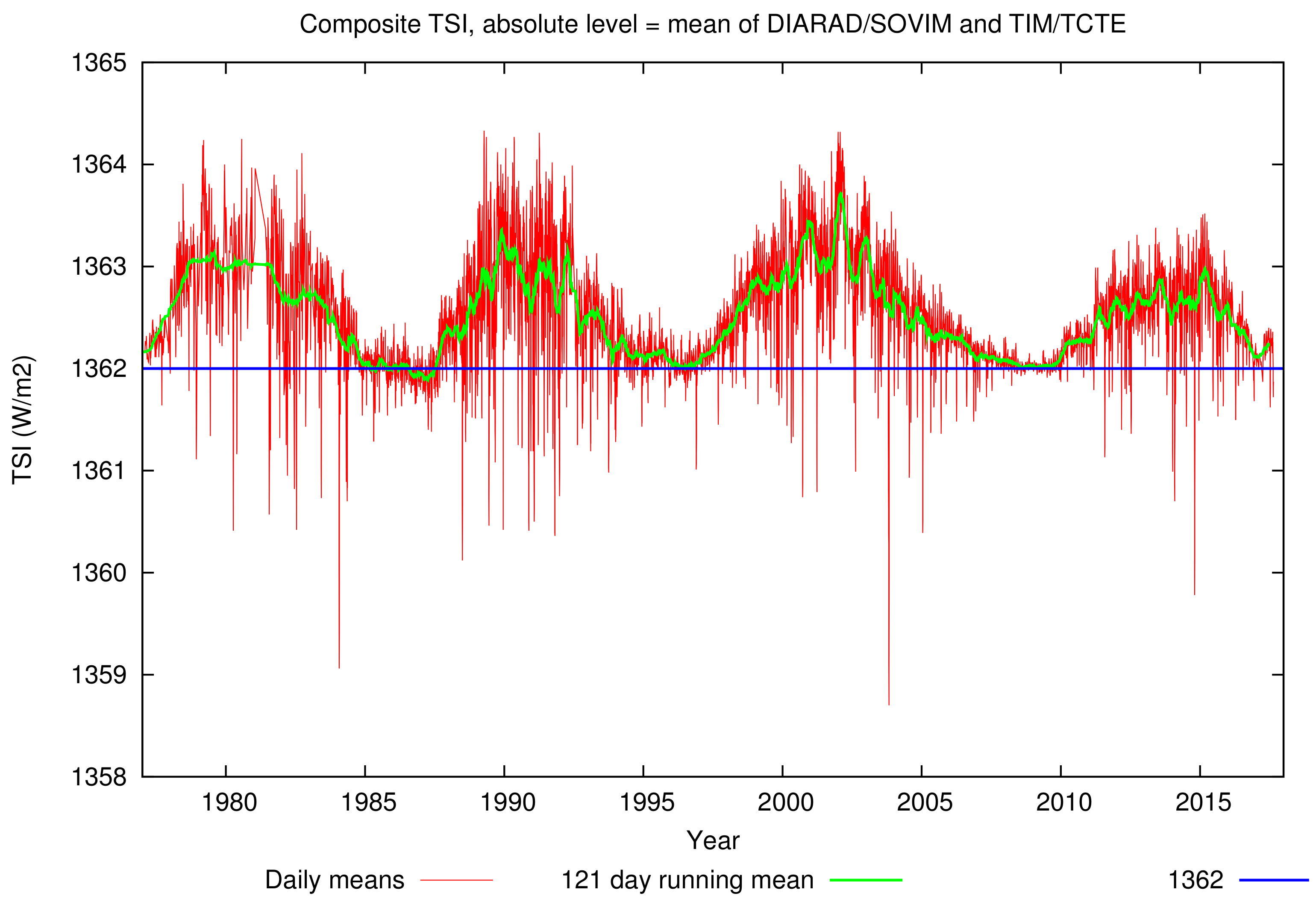
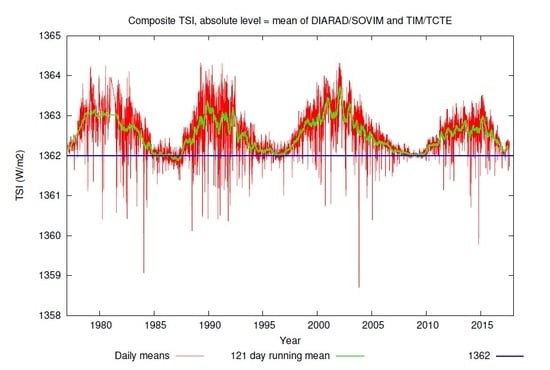
Figure 1 shows the composite TSI obtained following the methodology of Dewitte and Nevens [
21], adopting the mean level of DIARAD/SOVIM and TIM/TCTE, and with extension prior to 1984 of the TSI measurements by the Satire regression model from Ball et al. [
22] based on the Kitt Peak ground magnetograms.
3. Earth Radiation Budget Instruments
Measurement of the ERB from space started with the measurements of Explorer VI and VII in 1969, as reported by Vonder Haar and Raschke [
23]. Early measurements of the ERB have been reviewed by House et al. [
24]. Measurements with dedicated broadband instruments started on Nimbus 6 in 1975 by Jacobowitz et al. [
25]. Nimbus 6 contained two types of instruments: a Non-Scanning (NS) or Wide Field Of View (WFOV) instrument which measures the radiation of the earth from limb to limb, and a scanning Narrow Field Of View (NFOV) instrument, which measures the radiation from the Earth with higher resolution.
Table 3 lists the non-scanning ERB instruments flown in space.
Non-Scanning ERB instruments have a similar design to the TSI radiometers, e.g., the Earth Radiation Budget Experiment (ERBE) NS ERB instruments are a derivative of the ACRIM TSI radiometer (see Barkstrom and Smith [
26]). The main difference is in the opening angle which is 120
for a WFOV radiometer while it is a few degrees for a TSI radiometer. WFOV ERB radiometers measure the true radiative flux at satellite altitude. The reflected solar radiation with wavelengths shorter than 4 microns is also called ShortWave (SW) radiation. The emitted thermal radiation with wavelengths longer than 4 microns is also called LongWave (LW) radiation. A black radiometer without front window measures the total (TOT) radiation, which is the sum of the SW and the LW radiation. A SW radiometer is obtained by putting a quartz window in front of a TOT radiometer. LW radiation can be measured as TOT minus SW.
The size of the Field Of View (FOV) of a WFOV radiometer is several thousand kilometers, which prohibits, for example, the discrimination between clear sky and cloudy scenes. Higher spatial resolution is obtained with the NFOV instruments, with a spatial resolution of the order of 10 to 100 km. In order to capture the Earth’s radiation at all viewing zenith angles, these radiometers are scanning.
Table 4 lists the scanning ERB NFOV instruments flown in space on Low Earth Orbit satellites.
A NFOV instrument does not measure a flux but a radiance. To convert the radiance to a flux estimate, an Angular Dependency Model (ADM) is needed. The ADM’s used for ERBE were derived from the Nimbus 7 Scanner instrument by Suttles et al. [
36,
37]. The Clouds and the Earth’s Radiant Energy System (CERES) instruments have a rotating azimuth capability, which has been used to derive improved ADM’s by Loeb et al. [
38].
A polar satellite provides global spatial sampling, but has limited temporal sampling with only one daytime and one nighttime measurement per day for all locations but the polar regions. For a proper sampling of the diurnal cycle of the ERB, the Geostationary Earth Radiation Budget (GERB) instruments described by Harries et al. [
39] are flown on the Meteosat Second Generation (MSG) satellites described by Schmetz et al. [
40].
Table 5 lists the GERB instruments flown in space.
Nominally, the MSG satellites are located at a longitude close to 0. Since October 2016, the oldest of the MSG satllites, MSG-1 also called Meteosat-8, has been relocated to 41.5 east longitude.
4. Calibration
ERB instruments are calibrated on-ground with absolute calibration sources; typically a blackbody is used as a LW calibration source, and a lamp with an irradiance known relative to a primary standard is used as a SW calibration source. In flight, the stability of the calibration is checked or maintained using relative calibration sources.
When two ERB instruments are overlapping in time, their absolute calibration can be checked by in-flight intercomparsion of these two instruments. A compilation of the results of such intercomparisons up to 2006 was made by Smith et al. [
42]. We have completed this compilation with the results of Clerbaux et al. for Gerb-2 [
43], and Gerb-1 [
44], and Chomette et al. [
45] for the Scanning Radiometer for Radiation Balance (ScaRaB) 3.
Table 6 summarises the calibration biases of the different ERB instruments compared to the Earth Radiation Budget Satellite (ERBS) Scanner.
Combining the ERB intercomparison results from
Table 6 with the CERES data from Loeb et al. [
46], for the reference period from March 2000 to February 2005, we get a Reflected Solar Flux (RSF) of 99.6 +/− 2.7 W/m
and an OLR of 236.5 +/− 2.0 W/m
. The given uncertainties are absolute uncertainties; they are based on the observed instrument calibration differences of
Table 6. Following
Section 2, the TSI is 1362.9 +/− 0.9 W/m
. The corresponding incoming solar flux is 340.4 +/− 0.2 W/m
. The observed Earth’s Energy Imbalance (EEI) between incoming solar and outgoing terrestrial flux is then 4.3 +/− 4.9 W/m
.
An independent estimate of the EEI derived from Ocean Heat Content (OHC) of 0.9 +/− 0.3 W/m
is given in [
47]. The indirect estimate of the EEI from OHC is thus more precise than the direct radiative measurement. Following a method similar to Loeb et al. [
46], we can adjust the OLR and RSF within their observed uncertainty to make them consistent with the OHC EEI. We assume the uncertainties on the RSF and the OLR are independent and have Gaussian distributions. Then the most likely value of the RSF is 101.6 W/m
and the most likely value of the OLR is 238.0 W/m
. The corresponding Earth albedo is 29.8%.
Table 7 lists the adjustment factors by which the readings of an individual instrument have to be multiplied in order to reproduce the most likely RSF or OLR values.
5. Climatology
In this section we briefly discuss the multi-annual mean global spatial distributions of the ERB components.
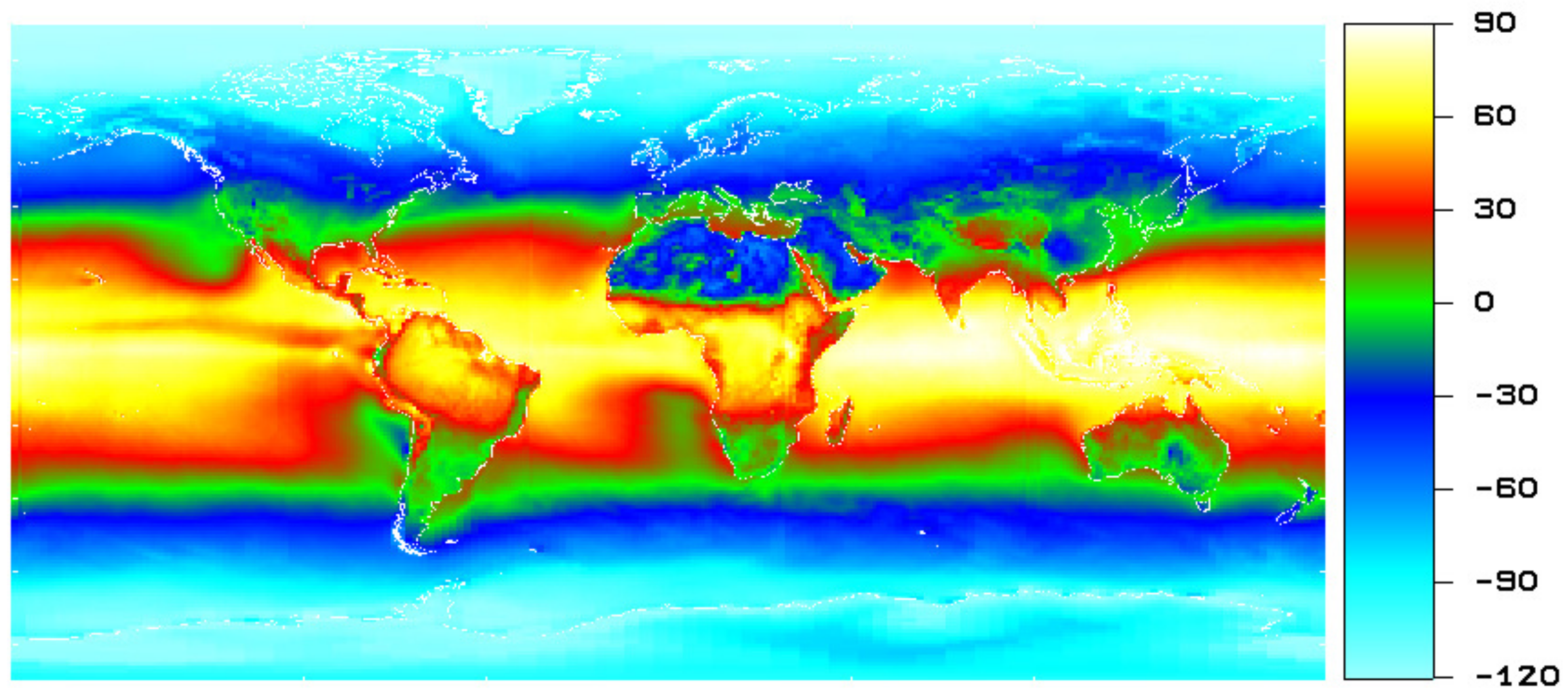
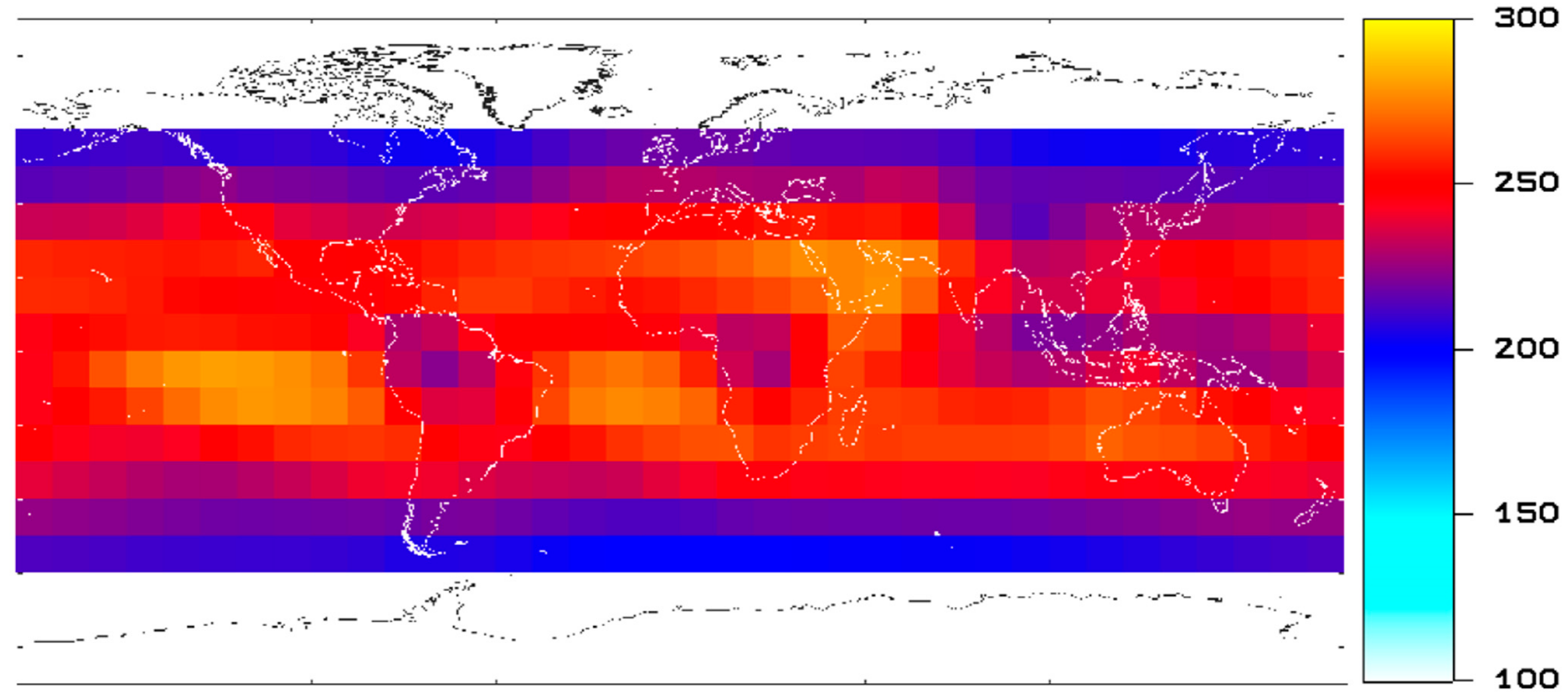
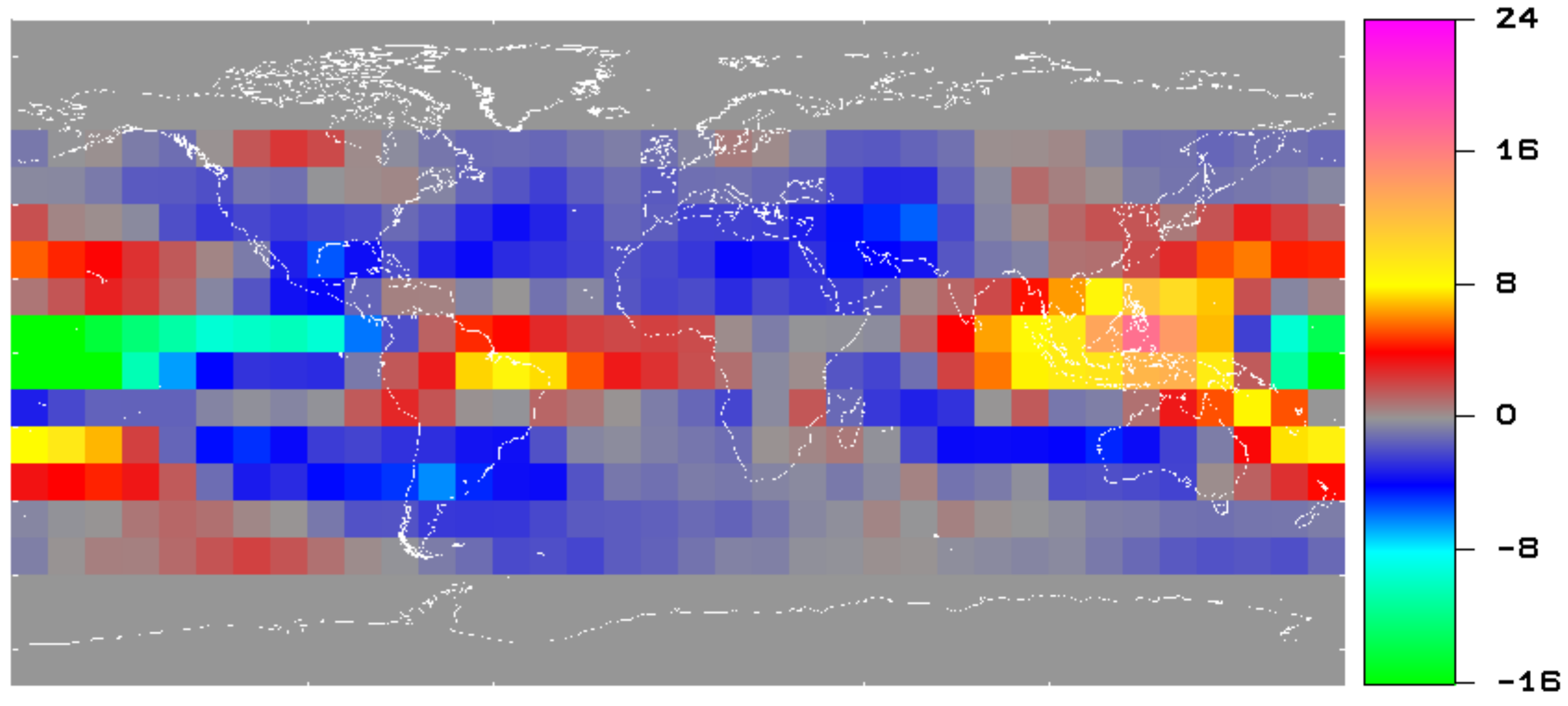
Figure 2 shows the climatology of the net radiation—defined as the absorbed solar radiation minus the OLR —obtained from the CERES Energy Balanced And Filled (EBAF) product—obtained following the methodology of Loeb et al. [
46] —from February 2000 to March 2010. Its spatial structure shows an equator to pole gradient, which is caused by the gradient of the incoming solar radiation. This equator to pole gradient is itself the driver of the general circulation in the atmosphere and in the oceans as described by Trenberth and Carron [
48].
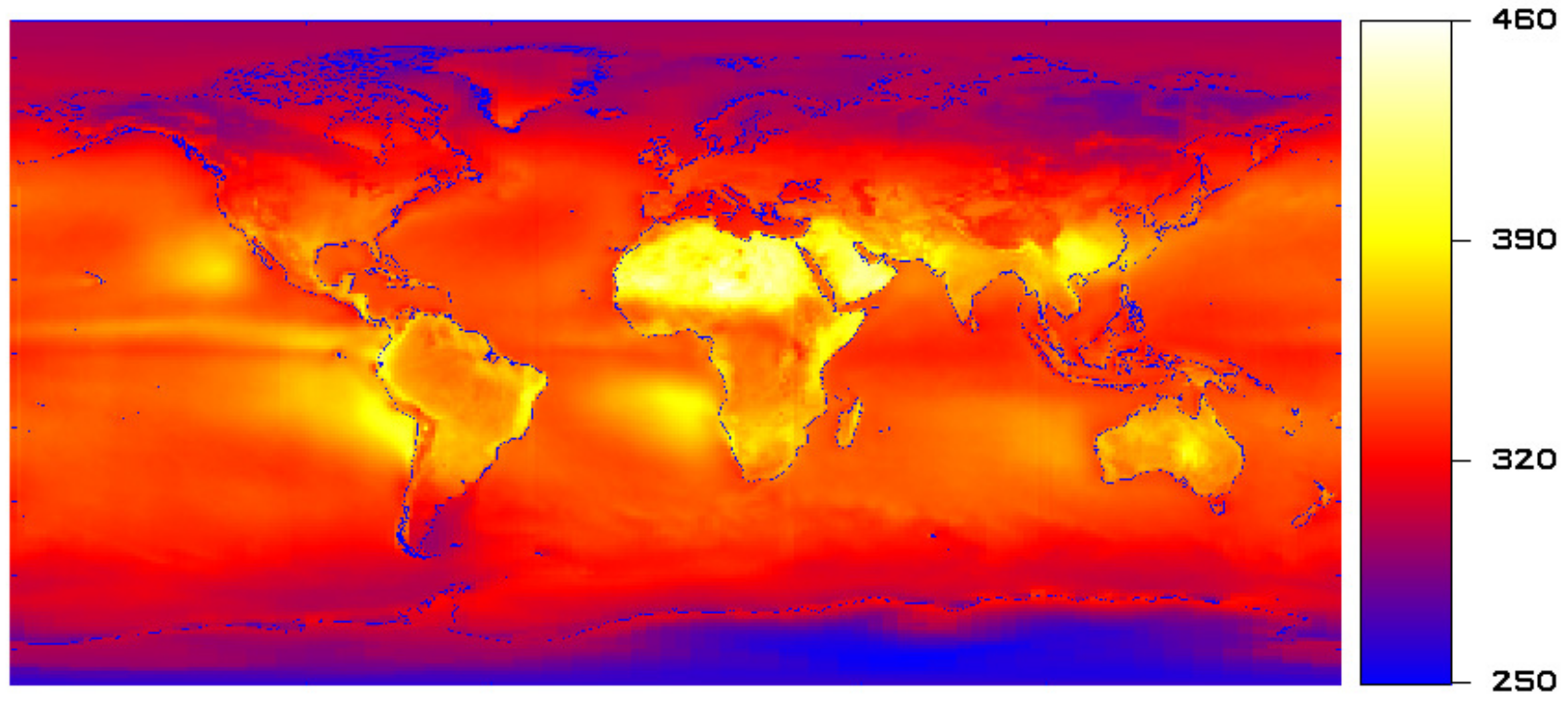
Figure 3 shows the climatology of the total outgoing radiation—defined as the OLR plus the RSF—from the CERES EBAF product for the same period.
It shows a strong radiative cooling for the marine stratocumulus regions west of the coasts of Namibia, Peru, California, and to a lesser extent west of Australia. The presence of these marine stratocumulus is provoked by the subsidence in the Hadley and Walker circulations, and their radiative cooling helps to maintain this circulation. They also play an important role in the so-called cloud feedback as described by Stephens [
49].
Figure 3 also shows a strong cooling over desert, particularly the Sahara and the Arabian desert. The strong cooling is caused by the relatively high surface albedo and the prevailence of clear sky conditions. It influences the local circulation as described by Charney [
50], pumping energy out of the circulation and radiating it to space as described by Blake et al. [
51].
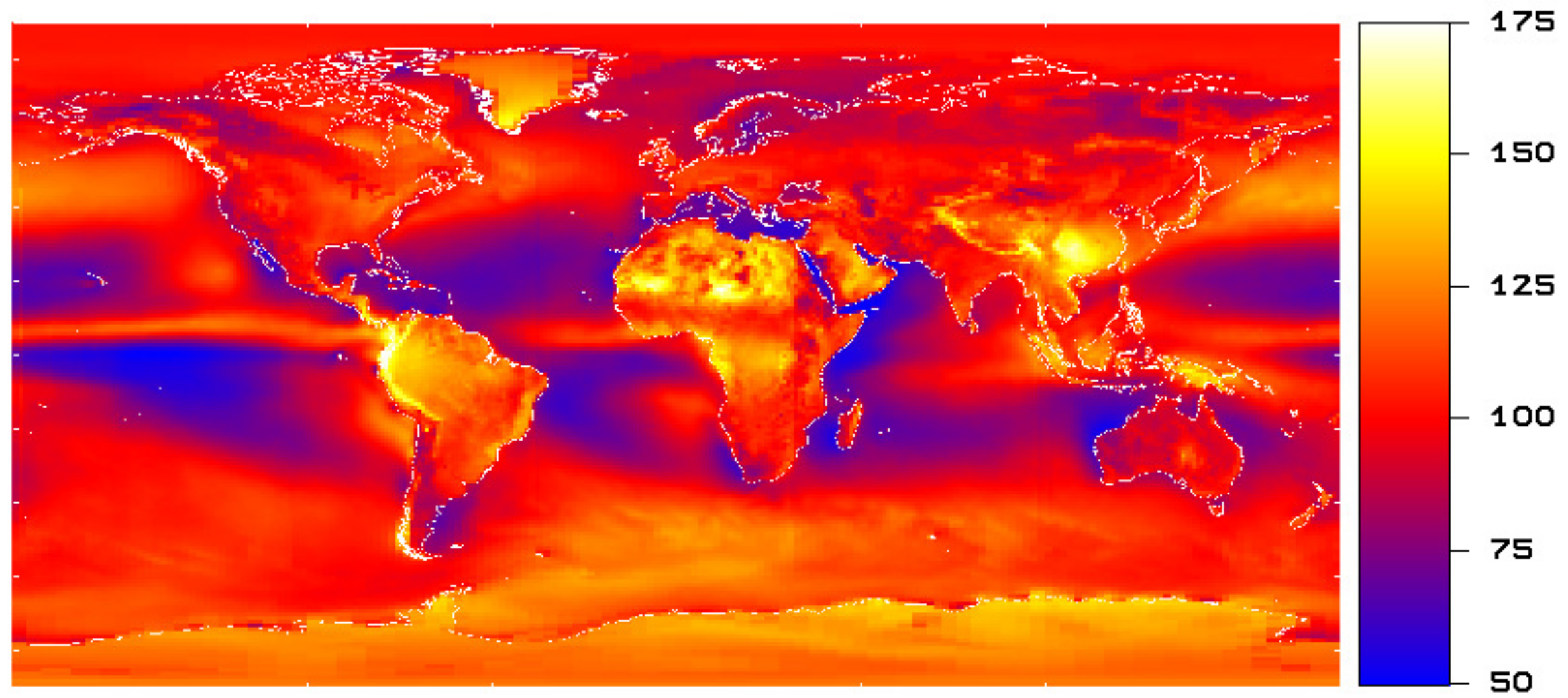
Figure 4 and
Figure 5 shows the CERES EBAF climatologies of the RSF and the OLR, respectively. High reflection by thick clouds and low emission by cold cloud tops is seen for the tropical convective regions and for the midlatitude regions with frontal cloudiness. For most cloud regions there is a compensation between RSF cooling and OLR heating. The exceptions are the marine stratocumulus clouds for which the RSF cooling is not compensated by OLR heating.
Figure 6 shows the climatology of the OLR from the ERBS WFOV between
57 degrees from 1985 to 1997. Although it clearly has a lower spatial resolution than CERES—see
Figure 5— it shows similar features.
6. Interannual Variability and Long-Term Changes
Tropical convection is caused by the diurnal wave of solar heating travelling around the Earth from east to west. Land masses heat up more quickly than oceans, and therefore tropical convection occurs preferentially over land. Two stable convection maxima—visible as OLR minima in
Figure 5—exist over the land masses of South America and Central Africa. A third convection maximum exists around Indonesia, with a western branch towards the Indian Ocean, and an eastern branch towards the Pacific. Since not much land is present in this area, the ‘Indonesian’ convection maximum is unstable; this instability gives rise to the well known El Nino/La Nina variability as described by Mc Phaden et al. [
52], which is the main mode of interannual climate variability.
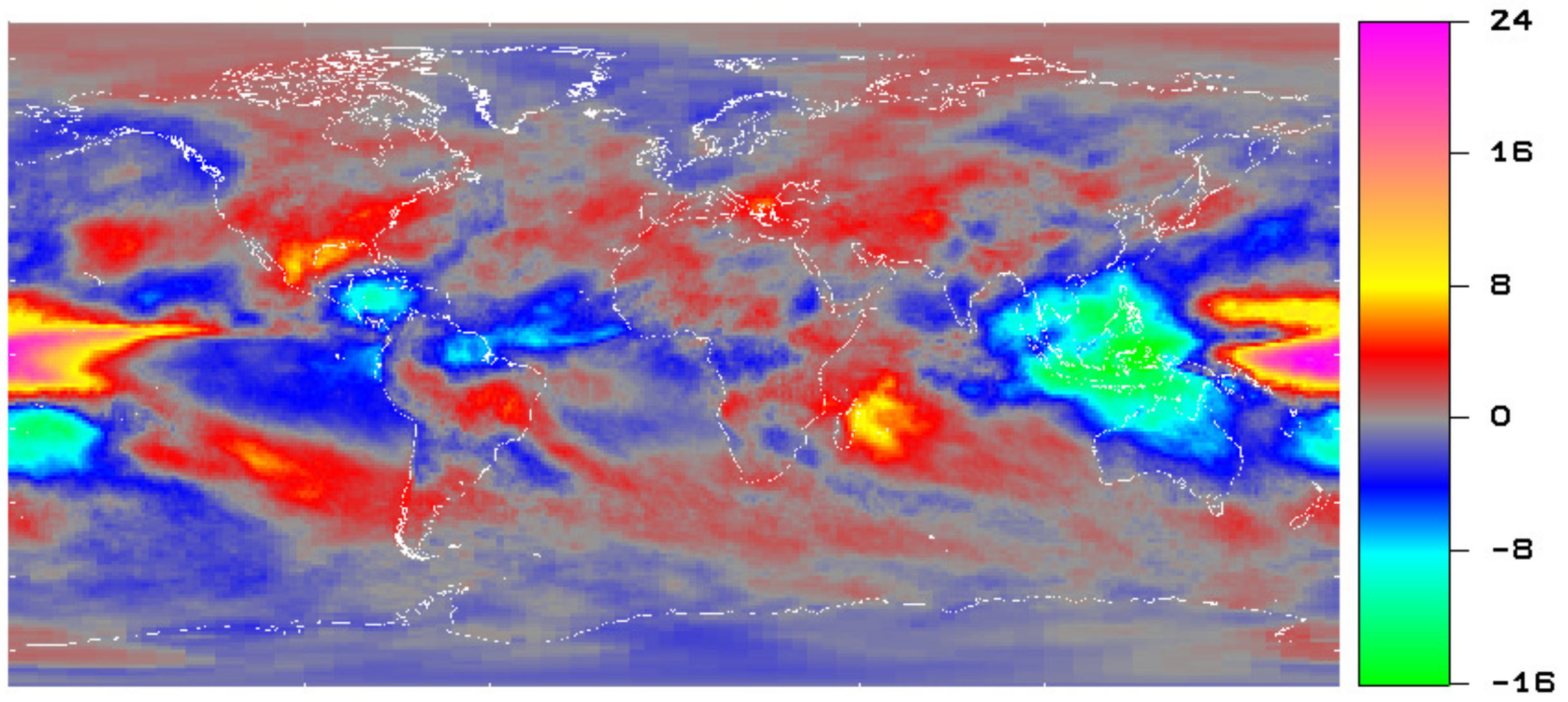
Figure 7 shows the variability of the OLR between La Nina years and El Nino years. The mean CERES EBAF OLR for the El Nino years 2002, 2003, 2004, 2006, and 2009 was subtracted from the mean OLR for the La Nina years 2000, 2001, 2005, 2007, and 2008. El Nino and La Nina years were identified using the Multivariate El Nino index by Wolter and Timlin [
53].
During La Nina the eastern and the western branches of the ‘Indonesian’ convection maximum move towards each other; as a result the OLR around Indonesia decreases as shown by the deep minimum around Indonesia in
Figure 7. The high precipitation corresponding to low OLR increases, causing flooding in Indonesia, South-East Asia, and Australia. Through the general Walker circulation there is a ‘communication’ between the three convection maxima, resulting in a teleconnected pattern of variation over the entire tropics, visible in
Figure 7. e.g., during La Nina there is an increase in OLR—and corresponding drought—over the Southern US.
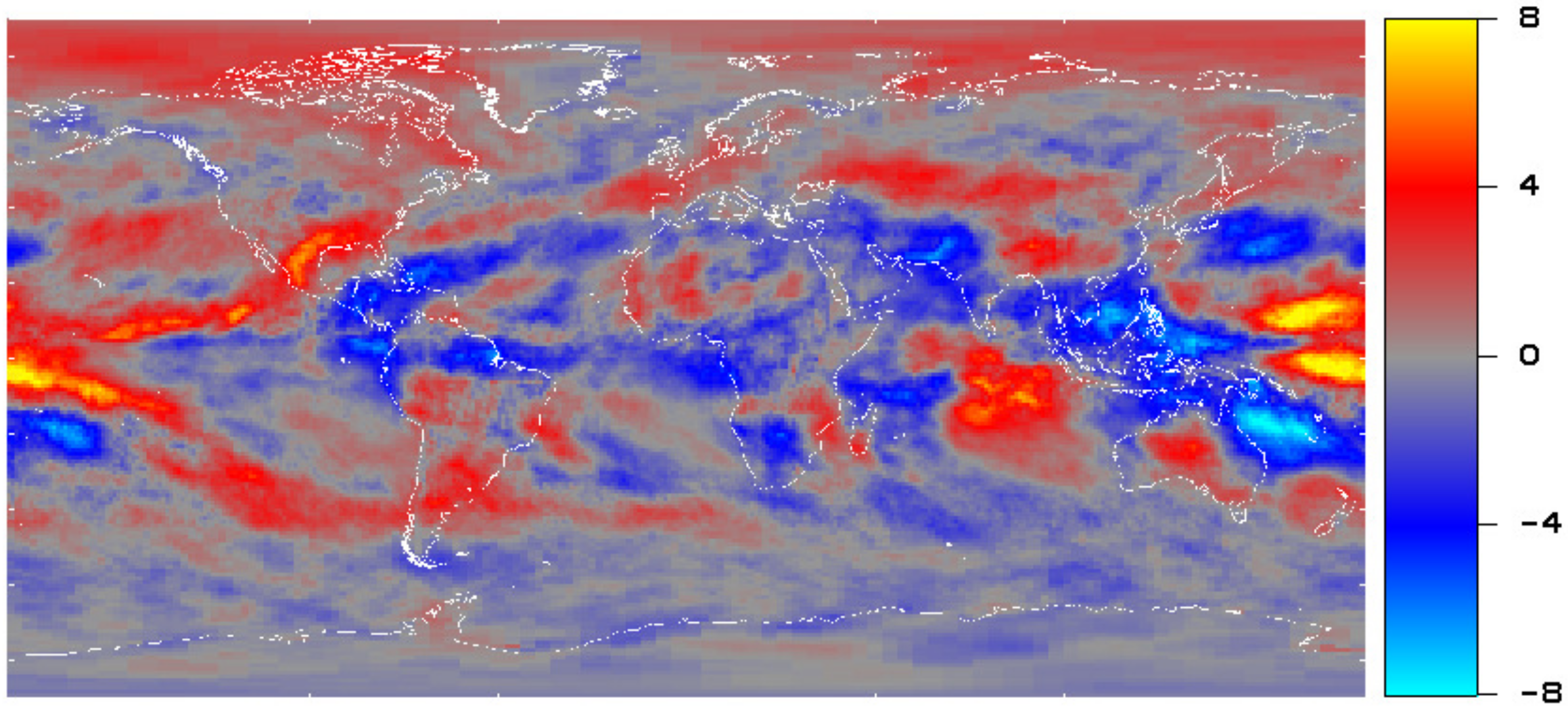
Figure 8 shows the long-term change of the OLR over the period 2000–2009. The mean CERES EBAF OLR for the period 2000–2004 was subtracted from the mean OLR for the period 2005–2009.
The spatial pattern of the 2000–2009 long-term change as shown in
Figure 8 is similar to the variation from El Nino to La Nina conditions shwon in
Figure 7. Thus, during 2000–2009 there was a general strengthening of La Nina conditions.
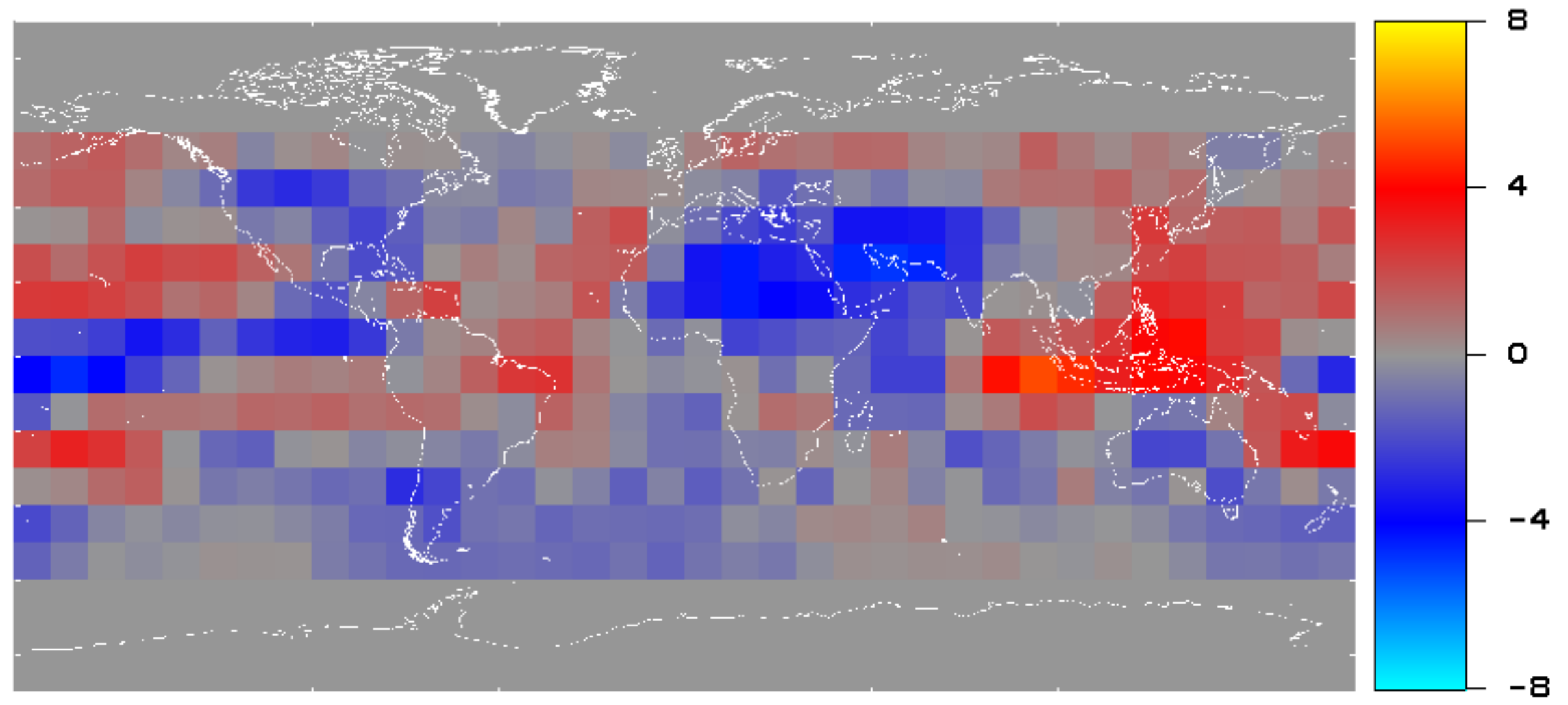
Figure 9 shows the long-term change of the OLR over the earlier period 1985–1997. The mean ERBS WFOV OLR for the period 1985–1990 was subtracted from the mean OLR for the period 1991–1997.
Figure 10 shows the variability of the OLR between El Nino years and La Nina years as seen by the ERBS WFOV instrument. The mean ERBS WFOV OLR for the La Nina years 1985, 1988, 1989, and 1996 was subtracted from the mean OLR for the El Nino years 1987, 1991, 1992, and 1997. El Nino and La Nina years were identified using the Multivariate El Nino index by Wolter and Timlin [
53].
The spatial pattern of the 1985–1997 long-term change as shown in
Figure 9 is similar to the variation from La Nina to El Nino conditions shown in
Figure 10. Thus, during 1985–1997 there was a general strengthening of El Nino conditions.
The period of El Nino strengthening from 1985–1997 corresponded to a period of strong global temperature rise as described by Hansen et al. [
54], but also to a period of increase of surface solar irradiance also called global brightening as described by Wild [
55] and Dewitte et al. [
56].
The period of La Nina strengthening from 2000–2009 corresponded to a period of global temperature stagnation, but also to a period of increase of decreasing surface solar irradiance due to increasing air pollution over South East Asia as described by Dewitte et al. [
56].
It should be noted that a period of temperature stagnation does not mean absence of heat uptake by the Earth. Following Allan et al. [
57] the EEI in the 2000–2012 period was 0.62 +/− 0.43 W/m
, while it was 0.34 +/− 0.67 W/m
for the 1985–1999 period. It seems that during the period of temperature stagnation the energy uptake by the Earth was actually higher than during the period of strong temperature rise.
7. Discussion
Due to its fundamental importance for climate and climate change, the long-lasting efforts to measure the ERB including the TSI from space are fully justified. These measurements are demanding both in terms of stability and absolute accuracy.
TSI measurements from space have been made since 1969. TSI measurements with good stability have been available since 1984. They reveal a variation of the TSI in phase with the 11-year sunspot cycle, with an amplitude of the order of 1 W/m. The currently-ending solar cycle 24 has a low amplitude compared to the preceding ones.
The TIM TSI instruments have a different viewing geometry as compared to the classical TSI instruments, which results in a lower absolute value of the measured TSI. Reconciling the classical DIARAD/SOVIM and the new TIM/TCTE instrument, the TSI level at solar minimum is estimated to be 1362.0 +/− 0.9 W/m.
The ERB measurements have sufficient stability to track the temporal variability of the EEI driving climate change, but they can not measure its absolute value with sufficient accuracy. Combining the ERB measurements with independent estimates of the EEI from OHC, we obtain the most likely values of the OLR of 238.0 W/m and of the RSF of 101.6 W/m—corresponding to an albedo of 29.8%—for the period 2000–2005.
Long-term changes of the OLR measured by the ERBS WFOV instrument reveal a general strengthening of El Nino conditions for the period 1985–1997, while the CERES measurements reveal an opposite strengthening of La Nina conditions for the period 2000–2009. There are possible links with surface solar irradiance brightening/dimming, temperature rise/stagnation and EEI level. Understanding these links is of fundamental importance for understanding climate change, and therefore deserves further study.