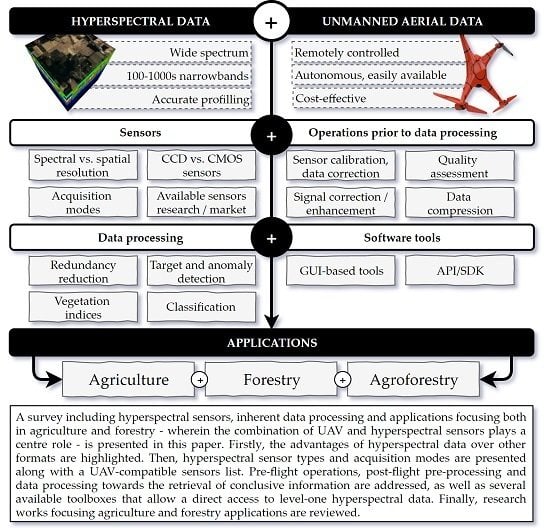
Hyperspectral Imaging: A Review on UAV-Based Sensors, Data Processing and Applications for Agriculture and Forestry

Abstract

Traditional imagery—provided, for example, by RGB and/or NIR sensors—has proven to be useful in many agroforestry applications. However, it lacks the spectral range and precision to profile materials and organisms that only hyperspectral sensors can provide. This kind of high-resolution spectroscopy was firstly used in satellites and later in manned aircraft, which are significantly expensive platforms and extremely restrictive due to availability limitations and/or complex logistics. More recently, UAS have emerged as a very popular and cost-effective remote sensing technology, composed of aerial platforms capable of carrying small-sized and lightweight sensors. Meanwhile, hyperspectral technology developments have been consistently resulting in smaller and lighter sensors that can currently be integrated in UAS for either scientific or commercial purposes. The hyperspectral sensors’ ability for measuring hundreds of bands raises complexity when considering the sheer quantity of acquired data, whose usefulness depends on both calibration and corrective tasks occurring in pre- and post-flight stages. Further steps regarding hyperspectral data processing must be performed towards the retrieval of relevant information, which provides the true benefits for assertive interventions in agricultural crops and forested areas. Considering the aforementioned topics and the goal of providing a global view focused on hyperspectral-based remote sensing supported by UAV platforms, a survey including hyperspectral sensors, inherent data processing and applications focusing both on agriculture and forestry—wherein the combination of UAV and hyperspectral sensors plays a center role—is presented in this paper. Firstly, the advantages of hyperspectral data over RGB imagery and multispectral data are highlighted. Then, hyperspectral acquisition devices are addressed, including sensor types, acquisition modes and UAV-compatible sensors that can be used for both research and commercial purposes. Pre-flight operations and post-flight pre-processing are pointed out as necessary to ensure the usefulness of hyperspectral data for further processing towards the retrieval of conclusive information. With the goal of simplifying hyperspectral data processing—by isolating the common user from the processes’ mathematical complexity—several available toolboxes that allow a direct access to level-one hyperspectral data are presented. Moreover, research works focusing the symbiosis between UAV-hyperspectral for agriculture and forestry applications are reviewed, just before the paper’s conclusions.

1. Introduction

Remote sensing relying on unmanned aircraft systems (UAS), although an emerging field of application, has been systematically applied for monitoring vegetation and environmental parameters aiming the optimization of agroforestry activities [1]. In this context, UAS have become suitable to assess crops’ conditions by gathering huge amounts of raw data that require further processing to enable a wide range of applications, such as water status [2], vigor assessment [3], biomass estimation [4] and disease monitoring [5]. Similarly, forestry and nature preservation can also greatly benefit from the use of UAS technology, allowing inspection of forestry operations [6], wildfire detection [7], health monitoring [8] and forest preservation [9].

In spite of the large number of successful works that have been applied to agroforestry and related areas using low-cost passive imagery sensors—such as visible (RGB) and near infrared (NIR)—many applications require higher spectral fidelity that only multispectral and hyperspectral [10,11,12,13] sensors can offer. Both of the referred spectral-based methods consist of the acquisition of images where, for each of the image’s spatially distributed elements, a spectrum of the energy reaching the respective sensor is measured. The main difference between them is the number of bands (also referred as channels) and their width [14]. While multispectral imagery generally ranges from 5 to 12 bands that are represented in pixels and each band is acquired using a remote sensing radiometer, hyperspectral imagery consists of a much higher band number—hundreds or thousands of them—arranged in a narrower bandwidth (5–20 nm, each). Figure 1 represents the differences between multi and hyperspectral imaging, which rely on a spectroscopic approach that has been used for laboratorial practices and in Astronomy for more than 100 years.

In fact, both multi- and hyperspectral imagery have the potential to take data mining to a whole new exploration level in many areas, including food quality assessment [11] and agriculture [12]. For instance, productivity and stress indicators in both agricultural and forest ecosystems can be assessed through photosynthetic light use efficiency quantification, which can be obtained by measuring the photochemical reflectance index (PRI) relying on narrowband absorbance of xanthophyll pigments at 531 and 570 nm [15]. However, while the higher spectral resolution present in hyperspectral data allows remote sensing of narrowband spectral composition—also known as spectra, signature or, according to [16], spectral signature—multispectral data manifests itself in larger intervals over the electromagnetic spectrum, which does not enable to reach the same level of detail. Thus, hyperspectral data has a better performance profiling materials and respective endmembers due to its almost continuous spectra. On the one hand, it covers spectral detail that might pass unnoticeable in multispectral data due to its discrete and sparse nature. For example, in Figure 2, since red-edge (RE, 670–780 nm) is not accessible through the broadband sensor, leaf chlorophyll content, phenological state and vegetation stress—which are parameters that manifest in that spectral range—cannot be assessed. On the other hand, hyperspectral has the ability to discriminate components that may be unwittingly grouped by multispectral bands (see, for example, [17] for more details).

Along with the resolution improvement, the hyperspectral sensing approach also increases data processing complexity, since such imagery ranges from hundreds to thousands of narrow bands that can be difficult to handle in real-time with reduced computational resources. Besides, spectral signatures can undergo through variations depending on light exposure and atmospheric conditions, which is an issue that has been leading the scientific community to propose processes for acquisition (to control environmental conditions) and/or analysis methodologies (to correct the noise resulting from environmental conditions). Such efforts allow accurately matching spectral data and identifying material compositions.

The first developments of imaging spectrometry in remote sensing applications started using satellites, more specifically to support Landsat-1 data analysis through field spectral measurements, according to [19]. Studies were mostly regarded to mineral exploration [20], but also landmine detection [21], agroforestry and related areas [22]. Back then, hyperspectral imaging technology did not have the supporting resources to go mainstream because developments in electronics, computing and software areas were required. Progress in the 1980s ended up to overcome technological limitations, opening the doors for the dissemination of this remote sensing technique for earth monitoring by the 1990s [23]. However, its development is still considered an ongoing process [24]. Currently, satellite capabilities for wide spatial range covering along with the improvements that have been carried out regarding spatial and spectral resolution [25] have been allowing the development of remote sensing works in—also but not limited to—agriculture, forestry and related areas (e.g., [26,27,28]). Notwithstanding, long distances relatively to earth surface raises recurrent problems, according to [29]. For example, Pölönen et al. [30] pointed out that for conditions involving cloudiness and short growing season, hyperspectral data acquired from traditional platforms can become useless in some cases. Other issues include the high cost of commercial satellite imagery, which only provide up to 30 cm resolution [31]. Even recent technology such as Sentinel 2 provides up to 10 m resolution in RGB and NIR [32], which is too coarse for some applications. For a better insight, considering a scenario with vines in which consecutive rows are parted by 4 m, such imagery would mix, at least, 2 rows with a significant portion of soil. An alternative to satellites started to be designed by National Aeronautics and Space Administration Jet Propulsion Laboratory (NASA/JPL) in 1983, with the development of hyperspectral hardware, specific for aircrafts, resulting in an Airborne Imaging Spectrometer (AIS). Later, in 1987, the airborne visible/infrared imaging spectrometer (AVIRIS) [33] came out as a high quality hyperspectral data provider that became popular among the scientific community [19]. However, besides the costs involved in the use of this solution, a certified pilot for manning the aerial vehicle and flight-related logistics is required. Lately, a remote sensing platform capable of overcoming not only satellite but also manned aircraft issues by bringing enhanced spectral and spatial resolutions, operational flexibility and affordability to the users is emerging: the UAS [34]. Together with specialized sensors, UAS are becoming powerful sensing systems [35] that complement the traditional sensing techniques rather than competing with them [1]. According to Pádua et al. [1], a UAS can be defined as a power-driven and reusable aircraft, operated without a human pilot on board [36]. Usually, it is composed of a UAV that, in turn, is capable of carrying remote sensing devices. UAS can be remotely controlled or have a programmed route to perform an autonomous flight using the embedded autopilot. Generally, it also requires a ground-control station and communication devices for carrying out flight missions [37]. Colomina and Molina [38] share a similar perspective by referring that a UAV is usually referred to as the remotely piloted platform, whereas the UAS is regarded as the platform and control segment. They also add that UAV and UAS are somewhat used interchangeably too. In what regards to hyperspectral data handling, a set of steps can be followed [13]: (1) image acquisition; (2) calibration; (3) spectral/spatial processing; (4) dimensionality reduction and; finally (5) computation related tasks (e.g., analysis, classification, detection, etc.). Similarly, in [39], file reduction and subsetting, spectral library definition (e.g., made by selecting a portion in the image) and classification are pointed out as valid operations to constitute a chain. Remote sensing, through the combination of UAV and on-board hyperspectral sensors and relying in many of the aforementioned steps/operations, has been applied both to agriculture and forestry (e.g., [40,41,42]). However, available works are not so numerous when compared with other platforms, since this is a relatively new research field. Even so, they provide a proper demonstration of this approach’s potential.

All in all, the main focus of this paper is, precisely, UAS-based remote sensing using hyperspectral sensors, applied both in agriculture and forestry. The acquisition equipment designed to be attached to UAVs is presented next, in Section 2. Then, Section 3 provides a discussion towards the operations that should be carried out before and after flight missions, as well as pre-processing data procedures for image calibration. Important approaches for data processing are reviewed in Section 4, specifically data dimension, target detection, classification and vegetation indices operations. Supporting software tools and libraries are presented in Section 5. Applications focusing the use of UAV’s and hyperspectral sensors in agriculture and forestry are addressed in Section 6, right before some conclusions within Section 7. To provide guidance along this paper’s reading, a glossary regarding the used abbreviations and acronyms is listed in Appendix A.

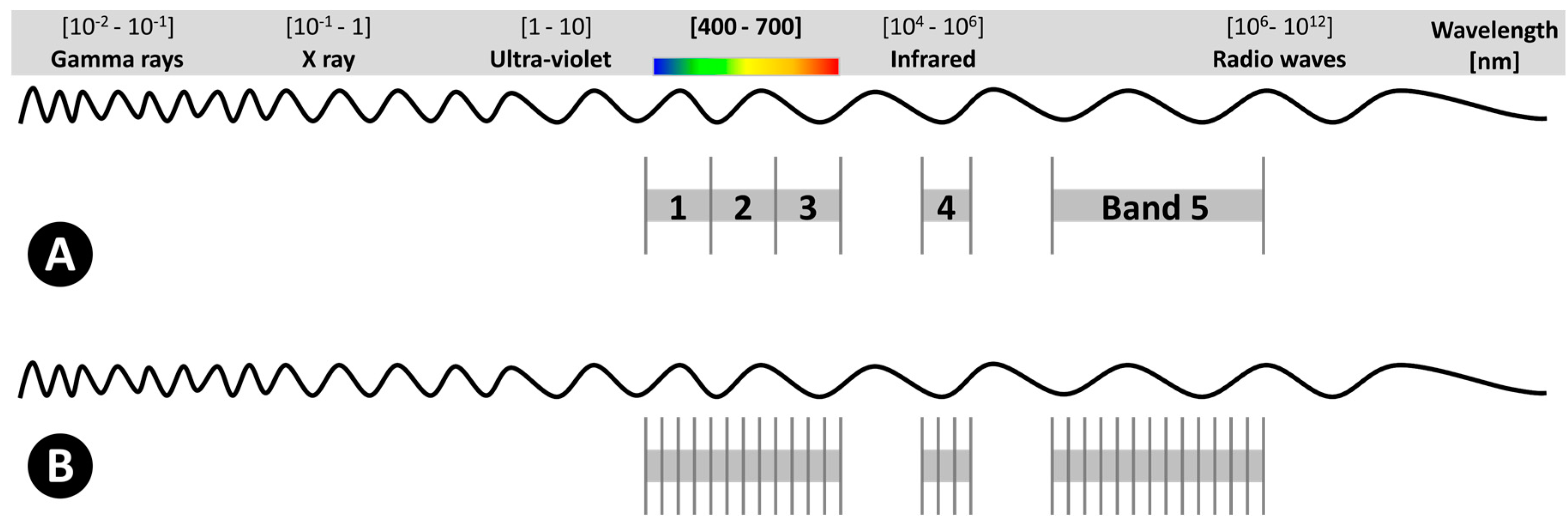
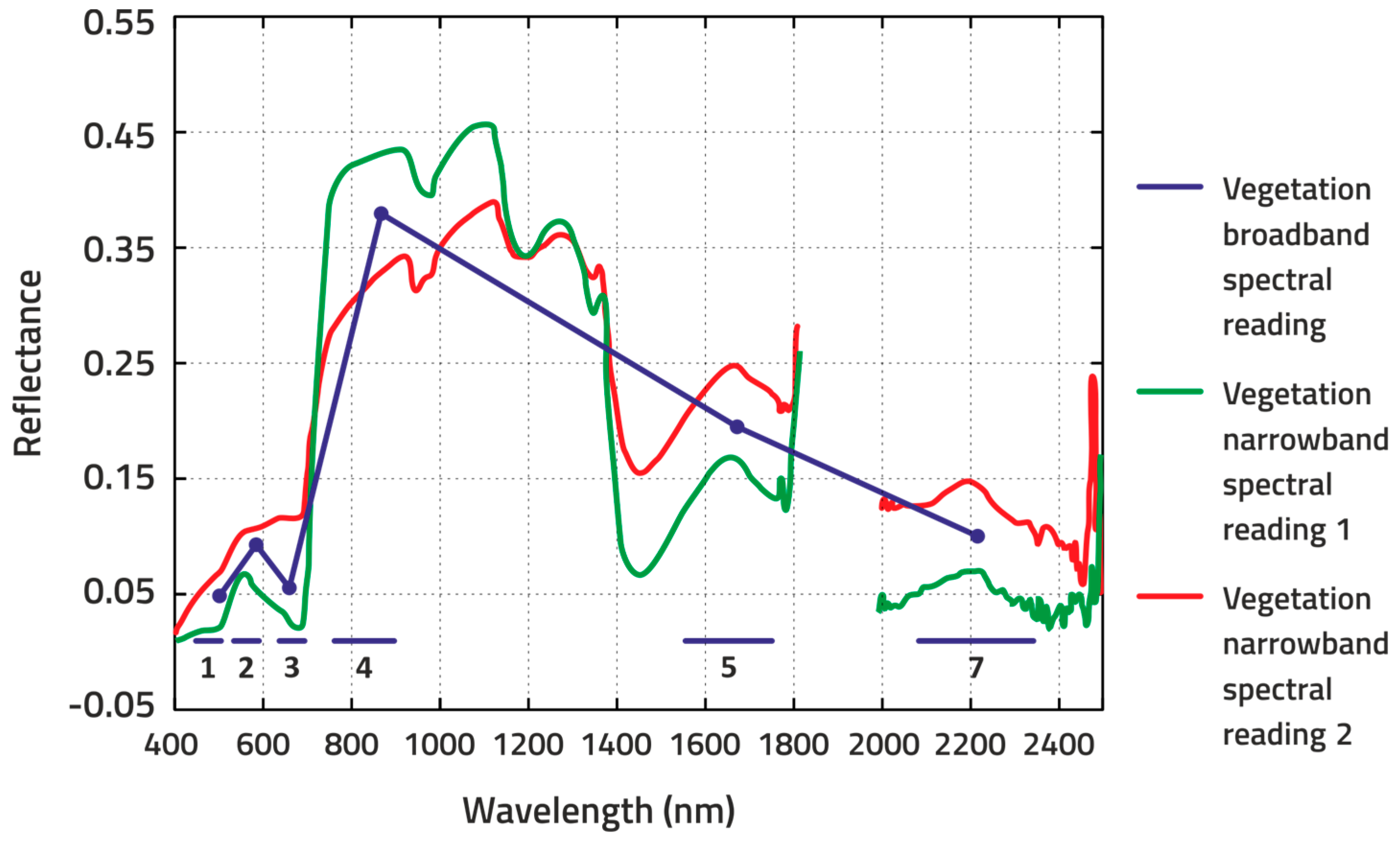
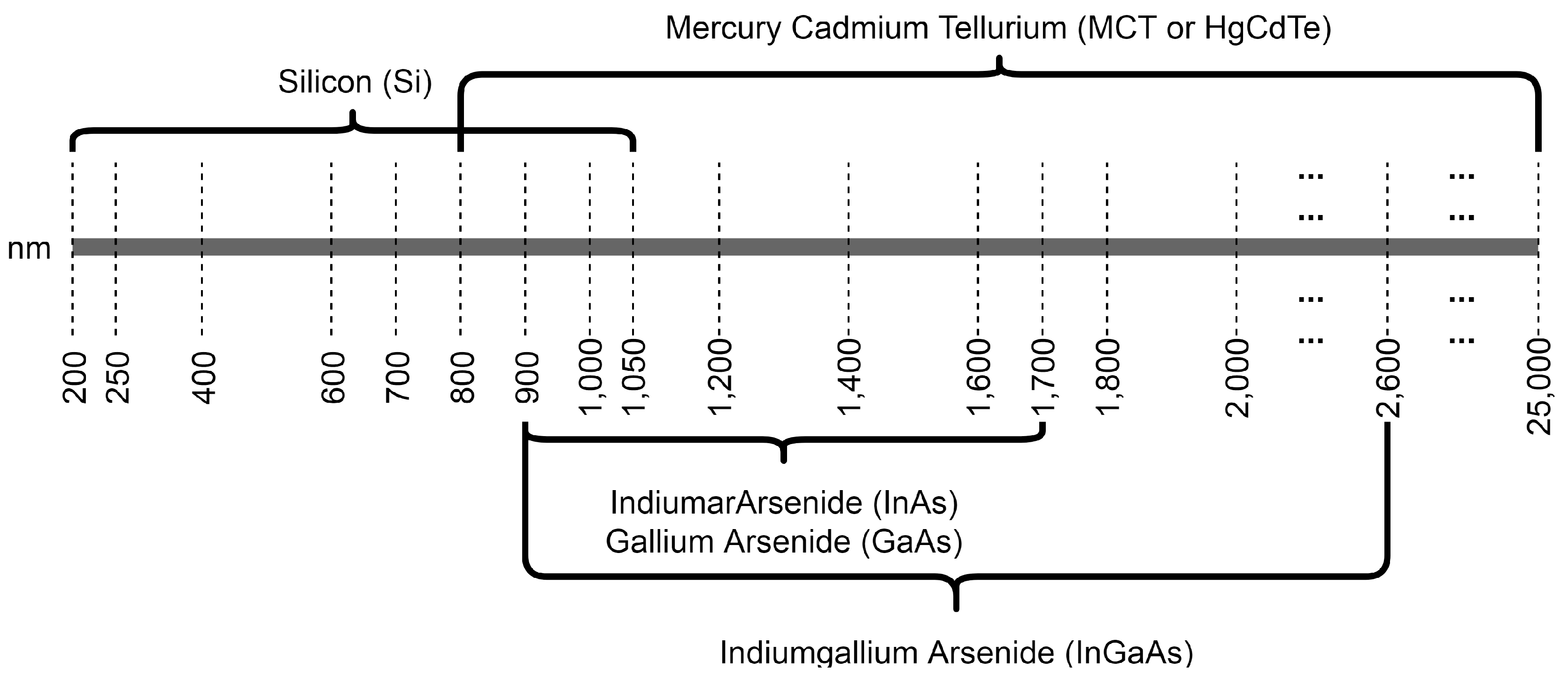
2. Hyperspectral Sensors

Independent of the aerial platform (Airborne, Satellite, UAV, etc.), sensors play an important role in data acquisition. According to [43], in which an extensive work addressing hyperspectral technology can be found, there are four main techniques for acquiring measurable data from a given target: by hyperspectral imaging, multispectral imaging, spectroscopy and RGB imagery. The most significant differences are synthetized in

Table 1. Main differences between hyperspectral and multispectral imaging, spectroscopy and RGB imagery (merging perspectives of [43,44]). A classification based on a bullet rate (1–3) was used to quantify both the spectral and spatial information associated to each acquisition technique, in relative terms.

	Spectral Information	Spatial Information
Hyperspectral Imaging	•••	•••
Multispectral Imaging	••	•••
Spectroscopy	•••	•
RGB Imagery	•	•••

, which considers not only the comparison carried out by [43] but also the vision of Sellar and Boreman [44], who stated that imaging sensors for remote sensing can be divided into the method by which they achieve (1) spatial discrimination and (2) spectral discrimination.

When compared with others, hyperspectral imaging sensors are effectively capable of capturing more detail in both spectral and spatial ranges. RGB imaging does not provide spectral information beyond the visible spectrum, which is of high importance for characterizing chemical and physical proprieties of a specimen. On the other hand, spectroscopy is a proximity technology mainly used for sensing tiny areas (e.g., leaf spots), aiming the acquisition of spectral samples without spatial definition. Regarding multispectral imaging and in spite of its capability for sensing both spectral and spatial data, there is a lack of spectral resolution that is only surpassed by hyperspectral imaging, as it was pointed out in the previous section. Thereby, hyperspectral sensing technology should be preferred when it comes to sense chemical and physical properties of a specimen.

In what regards to the concept of hyperspectral sensors, there are area detectors that have the ability of quantifying acquired light that results from the conversion of incident photons into electrons [43]. Two types of sensors are prominently used to achieve such conversion: charge-coupled device (CCD) and complementary metal-oxide-semiconductor (CMOS) sensors. Both consist in an array of photodiodes that might be built using different materials, as it is detailed in Figure 3.

CCD and CMOS sensors are different mainly in the way they treat incoming energy. On the one hand, CCD requires moving the electric charges accumulated in the photodiodes into another place wherein the quantity of charges can be measured. On the other hand, CMOS holds the photodetector and readout amplifier integrated as a single part capable of converting the voltage signal resulted from incoming electrons—converted photons—due to optically intensive transistors placed adjacently to photodiode. This seems to be the reason why CMOS technology is faster when acquiring and measuring light intensity. However, it is more prone to noise and dark currents than CCD due to the on-chip circuits used to transfer and amplify signals and as a result of lower dynamic range and sensitivity, as it is explained by [43]. A dark current is a temperature-dependent common phenomenon that contributes to introduce noise in a sensor’s reading and that needs to be considered in calibration tasks, for correction purposes. According to [45], such phenomenon can be generated by the Shockley–Read–Hall (SRH) process—that considers band gap by an impurity in the lattice to make the electron in transition pass through a new energy state—due to multiple factors, which end up resulting in the so-called blemish pixels. Additional information can be found in [15], in which is pointed out that CCD-based sensors have higher sensitivity regarding band data acquisition while, on the other hand, high grade CMOS have greater quantum efficiency in NIR.

Regarding acquisition modes, reference [43] categorizes them in four main ones (in fairly enough accordance with [44,46,47]): point scanning (or whiskbroom), line scanning (or pushbroom), plan scanning and single shot (Figure 4). While whiskbroom mode acquires all the bands pixel by pixel by moving the detector in the x-y space to store data in a band-interleaved-by-pixel (BIP) cube, pushbroom mode proceeds similarly but, instead of pixel-based scanning, an entire sequence of pixels forming a line is acquired, which ends up by constituting a band-interleaved-by-line (BIL) cube. Some other pushbroom characteristics include compact size, low weight, simpler operation and higher signal to noise ratio [10]. More comparisons between pushbroom and whiskbroom modes are presented in [48]. Plane scanning mode builds a band sequential (BSQ) cube constituted by several images taken at a time, each one holding spectral data regarding a whole given x-y space. Finally, there is a more recent mode that acquires all of the spatial and spectral data at once known as single shot. In [46], snapshot imager seems to be related with the referenced single shot mode inasmuch as it is presented as a device that collects an entire data cube within a single integration period. Additionally, some noteworthy issues are pointed out for each acquisition mode. Whiskbroom is a slow acquisition mode and pushbroom must use short enough time exposure to avoid the risk of inconsistencies at the spectral band level (saturation or underexposure). Plane scanning is not suitable for moving environments, while single shot was reported as an under development technology that still lacks support to higher spatial resolutions.

The combination of hyperspectral sensors with UAVs is commonly made available through pre-built systems that require dealing at least with three parties: the sensor manufacturer, the UAV manufacturer and the party that provides system integration [15]. The list of available commercial hyperspectral sensors is presented in

Table 2. List of hyperspectral sensors (and respective characteristics) available for being coupled with UAVs.

Manuf.	Sensor	Spectral Range (nm)	No. Bands	Spectral Resol. (nm)	Spatial Resol. (px)	Acquis. Mode	Weight (g)
BaySpec	OCI-UAV-1000	600–1000	100	<5 b	2048 d	P	272
Brandywine Photonics	CHAI S-640	825–2125	260	5 c	640 × 512	P	5000
	CHAI V-640	350–1080	256	2.5 c	640 × 512	P	480
				5 c
				10 c
Cubert GmbH	S 185—FIREFLEYE SE	450–950	125	4 c	50 × 50	S	490
	S 485—FIREFLEYE XL	355–750	125	4.5 c	70 × 70	S	1200
		450–950
		550–1000
	Q 285—FIREFLEYE QE	450–950	125	4 c	50 × 50	S	3000
Headwall Photonics Inc., Fitchburg, MA, USA	Nano HyperSpec	400–1000	270	6 b	640 d	P	1200 e
	Micro Hyperspec VNIR	380–1000	775 837 923	2.5 b	1004 d 1600 d	P	≤3900
HySpex	VNIR-1024	400–1000	108	5.4 c	1024 d	P	4000
	Mjolnir V-1240	400–1000	200	3 c	1240 d	P	4200
	HySpex SWIR-384	1000–2500	288	5.45 c	384 d	P	5700
MosaicMill	Rikola	500–900	50 a	10 b	1010 × 1010	S	720
NovaSol	vis-NIR microHSI	400–800 400–1000 380–880	120 180 150	3.3 c	680 d	P	<450
	Alpha-vis micro HSI	400–800 350–1000	40 60	10 c	1280 d	P	<2100
	SWIR 640 microHSI	850–1700 600–1700	170 200	5 c	640 d	P	3500
	Alpha-SWIR microHSI	900–1700	160	5 c	640 d	P	1200
	Extra-SWIR microHSI	964–2500	256	6 c	320 d	P	2600
PhotonFocus	MV1-D2048x1088-HS05-96-G2	470–900	150	10-12 b	2048 × 1088	P	265
Quest Innovations	Hyperea 660 C1	400–1000	660	-	1024 d	P	1440
Resonon	Pika L	400–1000	281	2.1 c	900 d	P	600
	Pika XC2	400–1000	447	1.3 c	1600 d	P	2200
	Pika NIR	900–1700	164	4.9 c	320 d	P	2700
	Pika NUV	350–800	196	2.3 c	1600 d	P	2100
SENOP	VIS-VNIR Snapshot	400–900	380	10 b	1010 × 1010	S	720
SPECIM	SPECIM FX10	400–1000	224	5.5 b	1024 d	P	1260
	SPECIM FX17	900–1700	224	8 b	640 d	P	1700
Surface Optics Corp., San Diego, CA, USA	SOC710-GX	400–1000	120	4.2 c	640 d	P	1250
XIMEA	MQ022HG-IM-LS100-NIR	600–975	100+	4 c	2048 × 8	P	32
	MQ022HG-IM-LS150-VISNIR	470–900	150+	3 c	2048 × 5	P	300

Note: ^a 380 in laboratory; ^b at FWHM; ^c by sampling; ^d Pushbroom length line (the other dimension depends on sensor’s sweep distance); ^e without lens and global positioning system (GPS); P—Pushbroom; S—Snapshot.

. Beside market options, others were developed in research initiatives (or projects). For example, in [49] a hyperspectral sensor was developed weighing 960 g, with support for capturing 324 spectral bands (or half in the binned mode) between 361 and 961 nm. In [50], another sensor was proposed to deal with rice paddies cultivated under water. It weighs 400 g and has a capturing range of 256 bands between 340 and 763 nm. In [51], a whiskbroom imager based on a polygon mirror and compact spectrometers with a promising low-cost applicability is presented. Sellar and Boreman [44] proposed a windowing approach, distinct from the time-delay integration technique used by some panchromatic imagers. Fabry-Perot interferometer (FPI) hyperspectral imager was alternatively developed by [30] as a Raman spectroscopy device [52] behaving like a single shot imager, since it acquires the whole 2D-plane at once. The data processing steps related with this sensor are described in [53].

Pre- and post-flight operations are required to reach level-one data, i.e., spatially and spectrally reliable hyperspectral cubes, ready to use and process. Next section is devoted to such operations.

3. Operations Prior to Flight and Post-Acquisition Data Pre-Processing

Regardless of the platform from which hyperspectral data is acquired (airborne, satellite, laboratory, etc.), its processing steps and methods are similar, with the exception of the pre-processing stage, which raises some issues. For example, radiometric noise is the prominent concern regarding UAS systems—mainly due to the light conditions—while atmospheric noise needs to be also considered as a major source of distortion when regarding satellite imagery. Therefore, it is very important to overcome such issues to obtain the proper conditions that will allow to subsequently apply the proper set of common processing stages, oriented for an intended outcome (for example, classification or pixel detection). Bioucas-Dias [54] addresses some approaches for data restoration and spectral resolution improvement that seem to be more suitable when applied to satellite imagery. Considering this work’s focus, calibration operations and methods for pre-processing UAS-based hyperspectral imagery are presented next.

Before starting to acquire hyperspectral data, all the hardware needs to be calibrated, including the inertial measurement unit (IMU) and the imager. In the latter, incoming light—under typical conditions—must be managed by reducing or increasing lens aperture. Currently, the simplest way of converting the sensor digital numbers (DN) to reflectance is via relative reflectance. In addition, [55] pointed out the low quality of UAV georeferencing and its negative impact, especially in pushbroom spectrometers. Indeed, navigation grade GPS sensors do not facilitate hyperspectral pushbroom scanning on a UAV [49]. The use of ground control points (GCPs) is absolutely necessary for improving georeferencing. However, recent advances in direct georeferencing and imaging technologies—like the integrated global navigation satellite systems (GNSS) and inertial navigation systems (INS)—enable precise mapping using a minimal number of GCPs. Foreseeing radiometric calibration at the pre-processing stage, white references are placed on the ground, at least at four pixels wide and preferably at 1 m². Low-cost (and low-quality) calibration panels can be used towards radiometric adjustments based on estimations that, however, cannot beat the accuracy provided by spectralon panels. Recently, Headwall [56] launched a VNIR E-series hyperspectral sensor with a built-in module for radiometric corrections, claiming that there is no need for placing such ground references. Still, validation tests are required. IMU’s calibration should be performed against the earth’s local magnetic field, otherwise the UAV’s orientation can get compromised [15].

After the hyperspectral data acquisition stage, some pre-processing operations are required. Duan et al. [57] consider pre-processing a mandatory prerequisite to extract quantitative information of the sensed area. Hyperspectral data acquired by traditional platforms like satellites—whose limitations were identified in [29]—and aircrafts is usually influenced by climate—among others factors pointed out by Pölönen [30]—and this hampers its use, especially in precision agriculture, where information detail matters. On the other hand, UAVs have the advantage of flying closer to the earth’s surface wherein the influence of atmosphere is not as significant. For this reason, there is no need for atmospheric corrections as it would be in traditional platforms. However, low acquisition height and unstable movement of the UAV, along with the viewing angle and high influence of micro-relief on illumination, make the pre-processing operations more difficult [58].

The need for radiometric and geometric corrections [59] and spectral calibration [49] while using UAV-carried hyperspectral sensors to preserve acquired data scientific rigor was highlighted. In addition, sensors need to be recalibrated regularly. Regarding radiometric calibration, coefficient might be obtained in the laboratory to achieve conversion to radiance [59]. In [49], optical integrating sphere USR-SR 2000S (Labsphere Inc., North Sutton, NH, USA) with four electric current stabilized light sources (labelled as SI and INGAAS lamps) producing calibrated irradiance levels of traceable uncertainties was used for radiometric correction purposes. Nevertheless, some factors—for example, sensor’s transportation and installation—are likely to lead to calibration loss that, in turn, results in a radiometric performance decreasing [57]. Such phenomenon can be assessed by using targets of known reflectance in the field to later check data radiometric quality. For geometric corrections, reference [49] suggests triangulation transformation. Both radiometric and geometric corrections can be done using software tools—whenever these are provided by the hyperspectral sensor’s manufacturer—, which should georegister and convert raw DN data cubes to radiance. One of the ways of achieving georegistration is to combine the external orientation data gathered during the flight with sensor model—interior orientation—and elevation model. In [58], it is mentioned that most of available pre-processing software uses the exact IMU position and orientation. Presumably, to be able of using IMUs on-board a UAV, a compromise between IMU weight and the UAV payload needs to be found. Moreover, spectral calibration needs be carried out by using standard methodologies like Lucieer et al. [49] did, using open-ray line source producing sharp gas absorption features of well-known wavelengths [60]. These pre-processing operations result in corrected data, which allows for comparisons between different time series and even data acquired by different hyperspectral sensors.

Quality assessment of hyperspectral data is a relevant topic for pre-processing [57]. An important criterion for hyperspectral data quality characterization is the signal-to-noise ratio (SNR). In [61], it was stated that quantitatively analyzing hyperspectral data requires the precise evaluation of the SNR. Essentially, for optimizing the use of data, high ratio is needed and, contrastingly, low ratio must be removed due to its negative effect on data.

According to Bioucas-Dias [54], signal correction/improvement fits in a group of approaches identified as data fusion, found in works such as [62,63,64], that refers to the class of methods capable of dealing with spectral and spatial data merging. Such methods include restoration (i.e., noise reduction and spectral improvement), spatial data fusion (for resolution enhancement based on subpixel information), spatial-spectral data fusion (refereeing to resolution improvement based on fusion of different parts of a hyperspectral imaging (HSI) cube, considering a cubes’ different bands) and multisource data fusion (resolution improvement considering more than one data provider, for example, satellites and UAVs).

A final remark on this section goes to data storage related issues during the data acquisition stage, mainly due to two reasons: on the one hand, (1) huge amounts of data are generated with the use of hyperspectral sensors and, on the other hand; (2) UAVs’ have a limited payload, which implies the use of a confined number of lightweight storage devices. To tackle these issues, authors in [65] proposed methods regarding hyperspectral images captured on-board UAVs during mission flights. There is a pre-processing step they used to transform hyperspectral data cubes into speech-like signals. Afterwards, those signals undergo a compression stage that processes them by means of a linear prediction.

After pre-processing operations over acquired data, the next stage is to perform data processing and analysis, which is addressed in the following section.

4. Data Processing and Analysis

This section focuses on approaches around hyperspectral data processing and analysis—including target detection, classification and vegetation indices (VI) operations—which are usually carried out after pre-processing operations that handle radiometric, geometric or even atmospheric calibrations.

4.1. Dimension Reduction

Hyperspectral data pre-processing stage is usually followed by a dimension reduction operation. Following this, Burger and Gowen [66] addressed the importance of handling hyperspectral data more efficiently to tackle dimensionality issues that have a malign effect in computational processing in general, as well as in approaches like neural networks (Hughes phenomenon), in particular [67]. According to the authors, there are some methods for compression (spatial domain in image processing) and dimension reduction (reducing of hyperspectral cubes’ dimensions) that aim to achieve efficient data handling: wavelet compression, band selection and projection methods. Within the former, there is the principal component analysis (PCA) method to concentrate the spectral variance that can be combined with others (like wavelet compression). Burger and Gowen [66] highlighted the maximum noise fraction (MNF) as a PCA-based method capable of achieving good performance in classification with low distortion rates, even better than the PCA alone [68,69]. Random projection and independent component analysis (ICA) are also mentioned as relevant projection methods, along with the multivariate curve resolution (MCR) analysis, which aims to decompose mixed spectra into pure components and corresponding concentrations. In [54], dimension reduction problems belong to the data fusion scope and are handled by spectral data fusion approaches, in which reduction is achieved by redundancy analysis.

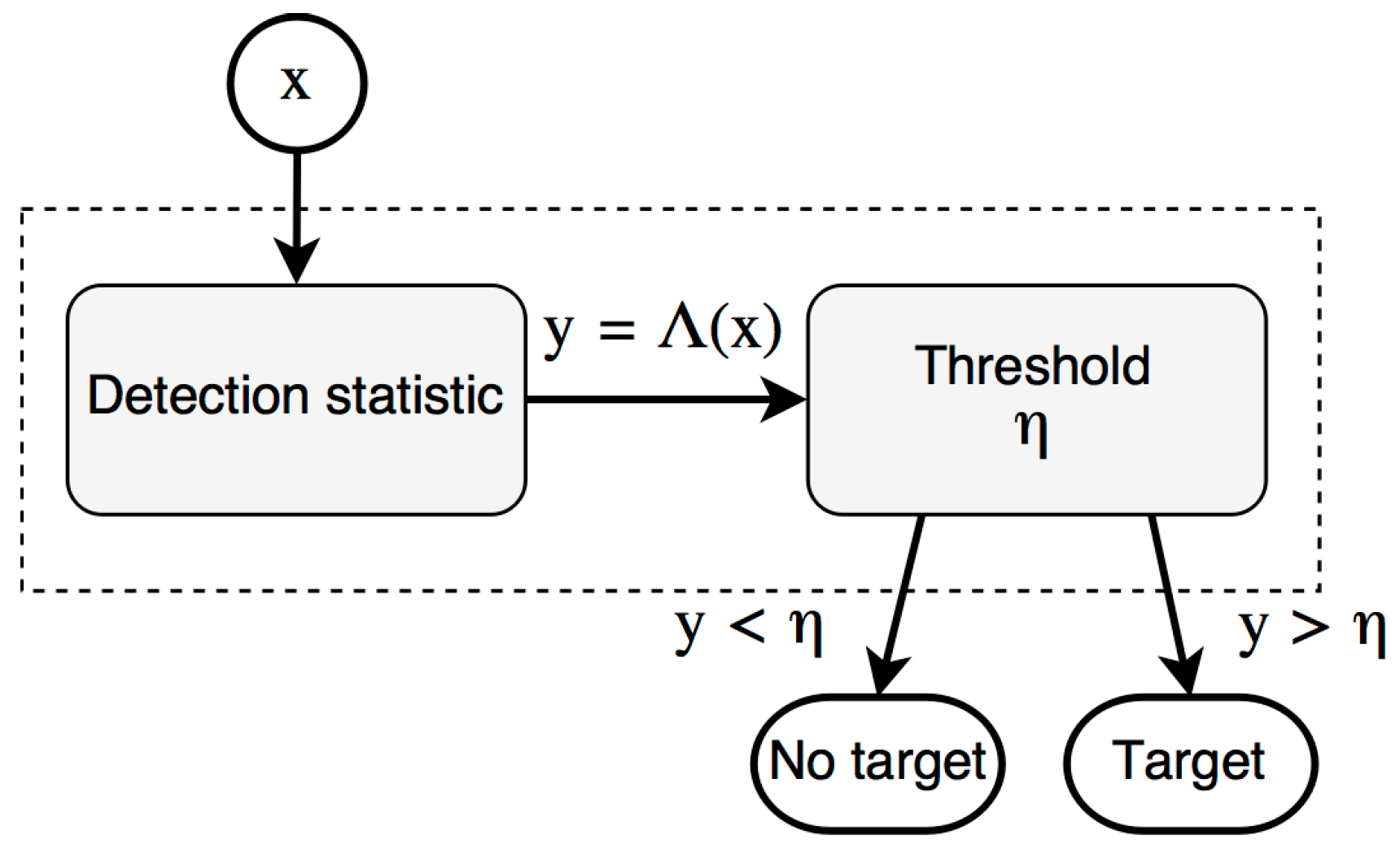
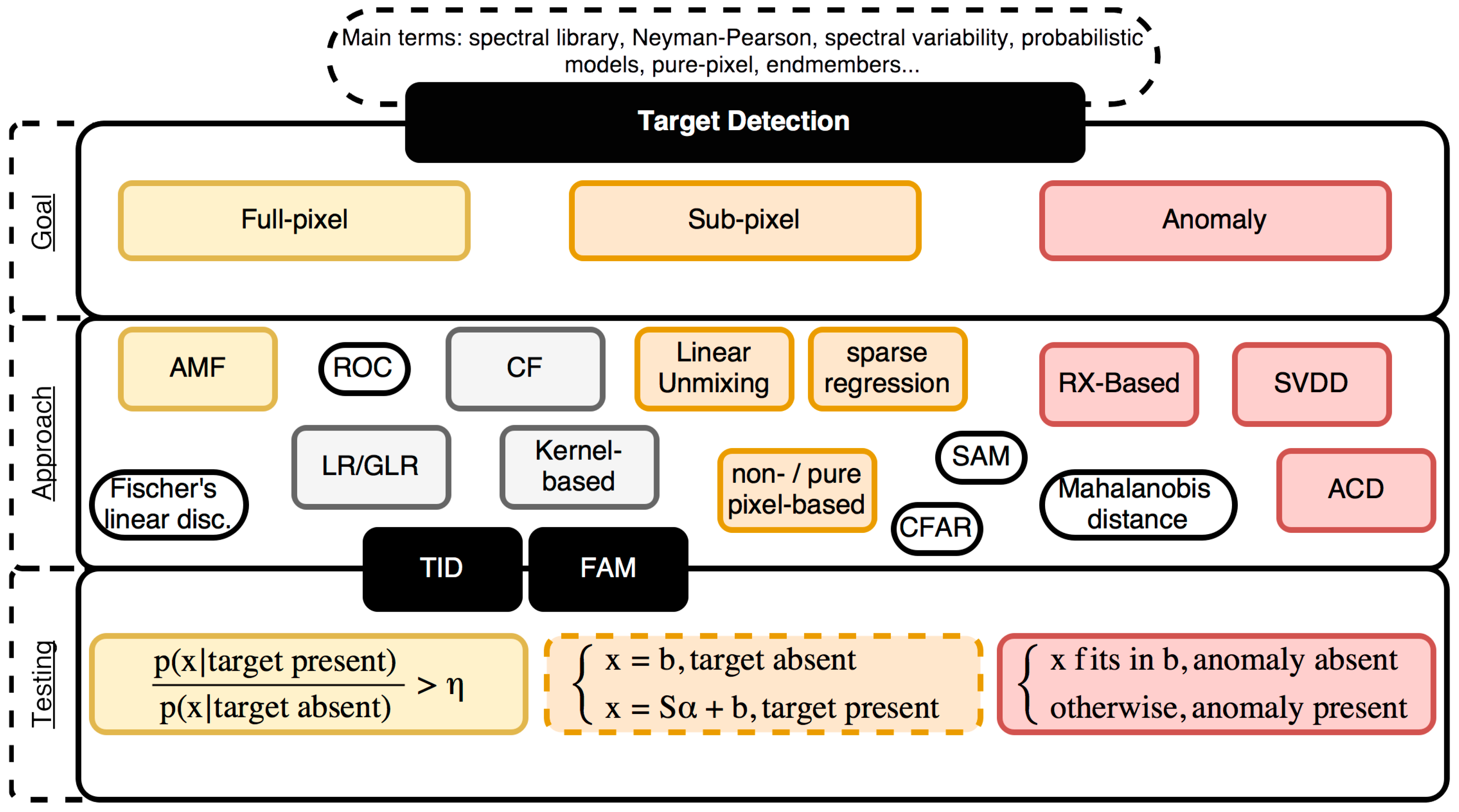
4.2. Target and Anomaly Detection

Essentially, target/anomaly detection consists in a binary classification technique that labels every pixel in the hyperspectral cube as belonging to target/background or outlier/background, respectively [70]. Due to some nuances establishing the specific goal of finding a target/anomaly among data through the classification of two classes, this detection approach was detached from the classification methods that will be addressed after this section. A graphical summary consisting of a taxonomy regarding target/anomaly detection is provided at the end of this subsection.

Manolakis and Shaw [71] have been bridging the gap between remote sensing and signal processing by providing an extensive overview on the statistical tools (mainly based on [72]) that can be used to handle hyperspectral data concerning pixels of interest. More specifically, they address target detection that refers to identifying a specific material in the HSI cube. It involves the binary hypothesis testing problem in which each pixel is assigned to a target or non-target label. In this task, the criterion is to maximize the detection probability while keeping false alarms at a predefined desirable rate (also known as Neyman-Person criterion [72]).

Reflectance spectra are stored in libraries and must then be compared with the acquired data, after conversion to reflectance and considering some corrections related with distortions such as atmospheric noise. The absence of a priori information (libraries or the needed data to work with a target reflectance) calls for an approach in which spectral signatures that differ from the background are searched (anomaly detection).

Likelihood ratio (LR) is one of the most known approaches to check the target probability. It is given by Equation (1):

$$\Delta \left(x\right)=\frac{p\left(x|\mathrm{signal}\mathrm{present}\right)}{p\left(x\right|\mathrm{signal}\mathrm{absent})}$$

(1)

in which Δ(x) > η (threshold). The threshold that separates targets from non-targets should be set to properly balance the probability of false alarms and detection. Receiving operating characteristic (ROC) curves are useful to analyze such a trade-off.

Whenever there are unknown targets and background parameters, a trick can be used: replacing unknown parameters in the LR by maximum likelihood estimates. Thresholds should be automatically figured out in practical applications (i.e., without an operator’s intervention), enabling a spontaneous detection. To that end, Manolakis and Shaw [71] underline the importance of the constant false alarm rate (CFAR) processor for dealing with misclassifications.

In [16], the importance of choosing a good threshold to minimize the occurrence of missing targets and false alarms is also highlighted. While a ROC provides the means to get the threshold variation involved in the detectors evaluation, Bayes and Newman-Pearson criterions are suitable methods for optimum threshold selection in cases wherein the conditional densities used in LR ratio calculus are completely known. However, in most real cases, probability densities rely on unknown targets and backgrounds. A widely used workaround is to replace unknown parameters with maximum-likelihood estimates through a process known as generalized likelihood ratio (GLR), from where adaptive detectors result. However, as the target class is very small, a problem arises related with adaptive detectors: target density parameters become difficult to estimate. In practice, target detection should rely on automatic threshold setters, considering that a high false alarm rate has its computational costs. Detectors based on CFAR represent a key approach to solve the referred issue inasmuch as they are immune to background variations and noise, according to another Manolakis and Shaw work [16]. After some performance considerations, they have proposed guidelines to design good detection methods, dividing them into main classes: full pixel and subpixel. Both will be addressed later in more detail.

Detection algorithms are many but their application depends on some factors, such as: type of models used for spectral variability, pixel purity and models used for describing mixed pixels. As for spectral variability, it is usually described in the following forms:

• geometrically: uses a subspace of the spectra in which the matrix defining the variability of the subspace can be a spectra signatures library (on data or even vectors), obtained from statistical techniques;
• statistically: spectral variability is described accordingly with probability distribution models. Calculus such as mean vector and covariance matrix are applied in different moments under a multivariate normal distribution assumption. Thus, variability can be measured from a uniform distribution of the data space.

Manolakis and Shaw [71] reinforced that variations in the material surface, along with factors induced by atmospheric conditions, sensor noise, materials composition and location (among others) usually change spectra readings. Moreover, most of the spectra readings acquired for real applications are likely to be random due to the combination of certain variability factors, which makes direct correlations to spectral libraries—reflectance spectra collections measured from materials of known composition [73]—infeasible. According to Manolakis and Shaw, the description of such statistical variability is more suitable to be analyzed using probabilistic models, which can include the following approaches:

• Probability Density Models: this kind of models consist in a scatter set of the reflectance values for a range of spectral bands that aims to identify different spectral classes in a scene using clustering algorithms (e.g., k-means) and classification methods (e.g., color attribution);
• Subspace models: are applied to analyze the variability within an M-dimensional band space, from a K-dimensional set, where M < K. PCA is one of the approaches within this probabilistic model;
• Linear spectral mixing models: are used to estimate the composition of the image’s pixels in those cases wherein there are pixels composed of a small number of unique spectral signatures corresponding to different components (endmembers).

As aforementioned, target detection methods can be classified into the following fundamental types: full pixel and subpixel [16,71]. The former refers to pure pixel that does not have “contaminating” interference from the background. On the other hand, sub-pixel methods are more challenging since they involve mixed spectra, corresponding to distinct materials.

There are two main ways of analyzing mixed spectra: (1) using linear mixed models (LMM) [72] that assume that a pixel is constituted by a linear small set of spectra known as endmembers (also in agreement with [16]); and (2) through stochastic mixing models in which there is a randomness and independency of the endmember spectra.

It turns out that mixed spectra can be faced as spectral unmixing problems. According to Bioucas-Dias [54] spectral unmixing (see, for example, [74,75]) purpose is to restore the ability of ascertain materials, i.e., to retrieve information of spectral endmembers and their abundances. Several conditions can compromise that ability, such as light, intimate mixtures and the spectral resolution of the sensor itself. The general name for the mathematical model that deals with this kind of issues is the radiative transfer theory (RTT). In the spectral unmixing scope, there are several approaches such as linear unmixing (inverse problem formulation for ICA analysis, widely used in the past decade), pure pixel-based (which assumes the presence in the data of one or more pure pixels per endmember), based on non-pure pixels (endmembers are inferred by fitting a minimum volume simplex to data in the case of lack of pure pixels) and sparse regression unmixing (a recent method that demands ground spectral libraries to find the optimal subset of signatures that can best model each pixel). Unmixing is associated to target detection by convenience but it can also be applied to classification problems.

For detection problems formulation, background only or background and target constitute the competing hypothesis. Unknown parameters such as the background covariance matrix have to be estimated. Then, a generalized likelihood ratio test (GLRT) approach [72] can be applied as an adaptive detector.

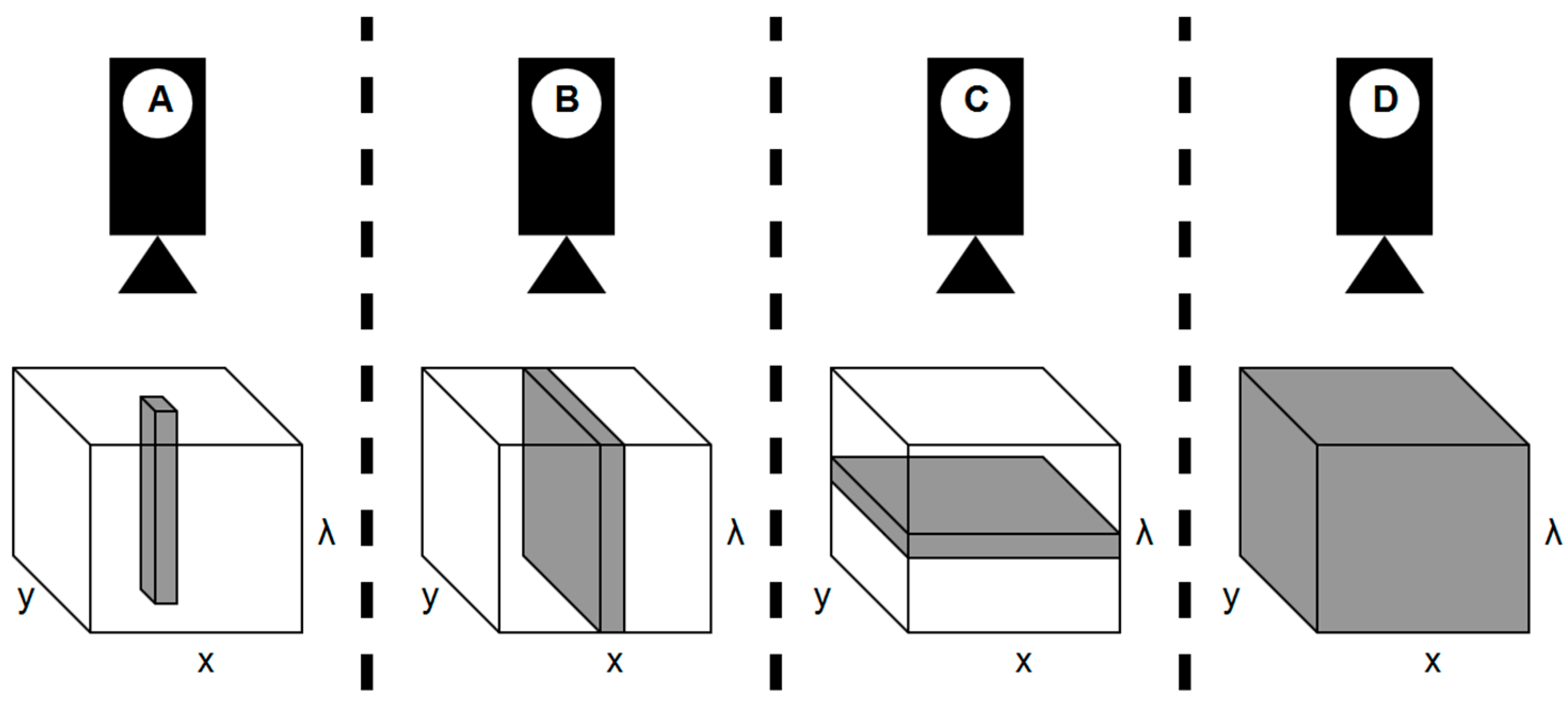
4.2.1. Full Pixel Detection

Usually, the process for full pixel detection includes clustering two groups of pixels separated by target and background. Then, a LR (concept depicted on Figure 5) or a GLR approach is applied to decide if a certain pixel falls in the target or in the background, by analyzing its position relatively to some scalar boundary decision curve (scalar threshold). According to [16], the use of normal probability models lead to a better performance.

To address the problem of the overlapping background and target classes that might lead to classification errors, some approaches are available: LR detectors and adaptive matched filters (AMF). The former uses multivariate normal vectors that can be checked for a spectrum through the probability density function that considers a mean vector and a covariance matrix. The design of a Neyman-Pearson detector can be made if the probability density function is satisfied, for example, with some matched filter like Fisher’s linear discriminant, which enables the detection by using an automatically calculated threshold. Alternatively, an AMF approach can also be applied to the same end. It uses a sample covariance matrix (from libraries or local data) distribution, determined by Richmond [76] and it is focused on the normal distribution of the background under the test “target absent” hypothesis. For target detection, Spectral Angle Mapper (SAM), Equation (2), can be used as a valid algorithm if the conditions comply with well separated distributions and small dispersions. Optimal properties are not applicable here, accordingly with Manolakis [71].

$$\mathrm{SAM}=\angle \left(x,y\right)=\arccos \left(\frac{x^{T}y}{\left|\left|x\right|\right|\left|\left|y!\right|\right|}\right)$$

(2)

where $x^{T}y$ is the dot product of vectors x and y.

4.2.2. Subpixel Target Detection

If it is known that the target of interest only occupies part of the pixel (presence of mixed background), another set of approaches should be applied, namely the unstructured and structured background models.

Unstructured background models are supposed to be used with backgrounds that include additive noise, multivariate normal distribution, mean 0 (forced) and a covariance matrix. The competing hypothesis in this approach is shown in Equation (3):

$$\{\begin{array}{c}\mathrm{H}0:\mathrm{x}=\mathrm{b}\left(\mathrm{target}\mathrm{absent}\right)\\ \mathrm{H}1:\mathrm{x}=\mathrm{S}\mathsf{\alpha }+\mathrm{b}\left(\mathrm{target}\mathrm{present}\right)\end{array}$$

(3)

where Sα corresponds to a spectral signature subspace model, b is the background and x are the testing pixels.

In the presence of such backgrounds, it is assumed that materials are spread independently and identically within a given pixel. According to Manolakis [16], the design of a practical detector could involve merging the GLR detector proposed by Kelly [77,78]—which includes the threshold to set up the probability of detection (Pd) and the probability of false alarm (Pfa)—and Reed and Yu [79] approach using a multivariate analysis of variance formulation. Such merge results in the ability of estimating Mahalanobis distance of the testing pixel, from background mean, which earns adaptability through CFAR propriety. The author highlighted its usefulness for anomaly detection in hyperspectral data applications (approach for spectral data with unknown target). Regarding target detection, one must consider that the amount of background is variable in unstructured cases. Thereby, estimators relying on variance—directly related with the fill factor of the target—can be used, such as adaptive coherence cosine (ACE) estimator [80,81]. On the other hand, structured background modelled by a subspace models have, as the only source of randomness, additive noise with unknown variance. Manolakis et al. [16] proposed a GLRT detector [72,82,83], relying in the substitution of likelihood ratio by maximum-likelihood estimates of the unknown quantities. Its geometrical interpretation is also provided to help understanding criteria for fitting testing pixels in the different models, namely full linear model (target plus background) and reduced model (background). Conclusions regarding target present/absent can be taken based on such fitting.

For materials that overlap with each other making their spectral distinction difficult, a nonlinear decision boundary can be used. Manolakis et al. [16] provided an example on how to distinguish cars and trees overlapping in a scene. The plot of two-band data as points in two-dimensional space with the reflectance values as coordinates gives origin to a couple of distinguishable data clusters related with the evolved elements. According to the authors, this is the essence of multiple spectra-band data exploitation in remote sensing spectroscopy. However, both UAS flight altitudes and sensors’ improved spatial resolution should relieve mixed spectra issues in tasks related with forestry and agriculture monitoring and assessment.

Meanwhile, other developments were made by Nasrabadi [70], who addressed anomaly and target detection with recent statistical signal processing and machine learning approaches. In spite of its experimental results being around full-pixel targets, he claimed that the addressed methods can be extended to sub-pixel. For such reason, this work was referred without being assigned either to one or other targeting method. According the author, anomaly detection aims the pattern recognition of detected objects that stand out the cluttered background. Along with some already mentioned anomaly detectors, such as Reed-Xiaoli (RX) [79] and subspace-based [84] detectors, others were highlighted as emerging approaches, more specifically, Kernel RX [85]—non-linear version of RX detector to deal with the lack of Gaussian distribution behavior of clutter background, which cannot be easily modelled due to insufficient training data and knowledge about Gaussian mixtures—and support vector data description (SVDD) [86], which is a classifier capable of estimating support region for a given data set, avoiding prior information of distribution. Anomalous change detection (ACD) was defined by [87] as an algorithm capable of suppressing environmental changes to highlight materials transformation, giving a couple of hyperspectral images. Additionally, they provided comparison data between several ACD algorithms. Regarding the target detection and besides spectral matched filter [88], matched subspace [82] and orthogonal subspace projection [89], also kernel-based target detectors (proposed considering [90])—capable of extending previous target detectors, thus enabling the analysis of nonlinear features through kernels—and continuum fusion (CF) detectors (e.g., [91])—for dealing with the variability of target detection models parameters—were presented. Additionally, theoretical background on sparse representation classifiers relying on training data regarding all the classes is provided.

Still concerned with target detection gaps (Figure 6)—related with material discrimination in the presence of pixel’s mixed spectra and the large number of false alarms outputted by algorithms relying on classical detection theory and physics-based signal models—, false alarm mitigation (FAM) and target identification (TID) algorithms were recently developed and presented, after a set of introductory subjects, including spectral variability, subpixel targets modelling, likelihood detectors, matched filters and ROC-based performance analysis [92]. While FAM [93] is considered a promising approach to deal with the aforementioned issue related with false alarm rates, TID is useful to determine if a given pixel within a certain detector contains or not the target. The latter is also suitable for mixed spectral problems, which are addressed by unmixing techniques and material identification through library spectra association. Typical approaches are inspired by existing methods (e.g., [94,95,96]).

To conclude this subsection devoted to the targets’ detection within hyperspectral data, there are other works that are worthy of being consulted [54] and some related references [71,97,98] that might complete and update some of the previously addressed approaches as, for example, anomaly detection (identification of pixels significantly different from neighboring background in which no prior knowledge is considered), signature-based target detection (a matched filter that finds pixels relying on prior spectra knowledge), sparse representation target detection (classification uses sparse representation given by a short sample of target and background libraries) and nonlinear detectors (machine learning applications).

4.3. Other Classification Methods

For Manolakis and Shaw [71], classification methods consist of the assignment of pixels to classes or themes (also known as thermographic maps). For instance, in land cover classification tasks, the user has to determine classes by using training sets, spectral libraries and/or ground truth information, considering a probability minimization of misclassification as criteria.

Burger and Gowen [66] point out the availability of a wide set of classification and regression algorithms, including unsupervised methods like k-nearest neighbor and hierarchal clustering supervised classification such as partial least squares discriminant and SAM. With regard to statistical methods, [67] starts by explaining that class discrimination must rely on some statistic measurement—like Bhattacharyya distance [99]—in which there are typically involved class conditional density functions, desirable for discrimination. Such functions have a mean value and a covariance matrix associated. It turns out that those classes result from maximum likelihood classifiers—that can be applied through, for example, the minimum distance to means, a Fischer’s linear discriminant and a Gaussian classifier—that should be applied considering two main aspects: variance behavior and spectra correlation. According to [67], neural networks perform well on classification but are demanding in terms of computation and training data sets. Feature extraction for class discrimination might be achieved using one of two approaches: decision boundary feature matrix (DAFE) or decision boundary feature extraction (DBFE). Finally, a data analysis paradigm was proposed as well as a concrete example using a mall—located in Washington, District of Columbia (DC), USA—in which the final result is the discrimination of the scene’s elements, including roofs, roads and grass.

Plaza et al. [100] revised some alternative approaches to the classical statistical analysis (e.g., [90,101,102,103,104,105]) and proposed some methods based on support vector machines (SVM) and Markov-based techniques. To perform, SVMs rely on kernel functions that can be one of the following three types: Gaussian radial basis function (RBF), polynomial and based on SAM. They noticed that with a small number of training sets, more specifically 10, 20, 40, 60, 80, and 100 pixels of a given class, randomly extracted from a wider set, all of the three kernel functions allowed the SVM approach to reach above 92% of classification accuracy with the 10-pixel sample. The full training sample (of the wider set) did not increase this rate significantly. Transductive SVM (TSVM) was also explored by the authors, who defined it as an approach “based on specific iterative algorithms, which gradually search the optimal discriminant hyperplane in the feature space with a transductive process that incorporates unlabeled samples in the training phase”. A comparison made between SVM and TSVM from a sample obtained of a training samples subset, which considered some nuances—like variables to control the error for misclassification—was carried out and the results for the TSVM approach were better, regarding the conditions specified by the authors. Kernel-based classifiers related with spectral (e.g., Euclidian [106]) and spatial (e.g., using means and standard deviations) domains were then presented for a contextual information integration approach that leads to better classification results when compared to both of the aforementioned approaches. Additionally, they proposed an enhanced approach based on extended morphological profiles and Markov’s random fields, along with a method for spectral unmixing. A recent study [107] shows that hyperspectral image transductive classification is still being used, this time as an approach based on a co-training process to manage spectral and spatial information. Three kinds of classifiers (spectral, frequency-based and morphology-based spatial profile) belonging to imagery are firstly learned from the originally labelled part of the input data. Then, an iterative co-training phase takes over wherein classifiers are learned from imagery data. Also, a separated set of classifiers is used to predict unlabeled pixels. According to the authors, this approach overcomes the accuracy of the ones found in the state-of-the-art referring to the same class of classifiers.

Bioucas-Dias [54] agrees with the previous authors by stating that the goal, underlying classification problems, is to attribute labels to each pixel (e.g., [108,109]). They have enumerated a set of techniques that can be applied to classification, including: feature mining (which, in turn, is subdivided in feature extraction and selection approaches), supervised classification (to discriminate classes of pixels based on, for example, SVM) and semi-supervised classification (enlargement of the training set composed by labelled samples by considering unlabeled ones).

4.4. Vegetation Indices

VIs enable the analysis of several proprieties in leaf area index (LAI) and the assessment of biophysical, physiological, or biochemical crop parameters. In [110], VIs were classified as broad and narrow bands, being the latter group considered more proper for hyperspectral data [111]. Some of the addressed narrowband indices include chlorophyll absorption ratio index (CARI), greenness index (GI), greenness vegetation index (GVI), modified chlorophyll absorption ratio index (MCARI), modified normalized difference vegetation index (MNDVI), simple ratio (SR, including narrowband variants 1–4), transformed chlorophyll absorption ratio index (TCARI), triangular vegetation index (TVI), modified vegetation stress ratio (MVSR), modified soil-adjusted vegetation index (MSAVI) and PRI.

Indeed, VIs have been widely applied in hyperspectral data for several purposes [40,112,113,114,115,116,117]. For example, Haboudane et al. [112] carried out a study to evaluate VIs sensitivity to green LAI, and to modify some of them in order to enhance their responsivity to LAI variations. Modified versions of TVI and MCARI popped out as the best to predict green in LAI. Vineyard conditions assessment was addressed in [113], pointing out the PRI as one of the most sensitives to carotenoids C_x+c and chlorophyll-carotenoid ratios C_ab/C_x+c. TCARI combined with a broadband index known as Optimized Soil-Adjusted Vegetation Index (OSAVI) was the most consistent for estimating C_ab on aggregated and pure vine pixels. Later, 12 VIs assessment was performed by Lin [114], in which TCARI/OSAVI combination was highlighted as the best for chlorophyll estimation while, simultaneously, resisting to LAI variations. TCARI/MSAVI occupied the second place in that ranking. In [40], 3 years of UAV-acquired hyperspectral data over vineyard fields were used to carry out a study with VIs that led to the conclusion that the combination of R515/R570 (sensitive to C_x+c) and TCARI/OSAVI (sensitive to C_a+b) narrow-band indices are suitable for mapping carotenoid concentration at the pure-vine level. According to Liang et al. [115], PRI and, once again, TCARI/OSVAI, are the most suitable indices for leaf chlorophyll content estimation. Regarding canopy chlorophyll content estimation, SR and SR₂ are at the top of their ranking. In a recent work on rice [117], MSAVI is among the VIs that presented the strong and significant relationships with the LAI estimation at different phenological stages. For more information in hyperspectral VIs, the fourteenth section of the fifth part of [116]—a book devoted to hyperspectral remote sensing of vegetation—is available for consultation.

In [12], a wide survey on optimal hyperspectral narrow bands (between 400–2500 nm) to study vegetation and agricultural crop biophysical and biochemical properties was presented in the form of a table containing sections regarding band classes, more specifically: blue, green, red, RE, NIR, far near infrared (FNIR), Early short-wave infrared (ESWIR) and Far short-wave infrared (FSWIR).

Alternatively to the presented hyperspectral data processing, emerging approaches for dealing with HSI complexity based on deep learning (DL) are worthy to be referred. For example, in [118], a framework that joins dimension reduction and deep learning to allow hyperspectral image classification based on spectral-spatial features is proposed. Discriminant algorithms for spectral features and convolutional neural networks (CNN) to deal with spatial features are at the basis of this proposal that is pointed out as an outperforming framework comparatively to commonly used methods for hyperspectral image classification. For saliency detection regarding to band selection in HSI, a manifold ranking approach—that is also extended to DL—is presented in [119]. The spectral-spatial residual network found in [120] consists of a supervised deep learning framework that is capable of discriminating features from abundant spectral signatures and spatial contexts in a HSI (provided as input and without the need for feature engineering). In [121], both attribute profile and DL approaches were merged with the goal of classifying HIS. Profiling working together with CNN showed better results than using each of the involved approaches individually. Also, the need for lighter network architectures and deep network types was highlighted. Even for anomaly detection, CNN demonstrated to outperform classical methods such as RX-based approaches [122].

To sum up this section, dimension reduction focuses on data simplification for computational performance improvement while ensuring information conservation. Target detection refers to the identification of some particular feature of interest through imagery spectral profile analysis using pure inference statistics. Full pixel and sub-pixel methods are available for different scenarios. Other types of classification provide extensive analysis and categorization of a whole scene. The machine learning-based approaches can be understood as general classification since their black boxes provide flexible ways of classifying a scene and detecting particular features. For estimating vegetation properties and status, several indices are available. Emerging DL approaches are also strongly contributing to HSI processing with methods that include dimension reduction, classification and anomaly detection.

To deal with the mathematical complexity entangled in pure statistical approaches, several efforts have been made towards the development of software and libraries focusing on hyperspectral data processing. In the next section, several results of such efforts are presented.

5. Software and Libraries for Dealing with Hyperspectral Data

Handling, processing and analyzing hyperspectral data demands skilled workmanship with advanced knowledge in statistics, as it is evidenced in Section 4. Thereby, professionals relying on remote sensing—for example farmers, foresters or even code developers serving agriculture, forestry and related areas—are required to hold that knowledge somehow, either by training courses or by hiring external resources. To tackle with that situation, some entities have been developing efforts to hide the mathematical complexity to those professionals. In this subsection, a brief overview on software tools and programming libraries that represent such efforts will be presented.

Regarding software tools, there are some mature solutions that allow interacting with hyperspectral data and that only demand awareness of the processes to carry out data analysis rather than the inherent mathematical knowledge. For example, Earth Resource Data Analysis System (ERDAS) [123] is a commercial and complex software with a graphical user interface for manipulating not only hyperspectral imagery—for which many of the operations addressed in the previous section, like supervised classification, are supported—but also optical panchromatic, multispectral, radio detection/direction and ranging (RADAR) and light detection and ranging (LIDAR) data. Another tool is the Environment for Visualizing Images (ENVI) software [124], which combines advanced image processing and proven geospatial technology to help in the extraction of meaningful information from all kinds of data and therefore improves the decision making process. Tactical Hyperspectral Operations Resource (THOR) is a special ENVI package that enables orthorectification, atmospheric corrections, and target detection, among other operations, with data cubes. There is also ImageLab [125], which processes data from various spectroscopic imaging techniques, such as submillimeter radiation (THz band), optical, ultraviolet-visible (UV-Vis), infrared, Raman or mass spectrometry. Based on multivariate statistical methods, it enables the user both to analyze and classify acquired hyperspectral images and to merge them with maps of physical properties and high-resolution RGB photos. The convenient user interface gives full control over the vast range of functions. EXPRESSO 13 [126] is the flagship software of Brandywine (a hyperspectral sensors manufacturer). It consists of real-time hyperspectral image processing and control with an intuitive interface and provides all of the standard algorithms (e.g., k-means clustering, matched filtering and MNF transform). Finally, Spectronon [127] is another analysis software that provides tools like hyperspectral classification (e.g., based on SAM and logistic regression) VIs determination, advanced visualization tools and support for user-written Python plugins. It is designed to deal with Resonon’s spectral sensors. Next, available programming libraries for dealing with hyperspectral data processing will be addressed, including some application programming interfaces (APIs) released by companies that also released the aforementioned software tools.

In fact, programming libraries, as it turns out, are in lesser numbers. A free open-source option that seems to be mature is the Spectral Python (SPy) module [128], which is released under GNU general public license (GPL). Documentation seems to be well structured and validated by some published works [79,99]. There is also Hyperspectral Python (HypPy) [129], which works with ENVI file format for images and it can be used along with other software, such as ENVI software. Another option is Hyperspectral Image Analysis Toolbox (HIAT) [130] that consists in a collection of functions for analysis of hyperspectral and multispectral data in Matlab environment. It provides processing methods like discriminant analysis, principal components analysis, Euclidean distance or maximum likelihood, but it seems not covered by developer support anymore [131]. MultiSpec [132] is a freeware processing system for analyzing multispectral and hyperspectral images developed by Landgrebe (author of [67], for example). Also, some of the addressed software tools provide libraries for programmers. For example, ENVI has a so-called interactive data language that is easy to learn and to use, enabling scientists and professionals to make a softer hyperspectral data handling. From Erdas, a C/C++ development kit is available, too. Resonon [127] also shares a programming interface in C++ for those who desire to control hyperspectral imagers, available from the company. However, hyperspectral data processing and analysis seem to not be supported by this API.

Just like for statistical-based hyperspectral data manipulation, some engines and libraries (e.g., Tensorflow [133] and Theano [134]) that support the development of machine/deep learning applications are available.

The next section presents a set of works that combine UAVs, hyperspectral sensors and data analysis, within the scope of agriculture, forestry and related areas.

6. Applications in Agriculture and Forestry Areas

In this section, applications employing hyperspectral data acquisition, processing and analysis for areas related with farming and wild vegetation management will be presented, with a special focus on matters that range from the earlier sowing tasks to post-crop stages, moving through the estimation of parameters (e.g., carotenoid content, biomass and nitrogen) to disease monitoring. Works are presented considering a clear division between agriculture, forestry and agroforestry areas.

6.1. Agriculture

Methods for leaf carotenoid content estimation in vineyards, using high resolution hyperspectral imagery acquired from an UAV are presented in [40]. The atmospheric correction was conducted using total incoming irradiance at 1 nm intervals, simulated with the simple model of the atmospheric radiative transfer of sunshine (SMARTS) developed by the National Renewable Energy Laboratory, Unites States of America (US) Department of Energy (Gueymard, 1995, 2001). Radiative transfer models and scaling-up methods were used to achieve estimations upon 2 years of hyperspectral imagery with good results, although slightly less accurate than in [135], which is a work with similar measuring purposes.

Pölönen et al. [30] used hyperspectral Fabry-Perot and UAVs to estimate biomass and nitrogen. Their approach was tested in field with plantations of wheat and barley. Pre-processing operations involved laboratory calibration, spectral and dark signal corrections. Feature extraction was done using NDVI spectral index, spectral unmixing and spatial features. Estimation was made using a machine learning approach that joins k-nearest neighbor (k-NN) for classification and training data acquired in a laboratory environment.

Corresponding objectives are pursued in [136] using a similar sensor for adverse meteorological conditions, which represented a challenge regarding data processing. According to the authors, varying illumination conditions caused significant radiometric differences between images. However, their radiometric correction was able to reduce grey values variation in overlapping images from 14–18% to 6–8%.

In [41], a multitemporal analysis process of hydrological soil surface characteristics (H-SSC) was applied to Mediterranean vineyards. It was capable of discriminating land classes and translating possible evolutions to decision rules. Classification consists of correcting H-SSC class maps, previously derived from any monotemporal classification (maps are pixel or image-object-based), relying on the comparison between expert knowledge reflected on H-SSC possible evolutions (successors) and a given monotemporal classification. Mechanical and chemical interventions in field are prone of being detected with this approach.

In [49], the authors built their own hyperspectral-based UAS that includes a 960 g hyperspectral sensor capable of capturing 324 spectral bands (or half in the binned mode) between 361 and 961 nm, a multirotor drone, positional/orientation sensors and a power supply unit. Validation experiments included the assessment of chlorophyll content and green biomass of pasture and barley crop, mainly based on calculus involving VIs.

Water status of a lemon orchard was investigated in [137] using field data collection, i.e., leaf-level measurements of chlorophyll fluorescence and PRI data, seasonal time-series of crown temperature and PRI under different regulated deficit irrigation (RDI) treatments. UAS—consisting in a UAV plus thermal and hyperspectral sensors—was used to gather data for analyzing pure crown temperature, radiance and reflectance spectra with the objective of estimate chlorophyll fluorescence, visible ratios and structural indices for water stress detection. Radiometric calibration was made in relation to a calibrated unit light source while atmospheric calibration was carried out by using SMARTS model. Indices-based measurements and FluorMOD model plus FLD3 were applied for fluorescence estimation, which was in agreement with ground measurements.

Verticillium wilt—which is a disease that affects olive cultures in the way that it blocks the water flow at the vascular plant level—was studied by [138] with the use of thermal imagery, chlorophyll fluorescence, structural and physiological indices (xanthophyll, chlorophyll a + b, carotenoids and blue/green/red B/G/R indices) calculated from multispectral and hyperspectral data as early indicators of the infection’s presence and severity.

In [50], chlorophyll densities estimation on rice paddies at low flight altitudes was the main concern. A hyperspectral sensor was assembled to that end, capable of reading 256 bands equally spaced between 340 and 763 nm. Comparisons of the sensor readings to ground truth demonstrated great accuracy in the estimations of chlorophyll density, more specifically at RE and NIR ranges.

The angular effect over several VIs using UAVs and a hyperspectral sensor was studied in [139] with a focus on wheat. The so-called goniometer system uses a structure for motion approach to assess pointing and position accuracy. As main conclusions, the authors stated that their UAV-based goniometer represents a useful mean-step towards the development of correction techniques to attenuate the effects of angular reflections on spectra.

Researchers from National Lab and State University of Idaho in the USA [140] presented several tests on their remote sensing system that evaluates the influence of improved flights on geometric accuracy, mosaicking capabilities and ability to discriminate non-vegetation targets, grasses and shrubs. Unsupervised classification based on k-mean was used for exploring data imagery acquired from the field and a matched filter based on SAM was applied for supervised classification of ground features (e.g., Sandberg bluegrass and bare soil). The former seems to support vegetation management objectives that rely on mapping shrub cover and distribution patterns, while the latter performed poorly, highlighting the need of improving supervised classification procedures.

A study demonstrating the relationship between steady-state fluorescence and net photosynthesis measured under natural light field conditions—both at the leaf and image levels—was carried out by Zarco-Tejada [42], who used a 260-band hyperspectral sensor attached to an UAV to perform tests in twelve production vineyards of Ribera del Duero (northern Spain). Several tests for acquiring parameters on biochemical determination of chlorophyll a + b, carotenoids and anthocyanins, while other parameters (e.g., Leaf steady-state and dark-adapted fluorescence) were collected on the ground to be compared to imagery data from which florescence estimations were taken by using the Fraunhofer Line Depth (FLD) principle. Results point out to a connection between both.

Focusing on wheat fields, Kaivosoja et al. [141] exploited classified raster maps from hyperspectral data to produce a work task for a precision fertilizer application. Flight campaigns were carried out in wheat fields (Finland) to then produce classified raster maps with biomass and nitrogen contents estimation. Such maps were combined with historic data (e.g., yield maps) to generate proper task maps for farm machinery. Some equations relating nitrogen with biomass were used for statistical purposes. Despite the potential usefulness of this kind of estimation practices, the authors stressed out some inaccuracies related with the hyperspectral data processing chain. Perhaps ground measures taken in sparser temporal data could contribute to a more accurate classification, thus improving the results.

6.2. Forestry

A method to derive 3D hyperspectral information from lightweight snapshot sensors on board of UAVs for vegetation monitoring was proposed in [142], based on a structure from motion approach that results in a digital surface model (DSM) as a representation of the 3D space linked to objects’ reflectance. The used sensor provides 125 bands of information the range of 450–950 nm and 21 cm of resolution. Operations around radiometric calibration are extensively documented. Since the center wavelengths and full width at half maximum (FWHM) were provided by the manufacturer, spectral calibration was not carried out.

To identify the presence of bark beetle infestations on Norway’s spruce, Näsi et al. [143] developed a new processing approach to analyze spectral characteristics for high spatial resolution photogrammetric and hyperspectral image data in a forested environment. The used hyperspectral sensor—FPI—is different from most of the others since it has stereoscopic capabilities, which suggest improved accuracy in point cloud gathering and further DSM production. The workflow for analysis includes images’ correction according to laboratory calibrations, creation of a 3D geometric model, determination of spectral image mosaics, identification of individual trees, spectral feature extraction and, finally, classification based on supervised k-NN [144]. For three color classes (healthy, infested, dead), an overall accuracy of 76% was obtained, while 90% was achieved when using 2 classes (healthy, dead).

Small tropical forests were the focus in [145], that presents a work for the assessment of altimetry accuracy involving Bundle Block Adjustment (BBA) with a couple of hyperspectral bands and GCPs. Conclusions were: (1) ground control is needed to improve altimetry accuracy and (2) fewer discrepancies were noticed for the GCPs placed in the image border rather than the ones placed in its corners. Preliminary results showed a discrepancy of around 40 cm in the Z coordinate, which is sufficient for forestry applications.

6.3. Agroforestry

Saari et al. [146] integrated Unmanned Aerial System Innovations (UASI), which is a project that aims to study how useful light weighted UAVs can be in fields related with forestry or agriculture. They start off by pointing out forestry requirements (e.g., tree height estimation and species identification) and crop monitoring applications (e.g., feedstock estimation and nitrogen status assessment) as well as the requirements of UASI systems (collaborative support for farmers or forest professionals). They conclude that FPI is a suitable sensor to be used in the several tasks concerning the system. This sensor was used to demonstrate the technical feasibility of false color and hyperspectral data in forest inventory and agriculture applications. Later, this research group [147] focused in precision agriculture with studies on biomass estimation based on support vector regression machine. Multi-temporal data and point clouds were their main data sources.

Summing up, several works ranging from vegetation status monitoring to disease detection demonstrate how versatile and useful hyperspectral remote sensing using UAVs can be for both agriculture and forestry.

7. Conclusions

UAS are getting increasingly popular in agricultural and forestry insofar as they represent a cost-effective and readily available tool for surveying land and crops, with the purpose of acquiring data for further analysis and to support decision-making and management processes. However, most of the sensors that are commonly applied to that end (e.g., RGB and multispectral sensors) usually only provide information on a very limited number of bands and/or spectral ranges which might not suffice some components that are part of a data set representing a scanned place, such as a forest section or a crop area.

To tackle this issue, hyperspectral sensors—commonly used on satellites or manned aircraft a few years ago—are getting redesigned to be lighter and smaller and, thus, more suitable to be carried by UAVs for earth surface surveying purposes, considering a wider spectral range and narrower bands. Several of these sensors are commercially available and were presented in Section 2, along with a few proposals based on scientific research.

Hyperspectral sensors usually generate huge amounts of data since they retrieve spectra sets composed of hundreds of bands across considerable spatial resolution images. Such dimensionality demands proper analysis and processing methods. The most important ones were presented in Section 4, right before some software tools and programming libraries that implement most of the addressed mathematical approaches. For remote sensing professionals, land surveying technicians and programmers working on applications for agroforestry and related areas, such tools may prove to be relevant.

Works on agriculture and forestry areas involving UAVs and hyperspectral sensors were reviewed, focusing on their main purposes and general processing and analysis approaches. Notwithstanding the considerable number of applications, they seem to be still scarce compared with applications involving UAVs and other types of sensors, probably because of the high prices of high-resolution spectroscopy that can compromise cost-effectiveness on applications around agroforestry and related areas. Another reason for the low number of studies is the complexity of data acquisition and analysis. A higher level of training is needed to acquire the data. Additionally, some researchers [148] expect that hyperspectral sensors will be applied only for research purposes. However, we refuse to agree with that perspective due to the increasing number of market solutions that are contributing to the wide spread of high-resolution spectroscopy devices. Moreover, it is expected that the technological development of upcoming years can bring smaller and more affordable devices, turning hyperspectral-based sensing into a mainstream approach for agriculture, forestry and related areas. Even knowing there is still a long way to go until UAS-based remote sensing using hyperspectral becomes effectively affordable for common farmers and foresters, there is, undoubtedly, a window of opportunity for the dissemination of business models relying on regionalized and cost-effective services supply focusing on this kind of survey and enabling more accurate decision-support tools. With this in mind and following the proposal already presented in [149], future efforts will be developed towards the identification and discrimination of phytosanitary issues affecting vineyards through hyperspectral-based remote sensing carried out using UAVs.