Abstract
We explore the potential of computing coastal ocean surface currents from Moderate-Resolution Imaging Spectroradiometer (MODIS) and Visible Infrared Imaging Radiometer Suite (VIIRS) satellite imagery using the maximum cross-correlation (MCC) method. To improve on past versions of this method, we evaluate combining MODIS and VIIRS thermal infrared (IR) and ocean color (OC) imagery to map the coastal surface currents and discuss the benefits of this combination of sensors and optical channels. By combining these two sensors, the total number of vectors increases by . In addition, we also make use of the different surface patterns of IR and OC imagery to improve the tracking performance of the MCC method. By merging the MCC velocity fields inferred from IR and OC products, the spatial coverage of each individual MCC field is increased by relative to the vectors derived from OC images. The root mean square (RMS) error of the merged currents is 18 compared with coincident HF radar surface currents. A 5-year long time serious of merged MCC computed currents was used to investigate the current structure of the California Current (CC). Weekly, seasonal, and 5-year mean flows provide a unique space-time picture of the oceanographic variability of the CC.
1. Introduction
Mapping of costal surface currents, and their space-time variability, is one of the major challenges in physical oceanography. Surface current estimation methods must have the capability of repeatedly resolving coastal circulation features and their temporal and spatial variations. Coastal ocean currents can be mapped from HF radars [1,2] at high spatial and temporal resolution over the area offshore within a distance of 50 km and up to 200 km off the coast with somewhat reduced spatial resolution and accuracy. But the radars must be deployed near the coast and the best mapping area is confined to the areas adjacent to the coast. In addition, it is hard to deploy them in remote areas and extreme environments without access to the power supply needed to maintain the radar systems. Space-based radar altimetry is extensively used to measure mesoscale currents, but these are geostrophic currents only [3]. Another limitation is that altimetry does not work well near the coastline or in shallow waters [4] due to land contamination of the altimeter signal and of the microwave water vapor radiometer used to correct the altimeter. The ocean surface currents also can be retrieved using Doppler anomaly from Sentinel-1 [5]. This is a new method that can be considered in the future.
The maximum cross-correlation (MCC) method [6], a feature tracking method using sequential satellite imagery, doesn’t have these limitations mentioned above for the coastal ocean. This method has been used to measure a variety of ocean surface currents over the past several decades [6,7,8,9,10,11,12,13,14,15,16,17,18,19]. Its effectiveness for retrieving ocean surface currents from Advanced Very High Resolution Radiometer (AVHRR) thermal infrared (IR) images has been repeatedly demonstrated [6,7,8,9,10,11]. Also, ocean color (OC) images collected from Coastal Zone Color Scanner (CZCS) [12], Moderate-Resolution Imaging Spectroradiometer (MODIS) and Sea-viewing Wide Field-of-view Sensor (SeaWiFS) [9], and Geostationary Ocean Color Imager (GOCI) [13,14,15] have been used successfully to compute the space-time variability of the surface currents. More recently, sequential synthetic aperture radar (SAR) images derived from ERS-2, Envisat [16], TerraSAR-X (TSX) [17], TanDEM-X (TDX) and COSMO-SkyMed (CSK) [18] have also been used with the MCC method to map the space-time variations of coastal currents. Moreover, this MCC method is not region-specific, and has been used to study the current structure in diverse regions such as the California Current [9,11], the Gulf Stream [7,10], the East Australian Current [8,19], the Tsushima Currents [14] and the Kuroshio Current [15].
Previous studies have validated the MCC derived currents as having root mean square (RMS) errors of 8–25 compared with ADCPs, drifters or HF radar currents [8,10,14,20]. Tokmakian et al. [20] proved that the RMS errors between the IR derived MCC currents, and the ADCP and geostrophic velocities estimated from hydrologic data were on the order of 25 . Bowen et al. [8] used 7 years of AVHRR images and compared the MCC currents with geostrophic currents and currents inferred from the trajectories of drifting buoys drifting buoys. The estimate accuracy of the MCC currents was 8–20 . Chubb et al. [10] extracted the surface currents from AVHHR sea surface temperature (SST) imagery and compared the four MCC current fields with HF radar results. The average angle and magnitude of the complex correlation coefficient were 0.663 and , respectively. Warren et al. [14] computed the ocean currents from GOCI imagery over the Tsushima Strait using the MCC method and compared four days of MCC derived currents with HF radar currents finding RMS errors on the order of 20 .
The MCC method using optical imagery is sensitive to cloud cover because it will result in missing data in the cloud covered area and the missing data will decrease the number of current vectors [8,14]. In addition, weak surface tracking features also fail to produce reliable MCC vectors. For thermal IR imagery, isothermal surface conditions nullify the MCC method and produce no vectors. OC imagery can offer complementary data to estimate surface currents under isothermal surface conditions. Crocker et al. [9] combined the IR and OC satellite imagery to compute currents using the MCC method. Their results demonstrated that the two velocity fields agreed well with a mean correlation of 0.74 and a mean RMS difference of 7.4 . By merging the two types of MCC fields, the spatial coverage increased by ∼25%. Yang et al. [13] applied a correlation coefficient based method to merge the individual MCC fields inferred from several OC products. In their study, they only showed one example of merging MCC fields retrieved from the Visible Infrared Imaging Radiometer Suite (VIIRS) satellite images of chlorophyll-a (Chl) concentration and remote sensing reflectance (Rrs) at 551 nm (Rrs551). The total spatial coverage of the merged field increased.
Sensors on polar orbiting satellite can provide global observations for the MCC method. The AVHRR thermal IR imagery was for many years the most commonly used data source for the surface current calculation with the MCC method. For the MCC application, these images must be well geolocated. Emery et al. [21] proposed an MCC-based method to accurately navigate the AVHRR images. This application of AVHRR IR data takes on only a historical perspective as the last and final AVHRR for the afternoon orbit was launched on 6 February 2009. The Earth Observing System (EOS) was intended to provide global observations by the instrumentation aboard the EOS satellites. MODIS, SeaWiFS and VIIRS are all components of the EOS missions. However, SeaWiFS imagery is no longer available for generating OC imagery. Even the two MODIS instruments have exceeded their initial design mission life times. The VIIRS onboard the Suomi National Polar-orbiting Partnership (SNPP) satellite, which launched on 28 October 2011, is the newest sensor producing OC and IR imagery. These images are available near-real-time and are deliverd to the user already navigated and calibrated. Hence, the MODIS and VIIRS provide global thermal IR and OC satellite datasets, which can be used to compute coastal surface currents with the MCC method.
In this paper, we explore the potential of mapping the coastal surface currents by combining MODIS and VIIRS satellite imagery. This paper proceeds as follows. Section 2 introduces our study region, satellite imagery employed and the validation datasets of HF radar currents. Section 3 describes the MCC method, then explores the combination of MODIS and VIIRS imagery to map surface currents with the MCC method. Subsequently, we compare the MCC derived currents with HF radar currents and introduce our MCC current merging method. Section 4 describes the routine computation of the coastal currents over the observation period. We then examine the current space-time variability over the study region in Section 5. Finally, the discussion and conclusion are in Section 6.
2. Study Region and Data
2.1. Study Region
In this paper, our study region is the U.S. West Coast (Figure 1) within the region – N and – W. This area covers a large part of the California Current System (CCS). Crocker et al. [9] and Matthews and Emery [11] mapped the surface currents in this region with the MCC method and their results can be compared with our results. In addition, many HF radars have been deployed along the U.S. West Coast [22] and the HF radar currents are available over our observation period covering the coastal areas out to 200 km off the coast, as marked in grey in Figure 1. These HF radar surface currents can be used to validate the accuracy of the MCC currents. We consider the study region selected in this paper as an example of how the MCC method could be applied to most non-polar coastal regions of the world.
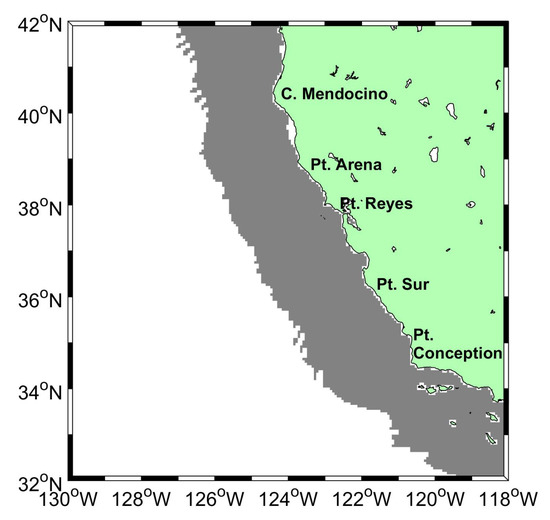
Figure 1.
Map of the study region of the U.S. West Coast, from – N to – W. The HF radar coverage area is in gray.
2.2. Satellite Imagery
MODIS (onboard Aqua (MODISA) and Terra (MODIST) satellites) and VIIRS are polar orbiting satellite sensors which provide global coverage of OC imagery during the day and IR imagery both day and night. We studied the statistics of the re-visit times over our study region based on the IR imagery over the year 2015 as shown in Figure 2. Aqua and SNPP satellites have a high overlap of the re-visit period both during daytime and nighttime, but they also exhibit important differences. The Terra satellite has few overlaps with Aqua and SNPP in the daytime and has totally different coverage during the nighttime. Table 1 shows the re-visit periods of the three satellites. By combining the satellite imagery collected from MODIS with VIIRS, we can acquire more image pairs for our MCC current calculations.
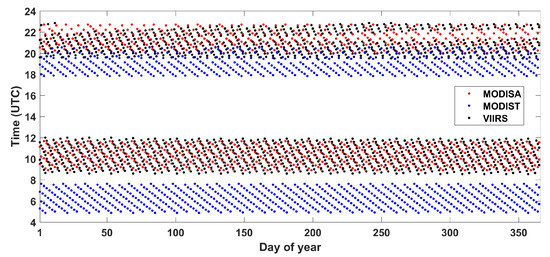
Figure 2.
Visit time of MODIS and VIIRS sensors over the study region in 2015.

Table 1.
The IR and OC products used in this paper.
MODIS and VIIRS can provide IR and many OC products derived from different channels. The imagery selected in this paper are shown in Table 1. Both MODIS and VIIRS can produce IR (11 m channel), Chl, diffuse attenuation coefficient at 490 nm (Kd490) and the Rrs() (where is the wavelengths, and MODIS has 10 bands including 412, 443, 469, 488, 531, 547, 555, 645, 667 and 678 nm while VIIRS instruments has 5 bands including 410, 443, 486, 551 and 671 nm) datasets. The common products of the MODIS and VIIRS are IR, Chl, Kd490 and Rrs443. Each of these products can be used to retrieve coastal surface currents independently. In this paper, we used the MODIS and VIIRS SST and OC images from 1 January 2012 to 31 December 2016.
2.3. HF Radar Currents
Coastal-based HF radars, along the California coast, provide real-time maps of coastal surface currents out to 50 km at high spatial and temporal resolution [1,22]. These currents extend out to 200 km but with slightly reduced spatial resolution and accuracy. HF radars cover the entire portion of the coast of the study region (see Figure 1) and provide hourly surface currents resampled to 6 km spatial resolution in any weather condition over the observation period and are available from the Coastal Observing Research and Development Center (http://cordc.ucsd.edu/projects/mapping/maps/). We use these results to validate the accuracy of the MCC derived currents.
3. Methodology
3.1. MCC Method
The MCC method is an ocean surface current retrieval method, which automatically calculates the current vector as the displacement of image features between a template window in the first image and the matching features found from the maximum MCC in the larger search window in the second image (Figure 3). The derived current is defined as the location of the maximum correlation in the search window in the second image from the starting position in the template window in the first image. The current vector is estimated by dividing the displacement vector by the time interval of the sequential images [6,9]. Previous studies have demonstrated the MCC method’s effectiveness using IR, OC and SAR satellite imagery.
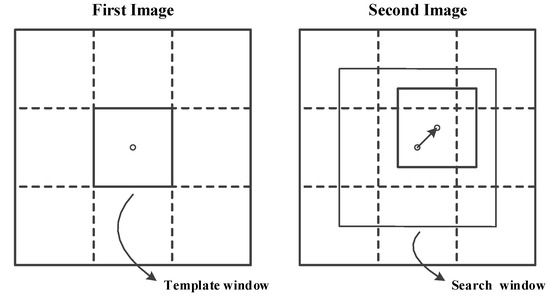
Figure 3.
Schematic of the MCC method.
The time separation of the sequential images, the sizes of the template and search windows are the primary parameters that determine the performance of the MCC method. Previous studies demonstrated that the MCC method performs well when the time separation of the IR and OC images is between 3 and 24 h. The size of a good template window is pixels ( km), which has been used in our study region as recommended by [9,11]. The size of the search window needs to be large enough to accommodate the maximum velocity expected in the study region. In our study region, the most probable maximum velocity is 70 [9]. After the initial MCC calculation, several post-filters are proposed to remove the noisy and including erroneous vectors [9]. This involves a correlation cut-off and a next neighbor smoothing function.
3.2. Combination of MODIS and VIIRS Imagery
In this section, we explore the possibility of retrieving ocean currents from sequential imagery at different spatial resolutions collected from MODIS and VIIRS, respectively. VIIRS has a higher spatial resolution of ∼0.75 km relative to MODIS with a resolution of ∼1.1 km (see Table 1). Hence, we resample the VIIRS imagery to the same spatial resolution as MODIS using a triangulation-based cubic interpolation method. Once the resampled imagery has the same georegistration accuracy, we can apply the MCC method to the combination of the MODIS and VIIRS imagery. Two images from MODIS and VIIRS, having a short time separation, were selected to assess the practicality of computing coastal currents from MODIS and VIIRS images with the MCC method. The bias, RMS and correlation coefficients are selected as metrics to evaluate the accuracy of the results.
First, we compare the resampled individual VIIRS images with MODIS. Figure 4a,b show two Chl images provided by MODIS and VIIRS with a time interval of 5 min. The VIIRS Chl image is resampled to the same spatial resolution of 1.1 km as is native for MODIS. The prominent pattern of the two images are similar. Areas close the coast have higher values. We assume that the Chl pattern over the study region in such a short time interval, experiences relatively little change. In Figure 4c, we present the spatial difference between Figure 4a,b where we have subtracted MODIS image from the resampled VIIRS image. Consistent with the cloud-detection algorithm, some pixels in the non-nadir area are omitted [23]. Both in Figure 4b,e, the area on the right of the dashed line exhibits a lack of data while to the left of the dashed line is the nadir area, which agrees well. We do not compare the non-nadir areas. There is a relatively large difference near the coast with values on the order of 0.8 . The area far off the cost exhibits almost no differences. The number of pixels, bias, RMS and correlation coefficients are 314,453, −0.04 , 0.22 and 0.94, respectively (see Figure 5a). In Figure 4d,e, we present two IR images obtained from nearly coincident MODIS and VIIRS images. These images also have similar patterns. Relative to the Chl images, the IR images have slightly better spatial coverage, even in the blank areas in the Chl image due to the very different cloud filter methods. However, these areas do exhibit larger errors in Figure 4f compared with the overlapping areas covered with data. In the southeast portion of the image, there is cloud cover both in Figure 4a,b, but in the same area, a cold feature is revealed in Figure 4d,e while the adjacent region has higher temperatures. The temperature difference of the two images is ∼4 K. In addition, the western portion of the study region is covered by cloud resulting in missing data in the Chl images. But in the IR images, many individual pixels with lower temperature appear in the cloud covered areas likely due to sub-pixel cloud contamination. The temperature difference in this area is ∼5 K. These results imply that the cloud covered area in the IR images has low reliability in the SST values because the cloud filtration, and atmospheric correction methods are different. These patterns may produce spurious vectors. Hence, we mark the cloudy pixels in the Chl images and apply this cloud filter to the SST images to remove the cloudy pixels in the SST images. Comparison of Figure 4d,e are shown in Figure 5b, the number of pixels, bias, RMS and correlation coefficients are 314,453, −0.28 K, 0.31 K and 0.99, respectively. The differences may come from the differences between the sensors of the two satellites, the proposed resampling and regridding method. Our results demonstrate the resampled VIIRS Chl and IR images have significantly similar characteristics with the MODIS images and they are on the order of accuracy of the results in [23].
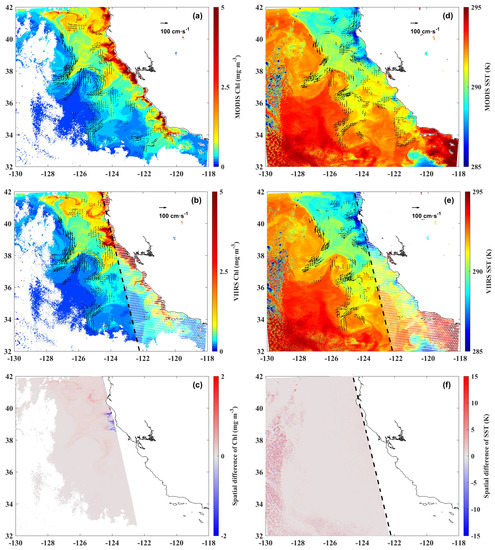
Figure 4.
Chl imagery from (a) MODISA at 21:47; and (b) VIIRS at 21:42, 1 October 2014 UTC and MCC vectors derived from these images and the corresponding Chl image from MODIST at 18:32, 1 October 2014 UTC. (c) is the spatial difference of (a,b); The non-nadir area of the VIIRS is avoided. SST imagery from (d) MODISA and (e) VIIRS at the same time and MCC vectors derived from these images and the MODIST images used in (a,b); (f) is the spatial difference of (d,e). Number of vectors in (a,b,d,e) is 773, 653, 609, 450, respectively.
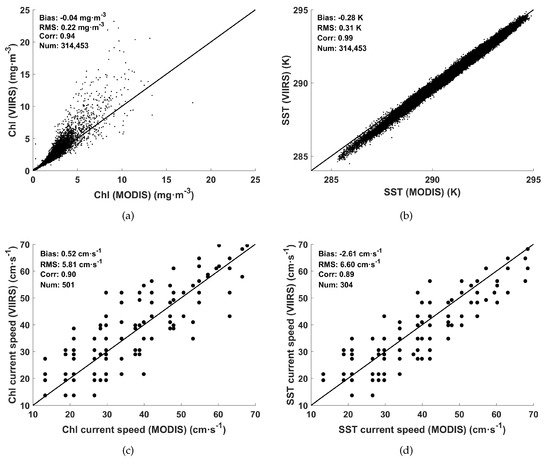
Figure 5.
Comparisons of (a) Chl and (b) SST images derived from MODISA (at 21:47) and VIIRS (at 21:42); (c) Chl MCC currents and (d) SST MCC currents derived from MODIST images (at 18:32) and MODISA (at 21:47) and VIIRS (at 21:42) images, respectively.
Second, we apply the MCC method to the combination of the resampled VIIRS and MODIS imagery. A MODIST image pair at 18:32 on the same day as the VIIRS image pair is used to retrieve the MCC coastal surface currents. There are strong similarities between the two velocity maps in Figure 4a,b, and Figure 4d,e, respectively. Additionally, we also quantitatively compare these velocity maps where the MCC vectors derived from MODISA are used to validate the accuracy of the VIIRS derived vectors. Figure 5c,d present the comparisons between the MODISA and VIIRS derived velocities. The number of vectors, bias, RMS and correlation coefficients of the Chl field are 501, 0.52 , 5.81 and 0.90, respectively and for the SST field, the results are 304, −2.61 , 6.60 and 0.89, respectively. These velocity differences between the MCC and HF radar vectors may come from the weighted average method, the depth of the estimated currents and the regridding method. The MODIS image produces more vector velocities than VIIRS because the non-nadir area of the VIIRS doesn’t produce any vectors. The quantitative results show that the VIIRS derived velocities have the same accuracy as MODIS derived velocities. It demonstrates that it’s possible to estimate the coastal surface currents by combining MODIS and VIIRS satellite imagery using the MCC method. By combining MODIS and VIIRS, more image pairs can be used to compute MCC velocities.
3.3. Comparison with HF Radar Currents
HF radar currents over the U.S. West Coast at 6 km spatial resolution are available over the entire observation period for comparisons with the MCC derived currents in our study region. To compare the MCC currents with HF radar currents, we selected an overlap of 17 pixels between the template windows in the first image in Figure 3 to get an output with ∼5.5 km spatial resolution. Then the MCC currents were regridded to the same grid points as the HF radar currents at a 6 km resolution. The HF radar currents with magnitudes less than the MCC velocity resolution or greater than the maximum expected velocity (70 ) for this area were discarded. The hourly HF radar currents were composited using a linear weighting method developed by [10] to coincide with the time interval of the MCC derived currents. In Figure 6, we show the plots of regridded MCC currents derived from the imagery products shown in Table 1 together with the HF radar currents. We show a small portion of the coastal region MCC currents and HF radar currents, which together indicate the same general circulation pattern. There are, however, are some disagreements between the MCC vectors and HF radar vectors in Figure 6. In addition, these plots also reveal the disagreements between the MCC currents derived from different datasets. Hence, several quantitative analysis methods are proposed below to evaluate the source of these disagreements.
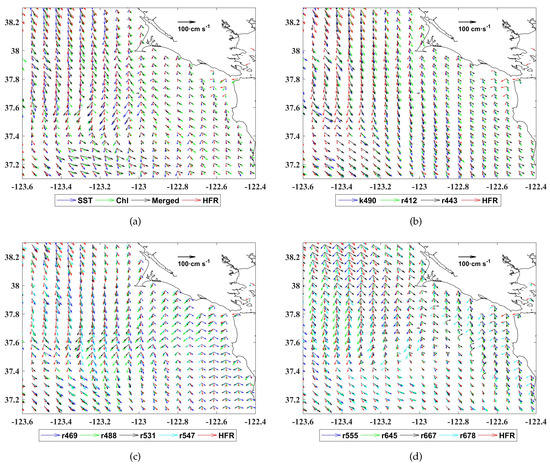
Figure 6.
Plots of the regridded MCC currents derived from (a) SST, Chl, Merged; (b) Kd490, Rrs412, Rrs443; (c) Rrs469, Rrs488, Rrs531, Rrs547; and (d) Rrs555, Rrs645, Rrs667 Rrs678 and the overlapping HF radar currents at 6 km spatial resolution, respectively. The maps of the MCC currents is from MODIST at 18:50 and MODISA at 22:07, 16 April 2015 UTC.
(1) Complex Correlation: To obtain a quantitative analysis of the agreement between of the MCC and HF radar derived currents, we calculated a complex correlation [24]
where the 2-D velocity field for either HF radar and MCC velocities is denoted as a complex number V defined by . and represent the MCC and HF radar derived current fields, respectively. Then the average magnitude correlation coefficient can be computed as
and the average angular phase difference between the derived velocity fields is defined as
The magnitude correlation indicates the relative magnitude difference between the two datasets. The phase angle is an average anticlockwise rotation of the HF radar vectors with the MCC vectors, and only when the magnitude correlation is high, it is meaningful.
(2) Residuals: To quantify the relationship between the MCC and HF radar currents, we computed the residuals between the two datasets
where i is the index of the corresponding pixel of the two datasets; is scalar value that represents the u- (zonal) component, v- (meridional) component, magnitude and direction of the current vector or the complex correlation coefficient estimated with the MCC method; is the corresponding value estimated from HF radar. In Figure 7, we present the histograms of the magnitude and phase angle residuals between the MCC vectors and HF radar vectors. The accuracy of these results is on the order of the results in [10,14].
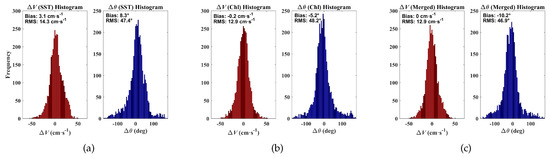
Figure 7.
Histograms of frequency of phase angle and magnitude between (a) SST; (b) Chl and (c) merged currents and HF radar currents.
The bias and RMS error of the residuals can be computed as
where N is the number of overlapping pixels of the datasets.
Without loss of generality, 60 pairs of cloud-free sequential images over the observation period, with overlapping areas near the coast with a time separation of ∼3 h, have been used to compute the coastal surface currents with the MCC method. These results are then compared with the HF radar currents to assess the accuracy of the MCC surface current fields derived from these different satellite datasets. As introduced, we calculated the RMS errors of the u- and v- components, magnitude and phase and complex correlation coefficient of each individual velocity field. Figure 8 shows boxplots of the RMS results derived from different satellite datasets. From Figure 8a, we see that the upper and lower limits of RMS of the u- and v- components derived from the Rrs412 and Rrs645 imagery are higher than those of the other parameters and they also have higher median RMS values. Also, the RMS of the magnitude of the two products is higher than other satellite datasets (Figure 8b). In addition, the currents extracted from the two datasets have a wider range of magnitude correlation coefficient that ranges from 0 to 0.78 with a median value lower than the others (Figure 8c). According to the above analysis, the Rrs412 and Rrs645 derived currents have relatively poor accuracy. They are not considered representative of coastal surface currents and are not used in the following sections.

Figure 8.
Comparisons of MCC and HF radar currents. Boxplot of RMS of (a) the u- and v- components; (b) magnitude and phase angle and (c) complex correlation coefficient from the 60 image pairs.
3.4. Multiple MCC Source Image Current Merging
AVHRR only provides IR imagery, while GOCI and SeaWiFS are limited to OC imagery only. MODIS and VIIRS can provide both IR and OC images during daytime and IR also at night. This makes it an advantage to merge the MCC currents derived from both IR and OC sequential images. Each gridded pixel area yields several vectors derived from different data sources. Each velocity has its own cross-correlation coefficient which denotes the degree of matching in the patterns of the sequential images. Hence, we can merge the MCC currents extracted from different kinds of imagery based on the cross-correlation coefficient. Considering the accuracy analysis in Section 3.3, the Rrs412 and Rrs645 derived MCC vectors have relative lower accuracies than the other data types. Moreover, the Rrs645 also produces fewer vectors than that of any other imagery (see Figure 9). Thus, we avoided using the MCC fields inferred from Rrs412 and Rrs645 in the following sections. Given that the currents derived from the other datasets have the same order of accuracy, we can merge these current fields using a linearly weighted sum. Assume M MCC fields do exist at a certain pixel, and the merged vector can be calculated as
where and () are the cross-correlation coefficient and u- (v-) component constructed from the ith satellite imagery, respectively.
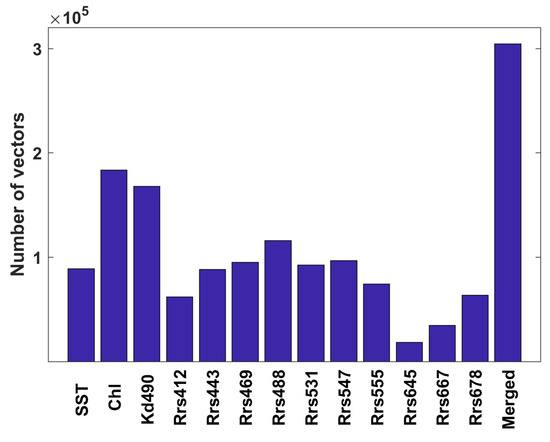
Figure 9.
Histogram of total number of vectors derived from different satellite datasets.
By merging the MCC surface current fields derived from different satellite imagery, the spatial coverage of each individual MCC current field will be increased because the various trackable surface features produce complimentary velocities in different areas. Since the California Coast is one of the most famous upwelling areas in the world and the phytoplankton production over this area is rich, the Chl imagery has stronger surface patterns. The Chl product produces more vectors than other features and are almost double the others in total number. The patterns defined by the various OC channels must have been sufficiently different that a different number of vectors was computed for each. OC channels are also very susceptible to atmospheric contamination and it may be that the atmospheric correction is better in one channel than in another, resulting in the difference of number of vectors of different channels. Also, the number of merged vectors significantly increases. Using the proposed merging method (6), the number of vectors increased by and over the number of Chl or SST only vectors, respectively.
We have also assessed the accuracy of the merged currents. The merged vectors show good agreement with the HF radar currents visually (Figure 6a) and the quantitative comparison of the merged currents with the coincident HF radar currents in Figure 7c demonstrates that the merged currents maintain the same order of accuracy as with the individual Chl and IR MCC currents. Furthermore, the boxplots of the RMS errors in Figure 8 imply that the merged currents are more stable and maintain the same level of accuracy as the Chl only derived MCC currents. Table 2 lists the mean RMS errors of the 60 samples. The merged results have the greatest number of vectors, and maintain the overall accuracy of the MCC method.

Table 2.
The IR and OC products used in this paper.
4. Routine MCC Current Computation
4.1. Image Selection
We grid the imagery to the array values we need for the MCC computation and the images with less than percent of data coverage (due primarily to cloud cover) are removed from consideration. In addition, the missing data will decrease the cross-correlation coefficients resulting in unreliable vectors [8]. Hence, the corresponding coverage between the sequential images needs to be considered. We computed the MCC currents from Chl images over the entire observation period. The computational results are shown in Table 2 where there are ∼4200 current fields each year and also for each year ∼3200 current fields have no vectors due to cloud cover or weak surface pattern features. An overlapping test technique is proposed to reduce the computation from sequential images that produce no vectors. We mark the overlapping area with data between the sequential images and calculate the percentage of the pixels that are identified as not being clouds. Then an overlapping threshold is set to identify those areas where no vector pairs will be available. We then set the threshold from to with an interval of . As displayed in Figure 10a, the vector loss increases as the threshold improves because there are more overlapping data between the sequential images. When this threshold is under , the number of vectors lost is within 200. If the threshold is higher than , the number of vectors lost increases significantly. Furthermore, higher thresholds imply the removal of more vector pairs that would need to be processed. From Figure 10b, we know that the percentage reduction in the number of no vector fields increases as the threshold increases. When the threshold is more than , the reduction ratio increases slowly. According to the above analysis, we set the overlapping threshold to to decrease the number of the computational image pairs having a reduction in the number of vectors.
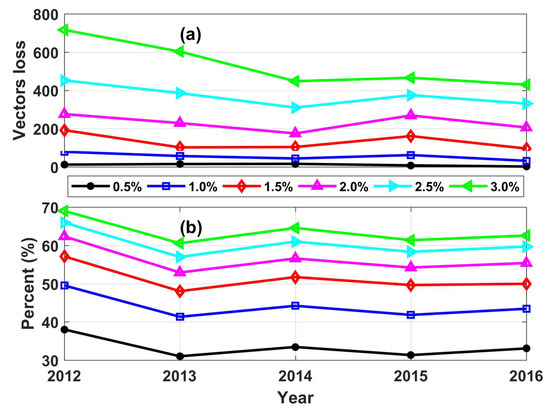
Figure 10.
To evaluate the influence of the overlapping threshold against (a) the number of vector loss and (b) percent of MCC fields avoided to be computed.
In addition, in an effort to improve the computational efficiency of each individual MCC field, we applied an efficient search method developed by Liu et al. [15] to decrease the computational time of the MCC method. More details can be found in their research. By combining these strategies, the computational performance and efficiency of the MCC method is improved making it easy to compute the coastal currents.
4.2. Number of Vectors
We computed the MCC currents over the study region for the observation period and the individual MCC fields estimated from different satellite imagery, which were then merged to increase the spatial coverage of the MCC current fields. In Figure 11, we present the total number of monthly MCC merged vectors for the entire observation period. The MODIS satellite datasets produce more vectors than that of the VIIRS (combination) datasets. By the combination of the current vectors computed from the VIIRS images, the total number of vectors increases over that of the MODIS alone. A seasonal trend was clearly exhibited in Figure 11 due to the sea surface trackable features and the cloud cover climatology of the study region.
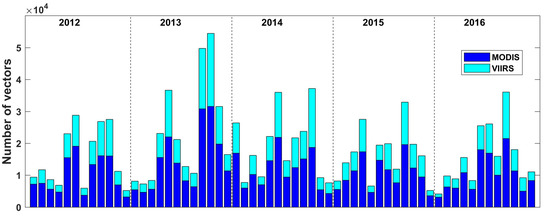
Figure 11.
Total number of monthly MCC merged vectors over the 5-year observation period.
4.3. MCC Current Composites
We have proposed merging MODIS and VIIRS imagery derived currents to improve the spatial and temporal coverage of the individual MCC velocity field presented in Section 3.4. Unfortunately, this method can’t always fill in the individual cloud covered areas. Thus, we made MCC current composites over time for period of 7 days. The 7-day MCC composites have the original grid box of pixels ( km) and the seasonal composites are with a grid box of pixels.
Figure 12a depicts the number of composite vectors over the observation period (261 weeks). The mean weekly number of vectors produced by the 7-day composites is 719. The histogram of the total number of vectors is shown in Figure 12b, where most of the weeks produce from 400 to 1300 vectors. In addition, we also analyzed the spatial coverage of the 7-day MCC composites in Figure 12c. The coastal areas offshore ∼400 km have the highest data coverage on the order of 60 and higher. The number of vectors declines as the distance offshore increases.
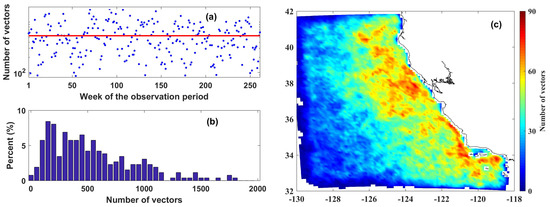
Figure 12.
(a) Number of the 7-day MCC composite vectors; (b) histogram of total percent of number of vectors and (c) spatial coverage of MCC vectors over the observation period. The red line in (a) is the mean number of vectors and the value is 719.
5. California Current System Observation
5.1. 5-Year MCC Mean Flows
To investigate the current system in our study region, we computed the multi-year mean flows based on the 7-day composites. Centurioni et al. [25] revealed four permanent meanders in the CCS. As our study region is slightly smaller, only three of them are captured in our 5-year mean flows (Figure 13), which has almost the same structure as the 12-year mean flows calculated by Matthews and Emery [11]. The first offshore jet structure originates north of Cape Mendocino, flows southward with a width of ∼200 km and mean current speeds of ∼15 . The second jet exits between Point Arena and Point Reyes, also with a width of ∼200 km and higher mean current speeds of 25 , extending to ∼350 km offshore. The third jet is investigated to the north of Point Conception and the offshore current flows southward quickly with mean current speeds of 20 .
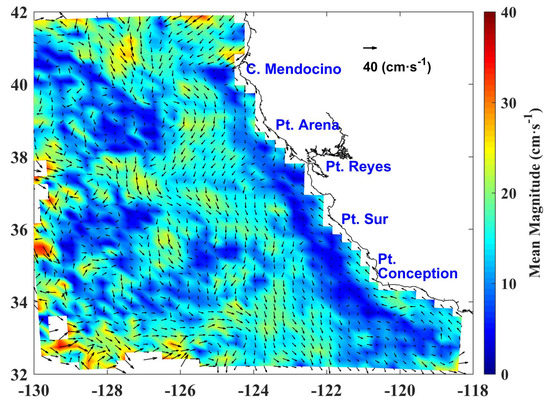
Figure 13.
Time-averaged mean currents (colors show magnitude while the vectors show the currents) from 5 years of MCC currents.
5.2. Weekly MCC Composites
To smooth the current fields and fill in the blank areas of the 7-day MCC composites, we used the optimal interpolation (OI) method based on the covariance matrix computed from the 5-year mean flows over the study region. More details can be found in [26]. The OI algorithm also provides the MCC-OI mapping errors. The mean mapping errors are presented in Figure 14. Reflecting on Figure 12c, the spatial distribution of the OI error map has many similarities with the MCC vector coverage as it should have. The lowest error is located in the center of the study region where the vector coverage is the highest. The offshore area within 500 km along the California coast has mapping errors under .
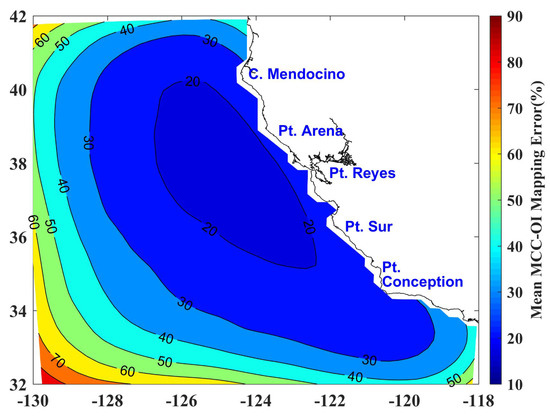
Figure 14.
The MCC-OI mapping error expressed as percent of the signal variance.
The CCS is eddy-rich [27,28] and the MCC-OI maps provide surface currents with sufficiently high spatial resolution to depict these mesoscale features and study their oceanographic variabilities over the study region. In Figure 15a,b, we present two continuous 7-day MCC-OI maps. The ocean circulation patterns of both weeks are similar. The coastal jet between N and N flows equatorward in late-April and early-May. An anticyclonic eddy centered at N, W is captured in the first week and it moves offshore and gets stronger from the first week to the second. One eddy dipole is revealed by Figure 15. The eddy dipole is in the southeast portion of the study region. Our results observe the evolution of this eddy dipole and a cyclonic eddy over the two weeks. A cyclonic eddy centered at N, W in the first week, moves southeastward, then interacts with the offshore cyclonic eddy of the eddy dipole, forming a new eddy dipole with a stronger cyclonic eddy, as discussed by Simpson and Lynn [29]. The third jet mentioned in Section 5.1 is also investigated in the two weeks.
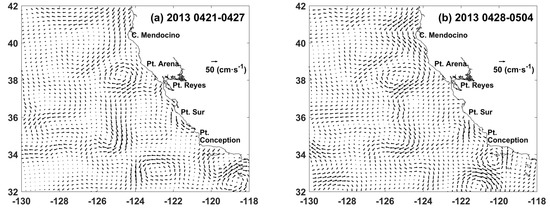
Figure 15.
7-day MCC-OI maps start from (a) 21 April 2013 and (b) 28 April 2013.
The 7-day surface current maps clearly show the evolution of these two eddy dipoles in the CCS. This provides strong evidence of the representativeness of the MCC method for estimating coastal surface currents and investigating the complex oceanography variability in coastal area.
5.3. Seasonal MCC Mean Flows
The study region is the central area of the CCS, including the persistent equatorward flow of the surface CC, the California Undercurrent (CU) that is a poleward subsurface current and the Davidson Current (DC) that is also a poleward current that occurs seasonally during the winter and fall near and north of Point Conception [30].
The CC in our study region exhibits significant seasonal variations. To investigate this variability, we computed the seasonal mean flows for 2013 since this year had the greatest number of MCC vectors for all the years that we studied. In winter (Figure 16a), the coastal velocities reveal a complex structure, but the poleward DC is not evident. The offshore CC tends to move closer to the shore in winter. One inshore cyclonic eddy lies along the path of the DC and it is located between Point Sur and Point Conception and the other one is near Point Reyes. Two eddy dipoles are observed, one is near Cape Mendocino and the other is near Point Arena. In spring (Figure 16b), the pattern of the surface flow over the study region is predominantly equatorward and more eddies are seen in the spring. The coastal jet flows equatorward from north of Point Conception. The eddy dipole near Cape Mendocino moves inshore from winter to spring and the eddy dipole near Point Mendocino moves westward during this period. The eddy in the path of the DC dissipates in spring. Several offshore eddies are also captured in our results. A cyclonic eddy forms to the south of Cape Mendocino in spring. The southwestward flow starts to meander at N, W, with the surface flows to the southwestward. In summer (Figure 16c), the inshore and offshore CC both flow equatorward and the offshore CC meanders are seen from the north ( N) to the south ( N). The CC weakens or reverses in the southern area. The offshore flows between Point Arena and Point Sur coincide with the strong upwelling during the summertime. The cyclonic eddy to the south of Point Conception in spring moves offshore over summer, and instead, an anticyclonic eddy forms in that area. Moreover, an eddy dipole forms at N, W. In fall (Figure 16d), the CC flows equatorward and the poleward DC is not evident inshore. The CC increases the complexity from summer to fall. Several eddies are captured in the fall plots.
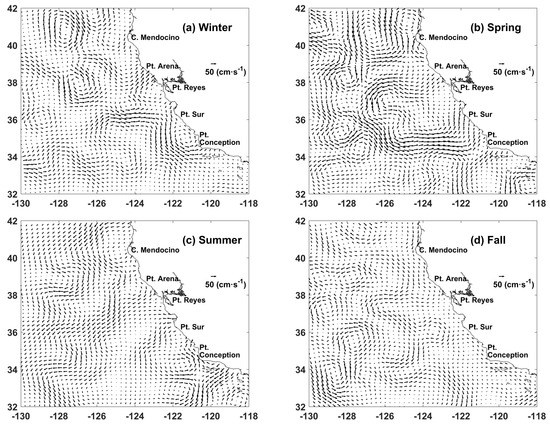
Figure 16.
Seasonal MCC mean flows of 2013. (a) winter (January–March); (b) spring (April–June); (c) summer (July–September); and (d) fall (October–December).
6. Discussion and Conclusions
In this paper, we explore the potential to map the coastal currents using the improved MCC method from the combination of MODIS and VIIRS imagery. We use imagery from the CC region off the western U.S. Evidence demonstrates the viability of the MCC method to compute reliable coastal surface currents. First, we examined coincident imagery over the study region to analyze the temporal resolution of the imagery (Figure 2). Second, we explored the possibility of extracting the coastal surface currents from the combination of MODIS and VIIRS satellite images. It is possible to apply the MCC method to sequential MODIS and VIIRS imagery merged together. The combination of the MODIS and VIIRS datasets increases the total number of vectors by . Third, the MCC surface currents computed from 60 pairs of cloud free images were examined to map the coastal surface currents and HF radar current maps are used as comparisons to validate the accuracy of the MCC current fields. Fourth, several satellite datasets were selected for merging the different MCC fields. This strategy makes use of different trackable surface features to improve the robustness of the MCC method for estimating surface currents. The merged surface current results increased by of the spatial coverage of the individual fields relative to the Chl fields alone. Moreover, after merging the MCC fields, the merged fields also maintain the same level of current accuracy. Based on the routine MCC maps, we compute the weekly, seasonal and 5-year mean flows, which are used to investigate the current structure of the study region. These results show substantial agreement with the previous studies [11,29,30].
In conclusion, we introduce a coastal surface current computational procedure based on the improved MCC method and demonstrated the effectiveness of this current retrieval method for our study region. By the combination of IR and OC datasets, we plan to estimate the surface displacement with these different surface features. In future work, we can explore the potential of computing the global coastal surface currents using the improved MCC method with MODIS and VIIRS data due to the MCC method’s non-region-specific character.
Acknowledgments
This work was supported in part by 863 High Technology Project of China under Grant 2012AA091701, in part by the National Natural Science Foundation of China under Grant 61401316, and in part by China Scholarship Council under Grant 201506270074. Thanks for NASA Goddard Space Flight Center, Ocean Ecology Laboratory and Ocean Biology Processing Group for support of the MODIS and VIIRS data (https://oceandata.sci.gsfc.nasa.gov/). The HF radar currents used in the paper are acquired from Coastal Observing Research and Development Center (http://cordc.ucsd.edu/projects/mapping/maps/).
Author Contributions
Jianfei Liu, William J. Emery and Xiongbin Wu conceived and designed the experiments; Jianfei Liu computed the MODIS and VIIRS data; Jianfei Liu, Lan Zhang, Miao Li and Chuan Li mapped and analysed the results; Jianfei Liu and William J. Emery wrote the paper.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Barrick, D.E.; Evans, M.; Weber, B. Ocean surface currents mapped by radar. Science 1977, 198, 138–144. [Google Scholar] [CrossRef] [PubMed]
- Georges, T.; Harlan, J.; Lematta, R. Large-scale mapping of ocean surface currents with dual over-the-horizon radars. Nature 1996, 379, 434–436. [Google Scholar] [CrossRef]
- Emery, W.J.; Baldwin, D.G.; Matthews, D.K. Sampling the mesoscale ocean surface currents with various satellite altimeter configurations. IEEE Trans. Geosci. Remote Sens. 2004, 42, 795–803. [Google Scholar] [CrossRef]
- Roesler, C.J.; Emery, W.J.; Kim, S.Y. Evaluating the use of high-frequency radar coastal currents to correct satellite altimetry. J. Geophys. Res. Oceans 2013, 118, 3240–3259. [Google Scholar] [CrossRef]
- Johnsen, H.; Nilsen, V.; Engen, G.; Mouche, A.A.; Collard, F. Ocean doppler anomaly and ocean surface current from Sentinel 1 tops mode. In Proceedings of the 2016 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Beijing, China, 10–15 July 2016; pp. 3993–3996. [Google Scholar]
- Emery, W.J.; Thomas, A.; Collins, M.; Crawford, W.R.; Mackas, D. An objective method for computing advective surface velocities from sequential infrared satellite images. J. Geophys. Res. Oceans 1986, 91, 12865–12878. [Google Scholar]
- Emery, W.J.; Fowler, C.; Clayson, C. Satellite-image-derived Gulf Stream currents compared with numerical model results. J. Atmos. Ocean. Technol. 1992, 9, 286–304. [Google Scholar] [CrossRef]
- Bowen, M.M.; Emery, W.J.; Wilkin, J.L.; Tildesley, P.C.; Barton, I.J.; Knewtson, R. Extracting multiyear surface currents from sequential thermal imagery using the maximum cross-correlation technique. J. Atmos. Ocean. Technol. 2002, 19, 1665–1676. [Google Scholar] [CrossRef]
- Crocker, R.I.; Matthews, D.K.; Emery, W.J.; Baldwin, D.G. Computing coastal ocean surface currents from infrared and ocean color satellite imagery. IEEE Trans. Geosci. Remote Sens. 2007, 45, 435–447. [Google Scholar] [CrossRef]
- Chubb, S.R.; Mied, R.P.; Shen, C.Y.; Chen, W.; Evans, T.E.; Kohut, J. Ocean surface currents from AVHRR imagery: Comparison with land-based HF radar measurements. IEEE Trans. Geosci. Remote Sens. 2008, 46, 3647–3660. [Google Scholar] [CrossRef]
- Matthews, D.K.; Emery, W.J. Velocity observations of the California Current derived from satellite imagery. J. Geophys. Res. Oceans 2009, 114. [Google Scholar] [CrossRef]
- Garcia, C.A.; Robinson, I.S. Sea surface velocities in shallow seas extracted from sequential coastal zone color scanner satellite data. J. Geophys. Res. Oceans 1989, 94, 12681–12691. [Google Scholar] [CrossRef]
- Yang, H.; Arnone, R.; Jolliff, J. Estimating advective near-surface currents from ocean color satellite images. Remote Sens. Environ. 2015, 158, 1–14. [Google Scholar] [CrossRef]
- Warren, M.; Quartly, G.; Shutler, J.; Miller, P.; Yoshikawa, Y. Estimation of ocean surface currents from maximum cross correlation applied to GOCI geostationary satellite remote sensing data over the Tsushima (Korea) Straits. J. Geophys. Res. Oceans 2016, 121, 6993–7009. [Google Scholar] [CrossRef]
- Liu, J.; Emery, W.J.; Wu, X.; Li, M.; Li, C.; Zhang, L. Computing Ocean Surface Currents from GOCI Ocean Color Satellite Imagery. IEEE Trans. Geosci. Remote Sens. 2017. [Google Scholar] [CrossRef]
- Qazi, W.A.; Emery, W.J.; Fox-Kemper, B. Computing ocean surface currents over the coastal California Current System using 30-min-lag sequential SAR images. IEEE Trans. Geosci. Remote Sens. 2014, 52, 7559–7580. [Google Scholar]
- Emery, W.J.; Gade, M.; Romeiser, R. Coastal Ocean Surface Current Retrievals from Sequences of TerraSAR-X Images. In Proceedings of the IEEE International Conference on Geoscience and Remote Sensing Symposium, IGARSS 2006, Denver, CO, USA, 31 July–4 August 2006; pp. 1926–1929. [Google Scholar]
- Ren, Y.; Li, X.M.; Gao, G.; Busche, T.E. Derivation of Sea Surface Tidal Current From Spaceborne SAR Constellation Data. IEEE Trans. Geosci. Remote Sens. 2017, 55, 3236–3247. [Google Scholar] [CrossRef]
- Bowen, M.M.; Wilkin, J.L.; Emery, W.J. Variability and forcing of the East Australian Current. J. Geophys. Res. Oceans 2005, 110. [Google Scholar] [CrossRef]
- Tokmakian, R.; Strub, P.T.; McClean-Padman, J. Evaluation of the maximum cross-correlation method of estimating sea surface velocities from sequential satellite images. J. Atmos. Ocean. Technol. 1990, 7, 852–865. [Google Scholar] [CrossRef]
- Emery, W.J.; Baldwin, D.; Matthews, D. Maximum cross correlation automatic satellite image navigation and attitude corrections for open-ocean image navigation. IEEE Trans. Geosci. Remote Sens. 2003, 41, 33–42. [Google Scholar] [CrossRef]
- Kim, S.Y.; Terrill, E.J.; Cornuelle, B.D.; Jones, B.; Washburn, L.; Moline, M.A.; Paduan, J.D.; Garfield, N.; Largier, J.L.; Crawford, G.; et al. Mapping the US West Coast surface circulation: A multiyear analysis of high-frequency radar observations. J. Geophys. Res. Oceans 2011, 116. [Google Scholar] [CrossRef]
- Cao, C.; Xiong, J.; Blonski, S.; Liu, Q.; Uprety, S.; Shao, X.; Bai, Y.; Weng, F. Suomi NPP VIIRS sensor data record verification, validation, and long-term performance monitoring. J. Geophys. Res. Atmos. 2013, 118. [Google Scholar] [CrossRef]
- Kundu, P.K. Ekman veering observed near the ocean bottom. J. Phys. Oceanogr. 1976, 6, 238–242. [Google Scholar] [CrossRef]
- Centurioni, L.; Ohlmann, J.; Niiler, P.P. Permanent meanders in the California current system. J. Phys. Oceanogr. 2008, 38, 1690–1710. [Google Scholar] [CrossRef]
- Wilkin, J.L.; Bowen, M.M.; Emery, W.J. Mapping mesoscale currents by optimal interpolation of satellite radiometer and altimeter data. Ocean Dyn. 2002, 52, 95–103. [Google Scholar] [CrossRef]
- Strub, P.T.; James, C. Altimeter-derived variability of surface velocities in the California Current System: 2. Seasonal circulation and eddy statistics. Deep Sea Res. Part II Top. Stud. Oceanogr. 2000, 47, 831–870. [Google Scholar] [CrossRef]
- Stegmann, P.M.; Schwing, F. Demographics of mesoscale eddies in the California Current. Geophys. Res. Lett. 2007, 34. [Google Scholar] [CrossRef]
- Simpson, J.J.; Lynn, R.J. A mesoscale eddy dipole in the offshore California Current. J. Geophys. Res. Oceans 1990, 95, 13009–13022. [Google Scholar] [CrossRef]
- Hickey, B.M. The California Current system—Hypotheses and facts. Prog. Oceanogr. 1979, 8, 191–279. [Google Scholar] [CrossRef]
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).