Spectrally-Spatially Regularized Low-Rank and Sparse Decomposition: A Novel Method for Change Detection in Multitemporal Hyperspectral Images
Abstract
:1. Introduction
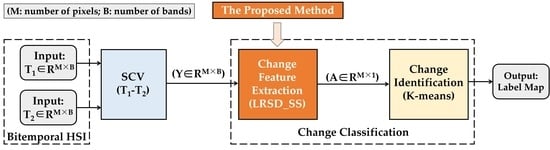
- It deals with a critical but not well solved problem with CD in HSI, which is to recover clean change data from noisy SCV of bitemporal HSI. Moreover, it addresses the issue from a relatively new angle for CD, which is to extract change features by exploiting inherent data structures exhibited in the SCV. To do so, this paper proposes a novel method, LRSD_SS, based on LRSD. Although the original LRSD has been applied in some areas of non-temporal HSI processing [38,49], it has not been used in temporal HSI change detection, to the best of our knowledge. This paper tries to fill the void by construction of LRSD_SS and demonstration of its capacity in solving the aforementioned problem of CD in multitemporal HSI.
- For better characterization of the underlying data structures, this paper designs a novel SS regularization superimposed on LRSD. The regularization enhances the local spectral-spatial smoothness, which normally exhibits in real change data, but is seldom observed from noise. Thus, the proposed LRSD_SS can further suppress the noise, especially those being as low-rank as the change features, which, however, has not been considered by the original LRSD. Experimental results show that LRSD_SS is robust to noise of various forms and intensities while being able to extract change features and increase change detection accuracy.
- This paper offers an implementation-friendly method for change detection in temporal HSI. The SS regularization processes all the bands of the SCV simultaneously and yields a closed form solution for the smoothed low-rank data matrix, thus ensuring efficiency.
2. Background Knowledge
2.1. The LRSD Model
2.2. Optimization for LRSD
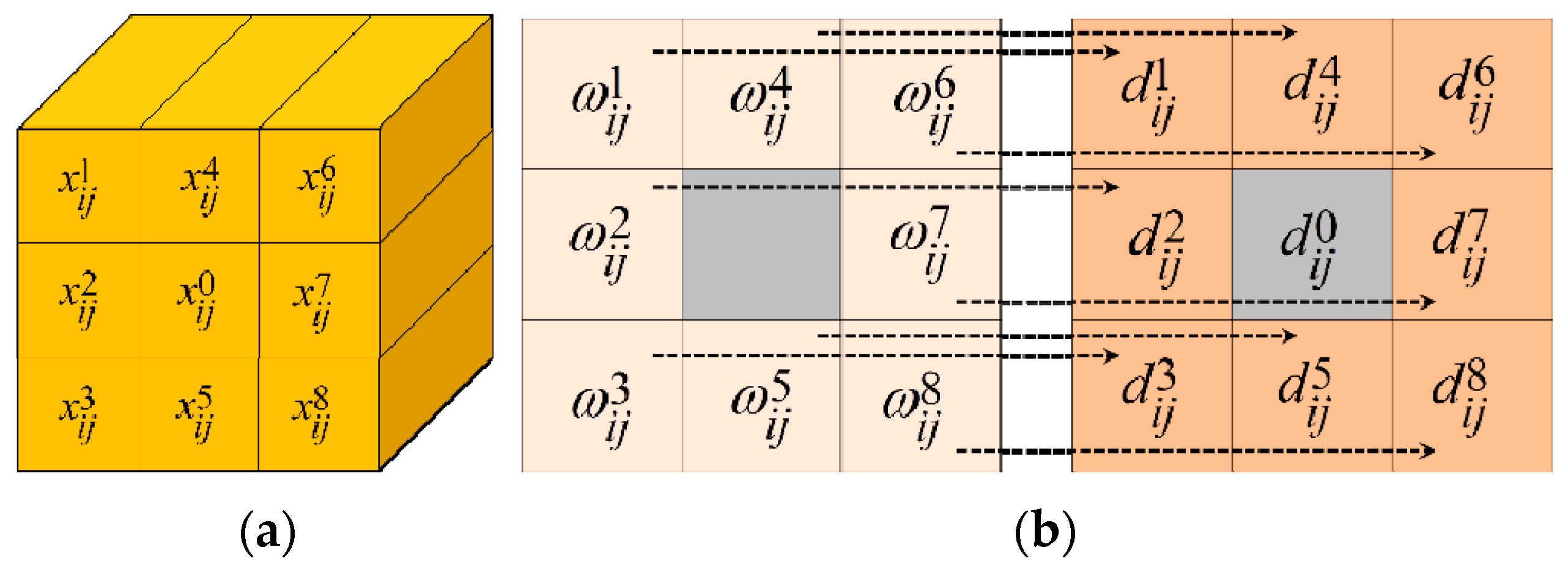
2.3. Spatial Regularization
3. Methodology
3.1. The Proposed Model: LRSD_SS
3.2. Optimization for LRSD_SS
| Algorithm 1: LRSD_SS |
| Input: |
| Output: (), and |
| Initialization: , , and ; |
| Do |
| Update by (11), by (14), and by (16). |
| Update by (17), by (18), and by (19). |
| Let and . |
| Set and . |
| while , and . |
3.3. Implementation
4. Results
4.1. Datasets
4.1.1. Simulated Bitemporal Hyperspectral Data
- Noise:
- Noise 1: random Gaussian noise with a low intensity (), superimposed on all the bands of all the pixels;
- Noise 2: random Gaussian noise with a high intensity (), superimposed on 20 randomly selected bands of some randomly selected pixels, which occupy of all the pixels;
- Noise 3: impulse noise with an intensity of the unitary distribution, superimposed on 20 randomly selected bands of some randomly selected pixels, which occupy 0.5% of all the pixels; and
- Noise 4: four dead lines with zero intensity, two of them superimposed on 20 randomly selected bands of all the pixels in two randomly selected rows and the other two superimposed on 20 randomly selected bands of all the pixels in two randomly selected columns.
- Bitemporal HSI:
- Data 1: Noise 1 () + Noise 2 () for both and ;
- Data 2: Noise 1 () + Noise 2 () for both and ;
- Data 3: Noise 1 () + Noise 2 () for both and ;
- Data 4: Noise 1 () + Noise 2 () for both and ;
- Data 5: Noise 1 () + Noise 3 for both and ;
- Data 6: Noise 1 () + Noise 4 for both and ;
- Data 7: Noise 1 () + Noise 2 () + Noise 3 for both and ;
- Data 8: Noise 1 () + Noise 2 () + Noise 4 for both and ;
- Data 9: Noise 1 () + Noise 3 + Noise 4 for both and ; and
- Data 10: Noise 1 () + Noise 2 () + Noise 3 + Noise 4 for both and .
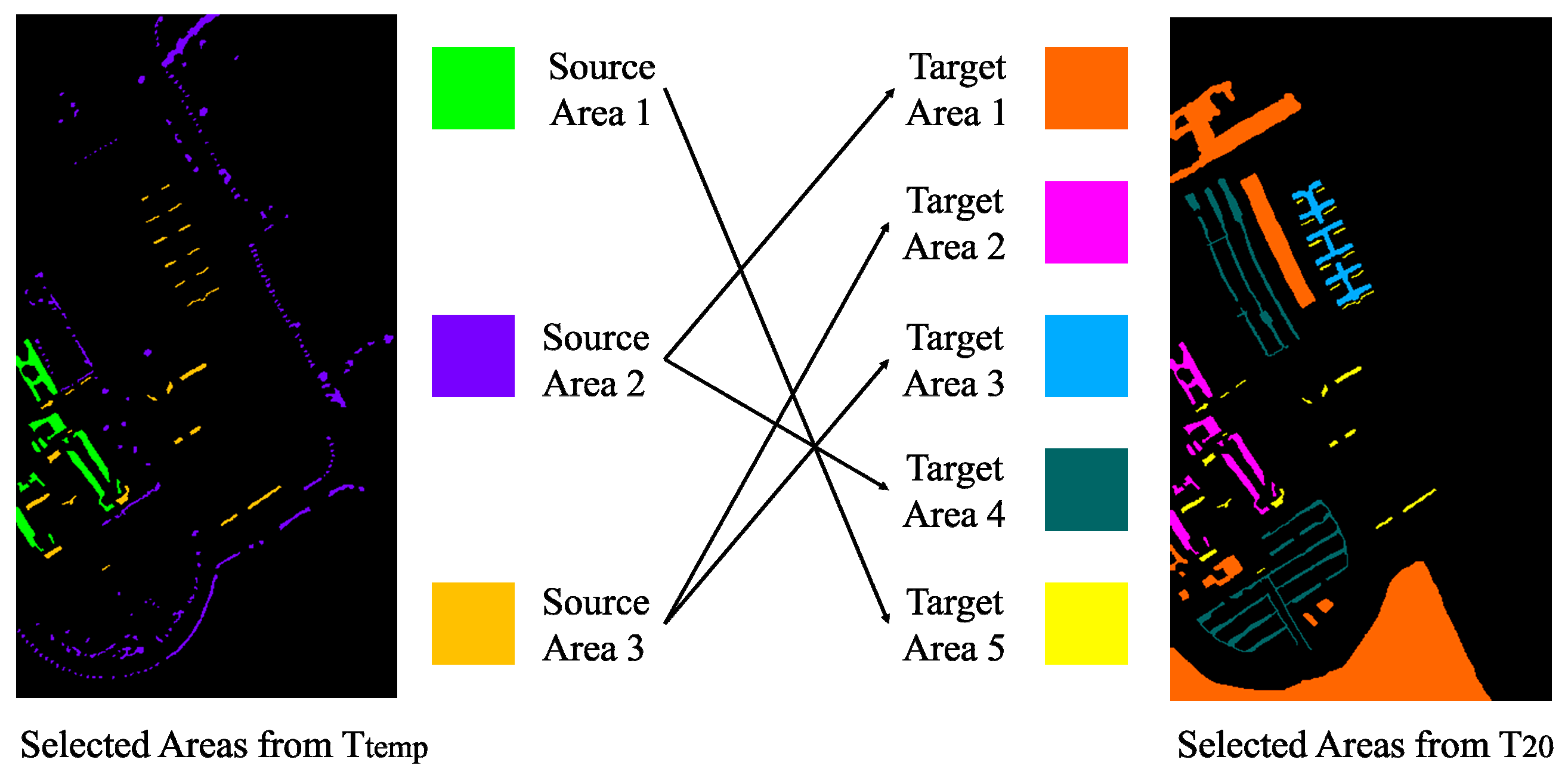
4.1.2. Real-World Dataset
4.2. Setup
4.3. Evaluation of LRSD_SS
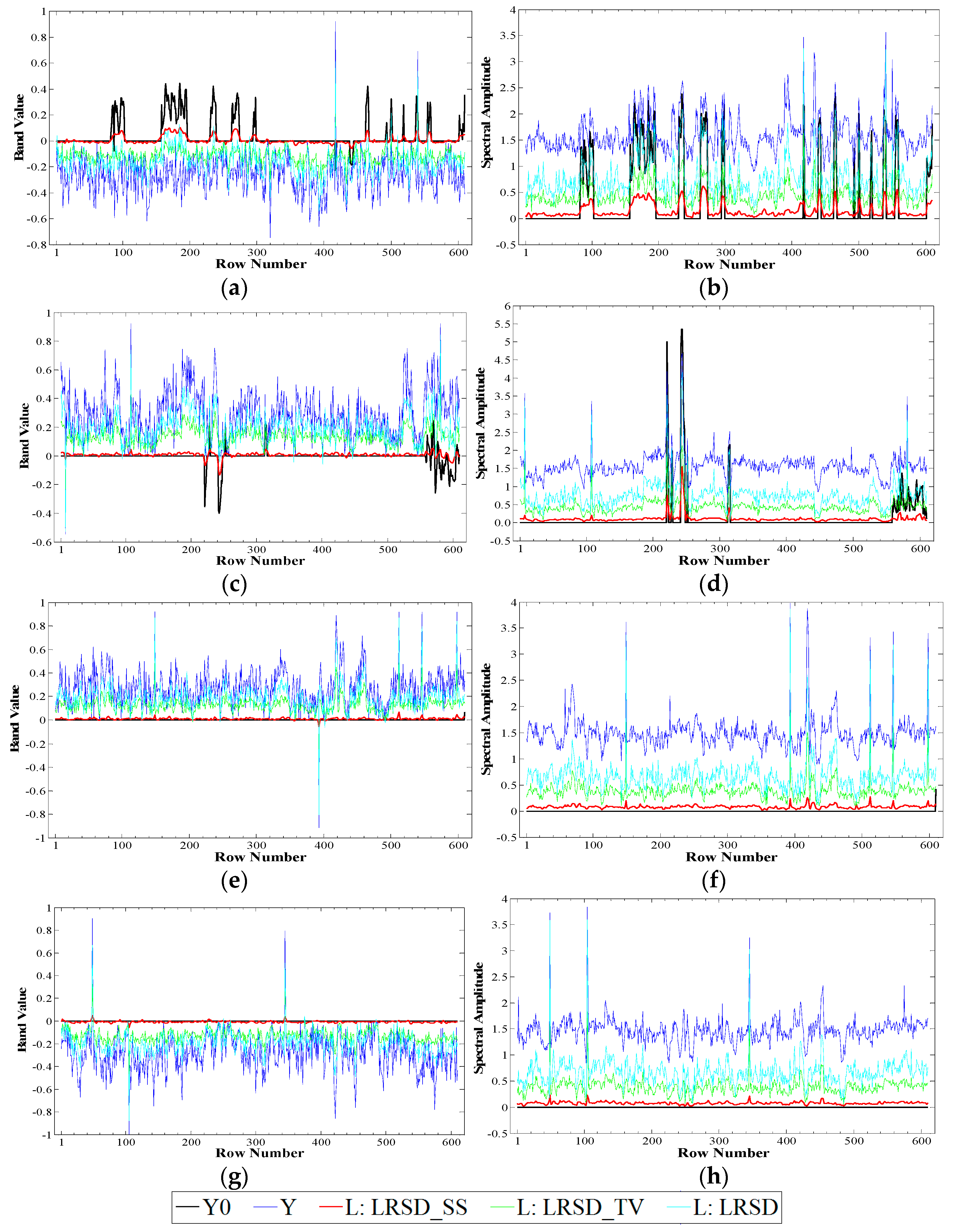
4.3.1. Efficacy
4.3.2. Efficiency
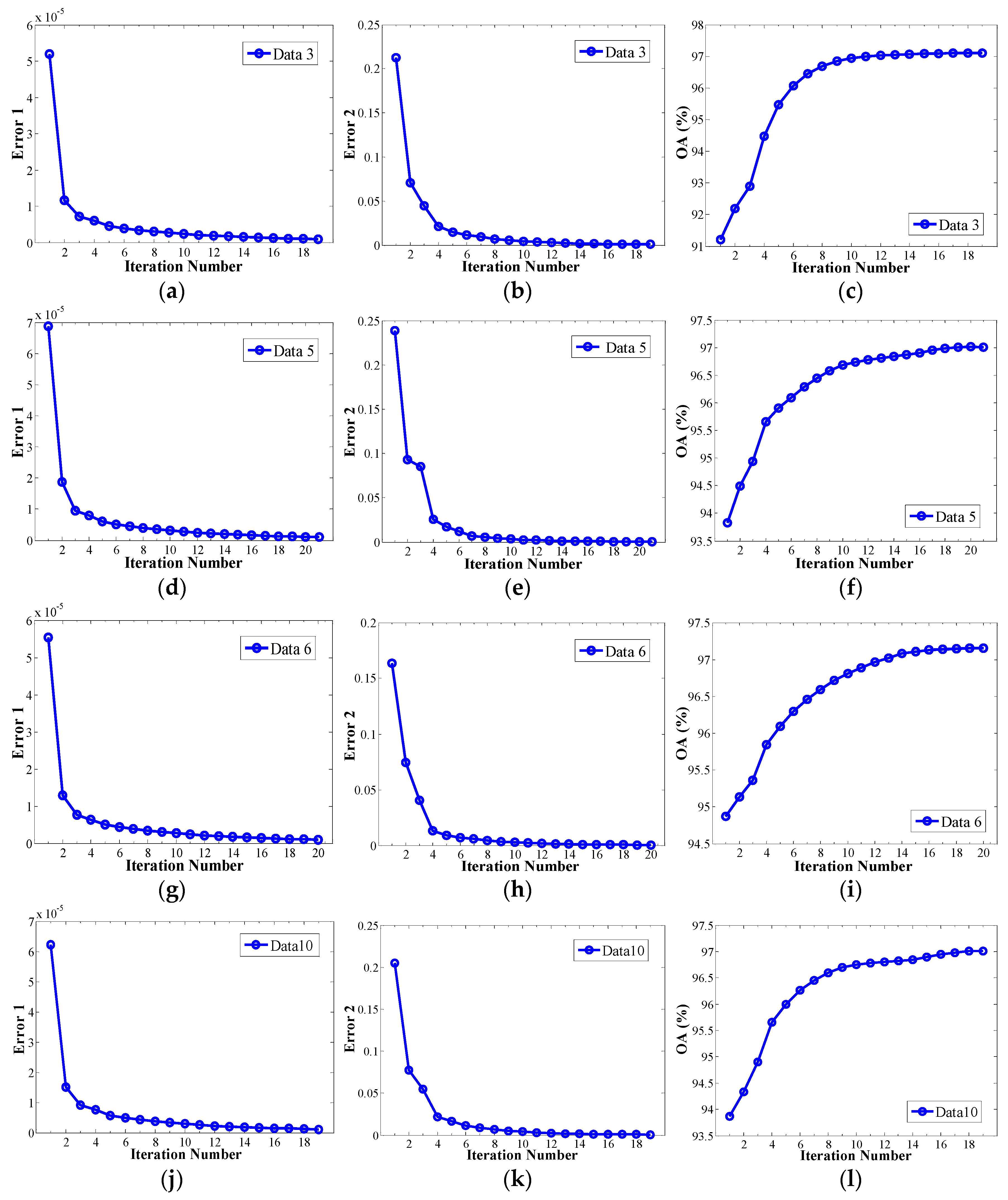
4.3.3. Stopping Criteria for Optimization
4.4. Discussion
- LRSD_SS effectively addresses the essential issue of change detection in multitemporal HSI by exploiting inherent data structures of SCV. With the proposed SS regularization which maintains the local patterns in the SCV, LRSD_SS can further characterize the nature of the change features, making it easier to separate the features from various types of noise and identify the changes. It is especially effective in recovering the clean background. Therefore, in the binary classification of the changed and the unchanged samples, LRSD_SS yields better results than many classic or state-of-the-art methods do.
- The proposed method is also efficient. The SS regularization extracts spectral-spatial features, processing all the bands of SCV simultaneously. Thus, it is much faster than the TV regularization on the LRSD model, which processes each band image separately. Moreover, the design of SS contributes a closed-form solution for the feature data within the ALM framework, so that the algorithm of LRSD_SS is implementation-friendly. As can be seen from the experimental results, only a few iterations are needed.
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Coppin, P.R.; Bauer, M. Digital change detection in forest ecosystems with remote sensing imagery. Remote Sens. Rev. 1996, 13, 207–304. [Google Scholar] [CrossRef]
- Yang, X.; Chen, L. Using multi-temporal remote sensor imagery to detect earthquake-triggered landslides. Int. J. Appl. Earth Obs. Geosci. 2010, 12, 487–495. [Google Scholar] [CrossRef]
- Singh, A. Digital change detection techniques using remotely sensed data. Int. J. Remote Sens. 1989, 10, 989–1003. [Google Scholar] [CrossRef]
- Coppin, P.R.; Jonckheere, I.; Nackaerts, K.; Muys, B. Digital change detection methods in ecosystem monitoring: A review. Int. J. Remote Sens. 2004, 25, 1565–1596. [Google Scholar] [CrossRef]
- Bovolo, F.; Marchesi, S.; Bruzzone, L. A framework for automatic and unsupervised detection of multiple changes in multitemporal images. IEEE Trans. Geosci. Remote Sens. 2012, 50, 2196–2212. [Google Scholar] [CrossRef]
- Bruzzone, L.; Fernandez Prieto, D. Automatic analysis of the difference image for unsupervised change detection. IEEE Trans. Geosci. Remote Sens. 2000, 38, 1170–1182. [Google Scholar] [CrossRef]
- Bovolo, F.; Bruzzone, L. Theoretical framework for unsupervised change detection based on change vector analysis in the polar domain. IEEE Trans. Geosci. Remote Sens. 2007, 45, 218–236. [Google Scholar] [CrossRef]
- Liu, S.; Bruzzone, L.; Bovolo, F.; Du, P. Hierarchical unsupervised change detection in multitemporal hyperspectral images. IEEE Trans. Geosci. Remote Sens. 2015, 53, 244–260. [Google Scholar] [CrossRef]
- Du, P.; Liu, S.; Gamba, P.; Tan, K.; Xia, J. Fusion of difference images for change detection over urban areas. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2012, 5, 1076–1086. [Google Scholar] [CrossRef]
- Wu, C.; Du, B.; Zhang, L. A subspace-based change detection method for hyperspectral images. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2013, 6, 815–830. [Google Scholar] [CrossRef]
- Deng, J.S.; Wang, K.; Deng, Y.H.; Qi, G.J. PCA-based Land-use change detection and analysis using multitemporal and multisensor satellite data. Int. J. Remote Sens. 2008, 29, 4823–4838. [Google Scholar] [CrossRef]
- Lu, D.; Mausel, P.; Brondi’Zio, E.; Moran, E. Change detection techniques. Int. J. Remote Sens. 2004, 25, 2365–2407. [Google Scholar] [CrossRef]
- Marchesi, S.; Bovolo, F.; Bruzzone, L. A context-sensitive technique robust to registration noise for change detection in VHR multispectral images. IEEE Trans. Geosci. Remote Sens. 2010, 19, 1877–1889. [Google Scholar] [CrossRef] [PubMed]
- Li, Y.; Gong, M.; Jiao, L.; Li, L.; Stolkin, R. Change-detection map learning using matching pursuit. IEEE Trans. Geosci. Remote Sens. 2015, 53, 4712–4723. [Google Scholar] [CrossRef]
- Fellouris, G.; Sokolov, G. Second-order asymptotic optimality in multisensor sequential change detection. IEEE Trans. Inf. Theory 2016, 62, 3662–3675. [Google Scholar] [CrossRef]
- Dalponte, M.; Bruzzone, L.; Vescovo, L.; Gianelle, D. The role of Spectral resolution and classifier complexity in the analysis of hyperspectral images of forest areas. Remote Sens. Environ. 2009, 113, 2345–2355. [Google Scholar] [CrossRef]
- Klaric, M.N.; Claywell, B.C.; Scott, G.J.; Hudson, N.J.; Sjahputera, O.; Li, Y.; Barratt, S.T.; Keller, J.M.; Davis, C.H. GeoCDX: An automated change detection and exploitation system for high-resolution satellite imagery. IEEE Trans. Geosci. Remote Sens. 2013, 51, 2067–2086. [Google Scholar] [CrossRef]
- Lu, J.; Li, J.; Chen, G.; Zhao, L.; Xiong, B.; Kuang, G. Improving pixel-based change detection accuracy using an object-based approach in multitemporal SAR flood images. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2015, 8, 3486–3496. [Google Scholar] [CrossRef]
- Zhou, Z.; Li, X.; Wright, J.; Candès, E.; Ma, Y. Stable principal component pursuit. In Proceedings of the 2010 IEEE International Symposium on Information Theory, Austin, TX, USA, 13–18 June 2010; pp. 1518–1522. [Google Scholar] [CrossRef]
- Nagy, G. Feature Extraction on Binary Patterns. IEEE Trans. Syst. Sci. Cybern. 1969, 5, 273–278. [Google Scholar] [CrossRef]
- Eismann, M.T.; Meola, J.; Stoker, A.; Beaven, S.; Schaum, A. Hyperspectral change detection in the presence of diurnal and seasonal variations. IEEE Trans. Geosci. Remote Sens. 2008, 46, 237–249. [Google Scholar] [CrossRef]
- Ertürk, A.; Iordache, M.; Plaza, A. Sparse unmixing-based change detection for multitemporal hyperspectral images. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2016, 9, 708–719. [Google Scholar] [CrossRef]
- Chen, Z.; Wang, B. Spectral-spatial classification based on affinity scoring for hyperspectral imagery. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2016, 9, 2305–2320. [Google Scholar] [CrossRef]
- Li, J.; Huang, X.; Gamba, P.; Bioucas-Dias, J.M.; Zhang, L.; Benediktsson, J.A.; Plaza, A. Multiple feature learning for hyperspectral image classification. IEEE Trans. Geosci. Remote Sens. 2015, 53, 1592–1606. [Google Scholar] [CrossRef]
- Chen, Z.; Wang, B. Semisupervised spectral–spatial classification of hyperspectral imagery with affinity scoring. IEEE Geosci. Remote Sens. Lett. 2015, 12, 1710–1714. [Google Scholar] [CrossRef]
- Chen, Z.; Wang, B.; Niu, Y.; Xia, W.; Zhang, J.; Hu, B. Semisupervised hyperspectral image classification based on affinity scoring. In Proceedings of the IEEE Geoscience and Remote Sensing Symposium, Milan, Italy, 26–31 July 2015; pp. 4967–4970. [Google Scholar] [CrossRef]
- Yuan, Y.; Lin, J.; Wang, Q. Dual-clustering-based hyperspectral band selection by contextual analysis. IEEE Trans. Geosci. Remote Sens. 2016, 54, 1431–1445. [Google Scholar] [CrossRef]
- Wang, Q.; Meng, Z.; Li, X. Locality adaptive discriminant analysis for spectral-spatial classification of hyperspectral images. IEEE Geosci. Remote Sens. Lett. 2017, 1–5. [Google Scholar] [CrossRef]
- Letexier, D.; Bourennane, S. Noise removal from hyperspectral images by multidimensional filtering. IEEE Trans. Geosci. Remote Sens. 2008, 46, 2061–2069. [Google Scholar] [CrossRef]
- Karami, A.; Yazdi, M.; Zolghadre-Asli, A. Noise reduction of hyperspectral images using kernel non-negative Tucker decomposition. IEEE J. Sel. Top. Signal Process. 2011, 5, 487–493. [Google Scholar] [CrossRef]
- Elad, M.; Aharon, M. Image denoising via sparse and redundant representations over learned dictionaries. IEEE Trans. Image Process. 2006, 15, 3736–3745. [Google Scholar] [CrossRef] [PubMed]
- Dabov, K.; Foi, A.; Katkovnik, V.; Egiazarian, K. Image denoising by sparse 3-D transform-domain collaborative filtering. IEEE Trans. Image Process. 2007, 16, 2080–2095. [Google Scholar] [CrossRef] [PubMed]
- Qian, Y.; Ye, M. Hyperspectral imagery restoration using nonlocal spectral spatial structured sparse representation with noise estimation. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2013, 6, 499–515. [Google Scholar] [CrossRef]
- Li, Q.; Li, H.; Lu, Z.; Lu, Q.; Li, W. Denoising of hyperspectral images employing two-phase matrix decomposition. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 7, 3742–3754. [Google Scholar] [CrossRef]
- Yuan, Q.; Zhang, L.; Chen, H. Hyperspectral image denoising employing a spectral spatial adaptive total variation model. IEEE Trans. Geosci. Remote Sens. 2012, 50, 3660–3677. [Google Scholar] [CrossRef]
- Dai, X.; Khorram, S. The effects of image misregistration on the accuracy of remotely sensed change detection. IEEE Trans. Geosci. Remote Sens. 1998, 36, 1566–1577. [Google Scholar] [CrossRef]
- Vongsy, K.; Eismann, M.T.; Mendenhall, M.J. Extension of the linear chromodynamics model for spectral change detection in the presence of residual spatial misregistration. IEEE Trans. Geosci. Remote Sens. 2015, 53, 3005–3021. [Google Scholar] [CrossRef]
- Bruzzone, L.; Cossu, R. An adaptive approach to reducing registration noise effects in unsupervised change detection. IEEE Trans. Geosci. Remote Sens. 2003, 41, 2455–2465. [Google Scholar] [CrossRef]
- Bovolo, F.; Bruzzone, L.; Marchesi, S. A multiscale technique for reducing registration noise in change detection on multitemporal VHR images. In Proceedings of the 2007 International Workshop on the Analysis of Multi-Temporal Remote Sensing Images, Leuven, Belgium, 18–20 July 2007; pp. 1–6. [Google Scholar] [CrossRef]
- Bovolo, F.; Bruzzone, L.; Marchesi, S. Analysis and adaptive estimation of the registration noise distribution in multitemporal VHR images. IEEE Trans. Geosci. Remote Sens. 2009, 47, 2658–2671. [Google Scholar] [CrossRef]
- Liu, G.; Lin, Z.; Yan, S.; Sun, J.; Yu, Y.; Ma, Y. Robust recovery of subspace structures by low-rank representation. IEEE Trans. Pattern Anal. Mach. Intell. 2013, 35, 171–184. [Google Scholar] [CrossRef] [PubMed]
- Zhang, H.; He, W.; Zhang, L.; Shen, H.; Yuan, Q. Hyperspectral image restoration using low-rank matrix recovery. IEEE Trans. Geosci. Remote Sens. 2014, 52, 4729–4743. [Google Scholar] [CrossRef]
- Zhou, T.; Tao, D. GoDec: Randomized low-rank & sparse matrix decomposition in noisy case. In Proceedings of the 28th International Conference on Machine Learning, Bellevue, Washington, DC, USA, 28 June–2 July 2011; pp. 33–40. [Google Scholar]
- He, W.; Zhang, H.; Zhang, L.; Shen, H. Total-variation-regularized low-rank matrix factorization for hyperspectral image restoration. IEEE Trans. Geosci. Remote Sens. 2016, 54, 176–188. [Google Scholar] [CrossRef]
- Candès, E.J.; Li, X.; Ma, Y.; Wright, J. Robust principal component analysis. J. ACM 2002, 58, 289–298. [Google Scholar] [CrossRef]
- Wright, J.; Ganesh, A.; Pao, S.; Peng, Y.; Ma, Y. Robust principal component analysis: Exact recovery of corrupted low-rank matrices via convex optimization. In Proceedings of the International Conference on Neural Information Processing Systems, Vancouver, BC, Canada, 7–10 December 2009; pp. 2080–2088. [Google Scholar]
- Candès, E.J.; Plan, Y. Matrix completion with noise. Proc. IEEE 2010, 98, 925–936. [Google Scholar] [CrossRef]
- Zhang, Y.; Du, B.; Zhang, L.; Wang, S. A low-rank and sparse matrix decomposition-based Mahalanobis distance method for hyperspectral anomaly detection. IEEE Trans. Geosci. Remote Sens. 2016, 54, 176–188. [Google Scholar] [CrossRef]
- Plaza, A.; Martinez, P.; Perez, R.; Plaza, J. A quantitative and comparative analysis of endmember extraction algorithms from hyperspectral data. IEEE Trans. Geosci. Remote Sens. 2004, 42, 650–663. [Google Scholar] [CrossRef]
- Qian, Y.; Jia, S.; Zhou, J.; Robles-Kelly, A. Hyperspectral unmixing via L1/2 sparsity-constrained nonnegative matrix factorization. IEEE Trans. Geosci. Remote Sens. 2011, 49, 4282–4297. [Google Scholar] [CrossRef]
- Beck, A.; Teboulle, M. Fast gradient-based algorithm for constrained total variation image denoising and deblurring problems. IEEE Trans. Image Process. 2009, 18, 2419–2434. [Google Scholar] [CrossRef] [PubMed]
- Rudin, L.I.; Osher, S.; Fatemi, E. Nonlinear total variation based noise removal algorithms. Phys. D Nonlinear Phenom. 1992, 60, 259–268. [Google Scholar] [CrossRef]
- Lin, Z.; Chen, M.; Ma, Y. The Augmented Lagrange Multiplier Method for Exact Recovery of Corrupted Low-Rank Matrices; University of Illinois at Urbana-Champaign: Champaign, IL, USA, 2009. [Google Scholar] [CrossRef]
- Bazi, Y.; Bruzzone, L.; Melgani, F. An unsupervised approach based on the generalized Gaussian model to automatic change detection in multitemporal SAR images. IEEE Trans. Geosci. Remote Sens. 2005, 43, 874–887. [Google Scholar] [CrossRef]
- Kusetogullari, H.; Yavariabdi, A.; Celik, T. Unsupervised change detection in multitemporal multispectral satellite images using parallel particle swarm optimization. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2015, 8, 2151–2164. [Google Scholar] [CrossRef]
- Fazel, M.; Candès, E.; Recht, B.; Parrilo, P. Compressed sensing and robust recovery of low rank matrices. In Proceedings of the 42nd Asilomar Conference on Signals, Systems and Computers, Pacific Grove, CA, USA, 26–29 October 2008; pp. 1043–1047. [Google Scholar]
- Zhou, T.; Tao, D. Bilateral random projections. In Proceedings of the IEEE International Symposium on Information Theory, Cambridge, MA, USA, 1–6 July 2012; pp. 1286–1290. [Google Scholar] [CrossRef]
- Recht, B.; Fazel, M.; Parrilo, P.A. Guaranteed minimum-rank solutions of linear matrix equations via nuclear norm minimization. J. SIAM Rev. 2010, 53, 471–501. [Google Scholar] [CrossRef]
- Candès, E.J.; Tao, T. The power of convex relaxation: near-optimal matrix completion. IEEE Trans. Inf. Theory 2010, 56, 2053–2080. [Google Scholar] [CrossRef]
- Boyd, S.; Parikh, N.; Chu, E.; Peleato, B.; Eckstein, J. Distributed optimization and statistical learning via the alternating direction method of multipliers. Found. Trends Mach. Learn. 2010, 3, 1–122. [Google Scholar] [CrossRef]
- Han, D.; Yuan, X. A note on the alternating direction method of multipliers. J. Optim. Theory Appl. 2012, 1–12. [Google Scholar] [CrossRef]
- Cai, J.F.; Candès, E.J.; Shen, Z. A singular value thresholding algorithm for matrix completion. SIAM J. Optim. 2010, 20, 1956–1982. [Google Scholar] [CrossRef]
- Beck, A.; Teboulle, M. A fast iterative shrinkage-thresholding algorithm for linear inverse problems. SIAM J. Imag. Sci. 2009, 2, 183–201. [Google Scholar] [CrossRef]





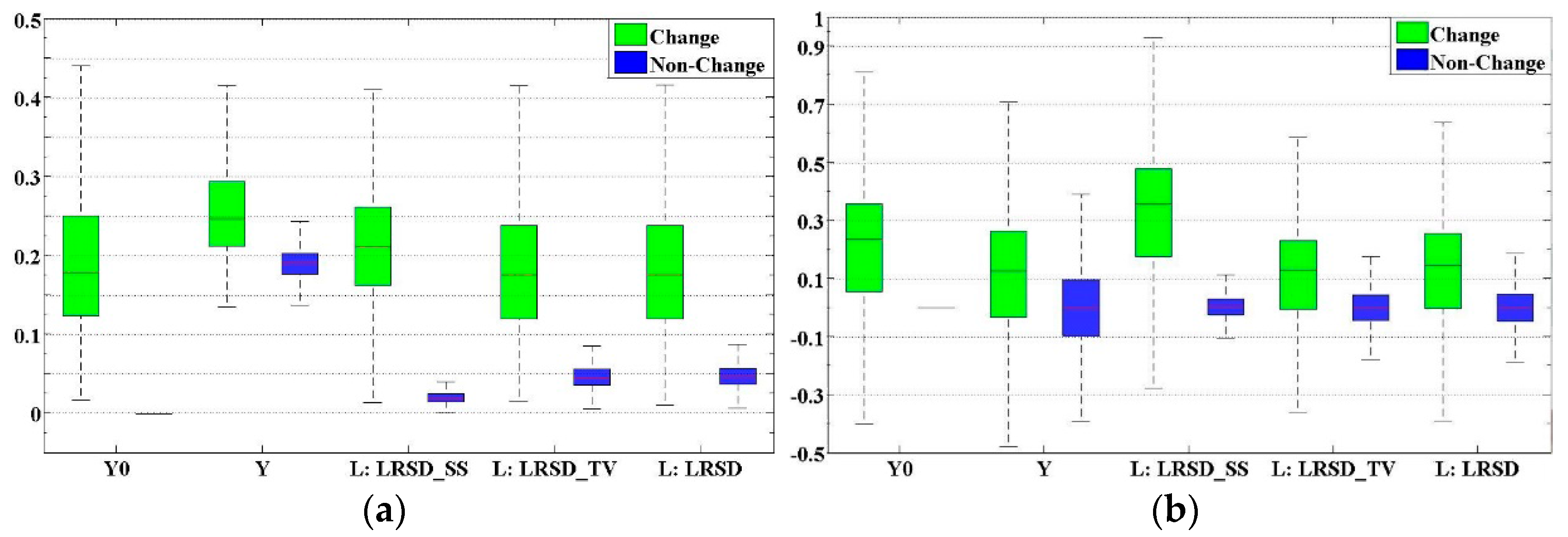
| Methods | Criteria | Data 1 | Data 2 | Data 3 | Data 4 | Data 5 | Data 6 | Data 7 | Data 8 | Data 9 | Data 10 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Original SCV + K-Means | OA (%) | 86.76 | 86.22 | 85.80 | 63.53 | 87.54 | 92.16 | 90.24 | 91.86 | 90.34 | 90.35 |
| AA (%) | 75.44 | 72.11 | 69.72 | 61.65 | 53.17 | 70.06 | 64.60 | 70.29 | 64.20 | 65.29 | |
| 0.46 | 0.42 | 0.38 | 0.13 | 0.10 | 0.53 | 0.40 | 0.53 | 0.40 | 0.42 | ||
| SAM + K-Means | OA (%) | 81.36 | 76.01 | 67.19 | 44.90 | 68.84 | 68.21 | 68.94 | 68.15 | 68.51 | 68.63 |
| AA (%) | 63.86 | 59.64 | 55.46 | 48.20 | 55.27 | 55.27 | 55.36 | 55.40 | 55.55 | 55.40 | |
| 0.25 | 0.15 | 0.07 | −0.01 | 0.07 | 0.07 | 0.07 | 0.07 | 0.07 | 0.07 | ||
| ASCD + K-Means | OA (%) | 83.97 | 79.56 | 69.56 | 42.93 | 69.70 | 68.95 | 69.69 | 69.00 | 69.53 | 69.58 |
| AA (%) | 60.53 | 57.56 | 53.28 | 44.02 | 52.93 | 52.60 | 52.86 | 52.64 | 53.03 | 53.00 | |
| 0.23 | 0.14 | 0.05 | −0.05 | 0.04 | 0.04 | 0.04 | 0.04 | 0.04 | 0.04 | ||
| PCA + K-Means | OA (%) | 90.88 | 90.90 | 90.69 | 89.37 | 93.81 | 94.75 | 93.87 | 94.82 | 93.81 | 93.93 |
| AA (%) | 85.95 | 83.73 | 82.22 | 78.37 | 77.61 | 81.75 | 78.32 | 81.99 | 78.69 | 78.65 | |
| 0.64 | 0.62 | 0.61 | 0.55 | 0.67 | 0.73 | 0.67 | 0.73 | 0.68 | 0.68 | ||
| LRSD + K-Means | OA (%) | 91.11 | 91.17 | 91.20 | 89.87 | 93.81 | 94.89 | 93.89 | 94.97 | 93.81 | 93.94 |
| AA (%) | 85.87 | 83.71 | 82.13 | 78.42 | 77.59 | 81.48 | 78.13 | 81.57 | 78.18 | 78.26 | |
| 0.64 | 0.63 | 0.62 | 0.56 | 0.67 | 0.73 | 0.67 | 0.74 | 0.67 | 0.68 | ||
| LRSD_TV + K-Means | OA (%) | 96.74 | 94.09 | 96.04 | 94.51 | 96.78 | 94.42 | 94.97 | 94.93 | 95.57 | 94.89 |
| AA (%) | 88.41 | 80.68 | 87.43 | 80.79 | 89.10 | 81.25 | 83.06 | 82.85 | 84.74 | 82.77 | |
| 0.84 | 0.70 | 0.81 | 0.72 | 0.84 | 0.72 | 0.75 | 0.74 | 0.78 | 0.74 | ||
| LRSD_SS + K-Means | OA (%) | 97.28 | 97.12 | 97.08 | 96.78 | 97.01 | 97.15 | 97.01 | 97.14 | 97.02 | 97.03 |
| AA (%) | 90.42 | 90.32 | 90.12 | 89.92 | 90.83 | 90.06 | 90.87 | 90.14 | 90.74 | 90.71 | |
| 0.87 | 0.86 | 0.86 | 0.85 | 0.86 | 0.86 | 0.86 | 0.86 | 0.86 | 0.86 |
| Criteria | Original SCV + K-Means | SAM + K-Means | ASCD + K-Means | PCA + K-Means | LRSD + K-Means | LRSD_TV + K-Means | LRSD_SS + K-Means |
|---|---|---|---|---|---|---|---|
| OA (%) | 98.04 | 97.79 | 93.13 | 98.03 | 98.03 | 98.17 | 98.56 |
| AA (%) | 98.24 | 97.06 | 87.92 | 98.23 | 98.23 | 98.29 | 98.39 |
| 0.95 | 0.95 | 0.82 | 0.95 | 0.95 | 0.96 | 0.96 |
| Components | L | S | X | |
|---|---|---|---|---|
| Methods | ||||
| LRSD_SS | 0.45 | 1.35 | 8.74 | |
| LRSD_TV | 0.44 | 1.37 | 419.22 | |
| LRSD | 0.34 | 1.28 | - | |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, Z.; Wang, B. Spectrally-Spatially Regularized Low-Rank and Sparse Decomposition: A Novel Method for Change Detection in Multitemporal Hyperspectral Images. Remote Sens. 2017, 9, 1044. https://doi.org/10.3390/rs9101044
Chen Z, Wang B. Spectrally-Spatially Regularized Low-Rank and Sparse Decomposition: A Novel Method for Change Detection in Multitemporal Hyperspectral Images. Remote Sensing. 2017; 9(10):1044. https://doi.org/10.3390/rs9101044
Chicago/Turabian StyleChen, Zhao, and Bin Wang. 2017. "Spectrally-Spatially Regularized Low-Rank and Sparse Decomposition: A Novel Method for Change Detection in Multitemporal Hyperspectral Images" Remote Sensing 9, no. 10: 1044. https://doi.org/10.3390/rs9101044
APA StyleChen, Z., & Wang, B. (2017). Spectrally-Spatially Regularized Low-Rank and Sparse Decomposition: A Novel Method for Change Detection in Multitemporal Hyperspectral Images. Remote Sensing, 9(10), 1044. https://doi.org/10.3390/rs9101044