Feature-Based Nonlocal Polarimetric SAR Filtering
Abstract
1. Introduction
2. Methodology
2.1. Characteristics of PolSAR Data
2.2. Scene Heterogeneity
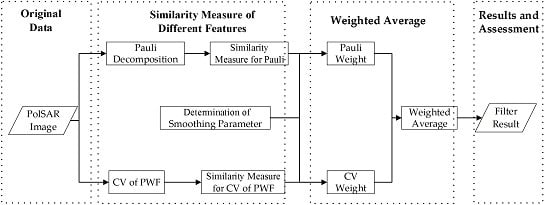
2.3. The NLM Filtering of and PB
2.3.1. Test for Similarity of the Features
2.3.2. Procedure of Weighted Average
2.3.3. Determination of Smoothing Parameters
| Algorithm 1: Nonlocal bilateral filtering based on heterogeneity and scattering. |
| INPUT: PolSAR image coherence matrix (or covariance matrix). |
| (1) For each pixel, the weight is calculated according to the test statistic between two patches. |
| (a) The is calculated from the PWF filtered image, and a heterogeneity map is generated. |
| (b) Calculate the parameter and according to the , the number of looks and the patch size . |
| (c) The test statistic is measured between two patches of the scalar values including the and the Pauli basis of the original image, respectively. |
| (d) The weights are performed based on the test statistic. |
| (2) The filtered coherence matrix (or covariance matrix) is performed by the weighted average based on the combination of the weights for the and the Pauli basis. |
| Output: the filtered image. |
3. Experiment and Results
3.1. Description of the Experimental Datasets
3.2. Evaluation and Comparision
3.2.1. Experiments on Simulated PolSAR Data
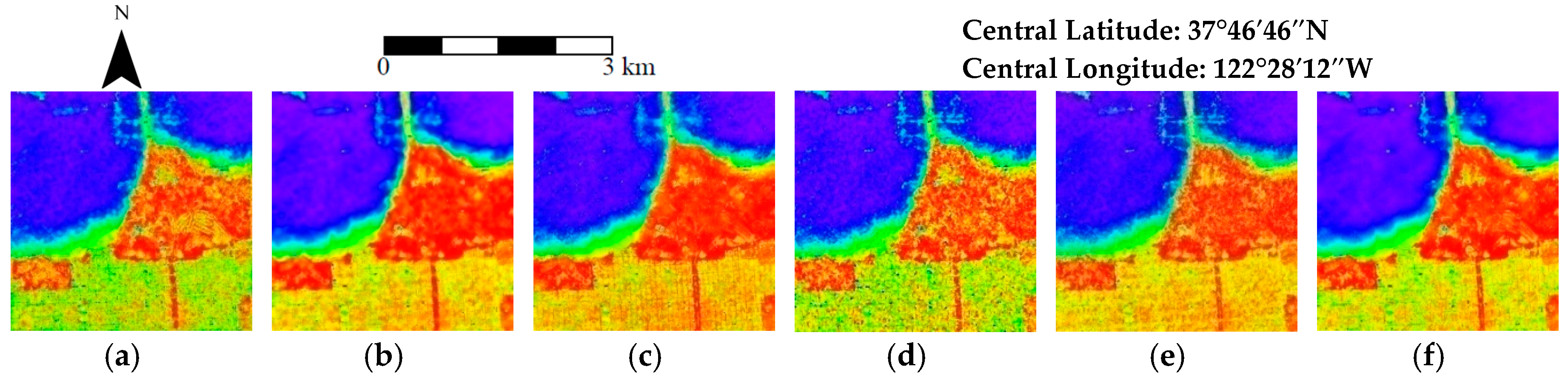
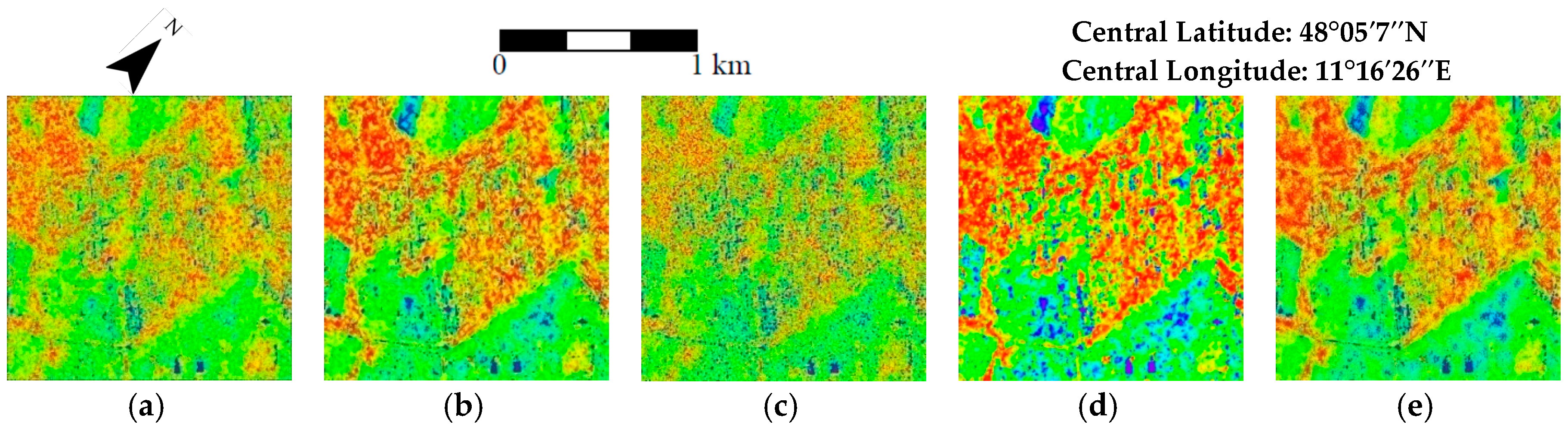
3.2.2. Experiments on Real PolSAR Data
4. Discussion
4.1. Main Features of the Proposed Method
4.2. Sensitivity Analysis of the Parameters
4.2.1. Sensitivity Analysis of the Smoothing Parameters
4.2.2. Size of the Patch
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Lee, J.S. Refined filtering of image noise using local statistics. Comput. Graph. Image Process. 1981, 15, 380–389. [Google Scholar] [CrossRef]
- Lee, J.S.; Grunes, M.R.; De Grandi, G. Polarimetric SAR speckle filtering and its implication for terrain classification. IEEE Trans. Geosci. Remote Sens. 1999, 37, 2363–2373. [Google Scholar]
- Lee, J.S. Digital image smoothing and the sigma filter. Comput. Vis. Graph. Image Process. 1983, 24, 255–269. [Google Scholar] [CrossRef]
- Lee, J.S.; Wen, J.H.; Ainsworth, T.L.; Chen, K.S.; Chen, A.J. Improved sigma filter for speckle filtering of SAR imagery. IEEE Trans. Geosci. Remote Sens. 2009, 47, 202–213. [Google Scholar]
- Lee, J.-S.; Ainsworth, T.L.; Wang, Y.T.; Chen, K.-S. Polarimetric SAR speckle filtering and the extended sigma filter. IEEE Trans. Geosci. Remote Sens. 2015, 53, 1150–1160. [Google Scholar] [CrossRef]
- Vasile, G.; Trouve, E.; Lee, J.S.; Buzuloiu, V. Intensity-driven adaptive-neighborhood technique for polarimetric and interferometric parameter estimation. IEEE Trans. Geosci. Remote Sens. 2006, 44, 1609–1621. [Google Scholar] [CrossRef]
- Tomasi, C.; Manduchi, R. Bilateral filtering for gray and color images. In Proceedings of the 6th International Conference on Computer Vision, Bombay, India, 7 January 1998; pp. 839–846. [Google Scholar]
- D’Hondt, O.; Guillaso, S.; Hellwich, O. Iterative bilateral filtering of polarimetric SAR data. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2013, 6, 1628–1639. [Google Scholar] [CrossRef]
- Alonso-Gonzalez, A.; Lopez-Martinez, C.; Salembier, P.; Deng, X.P. Bilateral distance based filtering for polarimetric SAR data. Remote Sens. 2013, 5, 5620–5641. [Google Scholar] [CrossRef]
- Buads, A.; Coll, B.; Morel, J.-M. A non-local algorithm for image denoisesing. In Proceedings of the IEEE Computer Society Conference Computer Vision and Pattern Recognition CVPR 2005, San Diego, CA, USA, 20–25 June 2005; Volume 2, pp. 60–65. [Google Scholar]
- Chen, J.; Chen, Y.; An, W.; Cui, Y.; Yang, J. Nonlocal filtering for polarimetric SAR data: A pretest approach. IEEE Trans. Geosci. Remote Sens. 2011, 49, 1744–1754. [Google Scholar] [CrossRef]
- Ni, W.P.; Gao, X.B. Despeckling of SAR image using generalized guided filter with Bayesian nonlocal means. IEEE Trans. Geosci. Remote Sens. 2016, 54, 567–579. [Google Scholar] [CrossRef]
- Zhong, H.; Zhang, J.J.; Liu, G.C. Robust polarimetric SARdespeckling based on nonlocal means and distributed lee filter. IEEE Trans. Geosci. Remote Sens. 2014, 52, 4198–4210. [Google Scholar] [CrossRef]
- Liu, G.C.; Zhong, H. Nonlocal means filter for polarimetric SAR data despeckling based on discriminative similarity measure. IEEE Geosci. Remote Sens. Lett. 2014, 11, 514–518. [Google Scholar] [CrossRef]
- Wang, Y.T.; Ainsworth, T.L.; Lee, J.S. Application of mixture regression for improved polarimetric SAR speckle filtering. IEEE Trans. Geosci. Remote Sens. 2017, 55, 453–467. [Google Scholar] [CrossRef]
- Zhang, L.; Sun, L.; Zou, B.; Moon, W. Fully polarimetric SAR image classification via sparse representation and polarimetric features. IEEE Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 8, 3923–3932. [Google Scholar] [CrossRef]
- Xie, W.; Jiao, L.C.; Zhao, J. PolSAR image classification via D-KSVD and NSCT-domain features extraction. IEEE Geosci. Remote Sens. Lett. 2016, 13, 227–231. [Google Scholar] [CrossRef]
- Uhlmann, S.; Kiranyaz, S. Integrating color features in polarimetric SAR image classification. IEEE Trans. Geosci. Remote Sens. 2014, 52, 2197–2216. [Google Scholar] [CrossRef]
- Chen, B.; Wang, S.; Jiao, L.C.; Stolkin, R.; Liu, H.Y. A three-component fisher-based feature weighting method for supervised PolSAR image classification. IEEE Geosci. Remote Sens. Lett. 2015, 12, 731–735. [Google Scholar] [CrossRef]
- Lopes, A.; Touzi, R.; Nezry, E. Adaptive speckle filters and scene heterogeneity. IEEE Trans. Geosci. Remote Sens. 1990, 6, 992–1000. [Google Scholar] [CrossRef]
- Frost, V.S.; Stiles, J.A.; Shanmugan, K.S.; Holtzman, J.C. A model for radar images and its application to adaptive digital filtering of multiplicative noise. IEEE Trans. Pattern Anal. Mach. Intell. 1982, 4, 157–165. [Google Scholar] [CrossRef] [PubMed]
- Lang, F.K.; Yang, J.; Li, D.R. Adaptive-window polarimetric SAR image speckle filtering based on a homogeneity measurement. IEEE Trans. Geosci. Remote Sens. 2015, 53, 5435–5446. [Google Scholar] [CrossRef]
- Dellepiane, S.G.; Angiati, E. Quality assessment of despeckled SAR images. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 7, 691–707. [Google Scholar] [CrossRef]
- Anfinsen, S.N.; Doulgeris, A.P.; Eltoft, T. Estimation of the equivalent number of looks in polarimetric synthetic aperture radar imagery. IEEE Trans. Geosci. Remote Sens. 2009, 47, 3795–3809. [Google Scholar] [CrossRef]
- Martino, G.D.; Simone, D.A.; Iodice, A.; Riccio, D. Scattering-based nonlocal means SAR despeckling. IEEE Trans. Geosci. Remote Sens. 2016, 54, 3574–3588. [Google Scholar] [CrossRef]
- Lee, J.S.; Grunes, M.R.; Schuler, D.L.; Pottier, E.; Ferro, L. Scattering-model-based speckle filtering of polarimetric SAR data. IEEE Trans. Geosci. Remote Sens. 2006, 44, 176–187. [Google Scholar]
- Liu, L.; Jiang, L.M.; Li, H.Z.; Hu, J.X. Improved scattering-model-based speckle filter in polarimetric SAR data with orientation angle compensation. In Proceedings of the 2011 International Conference on Remote Sensing, Environment and Transportation Engineering, Nanjing, China, 24–26 June 2011; pp. 5026–5029. [Google Scholar]
- Lee, J.S.; Eric, P. Polarimetric Radar Imaging: From Basics to Application; CRC Press: Boca Raton, FL, USA, 2009; pp. 160–161. [Google Scholar]
- Xu, Q.; Chen, Q.H.; Yang, S.; Liu, X.G. Superpixel-based classification using k distribution and spatia context for polarimetric SAR images. Remote Sens. 2016, 8, 619. [Google Scholar]
- Novak, L.M.; Burl, M.C. Optimal speckle reduction in polarimetric SAR imagery. IEEE Trans. Aerosp. Electron. Syst. 1990, 26, 293–305. [Google Scholar] [CrossRef]
- Lopes, A.; Sery, F. Optimal speckle reduction for the product model inmultilook polarimetric SAR imagery and the Wishartdistribution. IEEE Trans. Geosci. Remote Sens. 1997, 35, 632–647. [Google Scholar] [CrossRef]
- Conradsen, K.; Nielsen, A.A.; Schou, J. Atest statistic in the complex Wishart distribution and its application to change detection in polarimetric SAR data. IEEE Trans. Geosci. Remote Sens. 2003, 41, 4–19. [Google Scholar] [CrossRef]
- Lee, J.-S.; Grunes, M.R.; Kwok, R. Classification of multi-look polarimetric SAR imagery based on complex Wishart distribution. Int. J. Remote Sens. 1994, 15, 2299–2311. [Google Scholar] [CrossRef]
- Khan, S.; Guida, R. On fractional moments of multilook polarimetric whitening filter for polarimetric SAR data. IEEE Trans. Geosci. Remote Sens. 2014, 52, 3502–3512. [Google Scholar] [CrossRef]
- Foucher, S.; Lopez-Martinez, C. Analysis, evaluation, and comparison of polarimetric SAR speckle filtering techniques. IEEE Trans. Image Process. 2014, 23, 1751–1764. [Google Scholar] [CrossRef] [PubMed]
- Yu, Y.J.; Acton, S.T. Speckle reducing anisotropic diffusion. IEEE Trans. Image Process. 2002, 11, 1260. [Google Scholar] [PubMed]
- Foucher, S.; Farage, G.; Benie, G. Polarimetric SAR image filtering with trace-based partial differential equations. Can. J. Remote Sens. 2007, 33, 226–236. [Google Scholar] [CrossRef]
- Foucher, S.; Farage, G.; Benie, G. Speckle filtering of POLSAR and POLINSAR images using trace-based partial differential equations. In Proceedings of the 2006 IEEE International Geoscience and Remote Sensing Symposium, Denvor, CO, USA, 31 July–4 August 2006; pp. 2545–2548. [Google Scholar]
- Deledalle, C.-A.; Denis, L.; Tabti, S.; Tupin, F. MuLoG, or How to apply Gaussian denoisers to multi-channel SAR speckle reduction? IEEE Trans. Image Process. 2017, 26, 4389–4403. [Google Scholar] [CrossRef] [PubMed]
- Nie, X.L.; Qiao, H.; Zhang, B.; Huang, X.Y. A Nonlocal TV-based variational method for PolSAR data speckle reduction. IEEE Trans. Image Process. 2016, 25, 2620–2634. [Google Scholar] [CrossRef] [PubMed]
- Feng, H.; Hou, B.; Gong, M. SAR image despeckling based on local homogeneous region segmentation by using pixel-relativity measurement. IEEE Trans. Geosci. Remote Sens. 2011, 49, 2724–2737. [Google Scholar] [CrossRef]
- Leonardo, T.; Sidnei, J.S.; Corina, D.C.; Alejandro, C.F. Speckle reduction in polarimetric SAR imagery with stochastic distances and nonlocal means. Pattern Recognit. 2014, 47, 141–157. [Google Scholar]
- Yang, S.; Chen, Q.H.; Yuan, X.H.; Liu, X.G. Adaptive coherency matrix estimation forpolarimetric SAR imagery based onlocal heterogeneity coefficients. IEEE Trans. Geosci. Remote Sens. 2016, 54, 6732–6745. [Google Scholar] [CrossRef]
- Wu, J.; Liu, F.; Jiao, L.C.; Zhang, X.G. Local maximal homogeneous region search for SAR speckle reduction with sketch-based geometrical kernel function. IEEE Trans. Geosci. Remote Sens. 2014, 52, 5751–5764. [Google Scholar]


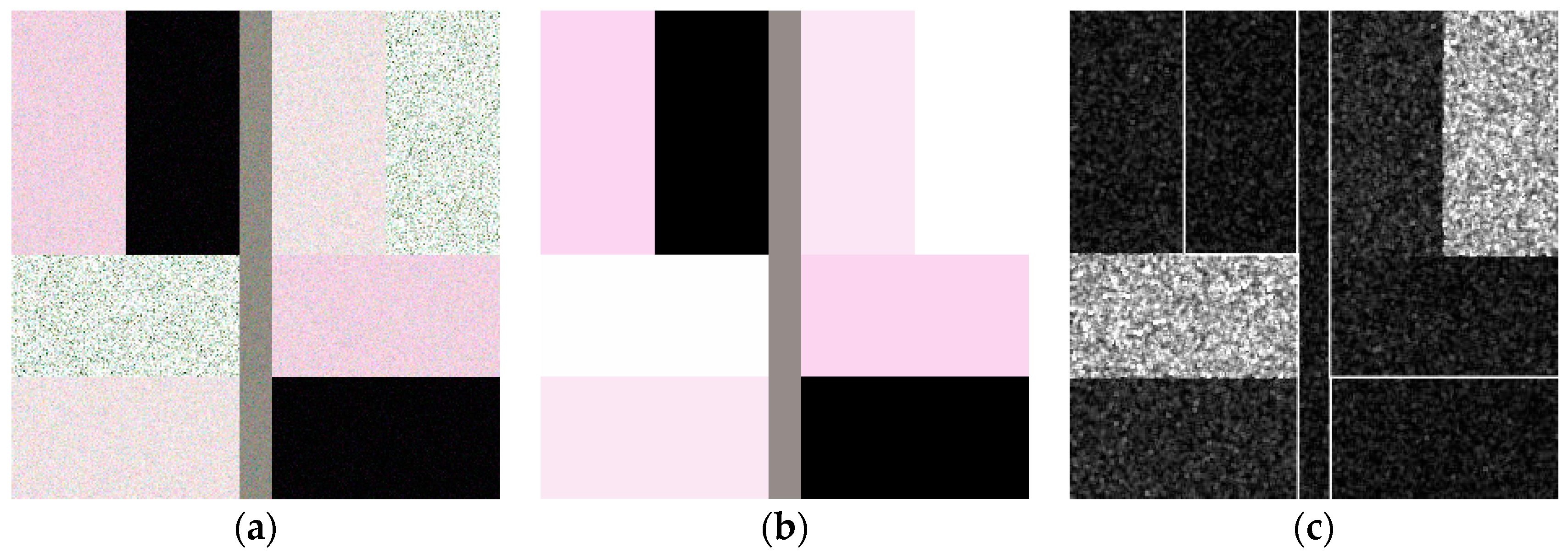











| Data | The One-Look Simulated PolSAR Data | ||||||||
| Methods/Indicators | ᾱ | A | H | Ca | Cp | P | ENL | EPI-HD | EPI-VD |
| Refined Lee | 0.007 | 0.060 | 0.102 | 0.585 | 0.591 | 0.218 | 45.942 | 0.620 | 0.369 |
| ite-bilateral | 0.005 | 0.138 | 0.015 | 0.077 | 0.544 | 0.222 | 53.421 | 0.710 | 0.555 |
| SRAD | 0.007 | 0.175 | 0.052 | 0.242 | 0.423 | 0.489 | 28.267 | 0.781 | 0.862 |
| MuLoG-TV | 0.023 | 0.391 | 0.070 | 0.515 | 0.430 | 0.164 | 54.775 | 0.709 | 0.602 |
| CVPB-NLM | 0.004 | 0.360 | 0.031 | 0.323 | 0.262 | 0.129 | 62.291 | 0.902 | 0.575 |
| Data | The Four-Look Simulated PolSAR Data | ||||||||
| Methods/Indicators | ᾱ | A | H | Ca | Cp | P | ENL | EPI-HD | EPI-VD |
| Refined Lee | 0.011 | 0.022 | 0.016 | 0.342 | 0.342 | 0.063 | 18.192 | 0.804 | 0.715 |
| ite-bilateral | 0.004 | 0.036 | 0.003 | 0.031 | 0.026 | 0.020 | 1.134 | 0.840 | 0.854 |
| NL-Lee | 0.004 | 0.032 | 0.003 | 0.079 | 0.028 | 0.017 | 18.772 | 0.747 | 0.913 |
| SRAD | 0.012 | 0.031 | 0.023 | 0.484 | 0.484 | 0.034 | 42.951 | 0.755 | 0.767 |
| MuLoG-TV | 0.016 | 0.074 | 0.022 | 0.444 | 0.052 | 0.053 | 35.108 | 0.675 | 0.708 |
| CVPB-NLM | 0.002 | 0.021 | 0.006 | 0.055 | 0.106 | 0.010 | 28.517 | 0.913 | 0.928 |
| Data | Method/Indicators | ᾱ | A | Ca | Cp | P | ENL | EPI-HD | EPI-VD |
| AIRSAR | Refined Lee | 0.178 | 0.658 | 0.087 | 0.063 | 0.119 | 0.489 | 0.749 | 0.969 |
| ite-bilateral | 0.166 | 0.803 | 0.097 | 0.074 | 0.090 | 1.388 | 0.758 | 0.902 | |
| NL-Lee | 0.171 | 0.777 | 0.080 | 0.071 | 0.070 | 0.424 | 0.723 | 0.918 | |
| SRAD | 0.167 | 0.657 | 0.098 | 0.071 | 0.098 | 0.810 | 0.708 | 0.926 | |
| MuLoG-TV | 0.134 | 0.647 | 0.232 | 0.073 | 0.256 | 0.732 | 0.775 | 0.927 | |
| CVPB-NLM | 0.168 | 0.806 | 0.096 | 0.071 | 0.086 | 1.224 | 0.806 | 0.998 | |
| Data | Method/Indicators | ᾱ | A | Ca | Cp | P | ENL | EPI-HD | EPI-VD |
| ESAR | Refined Lee | 0.056 | 0.411 | 0.561 | 0.686 | 0.245 | 18.992 | 0.413 | 0.788 |
| ite-bilateral | 0.075 | 0.421 | 0.330 | 0.323 | 0.158 | 18.522 | 0.524 | 0.824 | |
| SRAD | 0.075 | 0.366 | 1.030 | 0.710 | 0.140 | 12.061 | 0.941 | 0.863 | |
| MuLoG-TV | 0.080 | 0.391 | 0.302 | 0.210 | 0.173 | 28.905 | 0.505 | 0.770 | |
| CVPB-NLM | 0.075 | 0.439 | 0.340 | 0.260 | 0.163 | 22.990 | 0.623 | 0.780 |
| Data/Indicators | ᾱ | A | H | Ca | Cp | P | ENL | EPD-HD | EPD-VD | |
|---|---|---|---|---|---|---|---|---|---|---|
| one-look | 3 × 3 | 0.004 | 0.360 | 0.031 | 0.323 | 0.262 | 0.129 | 62.291 | 0.691 | 0.979 |
| 5 × 5 | 0.004 | 0.303 | 0.045 | 0.292 | 0.589 | 0.478 | 81.982 | 0.707 | 0.873 | |
| 7 × 7 | 0.003 | 0.238 | 0.078 | 0.480 | 0.518 | 0.751 | 72.076 | 0.750 | 0.860 | |
| 9 × 9 | 0.003 | 0.317 | 0.137 | 0.598 | 0.608 | 0.597 | 61.361 | 0.821 | 0.837 | |
| 11 × 11 | 0.003 | 0.343 | 0.222 | 0.603 | 0.737 | 0.537 | 39.299 | 0.842 | 0.935 | |
| four-look | 3 × 3 | 0.002 | 0.021 | 0.006 | 0.055 | 0.106 | 0.010 | 28.517 | 0.835 | 0.913 |
| 5 × 5 | 0.003 | 0.013 | 0.006 | 0.186 | 0.216 | 0.013 | 16.780 | 0.775 | 0.900 | |
| 7 × 7 | 0.004 | 0.028 | 0.014 | 0.308 | 0.366 | 0.013 | 12.542 | 0.912 | 0.943 | |
| 9 × 9 | 0.006 | 0.087 | 0.033 | 0.587 | 0.551 | 0.008 | 12.681 | 0.891 | 0.978 | |
| 11×11 | 0.009 | 0.168 | 0.062 | 0.957 | 0.703 | 0.009 | 16.365 | 0.967 | 0.994 | |
| Data | Indicators | ᾱ | A | Ca | Cp | P | ENL | EPI-HD | EPI-VD |
| AIRSAR | 3 × 3 | 0.168 | 0.806 | 0.096 | 0.071 | 0.086 | 1.224 | 0.806 | 0.998 |
| 5 × 5 | 0.166 | 0.790 | 0.098 | 0.076 | 0.092 | 0.621 | 0.807 | 0.962 | |
| 7 × 7 | 0.165 | 0.717 | 0.098 | 0.081 | 0.087 | 0.978 | 0.768 | 0.935 | |
| 9 × 9 | 0.167 | 0.598 | 0.100 | 0.079 | 0.087 | 0.995 | 0.822 | 0.975 | |
| 11 × 11 | 0.171 | 0.505 | 0.103 | 0.079 | 0.087 | 0.437 | 0.839 | 0.998 | |
| Data | Method/Indicators | ᾱ | A | Ca | Cp | P | ENL | EPI-HD | EPI-VD |
| ESAR | 3 × 3 | 0.075 | 0.439 | 0.340 | 0.260 | 0.163 | 22.990 | 0.623 | 0.780 |
| 5 × 5 | 0.075 | 0.423 | 0.368 | 0.250 | 0.162 | 24.652 | 0.580 | 0.788 | |
| 7 × 7 | 0.077 | 0.412 | 0.356 | 0.356 | 0.156 | 21.900 | 0.565 | 0.786 | |
| 9 × 9 | 0.077 | 0.393 | 0.614 | 0.567 | 0.152 | 16.090 | 0.615 | 0.791 | |
| 11 × 11 | 0.077 | 0.350 | 1.108 | 0.724 | 0.149 | 12.540 | 0.679 | 0.773 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xing, X.; Chen, Q.; Yang, S.; Liu, X. Feature-Based Nonlocal Polarimetric SAR Filtering. Remote Sens. 2017, 9, 1043. https://doi.org/10.3390/rs9101043
Xing X, Chen Q, Yang S, Liu X. Feature-Based Nonlocal Polarimetric SAR Filtering. Remote Sensing. 2017; 9(10):1043. https://doi.org/10.3390/rs9101043
Chicago/Turabian StyleXing, Xiaoli, Qihao Chen, Shuai Yang, and Xiuguo Liu. 2017. "Feature-Based Nonlocal Polarimetric SAR Filtering" Remote Sensing 9, no. 10: 1043. https://doi.org/10.3390/rs9101043
APA StyleXing, X., Chen, Q., Yang, S., & Liu, X. (2017). Feature-Based Nonlocal Polarimetric SAR Filtering. Remote Sensing, 9(10), 1043. https://doi.org/10.3390/rs9101043