A Graph-Based Approach for 3D Building Model Reconstruction from Airborne LiDAR Point Clouds
Abstract
:1. Introduction
2. Methodology
2.1. Building Contours Generation
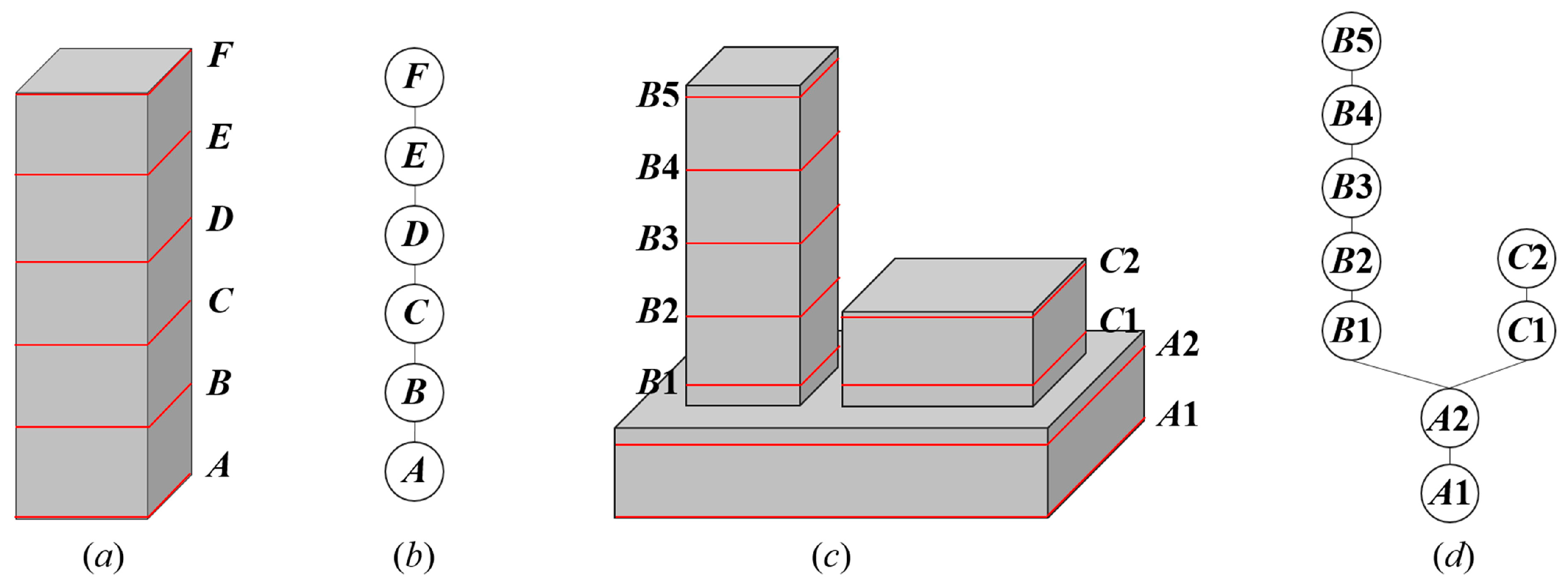
2.2. Graph-Based Localized Contour Tree Construction
2.3. Bipartite Graph Matching
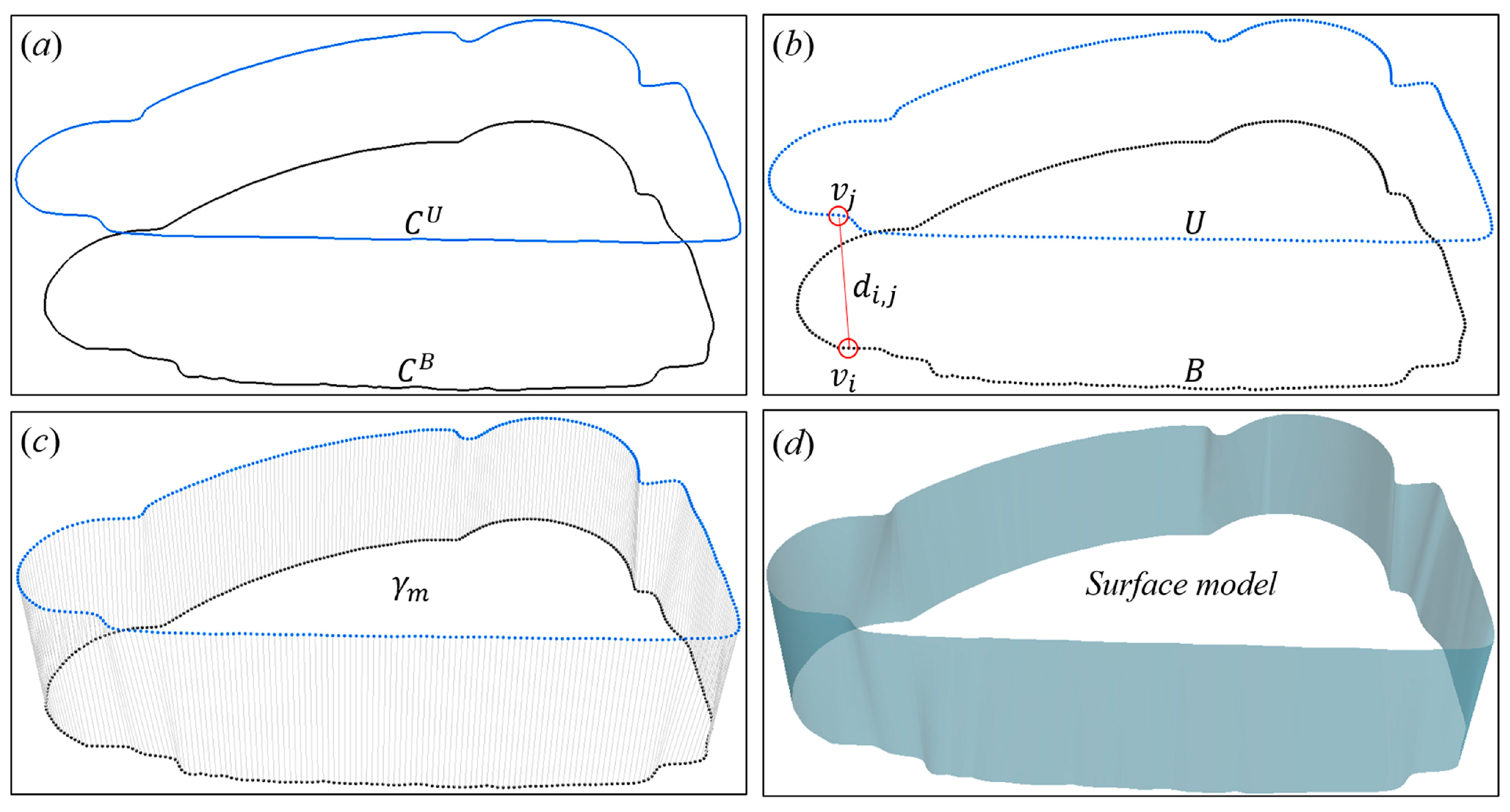
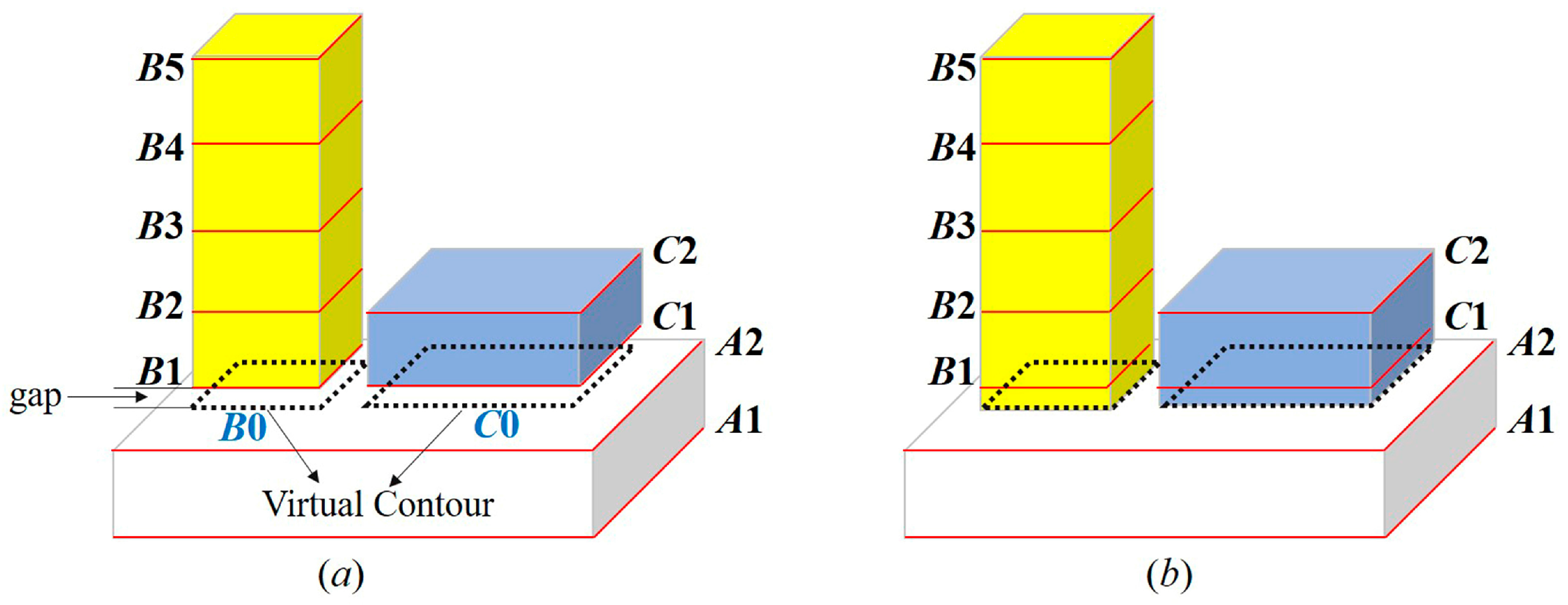
2.4. Building Model Reconstruction
2.5. Implementation
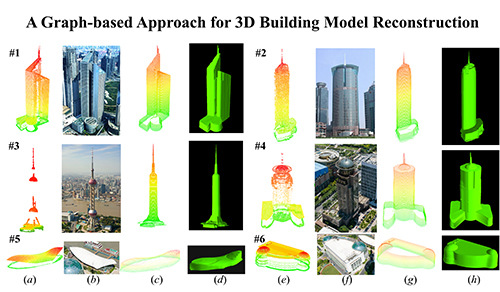
3. Experiment
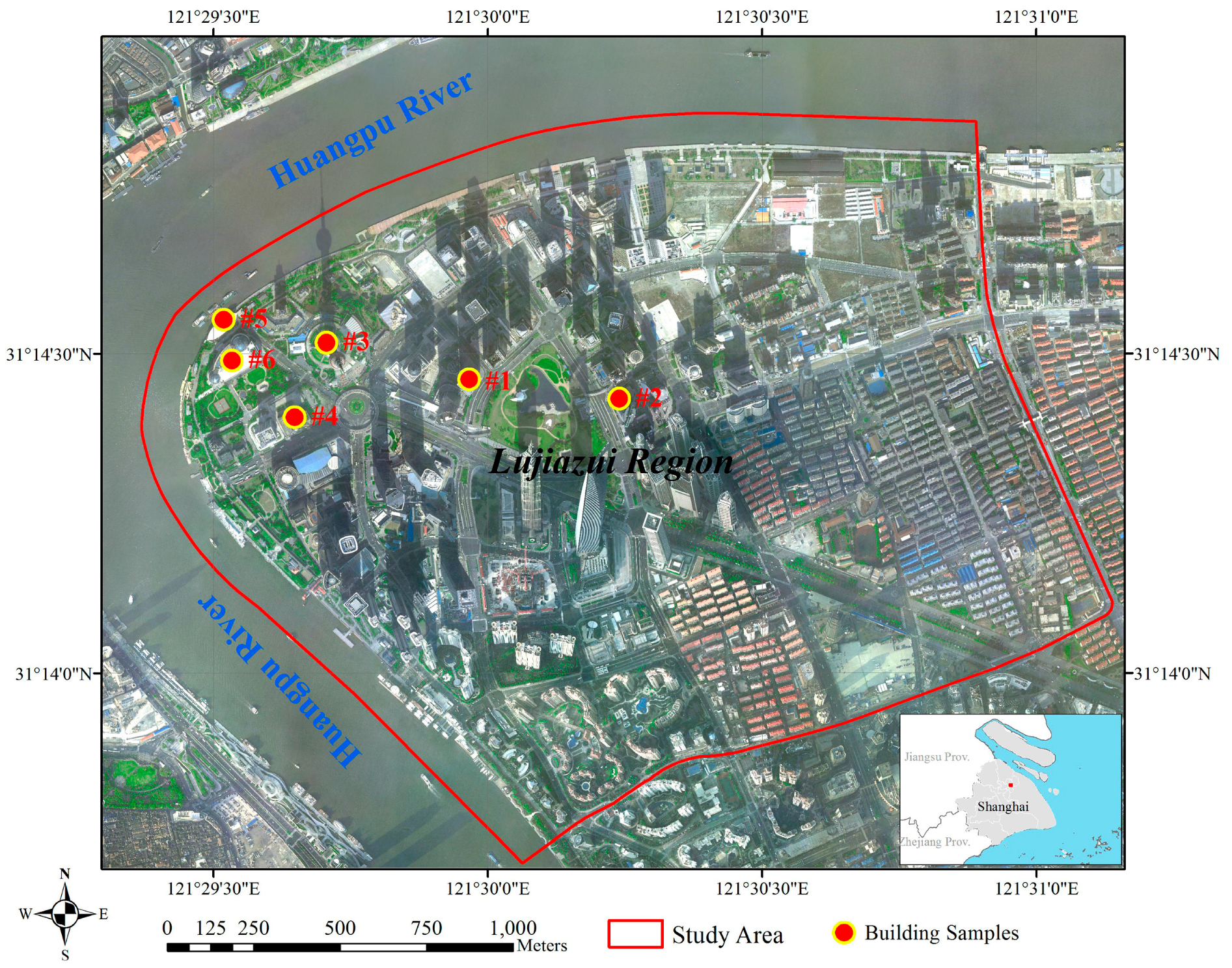
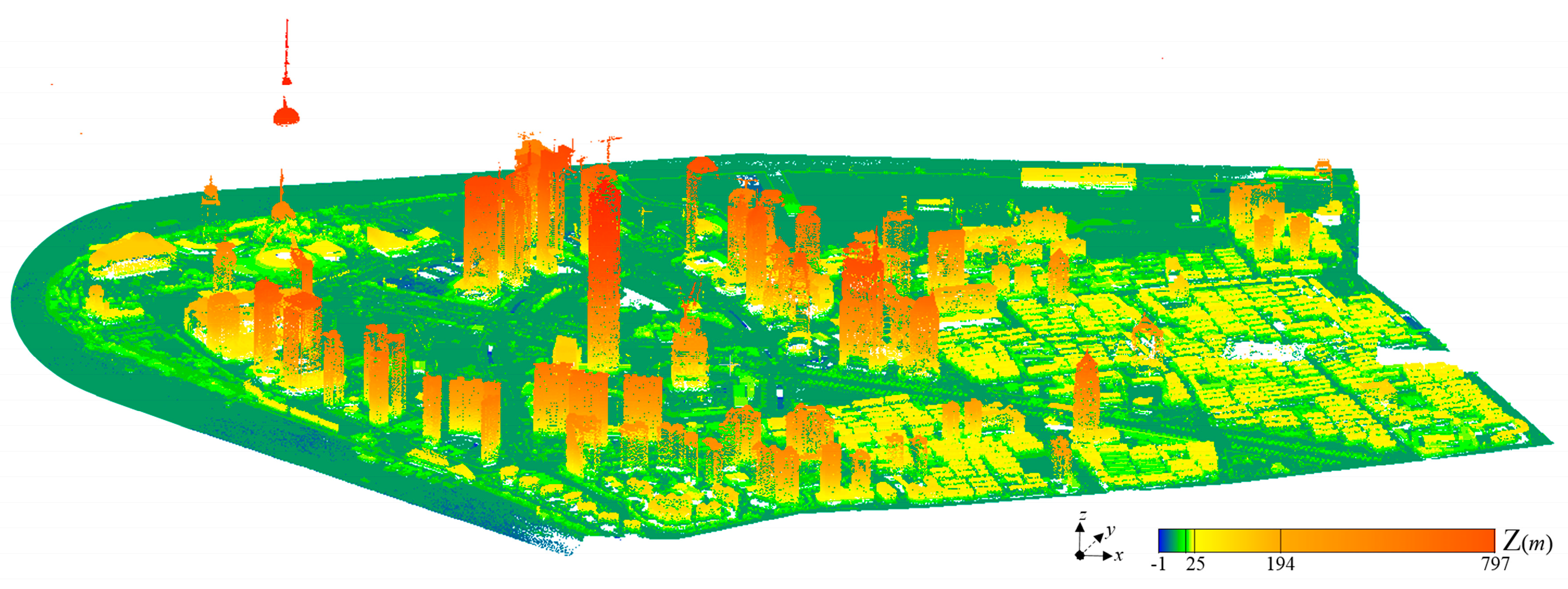
3.1. Study Area and Data
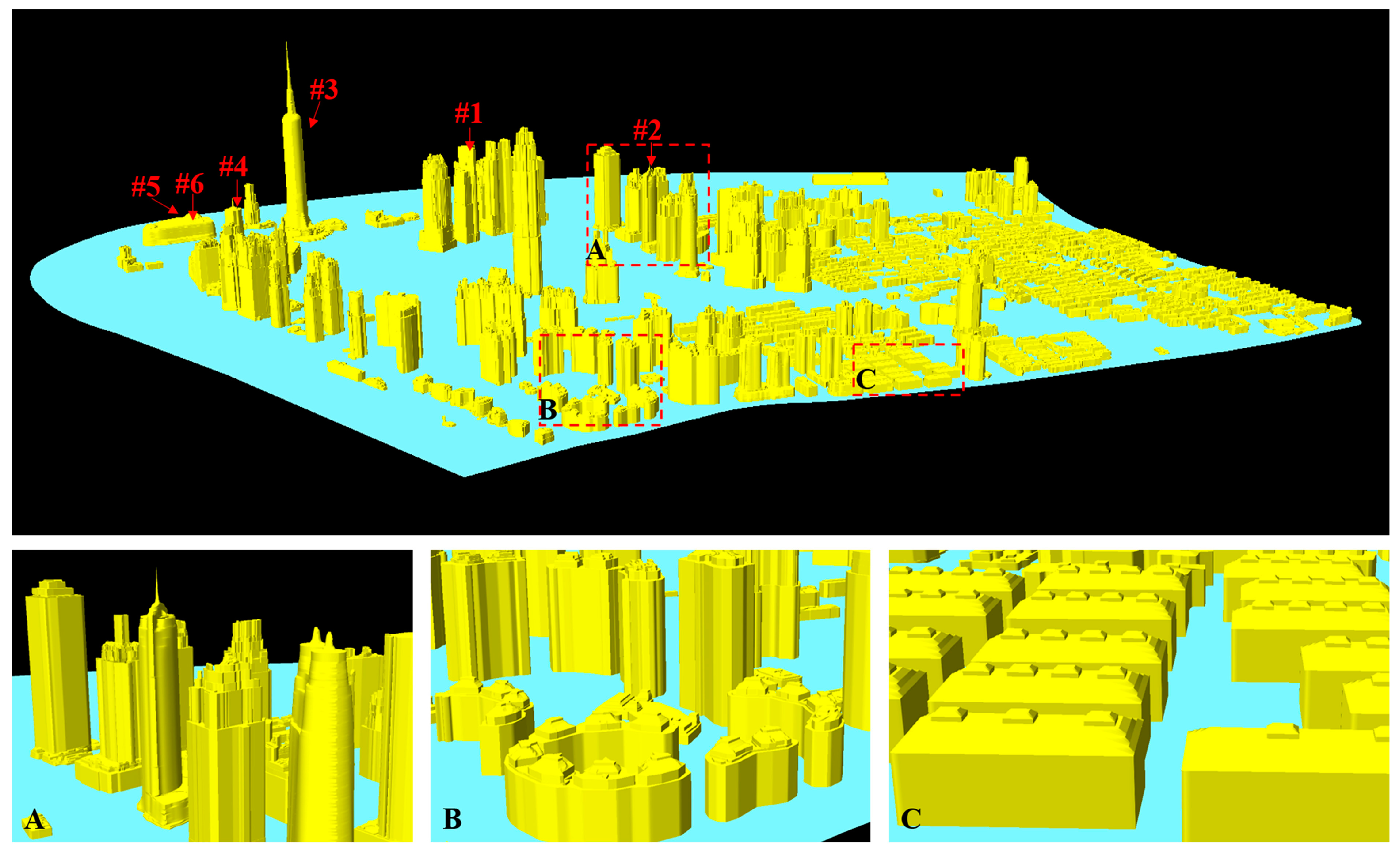
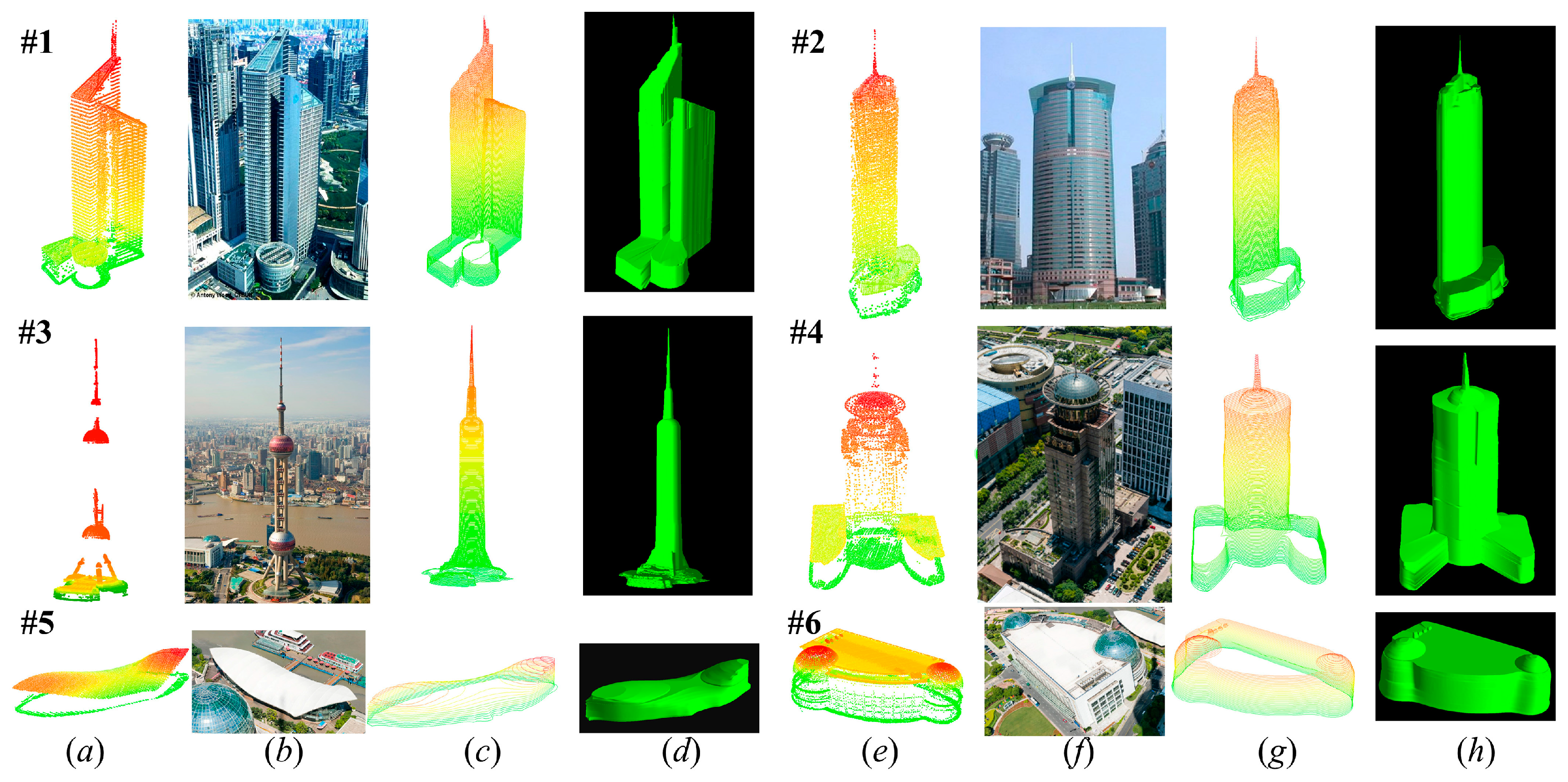
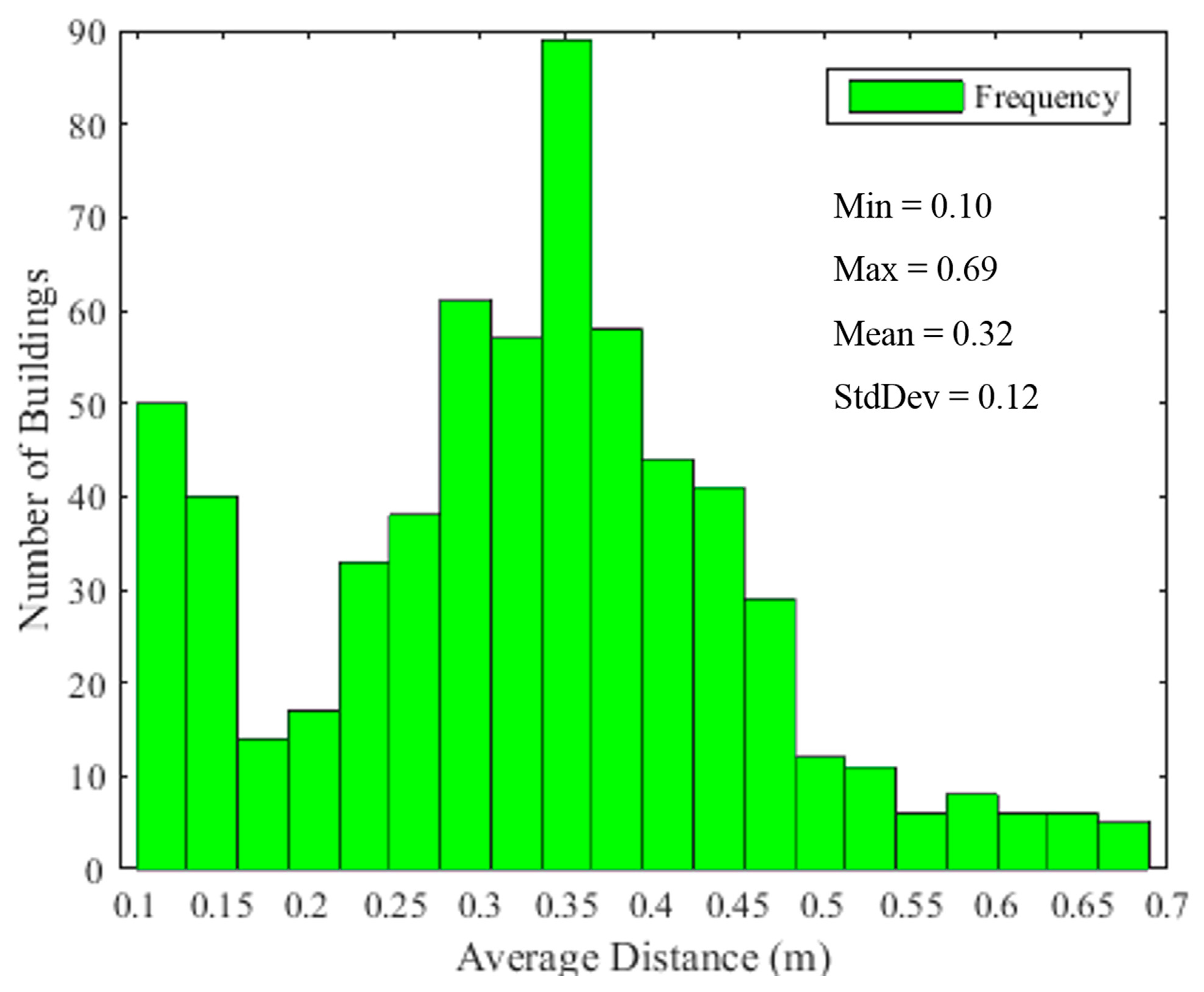
3.2. Results
4. Discussion
4.1. Performance
4.2. Tuning of Algorithm Parameters
4.3. Limitations
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Song, J.; Wu, J.; Jiang, Y. Extraction and reconstruction of curved surface buildings by contour clustering using airborne lidar data. Optik 2015, 126, 513–521. [Google Scholar] [CrossRef]
- Cheng, L.; Gong, J.; Li, M.; Liu, Y. 3D building model reconstruction from multi-view aerial imagery and lidar data. Photogramm. Eng. Remote Sens. 2011, 77, 125–139. [Google Scholar] [CrossRef]
- Vosselman, G.; Dijkman, S. 3D building model reconstruction from point clouds and ground plans. Int. Arch. Photogram. Rem. Sens. Spat. Inform. Sci. 2001, 34, 37–44. [Google Scholar]
- Suveg, I.; Vosselman, G. Reconstruction of 3D building models from aerial images and maps. ISPRS J. Photogramm. Remote Sens. 2004, 58, 202–224. [Google Scholar] [CrossRef]
- Verma, V.; Kumar, R.; Hsu, S. 3D building detection and modeling from aerial lidar data. In Proceedings of the 2006 IEEE Computer Society Conference on Computer Vision and Pattern Recognition, Washington, DC, USA, 17–22 June 2006.
- Gao, Y.; Dai, Q.; Wang, M.; Zhang, N. 3D model retrieval using weighted bipartite graph matching. Signal Process Image 2011, 26, 39–47. [Google Scholar] [CrossRef]
- Haala, N.; Kada, M. An update on automatic 3D building reconstruction. ISPRS J. Photogramm. Remote Sens. 2010, 65, 570–580. [Google Scholar] [CrossRef]
- Oude Elberink, S.; Vosselman, G. Quality analysis on 3D building models reconstructed from airborne laser scanning data. ISPRS J. Photogramm. Remote Sens. 2011, 66, 157–165. [Google Scholar] [CrossRef]
- Sohn, G.; Huang, X.; Tao, V. Using a binary space partitioning tree for reconstructing polyhedral building models from airborne lidar data. Photogramm. Eng. Remote Sens. 2008, 74, 1425–1438. [Google Scholar] [CrossRef]
- Zhou, Q.-Y.; Neumann, U. Fast and extensible building modeling from airborne lidar data. In Proceedings of the 16th ACM SIGSPATIAL International Conference on Advances in Geographic Information Systems, Irvine, CA, USA, 5–7 November 2008.
- Brenner, C. Building reconstruction from images and laser scanning. Int. J. Appl. Earth Obs. Geoinf. 2005, 6, 187–198. [Google Scholar] [CrossRef]
- Xiao, J.; Gerke, M.; Vosselman, G. Building extraction from oblique airborne imagery based on robust façade detection. ISPRS J. Photogramm. Remote Sens. 2012, 68, 56–68. [Google Scholar] [CrossRef]
- Rottensteiner, F. Automatic generation of high-quality building models from lidar data. IEEE Comput. Graph. Appl. 2003, 23, 42–50. [Google Scholar] [CrossRef]
- Pu, S.; Vosselman, G. Knowledge based reconstruction of building models from terrestrial laser scanning data. ISPRS J. Photogramm. Remote Sens. 2009, 64, 575–584. [Google Scholar] [CrossRef]
- Yang, B.; Fang, L.; Li, J. Semi-automated extraction and delineation of 3D roads of street scene from mobile laser scanning point clouds. ISPRS J. Photogramm. Remote Sens. 2013, 79, 80–93. [Google Scholar] [CrossRef]
- Arefi, H.; Reinartz, P. Building reconstruction using dsm and orthorectified images. Remote Sens. 2013, 5, 1681–1703. [Google Scholar] [CrossRef]
- Brédif, M.; Tournaire, O.; Vallet, B.; Champion, N. Extracting polygonal building footprints from digital surface models: A fully-automatic global optimization framework. ISPRS J. Photogramm. Remote Sens. 2013, 77, 57–65. [Google Scholar] [CrossRef]
- Yang, B.; Shi, W.; Li, Q. An integrated tin and grid method for constructing multi-resolution digital terrain models. Int. J. Geogr. Inf. Sci. 2005, 19, 1019–1038. [Google Scholar] [CrossRef]
- Wu, B.; Yu, B.; Yue, W.; Wu, J.; Huang, Y. Voxel-based marked neighborhood searching method for identifying street trees using vehicle-borne laser scanning data. In Proceedings of the Second International Workshop on Earth Observation and Remote Sensing Applications, Shanghai, China, 8–11 June 2012; pp. 327–331.
- Wu, B.; Yu, B.; Yue, W.; Shu, S.; Tan, W.; Hu, C.; Huang, Y.; Wu, J.; Liu, H. A voxel-based method for automated identification and morphological parameters estimation of individual street trees from mobile laser scanning data. Remote Sens. 2013, 5, 584–611. [Google Scholar] [CrossRef]
- Huang, Y.; Chen, Z.; Wu, B.; Chen, L.; Mao, W.; Zhao, F.; Wu, J.; Wu, J.; Yu, B. Estimating roof solar energy potential in the downtown area using a gpu-accelerated solar radiation model and airborne lidar data. Remote Sens. 2015, 7, 17212–17233. [Google Scholar] [CrossRef]
- Wu, B.; Yu, B.; Huang, C.; Wu, Q.; Wu, J. Automated extraction of ground surface along urban roads from mobile laser scanning point clouds. Remote Sens. Lett. 2016, 7, 170–179. [Google Scholar] [CrossRef]
- Wu, B.; Yu, B.; Wu, Q.; Huang, Y.; Chen, Z.; Wu, J. Individual tree crown delineation using localized contour tree method and airborne lidar data in coniferous forests. Int. J. Appl. Earth Obs. Geoinf. 2016, 52, 82–94. [Google Scholar] [CrossRef]
- Yu, S.; Yu, B.; Song, W.; Wu, B.; Zhou, J.; Huang, Y.; Wu, J.; Zhao, F.; Mao, W. View-based greenery: A three-dimensional assessment of city buildings’ green visibility using floor green view index. Landsc. Urban Plan. 2016, 152, 13–26. [Google Scholar] [CrossRef]
- Yu, B.; Liu, H.; Wu, J.; Hu, Y.; Zhang, L. Automated derivation of urban building density information using airborne lidar data and object-based method. Landsc. Urban Plan. 2010, 98, 210–219. [Google Scholar] [CrossRef]
- Huang, Y.; Yu, B.; Zhou, J.; Hu, C.; Tan, W.; Hu, Z.; Wu, J. Toward automatic estimation of urban green volume using airborne lidar data and high resolution remote sensing images. Front. Earth Sci. 2013, 7, 43–54. [Google Scholar] [CrossRef]
- Lafarge, F.; Mallet, C. Creating large-scale city models from 3D-point clouds: A robust approach with hybrid representation. Int. J. Comput. Vis. 2012, 99, 69–85. [Google Scholar] [CrossRef]
- Maas, H.-G.; Vosselman, G. Two algorithms for extracting building models from raw laser altimetry data. ISPRS J. Photogramm. Remote Sens. 1999, 54, 153–163. [Google Scholar] [CrossRef]
- Cheng, L.; Tong, L.; Chen, Y.; Zhang, W.; Shan, J.; Liu, Y.; Li, M. Integration of lidar data and optical multi-view images for 3D reconstruction of building roofs. Opt. Lasers Eng. 2013, 51, 493–502. [Google Scholar] [CrossRef]
- Kada, M.; McKinley, L. 3D building reconstruction from lidar based on a cell decomposition approach. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2009, 38, 47–52. [Google Scholar]
- Milde, J.; Brenner, C. Graph-based modeling of building roofs. In Proceedings of the 12th AGILE Conference on GIScience, Hannover, Germany, 2–5 June 2009.
- Vosselman, G.; Gorte, B.G.; Sithole, G.; Rabbani, T. Recognising structure in laser scanner point clouds. Int. Arch. Photogram. Rem. Sens. Spat. Inf. Sci 2004, 46, 33–38. [Google Scholar]
- Sampath, A.; Shan, J. Segmentation and reconstruction of polyhedral building roofs from aerial lidar point clouds. IEEE Trans. Geosci. Remote Sens 2010, 48, 1554–1567. [Google Scholar] [CrossRef]
- Wahl, R.; Schnabel, R.; Klein, R. From detailed digital surface models to city models using constrained simplification. Photogramm. Fernerkund. 2008, 12, 207–215. [Google Scholar]
- Schnabel, R.; Wahl, R.; Klein, R. Efficient ransac for point-cloud shape detection. Comput. Graph. Forum 2007, 26, 214–226. [Google Scholar] [CrossRef]
- Tarsha-Kurdi, F.; Landes, T.; Grussenmeyer, P. Hough-transform and extended ransac algorithms for automatic detection of 3D building roof planes from lidar data. In Proceedings of the ISPRS Workshop on Laser Scanning, Espoo, Finland, 12–14 September 2007.
- Kim, K.; Shan, J. Building roof modeling from airborne laser scanning data based on level set approach. ISPRS J. Photogramm. Remote Sens. 2011, 66, 484–497. [Google Scholar] [CrossRef]
- Tarsha-Kurdi, F.; Landes, T.; Grussenmeyer, P. Extended ransac algorithm for automatic detection of building roof planes from lidar data. Photogramm. J. Finl. 2008, 21, 97–109. [Google Scholar]
- Filin, S.; Pfeifer, N. Segmentation of airborne laser scanning data using a slope adaptive neighborhood. ISPRS J. Photogramm. Remote Sens. 2006, 60, 71–80. [Google Scholar] [CrossRef]
- Biosca, J.M.; Lerma, J.L. Unsupervised robust planar segmentation of terrestrial laser scanner point clouds based on fuzzy clustering methods. ISPRS J. Photogramm. Remote Sens. 2008, 63, 84–98. [Google Scholar] [CrossRef]
- Rottensteiner, F.; Trinder, J.; Clode, S.; Kubik, K. Automated delineation of roof planes from lidar data. Isprs Workshop Laser Scanning 2005, 36, 221–226. [Google Scholar]
- Lafarge, F.; Descombes, X.; Zerubia, J.; Pierrot-Deseilligny, M. Structural approach for building reconstruction from a single DSM. IEEE Trans. Pattern Anal. Mach. Intell. 2010, 32, 135–147. [Google Scholar] [CrossRef] [PubMed]
- Henn, A.; Gröger, G.; Stroh, V.; Plümer, L. Model driven reconstruction of roofs from sparse lidar point clouds. ISPRS J. Photogramm. Remote Sens. 2013, 76, 17–29. [Google Scholar] [CrossRef]
- Huang, H.; Brenner, C.; Sester, M. A generative statistical approach to automatic 3D building roof reconstruction from laser scanning data. ISPRS J. Photogramm. Remote Sens. 2013, 79, 29–43. [Google Scholar] [CrossRef]
- Truong-Hong, L.; Laefer, D. Validating computational models from laser scanning data for historic facades. J. Test. Eval. 2013, 41, 1–16. [Google Scholar] [CrossRef]
- Truong-Hong, L.; Laefer, D.F. Octree-based, automatic building façade generation from lidar data. Comput. Aided Des. 2014, 53, 46–61. [Google Scholar] [CrossRef]
- Castellazzi, G.; Altri, A.; Bitelli, G.; Selvaggi, I.; Lambertini, A. From laser scanning to finite element analysis of complex buildings by using a semi-automatic procedure. Sensors 2015, 15, 18360–18380. [Google Scholar] [CrossRef] [PubMed]
- Castellazzi, G.; D’Altri, A.M.; de Miranda, S.; Ubertini, F. An innovative numerical modeling strategy for the structural analysis of historical monumental buildings. Eng. Struct. 2017, 132, 229–248. [Google Scholar] [CrossRef]
- Zhang, J.; Li, L.; Lu, Q.; Jiang, W. Contour clustering analysis for building reconstruction from lidar data. In Proceedings of the International Archives of the Photogrammetry, Remote Sensing and Spatial Information Sciences, Beijing, China, 3–11 July 2008.
- Li, L.; Zhang, J.; Jiang, W. Automatic complex building reconstruction from lidar based on hierarchical structure analysis. Proc. SPIE 2009, 7496, 74961–74968. [Google Scholar]
- Chen, L.; Teo, T.; Rau, J.; Liu, J.; Hsu, W. Building reconstruction from lidar data and aerial imagery. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium, Boston, MA, USA, 6–11 July 2005.
- Yang, B.; Wei, Z.; Li, Q.; Li, J. Semiautomated building facade footprint extraction from mobile lidar point clouds. IEEE Geosci. Remote Sens. Lett. 2013, 10, 766–770. [Google Scholar] [CrossRef]
- Wu, Q.; Liu, H.; Wang, S.; Yu, B.; Beck, R.; Hinkel, K. A localized contour tree method for deriving geometric and topological properties of complex surface depressions based on high-resolution topographical data. Int. J. Geogr. Inf. Sci. 2015, 29, 2041–2060. [Google Scholar] [CrossRef]
- Yu, B.; Liu, H.; Wu, J.; Lin, W.-M. Investigating impacts of urban morphology on spatio-temporal variations of solar radiation with airborne lidar data and a solar flux model: A case study of downtown houston. Int. J. Remote Sens. 2009, 30, 4359–4385. [Google Scholar] [CrossRef]
- Zhang, K.; Chen, S.-C.; Whitman, D.; Shyu, M.-L.; Yan, J.; Zhang, C. A progressive morphological filter for removing nonground measurements from airborne lidar data. IEEE Trans. Geosci. Remote Sens. 2003, 41, 872–882. [Google Scholar] [CrossRef]
- Chen, Q.; Baldocchi, D.; Gong, P.; Kelly, M. Isolating individual trees in a savanna woodland using small footprint lidar data. Photogramm. Eng. Remote Sens. 2006, 72, 923–932. [Google Scholar] [CrossRef]
- Liu, H. The Automatic Recognition Software Technique of the Geometrical Elements about the Skeleton Map. Master’s Thesis, Tsinghua University, Beijing, China, 2006. [Google Scholar]
- Guilbert, E. Multi-level representation of terrain features on a contour map. GeoInformatica 2013, 17, 301–324. [Google Scholar] [CrossRef]
- West, D.B. Introduction to Graph Theory; Prentice hall Upper Saddle River: Bergen County, NJ, USA, 2001. [Google Scholar]
- Alper, Y.; Mubarak, S. Actions sketch: A novel action representation. In Proceedings of the 2005 IEEE Computer Society Conference on Computer Vision and Pattern Recognition, Washington, DC, USA, 20–26 June 2005.
- Wen, Y.; Gao, Y.; Hong, R.; Luan, H.; Liu, Q.; Shen, J.; Ji, R. View-based 3d object retrieval by bipartite graph matching. In Proceedings of the 20th ACM International Conference on Multimedia, Nara, Japan, 29 October–2 November 2012; pp. 897–900.
- Munkres, J. Algorithms for the assignment and transportation problems. SIAM J. Appl. Math 1957, 5, 32–38. [Google Scholar] [CrossRef]
- Kuhn, H.W. The hungarian method for the assignment problem. Nav. Res. Logist. Q. 1955, 2, 83–97. [Google Scholar] [CrossRef]
- You, S.; Hu, J.; Neumann, U.; Fox, P. Urban site modeling from lidar. In Computational Science and Its Applications—ICCSA 2003; Kumar, V., Gavrilova, M.L., Tan, C.J.K., L’Ecuyer, P., Eds.; Springer: Berlin/Heidelberg, Germany, 2003; pp. 579–588. [Google Scholar]
| No./ | 0.1 | 0.2 | 0.3 | 0.4 | 0.5 | 0.6 | 0.7 | 0.8 | 0.9 | 1.0 | 1.5 | 2.0 | 3.0 | 4.0 | 5.0 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| #1 | 0.39 | 0.41 | 0.42 | 0.43 | 0.43 | 0.52 | 0.65 | 0.96 | 0.98 | 0.99 | 1.04 | 1.07 | 1.10 | 1.44 | 1.84 |
| #2 | 0.33 | 0.35 | 0.35 | 0.36 | 0.36 | 0.37 | 0.39 | 0.39 | 0.43 | 0.45 | 0.59 | 0.72 | 0.97 | 1.02 | 1.43 |
| #3 | 0.49 | 0.49 | 0.50 | 0.52 | 0.54 | 0.57 | 0.60 | 0.67 | 0.77 | 0.91 | 1.03 | 1.57 | 2.22 | 3.28 | 4.05 |
| #4 | 0.28 | 0.29 | 0.29 | 0.37 | 0.42 | 0.42 | 0.48 | 0.54 | 0.67 | 0.79 | 0.90 | 1.28 | 2.00 | 2.93 | 4.42 |
| #5 | 0.17 | 0.19 | 0.20 | 0.22 | 0.28 | 0.30 | 0.30 | 0.32 | 0.39 | 0.44 | 0.51 | 0.70 | 1.32 | 1.97 | 2.56 |
| #6 | 0.26 | 0.28 | 0.30 | 0.31 | 0.31 | 0.43 | 0.46 | 0.47 | 0.59 | 0.65 | 0.67 | 0.81 | 1.70 | 2.23 | 3.19 |
| No./ | 20 | 40 | 60 | 80 | 100 | 120 | 140 | 160 | 180 | 200 | 250 | 300 | 350 | 400 | 500 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| #1 | 0.66 | 0.51 | 0.45 | 0.44 | 0.44 | 0.43 | 0.43 | 0.43 | 0.43 | 0.43 | 0.43 | 0.43 | 0.43 | 0.43 | 0.43 |
| #2 | 0.82 | 0.67 | 0.59 | 0.51 | 0.42 | 0.41 | 0.39 | 0.39 | 0.37 | 0.37 | 0.36 | 0.36 | 0.36 | 0.35 | 0.35 |
| #3 | 0.93 | 0.81 | 0.74 | 0.69 | 0.67 | 0.60 | 0.58 | 0.57 | 0.57 | 0.56 | 0.55 | 0.54 | 0.52 | 0.51 | 0.51 |
| #4 | 1.23 | 1.05 | 1.01 | 0.98 | 0.79 | 0.77 | 0.76 | 0.68 | 0.60 | 0.55 | 0.45 | 0.42 | 0.40 | 0.38 | 0.38 |
| #5 | 0.51 | 0.46 | 0.44 | 0.43 | 0.41 | 0.39 | 0.35 | 0.32 | 0.32 | 0.31 | 0.28 | 0.28 | 0.24 | 0.22 | 0.21 |
| #6 | 0.47 | 0.36 | 0.33 | 0.32 | 0.32 | 0.32 | 0.32 | 0.32 | 0.32 | 0.32 | 0.31 | 0.31 | 0.31 | 0.31 | 0.31 |
© 2017 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, B.; Yu, B.; Wu, Q.; Yao, S.; Zhao, F.; Mao, W.; Wu, J. A Graph-Based Approach for 3D Building Model Reconstruction from Airborne LiDAR Point Clouds. Remote Sens. 2017, 9, 92. https://doi.org/10.3390/rs9010092
Wu B, Yu B, Wu Q, Yao S, Zhao F, Mao W, Wu J. A Graph-Based Approach for 3D Building Model Reconstruction from Airborne LiDAR Point Clouds. Remote Sensing. 2017; 9(1):92. https://doi.org/10.3390/rs9010092
Chicago/Turabian StyleWu, Bin, Bailang Yu, Qiusheng Wu, Shenjun Yao, Feng Zhao, Weiqing Mao, and Jianping Wu. 2017. "A Graph-Based Approach for 3D Building Model Reconstruction from Airborne LiDAR Point Clouds" Remote Sensing 9, no. 1: 92. https://doi.org/10.3390/rs9010092
APA StyleWu, B., Yu, B., Wu, Q., Yao, S., Zhao, F., Mao, W., & Wu, J. (2017). A Graph-Based Approach for 3D Building Model Reconstruction from Airborne LiDAR Point Clouds. Remote Sensing, 9(1), 92. https://doi.org/10.3390/rs9010092