Satellite Attitude Determination and Map Projection Based on Robust Image Matching
Abstract
:1. Introduction
2. Datasets
2.1. Satellite Image: UNIFORM-1
2.2. Base Map Image: Landsat-8
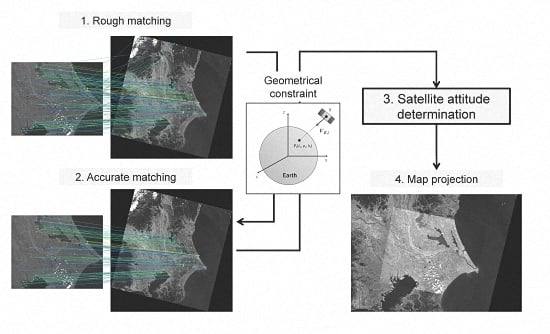
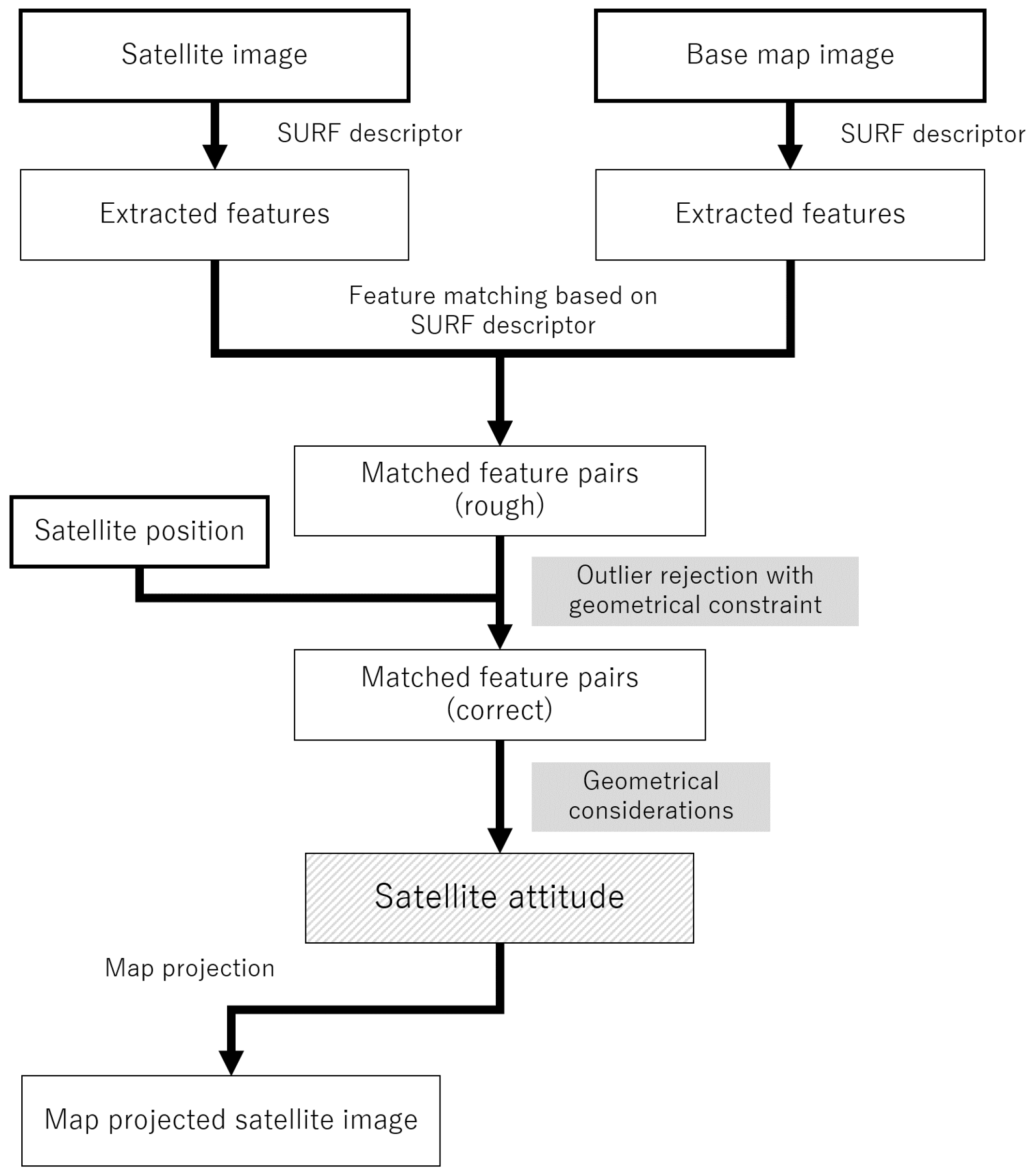
3. Method
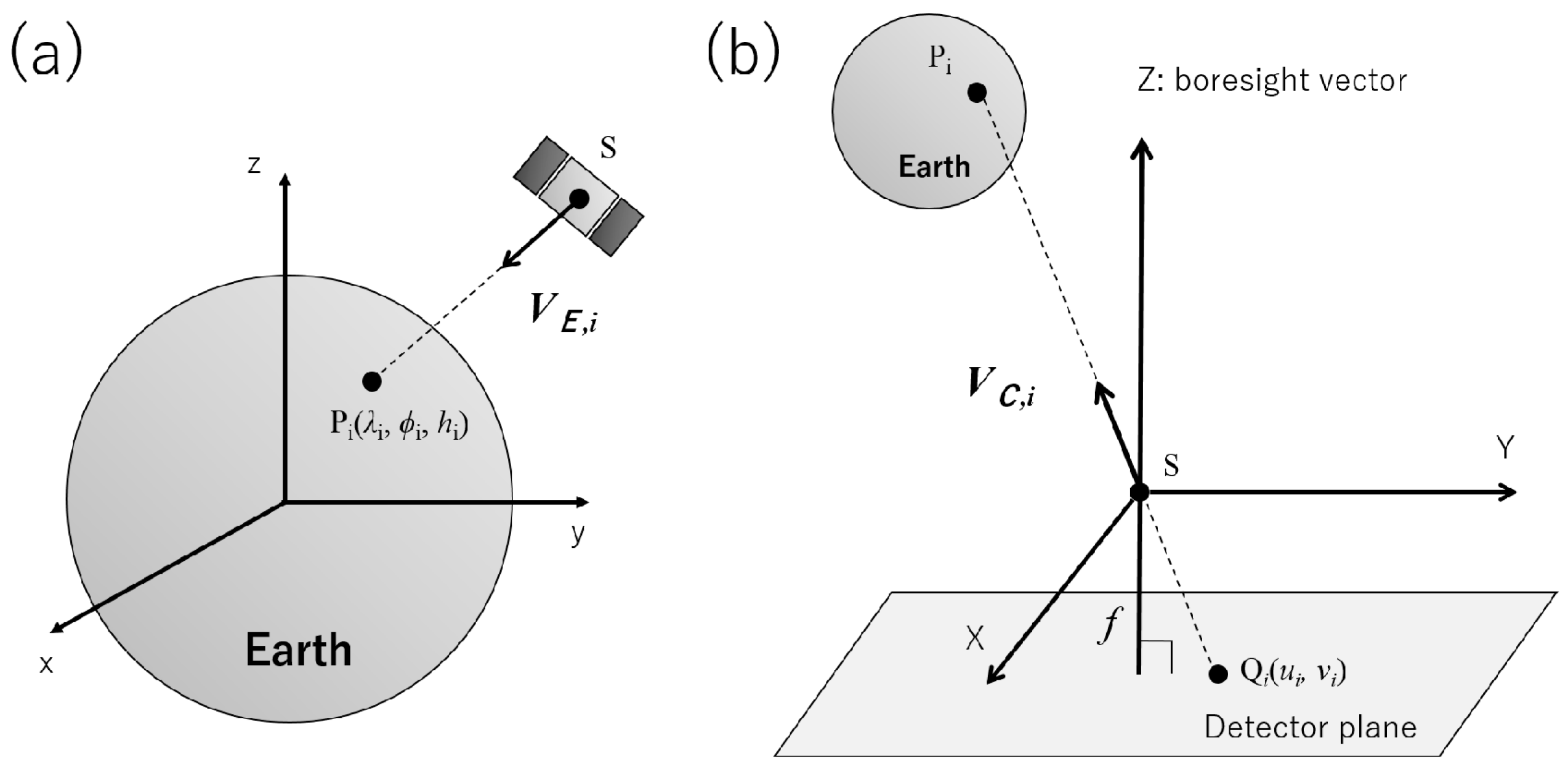
3.1. Satellite Attitude Determination from Images
- Calculate the cross product of and to form an orthogonal vector.
- Calculate the cross product of and to form an orthogonal vector.
- Normalize , , and to unit vectors.
- Construct .
3.2. Finding Matched Feature Points from Satellite and Base Images
3.2.1. Feature Descriptor
3.2.2. Rough Matching
3.2.3. Robust Feature Matching
- Randomly choose three feature pairs from the rough matching result.
- Estimate using three chosen feature pairs.
- Calculate the vector angles between andand find the largest angle in the three pairs (ideally ).
- If is less than a specified threshold, estimate the angles of and for all other feature pairs using the obtained , and find the inliers whose vector angles are less than the threshold.
- Repeat Steps 1–4 for a pre-specified number of times , and find a condition that maximizes the number of inliers L.
- Recalculate using all inliers in the maximized found in Step 5.
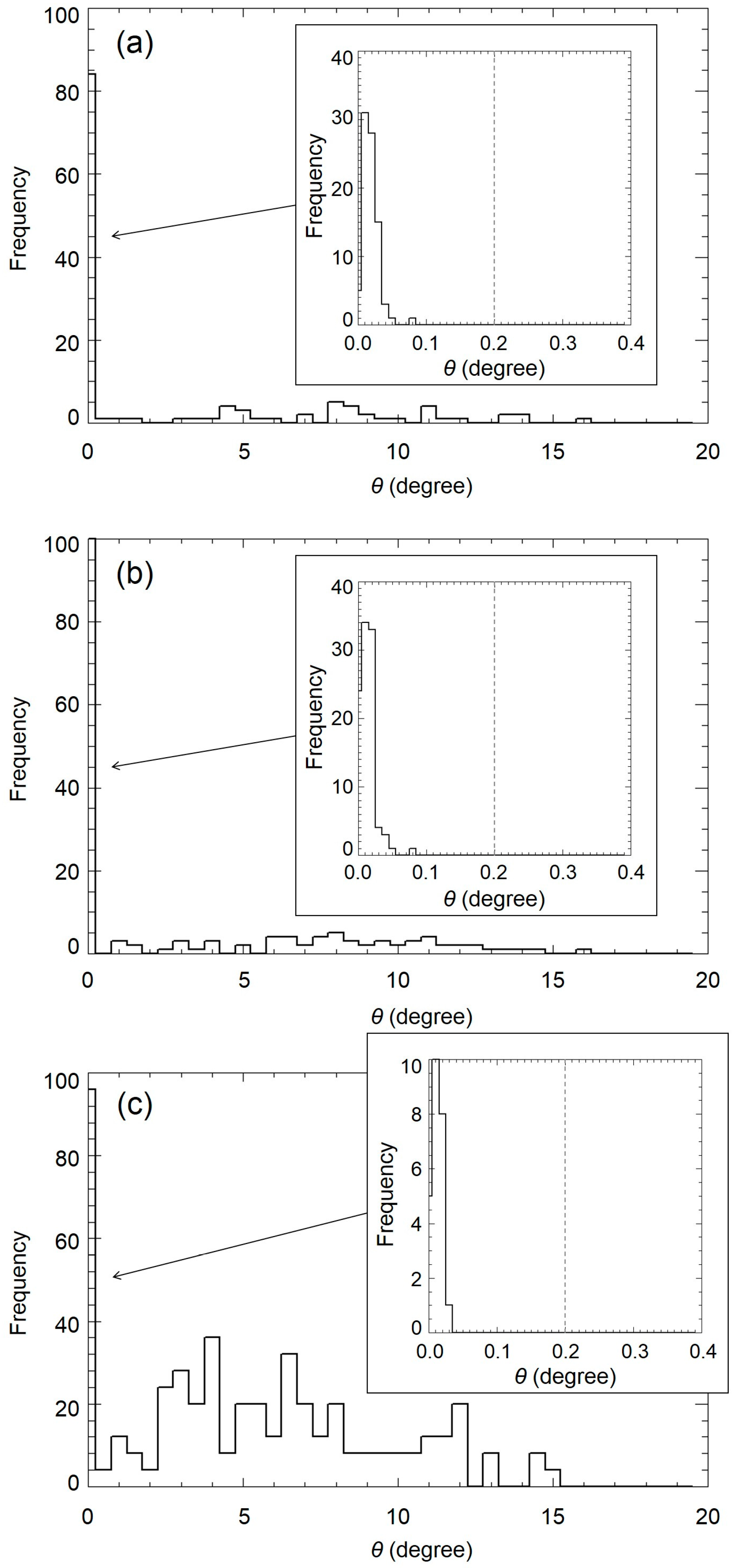
4. Results
4.1. Improvement of Feature Matching with Robust Estimation
4.2. Map Projection Accuracy
5. Discussion
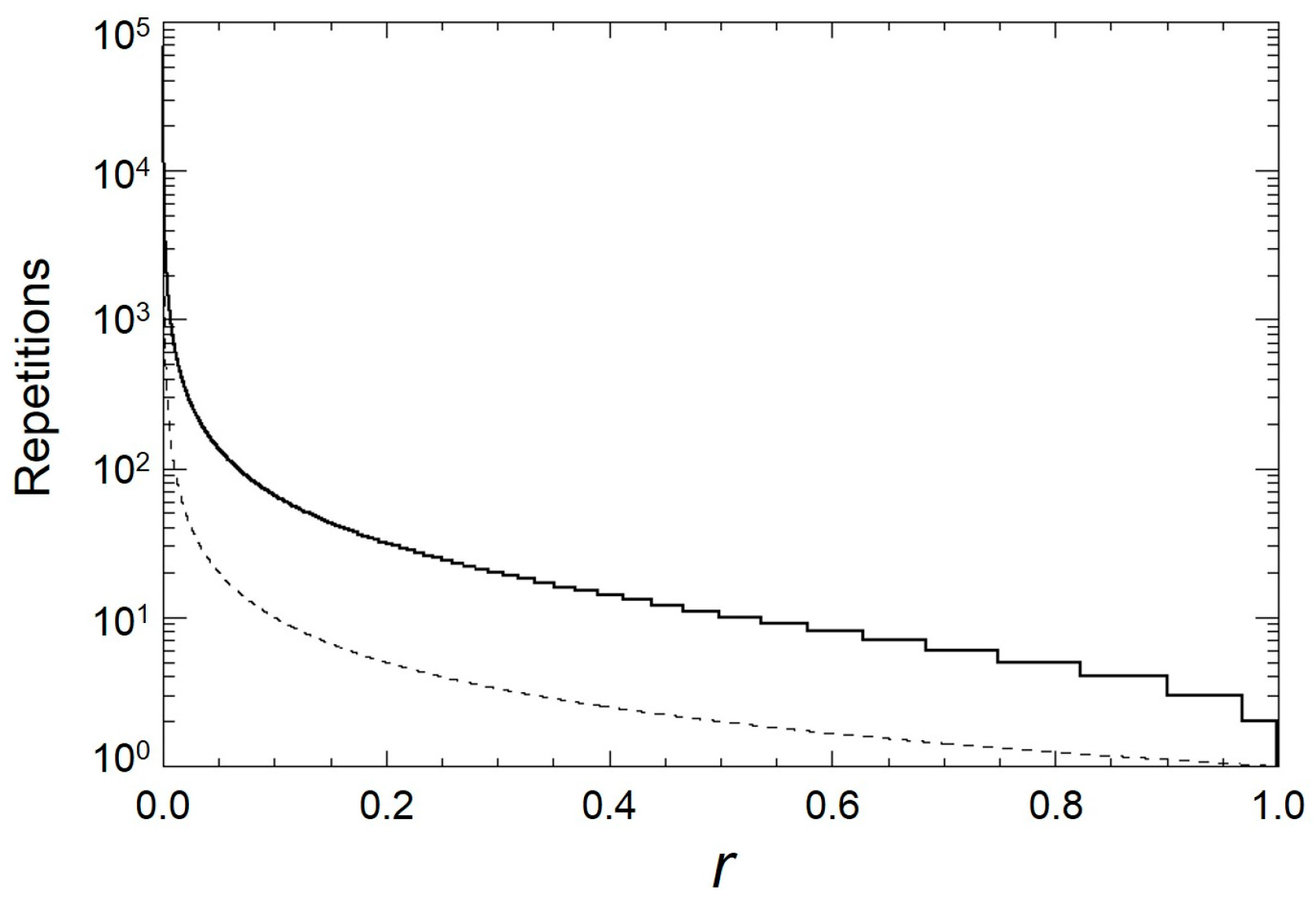
5.1. Inlier Rates and the Number of Repetitions in Robust Estimation
5.2. Combination with Sequential Observations
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Appendix A
Appendix B
References
- Buchen, E. Small satellite market observations. In Proceedings of the 29th Annual AIAA/USU Conference of Small Satellite, Logan, UT, USA, 8–13 August 2015.
- Guerra, A.G.C.; Francisco, F.; Villate, J.; Agelet, F.A.; Bertolami, O.; Rajan, K. On small satellites for oceanography: A survey. Acta Astronaut. 2016, 127, 404–423. [Google Scholar] [CrossRef]
- Yamaura, S.; Shirasaka, S.; Hiramatsu, T.; Ito, M.; Arai, Y.; Miyata, K.; Otani, T.; Sato, N.; Akiyama, H.; Fukuhara, T.; et al. UNIFORM-1: First micro-satellite of forest fire monitoring constellation project. In Proceedings of the 28th Annual AIAA/USU Conference of Small Satellite, Logan, UT, USA, 2–7 August 2014.
- Sakamoto, Y.; Sugimura, N.; Fukuda, K.; Kuwahara, T.; Yoshida, K. Flight verification of attitude determination methods for microsatellite RISING-2 using magnetometers, sun sensors, gyro sensors and observation images. In Proceedings of the 30th International Symposium on Space Technology and Science, Kobe, Japan, 4–10 July 2015.
- Tahoun, M.; Shabayayek, A.E.R.; Hassanien, A.E. Matching and co-registration of satellite images using local features. In Proceedings of the International Conference on Space Optical Systems and Applications, Kobe, Japan, 7–9 May 2014.
- Wang, X.; Li, Y.; Wei, H.; Lin, F. An ASIFT-based local registration method for satellite imagery. Remote Sens. 2015, 7, 7044–7061. [Google Scholar] [CrossRef]
- Bay, H.; Ess, A.; Tuytelaars, T.; Gool, L.V. Speeded-up robust features (SURF). Comput. Vis. Image Underst. 2008, 110, 346–359. [Google Scholar] [CrossRef]
- Fisher, M.A.; Bolles, R.C. Random sample consensus: A paradigm for model fitting with applications to image analysis and automated cartography. Commun. ACM 1981, 24, 381–395. [Google Scholar]
- Choi, S.; Kim, T.; Yu, W. Performance Evaluation of RANSAC Family. In Proceedings of the British Machine Vision Conference, London, UK, 7–10 September 2009.
- Markley, F.H.; Crassidis, J.L. Fundamentals of Spacecraft Attitude Determination and Control; Springer: Berlin/Heidelberg, Germany, 2014; pp. 287–343. [Google Scholar]
- Jing, L.; Xu, L.; Li, X.; Tian, X. Determination of Platform Attitude through SURF Based Aerial Image Matching. In Proceedings of the 2013 IEEE International Conference on Imaging Systems and Techniques, Beijing, China, 22–23 October 2013.
- Natraj, A.; Ly, D.S.; Eynard, D.; Demonceaux, C.; Vasseur, P. Omnidirectional vision for UAV: Applications to attitude, motion and altitude estimation for day and night conditions. J. Intell. Robot. Syst., 2013, 69, 459–473. [Google Scholar] [CrossRef]
- Hiramatsu, T.; Yamaura, S.; Akiyama, H.; Sato, N.; Morita, K.; Otani, T.; Miyata, K.; Kouyama, T.; Kato, S.; Ito, M.; et al. Early results of a wildfire monitoring microsatellite UNIFORM-1. In Proceedings of the 29th Annual AIAA/USU Conference of Small Satellite, Logan, UT, USA, 8–13 August 2015.
- Fukuhara, T. An application to the wild fire detection of the uncooled micro bolometer camera onboard a small satellite. In Proceedings of the International Conference on Space, Aeronautical and Navigational Electronics, Hanoi, Vietnam, 2–3 December 2013.
- UNIFORM Browser. Available online: http://legacy.geogrid.org/uniform1/ (accessed on 7 August 2016).
- ASTER GDEM Validation Team. ASTER Global Digital Elevation Model Version 2—Summary of Validation Results 2011. Available online: http://www.jspacesystems.or.jp/ersdac/GDEM/ver2Validation/Summary_GDEM2_validation_report_final.pdf (accessed on 8 August 2016).
- Athmania, D.; Achour, H. External validation of the ASTER GDEM2, GMTED2010 and CGIAR-CSI- SRTM v4.1 free access digital elevation models (DEMs) in Tunisia and Algeria. Remote Sens. 2014, 6, 4600–4620. [Google Scholar] [CrossRef]
- Archinal, B.A.; A’Hearn, M.F.; Bowell, E.; Conrad, A.; Consolmagno, G.J.; Courtin, R.; Fukushima, T.; Hestroffer, D.; Hilton, J.L.; Krasinsky, G.A.; et al. Report of the IAU Working Group on cartographic coordinates and rotational elements: 2009. Celest. Mech. Dyn. Astron. 2011, 109, 101–135. [Google Scholar] [CrossRef]
- Ogohara, K.; Kouyama, T.; Yamamoto, H.; Sato, N.; Takagi, M.; Imamura, T. Automated cloud tracking system for the Akatsuski Venus Climate Orbiter data. Icarus 2012, 217, 661–668. [Google Scholar] [CrossRef]
- Acton, C.H. Ancillary Data services of NASA’s navigation and ancillary information facility. Planet. Space Sci. 1996, 44, 65–70. [Google Scholar] [CrossRef]
- Kelso, T.S. Validation of SGP4 and IS-GPS-200D against GPS precision ephemerides. In Proceedings of the 17th AAS/AIAA Space Flight Mechanics Conference, Sedona, AZ, USA, 28 January–1 February 2007.
- Kouyama, T.; Yamazaki, A.; Yamada, M.; Imamura, T. A method to estimate optical distortion using planetary images. Icarus 2013, 86, 86–90. [Google Scholar] [CrossRef]
- Lowe, D. Distinctive image features from scale-invariant keypoints. Int. J. Comput. Vis. 2004, 60, 91–110. [Google Scholar] [CrossRef]
- Bradski, G.; Kaehler, A. Learning OpenCV; O’Reilly: Sebastopol, CA, USA, 2008; pp. 521–526. [Google Scholar]
- Strugnell, N.; Lucht, W.; Schaaf, C. A global data set derived from AVHRR data for use in climate simulations. Geophys. Res. Lett. 2001, 28, 191–194. [Google Scholar] [CrossRef]
- Ramisa, A.; Vasudevan, S.; Aldavert, D.; Toledo, R.; de Mantaras, R.L. Evaluation of the SIFT object recognition method in mobile robots. In Proceedings of the Catalan Conference on Artificial Intelligence (CCIA), Cardona, Spain, 21–23 October 2009; pp. 9–18.
- Torr, P.H.S.; Zisserman, A. MLESAC: A new robust estimator with application to estimating image geometry. Comput. Vis. Image Underst. 2000, 78, 138–156. [Google Scholar] [CrossRef]
- Chum, O.; Matas, J. Matching with PROSAC—Progressive Sample Consensus. In Proceedings of the International Conference on Computer Vision and Pattern Recognition, San Diego, CA, USA, 20–26 June 2005.
- Cetin, M.; Toka, O. The Comparing of S-estimator and M-estimators in Linear Regression. Gazi Univ. J. Sci. 2011, 24, 747–752. [Google Scholar]
- Kneip, L.; Scaramuzza, D.; Siegwart, R. A novel parametrization of the Perspective-Three-Point problem for a direct computation of absolute camera position and orientation. In Proceeding of the International Conference on Computer Vision and Pattern Recognition, Colorado Springs, CO, USA, 21–23 June 2011; pp. 2926–2976.
- Nakano, G. Globally optimal DLS method for PnP Problem with Cayley parameterization. In Proceedings of the British Machine Vision Conference, Swansea, UK, 7–10 September 2015; pp. 78.1–78.11.
- Strorey, J.; Choate, M.; Lee, K. Landsat 8 operational land imager on-orbit geometric calibration and performance. Remote Sens. 2014, 6, 11127–11152. [Google Scholar] [CrossRef]
- Leutenegger, S.; Chli, M.; Siegwart, R.Y. BRISK: Binary robust invariant scalable keypoints. In Proceedings of the IEEE International Conference on Computer Vision, Barcelona, Spain, 6–13 November 2011; pp. 2548–2555.
- Rublee, E.; Rabaud, V.; Konolige, K.; Bradski, G. ORB: An efficient alternative to SIFT or SURF. In Proceedings of the IEEE International Conference on Computer Vision (ICCV), Barcelona, Spain, 6–13 November 2011; pp. 2564–2571.
- Alcantarilla, P.F.; Bartoli, A.; Davison, A.D. KAZE features. In Proceedings of the European Conference on Computer Vision (ECCV), Firenze, Italy, 7–13 October 2012; pp. 214–227.
- Aguiler, M.; Frauel, Y.; Escolano, F.; Martinez-Perez, M.E.; Espinosa-Romero, A.; Lozano, M.A. A robust Graph Transformation Matching for non-rigid registration. Image Vis. Comput. 2009, 27, 897–910. [Google Scholar] [CrossRef]





| Wavelength (μm) | Pixel Scale (degree/pixel) | GSD (m) | Image Width (km) | Bit Depth (bit) | |
|---|---|---|---|---|---|
| BOL | 8–14 | 0.0142 | 156 | 100 × 75 | 12 |
| VIS | 0.4–1.0 | 0.00774 | 85 | 109 × 87 | 10 |
| Wavelength (μm) | GSD (m) | Swath (km) | Bit Depth (bit) | |
|---|---|---|---|---|
| OLI Band 4 | 0.64–0.67 | 30 | 185 | 16 |
| L | N | Inlier Ratio | ||||
|---|---|---|---|---|---|---|
| (a) Kanto, Japan | 84 | 0.018° | 125 | 2.7° | 0.67 | 0.30 |
| (b) Yosemite, US | 100 | 0.019° | 162 | 3.1° | 0.62 | 0.23 |
| (c) Kyushu, Japan | 24 | 0.016° | 120 | 5.3° | 0.20 | 0.0072 |
| Npair | (m) | (m) | (m) | (m) | |
|---|---|---|---|---|---|
| (a) Kanto, Japan | 92 | 7 | 47 | 123 | 102 |
| (b) Yosemite, US | 107 | −25 | −6 | 121 | 181 |
| (c) Kyushu, Japan | 23 | −11 | −9 | 156 | 170 |
| RANSAC (Expected) | RANSAC (Actual) | PROSAC (Actual) | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Mean | 99.9% Guarantee | Mean | SD | Max | Min | Mean | SD | Max | Min | |
| (a) Kanto, Japan | 3.3 | 19 | 3.5 | 3.1 | 25 | 1 | 6.1 | 5.8 | 24 | 2 |
| (b) Yosemite, US | 4.3 | 26 | 4.9 | 4.7 | 28 | 1 | 3.6 | 1.8 | 11 | 2 |
| (c) Kyushu, Japan | 145 | 956 | 139 | 139 | 1058 | 1 | 28.2 | 16.2 | 86 | 11 |
| Observation Date | 1: 2015-10-16T03:31:07 | 2: 2015-10-16T03:31:15 |
|---|---|---|
| Rotation matrix () | ||
| Rotation angle between two matrices | 0.18° | |
© 2017 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kouyama, T.; Kanemura, A.; Kato, S.; Imamoglu, N.; Fukuhara, T.; Nakamura, R. Satellite Attitude Determination and Map Projection Based on Robust Image Matching. Remote Sens. 2017, 9, 90. https://doi.org/10.3390/rs9010090
Kouyama T, Kanemura A, Kato S, Imamoglu N, Fukuhara T, Nakamura R. Satellite Attitude Determination and Map Projection Based on Robust Image Matching. Remote Sensing. 2017; 9(1):90. https://doi.org/10.3390/rs9010090
Chicago/Turabian StyleKouyama, Toru, Atsunori Kanemura, Soushi Kato, Nevrez Imamoglu, Tetsuya Fukuhara, and Ryosuke Nakamura. 2017. "Satellite Attitude Determination and Map Projection Based on Robust Image Matching" Remote Sensing 9, no. 1: 90. https://doi.org/10.3390/rs9010090
APA StyleKouyama, T., Kanemura, A., Kato, S., Imamoglu, N., Fukuhara, T., & Nakamura, R. (2017). Satellite Attitude Determination and Map Projection Based on Robust Image Matching. Remote Sensing, 9(1), 90. https://doi.org/10.3390/rs9010090