A Self-Calibrating Runoff and Streamflow Remote Sensing Model for Ungauged Basins Using Open-Access Earth Observation Data
Abstract
:1. Introduction
2. Materials and Methods
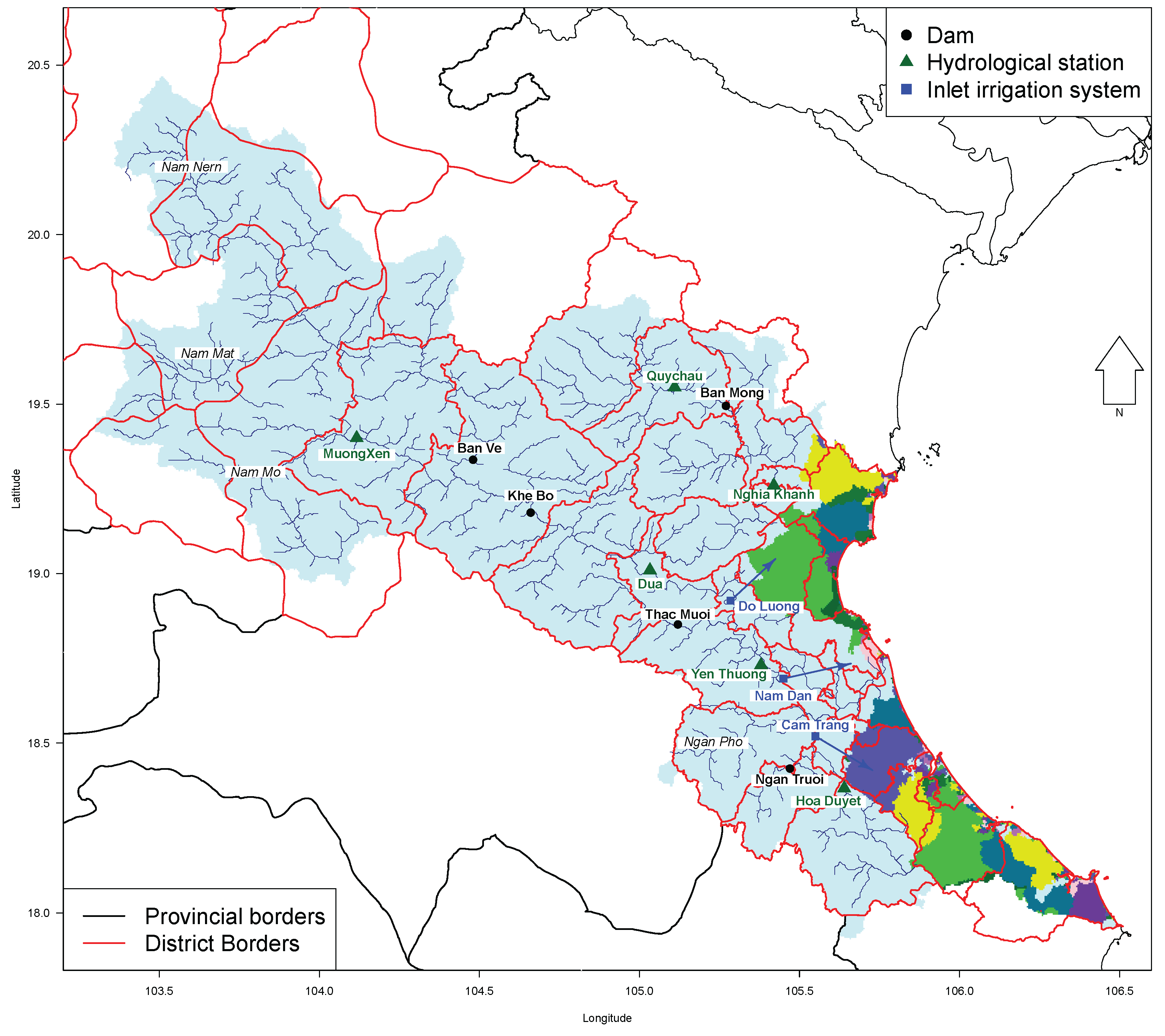
2.1. Study Area
2.2. Climatic Setting
2.3. Input Products
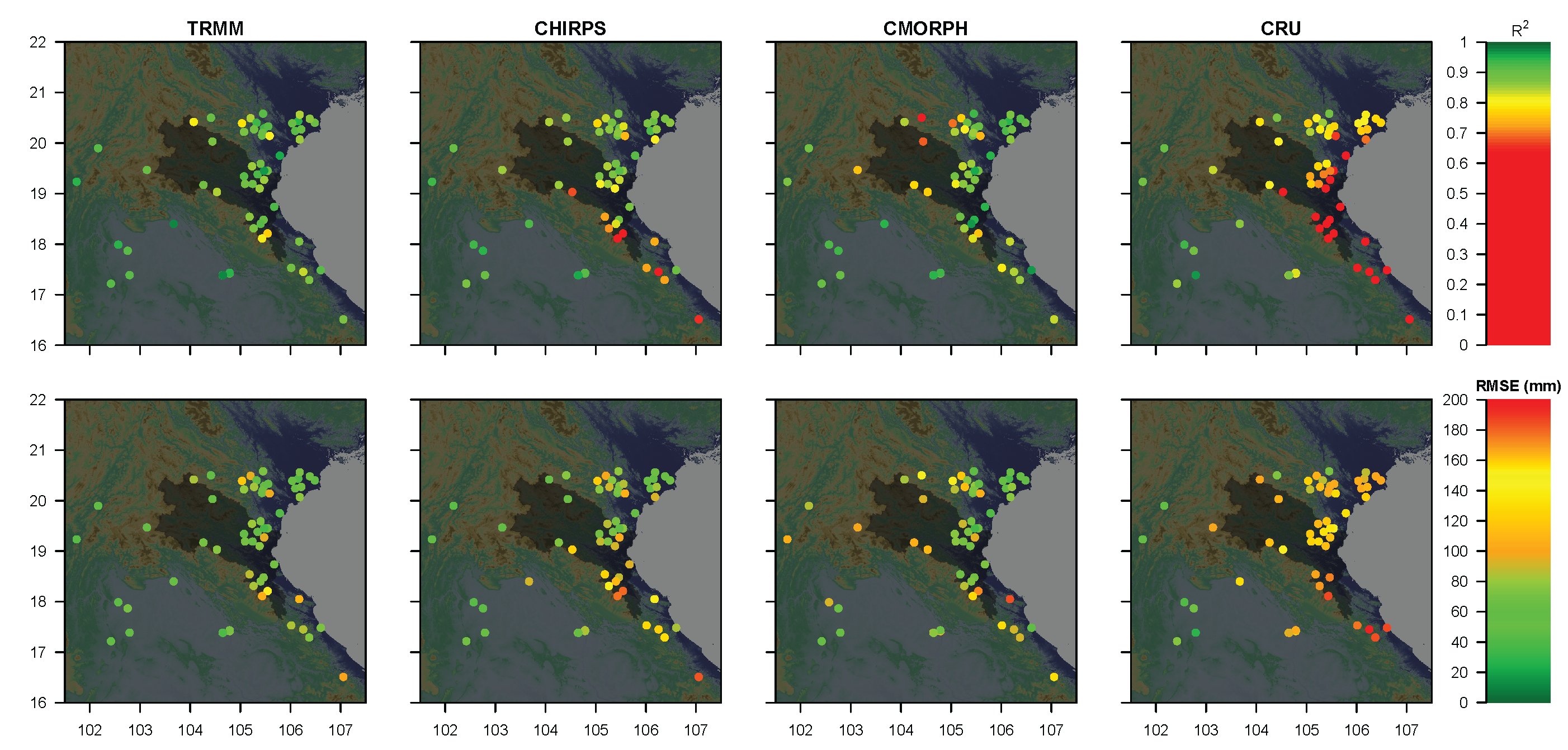
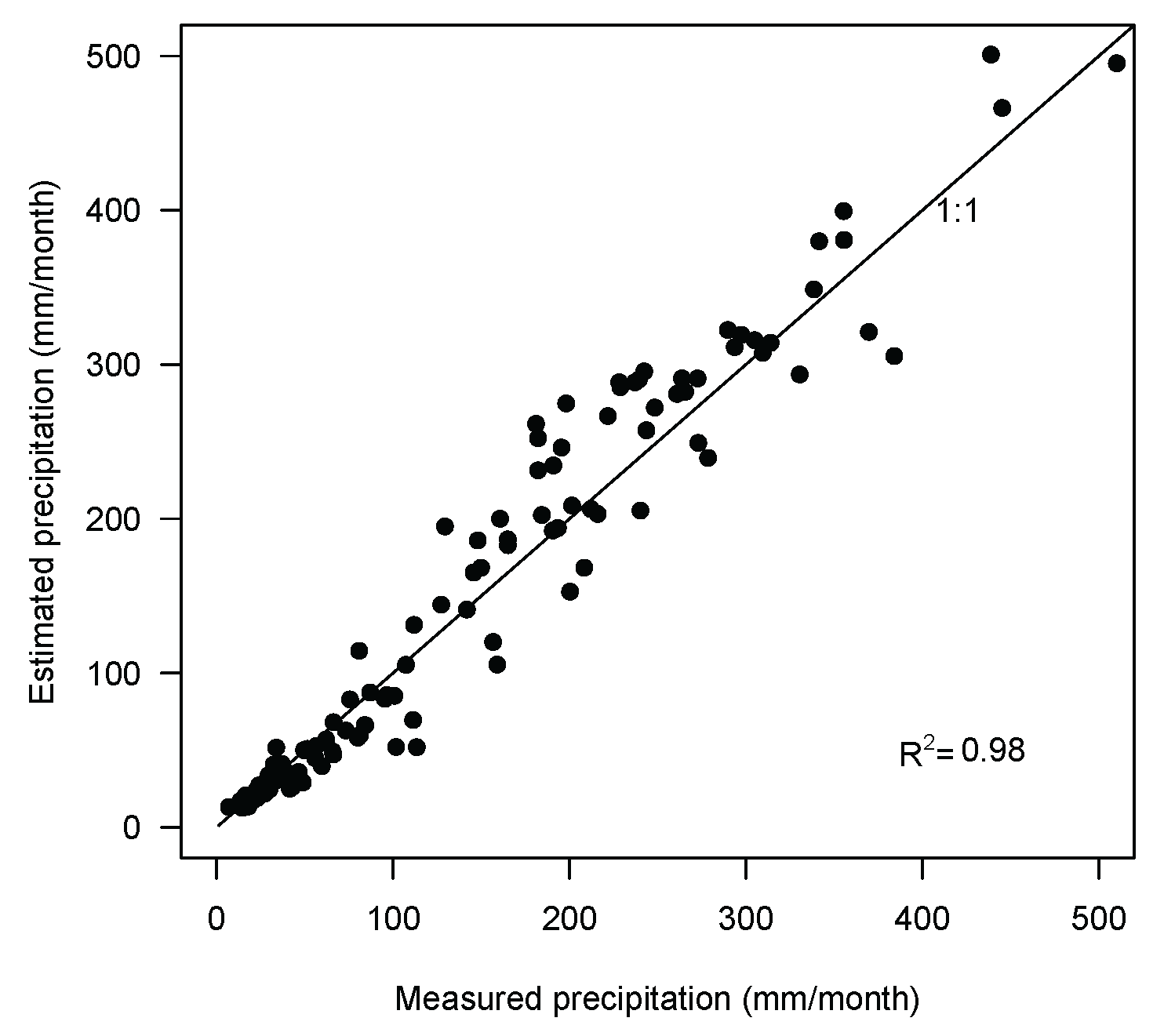
2.3.1. Precipitation
2.3.2. Evapotranspiration
2.4. Interception
2.4.1. Soil Water and Groundwater
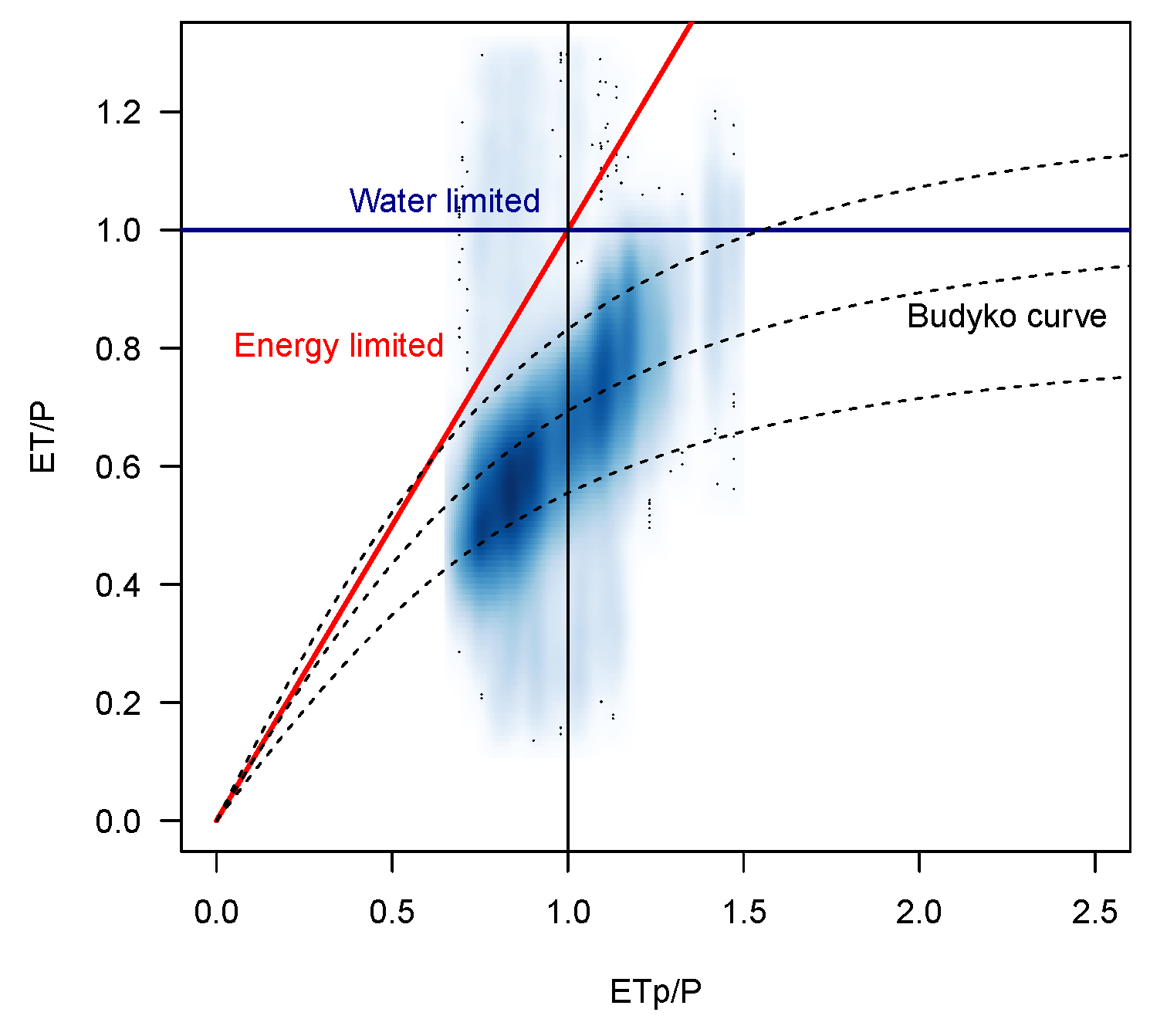
2.5. The Water Balance Model
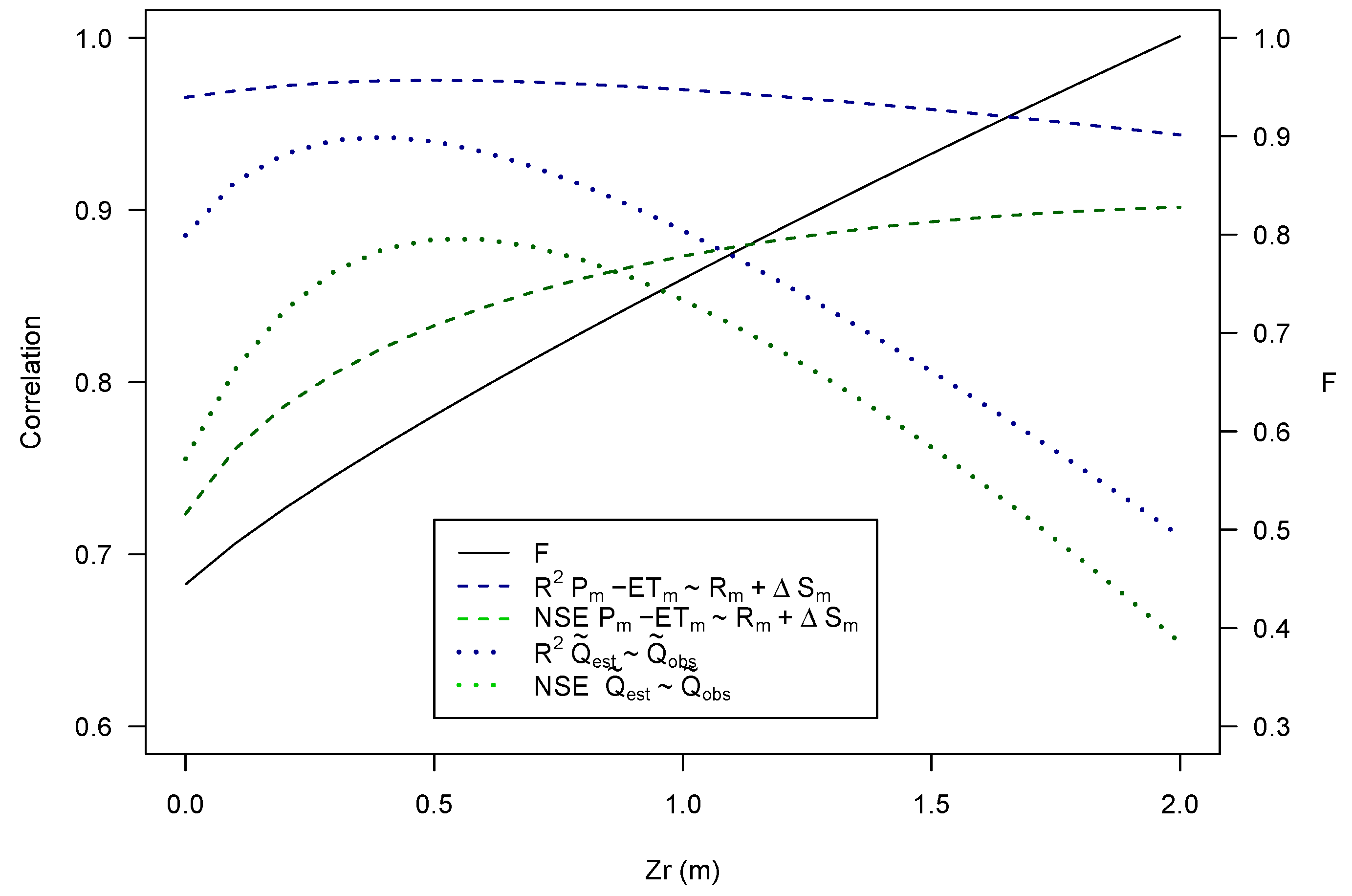
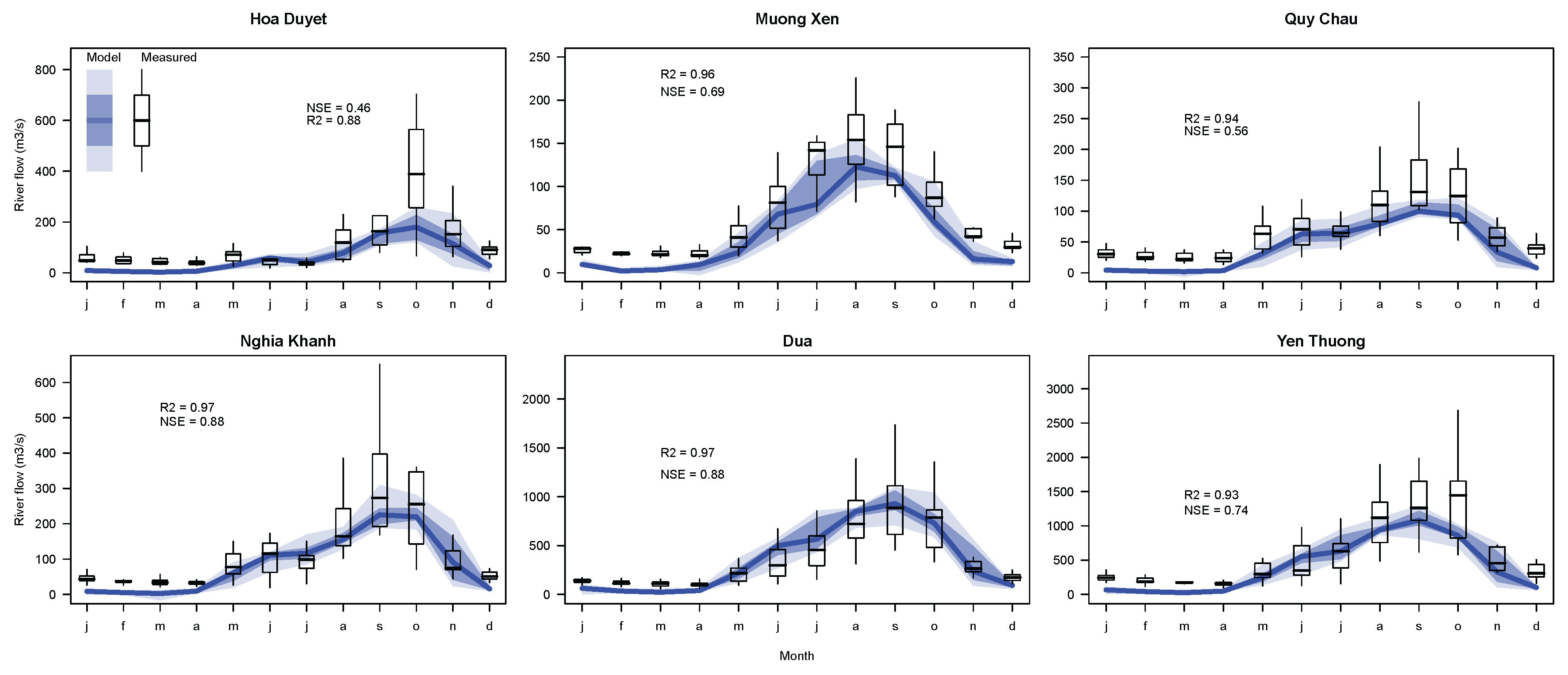
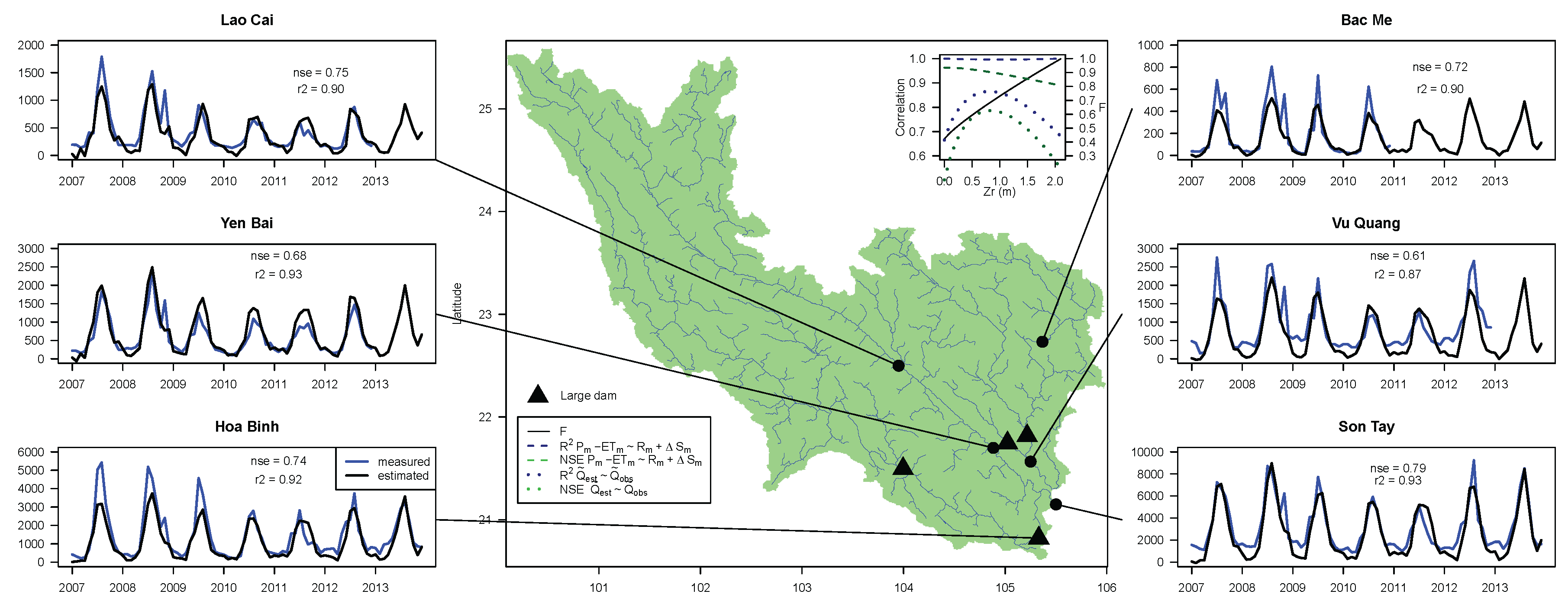
3. Results
4. Discussion
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Rijsberman, F.R. Water scarcity: Fact or fiction? Agric. Water Manag. 2006, 80, 5–22. [Google Scholar] [CrossRef]
- Mekonnen, M.M.; Hoekstra, A.Y. Four billion people facing severe water scarcity. Sci. Adv. 2016, 2. [Google Scholar] [CrossRef] [PubMed]
- Tolentino, P.L.M.; Poortinga, A.; Kanamaru, H.; Keesstra, S.; Maroulis, J.; David, C.P.C.; Ritsema, C.J. Projected Impact of Climate Change on Hydrological Regimes in the Philippines. PLoS ONE 2016, 11. [Google Scholar] [CrossRef] [PubMed]
- Lakshmi, V. The role of satellite remote sensing in the prediction of ungauged basins. Hydrol. Process. 2004, 18, 1029–1034. [Google Scholar] [CrossRef]
- Bastiaanssen, W.G.; Karimi, P.; Rebelo, L.M.; Duan, Z.; Senay, G.; Muthuwatte, L.; Smakhtin, V. Earth observation based assessment of the water production and water consumption of Nile Basin agro-ecosystems. Remote Sens. 2014, 6, 10306–10334. [Google Scholar] [CrossRef]
- Simons, G.; Bastiaanssen, W.; Ngô, L.A.; Hain, C.R.; Anderson, M.; Senay, G. Integrating Global Satellite-Derived Data Products as a Pre-Analysis for Hydrological Modelling Studies: A Case Study for the Red River Basin. Remote Sens. 2016, 8, 279. [Google Scholar] [CrossRef]
- Karimi, P.; Bastiaanssen, W.; Sood, A.; Hoogeveen, J.; Peiser, L.; Bastidas Obando, E.; Dost, R. Spatial evapotranspiration, rainfall and land use data in water accounting. Part 2: Reliability of water accounting results for policy decisions in the Awash basin. Hydrol. Earth Syst. Sci. 2015, 19, 533–550. [Google Scholar] [CrossRef]
- Karimi, P.; Bastiaanssen, W.; Molden, D. Water Accounting Plus (WA+)—A water accounting procedure for complex river basins based on satellite measurements. Hydrol. Earth Syst. Sci. 2013, 17, 2459–2472. [Google Scholar] [CrossRef]
- Molden, D.; Sakthivadivel, R. Water accounting to assess use and productivity of water. Int. J. Water Resour. Dev. 1999, 15, 55–71. [Google Scholar] [CrossRef]
- Karimi, P.; Bastiaanssen, W. Spatial evapotranspiration, rainfall and land use data in water accounting. Part 1: Review of the accuracy of the remote sensing data. Hydrol. Earth Syst. Sci. 2015, 19, 507–532. [Google Scholar] [CrossRef]
- Immerzeel, W.; Droogers, P. Calibration of a distributed hydrological model based on satellite evapotranspiration. J. Hydrol. 2008, 349, 411–424. [Google Scholar] [CrossRef]
- Bui, Y.T.; Orange, D.; Visser, S.; Hoanh, C.T.; Laissus, M.; Poortinga, A.; Tran, D.T.; Stroosnijder, L. Lumped surface and sub-surface runoff for erosion modeling within a small hilly watershed in northern Vietnam. Hydrol. Process. 2014, 28, 2961–2974. [Google Scholar] [CrossRef]
- Valentin, C.; Agus, F.; Alamban, R.; Boosaner, A.; Bricquet, J.P.; Chaplot, V.; De Guzman, T.; De Rouw, A.; Janeau, J.L.; Orange, D.; et al. Runoff and sediment losses from 27 upland catchments in Southeast Asia: Impact of rapid land use changes and conservation practices. Agric. Ecosyst. Environ. 2008, 128, 225–238. [Google Scholar] [CrossRef]
- Cheang, B.K. Short-and Long-Range Monsoon Prediction in Southeast Asia; Malaysia Meteoorlogical Service: Petaling Jaya, Malaysia, 1987.
- Nguyen, D.Q.; Renwick, J.; McGregor, J. Variations of surface temperature and rainfall in Vietnam from 1971 to 2010. Int. J. Climatol. 2014, 34, 249–264. [Google Scholar] [CrossRef]
- Yen, M.C.; Chen, T.C.; Hu, H.L.; Tzeng, R.Y.; Dinh, D.T.; Nguyen, T.T.T.; Wong, C.J. Interannual variation of the fall rainfall in Central Vietnam. J. Meteorol. Soc. Jpn. 2011, 89, 193–204. [Google Scholar] [CrossRef]
- Nguyen, T.D.; Uvo, C.; Rosbjerg, D. Relationship between the tropical Pacific and Indian Ocean sea-surface temperature and monthly precipitation over the central highlands, Vietnam. J. Meteorol. Soc. Jpn. 2007, 27, 1439–1454. [Google Scholar] [CrossRef]
- Thomas, T.; Christiaensen, L.; Do, Q.T.; Trung, L.D. Natural Disasters and Household Welfare: Evidence from Vietnam; World Bank Policy Research Working Paper Series; World Bank: Washington, DC, USA, 2010. [Google Scholar]
- NCDC. Available online: http://land.copernicus.vgt.vito.be (accessed on 16 January 2016).
- Funk, C.C.; Peterson, P.J.; Landsfeld, M.F.; Pedreros, D.H.; Verdin, J.P.; Rowland, J.D.; Romero, B.E.; Husak, G.J.; Michaelsen, J.C.; Verdin, A.P. A Quasi-Global Precipitation Time Series for Drought Monitoring; US Geological Survey Data Series: Reston, VA, USA, 2013; Volume 832.
- Joyce, R.J.; Janowiak, J.E.; Arkin, P.A.; Xie, P. CMORPH: A method that produces global precipitation estimates from passive microwave and infrared data at high spatial and temporal resolution. J. Hydrometeorol. 2004, 5, 487–503. [Google Scholar] [CrossRef]
- Harris, I.; Jones, P.; Osborn, T.; Lister, D. Updated high-resolution grids of monthly climatic observations—The CRU TS3. 10 Dataset. Int. J. Climatol. 2014, 34, 623–642. [Google Scholar] [CrossRef]
- Vernimmen, R.R.E.; Hooijer, A.; Mamenun; Aldrian, E.; van Dijk, A.I.J.M. Evaluation and bias correction of satellite rainfall data for drought monitoring in Indonesia. Hydrol. Earth Syst. Sci. 2012, 16, 133–146. [Google Scholar] [CrossRef]
- Cheema, M.J.M.; Bastiaanssen, W.G. Local calibration of remotely sensed rainfall from the TRMM satellite for different periods and spatial scales in the Indus Basin. Int. J. Remote Sens. 2012, 33, 2603–2627. [Google Scholar] [CrossRef]
- Huang, Y.; Chen, S.; Cao, Q.; Hong, Y.; Wu, B.; Huang, M.; Qiao, L.; Zhang, Z.; Li, Z.; Li, W.; et al. Evaluation of version-7 TRMM multi-satellite precipitation analysis product during the Beijing extreme heavy rainfall event of 21 July 2012. Water 2013, 6, 32–44. [Google Scholar] [CrossRef]
- Senay, G.B.; Budde, M.; Verdin, J.P.; Melesse, A.M. A coupled remote sensing and simplified surface energy balance approach to estimate actual evapotranspiration from irrigated fields. Sensors 2007, 7, 979–1000. [Google Scholar] [CrossRef]
- Senay, G.; Gowda, P.; Bohms, S.; Howell, T.; Friedrichs, M.; Marek, T.; Verdin, J. Evaluating the SSEBop approach for evapotranspiration mapping with landsat data using lysimetric observations in the semi-arid Texas High Plains. Hydrol. Earth Syst. Sci. Discuss. 2014, 11, 723–756. [Google Scholar] [CrossRef]
- Chen, M.; Senay, G.B.; Singh, R.K.; Verdin, J.P. Uncertainty analysis of the Operational Simplified Surface Energy Balance (SSEBop) model at multiple flux tower sites. J. Hydrol. 2016, 536, 384–399. [Google Scholar] [CrossRef]
- Budyko, M. Climate and Life; Academic Press: San Diego, CA, USA, 1974; pp. 72–191. [Google Scholar]
- Rodell, M.; Houser, P.; Jambor, U.E.A.; Gottschalck, J.; Mitchell, K.; Meng, C.; Arsenault, K.; Cosgrove, B.; Radakovich, J.; Bosilovich, M.; et al. The global land data assimilation system. Bull. Am. Meteorol. Soc. 2004, 85, 381–394. [Google Scholar] [CrossRef]
- Gentine, P.; D’Odorico, P.; Lintner, B.R.; Sivandran, G.; Salvucci, G. Interdependence of climate, soil, and vegetation as constrained by the Budyko curve. Geophys. Res. Lett. 2012, 39. [Google Scholar] [CrossRef]
- Boegh, E.; Søgaard, H.; Broge, N.; Hasager, C.; Jensen, N.; Schelde, K.; Thomsen, A. Airborne multispectral data for quantifying leaf area index, nitrogen concentration, and photosynthetic efficiency in agriculture. Remote Sens. Environ. 2002, 81, 179–193. [Google Scholar] [CrossRef]
- Von Hoyningen-Huene, J. Die Interzeption des Niederschlags in Landwirtschaftlichen Pflanzenbeständen; Arbeitsbericht Deutscher Verband für Wasserwirtschaft und Kulturbau (DVWK): Braunschweig, Germany, 1981; p. 63. [Google Scholar]
- Braden, H. Ein energiehaushalts- und verdunstungsmodell fur wasser und stoffhaushaltsuntersuchungen landwirtschaftlich genutzter einzugsgebiete. Mitt. Deutsch. Bodenk. Ges. 1985, 42, 294–299. [Google Scholar]
- Yeh, P.J.F.; Swenson, S.; Famiglietti, J.; Rodell, M. Remote sensing of groundwater storage changes in Illinois using the Gravity Recovery and Climate Experiment (GRACE). Water Resour. Res. 2006, 42. [Google Scholar] [CrossRef]
- Rodell, M.; Chen, J.; Kato, H.; Famiglietti, J.S.; Nigro, J.; Wilson, C.R. Estimating groundwater storage changes in the Mississippi River basin (USA) using GRACE. Hydrogeol. J. 2007, 15, 159–166. [Google Scholar] [CrossRef]
- Nolet, C.; Poortinga, A.; Roosjen, P.; Bartholomeus, H.; Ruessink, G. Measuring and modeling the effect of surface moisture on the spectral reflectance of coastal beach sand. PLoS ONE 2014, 9, e112151. [Google Scholar] [CrossRef] [PubMed]
- Wagner, W.; Lemoine, G.; Rott, H. A method for estimating soil moisture from ERS scatterometer and soil data. Remote Sens. Environ. 1999, 70, 191–207. [Google Scholar] [CrossRef]
- Naeimi, V.; Scipal, K.; Bartalis, Z.; Hasenauer, S.; Wagner, W. An improved soil moisture retrieval algorithm for ERS and METOP scatterometer observations. IEEE Trans. Geosci. Remote Sens. 2009, 47, 1999–2013. [Google Scholar] [CrossRef]
- Naeimi, V.; Paulik, C.; Bartsch, A.; Wagner, W.; Kidd, R.; Park, S.E.; Elger, K.; Boike, J. ASCAT Surface State Flag (SSF): Extracting information on surface freeze/thaw conditions from backscatter data using an empirical threshold-analysis algorithm. IEEE Trans. Geosci. Remote Sens. 2012, 50, 2566–2582. [Google Scholar] [CrossRef]
- Copernicus Global Land Service. Available online: http://land.copernicus.vgt.vito.be (accessed on 16 January 2016).
- Albergel, C.; Rüdiger, C.; Pellarin, T.; Calvet, J.C.; Fritz, N.; Froissard, F.; Suquia, D.; Petitpa, A.; Piguet, B.; Martin, E. From near-surface to root-zone soil moisture using an exponential filter: An assessment of the method based on in-situ observations and model simulations. Hydrol. Earth Syst. Sci. Discuss. 2008, 12, 1323–1337. [Google Scholar] [CrossRef]
- Ceballos, A.; Scipal, K.; Wagner, W.; Martínez-Fernández, J. Validation of ERS scatterometer-derived soil moisture data in the central part of the Duero Basin, Spain. Hydrol. Process. 2005, 19, 1549–1566. [Google Scholar] [CrossRef]
- De Boer, F. HiHydroSoil: A High Resolution Soil Map of Hydraulic Properties—Version 1.2; Technical Report; FutureWater: Wageningen, The Netherlands, 2016. [Google Scholar]
- Hengl, T.; de Jesus, J.M.; MacMillan, R.A.; Batjes, N.H.; Heuvelink, G.B.; Ribeiro, E.; Rosa, A.S.; Kempen, B.; Leenaars, J.G.; Walsh, M.G.; et al. SoilGrids1km—Global soil information based on automated mapping. PLoS ONE 2014, 9, e105992. [Google Scholar] [CrossRef] [PubMed]
- Scott, C.A.; Bastiaanssen, W.G.; Ahmad, M.u.D. Mapping root zone soil moisture using remotely sensed optical imagery. J. Irrig. Drain. Eng. 2003, 129, 326–335. [Google Scholar] [CrossRef]
- Duan, Z.; Bastiaanssen, W. First results from Version 7 TRMM 3B43 precipitation product in combination with a new downscaling–calibration procedure. Remote Sens. Environ. 2013, 131, 1–13. [Google Scholar] [CrossRef]
- Choudhury, B.J.; DiGirolamo, N.E. A biophysical process-based estimate of global land surface evaporation using satellite and ancillary data I. Model description and comparison with observations. J. Hydrol. 1998, 205, 164–185. [Google Scholar] [CrossRef]
- Schaake, J.C.; Koren, V.I.; Duan, Q.Y.; Mitchell, K.; Chen, F. Simple water balance model for estimating runoff at different spatial and temporal scales. J. Geophys. Res. Atmos. 1996, 101, 7461–7475. [Google Scholar] [CrossRef]
- Nash, J.; Sutcliffe, J.V. River flow forecasting through conceptual models part I—A discussion of principles. J. Hydrol. 1970, 10, 282–290. [Google Scholar] [CrossRef]
- Foglia, L.; Hill, M.C.; Mehl, S.W.; Burlando, P. Sensitivity analysis, calibration, and testing of a distributed hydrological model using error-based weighting and one objective function. Water Resour. Res. 2009, 45. [Google Scholar] [CrossRef]
- Ghaffari, G.; Keesstra, S.; Ghodousi, J.; Ahmadi, H. SWAT-simulated hydrological impact of land-use change in the Zanjanrood Basin, Northwest Iran. Hydrol. Process. 2010, 24, 892–903. [Google Scholar] [CrossRef]
- Stürck, J.; Poortinga, A.; Verburg, P.H. Mapping ecosystem services: The supply and demand of flood regulation services in Europe. Ecol. Indic. 2014, 38, 198–211. [Google Scholar] [CrossRef]
- Poortinga, A.; Delobel, F.; Rojas, O.; Peters, S.; Ward, P. MOSAICC: An inter-disciplinary system of models to evaluate the impact of climate change on agriculture. In Proceedings of The 8th International Symposium Agro Environ, Wageningen, The Netherlands, 1–4 May 2012.
- Terink, W.; Lutz, A.F.; Simons, G.W.H.; Immerzeel, W.W.; Droogers, P. SPHY v2.0: Spatial Processes in Hydrology. Geosci. Model Dev. 2015, 8, 2009–2034. [Google Scholar] [CrossRef]
- Wada, Y.; van Beek, L.P.; van Kempen, C.M.; Reckman, J.W.; Vasak, S.; Bierkens, M.F. Global depletion of groundwater resources. Geophys. Res. Lett. 2010, 37. [Google Scholar] [CrossRef]
- Bierkens, M.; Van Beek, L. Seasonal predictability of European discharge: NAO and hydrological response time. J. Hydrometeorol. 2009, 10, 953–968. [Google Scholar] [CrossRef]
- Singh, R.K.; Senay, G.B. Comparison of four different energy balance models for estimating evapotranspiration in the Midwestern United States. Water 2016, 8. [Google Scholar] [CrossRef]
- Bhattarai, N.; Shaw, S.B.; Quackenbush, L.J.; Im, J.; Niraula, R. Evaluating five remote sensing based single-source surface energy balance models for estimating daily evapotranspiration in a humid subtropical climate. Int. J. Appl. Earth Obs. Geoinf. 2016, 49, 75–86. [Google Scholar] [CrossRef]
- Asadullah, A.; McINTYRE, N.; Kigobe, M. Evaluation of five satellite products for estimation of rainfall over Uganda/Evaluation de cinq produits satellitaires pour l’estimation des précipitations en Ouganda. Hydrol. Sci. J. 2008, 53, 1137–1150. [Google Scholar] [CrossRef]
| Abbreviation | Product | Institute |
|---|---|---|
| TRMM | Tropical Rainfall Measurement Mission | NASA |
| CHIRPS | Climate Hazards Group InfraRed Precipitation Station | Climate Hazards Group |
| CMORPH | Climate Prediction Center Morphing Technique | NOAA /CPC |
| CRU | Climate Research Unit | University of East Anglia |
| Abbreviation | Method | Resolution |
|---|---|---|
| TRMM (3B43) | Microwave (TMI, SSMI, AMSU and AMSR) | 0.25° |
| Infrared (GMS), Gauge data | ||
| CHIRPS | CHPClim, Infrared & Microwave (TRMM (3B43) | 0.05° |
| CFSv2. Gauge data | ||
| CMORPH | Microwave estimates (DMSP F-13, 1415 (SSM/I) | 0.25° |
| NOAA-15, 16, 17 & 18 | ||
| (AMSU-B), AMSR-E, and TRMM TMI | ||
| IR motion vectors, Gauge data | ||
| CRU | Surface station observations | 0.50° |
© 2017 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Poortinga, A.; Bastiaanssen, W.; Simons, G.; Saah, D.; Senay, G.; Fenn, M.; Bean, B.; Kadyszewski, J. A Self-Calibrating Runoff and Streamflow Remote Sensing Model for Ungauged Basins Using Open-Access Earth Observation Data. Remote Sens. 2017, 9, 86. https://doi.org/10.3390/rs9010086
Poortinga A, Bastiaanssen W, Simons G, Saah D, Senay G, Fenn M, Bean B, Kadyszewski J. A Self-Calibrating Runoff and Streamflow Remote Sensing Model for Ungauged Basins Using Open-Access Earth Observation Data. Remote Sensing. 2017; 9(1):86. https://doi.org/10.3390/rs9010086
Chicago/Turabian StylePoortinga, Ate, Wim Bastiaanssen, Gijs Simons, David Saah, Gabriel Senay, Mark Fenn, Brian Bean, and John Kadyszewski. 2017. "A Self-Calibrating Runoff and Streamflow Remote Sensing Model for Ungauged Basins Using Open-Access Earth Observation Data" Remote Sensing 9, no. 1: 86. https://doi.org/10.3390/rs9010086
APA StylePoortinga, A., Bastiaanssen, W., Simons, G., Saah, D., Senay, G., Fenn, M., Bean, B., & Kadyszewski, J. (2017). A Self-Calibrating Runoff and Streamflow Remote Sensing Model for Ungauged Basins Using Open-Access Earth Observation Data. Remote Sensing, 9(1), 86. https://doi.org/10.3390/rs9010086







