Decline of Geladandong Glacier Elevation in Yangtze River’s Source Region: Detection by ICESat and Assessment by Hydroclimatic Data
Abstract
:1. Introduction
2. Data and Methods
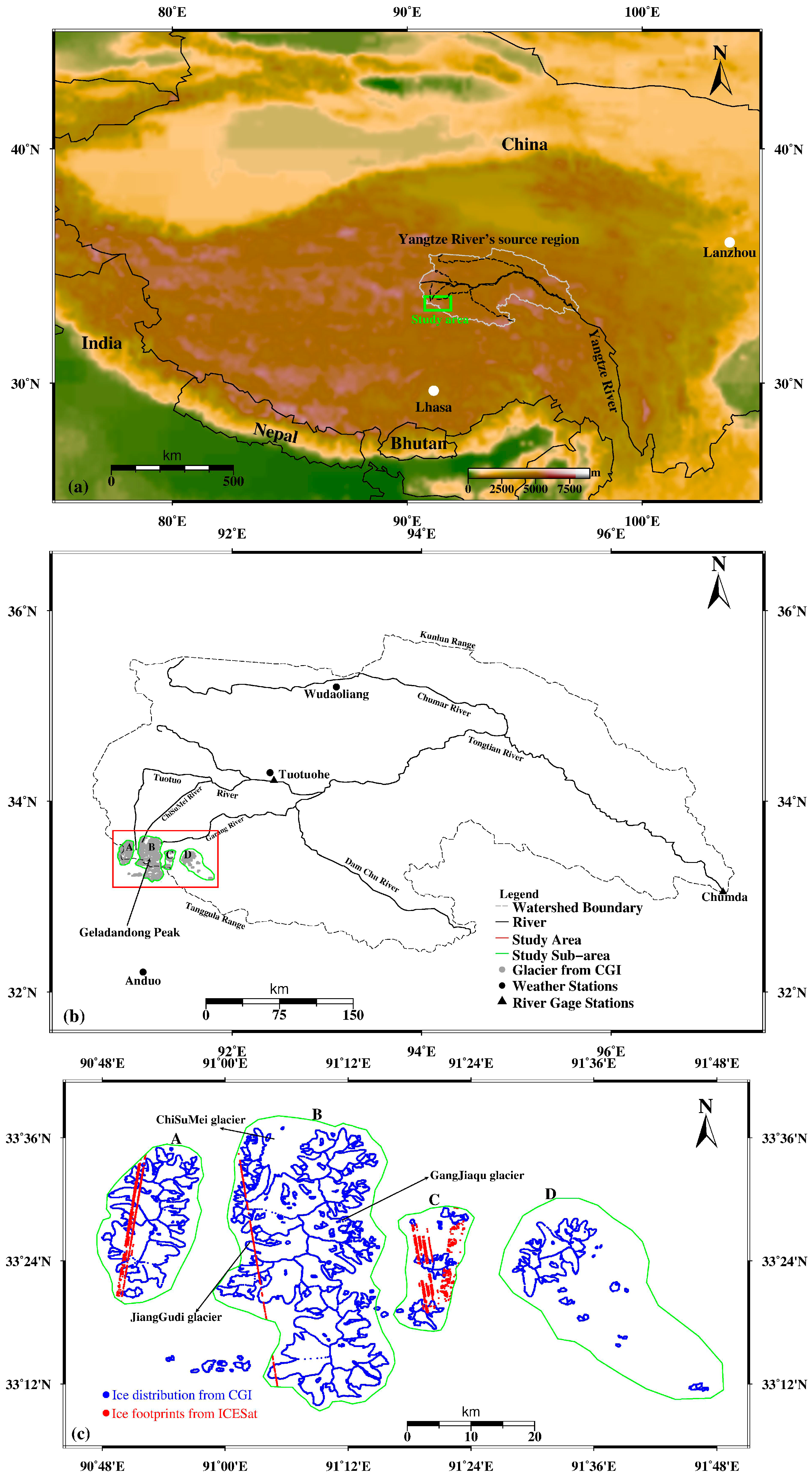
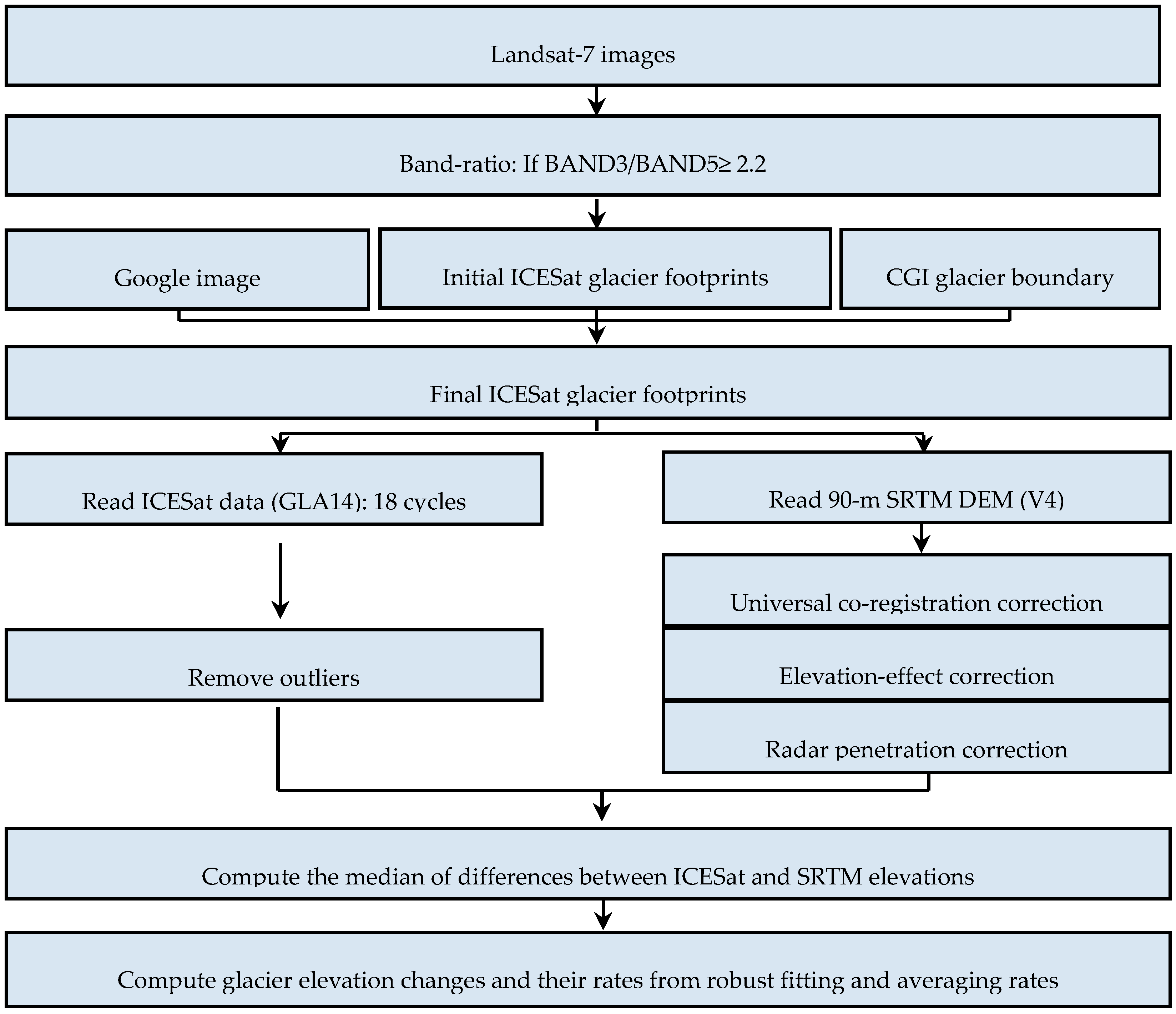
2.1. Landsat-7 Imagery for Glacier Identification
- (1)
- If the ratio Band3/Band5 is greater than 2.2, the footprint is a candidate point over glacier;
- (2)
- If the candidate point is not within a polygon of glaciers (Figure 1b) but is over an ice surface given by an Google Earth Image (23 June 2007 from CNES/Spot image), it is regarded as a point over glaciers;
- (3)
- If the candidate is neither within a glacier polygon nor over an ice surface defined by a Google image, it is not regarded as a point over glaciers.
2.2. Reference Elevations from SRTM
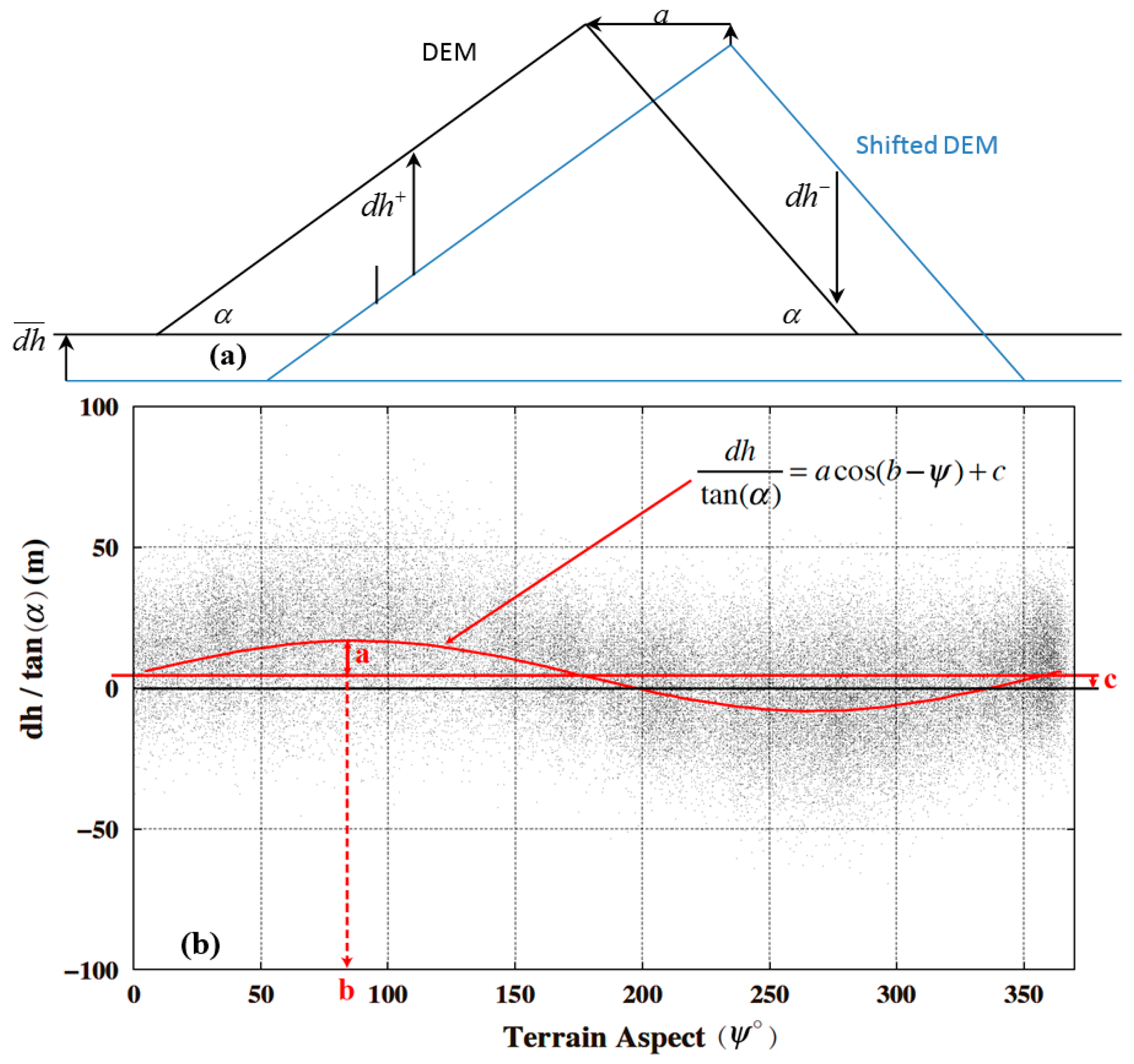
2.3. ICESat Altimetry for Determining Glacier Elevation Changes and Change Rates
- (1)
- Remove ICESat elevations exceeding the minimum and maximum of the SRTM elevations within the study region.
- (2)
- Remove the elevations at two consecutive along-track footprints that have a difference exceeding 300 m. Rationale: If we allow a maximum glacier slope of 60° for two neighboring along-track footprints spaced at about 172 m, the maximum elevation difference will be about 294 m.
- (3)
- Determine a smoothed value at a given point using n neighboring points (n = 100 in this paper). First, along a sufficiently long ground track, the differences between the original and smoothed heights are computed to determine a standard deviation . Then, if an original height, , meets the condition that , then is removed.
- (4)
- Remove the ICESat elevations that differ from the SRTM elevations by more than 150 m [23].
2.3.1. Method 1: Robust Fitting
2.3.2. Method 2: Rate Averaging
2.4. In Situ Hydroclimatic Data
3. Results
3.1. Glacier Elevation Changes and Their Rates from ICESat
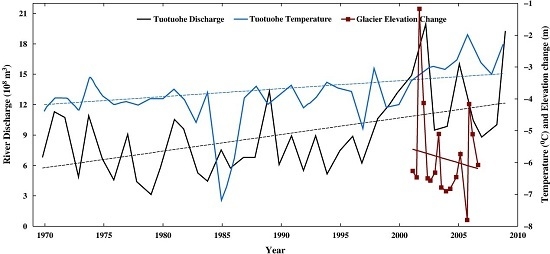
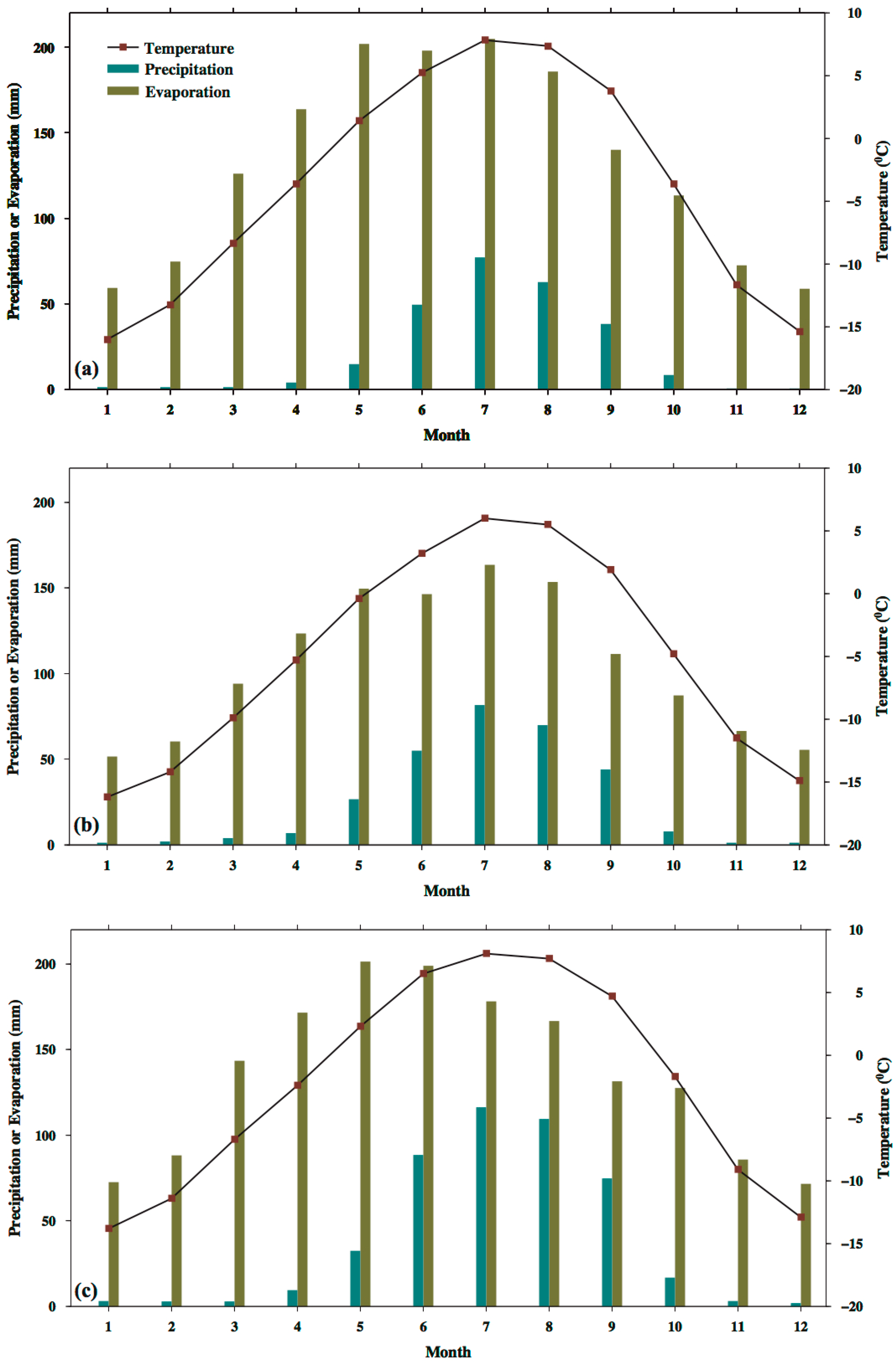
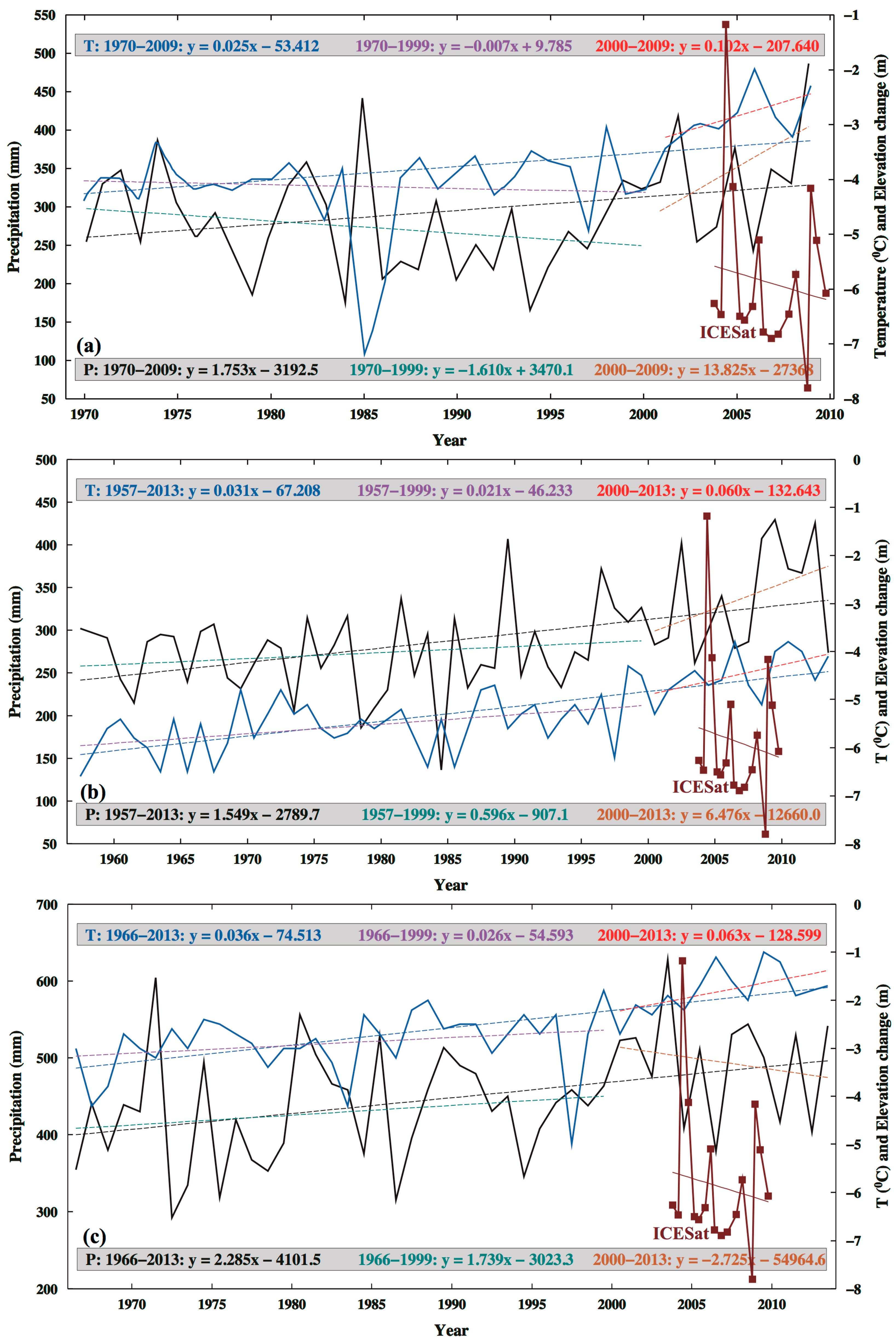
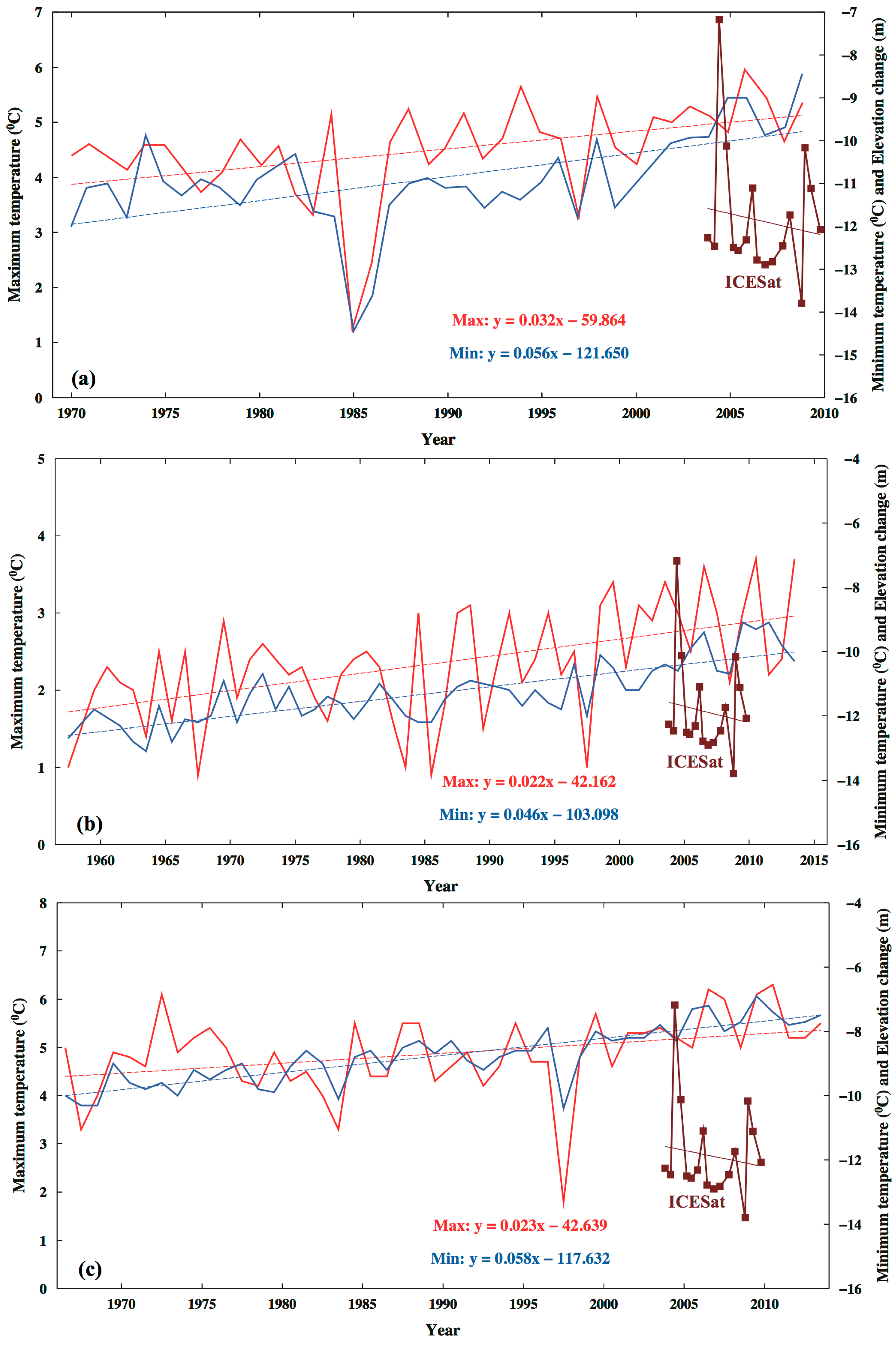
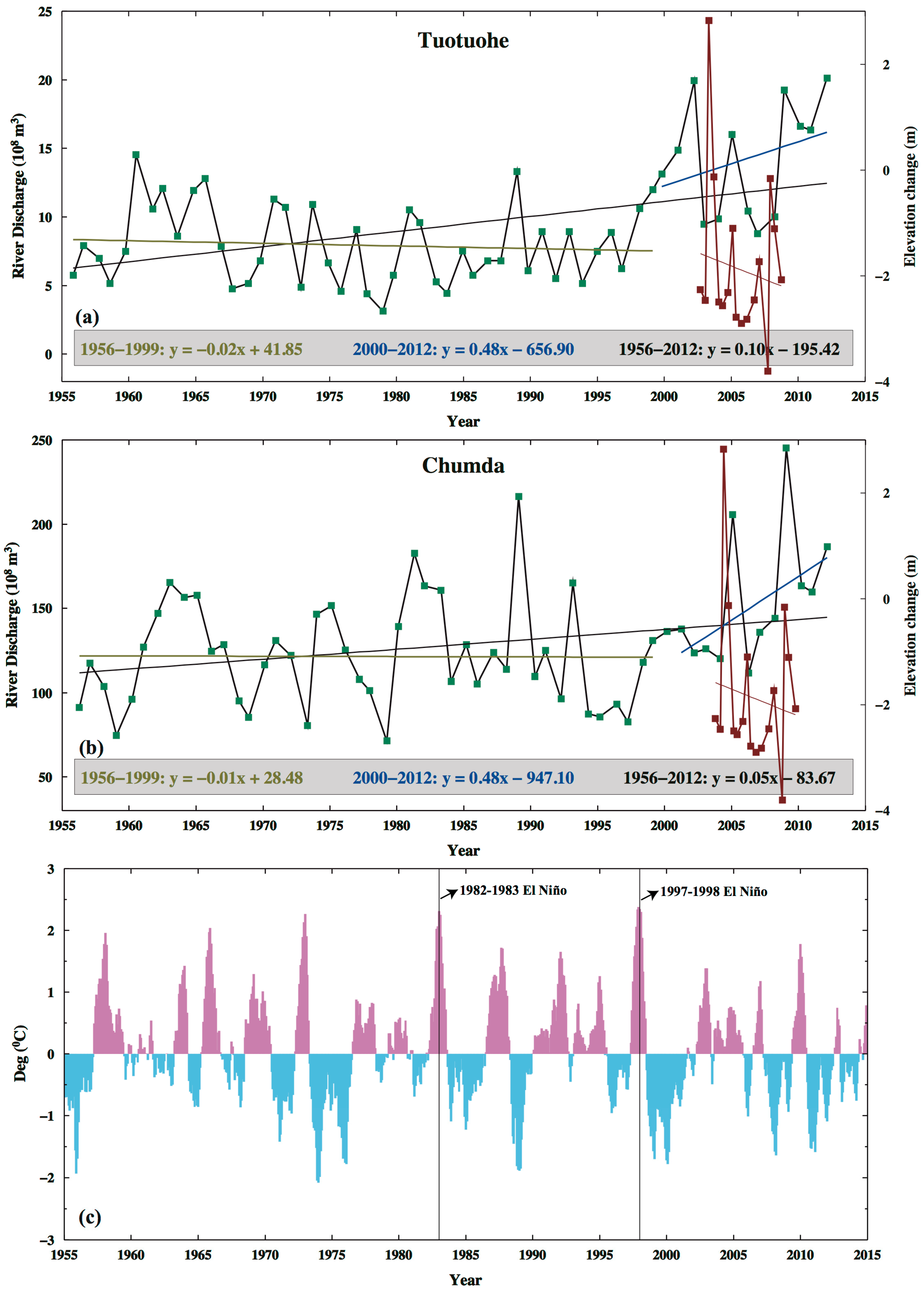
3.2. Decline of Geladandong Glacier Elevation: Its Correlation with Evaporation, Temperature, Precipitation, and River Discharge
4. Discussion
4.1. Mechanism for the Geladandong Glacier Surface Decline
4.2. The Limitations and Development of ICESat Determination of Glacier Elevation Change
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Farrington, D.F. Impacts of Climate Change on the Yangtze Source Region and Adjacent Areas; China Meteorological Press, World Wide Fund China-Lhasa Programme Office: Beijing, China, 2010. [Google Scholar]
- Yang, J.P.; Ding, Y.J.; Liu, S.Y.; Lu, A.-X.; Chen, R.-S. Glacier change and its effect on surface runoff in the source region of the Yangtze and Yellow rivers. J. Nat. Res. 2003, 18, 595–602. (In Chinese) [Google Scholar]
- Zhang, J.; Braaten, D.; Li, X.; She, J.; Tao, F. An inventory of glacier changes between 1973 and 2011 for the Geladandong Mountain area, China. Cryosphere 2013, 7, 507–531. [Google Scholar] [CrossRef]
- Neckel, N.; Kropáček, J.; Bolch, T.; Hochschild, V. Glacier mass changes on the Tibetan Plateau 2003–2009 derived from ICESat laser altimetry measurements. Environ. Res. Lett. 2014, 9, 014009. [Google Scholar] [CrossRef]
- Gardner, A.S.; Moholdt, G.; Cogley, J.G.; Wouters, B.; Arendt, A.A.; Wahr, J.; Berthier, E.; Hock, R.; Pfeffer, W.T.; Kaser, G.; et al. A Reconciled Estimate of Glacier Contributions to Sea Level Rise: 2003 to 2009. Science 2013, 340, 852–857. [Google Scholar] [CrossRef] [PubMed]
- Oerlemans, J. Glaciers and Climate Change; A. A. Balkema Publishers: Leiden, The Netherlands, 2001. [Google Scholar]
- Vincent, C. Influence of climate change over the 20th Century on four French glacier mass balances. J. Geophys. Res. 2002, 107, 4375–4386. [Google Scholar] [CrossRef]
- Jacob, T.; Wahr, J.; Pfeffer, W.; Swenson, S. Recent contributions of glaciers and ice caps to sea level rise. Nature 2012, 482, 514–518. [Google Scholar] [CrossRef] [PubMed]
- Yao, T.; Thompson, L.; Yang, W.; Yu, W.; Gao, Y.; Guo, X.; Yang, X.; Duan, K.; Zhao, H.; Xu, B.; et al. Different glacier status with atmospheric circulations in Tibetan Plateau and surroundings. Nat. Clim. Chang. 2012, 2, 663–667. [Google Scholar] [CrossRef]
- Dobhal, D.; Gergan, J.; Thayyen, R. Mass balance studies of the Dokirani Glacier from 1992 to 2000 Garhwal Himalaya. India Bull. Glaciol. Res. 2008, 25, 9–17. [Google Scholar]
- Fujita, K.; Nuimura, T. Spatially heterogeneous wastage of Himalayan glaciers. Proc. Natl. Acad. Sci. USA 2011, 108, 14011–14014. [Google Scholar] [CrossRef] [PubMed]
- Azam, M.; Wagnon, P.; Ramanathan, A.; Vincent, C.; Sharma, P.; Arnaud, Y.; Linda, A.; Pottakkal, J.G.; Chevallier, P.; Singh, V.B.; et al. From balance to imbalance: A shift in the dynamic behaviour of Chhota Shigri glacier, western Himalaya, India. J. Glaciol. 2012, 58, 315–324. [Google Scholar] [CrossRef]
- Bolch, T.; Kulkarni, A.; Kääb, A.; Huggel, C.; Paul, F.; Cogley, J.G.; Frey, H.; Kargel, J.S.; Fujita, K.; Scheel, M.; et al. The state and fate of Himalayan Glaciers. Science 2012, 336, 310–314. [Google Scholar] [CrossRef] [PubMed]
- Vincent, C.; Ramanathan, A.; Wagnon, P.; Dobhal, D.P.; Linda, A.; Berthier, E.; Sharma, P.; Arnaud, Y.; Azam, M.F.; Jose, P.G.; et al. Balanced conditions or slight mass gain of glaciers in the Lahaul and Spiti region (northern India, Himalaya) during the nineties preceded recent mass loss. Cryosphere 2013, 7, 569–582. [Google Scholar] [CrossRef]
- World Glacier Monitoring Service. Available online: http://wgms.ch/ (accessed on 12 January 2017).
- Rabatel, A.; Dedieu, J.; Vincent, C. Using remote-sensing data to determine equilibrium-line altitude and mass-balance time series: Validation on three French glaciers, 1994–2002. J. Glaciol. 2005, 51, 539–546. [Google Scholar] [CrossRef]
- Kulkarni, A.; Rathore, B.; Singh, S.; Bahuguna, I. Understanding changes in the Himalayan cryosphere using remote sensing techniques. Int. J. Remote Sens. 2011, 32, 601–615. [Google Scholar] [CrossRef]
- Immerzeel, W.W.; Pellicciotti, F.; Shrestha, A. Glaciers as a proxy to quantify the spatial distribution of precipitation in the Hunza basin. Mt. Res. Dev. 2012, 32, 30–38. [Google Scholar] [CrossRef]
- Matsuo, K.; Heki, K. Time-variable ice loss in Asian high mountains from satellite gravimetry. Earth Planet. Sci. Lett. 2010, 290, 30–36. [Google Scholar] [CrossRef]
- Zhang, G.; Yao, T.; Xie, H.; Kang, S.; Lei, Y. Increased mass over the Tibetan Plateau: From lakes or glaciers? Geophys. Res. Lett. 2013, 40, 2125–2130. [Google Scholar] [CrossRef]
- Berthier, E.; Arnaud, Y.; Kumar, R.; Ahmad, S.; Wagnon, P.; Chevallier, P. Remote sensing estimates of glacier mass balances in the Himachal Pradesh (Western Himalaya, India). Remote Sens. Environ. 2007, 108, 327–338. [Google Scholar] [CrossRef]
- Bolch, T.; Pieczonka, T.; Benn, D.I. Multi-decadal mass loss of glaciers in the Everest area (Nepal Himalaya) derived from stereo imagery. Cryosphere 2011, 5, 349–358. [Google Scholar] [CrossRef]
- Kääb, A.; Berthier, E.; Nuth, C.; Gardelle, J.; Arnaud, Y. Contrasting patterns of early 21st century glacier mass change in the Himalayas. Nature 2012, 488, 495–498. [Google Scholar] [CrossRef] [PubMed]
- Nuimura, T.; Fujita, K.; Yamaguchi, S.; Sharma, R. Elevation changes of glaciers revealed by multitemporal digital elevation models calibrated by GPS survey in the Khumbu region, Nepal Himalaya, 1992–2008. J. Glaciol. 2012, 58, 648–656. [Google Scholar] [CrossRef]
- Pieczonka, T.; Bolch, T.; Wei, J.F.; Liu, S.Y. Heterogeneous mass loss of glaciers in the Aksu-Tarim Catchment (Central Tien Shan) revealed by 1976 KH-9 Hexagon and 2009 SPOT-5 stereo imagery. Remote Sens. Environ. 2013, 130, 233–244. [Google Scholar] [CrossRef]
- Gardelle, J.; Berthier, E.; Arnaud, Y. Slight mass gain of Karakorum glaciers in the early 21st century. Nat. Geosci. 2012, 5, 322–325. [Google Scholar] [CrossRef]
- Huss, M. Density assumptions for converting geodetic glacier volume change to mass change. Cryosphere 2013, 7, 877–887. [Google Scholar] [CrossRef]
- Paul, F.; Kääb, A.; Maisch, M.; Kellenberger, T.; Haeberli, W. The new remote-sensing-derived Swiss glacier inventory: I. Methods. Ann. Glaciol. 2002, 34, 355–361. [Google Scholar] [CrossRef]
- Scherler, D.; Bookhagen, B.; Strecker, M.R. Hillslope-glacier coupling: The interplay of topography and glacial dynamics in High Asia. J. Geophys. Res. Earth 2011, 116. [Google Scholar] [CrossRef]
- Li, X. GLIMS Glacier Database (Boulder, CO: National Snow and Ice Data Center/World Data Center for Glaciology) Digital Media. 2003. Available online: http://www.glims.org/ (accessed on 12 January 2017).
- Guo, W.Q.; Liu, S.Y.; Xu, J.L.; Wu, L.Z.; Shangguan, D.H.; Yao, X.J.; Wei, J.F.; Bao, W.J.; Yu, P.C.; Liu, Q.; et al. The second Chinese glacier inventory: Data, methods and results. J. Glaciol. 2015, 61, 357–372. [Google Scholar] [CrossRef]
- SRTM Data Search. Available online: http://srtm.csi.cgiar.org/SELECTION/inputCoord.asp (accessed on 10 May 2016).
- Nuth, C.; Kääb, A. Co-registration and bias corrections of satellite elevation data sets for quantifying glacier thickness change. Cryosphere 2011, 5, 271–290. [Google Scholar] [CrossRef]
- Gardelle, J.; Berthier, E.; Arnaud, Y. Impact of resolution and radar penetration on glacier elevation changes computed from multi-temporal DEMs. J. Glaciol. 2012, 58, 419–422. [Google Scholar] [CrossRef]
- Advanced Spaceborne Thermal Emission and Reflection Radiometer (ASTER). Available online: http://gdem.ersdac.jspacesystems.or.jp/ (accessed on 11 May 2016).
- Kääb, A. Glacier Volume Changes Using ASTER Satellite Stereo and ICESat GLAS Laser Altimetry, A Test Study on Edgeya, Eastern Svalbard. IEEE Int. Geosci. Remote Sens. 2008, 46, 2823–2830. [Google Scholar] [CrossRef]
- Huber, P.J. Robust Statistics; John Wiley and Sons: Hoboken, NJ, USA, 1981. [Google Scholar]
- Nicolas, B.; Nicolas, L.; Hani, A.; Jean, S.B. The Relevance of GLAS/ICESat Elevation Data for the Monitoring of River Networks. Remote Sens. 2011, 3, 708–720. [Google Scholar]
- Moholdt, G.; Nuth, C.; Hagen, J.; Kohler, J. Recent elevation changes of Svalbard glaciers derived from ICESat laser altimetry. Remote Sens. Environ. 2010, 114, 2756–2767. [Google Scholar] [CrossRef]
- Surazakov, A.B.; Aizen, V.B. Estimating volume change of mountain glaciers using SRTM and map-based topographic data. IEEE Trans. Geosci. Remote Sens. 2006, 44, 2991–2995. [Google Scholar] [CrossRef]
- Brenner, A.C.; Bentley, C.R.; Csatho, B.M.; Harding, D.J.; Hofton, M.A.; Minster, J.; Roberts, L.; Saba, J.L.; Schutz, R.; Thomas, R.H.; et al. Derivation of Range and Range Distributions From Laser Pulse Waveform Analysis for Surface Elevations, Roughness, Slope, and Vegetation Heights, version 3.0; Algorithm Theoretical Basis Document; Goddard Space Flight Center: Greenbelt, MD, USA, 2003. [Google Scholar]
- Bliss, A.; Hock, R.; Radić, V. Global response of glacier runoff to twenty-first century climate change. J. Geophys. Res. Earth Surf. 2014, 119, 717–730. [Google Scholar] [CrossRef]
- Pu, J.; Yao, T.; Yang, M.; Tian, L.; Wang, L.N.; Ageta, Y.; Fujita, K. Rapid decrease of mass balance observed in the Xiao (Lesser) Dongkemadi Glacier, in the central Tibetan Plateau. Hydrol. Process. 2008, 22, 2953–2958. [Google Scholar] [CrossRef]
- Moholdt, G.; Wouters, B.; Gardner, A.S. Recent mass changes of glaciers in the Russian High Arctic. Geophys. Res. Lett. 2012, 39, L10502. [Google Scholar] [CrossRef]
- Zong, J.B.; Ye, Q.H.; Tian, L.D. Recent Naimona’Nyi glacier surface elevation changes on the Tibetan Plateau based on ICESat/GLAS, SRTM DEM and GPS measurements. Chin. Sci. Bull. 2013, 58, 2108–2118. (In Chinese) [Google Scholar] [CrossRef]
- China Meteorological Data Service Center. Available online: http://cdc.nmic.cn/home.do (accessed on 13 January 2017).
- Sun, Y.S.; Duan, S.Q.; Li, Y.; Cao, G.C. Variation characteristics and trend analysis of runoff at the source regions of the three rivers in Qinghai during recent years. J. Water Resour. Eng. 2015, 26, 52–57. (In Chinese) [Google Scholar]
- Niño 3.4 Sea Surface Temperature Index. Available online: http://www.esrl.noaa.gov/psd/gcos_wgsp/Timeseries/Nino34/ (accessed on 26 May 2016).
- Kang, E.; Cheng, G.D.; Dong, Z.C. Glacier-Snow Water Resources and Mountain Runoff in the Arid Area of Northwest China; Science Press: Beijing, China, 2002; pp. 14–54. (In Chinese) [Google Scholar]
- Shi, Y.F. Concise Glacier Inventory of China; Shanghai Popular Science Press: Shanghai, China, 2008; pp. 1–205. [Google Scholar]
- Oerlemans, J. Extracting a climate signal from 169 glacier records. Science 2005, 308, 675–677. [Google Scholar] [CrossRef] [PubMed]
- Raper, S.; Brown, O.; Braithwaite, R.J. A geometric glacier model for sea-level change calculations. J. Glaciol. 2000, 46, 357–368. [Google Scholar] [CrossRef]
- Zhang, Y.; Fujita, K.; Ageta, Y.; Nakawo, M.; Yao, T.; Pu, J. The response of glacier ELA to climate fluctuations on High-Asia. Bull. Glacier Res. 1998, 16, 1–11. [Google Scholar]
- Liu, S.Y.; Xie, Z.C.; Wang, N.L.; Ye, B. Mass balance sensitivity to climate change: A case study of Glacier No. 1 at Urumqi Riverhead, Tianshan Mountains, China. Chin. Geogr. Sci. 1999, 9, 134–140. [Google Scholar] [CrossRef]
- Li, Z.Q.; Han, T.D.; Jing, Z.F.; Yang, H.A.; Jiao, K.Q. A summary of 40-year observed variation facts of climate and Glacier No. 1 at headwater of Urumqi River, Tianshan, China. J. Glaciol. Geocryol. 2003, 25, 117–123. (In Chinese) [Google Scholar]
- Singh, P.; Bengtsson, L. Impact of warmer climate on melt and evaporation for the rainfed, snowfed and glacierfed basins in the Himalayan region. J. Hydrol. 2005, 300, 140–154. [Google Scholar] [CrossRef]
- Wang, S.; Zhang, M.; Li, Z.; Wang, F.; Li, H.; Li, Y.; Huang, X. Glacier area variation and climate change in the Chinese Tianshan Mountains since 1960. J. Geogr. Sci. 2011, 21, 263–273. [Google Scholar] [CrossRef]
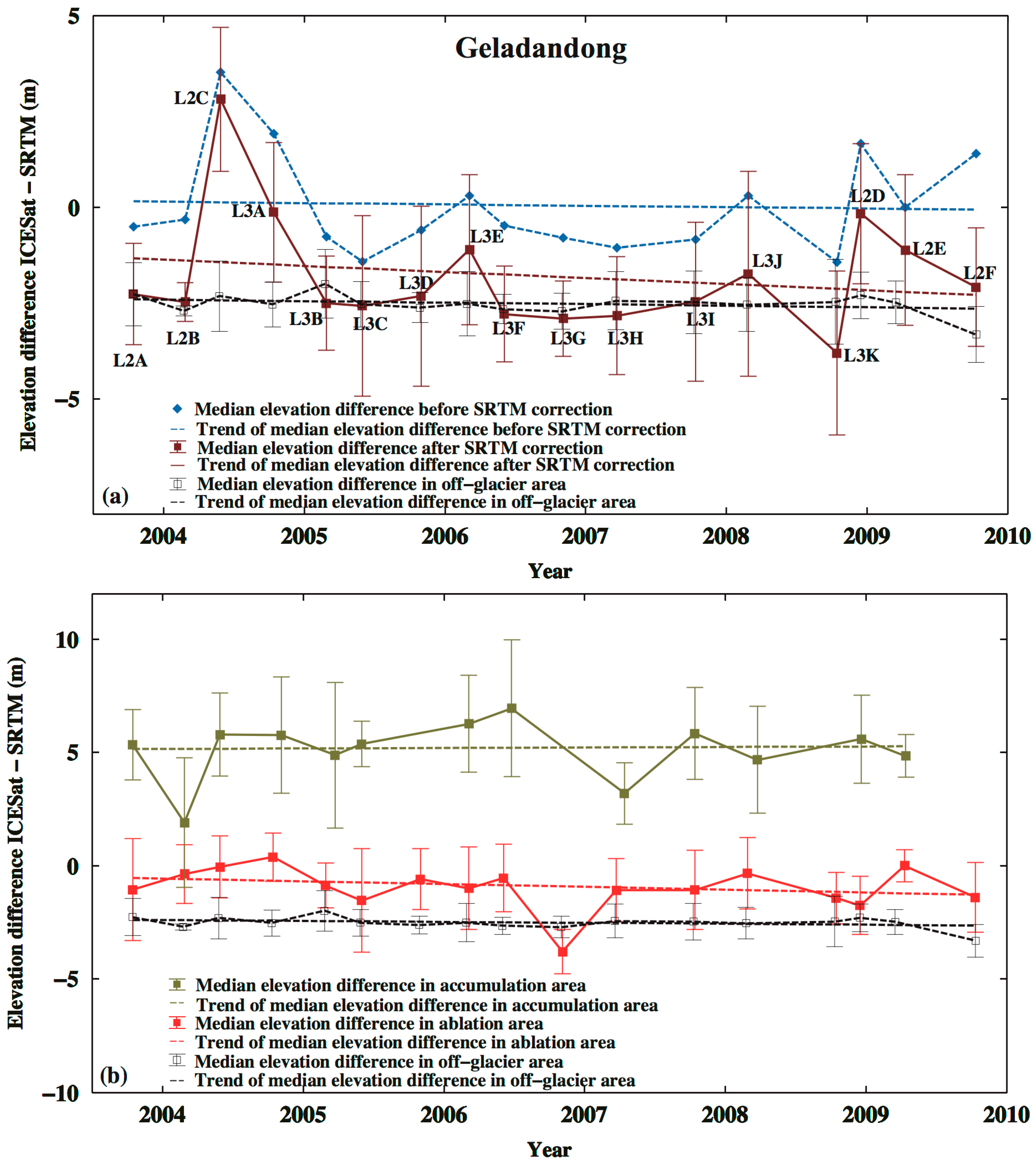
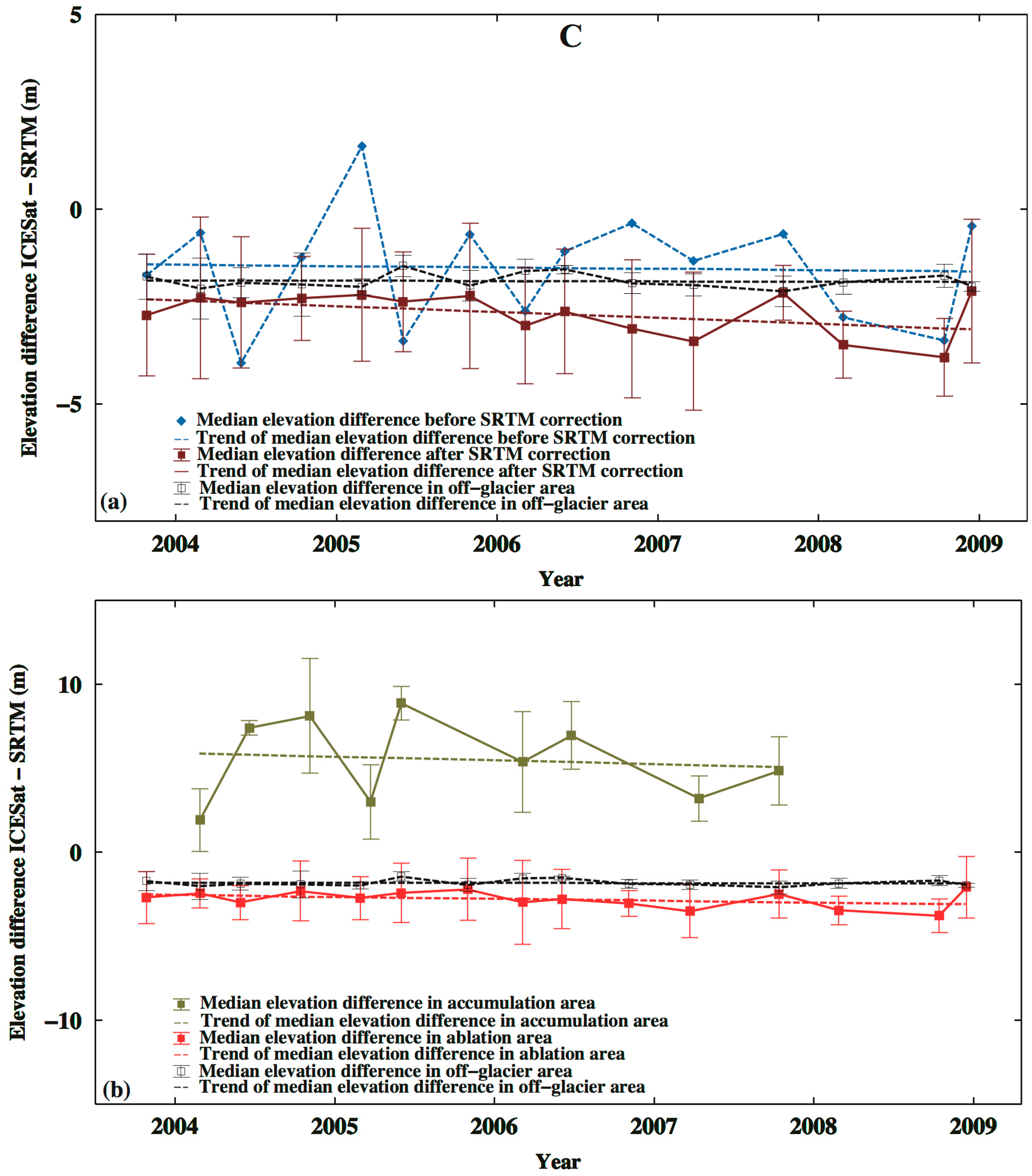
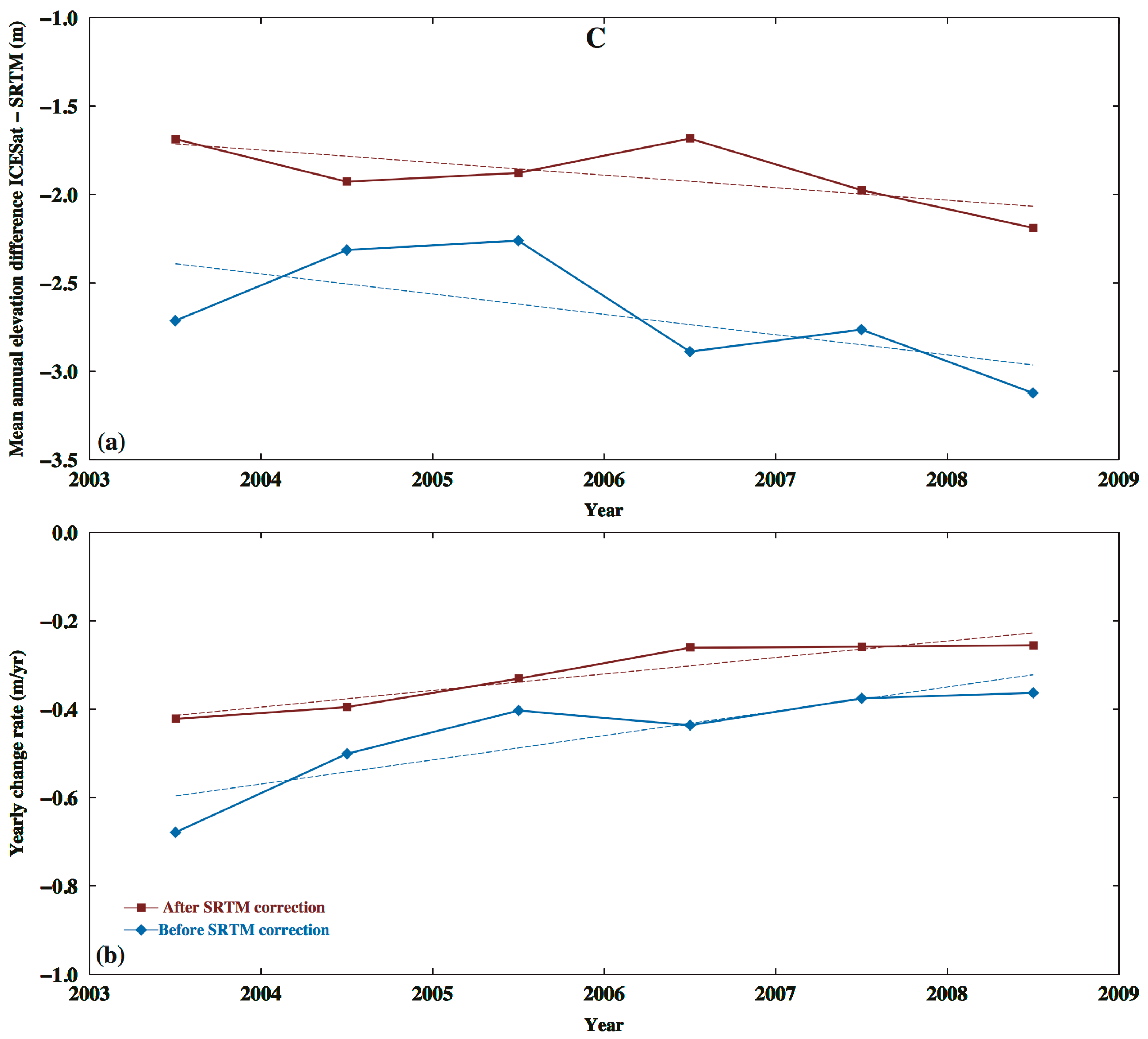
| Region and Time Period | Rate of Elevation Change from Robust Fitting * | |||
|---|---|---|---|---|
| Accumulation Area (m·a−1) | Ablation Area (m·a−1) | Entire Area (m·a−1) | Off-Glacier Area (m·a−1) | |
| Geladandong (2003–2009) | +0.075 ± 0.223 | −0.123 ± 0.109 | −0.158 ± 0.066 | −0.010 ± 0.059 |
| C (2003–2008) | −0.291 ± 0.818 | −0.128 ± 0.097 | −0.176 ± 0.102 | −0.007 ± 0.063 |
| Region | Year | Season | ICESat Cycle | No. of ICESat over Non-Glacier | No. of ICESat over Glacier | Time Difference with SRTM (Year) | Elevation Range (m) | Difference before Corrections (m) | Difference after Corrections (m) | Rate before Corrections (m·a−1) | Rate after Corrections (m·a−1) | Mean Rate (m·a−1) |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| A | 2004 | Winter | L2C | 14 | 42 | 5 | 5389.74/6013.87 | −4.830 | −2.988 | −0.966 | −0.598 | −0.598 ± 0.368 |
| Fall | L3A | 30 | 118 | 5 | 5264.05/6044.73 | −2.854 | −2.702 | −0.571 | −0.540 | −0.540 ± 0.031 | ||
| Mean | −3.842 | −2.845 | −0.769 | −0.569 | −0.569 ± 0.200 | |||||||
| 2006 | Winter | L3E | 37 | 108 | 6 | 5352.27/5970.55 | −7.281 | −1.838 | −1.214 | −0.306 | −0.306 ± 0.908 | |
| 2008 | Winter | L3J | 44 | 117 | 8 | 5356.57/6036.16 | −0.202 | −1.480 | −0.025 | −0.185 | −0.185 ± 0.160 | |
| Fall | L2D | 22 | 112 | 9 | 5259.85/6040.47 | −2.813 | −2.247 | −0.313 | −0.250 | −0.250 ± 0.063 | ||
| Mean | −1.508 | −1.864 | −0.169 | −0.218 | −0.218 ± 0.049 | |||||||
| 2009 | Winter | L2E | 4 | 8 | 9 | 5696.00/5818.38 | −7.281 | −5.169 | −0.809 | −0.574 | −0.574 ± 0.235 | |
| Mean | −0.740 | −0.418 | −0.418 ± 0.322 | |||||||||
| B | 2003 | Fall | L2A | 42 | 167 | 4 | 5320.61/6052.85 | −1.674 | −1.728 | −0.412 | −0.432 | −0.432 ± 0.020 |
| C | 2003 | Fall | L2A | 185 | 57 | 4 | 5157.24/5657.92 | −2.714 | −1.687 | −0.679 | −0.422 | −0.422 ± 0.257 |
| 2004 | Winter | L2B | 184 | 67 | 4 | 5174.79/5895.91 | −2.269 | −0.597 | −0.567 | −0.149 | −0.149 ± 0.418 | |
| Summer | L2C | 17 | 17 | 5 | 5213.84/5811.41 | −2.391 | −3.947 | −0.478 | −0.789 | −0.789 ± 0.311 | ||
| Fall | L3A | 122 | 52 | 5 | 5215.5/5888.92 | −2.283 | −1.237 | −0.457 | −0.247 | −0.247 ± −0.210 | ||
| Mean | −2.314 | −1.927 | −0.501 | −0.395 | −0.395 ± 0.106 | |||||||
| 2005 | Winter | L3B | 102 | 62 | 5 | 5219.9/5984.17 | −2.194 | −1.623 | −0.439 | −0.324 | −0.324 ± 0.115 | |
| Summer | L3C | 103 | 44 | 6 | 5204.58/5745.15 | −2.373 | −3.373 | −0.400 | −0.562 | −0.562 ± 0.162 | ||
| Fall | L3D | 187 | 64 | 6 | 5202.93/5702.13 | −2.219 | −0.642 | −0.370 | −0.107 | −0.107 ± 0.263 | ||
| Mean | −2.262 | −1.879 | −0.403 | −0.331 | −0.331 ± 0.072 | |||||||
| 2006 | Winter | L3E | 154 | 51 | 6 | 5208.13/5856.86 | −2.986 | −2.616 | −0.498 | −0.436 | −0.436 ± 0.062 | |
| Summer | L3F | 123 | 63 | 7 | 5141.87/5961.69 | −2.619 | −1.074 | −0.374 | −0.153 | −0.153 ± 0.221 | ||
| Fall | L3G | 195 | 56 | 7 | 5185.33/5696.44 | −3.066 | −1.359 | −0.438 | −0.194 | −0.194 ± 0.244 | ||
| Mean | −2.890 | −1.683 | −0.437 | −0.261 | −0.261 ± 0.176 | |||||||
| 2007 | Winter | L3H | 92 | 57 | 7 | 5214.19/5938.8 | −3.386 | −1.321 | −0.484 | −0.188 | −0.188 ± 0.296 | |
| Fall | L3I | 191 | 58 | 8 | 5199.65/5855.53 | −2.144 | −2.630 | −0.268 | −0.329 | −0.329 ± 0.061 | ||
| Mean | −2.765 | −1.976 | −0.376 | −0.259 | −0.259 ± 0.117 | |||||||
| 2008 | Winter | L3J | 56 | 45 | 8 | 5197.92/5655.95 | −3.474 | −2.775 | −0.434 | −0.346 | −0.346 ± 0.088 | |
| Fall | L3K | 107 | 21 | 9 | 5188.28/5723.47 | −3.798 | −3.356 | −0.422 | −0.373 | −0.373 ± 0.049 | ||
| Fall | L2D | 76 | 39 | 9 | 5259.42/5643.58 | −2.095 | −0.438 | −0.233 | −0.049 | −0.049 ± 0.184 | ||
| Mean | −3.122 | −2.190 | −0.363 | −0.256 | −0.256 ± 0.107 | |||||||
| Mean | −0.460 | −0.321 | −0.321 ± 0.139 |
© 2017 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chao, N.; Wang, Z.; Hwang, C.; Jin, T.; Cheng, Y.-S. Decline of Geladandong Glacier Elevation in Yangtze River’s Source Region: Detection by ICESat and Assessment by Hydroclimatic Data. Remote Sens. 2017, 9, 75. https://doi.org/10.3390/rs9010075
Chao N, Wang Z, Hwang C, Jin T, Cheng Y-S. Decline of Geladandong Glacier Elevation in Yangtze River’s Source Region: Detection by ICESat and Assessment by Hydroclimatic Data. Remote Sensing. 2017; 9(1):75. https://doi.org/10.3390/rs9010075
Chicago/Turabian StyleChao, Nengfang, Zhengtao Wang, Cheinway Hwang, Taoyong Jin, and Yung-Sheng Cheng. 2017. "Decline of Geladandong Glacier Elevation in Yangtze River’s Source Region: Detection by ICESat and Assessment by Hydroclimatic Data" Remote Sensing 9, no. 1: 75. https://doi.org/10.3390/rs9010075
APA StyleChao, N., Wang, Z., Hwang, C., Jin, T., & Cheng, Y.-S. (2017). Decline of Geladandong Glacier Elevation in Yangtze River’s Source Region: Detection by ICESat and Assessment by Hydroclimatic Data. Remote Sensing, 9(1), 75. https://doi.org/10.3390/rs9010075