Identification of Statistically Homogeneous Pixels Based on One-Sample Test
Abstract
:1. Introduction
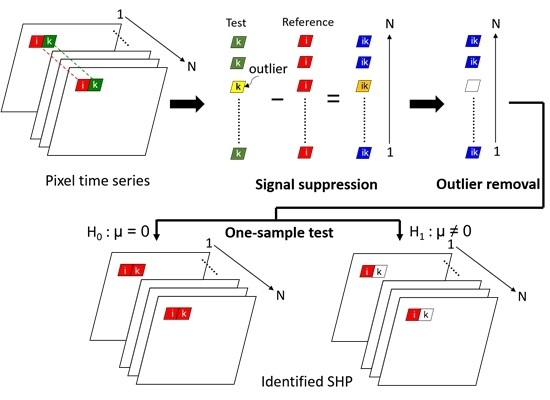
2. Methodology
2.1. Signal Suppression
2.2. Outlier Removal
2.3. One-Sample Test
3. Experiments and Discussion
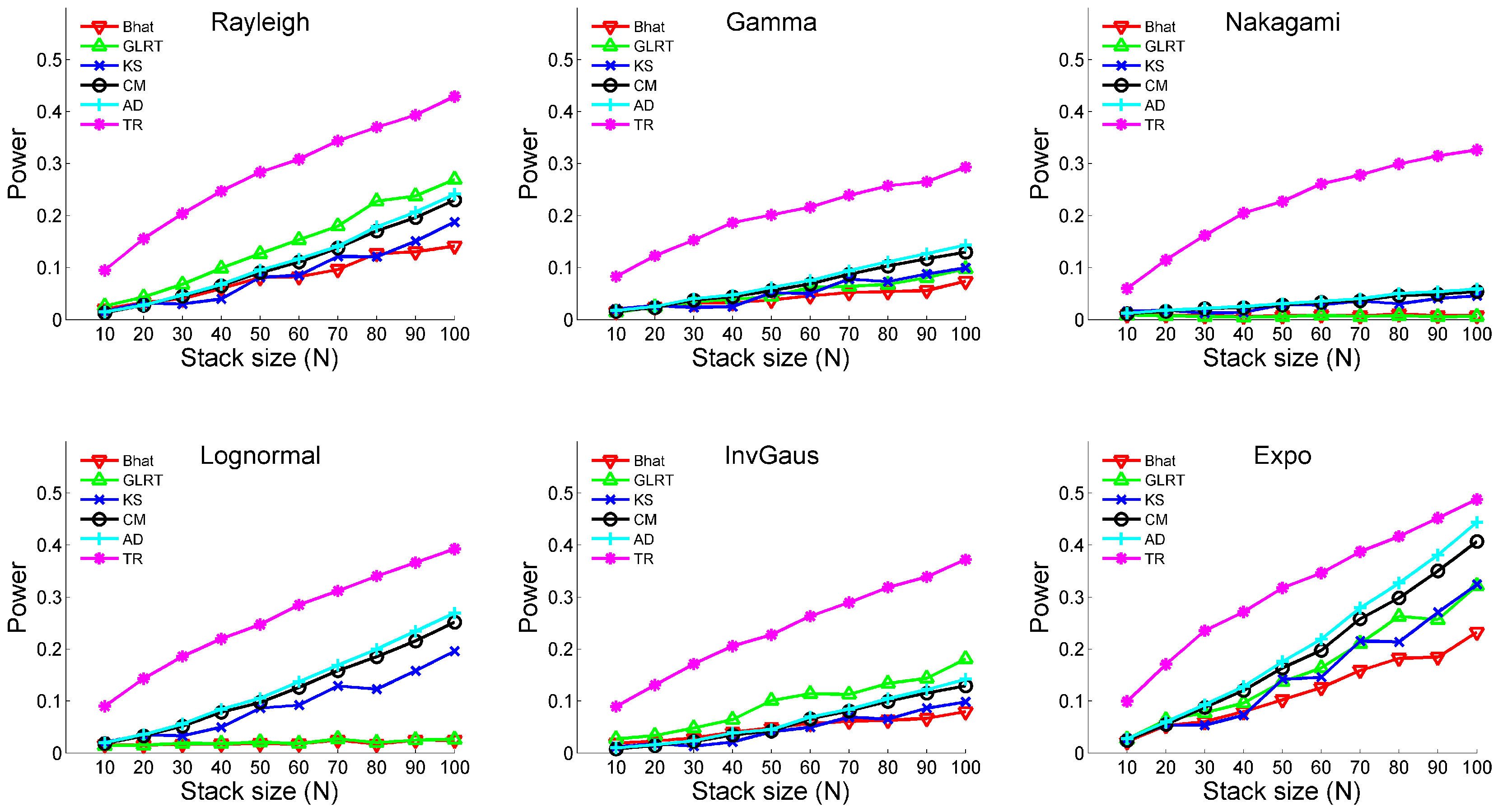
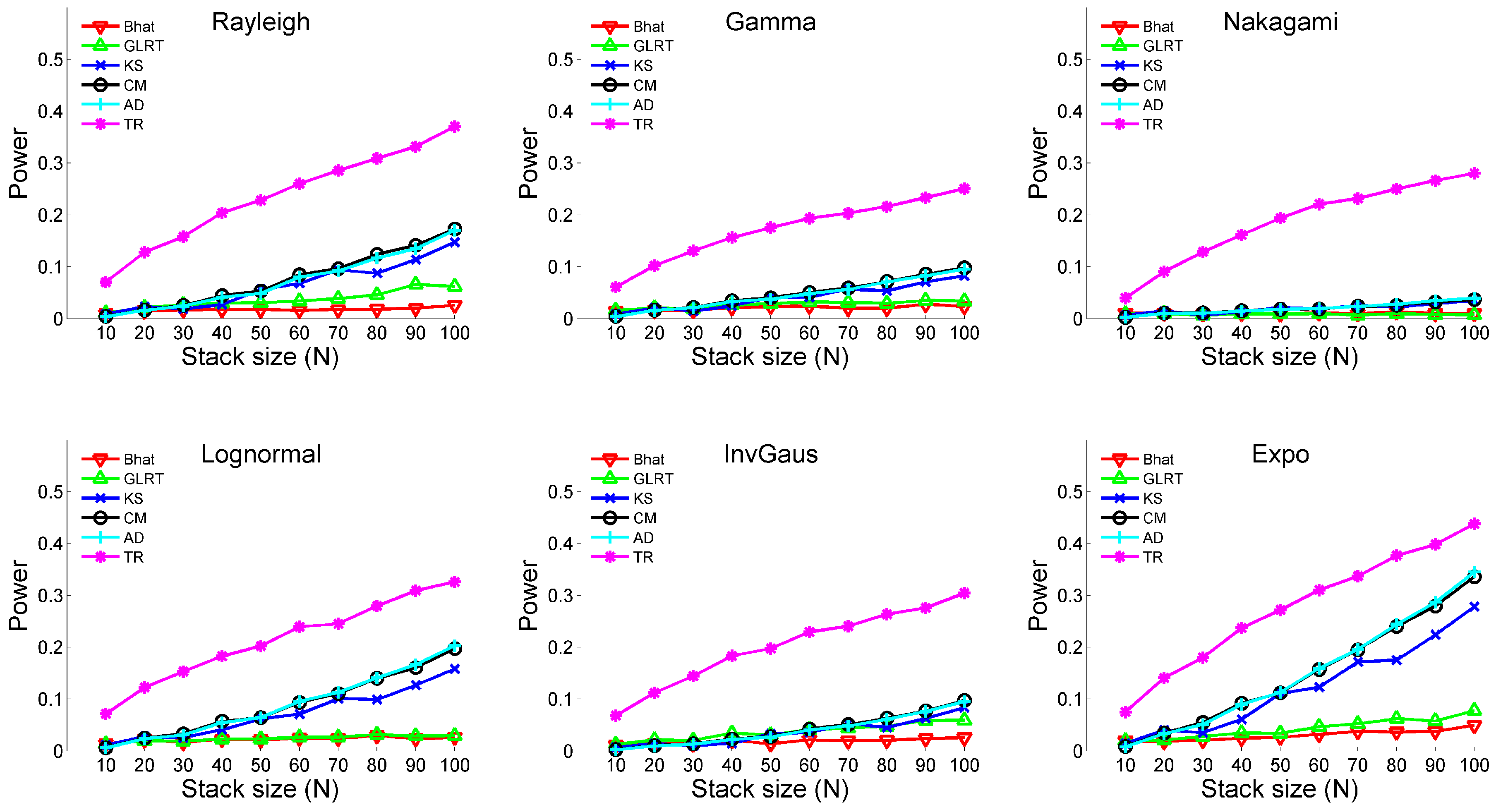
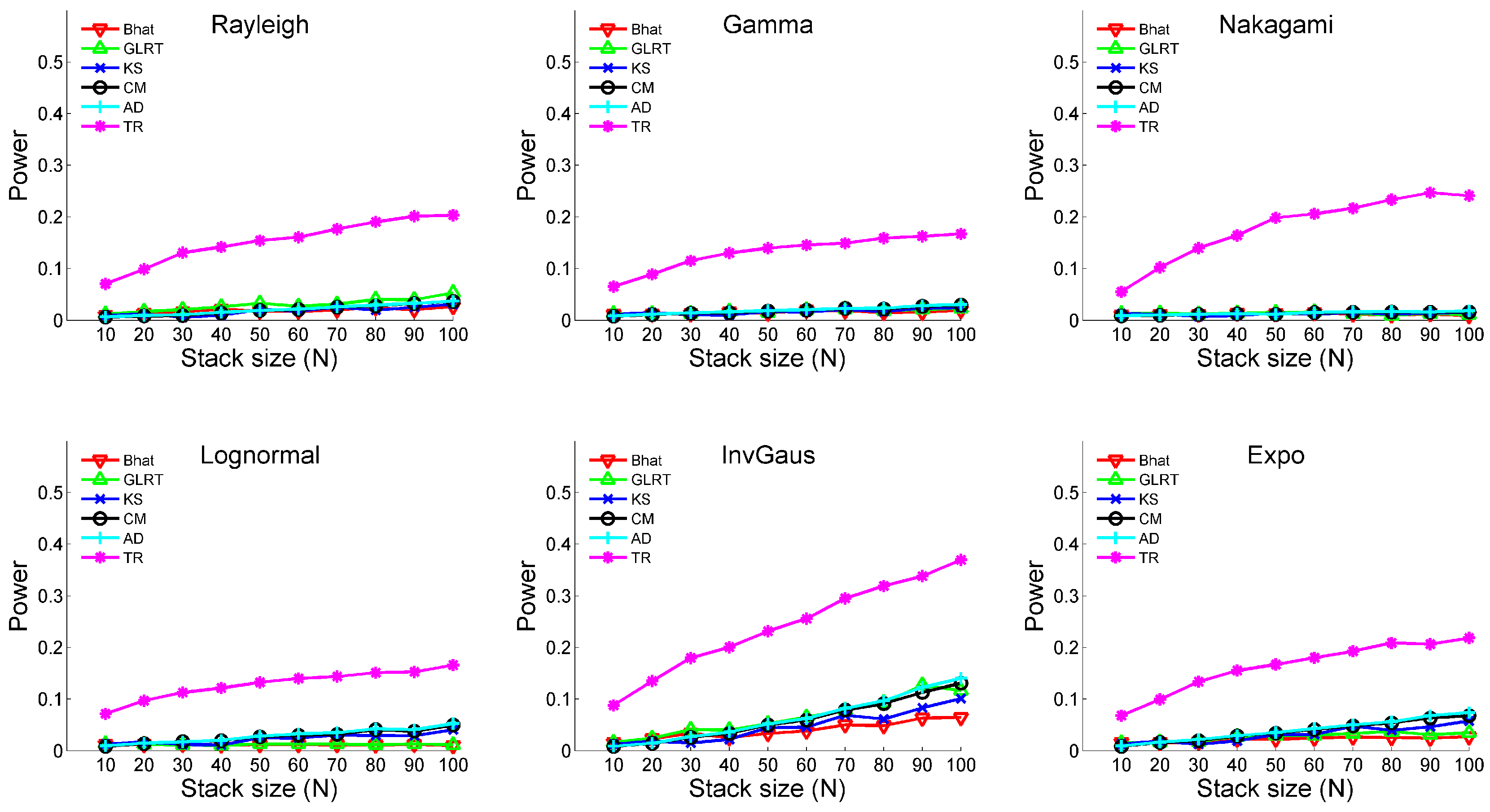
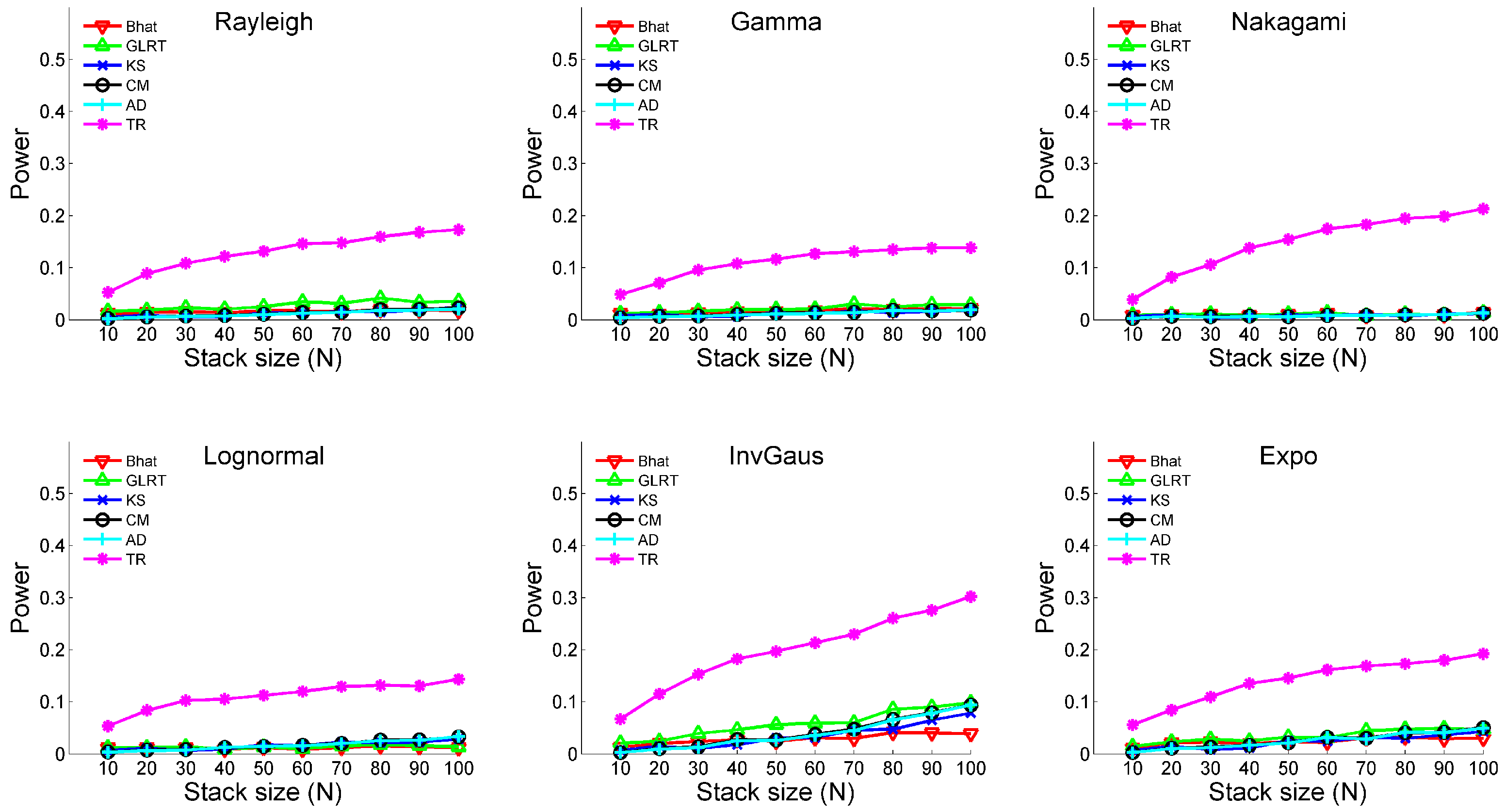
3.1. Monte Carlo Simulation
- (i)
- Temporal change: No; Outlier: NoThe two samples possess neither temporal changes nor outliers. Three types of distributions are analyzed. The distributional parameters are shown in Table 1.
- (ii)
- Temporal change: No; Outlier: YesThe two samples possess outliers without temporal changes. The distributional parameters are the same as Table 1; however, both samples include 5% outliers. The magnitudes of outliers are set to be , where μ and σ represent the mean and standard deviation of the sample.
- (iii)
- Temporal change: Yes; Outlier: NoA temporal change is designed in the first sample. The time of change is always at for different sample sizes, meaning that observations before and after follow different distributional parameters. The corresponding parameters are shown in Table 2.
- (iv)
- Temporal change: Yes; Outlier: YesA temporal change is designed in the first sample. The distributional parameters are the same as Table 2; however, both samples include 5% outliers. The magnitudes of outliers are set to be .
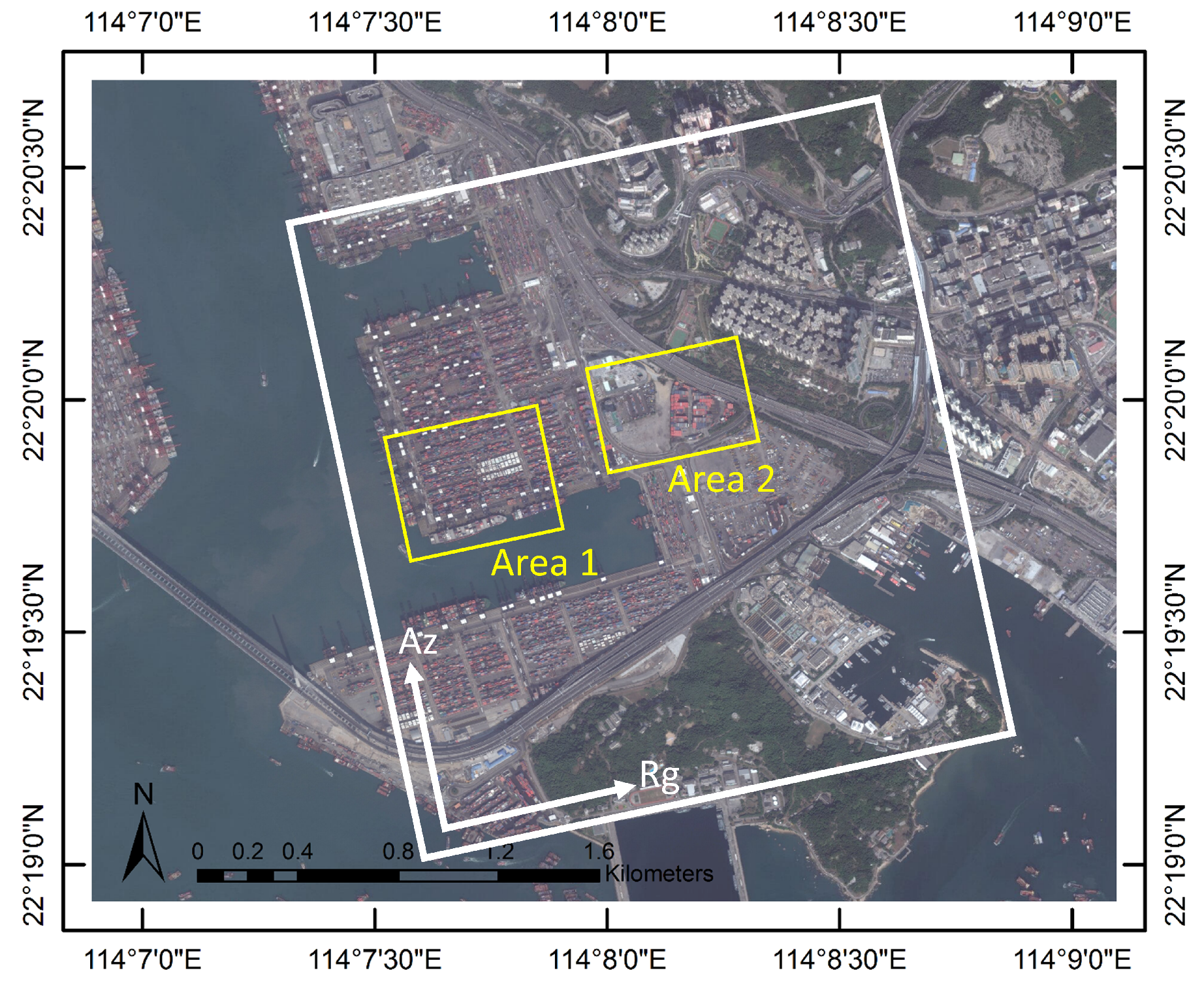
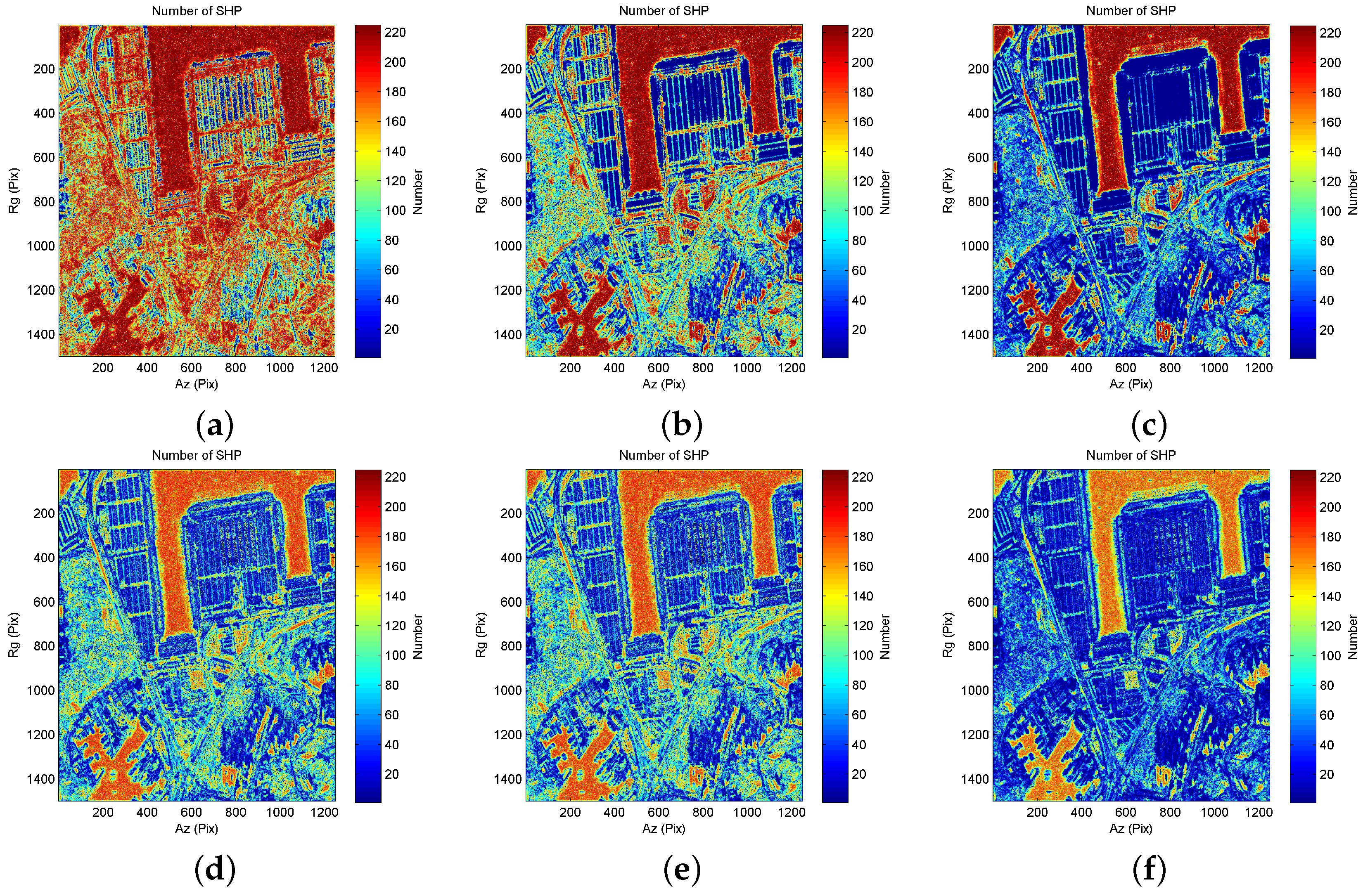
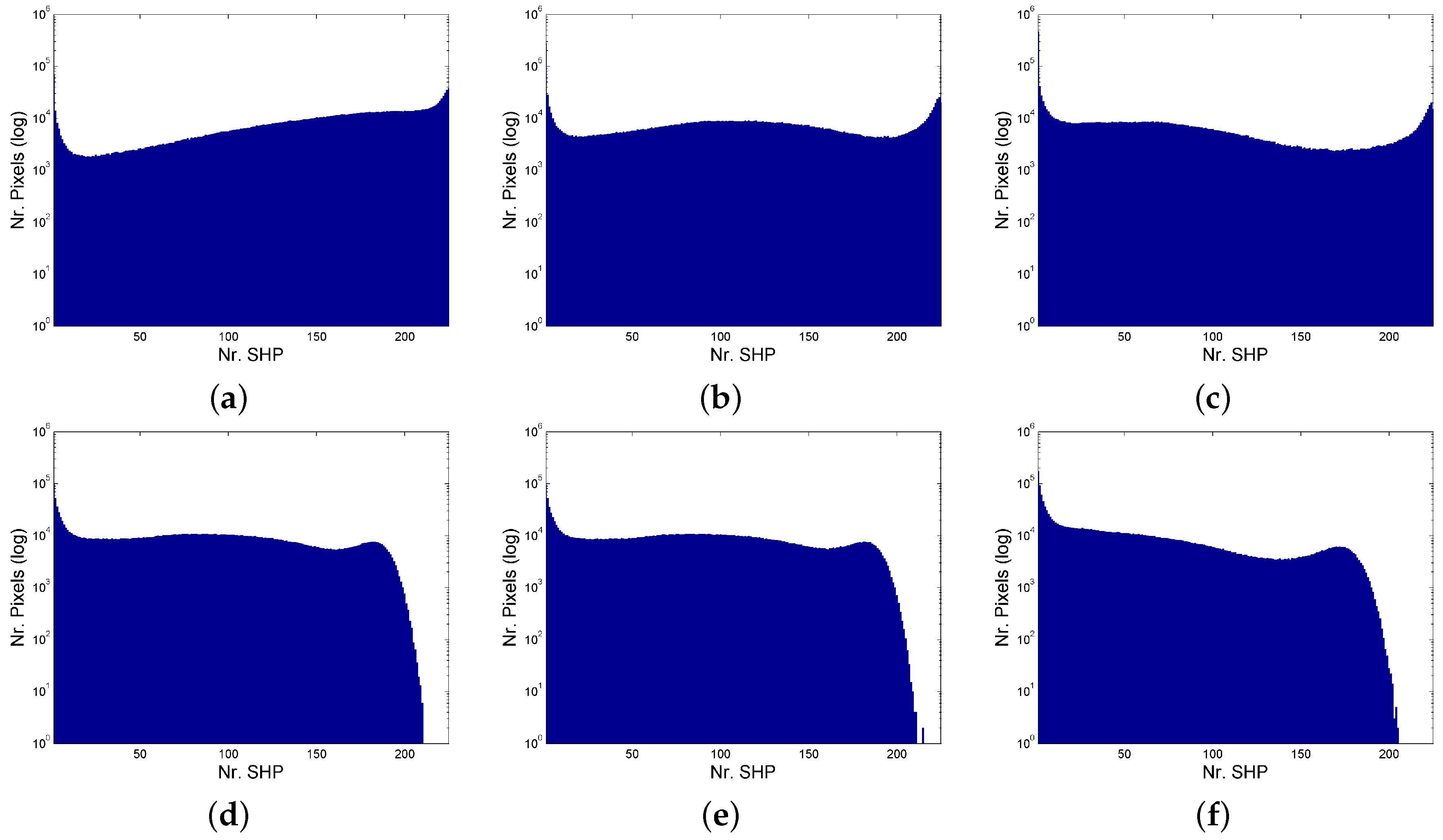
3.2. Experiments with SAR Data Stack
4. Conclusions
- Removing signals and outliers before conducting any hypothesis tests is advantageous. By reducing the impacts of these measurements, the hypothesis testing can deal only with the stochastic processes. This not only makes the parametric tests applicable, but also augments the power of the test operation.
- Considering temporal variabilities is pragmatically necessary, especially when dealing with data stacks crossing through a large temporal spacing. The proposed approach helps to identify SHP family even with temporal variations.
- Since having large sample sizes can lower the probability of conducting type I and II errors, the proposed approach becomes useful in mitigating the impact of temporal variabilities while keeping the large temporal spacing.
- The difference of two time series (i.e., ) keeps the temporal sequence that would be lost when building sample CDF in tests like KS or AD. This also helps to improve the effectiveness of hypothesis tests.
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Ferretti, A.; Fumagalli, A.; Novali, F.; Prati, C.; Rocca, F.; Rucci, A. A new algorithm for processing interferometric data-stacks: SqueeSAR. IEEE Trans. Geosci. Remote Sens. 2011, 49, 3460–3470. [Google Scholar] [CrossRef]
- Parizzi, A.; Brcic, R. Adaptive InSAR stack multilooking exploiting amplitude statistics: A comparison between different techniques and practical results. IEEE Geosci. Remote Sens. Lett. 2011, 8, 441–445. [Google Scholar] [CrossRef]
- Goel, K. Advanced Stacking Techniques and Applications in High Resolution SAR Interferometry. Ph.D. Thesis, Technical University of Munich, Munich, Germany, 2014. [Google Scholar]
- Goel, K.; Adam, N. A distributed scatterer interferometry approach for precision monitoring of known surface deformation phenomena. IEEE Trans. Geosci. Remote Sens. 2014, 52, 5454–5468. [Google Scholar] [CrossRef]
- Schmitt, M.; Stilla, U. Adaptive multilooking of airborne single-pass multi-baseline InSAR stacks. IEEE Trans. Geosci. Remote Sens. 2014, 52, 305–312. [Google Scholar] [CrossRef]
- Sica, F.; Reale, D.; Poggi, G.; Verdoliva, L.; Fornaro, G. Nonlocal adaptive multilooking in SAR multipass differential interferometry. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2015, 8, 1727–1742. [Google Scholar] [CrossRef]
- Deledalle, C.A.; Denis, L.; Tupin, F. NL-InSAR: Nonlocal interferogram estimation. IEEE Trans. Geosci. Remote Sens. 2011, 49, 1441–1452. [Google Scholar] [CrossRef]
- Deledalle, C.A.; Denis, L.; Tupin, F.; Reigber, A.; Jäger, M. NL-SAR: A unified nonlocal framework for resolution-preserving (Pol)(In) SAR Denoising. IEEE Trans. Geosci. Remote Sens. 2015, 53, 2021–2038. [Google Scholar] [CrossRef]
- Jiang, M.; Ding, X.; Li, Z. Hybrid approach for unbiased coherence estimation for multitemporal InSAR. IEEE Trans. Geosci. Remote Sens. 2014, 52, 2459–2473. [Google Scholar] [CrossRef]
- Jiang, M.; Ding, X.; Li, Z.; Tian, X.; Wang, C.; Zhu, W. InSAR coherence estimation for small data sets and its impact on temporal decorrelation extraction. IEEE Trans. Geosci. Remote Sens. 2014, 52, 6584–6596. [Google Scholar] [CrossRef]
- Schmitt, M.; Schönberger, J.L.; Stilla, U. Adaptive covariance matrix estimation for multi-baseline InSAR data stacks. IEEE Trans. Geosci. Remote Sens. 2014, 52, 6807–6817. [Google Scholar] [CrossRef]
- Jiang, M.; Ding, X.; Hanssen, R.F.; Malhotra, R.; Chang, L. Fast statistically homogeneous pixel selection for covariance matrix estimation for multitemporal InSAR. IEEE Trans. Geosci. Remote Sens. 2015, 53, 1213–1224. [Google Scholar] [CrossRef]
- Carvalho, E.A.; Ushizima, D.M.; Medeiros, F.N.; Martins, C.I.O.; Marques, R.C.; Oliveira, I. SAR imagery segmentation by statistical region growing and hierarchical merging. Digit. Signal Process. 2009, 20, 1365–1378. [Google Scholar] [CrossRef]
- Walpole, R.E.; Myers, R.H. Probability and Statistics for Engineers and Scientists, 5th ed.; Macmillan: New York, NY, USA, 1993; pp. 671–672. [Google Scholar]
- Tison, C.; Nicolas, J.M.; Tupin, F.; Maître, H. A new statistical model for Markovian classification of urban areas in high-resolution SAR images. IEEE Trans. Geosci. Remote Sens. 2004, 42, 2046–2057. [Google Scholar] [CrossRef]
- Goodman, J.W. Statistical properties of laser speckle patterns. In Laser Speckle and Related Phenomena; Springer: Heidelberg, Germany, 1975; pp. 9–75. [Google Scholar]
- Jao, J. Amplitude distribution of composite terrain radar clutter and the κ-distribution. IEEE Trans. Antennas Propag. 1984, 32, 1049–1062. [Google Scholar]
- Frery, A.C.; Muller, H.J.; Yanasse, C.C.F.; Sant’Anna, S.J.S. A model for extremely heterogeneous clutter. IEEE Trans. Geosci. Remote Sens. 1997, 35, 648–659. [Google Scholar] [CrossRef]
- Moser, G.; Zerubia, J.; Serpico, S.B. SAR amplitude probability density function estimation based on a generalized Gaussian model. IEEE Trans. Image Process. 2006, 15, 1429–1442. [Google Scholar] [CrossRef] [PubMed]
- Touzi, R. A review of speckle filtering in the context of estimation theory. IEEE Trans. Geosci. Remote Sens. 2002, 40, 2392–2404. [Google Scholar] [CrossRef]
- Mascarenhas, N.D.A. An overview of speckle noise filtering in SAR images. In Proceedings of the First Latino-American Seminar on Radar Remote Sensing—Image Processing Techniques, Buenos Aires, Argentina, 2–4 December 1996; Volume 407, p. 71.
- Wilcox, R.R. Introduction to Robust Estimation and Hypothesis Testing, 3rd ed.; Elsevier Science: Burlington, MA, USA, 2011. [Google Scholar]
- Hubert, M.; Vandervieren, E. An adjusted boxplot for skewed distributions. Computat. Stat. Data Anal. 2008, 52, 5186–5201. [Google Scholar] [CrossRef]
- Brys, G.; Hubert, M.; Struyf, A. A robust measure of skewness. J. Comput. Graph. Stat. 2004, 13, 996–1018. [Google Scholar] [CrossRef]


| Rayleigh | Gamma | Nakagami | Lognormal | Inverse Gaussian | Exponential | |
|---|---|---|---|---|---|---|
| Sample 1 | ||||||
| Sample 2 |
| Rayleigh | Gamma | Nakagami | Lognormal | Inverse Gaussian | Exponential | |
|---|---|---|---|---|---|---|
| Sample 1 | ||||||
| Sample 2 |
© 2017 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lin, K.-F.; Perissin, D. Identification of Statistically Homogeneous Pixels Based on One-Sample Test. Remote Sens. 2017, 9, 37. https://doi.org/10.3390/rs9010037
Lin K-F, Perissin D. Identification of Statistically Homogeneous Pixels Based on One-Sample Test. Remote Sensing. 2017; 9(1):37. https://doi.org/10.3390/rs9010037
Chicago/Turabian StyleLin, Keng-Fan, and Daniele Perissin. 2017. "Identification of Statistically Homogeneous Pixels Based on One-Sample Test" Remote Sensing 9, no. 1: 37. https://doi.org/10.3390/rs9010037
APA StyleLin, K.-F., & Perissin, D. (2017). Identification of Statistically Homogeneous Pixels Based on One-Sample Test. Remote Sensing, 9(1), 37. https://doi.org/10.3390/rs9010037