Abstract
Differential Interferometric SAR (DInSAR) time-series techniques can be used to derive surface displacement rates with accuracies of 1 mm/year, by measuring the one-dimensional distance change between a satellite and the surface over time. However, the slanted direction of the measurements complicates interpretation of the signal, especially in regions that are subject to multiple deformation processes. The Simultaneous and Integrated Strain Tensor Estimation from Geodetic and Satellite Deformation Measurements (SISTEM) algorithm enables decomposition into a three-dimensional velocity field through joint inversion with GNSS measurements, but has never been applied to interseismic deformation where strain rates are low. Here, we apply SISTEM for the first time to detect tectonic deformation on the Hyblean Foreland Plateau in South-East Sicily. In order to increase the signal-to-noise ratio of the DInSAR data beforehand, we reduce atmospheric InSAR noise using a weather model and combine it with a multi-directional spatial filtering technique. The resultant three-dimensional velocity field allows identification of anthropogenic, as well as tectonic deformation, with sub-centimeter accuracies in areas of sufficient GPS coverage. Our enhanced method allows for a more detailed view of ongoing deformation processes as compared to the single use of either GNSS or DInSAR only and thus is suited to improve assessments of regional seismic hazard.
Keywords:
DInSAR time-series; StaMPS; TRAIN; SISTEM; tropospheric correction; GPS; joint inversion; neotectonics 1. Introduction
The use of space-borne Synthetic Aperture Radar (SAR) imagery has had considerable success during the last two decades for the monitoring of the seismic cycle [1,2]. Due to the coherent measurement principle of a SAR system, the interference of the signal of two SAR images (i.e., Interferometric SAR-InSAR) can be calculated. Using a reference of the a priori distance between the satellite and the sensed object in form of a Digital Elevation Model (DEM), the differential phase of 2 images, acquired at different dates, can be exploited (i.e., Differential InSAR-DInSAR). This results in measurements of change in distance between the antenna and the ground in the 1-dimensional line-of-sight (LOS) direction of the radar aperture, with centimeter accuracies for the time span of the 2 acquisitions [3].
More recent developments of time-series DInSAR methods exploit the temporal evolution of the phase signal in time by using a stack of multiple SAR images, whereby the respective accuracies increase significantly. Advanced techniques referred to as Persistent Scatterers (PS) [4,5,6] and Small BASeline (SBAS) [7,8,9] have already demonstrated their potential in assessing ground surface motion for active tectonic zones such as plate boundaries (e.g., [10,11]), volcanoes (e.g., [12,13,14]), landslides (e.g., [15]) as well as urban areas (e.g., [16,17,18,19,20,21]), where local deformation rates exceed the expected error and enough pixels per area contain a relatively stable phase in time (i.e., coherent areas). Instead, the application of time-series DInSAR techniques for the detection of local seismicity at secondary faults of wider plate boundary areas is more challenging, since respective ground displacements are usually less than 1 cm/year. Under ideal circumstances, accuracies of 1 mm/year and less are reported for LOS measurements using time-series DInSAR methods [19,21,22]. This, however, is often not the case.
Furthermore, detected ground displacements in LOS are directional ambiguous and can originate both from horizontal as well as vertical deformations, which, in turn, may be results of different processes taking place. This hampers the 3-dimensional characterization of tectonic processes and may mislead their differentiation from other drivers of surface deformation such as anthropogenic induced subsidence due to construction, mining or water pumping.
In order to enhance robustness and enable the use in operational scenarios of (seismic) hazard assessments, two challenges need to be overcome: (1) to account properly for atmospheric noise due to changes in the atmospheric state between two or more SAR acquisitions and (2) to resolve the ambiguity of the measurements with respect to the direction of the ground movement due to the 1-dimensionality of the LOS measurement.
In this paper, we present a combination of recent advances in order to address both challenges over the area of the Hyblean plateau in south-east Sicily, Italy. This region experienced the largest earthquake (Mw 7.4) that struck Italy during historical times. The mainshock on the 11th of January 1693 was accompanied by a large tsunami wave affecting the eastern Sicilian coast [23]. As the north-easternmost part of the Pelagian block the area is located in the Eurasian-Nubian convergence zone along the Maghrebian belt and is characterized by complex geodynamic processes. Additionally, karst processing on the carbonatic massif [24] and water pumping for agricultural and industrial water supply may deform the surface locally [25]. While local studies of time-series DInSAR already showed anthropogenic induced subsidence along the coast [25], there have not been any analyses by means of combined usage of Global Positioning System (GPS) and time-series DInSAR over the whole region so far.
1.1. Techniques of Atmospheric Correction
Atmospheric noise forms one of the largest challenges faced by the InSAR community as it typically masks smaller magnitude signals [2,3,26,27,28]. The atmospheric noise is split in an ionospheric and tropospheric component. Free electrons in the ionosphere lead to partial dispersion of the electro-magnetic wave, which generates an apparent noise signal within an interferogram. This influence is however frequency-dependent and becomes more prominent in the longer wavelength spectra of L- and P-Band. For our study, which deals with standard image mode C-band imagery from the ENVISAT Advanced SAR (ASAR) instrument, the effect is expected to be small and we neglect it. It should be noted, however, that for recently launched C-band sensors covering a wider area (e.g., Sentinel-1), those effects are more significant.
Tropospheric path delays, instead, are caused by differences in temperature, atmospheric pressure, and foremost the water vapor (i.e., relative humidity). Those differences introduce a noise signal on various spatial scales [29] and can exhibit up to a 14 cm error in a single interferogram [3]. As tropospheric delays are integrated along the radar traveled path, the introduced noise can exhibit a strong topography-correlated component as well. Different methods exist that either estimate the tropospheric correction based on the interferometric phase or by using auxiliary data.
Traditionally, phase-based corrections are used by applying a spatiotemporal filter on DInSAR stacks. This approach aims to reduce the spatially-correlated atmospheric noise, assuming that the atmosphere behaves randomly in time while being correlated in space [6,9,14]. Other attempts estimate linear and power-law relationships between the interferometric phase and the topography, with the aim to reduce the topography-correlated as well as the long-wavelength tropospheric noise [29,30]. For all of those methods the challenge lies in avoiding leakage of the deformation signal in the atmospheric correction. Alternative approaches based on auxiliary data include corrections estimated from GPS data [31,32], spectrometer measurements [33], meteorological model data [27,34,35] as well as combined approaches [36,37,38]. While each of these techniques is capable of reducing the tropospheric InSAR noise, the success rate is often limited by the lower spatial resolution or availability of the auxiliary data [29].
Here we utilize the Toolbox for Reducing Atmospheric InSAR Noise (TRAIN, www.davidbekaert.com), which includes all the current state of the art methods [39]. For our study we chose a correction technique based on the 75 km resolution ERA-INTERIM weather model data from the European Center for Meteorological Weather Forecast (ECMWF) [40]. Due to the coarse resolution, weather models often fail to correctly represent the turbulent atmosphere, but they do reduce the topography-correlated and long-wavelength signal on average [39,41,42]. Therefore, diurnal, semi-diurnal as well as seasonal signals can be reduced within single interferograms. Furthermore, the approach holds the advantage of being non-parametric and thus can be applied fully automatic. Since the dataset provides global atmospheric reanalysis from 1979 onwards, it is universally applicable to all past, present and future InSAR data, hence providing improved estimates of the LOS measurements.
1.2. Techniques for Decomposing the DInSAR Signal into a 3-Dimensional Velocity Field
Regional seismic hazard assessments greatly benefit from a decomposed (i.e., 3-dimensional) velocity field as provided by geodetic GPS measurements due to the directional unambiguity in the assessment of ground motion. In addition, it becomes easier to distinguish tectonic processes from other causes of surface deformations. While DInSAR provides a much higher spatial resolution as a GPS network, it is limited to the 1-dimensionality of the LOS measurement, being a superposition from horizontal and vertical displacements.
Decomposing multiple tracks of DInSAR observations is not trivial and has been subject to recent research activities [43]. Once deformation rates are decomposed in the horizontal and vertical directions, parameters like slip rate, dilatation or strain can be estimated more precisely. Those parameters, in turn, are of importance for defining the boundary conditions of the respective faults within seismic hazard models [44].
In general, a first aspect takes into consideration the different viewing geometries of the descending and ascending orbits, which allows for untangling the horizontal from the vertical motion. However, due to the orbital configuration of space-borne SAR systems, the signal remains almost insensitive to north-south directional movements. By neglecting north-south displacements, it becomes mathematically feasible to disentangle the east-west and up-down directions from DInSAR data alone [45].
Pixel offset tracking [46] and Multiple-Aperture Interferometry (MAI) [47,48] are alternative SAR based techniques that allow for displacement mapping along the azimuth direction of the satellite flight path and exhibit more sensitivity to north-south displacements (e.g., [49,50,51]). Accuracies are however on the order of a few centimeters, which in most cases exceed the actual deformation rate of interseismic motion.
The integration of evenly distributed GPS stations together with DInSAR datasets is considered the only appropriate method to obtain a spatially dense, 3-dimensional velocity field with sub-centimeter accuracies [43]. While GPS measurements usually provide precise measures with millimeter accuracies in all 3 directions of the velocity field, the distance between the GPS stations is often too large to capture local variations in the tectonic signal. The complementary use of both methods allows combining the 3-dimensional information of the GPS data with the dense spatial sampling of the DInSAR and thus to overcome the limitations of both techniques.
While various methods have been proposed to integrate the two different observations, there is no consensus yet on an ideal strategy [52]. The main issue relates to the question of how surrounding GPS measurements are used to disentangle the LOS displacements for pixels that do not overlap with the GPS stations. First attempts were based on an a priori interpolation of the GPS velocity field. Its consequent integration with the DInSAR datasets from ascending and descending orbits is based on either a Bayesian statistical approach in combination with a Markov random field [53] or an analytical optimization [11]. Both approaches have in common that the optimization procedures used are not based on the physics of the deformation. Additionally, both rely on the result of the a priori interpolation usually done by means of the kriging technique for each component. This technique, in turn, requires an appropriate choice of a theoretical semivariogram model for each component which depicts one of the main critics in geostatistics [54]. A slightly different method has been proposed by Catalão et al., 2011, which uses the horizontal displacements derived from interpolated GPS measurements to subsequently calculate the vertical displacements from the time-series DInSAR in ascending and descending orbits separately. The latter are then adjusted to the vertical GPS velocities by minimizing the bias between both observations and an improved estimate of the vertical velocity field is obtained [55].
Wang & Wright [56] adapted a method that was previously developed for GPS measurements solely [57]. The original method is based on a triangulation network, whereas a constant linear motion gradient in space is assumed. The data integration is based on the interpolation of the GPS and DInSAR data by using a biconjugate gradients method. Additionally, long-wavelength orbital and topographical correlated atmospheric noise is attributed and a Laplacian smoothing operator is incorporated to remove short-wavelength features of non-tectonic motion. While the method shows great potential for large-scale applications with regard to tectonic motion only, the velocity field model is calculated for the vertices of the triangles. Thus, the resolution of the original InSAR data is reduced to the distance of the vertices and small-scale phenomena in fragmented areas like the Hyblean foreland might be smoothed out.
For our study we have tested the Simultaneous and Integrated Strain Tensor Estimation from Geodetic and Satellite Deformation Measurements (SISTEM) approach [58], which is capable of simultaneously integrating various geodetic measurements to disentangle the 1-dimensional LOS displacements estimates and derive a spatially dense, 3-dimensional velocity field. With respect to the other techniques it features the advantage that it operates on the full resolution of the DInSAR data while no preliminary interpolation of the GPS data is necessary. Furthermore, it follows the physically based concept of the elastic theory, which is commonly applied for interseismic strain accumulation [59] as well as aquifer compression where intergranular pressure is increased due to water pumping [60]. As demonstrated by Guglielmino et al. [61] the integration of additional geodetic measurements such as leveling and DInSAR time-series from different sensors is straightforward. Hence, one can take full advantage of available data sources over a certain area of interest. SISTEM has already been applied successfully to volcanic [58] as well as for coseismic events [61,62], but has not before been applied to the derivation of small deformation rates associated with interseismic strain accumulation. This study aims to demonstrate its usefulness also for such types of deformation by concurrently providing information on other types of displacements such as anthropogenic induced subsidence.
It has been shown that under the assumption of infinitesimal and homogeneous strain, geodetic benchmark measurements can be used to derive the full strain field adopting a linear approach [63,64]. Under this assumption the 3-dimensional displacement components of an arbitrary point P with the position can be estimated by using N surrounding displacements measurements of the experimental points () with the positions in the form of N equations:
where describes the distance between the nth and P, while represents the elements of the displacement gradient tensor which can be broken down into the symmetric (i.e., the strain tensor E) and asymmetric part (i.e., the rigid body rotation tensor Ω) in the form of .
For every arbitrary point, equations of type (1) can be transformed into the form of a linear matrix equation and subsequently solved by the weighted least-square (WLS) approach. A represents the design matrix, l refers to the column vector of unknown parameters consisting of the 3D displacements and the elements of the strain tensor as well as the rigid body rotation tensor and u is the column observation vector with the displacement measurements of the N geodetic benchmarks. The term e is the residual vector that contains the standard errors of the solution due to the stochastic nature of the estimation problem.
It should be noted that the inverse of the covariance matrix C for the WLS solution is modified by introducing a weighting factor as described by Shen et al. [64] in the form of:
where represents the distance between the nth and the arbitrary Point P. In this way, the nearby s have a higher influence on the estimation of P.
Instead of the weighted interpolation between the geodetic benchmarks, SISTEM integrates the DInSAR measurements into the framework of the linear matrix equations by relating a number K of DInSAR datasets to the components of the displacements vector of an arbitrary point P as follows:
where is the Sth known LOS displacement of the point P and is the unit vector pointing from point P towards the Sth satellite acquisition. Consequently, the final design matrix A is constructed by rows and has the following form:
It can be noted that the first rows refer to the N blocks of three equations containing the positional information of the 3D geodetic measurements by GPS. The last K rows, instead, correspond to the DInSAR data. Consequently, the observation vector u and the column vector of unknown parametersl are defined as follows:
where represents the components of the strain tensor E defined as:
and represents the components of the rigid body rotation tensor Ω defined as:
By combining SISTEM with the tropospheric corrected time-series DInSAR data, we demonstrate that sub-centimeter measurements of the 3-dimensional velocity field are feasible on a routine basis if sufficient spatial coverage of the geodetic input data is given. Such information can then be used to identify previously unknown surface deformation as well as characterizing and constraining seismic source parameters for respective hazard assessments in the presence of tectonic activity.
2. Method and Data Collection
2.1. Study Area
The Hyblean plateau is located in the south-east of the Italian island of Sicily, in the center of the Mediterranean Sea (Figure 1). The region features a complex tectonic setting of the Eurasia-Nubian convergence zone along the Maghrebian Belt. A manifold geodynamic evolution and a set of different crustal blocks trapped between the Eurasian and African rigid plates, led to a fragmented and irregularly shaped convergence zone of the African and European plate [65,66]. According to Ben Avraham & Grasso 1991 [67], the plateau is considered as a block of the African foreland that resists the underthrusting beneath the Maghrebian belt due to its high buoyancy. In turn, this formed the arc-shaped deflection of the Maghrebian belt along the northern edge of the Hyblean foreland.
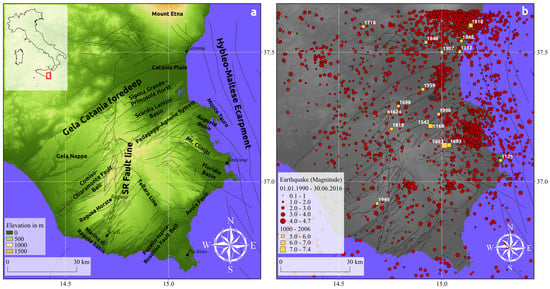
Figure 1.
Location of the study area: (a) Topographic map of the study area with its toponomy (SR-Fault: Scicli-Ragusa fault); (b) Recent and historical earthquakes over the study area [68,69].
On the eastern side, this block is bounded by the Hyblean-Maltese escarpment, a normal NNW-SSE trending and ENE dipping fault system that decouples the thick inland continental crust from the Ionian Mesozoic oceanic crust underthrusting the Calabrian arc [23]. The Ionian margin is thereby characterized by a typical horst and graben sequence, oblique with respect to the Hybleo-Maltese escarpment.
Downbending of the foreland takes place along the Gela-Catania foredeep. NE-SW trending normal faults characterize the area and form wide structures along the Scordia-Lentini graben. On the western side, the Scicli-Ragusa fault extends from the Scordia-Lentini basin in the north towards the Marina di Ragusa graben in the south and divides the foreland into two crustal blocks. The NE-SW normal faults controlling the Scordia-Lentini and the Marina di Ragusa extensional basins as well as the fault segments of the Scicli line have been partially reactivated by both reverse and left-lateral motions, respectively [70,71,72].
Historically, major destructive earthquakes hit the region in 1196, 1542 and 1693, though their location is still debated [23,73,74]. The last major earthquake (M = 5.4) occurred on 13 December 1990 located at the offshore part of the Lentini Graben [75,76]. The understanding of the neotectonics is of major interest for assessments regarding the regional seismic hazard. According to the national hazard maps it belongs to one of Italy’s most endangered regions with a 10% probability of exceeding a peak ground acceleration of more than 0.25 g within the next 50 years [77]. As shown in Figure 1b, there have been more than 450 small to medium strong earthquakes (M > 1) throughout the last 2 decades [66,78]. Despite numerous research activities it is still debated how the internal deformation of Sicily is accommodated by the faults and the number of faults that may take up this deformation [71].
2.2. Data Collection & Processing
2.2.1. DInSAR Processing
The multi-temporal DInSAR analysis has been performed using 49 ascending and 58 descending Envisat ASAR images that cover the time period from 2003 until 2010 (Figure 2). The SAR imagery has been focused using the ROI_PAC processor version 3.01 [79]. Subsequently, the interferograms were generated with the DORIS software [80]. We used the 30 m SRTM data for the topographic phase removal [81]. For the time-series processing the StaMPS Small Baseline (SB) approach was applied [7,82]. Due to the specific selection process of stable targets, this approach favors the detection of distributed scatterers which occur usually in rural regions. Furthermore, we could validate the phase unwrapping procedure by comparing the residuals of the phase between the SB interferograms and the modeled inversion for the single-master interferogram with the closed-loop test [7,8]. Noisy interferograms with spatially correlated phase unwrapping errors have been subsequently sorted out and the mean LOS velocities have been recalculated. In total we obtained a network of 119 interferograms for the descending and 148 interferograms for the ascending track. We then decreased further noise by resampling the pixel size to 300 m. The contribution related to associated DEM errors has been removed as part of the StaMPS time-series inversion. We corrected for the Envisat oscillator drift as described by Marinkovic & Larsen 2013 [83]. We further accounted for the long-wavelength orbit errors in our decomposition by using the GPS as constrain.
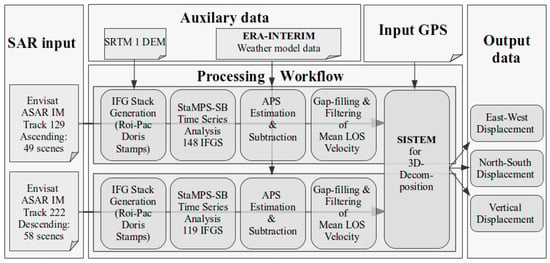
Figure 2.
Data collection, processing and integration workflow.
2.2.2. Tropospheric Correction
We corrected for tropospheric delays in the single interferograms by using ERA-INTERIM (75 km resolution) weather model data from the European Centre for Meteorological Weather Forecast (ECWMF) [40], which provides daily estimates of pressure, temperature and relative humidity at 0:00 h, 6:00 h, 12:00 h and 18:00 h UTC. These model outputs are used to estimate the tropospheric delay in the radar LOS for each interferogram. We used the routines available in the Toolbox for Reducing Atmospheric InSAR Noise (TRAIN) [84] described in Bekaert et al. 2015 [39]. The procedure performs a horizontal and vertical spline interpolation for the pressure, temperature and relative humidity. The slant tropospheric delay is then calculated by integrating the refractivity from the surface upwards, projected into the radar LOS. A linear interpolation is done in the temporal domain to match the SAR acquisition time of 22:00 h UTC for the ascending pass and 10:00 h UTC for the descending pass.
2.2.3. Spatial Enhancement
The coverage of the DInSAR datasets depends on the phase stability of every pixel. Since SISTEM only considers valid DInSAR pixels and does not interpolate per se over areas without information, a combined gap-filling and subsequent filtering procedure has been applied to enhance the spatial coverage of the DInSAR data prior to the data integration. This approach has been originally used to improve interferometric elevation data from the SRTM mission for land surface process applications [85]. The underlying problem is somewhat similar, since small-sized no-data areas are filled and residual artifacts from phase noise are removed by simultaneously preserving actual features like edges and ditches.
In our case, we assumed that for nearby areas the expected deformation signals are spatially correlated. As a first step, the gap-filling, which is based on a spline interpolation, has been applied for areas with less or equal than 100 pixels. In order to remove local artifacts that feature sort of a “salt and pepper” noise, we subsequently applied the multi-directional Lee filter [86]. The filter operates in the direction of the minimal variance across 16 directions within a windows size of 9 by 9 pixels. The actual distance of the filter operation is weighted by a parameter that takes the local noise into account.
2.2.4. GPS Data
GPS based ground deformation measurements over the Hyblean plateau have been routinely carried out since 1991 as a consequence of the M = 5.4 Augusta earthquake. The data used in this work has been collected during different geodetic surveys between 1993 and 2006 [70,87] as well as from continuously running GPS stations lying on the Hyblean plateau (Figure 3). We used the final precise velocities of 24 selected stations matching the DInSAR coverage. The velocities have been calculated and reported in Angelica et al. 2013 [65] and Mastrolembo Ventura et al. [71].
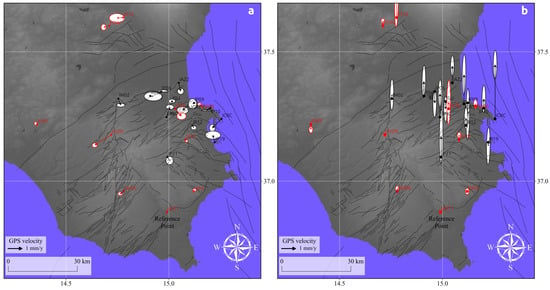
Figure 3.
GPS velocity field: Horizontal (a) and vertical (b) velocities with respect to the NOTO reference station (NOTO). Black stations have been installed between 1993 and 1997, while red stations were installed after 2000. The velocity field was originally calculated by Angelica et al. 2013 [65]).
2.2.5. SISTEM Integration
SISTEM simultaneously decomposes the input measurements into a 3-dimensional field vector based on the elasticity theory. The original SISTEM approach, as described by Guglielmino et al. [58], considers only one DInSAR dataset that is combined with the GPS data. The simultaneous integration of GPS and DInSAR measurements into a linear matrix equation is then solved by the WLS method. However, SISTEM can be easily extended by other DInSAR datasets as well as other geodetic measurements. Since the algorithm calculates every pixel singularly, SISTEM is capable of adapting the DInSAR-GPS integration according to the number of available DInSAR measurements for a particular pixel. In our case, conditioned by the expected small displacement rates, preference was given to the highest possible constrain of the WLS solution considering only overlapping pixels of both DInSAR datasets used.
Another important factor is the weighting of the GPS measurements based on the distance-decay function with respect to the nearest stations, expressed as the level of locality. This level of locality drops after a certain distance threshold. Beyond this radius the DInSAR data becomes the dominant information source. The threshold can be set for every component of the 3-dimensional velocity vector separately. For this study, the thresholds have been set to 4, 2 and 1 km for the north-south, east-west and up-down component, respectively. The highest threshold for the north-south component has been chosen because it is theoretically not possible to derive this component from the DInSAR data due to the acquisition geometry. Information outside this radius, which is predominantly constrained by the DInSAR data, becomes therefore unreliable. The threshold of 2 km for the east-west component instead was chosen in order to pick up a higher degree of spatial variation by utilizing the DInSAR data. For the vertical component the lowest threshold was used for 2 reasons. Firstly, DInSAR is most sensitive to vertical displacements due to its steep look-angle (∼23 degree). Secondly, the GPS data exhibits the highest uncertainties in the vertical direction. This is especially true for the GPS stations that have been installed in the 1990’s for which the standard deviations within the vertical direction ranges from 1.2 to 3 mm/year so that the DInSAR measurements have been considered as equally accurate, if not better.
For the final computation the structure of the covariance matrix has to be modified by adding the variances of the observations. Instead of estimating them on the DInSAR and GPS measurements itself, fixed values have been used for computational effectiveness. In order to account for the spatially correlated noise, a fixed variance of 7 mm/year has been used for the DInSAR data, while for the horizontal and vertical GPS measurements the variances were set to 3 mm/year and 1 cm/year, respectively. This, however, entails biases in the estimations of the standard error of the solution. While areas of higher standard errors indicate either non-elastic displacements or poor input data quality, they are not suited to determine the actual accuracy of the output data due to the arbitrarily chosen variances. In order to evaluate the overall performance of the data integration, the 3-dimensional velocity field was therefore used to recalculate the LOS velocities. The resultant residuals with respect to the input LOS measurements give a proper indication of the actual accuracy.
3. Results & Discussion
3.1. Tropospheric Correction
In order to validate the expected improvements of the mean LOS velocities after the tropospheric correction, two measures have been carried out. First, we compared the GPS velocities projected to the LOS of both tracks with our DInSAR results. We find a reduction of the Root Mean Square Error (RMSE) that amounts to about 15% for both tracks (Table 1). The high RMSE of 2.8 mm/year is conditioned by stations with older GPS instrumentation and larger uncertainties foremost in the vertical direction. By excluding these stations, the RMSE drops to 1.4 mm/year for the descending, and 1.5 mm/year for the ascending track, whereas the absolute residuals range from 0.1 mm/year up to 1.5 mm/year. Additional confirmation comes from the assessment of the variability of the mean LOS measurements within each single interferograms by calculating the RMSE. A reduction in RMSE of the tropospherically-corrected interferogram with respect to the uncorrected one indicates a general smoothing of the data, which would be expected due to the partial elimination of the tropospheric noise. Indeed, a reduction of about 10% could be achieved for the interferograms of both tracks on average (Table 1), indicating a decrease of long-wavelength tropospheric noise. These improvements are on the order of what was observed for a similar study over Eastern Turkey [41].

Table 1.
Accuracy of DInSAR results before and after tropospherical correction. RMSE of GPS velocities projected into the LOS against the DInSAR results is given (middle column) as well as the mean RMSE for all interferograms used in the LOS velocity inversion (right column).
The generally smoother deformation field of the tropospherically corrected mean LOS velocities is also visible in the LOS displacement maps (Figure 4b,f). The eastern part of the Plateau, in particular, shows a decrease in variability, which further indicates the improvement.
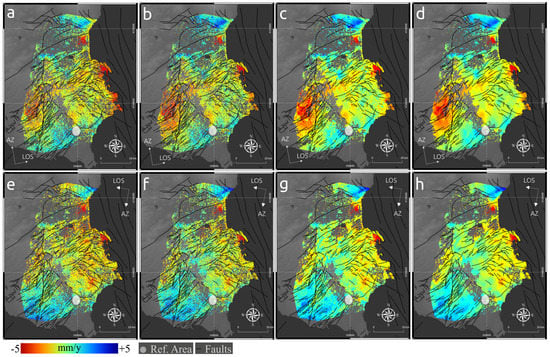
Figure 4.
(a–h) Mean LOS velocities (upper row: ascending track; lower row: descending track): (a,e) corrected for orbital and DEM error; (b,f) tropospheric corrected datasets; (c,g) gap-filled dataset; (d,h) multi-directional Lee filtered dataset.
It is worth mentioning that we also tested high-resolution NWM data as proposed in Catalão et al., 2011, but similar to the results of Bekaert et al., 2015 over central Italy, the higher resolution did not improve our estimates.
3.2. Spatial Enhancement
In contrast to prior studies that applied SISTEM, we found that when observations are not present for both, ascending and descending data, artifacts appear within our inversion result. In order to avoid a significant drop in spatial coverage when limiting the observations to the mutual coverage of both tracks, we performed a preceding gap-filling procedure. Under the assumption that the detected displacements and the DInSAR signal are spatially correlated, the gap-filling procedure led to a significant increase in the number of overlapping pixels of the two datasets (Figure 4c,g). Since the study area is structurally fragmented, a spatial area threshold of 100 pixels (∼9 km) has been set as a maximum size for the gap closed areas.
However, isolated pixels within such enclosed areas often suffer from increased phase noise so that in some of the gap filled areas a “salt and pepper” noise becomes apparent due to the higher weight in the interpolation process of those pixels. In order to smooth those areas, the multi-directional Lee filter was applied subsequently (Figure 4d,h). Since it is an anisotropic filtering approach, gradients along faults have not been affected as it would be the case for standard mean filters. By integrating the combined application of the gap-filling and anisotropic filtering in our workflow, it became possible to exploit the spatial correlation of the DInSAR data and enhance the coverage for the subsequent SISTEM data integration without introducing further noise. Indeed, the difference of the RMSE between the GPS velocities projected in the LOS and the tropospherically-corrected DInSAR LOS before and after this procedure amounts to 0.02.
3.3. SISTEM Decomposition
By integrating the GPS velocities (Figure 3) with the corrected and spatially enhanced mean LOS velocities (Figure 4d,h) into the SISTEM framework, the complementary features of both measurements are utilized to retrieve three-dimensional displacement estimates in the north-south, east-west and up-down direction (Figure 5a–c). The corresponding standard errors from the WLS solution are also provided as well (Figure 5a’–c’). In addition, the absolute residuals with respect to the original GPS data have been computed (Figure 5). However, this information should not be regarded as an independent validation source since the GPS data were used as an input into the decomposition. It rather indicates how the GPS measurements are affected by the integration with the DInSAR dataset. The standard error, instead, is biased by the fixed covariance values used for the WLS solution. The estimates are therefore unreliable in absolute terms, but can indicate relative errors that are related either to data input issues, or the circumstance that the surface is not deforming in an elastic manner. In order to realistically access the overall performance of SISTEM in terms of numerical accuracy, the retrieved velocity field has been used to recalculate the LOS velocities of the two SAR tracks. The residuals between the predicted LOS velocities from the SISTEM estimates and the original LOS (Figure 6) reveal a mean value of −0.45 mm/year with a standard deviation of 1.12 mm/year for the ascending, and a mean value of 0.76 mm/year with a standard deviation of 1.67 mm/year for the descending track. This result, in addition to the aforementioned deviations, ranging from 0.1 mm/year to 1.5 mm/year, between the GPS and the original LOS velocities into account, demonstrate the ability of this method to retrieve three-dimensional sub-centimeter surface deformation.
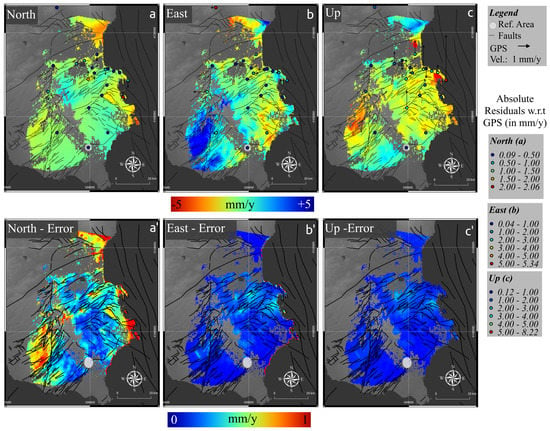
Figure 5.
Decomposed velocity field in reference to the Noto GPS station (a,a’) North-South component and WLS error; (b,b’) East-West component and WLS error; (c,c’) Up-Down component (from blue to red) and WLS errors. The corresponding GPS directional velocities have been plotted over the SISTEM output. The colour scale reflects the absolute residual of the GPS component with respect to the SISTEM solution.
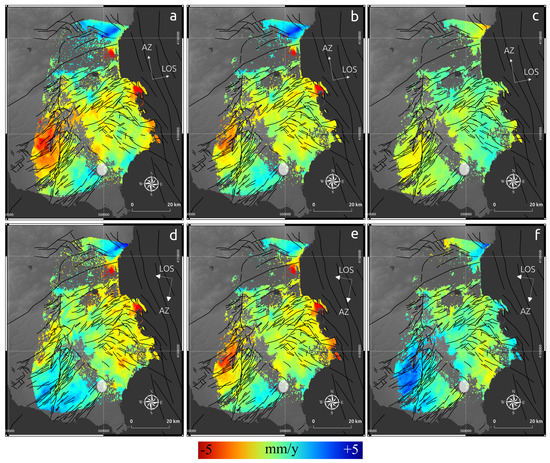
Figure 6.
(a–f) Recalculation of the mean LOS velocities from the SISTEM output; upper row ascending track; lower row: descending track. (a,d) original LOS mean velocities; (b,e) predicted LOS mean velocities from the 3-dimensional SISTEM components; (c,f) residuals of the predicted mean LOS velocities with respect to the original LOS velocities.
3.3.1. Vertical Component
As can be seen from the vertical displacement field (Figure 5c), the covered area is characterised by various zones of subsidence and uplift ranging from −10 to 5 mm/year. The comparison of the SISTEM output with the GPS data reveals the highest deviations of all three components. As mentioned earlier, older GPS stations suffer from poor vertical estimates as in the case of the ICRC station on the Monte Tauro Horst, northeast of the Augusta basin. Despite a significant uplift of about 6 mm/year indicated by the GPS velocity, the subsidence estimate of SISTEM in the neighbouring Augusta basin predominantly resembles the LOS displacements. Due to the high sensitivity of the DInSAR data with respect to the vertical component, and the lower weight given by the distance-decay function to the GPS station, SISTEM reinforces the respective estimation and reduces the magnitude of the standard error (Figure 5c’), as shown as well in the original approach [58]. Both tracks exhibit a LOS displacement of down to −10 mm/year for the Augusta basin, which translated into pure vertical movement, would result in about −11 mm/year for the acquisition geometry of ENVISAT Image mode. It is therefore underlined that despite the vicinity of a GPS station with contradictory vertical estimates, the SISTEM output is only marginally influenced by the GPS measurement, and thus improves the vertical displacement estimates using more accurate information provided by the mean LOS velocities of both DInSAR datasets. Indeed, this, and other areas affected by uplift and subsidence reveal low residuals of −1.5 to 1.5 mm/year when comparing the original LOS velocities to the predicted ones from the SISTEM decomposition (Figure 6). Nonetheless, GPS stations affected by low vertical accuracy have been kept for to their valuable, and more accurate horizontal components.
3.3.2. Horizontal Components
The retrieval of the north-south component (Figure 5a) as well as the east-west component (Figure 5b) is more critical since the DInSAR is less sensitive to this component. A good coverage of GPS stations is crucial for the retrieval of reliable estimates, especially for the north-south component, where the DInSAR cannot contribute sensible information for sub-centimeter surface displacements. Nonetheless, different zones of sub-centimeter deformation are revealed, but the decrease of accuracy is clearly linked to the vicinity of available GPS measurements by which the joint inversion is constrained.
In general, the north-south component shows a much smoother velocity field than for the other components (Figure 5a). This is because the DInSAR estimates cannot significantly contribute additional information so that the influence of the GPS predominates the most. This is reflected in the deviations between the input GPS and the SISTEM velocity field, which are the smallest in this directional component, with less than 0.5 mm/year for almost all GPS stations. In areas of LOS displacements with no GPS stations, the WLS solution cannot be sufficiently constrained, which becomes visible in the standard error estimates of the WLS solution, with significantly higher values (Figure 5a’). For those areas the distance-decay function weakens the influence of the distant GPS stations that are used for the decomposition. Their estimates, however, do have an influence on the decomposition and might contradict the actual DInSAR data by being part of another kinematic regime. This is especially visible along the coastal part of the Siracusa bay and the horst structure in the hinterland of Ragusa. Since north-south directed motions cannot be captured from the DInSAR datasets alone, the solution fails to disentangle the DInSAR data in the proper way.
The most obvious case is the southern part of the Scicli-Ragusa fault belt, where GPS stations are absent on the western part of the fault line. As a left-lateral strike-slip fault, the expected main direction of horizontal deformation should be in the north-south direction. The nearest GPS station HMDC, which is located about 4 km east of the fault, shows a 0.4 mm/year westwards and a 0.2 mm/year southwards movement with respect to the Noto reference station. The influence of the GPS measurement is therefore lower on the western side than the contradictory DInSAR estimates. In addition, the information west of the fault is weighted more strongly from the DInSAR in the east-west direction due to the lower distance thresholds for the distance-decay function. As a result, the motion could not be well constrained by the DInSAR data, which is not sensitive to the north-south direction and causes large standard errors of the WLS solution. This partly explains the predominant eastwards motion that does not match the expected north-south direction. Also the high values are most likely unrealistic. Indeed, the area features the highest residuals of up to 5 mm/year between the predicted LOS velocities from the SISTEM decomposition compared to the original ones used as input (Figure 6). It cannot be fully excluded that a part of the signal might be influenced by residual atmospheric noise that can be correlated to orographic effects by the local topography. On the other hand, the clear alignment along the fault and the expected active tectonics in this part of the study area allow us to speculate that the method may pick up the respective tectonics in an unprecedented spatial detail, but fails to estimate the right direction and velocity.
The same rationale applies to the Avola fault and its secondary structures in the south-east of the study area. A westward movement of about 2–4 mm/year has been detected which is bounded along the fault. Due to the absence of GPS measurements on the eastern side of the fault, the quantitative and directional displacements might not reflect the actual deformation, but the fault location is obtained in an unprecedented spatial detail.
The distinctive gradient of southwards motion along the Catania-Gela foredeep south of Mount Etna highlights the importance of the presence of GPS measurements in the vicinity for the retrieval of the north-south component. By excluding the IAZZ station south of Catania, which exhibits a southwards directed motion of about −1 mm/year with respect to the NOTO reference station, the spatial pattern of local shortening disappears within the SISTEM result. Other studies, however, have already described this shortening using additional campaign GPS data for this particular zone [88]. Even though the predicted LOS from this station deviates by 2.6 mm/year for the ascending and 2.9 mm/year for the descending track, the information was crucial to derive a realistic velocity field for this part of the study area.
3.4. The Velocity Field in Its Geological Context
Although outside of the main scope of this study, this section seeks to put the obtained velocity field in a geological context and underline the significance of the obtained results. Most recently, structural, seismological, geodetic as well as combined studies strengthen the idea that the Hyblean plateau acts as an independent crustal unit with respect to the kinematic behaviour of the Nubian plate [70,71,88]. The boundaries are located along the Gela-Catania foredeep, the rift zone along the Malta Escarpment and the Scicli-Ragusa line. The retrieved deformation field depicts displacements on all three parts of the plateau as well as various local zones of vertical motions that will be discussed below.
3.4.1. Northern Rim of the Hyblean Plateau
The northern rim of the Hyblean plateau resides in a triangle zone between the collisional belt along the Gela-Catania foredeep, and a N-S oriented rift zone towards the east along the Malta Escarpment (Figure 1). While this area was part of an extensional basin until the Lower-Middle Pleistocene, tectonic inversion set in about 0.85 my ago. This process has been indicated by structural analysis of outcrops within the Scordia-Lentini basin [89]. The area of maximum compression in the SISTEM result is located further north with values of −2.4 mm/year along the Gela-Catania foredeep, while only minor velocity gradients of about −1.1 mm/year are detectable over the horst structures bounding the Scordia-Lentini graben (Figure 5a). This fits with prior geodetic studies based on GPS data solely, that could not detect significant GPS strain over the Scordia-Lentini graben [71]. The authors of this study, however, indicate that during tectonic inversion, faults are reactivated selectively, and argue that active faulting has been displaced northwards. Structural analyses confirm this assumption and locate current associated processes within the Catania plain and its northwards bounding structures [90]. In the Catania plain the SISTEM results are in line with prior GPS based geodetic measurements that report shortening rates of circa 2.4 mm/year [71]. More elevated southwards displacements up to −3.4 mm/year are visible farther north towards the foothills of Mount Etna. This is assumed to be associated with the outward thrusting that originates from the basal decollement of Mount Etna, already reported by past DInSAR studies [91,92,93], and coincides with an anticline visible in the vertical component (Figure 5c).
3.4.2. Scicli-Ragusa Fault Belt
The Scicli-Ragusa fault belt extends from the western side of the horst structures at the northern rim of the plateau, southwards to the coast and continues off-shore up to the Pantelleria-Linosa-Malta rift zone [94]. It is considered to play a key role for the understanding of the kinematics of the central Mediterranean as it divides the eastern part of the plateau from the western part. Indeed, geodetic measurements indicate that the area west of the fault moves in agreement with the entire western Sicilian domain. Consequently, a sinistral strike-slip is present and according to Musumeci et al., 2014 [88] amounts to circa 1.2–1.5 mm/year for the northern part of the fault belt, while the southern branch exhibits lower values around 0.5 mm/year. The SISTEM estimates presented in the previous section are dominated by a strong eastwards motion over the horst around the city of Ragusa, which does not match any other geodetic observations or kinematic models that have been published so far. However, the north-south velocity field, despite being associated with large errors, matches the observations from Musumeci et al., 2014 [88] (Figure 7a). Moreover, the Comiso-Chiaramonte fault belt seems to be associated with accommodated tectonic stress. From this consideration it could be speculated that not the entire Scicli-Ragusa fault belt acts as a transfer zone and that part of the collisional force driven by the Nubian-Eurasian convergence superimposes the local geodynamics. The eastwards driven motion of the SISTEM result could then be partly explained by the NW-SE extension of the Pantelleria-Linosa-Malta rift zone, which according to Serpelloni et al., 2007 [95] amounts to about 1.5 mm/year. Low seismic activity and the absence of GPS measurements in this zone do not allow for an in-depth interpretation. Furthermore, the extension of the observed deformation towards the western side needs to be revealed by additional A-DInSAR data.
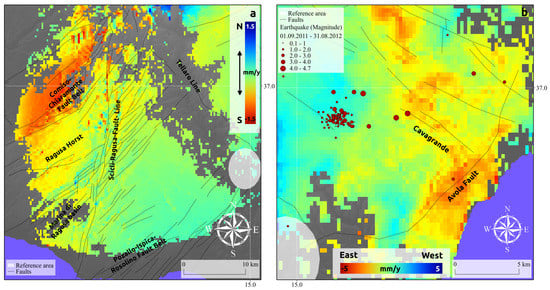
Figure 7.
Zoom-in on the (a) north-south velocity field along the Scicli-Ragusa fault; and (b) the east-west velocity field of the area around the Avola fault with the overlay of the earthquakes associated with 2011/2012 seismic swarm event [69].
3.4.3. Ionian Boundary of the Hyblean Plateau
The eastern part of the Hyblean plateau is influenced by a seismogenic rift zone, which extends NNW-SSE oriented along the entire Ionian coast. Active extension takes place off-shore further to the north with a rate of about 3.4 mm/year [96]. Towards the south, part of this rift zone swings into a SE-NW oriented fault belt, consisting of the Avola fault and the Pozallo-Ispica-Rosolino fault belt, exhibiting extensional rates of about 1.5 mm/year estimated by structural analysis [96]. The SISTEM results do not reveal any of the E-W extensional character on the northern part of the Hyblean plateau, which indicates that most of the seismic potential originating from the rift zone is located off-shore. Farther towards the south, fault-aligned displacements are revealed by both horizontal components. The strongest displacement is notable along the Avola fault line. This is a SW-NE directed normal fault with an expressive scarp of about 290 m and is considered to have caused the foreshock (M = 6.2) of the M = 7.4 earthquake on the 11th of January in 1693 [97]. The horizontal velocities from SISTEM indicate a WNW directed displacement of up to 3 mm/year. This is somewhat contradictory to its extensional character and would indicate that it accommodates part of the main tectonic stress originating from the Nubia-Eurasian convergence, which, in turn, is underlined by a slight uplift of the coastal part up to 1 mm/year. Part of this WNW directed displacement continues along linear fault structures towards the centre of the plateau, which is indeed seismically active. Focal mechanisms of this area indicate strike-slip faulting within this direction [88], and a seismic swarm taking place between October 2011 and July 2012 represents the biggest strain release over the whole plateau over the last 10 years [98]. Interestingly, the horizontal velocity field given by SISTEM indicates local variation over the area of this seismic swarm that took place roughly 1 year after the last acquisition of the A-DInSAR time-series (Figure 7b). This provides further indication that the diffuse displacements captured by the SISTEM decomposition over this area are associated with active tectonic driven deformation.
3.4.4. The Presence of Subsidence
The interpretation of the tectonic deformation over the Hyblean plateau is hampered by various other displacements present in the dataset and partly overlaying the above mentioned tectonically driven processes (Figure 5c). Water pumping is a wide-spread practice in Sicily for agricultural and industrial water use. The extraction of ground water leads to a compression of the aquifer which, in turn, induces the subsidence of the surface. Canova et al., 2012 [25] detected areas of subsidence related to ground water exploitation within the Augusta bay and the area around Villasmundo, about 15 km west of Augusta. They used ERS time-series data for the period of the 1990s and decomposed the DInSAR signals of both tracks by neglecting the north-south directed motion. While the extent of the subsidence areas is comparable, their estimates are about twice as high as the ones retrieved by the SISTEM decomposition. The rates of subsidence depicted within our study exhibit up to −10 mm/year in the Augusta bay and range between −2 to −4 mm/year in the surroundings of the village of Villasmundo. While this might show the consolidation of the soil in time, it could be also related to differences of the DInSAR reference point, which is not indicated in the comparative study.
Another zone of subsidence resides in the south of Catania that has not been reported before. Due to the localised extension it is likely being caused by local water pumping. Values amount up to −8 mm/year, which can cause damages to local infrastructures and industrial buildings located within this zone. Other areas of subsidence are seen towards the Gela-Nappe along the Comiso-Chiaramonte fault belt in the west of the plateau and over the south-eastern part. However, the lack of more detailed information does not allow for a definite interpretation. While tectonic induced stress is speculated along the Comiso-Chiaramonte fault belt indicated by the horizontal velocity field, the revealed subsidence might be driven by the gravitational creeping of the alluvial soils in this zone. In the south-eastern part, the subsidence does also overlap with horizontal displacements, and thus might be partly caused by active tectonic deformation. On the other hand, this area has been reported to be affected by diffuse karst processes [24] that may lead to subsidence, too.
4. Conclusions
In this paper we describe a complete workflow for combining advanced time-series DInSAR with GPS data for the retrieval of a full 3-dimensional velocity field of the Hyblean plateau in south-east Sicily. Due to expected small deformations we applied a data-driven approach and corrected the tropospheric InSAR noise using auxiliary data rather than spatio-temporal filtering. We used the TRAIN toolbox, which is fully compatible with the StaMPS data structure, to estimate a tropospheric correction using the ERA-Interim weather model.
An additional post-processing procedure that enhanced the mean LOS velocities with a gap-filling and consequent multi-directional filtering technique was proposed and proved to be successful. The spatially-limited gap-filling resulted in an increase of coverage and of overlapping pixels which is favorable for further processing of multiple datasets. Due to the multi-directional filter, pixels with increased phase noise were filtered leading to a smoother deformation signal in space, while steep gradients along faults were not affected. Again, this is a straightforward approach that can be easily implemented in post-processing procedures.
For the first time, we applied the SISTEM approach for interseismic deformation retrieval. In accordance to prior studies, the approach seems to work well in areas where a sufficient density of accurate GPS data is available. Predicted LOS velocities from the SISTEM output show generally low residuals of about ±1.5 mm/year and less with respect to the original ones in areas of subsidence and uplift. Despite these errors, patterns of detailed horizontal displacements are revealed and are in line with prior studies for various zones of the plateau. Considerable improvements can be expected by incorporating data from the recently launched SAR satellites, such as Sentinel-1, which allow for much higher temporal sampling and offer a more favorable configuration for A-DInSAR time-series approaches. Together with additional GPS measurements, our approach should be capable of providing more reliable estimates of the actual velocity field and thus allow for an improved understanding of the ongoing kinematics as well as the regional seismic hazard. Given these preconditions, the procedure is transferable also to other tectonic zones. Especially along continental plate boundaries, where the tectonic stress is often distributed over a diffuse network of active faults, the preservation of the DInSAR resolution of our approach allows for the identification of fault locations.
Acknowledgments
This research was funded by the Ministry of Education, Universities and Research (MIUR), University of Pavia, Italy. The work was conducted at the INGV in Rome and Catania as well as the COMET School of Environment, Leeds. Part of this work was carried out at the Jet Propulsion Laboratory, California Institute of Technology, under a contract with the National Aeronautics and Space Administration. COMET is the NERC Centre for the Observation and Modelling of Earthquakes, Volcanoes and Tectonics. Fruitful discussions and valuable input was given by Carlo-Alberto Brunori (INGV Roma), Guido Ventura (INGV Roma), Fabiano Costantini (Univ. di Tor Vergata/ESA), Christian Bignami (INGV Roma), Pablo J. González (Univ. of Liverpool) and Karsten Spaans (COMET). Additionally the authors want to acknowledge the European Space Agency for the kind provision of ENVISAT data under the project ID 13948 and INGV, who provided the GPS time-series data.
Author Contributions
Andreas Vollrath, Salvatore Stramondo and Francesco Zucca led the study design and wrote the article. David Bekaert, formerly at COMET School of Environment, Leeds, now at JPL, California Institute of Technology and Andrew J. Hooper wrote the code for the orbital and atmospheric correction of the SBAS time-series analysis and provided substantial support for processing. Alessandro Bonforte processed and analysed the GPS velocities and gave substantial support for the geological interpretation. Francesco Guglielmino wrote the code of SISTEM, processed the SISTEM decomposition and gave substantial support for the geological interpretation.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Salvi, S.; Stramondo, S.; Funning, G.J.; Ferretti, A.; Sarti, F.; Mouratidis, A. The Sentinel-1 mission for the improvement of the scientific understanding and the operational monitoring of the seismic cycle. Remote Sens. Environ. 2012, 120, 164–174. [Google Scholar] [CrossRef]
- Hooper, A.; Bekaert, D.; Spaans, K.; Arikan, M. Recent advances in SAR interferometry time series analysis for measuring crustal deformation. Tectonophysics 2012, 514–517, 1–13. [Google Scholar] [CrossRef]
- Zebker, H.A.; Rosen, P.A.; Hensley, S. Atmospheric effects in interferometric synthetic aperture radar surface deformation and topographic maps. J. Geophys. Res. 1997, 102, 7547–7563. [Google Scholar] [CrossRef]
- Kampes, B.M. Radar Interferometry: Persistent Scatterer Technique; Springer: Heidelberg, Germany, 2006. [Google Scholar]
- Hooper, A.; Zebker, H.A.; Segall, P.; Kampes, B. A new method for measuring deformation on volcanoes and other natural terrains using InSAR persistent scatterers. Geophys. Res. Lett. 2004, 31, 1–5. [Google Scholar] [CrossRef]
- Ferretti, A.; Prati, C.; Rocca, F. Nonlinear subsidence rate estimation using permanent scatterers in differential SAR interferometry. IEEE Trans. Geosci. Remote Sens. 2000, 38, 2202–2212. [Google Scholar] [CrossRef]
- Hooper, A. A multi-temporal InSAR method incorporating both persistent scatterer and small baseline approaches. Geophys. Res. Lett. 2008, 35, 1–5. [Google Scholar] [CrossRef]
- Usai, S. A Least Squares Database Approach for SAR Interferometric Data. IEEE Trans.Geosci. Remote Sens. 2003, 41, 753–760. [Google Scholar] [CrossRef]
- Berardino, P.; Fornaro, G.; Lanari, R.; Sansosti, E. A New Algorithm for Surface Deformation Monitoring Based on Small Baseline Differential SAR Interferograms. IEEE Trans. Geosci. Remote Sens. 2002, 40, 2375–2383. [Google Scholar] [CrossRef]
- Cavalié, O.; Pathier, E.; Radiguet, M.; Vergnolle, M.; Cotte, N.; Walpersdorf, A.; Kostoglodov, V.; Cotton, F. Slow slip event in the Mexican subduction zone: Evidence of shallower slip in the Guerrero seismic gap for the 2006 event revealed by the joint inversion of InSAR and GPS data. Earth Planet. Sci. Lett. 2013, 367, 52–60. [Google Scholar] [CrossRef]
- Samsonov, S.; Tiampo, K.; Rundle, J. Application of DInSAR-GPS optimization for derivation of three-dimensional surface motion of the southern California region along the San Andreas fault. Comput. Geosci. 2008, 34, 503–514. [Google Scholar] [CrossRef]
- Brunori, C.A.; Bignami, C.; Stramondo, S.; Bustos, E. 20 years of active deformation on volcano caldera: Joint analysis of InSAR and AInSAR techniques. Int. J. Appl. Earth Obs. Geoinf. 2013, 23, 279–287. [Google Scholar] [CrossRef]
- Currenti, G.; Solaro, G.; Napoli, R.; Pepe, A.; Bonaccorso, A.; Del Negro, C.; Sansosti, E. Modeling of ALOS and COSMO-SkyMed satellite data at Mt Etna: Implications on relation between seismic activation of the Pernicana fault system and volcanic unrest. Remote Sens. Environ. 2012, 125, 64–72. [Google Scholar] [CrossRef]
- Hooper, A.; Segall, P.; Zebker, H.A. Persistent scatterer interferometric synthetic aperture radar for crustal deformation analysis, with application to Volcán Alcedo, Galápagos. J. Geophys. Res. 2007, 112, 1–21. [Google Scholar] [CrossRef]
- Del Ventisette, C.; Ciampalini, A.; Manunta, M.; Calò, F.; Paglia, L.; Ardizzone, F.; Mondini, A.C.; Reichenbach, P.; Mateos, R.M.; Bianchini, S.; et al. Exploitation of Large Archives of ERS and ENVISAT C-Band SAR Data to Characterize Ground Deformations. Remote Sens. 2013, 5, 3896–3917. [Google Scholar] [CrossRef]
- Jones, C.; An, K.; Blom, R.; Kent, J.D.; Ivins, E.; Bekaert, D. Anthropogenic and geologic influences on subsidence in the vicinity of New Orleans, Louisiana. J. Geophys. Res. Solid Earth 2016, 121, 3867–3887. [Google Scholar] [CrossRef]
- Bonano, M.; Manunta, M.; Pepe, A.; Paglia, L.; Lanari, R. From Previous C-Band to New X-Band SAR Systems: Assessment of the DInSAR Mapping Improvement for Deformation Time-Series Retrieval in Urban Areas. IEEE Trans. Geosci. Remote Sens. 2013, 51, 1973–1984. [Google Scholar] [CrossRef]
- Ketelaar, V. Satellite Radar Interferometry Subsidence Monitoring Techniques; Springer: Assen, The Netherlands, 2009. [Google Scholar]
- Adam, N.; Parizzi, A.; Eineder, M.; Crosetto, M. Practical persistent scatterer processing validation in the course of the Terrafirma project. J. Appl. Geophys. 2009, 69, 59–65. [Google Scholar] [CrossRef]
- Stramondo, S.; Bozzano, F.; Marra, F.; Wegmuller, U.; Cinti, F.R.; Moro, M.; Saroli, M. Subsidence induced by urbanisation in the city of Rome detected by advanced InSAR technique and geotechnical investigations. Remote Sens. Environ. 2008, 112, 3160–3172. [Google Scholar] [CrossRef]
- Casu, F.; Manzo, M.; Lanari, R. A quantitative assessment of the SBAS algorithm performance for surface deformation retrieval from DInSAR data. Remote Sens. Environ. 2006, 102, 195–210. [Google Scholar] [CrossRef]
- Ferretti, A.; Savio, G.; Barzaghi, R.; Borghi, A.; Musazzi, S.; Novali, F.; Prati, C.; Rocca, F. Submillimeter Accuracy of InSAR Time Series: Experimental Validation. IEEE Trans. Geosci. Remote Sens. 2007, 45, 1142–1153. [Google Scholar] [CrossRef]
- Argnani, A.; Armigliato, A.; Pagnoni, G.; Zaniboni, F.; Tinti, S.; Bonazzi, C. Active tectonics along the submarine slope of south-eastern Sicily and the source of the 11 January 1693 earthquake and tsunami. Nat. Hazards Earth Syst. Sci. 2012, 12, 1311–1319. [Google Scholar] [CrossRef]
- Di Maggio, C.; Madonia, G.; Parise, M.; Vattano, M. Karst of Sicily and its conservation. J. Cave Karst Stud. 2012, 74, 157–172. [Google Scholar] [CrossRef]
- Canova, F.; Tolomei, C.; Salvi, S.; Toscani, G.; Seno, S. Land subsidence along the Ionian coast of SE Sicily (Italy), detection and analysis via Small Baseline Subset (SBAS) multitemporal differential SAR interferometry. Earth Surf. Process. Landf. 2012, 286, 273–286. [Google Scholar] [CrossRef]
- Hobiger, T.; Kinoshita, Y.; Shimizu, S.; Ichikawa, R.; Furuya, M.; Kondo, T.; Koyama, Y. On the importance of accurately ray-traced troposphere corrections for Interferometric SAR data. J. Geod. 2010, 84, 537–546. [Google Scholar] [CrossRef]
- Doin, M.P.; Lasserre, C.; Peltzer, G.; Cavalié, O.; Doubre, C. Corrections of stratified tropospheric delays in SAR interferometry: Validation with global atmospheric models. J. Appl. Geophys. 2009, 69, 35–50. [Google Scholar] [CrossRef]
- Hanssen, R.F. Radar Interferometry: Data Interpretation and Error Analysis; Kluwer Academic Publishers: New York, NY, USA, 2001. [Google Scholar]
- Bekaert, D.; Hooper, A.; Wright, T. A spatially variable power law tropospheric correction technique for InSAR data. J. Geophys. Res. Solid Earth 2015, 120, 1345–1356. [Google Scholar] [CrossRef]
- Lin, Y.N.; Simons, M.; Hetland, E.A.; Muse, P.; DiCaprio, C. A multiscale approach to estimating topographically correlated propagation delays in radar interferograms. Geochem. Geophys. Geosyst. 2010, 11, Q09002. [Google Scholar] [CrossRef]
- Li, Z.; Fielding, E.; Cross, P.; Muller, J. Interferometric synthetic aperture radar atmospheric correction: GPS topography-dependent turbulence model. J. Geophys. Res. 2010, 111, 1–12. [Google Scholar] [CrossRef]
- Williams, S.; Bock, Y.; Fang, P.; Cecil, H. Integrated satellite interferometry’ Tropospheric noise, GPS estimates and implications for interferometric synthetic aperture radar products. J. Geophys. Res. Solid Earth 1998, 103, 27051–27067. [Google Scholar] [CrossRef]
- Li, Z.; Fielding, E.; Cross, P.; Muller, J.P. Interferometric synthetic aperture radar atmospheric correction: Medium Resolution Imaging Spectrometer and Advanced Synthetic Aperture Radar integration. Geophys. Res. Lett. 2006, 33, 4–7. [Google Scholar] [CrossRef]
- Jolivet, R.; Grandin, R.; Lasserre, C.; Doin, M.P.; Peltzer, G. Systematic InSAR tropospheric phase delay corrections from global meteorological reanalysis data. Geophys. Res. Lett. 2011, 38, 1–6. [Google Scholar] [CrossRef]
- Nico, G.; Tome, R.; Catalão, J.; Miranda, P.M.A. On the Use of the WRF Model to Mitigate Tropospheric Phase Delay Effects in SAR Interferograms. IEEE Trans. Geosci. Remote Sens. 2011, 49, 4970–4976. [Google Scholar] [CrossRef]
- Li, Z.; Fielding, E.; Cross, P.; Preusker, R. Advanced InSAR atmospheric correction: MERIS/MODIS combination and stacked water vapour models. Int. J. Remote Sens. 2009, 30, 3343–3363. [Google Scholar] [CrossRef]
- Bonforte, A.; Ferretti, A.; Prati, C.; Puglisi, G.; Rocca, F. Calibration of atmospheric effects on SAR interferograms by GPS and local atmosphere models: First results. J. Atmos. Sol. Terr. Phys. 2002, 63, 1343–1357. [Google Scholar] [CrossRef]
- Mateus, P.; Nico, G.; Tome, R.; Catalão, J.; Miranda, P.M.A. Experimental Study on the Atmospheric Delay Based on GPS, SAR Interferometry, and Numerical Weather Model Data. IEEE Trans. Geosci. Remote Sens. 2013, 51, 6–11. [Google Scholar] [CrossRef]
- Bekaert, D.; Walters, R.; Wright, T.; Hooper, A.; Parker, D. Statistical comparison of InSAR tropospheric correction techniques. Remote Sens. Environ. 2015, 170, 40–47. [Google Scholar] [CrossRef]
- Dee, D.P.; Uppala, S.M.; Simmons, A.J.; Berrisford, P.; Poli, P.; Kobayashi, S.; Andrae, U.; Balmaseda, M.A.; Balsamo, G.; Bauer, P.; et al. The ERA-Interim reanalysis: Configuration and performance of the data assimilation system. Q. J. R. Meteorol. Soc. 2011, 137, 553–597. [Google Scholar] [CrossRef]
- Walters, R.J.; Parsons, B.; Wright, T.J. Constraining crustal velocity fields with InSAR for Eastern Turkey: Limits to the block-like behavior of eastern Anatolia. J. Geophys. Res. Solid Earth 2014, 119, 5215–5234. [Google Scholar] [CrossRef]
- Perissin, D.; Rocca, F.; Pierdicca, M.; Pichelli, E.; Cimini, D.; Venuti, G.; Rommen, B. Mitigation of athmospheric delay in INSAR: The ESA Metawave Project. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium, Vancouver, BC, Canada, 24–29 July 2011; pp. 2558–2561.
- Hu, J.; Li, Z.; Ding, X.; Zhu, J.; Zhang, L.; Sun, Q. Resolving three-dimensional surface displacements from InSAR measurements: A review. Earth-Sci. Rev. 2014, 133, 1–17. [Google Scholar] [CrossRef]
- Atzori, S.; Salvi, S. SAR Data Analysis in Solid Earth Geophysics: From Science to Risk Management. In Land Applications of Radar Remote Sensing; Closson, D., Ed.; InTech: Rijeka, Croatia, 2014; pp. 2–43. [Google Scholar]
- Ng, A.H.M.; Chang, H.C.; Zhang, K.; Ge, L.; Rizos, C.; Omura, M. Deformation mapping in three dimensions for underground mining using InSAR—Southern highland coal field in New South Wales, Australia. Int. J. Remote Sens. 2011, 32, 7227–7256. [Google Scholar] [CrossRef]
- Michel, R.; Avouac, J.P. Measuring ground displacement from SAR amplitude images: Application to the Landers earthquake. Geophys. Res. Lett. 1999, 26, 875–878. [Google Scholar] [CrossRef]
- Bechor, N.B.D.; Zebker, H.A. Measuring two-dimensional movements using a single InSAR pair. Geophys. Res. Lett. 2006, 33, 1–5. [Google Scholar] [CrossRef]
- Scheiber, R.; Moreira, A. Coregistration of Interferometric SAR Images Using Spectral Diversity. IEEE Trans. Geosci. Remote Sens. 2000, 38, 2179–2191. [Google Scholar] [CrossRef]
- Fielding, E.J.; Lundgren, P.R.; Taymaz, T.; Yolsal-Cevikbilen, S.; Owen, S.E. Fault-Slip Source Models for the 2011 M 7.1 Van Earthquake in Turkey from SAR Interferometry, Pixel Offset Tracking, GPS, and Seismic Waveform Analysis. Seismol. Res. Lett. 2013, 84, 579–593. [Google Scholar] [CrossRef]
- Jung, H.S.; Lu, Z.; Won, J.S.; Poland, M.P.; Miklius, A. Mapping three-dimensional surface deformation by combining multiple-aperture interferometry and conventional interferometry: Application to the June 2007 eruption of kilauea volcano, Hawaii. IEEE Geosci. Remote Sens. Lett. 2011, 8, 34–38. [Google Scholar] [CrossRef]
- Fialko, Y.; Simons, M.; Agnew, D. The complete (3-D) surface displacement field in the epicentral area of the 1999 Mw 7.1 Hector Mine earthquake, California, from space geodetic observations. Geophys. Res. Lett. 2001, 28, 3063–3066. [Google Scholar] [CrossRef]
- Bally, P. Satellite Earth Observation for Geohazard Risk Mangement; Technical Report; European Space Agency: Santorini, Greece, 2012. [Google Scholar]
- Gudmundsson, S. Three-dimensional surface motion maps estimated from combined interferometric synthetic aperture radar and GPS data. J. Geophys. Res. 2002, 107, 1–14. [Google Scholar] [CrossRef]
- Knospe, S.; Jónsson, S. Covariance estimation for DInSAR surface-deformation measurements in presence of anisotropic atmospheric noise. IEEE Trans. Geosci. Remote Sens. 2010, 48, 2057–2065. [Google Scholar] [CrossRef]
- Catalao, J.; Nico, G.; Hanssen, R.; Catita, C. Merging GPS and Atmospherically Corrected InSAR Data to Map 3-D Terrain Displacement Velocity. IEEE Trans. Geosci. Remote Sens. 2011, 49, 2354–2360. [Google Scholar] [CrossRef]
- Wang, H.; Wright, T.J. Satellite geodetic imaging reveals internal deformation of western Tibet. Geophys. Res. Lett. 2012, 39, 1–5. [Google Scholar] [CrossRef]
- England, P.; Molnar, P. Late Quaternary to decadal velocity fields in Asia. J. Geophys. Res. Solid Earth 2005, 110, 1–27. [Google Scholar] [CrossRef]
- Guglielmino, F.; Nunnari, G.; Puglisi, G.; Spata, A. Simultaneous and Integrated Strain Tensor Estimation From Geodetic and Satellite Deformation Measurements to Obtain Three-Dimensional Displacement Maps. IEEE Trans. Geosci. Remote Sens. 2011, 49, 1815–1826. [Google Scholar] [CrossRef]
- Segall, P. Earthquake and Volcano Deformation; Princeton University Press: Princeton, NJ, USA, 2010; pp. 1–432. [Google Scholar]
- Bouwer, H. Land Subsidence and Cracking Due to Ground-Water Depletion. Ground Water 1977, 15, 358–364. [Google Scholar] [CrossRef]
- Guglielmino, F.; Bignami, C.; Bonforte, A.; Briole, P.; Obrizzo, F.; Puglisi, G.; Stramondo, S.; Wegmüller, U. Analysis of satellite and in situ ground deformation data integrated by the SISTEM approach: The April 3, 2010 earthquake along the Pernicana fault (Mt. Etna—Italy) case stud. Earth Planet. Sci. Lett. 2011, 312, 327–336. [Google Scholar] [CrossRef]
- Guglielmino, F.; Anzidei, M.; Briole, P.; Elias, P.; Puglisi, G. 3D displacement maps of the 2009 L’Aquila earthquake (Italy) by applying the SISTEM method to GPS and DInSAR data. Terra Nova 2013, 25, 79–85. [Google Scholar] [CrossRef]
- Teza, G.; Pesci, A.; Galgaro, A. Grid _ strain and grid _ strain3: Software packages for strain field computation in 2D and 3D environments. Comput. Geosci. 2008, 34, 1142–1153. [Google Scholar] [CrossRef]
- Shen, Z.K.; Jackson, D.D.; Ge, B.X. Crustal deformation across and beyond the Los Angeles basin from geodetic measurements. J. Geophys. Res. 1996, 101, 27957–27980. [Google Scholar] [CrossRef]
- Angelica, C.; Bonforte, A.; Distefano, G.; Serpelloni, E.; Gresta, S. Seismic potential in Italy from integration and comparison of seismic and geodetic strain rates. Tectonophysics 2013, 608, 996–1006. [Google Scholar] [CrossRef]
- Scarfi, L.; Messina, A.; Cassisi, C. Sicily and southern Calabria focal mechanism database: A valuable tool for local and regional stress-field determination. Ann. Geophys. 2013, 56, D0109. [Google Scholar]
- Ben-Avraham, Z.; Grasso, M. Crustal structure variations and transcurrent faulting at the eastern and western margins of the eastern Mediterranean. Tectonophysics 1991, 196, 269–277. [Google Scholar] [CrossRef]
- Rovida, A.; Camassi, R.; Gasperini, P.; Stucchi, M. CPTI11, the 2011 Version of the Parametric Catalogue of Italian Earthquakes; Istituto Nazionale di Geofisica e Vulcanologia: Milano, Italy, 2011. [Google Scholar]
- ISIDe. Italian Seismological, Instrumental and Parametric Database, 2016. Available online: http://iside.rm.ingv.it/iside/standard/?lang=en (accessed on 27 Dcember 2016).
- Bonforte, A.; Catalano, S.; Maniscalco, R.; Pavano, F.; Romagnoli, G.; Sturiale, G.; Tortorici, G. Geological and geodetic constraints on the active deformation along the northern margin of the Hyblean Plateau (SE Sicily). Tectonophysics 2014, 640–641, 80–89. [Google Scholar] [CrossRef]
- Mastrolembo Ventura, B.; Serpelloni, E.; Argnani, A.; Bonforte, A.; Bürgmann, R.; Anzidei, M.; Baldi, P.; Puglisi, G. Fast geodetic strain-rates in eastern Sicily (southern Italy): New insights into block tectonics and seismic potential in the area of the great 1693 earthquake. Earth Planet. Sci. Lett. 2014, 404, 77–88. [Google Scholar] [CrossRef]
- Bousquet, J.; Lanzafame, G. Compression and Quaternary tectonic inversion onthe Northern edge of the Hyblean Mountains, foreland of the Appenine–Maghrebian chain in Eastern Sicily (Italy). GeoActa 2004, 3, 165–177. [Google Scholar]
- Di Bucci, D.; Burrato, P.; Vannoli, P.; Valensise, G. Tectonic evidence for the ongoing Africa-Eurasia convergence in central Mediterranean foreland areas: A journey among long-lived shear zones, large earthquakes, and elusive fault motions. J. Geophys. Res. 2010, 115, B12404. [Google Scholar] [CrossRef]
- Visini, F.; de Nardis, R.; Barbano, M.S.; Lavecchia, G. Testing the seismogenic sources of the January 11th 1693 Sicilian earthquake (Io X/XI): Insights from macroseismic field simulations. Ital. J. Geosci. 2009, 128, 147–156. [Google Scholar]
- Brancato, A.; Hole, J.A.; Gresta, S.; Beale, J.N. Determination of Seismogenic Structures in Southeastern Sicily (Italy) by High-Precision Relative Relocation of Microearthquakes. Bull. Seismol. Soc. Am. 2009, 99, 1921–1936. [Google Scholar] [CrossRef]
- Amato, A.; Azzara, R.; Basili, A.; Chiarabba, C.; Cocco, M.; Bona, M.D.; Selvaggi, G. Mainshock and aftershocks of the December 13, 1990, eastern Sicily earthquake. Ann. Geofis. 1995, 18, 255–266. [Google Scholar]
- Working Group MPS. Redazione Della Mappa di Pericolosità Sismica Prevista Dall’Ordinanza PCMdel 20 Marzo 2003; Rapporto Conclusivo per il Dipartimento Della Protezione Civile; INGV: Milano, Italy, 2004. [Google Scholar]
- Musumeci, C.; Patane, D.; Scarfi, L.; Gresta, S. Stress Directions and Shear-Wave Anisotropy: Observations from Local Earthquakes in Southeastern Sicily, Italy. Bull. Seismol. Soc. Am. 2005, 95, 1359–1374. [Google Scholar] [CrossRef]
- Rosen, P.A.; Henley, S.; Peltzer, G.; Simons, M. Updated Repeat Orbit Interferometry Package Released. EOS Trans. AGU 2004, 85, 47. [Google Scholar] [CrossRef]
- Kampes, B.M.; Hanssen, R.F.; Perski, Z. Radar interferometry with public domain tools. In Proceedings of the FRINGE 2003, Frascati, Italy, 1–5 December 2003; Volume 2003, pp. 6–11.
- Farr, T.G.; Rosen, P.A.; Caro, E.; Crippen, R.; Duren, R.; Hensley, S.; Kobrick, M.; Paller, M.; Rodriguez, E.; Roth, L.; et al. The Shuttle Radar Topography Mission. Rev. Geophys. 2007, 45, 1–33. [Google Scholar] [CrossRef]
- Hooper, A.J. Stanford Model for Persistent Scatterer Interferometry (StaMPS). Available online: https://homepages.see.leeds.ac.uk/earahoo/stamps/ (accessed on 27 December 2016).
- Marinkovic, P.; Larsen, Y. Consequences of Long-Term ASAR Local Oscillator Frequency Decay—An Empirical Study of 10 Years of Data. In Proceedings of the European Space Agency Living Planet Symposium, Edinburgh, UK, 9–13 September 2013.
- Bekaert, D. Toolbox for Reducing Atmospheric InSAR Noise (TRAIN). Available online: http://www.davidbekaert.com (accessed on 27 Dcember 2016).
- Selige, T.; Böhner, J.; Ringeler, A. Processing of SRTM X-SAR data to correct interferometric elevation models for land surface process applications. Göttinger Geogr. Abh. 2003, 115, 97–104. [Google Scholar]
- Lee, J.; Papathanassiou, K.; Ainsworth, T.; Grunes, M.; Reigber, A. A new technique for noise filtering of SAR interferometric phase images. IEEE Trans. Geosci. Remote Sens. 1998, 36, 1456–1465. [Google Scholar]
- Bonforte, A. Study of the Northeastern Sector of the Hyblean Plateau and of the Eastern Flank of Mt, Etna by GPS Spatial Techniques. Ph.D. Thesis, Univerita degli Studi di Catania, Catania, Italy, 2002. [Google Scholar]
- Musumeci, C.; Scarfì, L.; Palano, M.; Patanè, D. Foreland segmentation along an active convergent margin: New constraints in southeastern Sicily (Italy) from seismic and geodetic observations. Tectonophysics 2014, 630, 137–149. [Google Scholar] [CrossRef]
- Catalano, S.; De Guidi, G.; Lanzafame, G.; Monaco, C.; Torrisi, S.; Sturiale, G.; Tortorici, G.; Tortorici, L. Inversione tettonica positiva tardo-quaternaria nel Plateau Ibleo (Sicilia SE). Rend. Soc. Geol. It. 2006, 2, 118–120. [Google Scholar]
- Catalano, S.; Torrisi, S.; Tortorici, G.; Romagnoli, G. Active folding along a rift-flank: The Catania region case history (SE Sicily). J. Geodyn. 2011, 51, 53–63. [Google Scholar] [CrossRef]
- Bonforte, A.; Guglielmino, F.; Coltelli, M.; Ferretti, A.; Puglisi, G. Structural assessment of mount Etna volcano from permanent scatterers analysis. Geochem. Geophys. Geosyst. 2011, 12. [Google Scholar] [CrossRef]
- Borgia, A.; Lanari, R.; Sansosti, E.; Tesauro, M.; Berardino, P.; Fornaro, G.; Neri, M.; Murray, J.B. Actively growing anticlines beneath Catania from the distal motion of Mount Etna’s Decollement measured by SAR interferometry and GPS. Geophys. Res. Lett. 2000, 27, 3409–3412. [Google Scholar] [CrossRef]
- Lundgren, P.; Casu, F.; Manzo, M.; Pepe, A.; Berardino, P.; Sansosti, E.; Lanari, R. Gravity and magma induced spreading of Mount Etna volcano revealed by satellite radar interferometry. Geophys. Res. Lett. 2004, 31, 1–4. [Google Scholar] [CrossRef]
- Ben-Avraham, Z.; Grasso, M. Collision zone segmentation in Sicily and adjacent area (central Mediterranean). Ann. Tecton. 1990, 5, 131–139. [Google Scholar]
- Serpelloni, E.; Vannucci, G.; Pondrelli, S.; Argnani, A.; Casula, G.; Anzidei, M.; Baldi, P.; Gasperini, P. Kinematics of the Western Africa-Eurasia plate boundary from focal mechanisms and GPS data. Geophys. J. Int. 2007, 169, 1180–1200. [Google Scholar] [CrossRef]
- Catalano, S.; De Guidi, G.; Monaco, C.; Tortorici, G.; Tortorici, L. Active faulting and seismicity along the Siculo-Calabrian Rift Zone (Southern Italy). Tectonophysics 2008, 453, 177–192. [Google Scholar] [CrossRef]
- Bianca, M.; Monaco, C.; Tortorici, L.; Cernobori, L. Quaternary normal faulting in southeastern Sicily (Italy): A seismic source for the 1693 large earthquake. Geophys. J. Int. 1999, 139, 370–394. [Google Scholar] [CrossRef]
- Cultrera, F.; Barreca, G.; Scarfì, L.; Monaco, C. Fault reactivation by stress pattern reorganization in the Hyblean foreland domain of SE Sicily (Italy) and seismotectonic implications. Tectonophysics 2015, 661, 215–228. [Google Scholar] [CrossRef]
© 2017 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).