Improved Detection of Human Respiration Using Data Fusion Basedon a Multistatic UWB Radar
Abstract
:1. Introduction
2. Materials and Methods
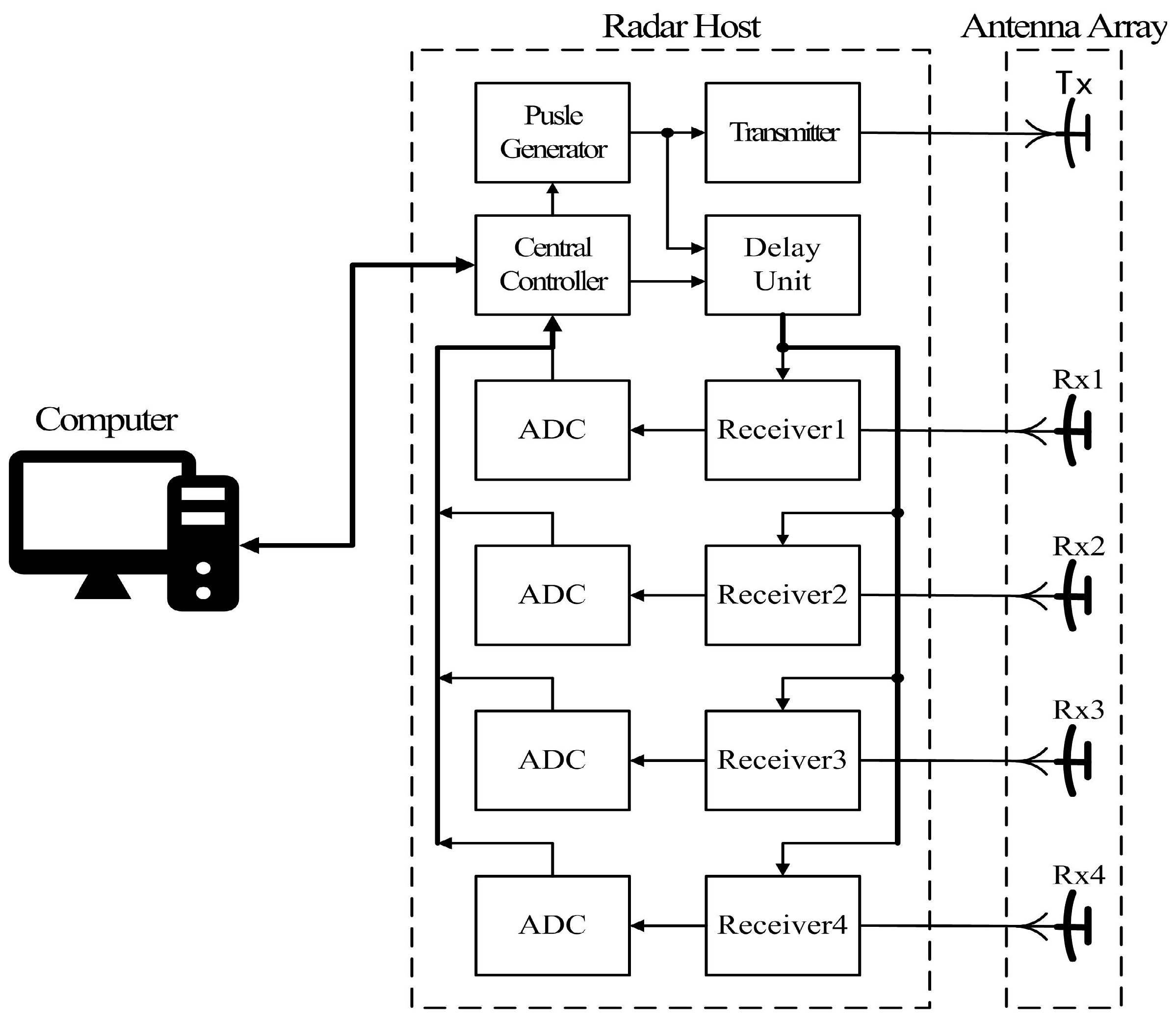
2.1. The Multistatic UWB Radar
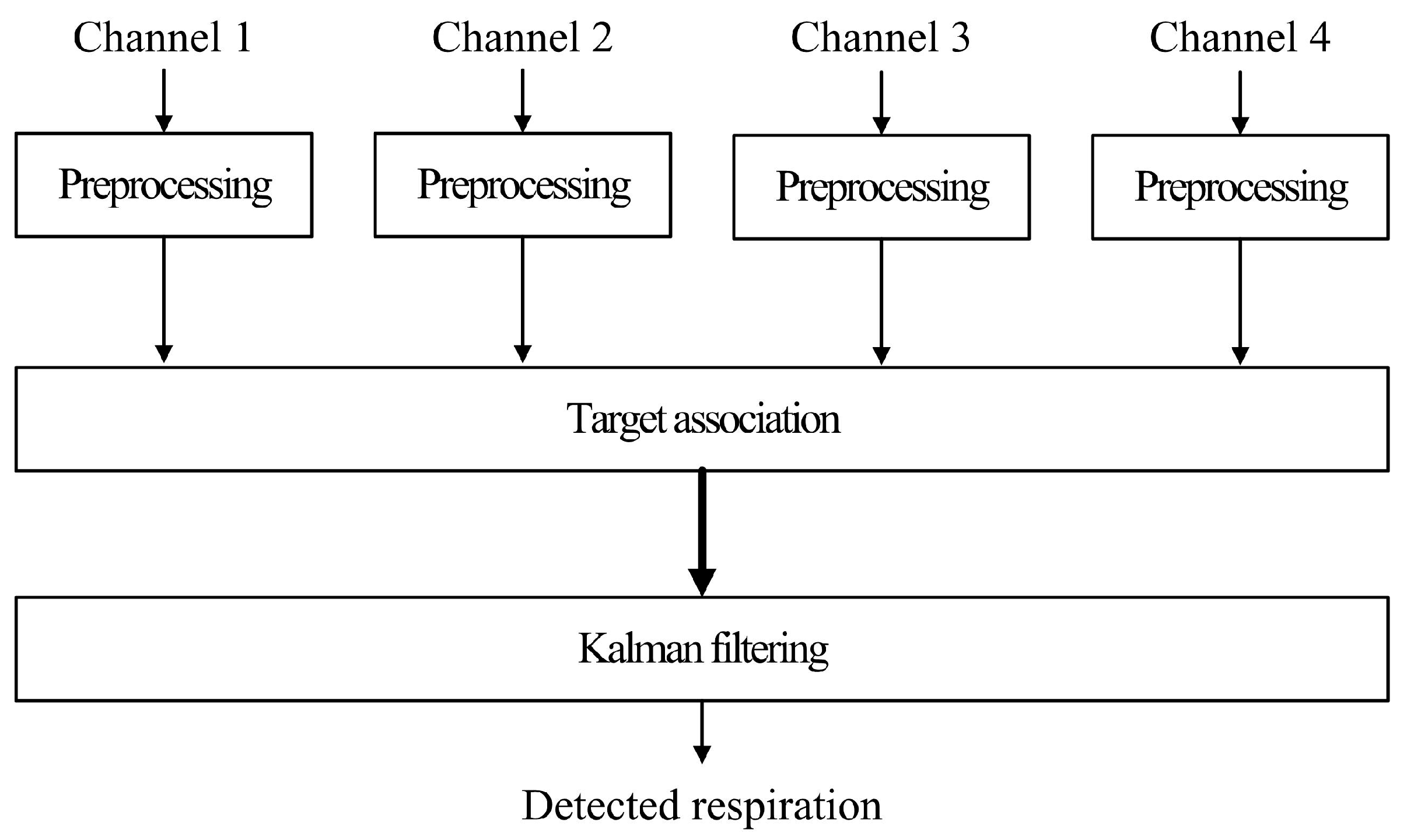
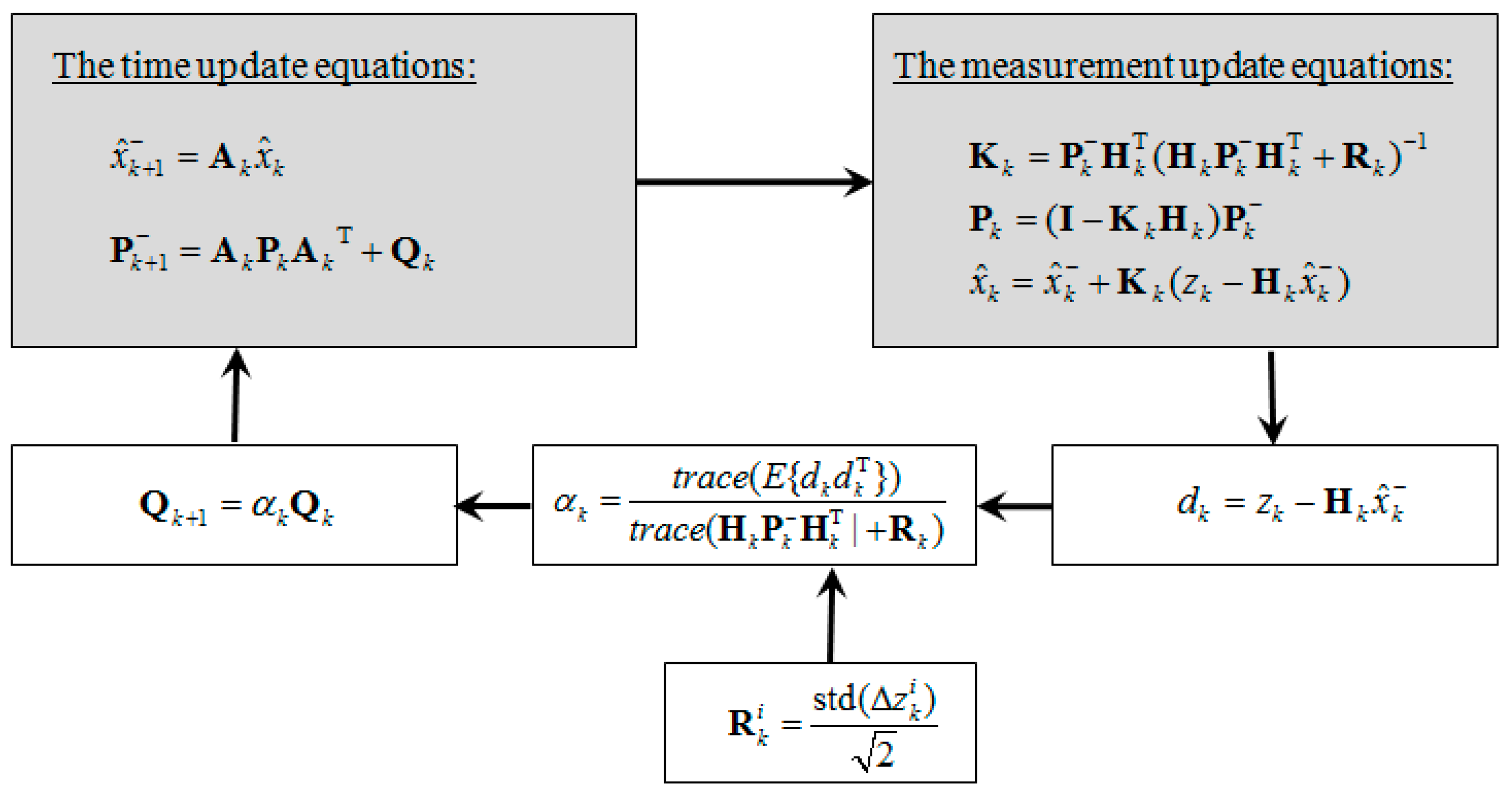
2.2. The Data Fusion Algorithm
2.3. The Experiment Setup
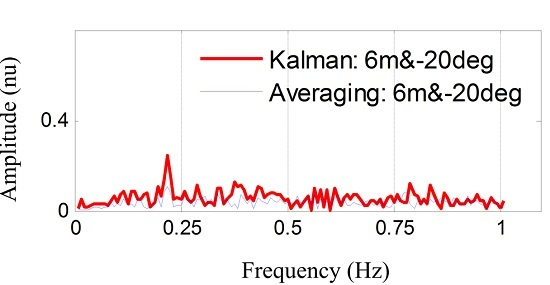
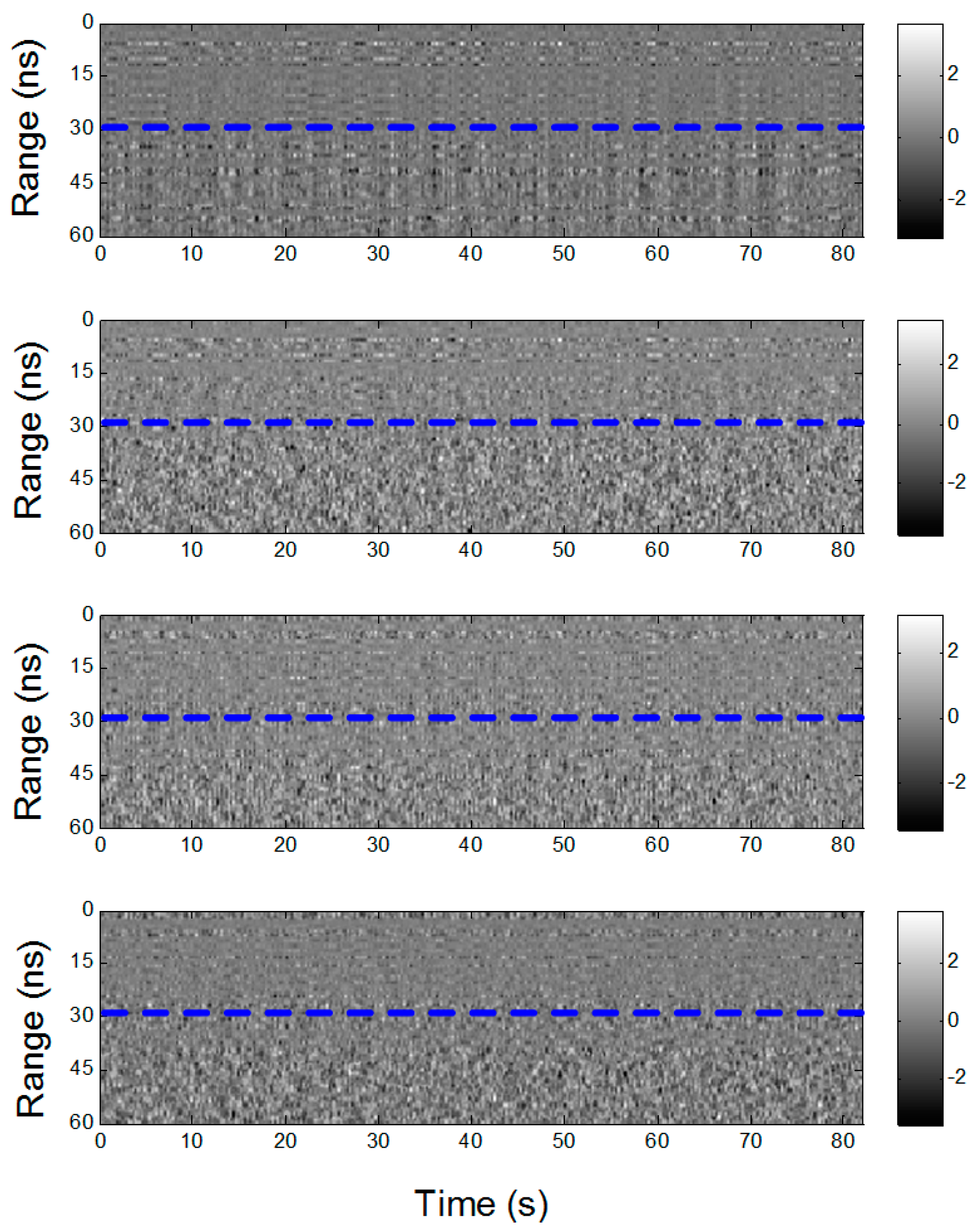
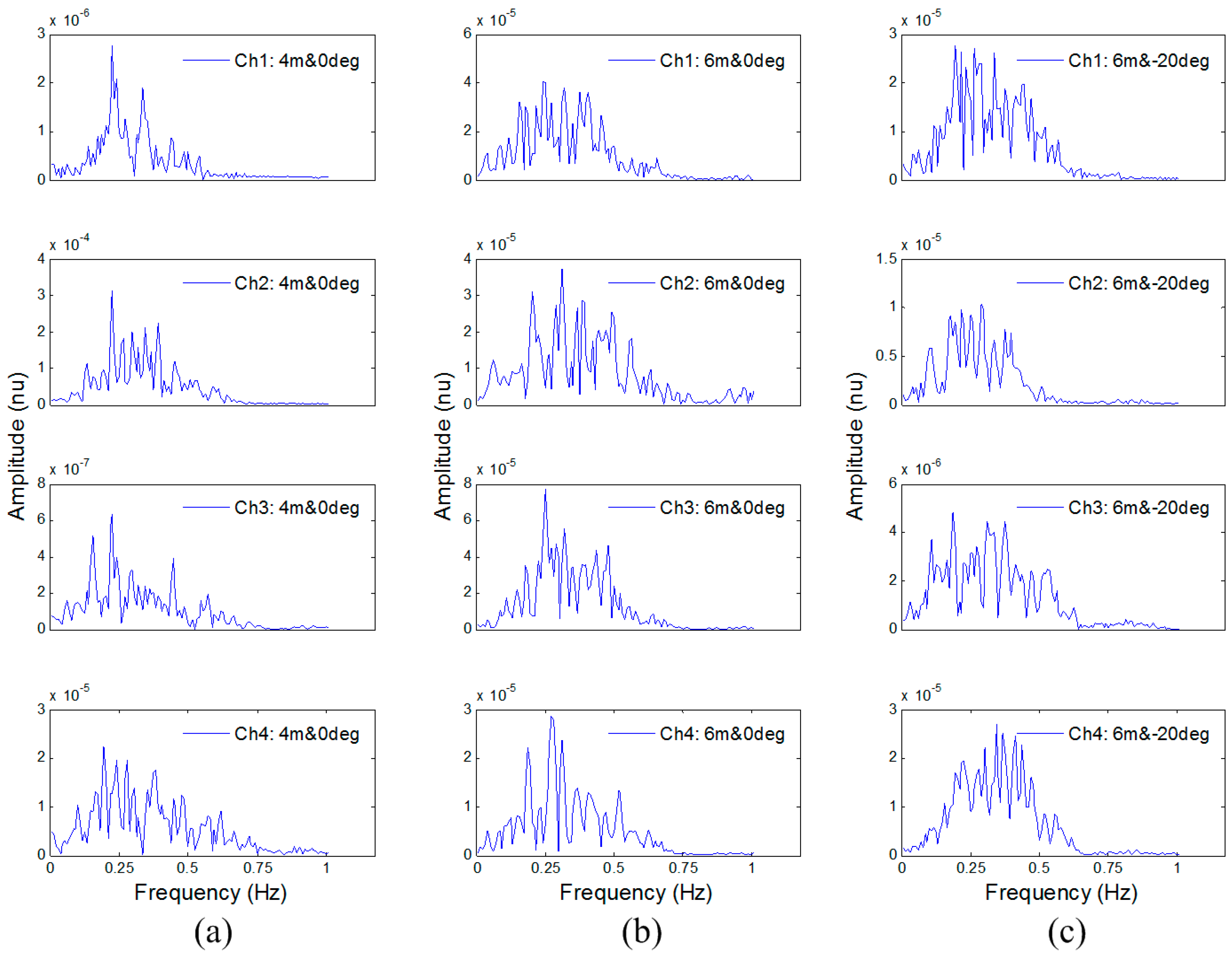
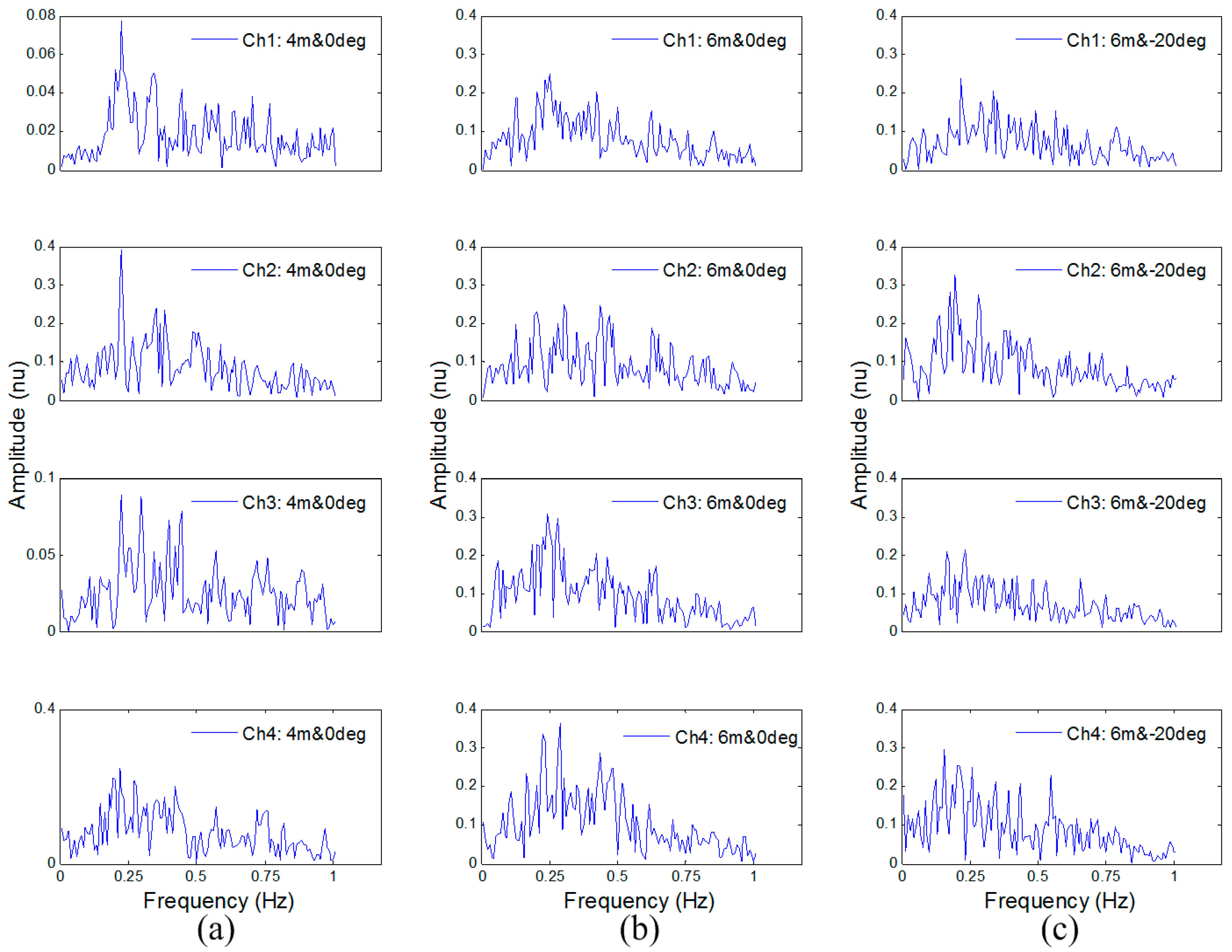
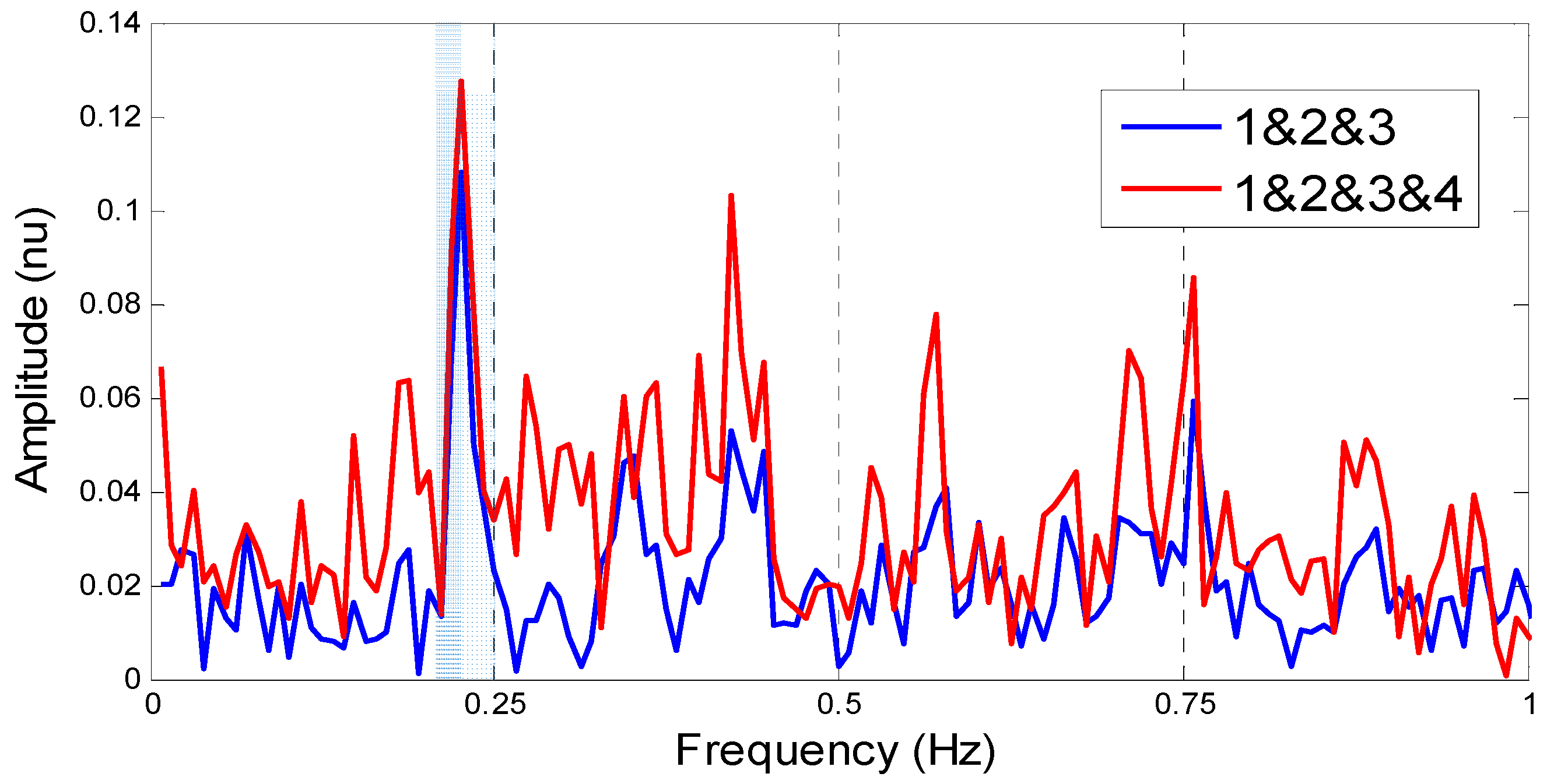
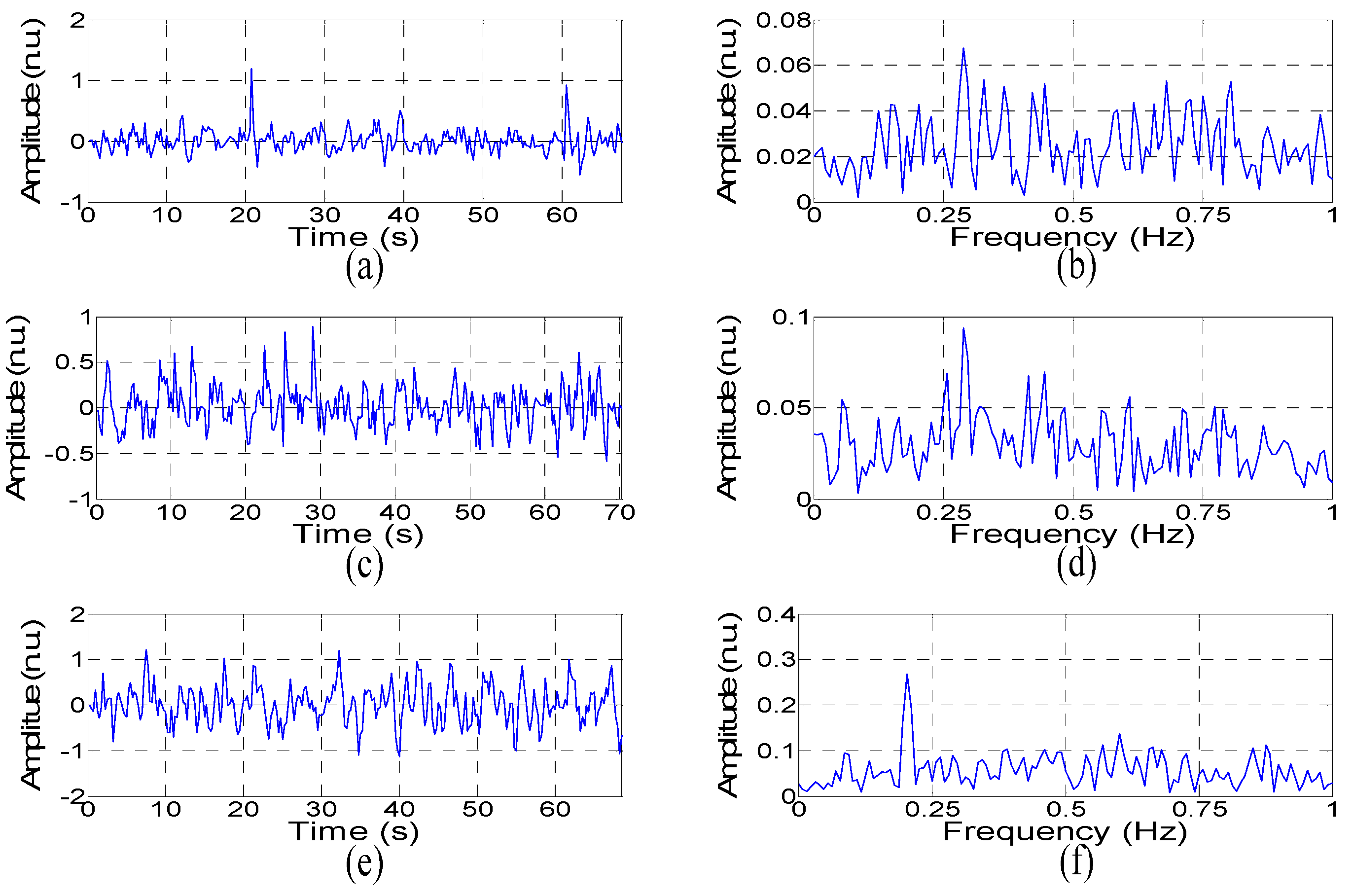
3. Experimental Results
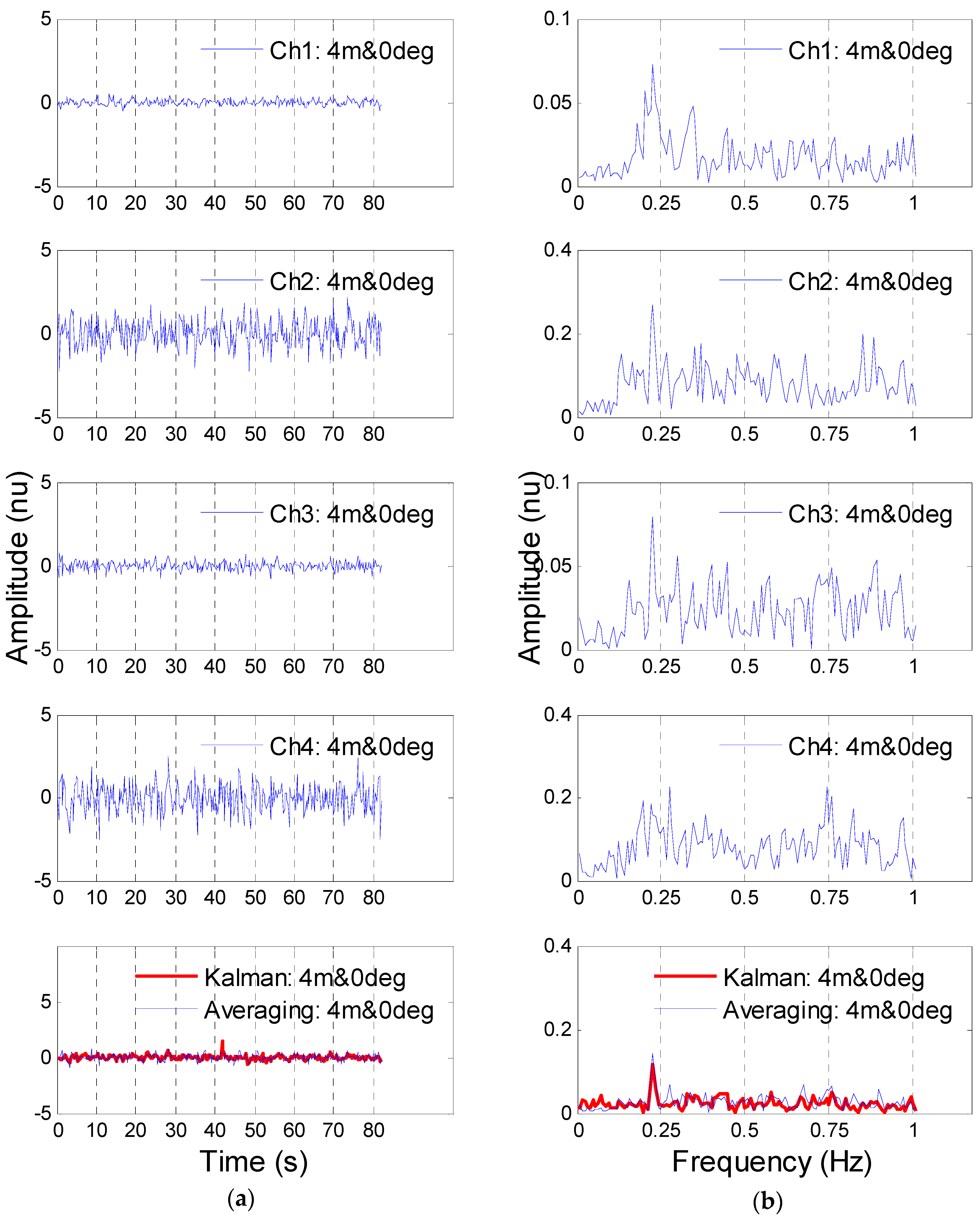
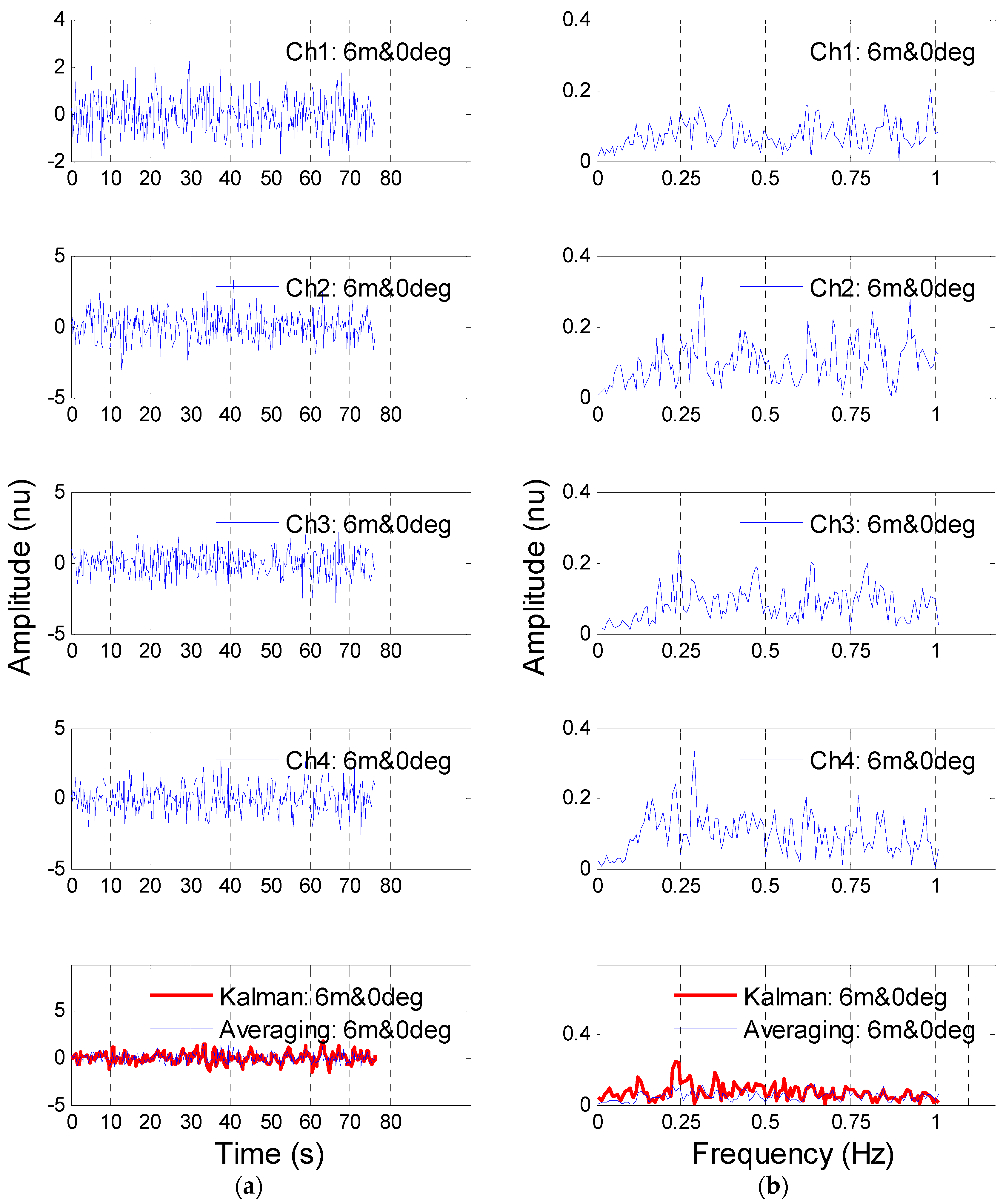
3.1. Detection Results of the Volunteer Target
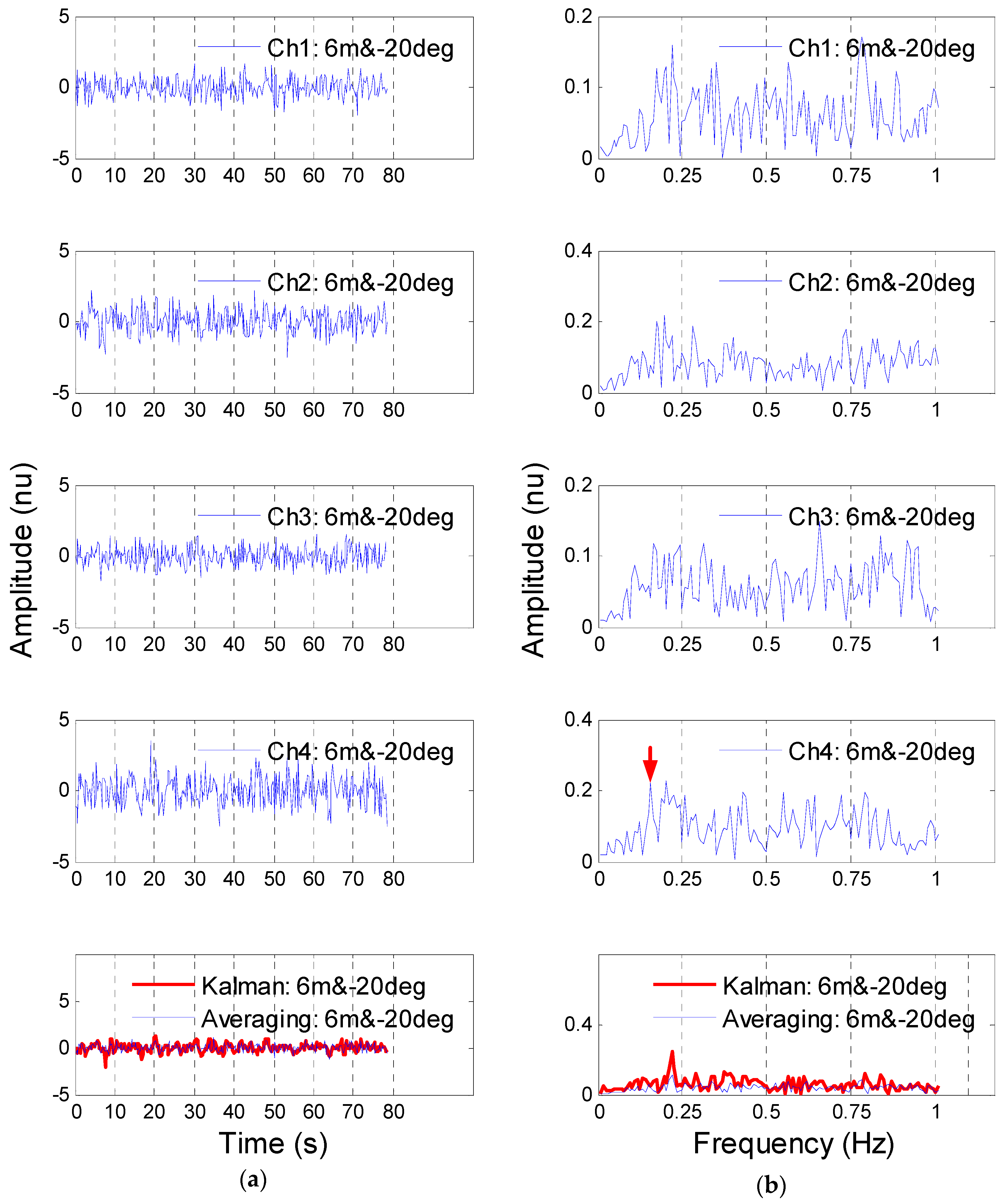
3.2. Detection Results of the Artificial Object
4. Discussion
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Immoreev, I.; Samkov, S.; Tao, T.H. Short-distance ultra-wideband radars. IEEE Aerosp. Electron. Syst. Mag. 2005, 6, 9–14. [Google Scholar] [CrossRef]
- Yarovoy, A.; Ligthart, L.P.; Matuzas, J.; Levitas, B. UWB radar for human being detection. IEEE Aerosp. Electron. Syst. Mag. 2006, 21, 10–14. [Google Scholar] [CrossRef]
- Sachs, J.; Helbig, M.; Herrmann, R.; Kmec, M.; Schilling, K.; Zaikov, E. Remote vital sign detection for rescue, security, and medical care by ultra-wideband pseudo-noise radar. Ad. Hoc. Netw. 2014, 13, 42–53. [Google Scholar] [CrossRef]
- Baldi, M.; Cerri, G.; Chiaraluce, F.; Eusebi, L.; Russo, P. Non-invasive UWB sensing of astronauts’ breathing activity. Sensors 2014, 15, 565–591. [Google Scholar] [CrossRef] [PubMed]
- Nezirovic, A.; Yarovoy, A.G.; Ligthart, L.P. Signal processing for improved detection of trapped victims using UWB radar. IEEE Trans. Geosci. Remote Sens. 2010, 48, 2005–2014. [Google Scholar] [CrossRef]
- Lv, H.; Li, W.; Li, Z.; Zhang, Y.; Jiao, T.; Xue, H.; Liu, M.; Jing, X.; Wang, J. Characterization and Identification of IR-UWB Respiratory-Motion Response of Trapped Victims. IEEE Trans. Geosci. Remote Sens. 2014, 52, 7195–7204. [Google Scholar] [CrossRef]
- Nezirovic, A.; Tesfay, S.; Valavan, A.S.E.; Yarovoy, A. Experimental study on human breathing cross section using UWB impulse radar. In Proceedings of Radar Conference, Amsterdam, The Netherlands, 30–31 October 2008.
- Nijsure, Y.; Tay, W.P.; Gunawan, E.; Wen, F.; Yang, Z.; Guan, Y.L.; Chua, A.P. An impulse radio ultrawideband system for contactless noninvasive respiratory monitoring. IEEE Trans. Geosci. Remote Sens. 2013, 60, 1509–1517. [Google Scholar] [CrossRef] [PubMed]
- Lazaro, A.; Girbau, D.; Villarino, R. Techniques for clutter suppression in the presence of body movements during the detection of respiratory activity through UWB radars. Sensors 2014, 14, 2595–2618. [Google Scholar] [CrossRef] [PubMed]
- Liu, L.; Liu, S. Remote detection of human vital sign with stepped-frequency continuous wave radar. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 7, 775–782. [Google Scholar] [CrossRef]
- Lv, H.; Liu, M.; Jiao, T.; Zhang, Y.; Yu, X.; Li, S.; Jing, X.; Wang, J. Multi-target human sensing via UWB bio-radar based on multiple antennas. IEEE 2013. [Google Scholar] [CrossRef]
- Wu, S.; Yao, S.; Liu, W.; Tan, K.; Xia, Z.; Meng, S.; Chen, J.; Fang, G.; Yin, H. Study on a novel UWB Linear array human respiration model and detection method. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2016, 9, 125–140. [Google Scholar] [CrossRef]
- Thiel, M.; Sarabandi, K. Ultra wideband multi-static scattering analysis of human movement within buildings for the purpose of stand-off detection and localization. IEEE Trans. Antennas Propag. 2011, 59, 1261–1268. [Google Scholar] [CrossRef]
- Salmi, J.; Molisch, A.F. Propagation parameter estimation, modeling and measurements for ultrawideband MIMO radar. IEEE Trans. Antennas Propag. 2011, 59, 4257–4267. [Google Scholar] [CrossRef]
- Kocur, D.; Švecová, M.; Rovňáková, J. Through-the-wall localization of a moving target by two independent ultra wideband (UWB) radar systems. Sensors 2013, 13, 11969–11997. [Google Scholar] [CrossRef] [PubMed]
- He, Y.; Aubry, P.; Le Chevalier, F.; Yarovoy, A. Decentralised tracking for human target in multistatic ultra-wideband radar. IET Radar Sonar Navig. 2014, 8, 1215–1223. [Google Scholar] [CrossRef]
- Nguyen, V.H.; Pyun, J.Y. Location detection and tracking of moving targets by a 2D IR-UWB radar system. Sensors 2015, 15, 6740–6762. [Google Scholar] [CrossRef] [PubMed]
- Li, C.; Xiao, Y.; Lin, J. Experiment and spectral analysis of a low-power-band heartbeat detector measuring from four sides of a human body. IEEE Trans. Microw. Theory Tech. 2006, 54, 4464–4471. [Google Scholar] [CrossRef]
- Chiani, B.; Paolini, E.; Giorgetti, A.; Mazzotti, M.; Chiani, M. Target Tracking for UWB Multistatic Radar Sensor Networks. IEEE J. Sel. Top. Signal Process. 2014, 8, 125–136. [Google Scholar]
- Conti, S.; Giorgetti, A.; Win, M.Z.; Conti, A. Blind Selection of representative observations for sensor radar networks. IEEE Trans. Veh. Technol. 2015, 64, 1388–1400. [Google Scholar]
- Gao, J.; Harris, C.J. Some remarks on Kalman filters for the multisensor fusion. Inf. Fusion 2002, 3, 191–201. [Google Scholar] [CrossRef]
- Khaleghi, B.; Khamis, A.; Karray, F.O.; Razavi, S.N. Multisensor data fusion: A review of the state-of-the-art. Inf. Fusion 2013, 14, 28–44. [Google Scholar] [CrossRef]
- Ding, W.; Wang, J.; Rizos, C.; Kinlyside, D. Improving adaptive Kalman estimation in GPS/INS integration. J. Navig. 2007, 60, 517–529. [Google Scholar] [CrossRef]
- Vullings, R.; De Vries, B.; Bergmans, J.W. An adaptive Kalman filter for ECG signal enhancement. IEEE Trans. Biomed. Eng. 2011, 58, 1094–1103. [Google Scholar] [CrossRef] [PubMed]
- Foussier, J.; Teichmann, D.; Jia, J.; Misgeld, B.; Leonhardt, S. An adaptive Kalman filter approach for cardiorespiratory signal extraction and fusion of non-contacting sensors. BMC Med. Inform. Decis. Mak. 2014. [Google Scholar] [CrossRef] [PubMed]
- Putra, D.; Haas, O.C.; Mills, J.A.; Burnham, K.J. A multiple model approach to respiratory motion prediction for real-time IGRT. Phys. Med. Biol. 2008, 53, 1651–1663. [Google Scholar] [CrossRef] [PubMed]
- Gan, Q.; Harris, C.J. Comparison of two measurement fusion methods for Kalman-filter-based multisensor data fusion. IEEE Trans. Aerosp. Electron. Syst. 2001, 37, 273–279. [Google Scholar] [CrossRef]
- Roecker, J.; McGillem, C. Comparison of two-sensor tracking methods based on state vector fusion and measurement fusion. IEEE Trans. Aerosp. Electron. Syst. 1988, 24, 447–449. [Google Scholar] [CrossRef]



| Parameter | Value |
|---|---|
| Signal mode | impulse |
| Transmission peak power | 0.26 W |
| Pulse repetition frequency | 128 kHz |
| Operating frequency | 250–750 MHz |
| Receiver dynamic range | 80 dB |
| Receiver sensitivity | 3 dB |
| ADC accuracy | 16 bits |
| Minimum step | 10 ps |
| Channel Combinations | BRIR | |||||||
|---|---|---|---|---|---|---|---|---|
| 2 channels | 1 and 2 | 1 and 3 | 1 and 4 | 2 and 3 | 2 and 4 | 3 and 4 | ||
| 5.18% | 5.55% | 5.23% | 3.88% | 5.02% | 4.59% | |||
| 3 channels | 1, 2, and 3 | 1, 2, and 4 | 1, 3, and 4 | 2, 3, and 4 | ||||
| 5.26% | 5.49% | 5.76% | 4.38% | |||||
| 4 channels | 4.51% | |||||||
| Channel Combinations | BRIR | |||||||
|---|---|---|---|---|---|---|---|---|
| 2 channels | 1 and 2 | 1 and 3 | 1 and 4 | 2 and 3 | 2 and 4 | 3 and 4 | ||
| 2.66% | 5.63% | 6.63% | 3.19% | 4.02% | 2.52% | |||
| 3 channels | 1, 2, and 3 | 1, 2, and 4 | 1, 3, and 4 | 2, 3, and 4 | ||||
| 4.04% | 5.31% | 6.11% | 2.21% | |||||
| 4 channels | 2.78% | |||||||
| Channel Combinations | BRIR | |||||||
|---|---|---|---|---|---|---|---|---|
| 2 channels | 1 and 2 | 1 and 3 | 1 and 4 | 2 and 3 | 2 and 4 | 3 and 4 | ||
| 4.03% | 3.62% | 4.73% | 3.99% | 5.54% | 5.22% | |||
| 3 channels | 1, 2, and 3 | 1, 2, and 4 | 1, 3, and 4 | 2, 3, and 4 | ||||
| 4.15% | 5.49% | 4.54% | 5.83% | |||||
| 4 channels | 5.33% | |||||||
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lv, H.; Qi, F.; Zhang, Y.; Jiao, T.; Liang, F.; Li, Z.; Wang, J. Improved Detection of Human Respiration Using Data Fusion Basedon a Multistatic UWB Radar. Remote Sens. 2016, 8, 773. https://doi.org/10.3390/rs8090773
Lv H, Qi F, Zhang Y, Jiao T, Liang F, Li Z, Wang J. Improved Detection of Human Respiration Using Data Fusion Basedon a Multistatic UWB Radar. Remote Sensing. 2016; 8(9):773. https://doi.org/10.3390/rs8090773
Chicago/Turabian StyleLv, Hao, Fugui Qi, Yang Zhang, Teng Jiao, Fulai Liang, Zhao Li, and Jianqi Wang. 2016. "Improved Detection of Human Respiration Using Data Fusion Basedon a Multistatic UWB Radar" Remote Sensing 8, no. 9: 773. https://doi.org/10.3390/rs8090773
APA StyleLv, H., Qi, F., Zhang, Y., Jiao, T., Liang, F., Li, Z., & Wang, J. (2016). Improved Detection of Human Respiration Using Data Fusion Basedon a Multistatic UWB Radar. Remote Sensing, 8(9), 773. https://doi.org/10.3390/rs8090773