Using VIIRS Day/Night Band to Measure Electricity Supply Reliability: Preliminary Results from Maharashtra, India
Abstract
:1. Introduction
2. Materials and Methods
2.1. Study Area
2.2. Representativeness
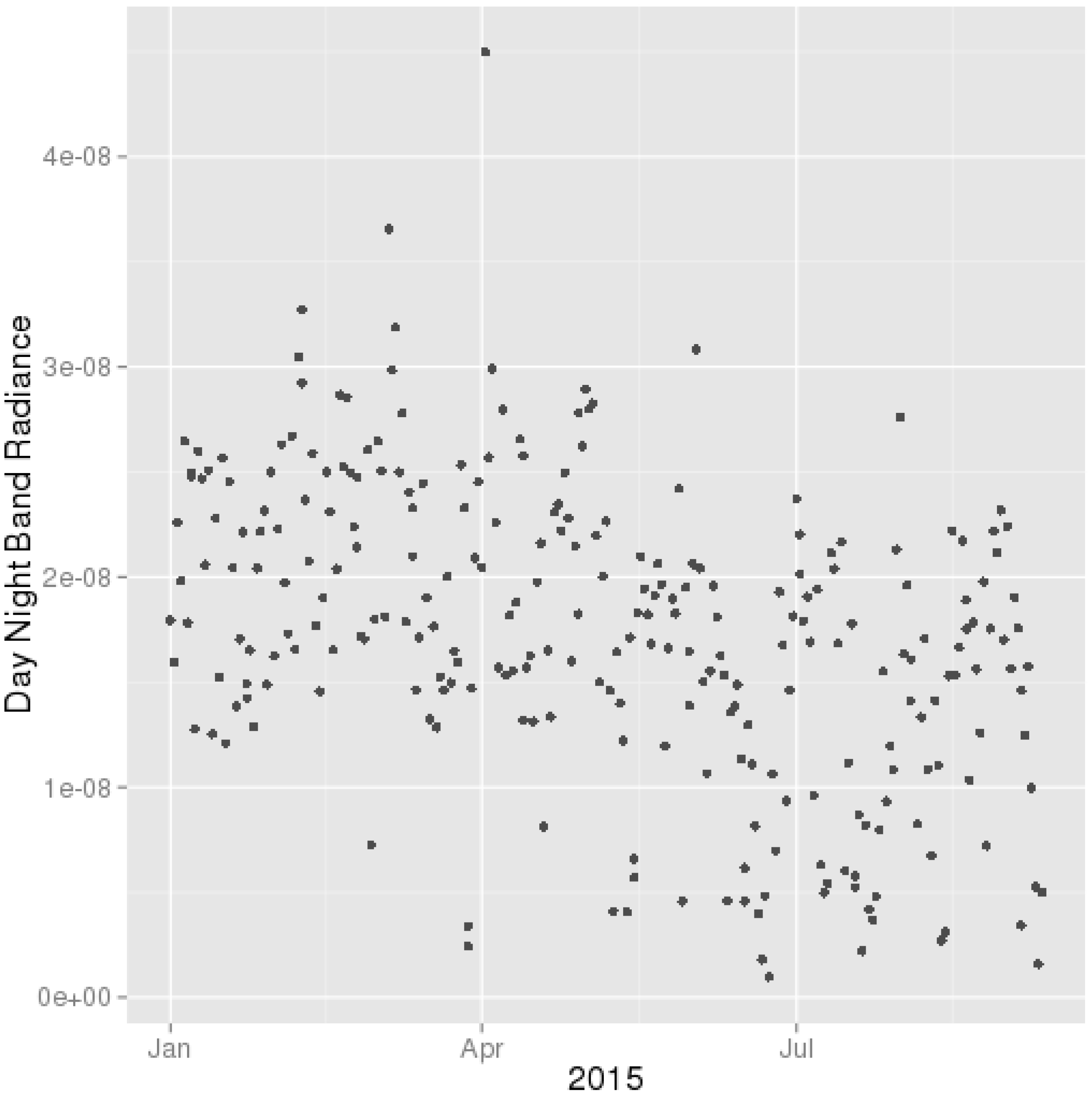
2.3. Remote Sensing
2.4. Voltage Monitors
2.5. Power Outage Classifier
2.6. Individual Power Outages and Power Outage Rates
2.7. Sensitivity Analysis
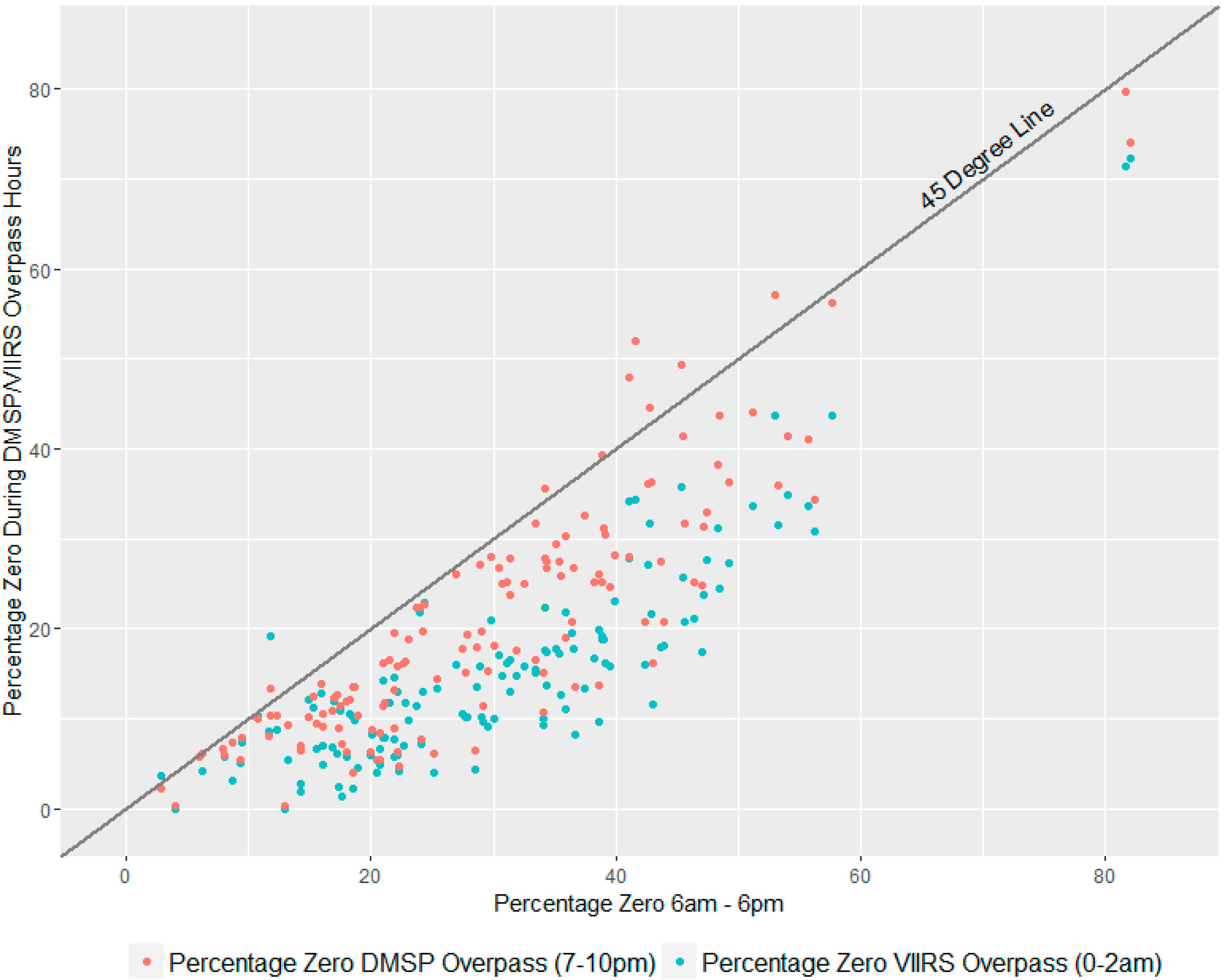
2.8. Validation
3. Results
3.1. Representativeness
3.2. Individual Power Outages
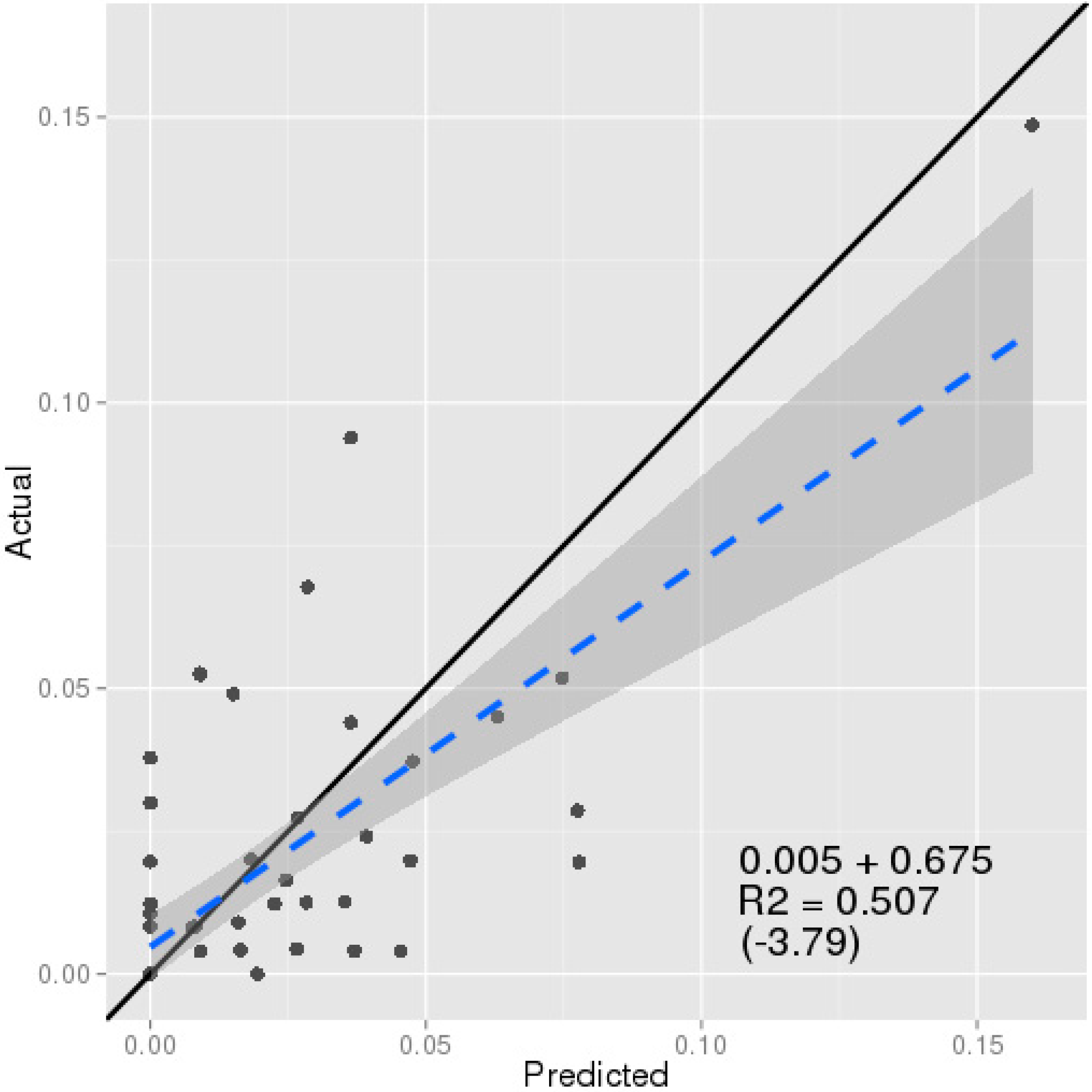
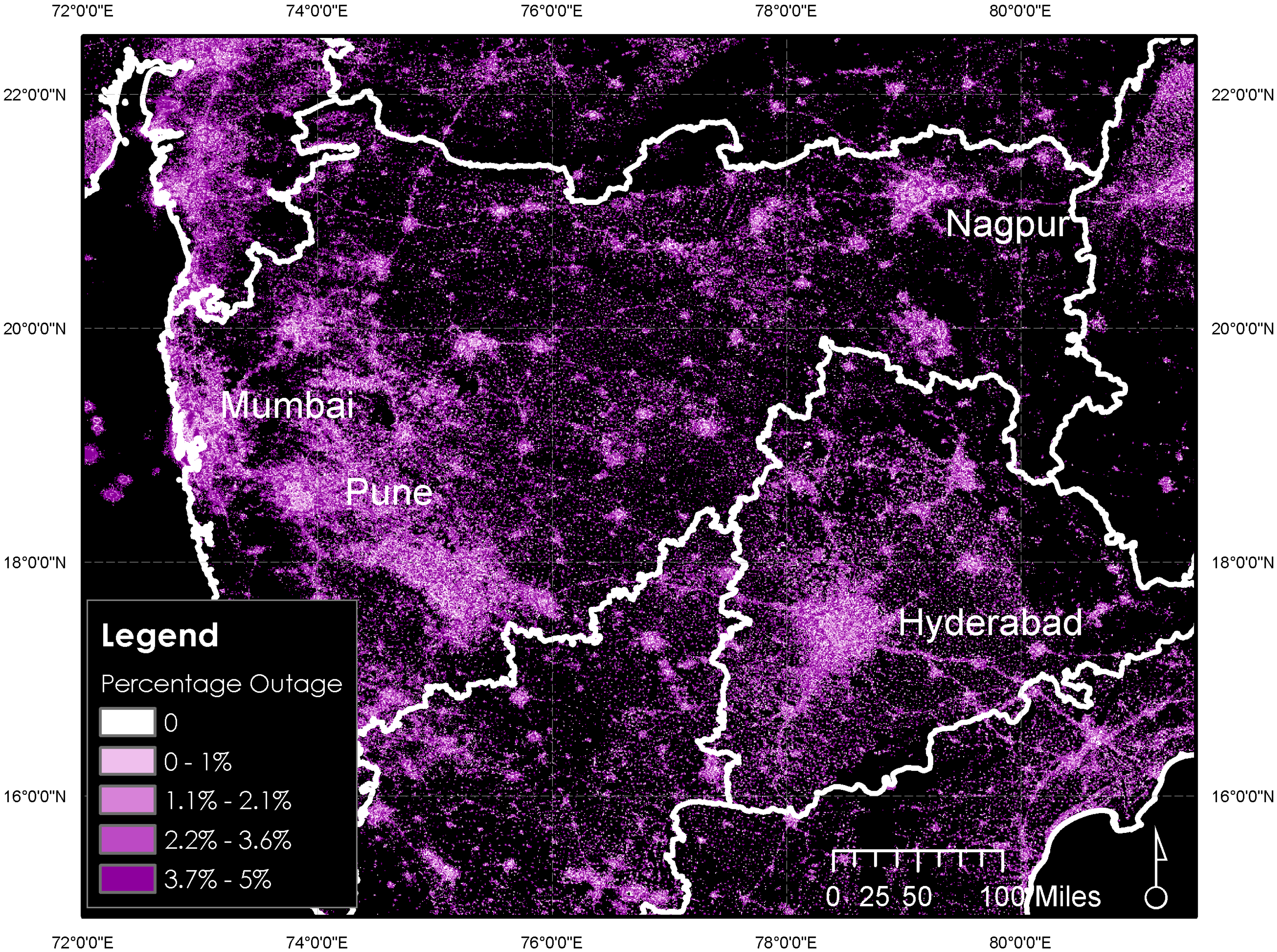
3.3. Power Outage Rates
4. Discussion
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Fisher-Vanden, K.; Mansur, E.T.; Wang, Q.J. Electricity shortages and firm productivity: Evidence from China’s industrial firms. J. Dev. Econ. 2015, 114, 172–188. [Google Scholar] [CrossRef]
- Alam, M. Coping with Blackouts: Power Outages and Firm Choices. Ph.D. Thesis, Yale University, New Haven, CT, USA, 2014. [Google Scholar]
- Allcott, H.; Collard-Wexler, A.; O’Connell, S.D. How do electricity shortages affect productivity? Evidence from India. Am. Econ. Rev. 2016, 106, 587–624. [Google Scholar] [CrossRef]
- Zuberi, J. Estimating the Cost of Power Outages for Large Scale Manufacturing Firms. University of California: Berkeley, CA, USA, Unpublished work. 2012. [Google Scholar]
- Anderson, G.B.; Bell, M.L. Lights out: Impact of the August 2003 power outage on mortality in New York, NY. Epidemiology 2012, 23, 189. [Google Scholar] [CrossRef] [PubMed]
- Burlando, A. Transitory shocks and birth weights: Evidence from a blackout in Zanzibar. J. Dev. Econ. 2014, 108, 154–168. [Google Scholar] [CrossRef]
- Chakravorty, U.; Pelli, M.; Marchand, B.U. Does the quality of electricity matter? Evidence from rural India. J. Econ. Behav. Organ. 2014, 107, 228–247. [Google Scholar] [CrossRef]
- Fetzer, T.; Pardo, O.; Shanghavi, A. An Urban Legend?! Power Rationing, Fertility and Its Effects on Mothers. Available online: http://cep.lse.ac.uk/pubs/download/dp1247.pdf (accessed on 24 May 2016).
- Seetharam, D.P.; Agrawal, A.; Ganu, T.; Hazra, J.; Rajaraman, V.; Kunnath, R. Hidden costs of power cuts and battery backups. In Proceedings of the Fourth International Conference on Future Energy Systems, ACM, Berkeley, CA, USA, 22–24 May 2013; pp. 39–50.
- Steinbuks, J.; Foster, V. When do firms generate? Evidence on in-house electricity supply in Africa. Energy Econ. 2010, 32, 505–514. [Google Scholar] [CrossRef]
- Guttikunda, S.K.; Jawahar, P. Application of SIM-air modeling tools to assess air quality in Indian cities. Atmos. Environ. 2012, 62, 551–561. [Google Scholar] [CrossRef]
- Elvidge, C.D.; Baugh, K.E.; Zhizhin, M.; Hsu, F.-C. Why VIIRS data are superior to DMSP for mapping nighttime lights. Proc. Asia-Pac. Adv. Netw. 2013, 35, 62–69. [Google Scholar] [CrossRef]
- Kyba, C.; Garz, S.; Kuechly, H.; de Miguel, A.S.; Zamorano, J.; Fischer, J.; Hölker, F. High-resolution imagery of Earth at night: New sources, opportunities and challenges. Remote Sens. 2014, 7, 1–23. [Google Scholar] [CrossRef]
- MahaDiscom Hourly Feeder Load Information. Available online: http://www.mahadiscom.com/feeder-hourly-data/hourly-feeder-load-information.shtm (accessed on 24 May 2016).
- Web LAADS Level Land Atmosphere Archive and Distribution System. Available online: https://earthdata.nasa.gov/about/daacs/daac-laads (accessed on 24 May 2016).
- Prayas Electricity Monitoring Initiative. Available online: http://www.watchyourpower.org/the_initiative.php (accessed on 24 May 2016).
- Varian, H.R. Big data: New tricks for econometrics. J. Econ. Perspect. 2014, 28, 3–27. [Google Scholar] [CrossRef]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Kulkarni, S.; Prayas Energy Group, Maharashtra, India. Personal communication, 2015.
- Meyer, D.; Hornik, K.; Weingessel, A.; Chang, C.; Lin, C. Package e1071. Available online: https://cran.r-project.org/web/packages/e1071/e1071.pdf (accessed on 24 May 2016).
- Central Electricity Authority of India. Load Generation Balance Report 2014–2015; Central Electricity Authority: New Delhi, India, 2015.
- Huang, Q.; Yang, X.; Gao, B.; Yang, Y.; Zhao, Y. Application of DMSP/OLS nighttime light images: A meta-analysis and a systematic literature review. Remote Sens. 2014, 6, 6844–6866. [Google Scholar] [CrossRef]
- Zhang, Q.; Seto, K.C. Can night-time light data identify typologies of urbanization? A global assessment of successes and failures. Remote Sens. 2013, 5, 3476–3494. [Google Scholar] [CrossRef]
- Liao, L.B.; Weiss, S.; Mills, S.; Hauss, B. Suomi NPP VIIRS day-night band on-orbit performance. J. Geophys. Res. Atmos. 2013, 118, 12705–12718. [Google Scholar] [CrossRef]
- Wang, J.; Aegerter, C.; Xu, X.; Szykman, J.J. Potential application of VIIRS Day/Night Band for monitoring nighttime surface PM 2.5 air quality from space. Atmos. Environ. 2016, 124, 55–63. [Google Scholar] [CrossRef]


| Predicted | ||||
|---|---|---|---|---|
| No Lights | Lights On | Outage | ||
| Actual | No Lights | 1741 | 0 | 0 |
| Lights On | 0 | 1737 | 48 | |
| Outage | 0 | 83 | 31 | |
| Overall Error Rate: 2.69% | ||||
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mann, M.L.; Melaas, E.K.; Malik, A. Using VIIRS Day/Night Band to Measure Electricity Supply Reliability: Preliminary Results from Maharashtra, India. Remote Sens. 2016, 8, 711. https://doi.org/10.3390/rs8090711
Mann ML, Melaas EK, Malik A. Using VIIRS Day/Night Band to Measure Electricity Supply Reliability: Preliminary Results from Maharashtra, India. Remote Sensing. 2016; 8(9):711. https://doi.org/10.3390/rs8090711
Chicago/Turabian StyleMann, Michael L., Eli K. Melaas, and Arun Malik. 2016. "Using VIIRS Day/Night Band to Measure Electricity Supply Reliability: Preliminary Results from Maharashtra, India" Remote Sensing 8, no. 9: 711. https://doi.org/10.3390/rs8090711
APA StyleMann, M. L., Melaas, E. K., & Malik, A. (2016). Using VIIRS Day/Night Band to Measure Electricity Supply Reliability: Preliminary Results from Maharashtra, India. Remote Sensing, 8(9), 711. https://doi.org/10.3390/rs8090711