Flood Damage Analysis: First Floor Elevation Uncertainty Resulting from LiDAR-Derived Digital Surface Models
Abstract
:1. Introduction
2. Materials and Methods
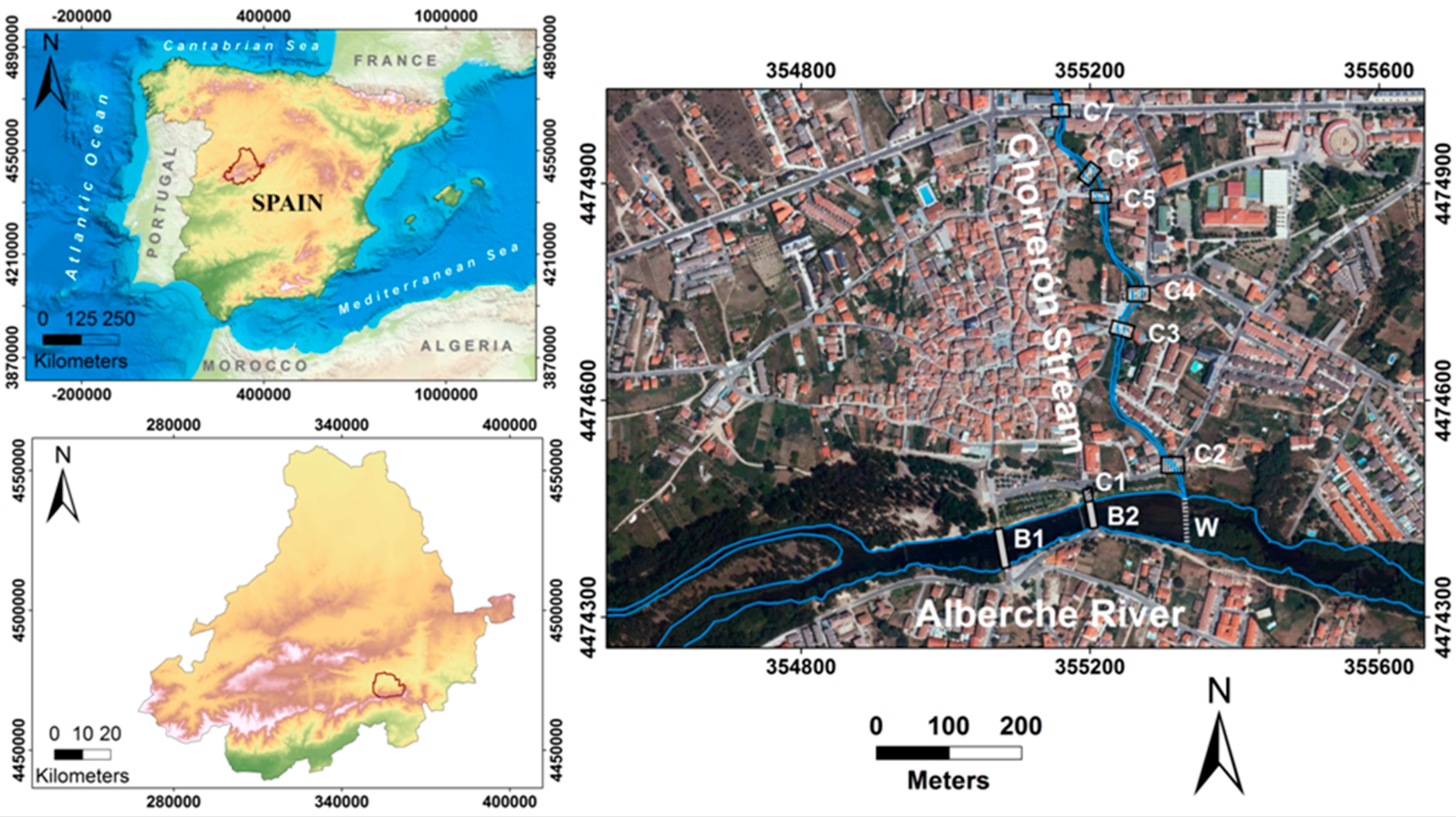
2.1. Study Area
2.2. DSM Construction
2.3. 2D Hydrodynamic Modelling
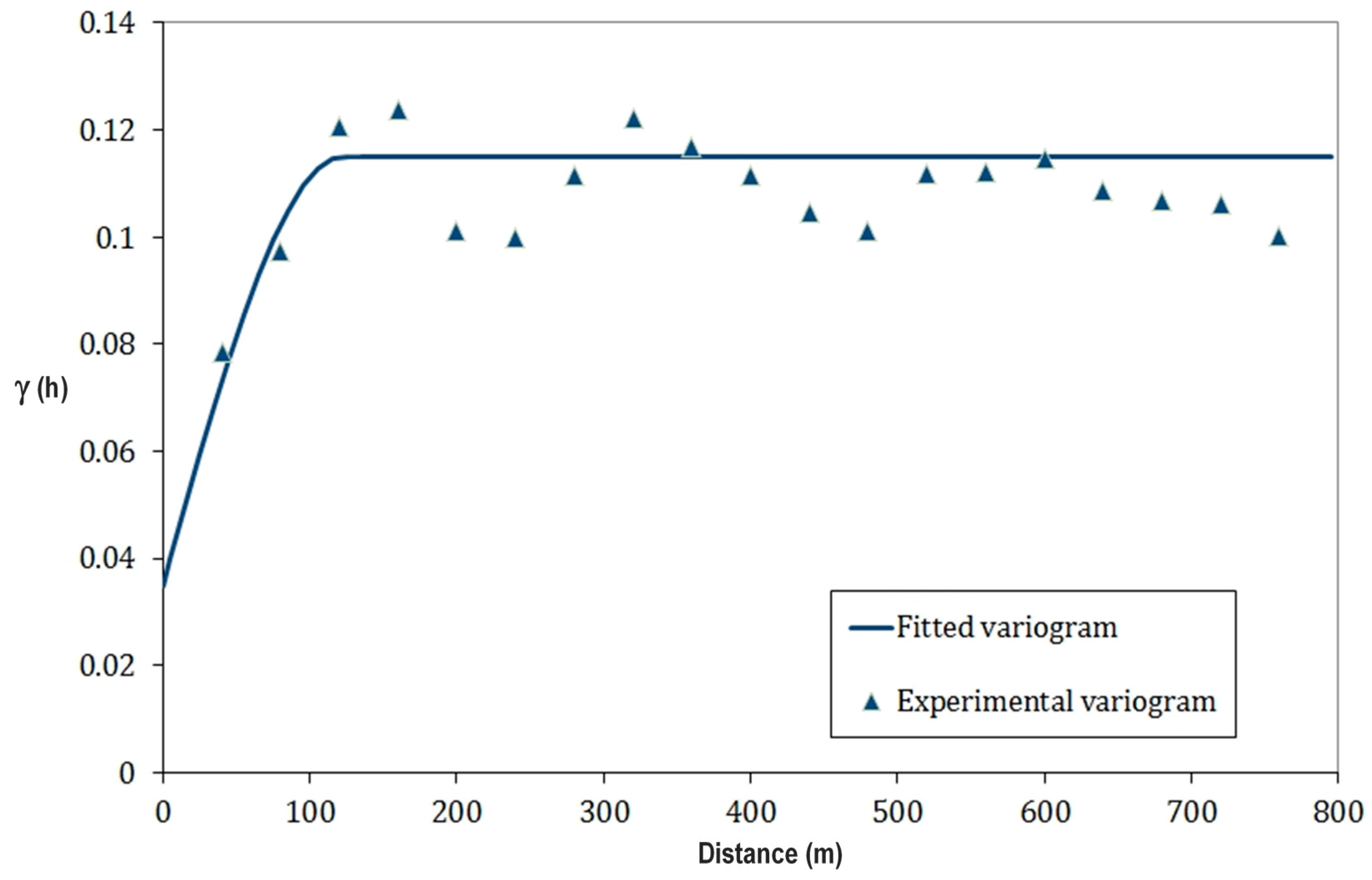
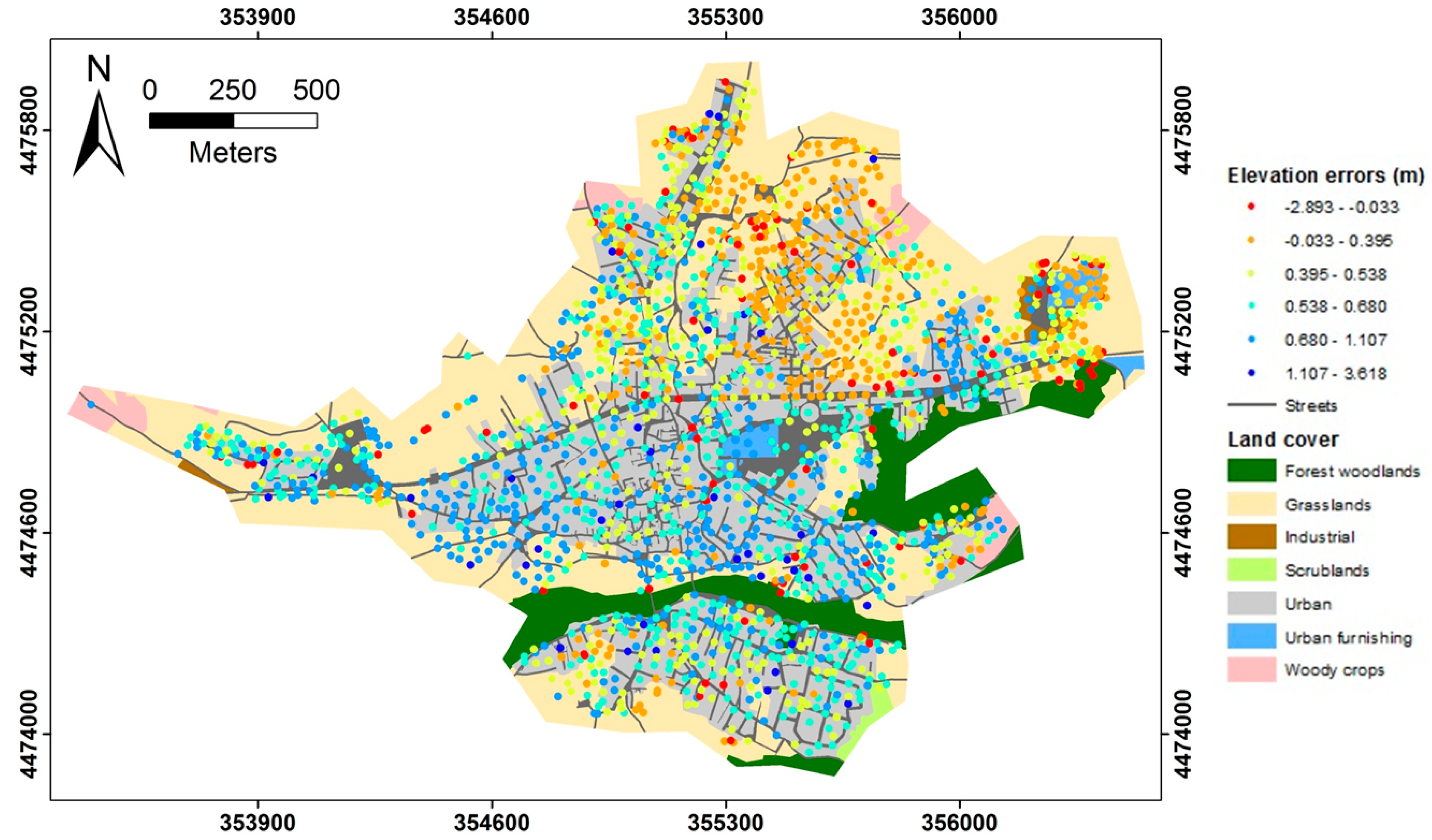
2.4. Geostatistical Uncertainty Analysis
3. Results
3.1. 500-Year Flood Zone
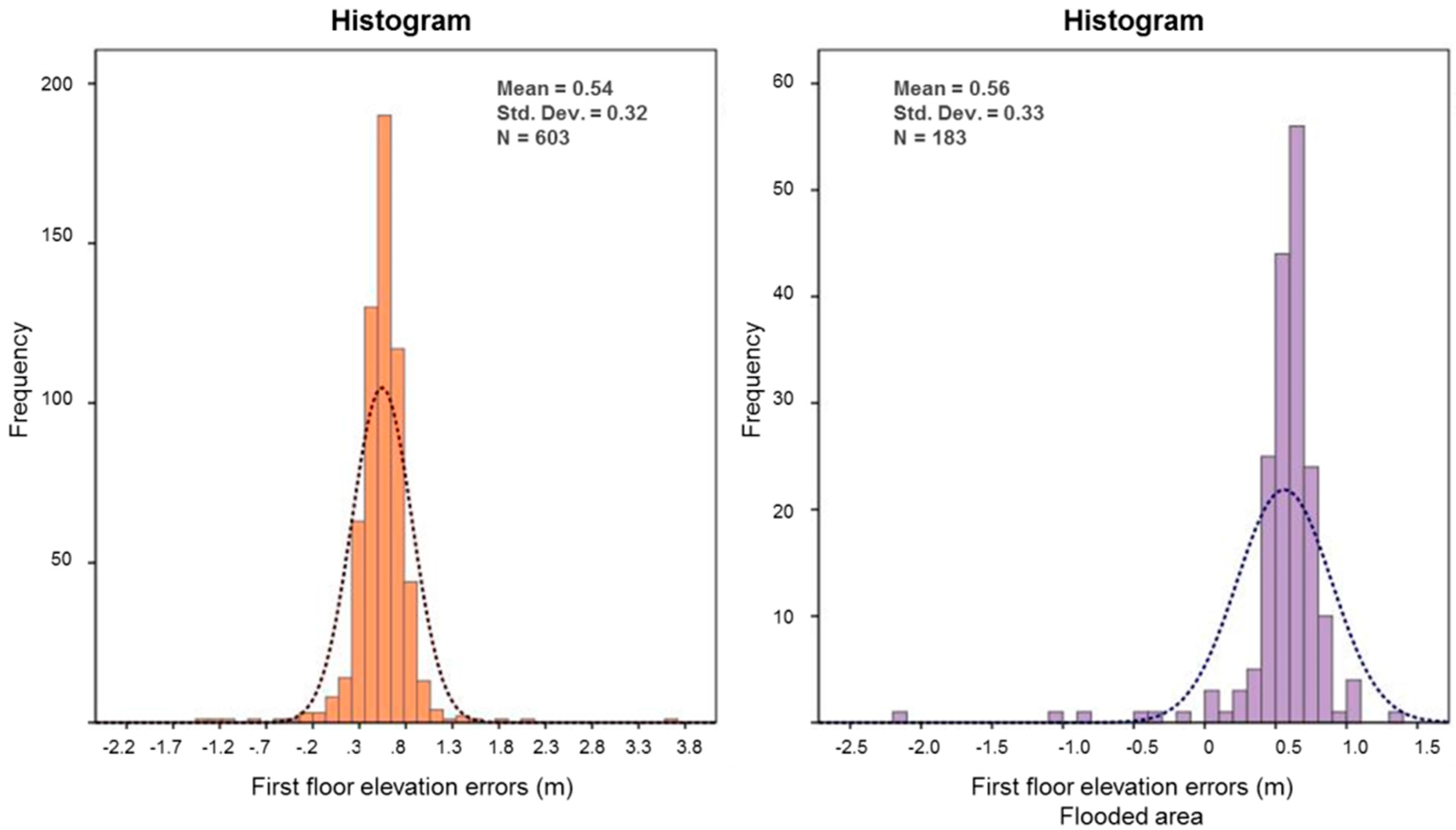
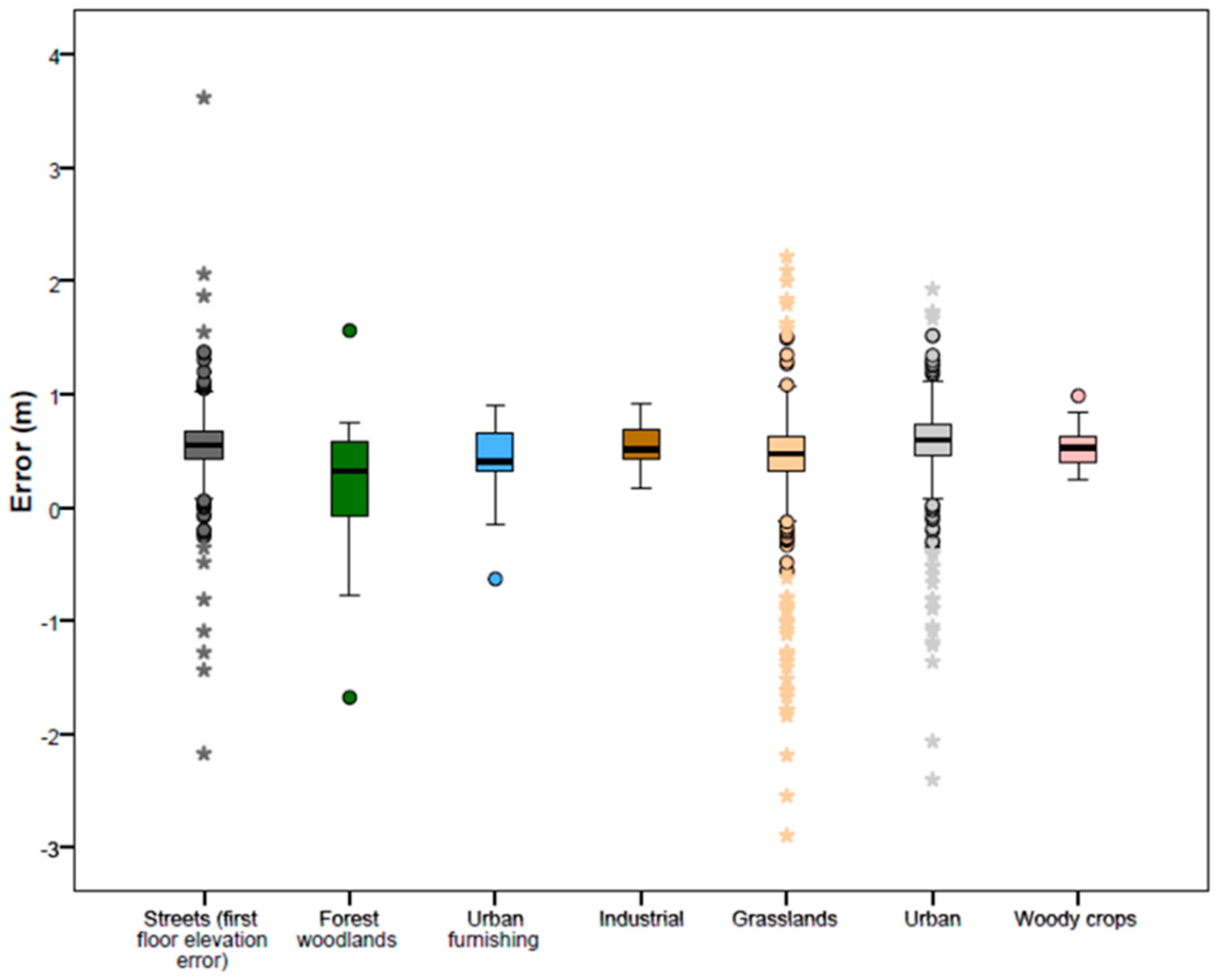
3.2. First Floor Elevation Uncertainty
4. Discussion
4.1. 2D Hydrodynamic Modelling
4.2. Geostatistical Analysis
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Nones, M. Implementation of the floods directive in selected eu member states. Water Environ. J. 2015, 29, 412–418. [Google Scholar] [CrossRef]
- Hubbard, S.; Stewart, K.; Fan, J. Modeling spatiotemporal patterns of building vulnerability and content evacuations before a riverine flood disaster. Appl. Geogr. 2014, 52, 172–181. [Google Scholar] [CrossRef]
- Webster, T.L.; Forbes, D.L.; Dickie, S.; Shreenan, R. Using topographic LiDAR to map flood risk from storm-surge events for Charlottetown, Prince Edward Island, Canada. Can. J. Remote Sens. 2004, 30, 64–76. [Google Scholar] [CrossRef]
- Webster, T.L. Flood risk mapping using LiDAR for Annapolis Royal, Nova Scotia, Canada. Remote Sens. 2010, 2, 2060–2082. [Google Scholar] [CrossRef]
- Abdullah, A.F.; Vojinovic, Z.; Price, R.K.; Aziz, N.A.A. Improved methodology for processing raw LiDAR data to support urban flood modelling—Accounting for elevated roads and bridges. J. Hydroinform. 2012, 14, 253–269. [Google Scholar] [CrossRef]
- Hohenthal, J.; Alho, P.; Hyyppa, J.; Hyyppa, H. Laser scanning applications in fluvial studies. Prog. Phys. Geogr. 2011, 35, 782–809. [Google Scholar] [CrossRef]
- Susaki, J. Adaptive slope filtering of airborne LiDAR data in urban areas for digital terrain model (DTM) generation. Remote Sens. 2012, 4, 1804–1819. [Google Scholar] [CrossRef]
- Maiman, T.H. Stimulated optical radiation in ruby. Nature 1960, 187, 493–494. [Google Scholar] [CrossRef]
- Smullin, L.D.; Fiocco, G. Optical echoes from moon. Nature 1962, 194, 1267. [Google Scholar] [CrossRef]
- Lim, K.; Treitz, P.; Wulder, M.; St-Onge, B.; Flood, M. LiDAR remote sensing of forest structure. Prog. Phys. Geogr. 2003, 27, 88–106. [Google Scholar] [CrossRef]
- Sithole, G.; Vosselman, G. Experimental comparison of filter algorithms for bare-earth extraction from airborne laser scanning point clouds. ISPRS J. Photogramm. Remote Sens. 2004, 59, 85–101. [Google Scholar] [CrossRef]
- Candela, T.; Renard, F.; Bouchon, M.; Brouste, A.; Marsan, D.; Schmittbuhl, J.; Voisin, C. Characterization of fault roughness at various scales: Implications of three-dimensional high resolution topography measurements. Pure Appl. Geophys. 2009, 166, 1817–1851. [Google Scholar] [CrossRef]
- Perroy, R.L.; Bookhagen, B.; Asner, G.P.; Chadwick, O.A. Comparison of gully erosion estimates using airborne and ground-based LiDAR on Santa Cruz Island, California. Geomorphology 2010, 118, 288–300. [Google Scholar] [CrossRef]
- Goulden, T.; Hopkinson, C.; Jamieson, R. Sensitivity of topographic slope and modelled watershed soil loss to DEM resolution. Remote Sens. Hydrol. 2012, 352, 345–349. [Google Scholar]
- Rogers, R.R.; Vaughan, M.A.; Hostetler, C.A.; Burton, S.P.; Ferrare, R.A.; Young, S.A.; Hair, J.W.; Obland, M.D.; Harper, D.B.; Cook, A.L.; et al. Looking through the haze: Evaluating the Calipso level 2 aerosol optical depth using airborne high spectral resolution LiDAR data. Atmos. Meas. Tech. 2014, 7, 4317–4340. [Google Scholar] [CrossRef]
- Croke, J.; Todd, P.; Thompson, C.; Watson, F.; Denham, R.; Khanal, G. The use of multi temporal LiDAR to assess basin-scale erosion and deposition following the catastrophic January 2011 lockyer flood, SE Queensland, Australia. Geomorphology 2013, 184, 111–126. [Google Scholar] [CrossRef]
- Del Val, M.; Iriarte, E.; Arriolabengoa, M.; Aranburu, A. An automated method to extract fluvial terraces from LiDAR based high resolution digital elevation models: The Oiartzun Valley, a case study in the Cantabrian margin. Q. Int. 2015, 364, 35–43. [Google Scholar] [CrossRef]
- Aggett, G.R.; Wilson, J.P. Creating and coupling a high-resolution dtm with a 1-d hydraulic model in a GIS for scenario-based assessment of avulsion hazard in a gravel-bed river. Geomorphology 2009, 113, 21–34. [Google Scholar] [CrossRef]
- Meesuk, V.; Vojinovic, Z.; Mynett, A.E.; Abdullah, A.F. Urban flood modelling combining top-view LiDAR data with ground-view SFM observations. Adv. Water Resour. 2015, 75, 105–117. [Google Scholar] [CrossRef]
- Dorn, H.; Vetter, M.; Hoefle, B. Gis-based roughness derivation for flood simulations: A comparison of orthophotos, LiDAR and crowdsourced geodata. Remote Sens. 2014, 6, 1739–1759. [Google Scholar] [CrossRef]
- Mandlburger, G.; Hauer, C.; Hoefle, B.; Habersack, H.; Pfeifer, N. Optimisation of LiDAR derived terrain models for river flow modelling. Hydrol. Earth Syst. Sci. 2009, 13, 1453–1466. [Google Scholar] [CrossRef]
- Costabile, P.; Macchione, F. Enhancing river model set-up for 2-d dynamic flood modelling. Environ. Model. Softw. 2015, 67, 89–107. [Google Scholar] [CrossRef]
- Cook, A.; Merwade, V. Effect of topographic data, geometric configuration and modeling approach on flood inundation mapping. J. Hydrol. 2009, 377, 131–142. [Google Scholar] [CrossRef]
- Mason, D.C.; Cobby, D.M.; Horritt, M.S.; Bates, P.D. Floodplain friction parameterization in two-dimensional river flood models using vegetation heights derived from airborne scanning laser altimetry. Hydrol. Process. 2003, 17, 1711–1732. [Google Scholar] [CrossRef]
- Webster, T.L.; Forbes, D.L.; MacKinnon, E.; Roberts, D. Flood-risk mapping for storm-surge events and sea-level rise using LiDAR for southeast new brunswick. Can. J. Remote Sens. 2006, 32, 194–211. [Google Scholar] [CrossRef]
- Pfurtscheller, C.; Vetter, M. Assessing entrepreneurial and regional-economic flood impacts on a globalized production facility. J. Flood Risk Manag. 2015, 8, 329–342. [Google Scholar] [CrossRef]
- Haynes, H.; Haynes, R.; Pender, G. Integrating socio-economic analysis into decision-support methodology for flood risk management at the development scale (Scotland). Water Environ. J. 2008, 22, 117–124. [Google Scholar] [CrossRef]
- Apel, H.; Thieken, A.H.; Merz, B.; Bloschl, G. Flood risk assessment and associated uncertainty. Nat. Hazard. Earth Syst. Sci. 2004, 4, 295–308. [Google Scholar] [CrossRef]
- Ballesteros-Canovas, J.A.; Sanchez-Silva, M.; Bodoque, J.M.; Diez-Herrero, A. An integrated approach to flood risk management: A case study of Navaluenga (central Spain). Water Resour. Manag. 2013, 27, 3051–3069. [Google Scholar] [CrossRef]
- Hodgson, M.E.; Bresnahan, P. Accuracy of airborne LiDAR-derived elevation: Empirical assessment and error budget. Photogramm. Eng. Remote Sens. 2004, 70, 331–339. [Google Scholar] [CrossRef]
- Naesset, E. Vertical height errors in digital terrain models derived from airborne laser scanner data in a boreal-alpine ecotone in Norway. Remote Sens. 2015, 7, 4702–4725. [Google Scholar] [CrossRef]
- Díez-Herrero, A. Geomorfología e Hidrología Fluvial del Río Alberche: Modelos y Sig para la Gestión de Riberas. Ph.D. Tesis, Universidad Complutense de Madrid, Madrid, Spain, 2004. [Google Scholar]
- Instituto Geográfico Nacional (IGN). Centro de Descargas del CNIG. Available online: http://centrodedescargas.cnig.es/CentroDescargas/ (accessed on 15 February 2016).
- Luis Montealegre, A.; Teresa Lamelas, M.; de la Riva, J. A comparison of open-source LiDAR filtering algorithms in a mediterranean forest environment. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2015, 8, 4072–4085. [Google Scholar] [CrossRef]
- Liu, X.; Zhang, Z. Effects of LiDAR data reduction and breaklines on the accuracy of digital elevation model. Surv. Rev. 2011, 43, 614–628. [Google Scholar] [CrossRef]
- Choung, Y. Accuracy assessment of the levee lines generated using LiDAR data acquired in the nakdong river basins, South Korea. Remote Sens. Lett. 2014, 5, 853–861. [Google Scholar] [CrossRef]
- Bladé, E.; Cea, L.; Corestein, G.; Escolano, E.; Puertas, J.; Vázquez-Cendón, E.; Dolz, J.; Coll, A. Iber-river modelling simulation tool. Rev. Int. Metodos Numer. Calc. Diseno Ing. 2014, 30, 1–10. [Google Scholar]
- Bodoque, J.M.; Diez-Herrero, A.; Eguibar, M.A.; Benito, G.; Ruiz-Villanueva, V.; Ballesteros-Canovas, J.A. Challenges in paleoflood hydrology applied to risk analysis in mountainous watersheds—A review. J. Hydrol. 2015, 529, 449–467. [Google Scholar] [CrossRef]
- Sistema de Información de Ocupación del Suelo en España (SIOSE). Available online: http://www.siose.es (accessed on 10 January 2016).
- Chow, V.T. Open Channel Hydraulics; McGraw-Hill: Singapore, Singapore, 1959; p. 688. [Google Scholar]
- Vazquez-Cendon, M.E. Improved treatment of source terms in upwind schemes for the shallow water equations in channels with irregular geometry. J. Comput. Phys. 1999, 148, 497–526. [Google Scholar] [CrossRef]
- Sede Electrónica del Catastro (SEC). Available online: https://www.sedecatastro.gob.es (accessed on 25 March 2016).
- Journel, A.G. Modelling uncertainty and spatial dependence: Stochastic imaging. Int. J. Geogr. Inf. Syst. 1996, 10, 517–522. [Google Scholar] [CrossRef]
- Gomez-Hernandez, J.J.; Journel, A.G. Joint sequential simulation of multigaussian fields. Geostat. Troia ’92 1993, 1, 85–94. [Google Scholar]
- Matheron, G. The Theory of Regionalized Variables and Its Applications; École National Supérieure des Mines: Paris, France, 1971. [Google Scholar]
- Remy, N.; Boucher, A.; Wu, J. Applied Geostatistics with Sgems : A User’s Guide; Cambridge University Press: Cambridge, UK, 2009. [Google Scholar]
- Heuvelink, G.B.M. Error Propagation in Environmental Modelling with Gis; Taylor & Francis: London, UK, 1998. [Google Scholar]
- Costabile, P.; Macchione, F.; Natale, L.; Petaccia, G. Flood mapping using LiDAR dem. Limitations of the 1-d modeling highlighted by the 2-d approach. Nat. Hazard. 2015, 77, 181–204. [Google Scholar] [CrossRef]
- Shen, D.; Wang, J.; Cheng, X.; Rui, Y.; Ye, S. Integration of 2-d hydraulic model and high-resolution LiDAR-derived dem for floodplain flow modeling. Hydrol. Earth Syst. Sci. 2015, 19, 3605–3616. [Google Scholar] [CrossRef]
- Merwade, V.; Cook, A.; Coonrod, J. Gis techniques for creating river terrain models for hydrodynamic modeling and flood inundation mapping. Environ. Model. Softw. 2008, 23, 1300–1311. [Google Scholar] [CrossRef]
- Liu, X. Airborne LiDAR for dem generation: Some critical issues. Prog. Phys. Geogr. 2008, 32, 31–49. [Google Scholar]
- Brzank, A.; Heipke, C.; Goepfert, J.; Soergel, U. Aspects of generating precise digital terrain models in the wadden sea from LiDAR-water classification and structure line extraction. ISPRS J. Photogramm. Remote Sens. 2008, 63, 510–528. [Google Scholar] [CrossRef]
- U.S. Army Corps of Engineers (USACE). Risk-Based Analysis for Flood Damage Reduction Studies; USACE: Washington, DC, USA, 1996.
- Merz, B.; Kreibich, H.; Thieken, A.; Schmidtke, R. Estimation uncertainty of direct monetary flood damage to buildings. Nat. Hazard. Earth Syst. Sci. 2004, 4, 153–163. [Google Scholar] [CrossRef]
- Leon, J.X.; Heuvelink, G.B.M.; Phinn, S.R. Incorporating dem uncertainty in coastal inundation mapping. PLoS ONE 2014, 9, e108727. [Google Scholar] [CrossRef] [PubMed]
- Matkan, A.A.; Hajeb, M.; Mirbagheri, B.; Sadeghian, S.; Ahmadi, M. Spatial analysis for outlier removal from LiDAR data. In Proceedings of the 1st ISPRS International Conference on Geospatial Information Research, Tehran, Iran, 15 November 2014; Volume 40, pp. 187–190.
- Aerts, J.C.J.H.; Heuvelink, G.B.M.; Goodchild, M.F. Accounting for spatial uncertainty in optimization with spatial decision support systems. Trans. GIS 2003, 7, 211–230. [Google Scholar] [CrossRef]
- Journel, A.G.; Huijbregts, C.J. Mining Geostatistics; Academic Press: London, UK, 1978. [Google Scholar]
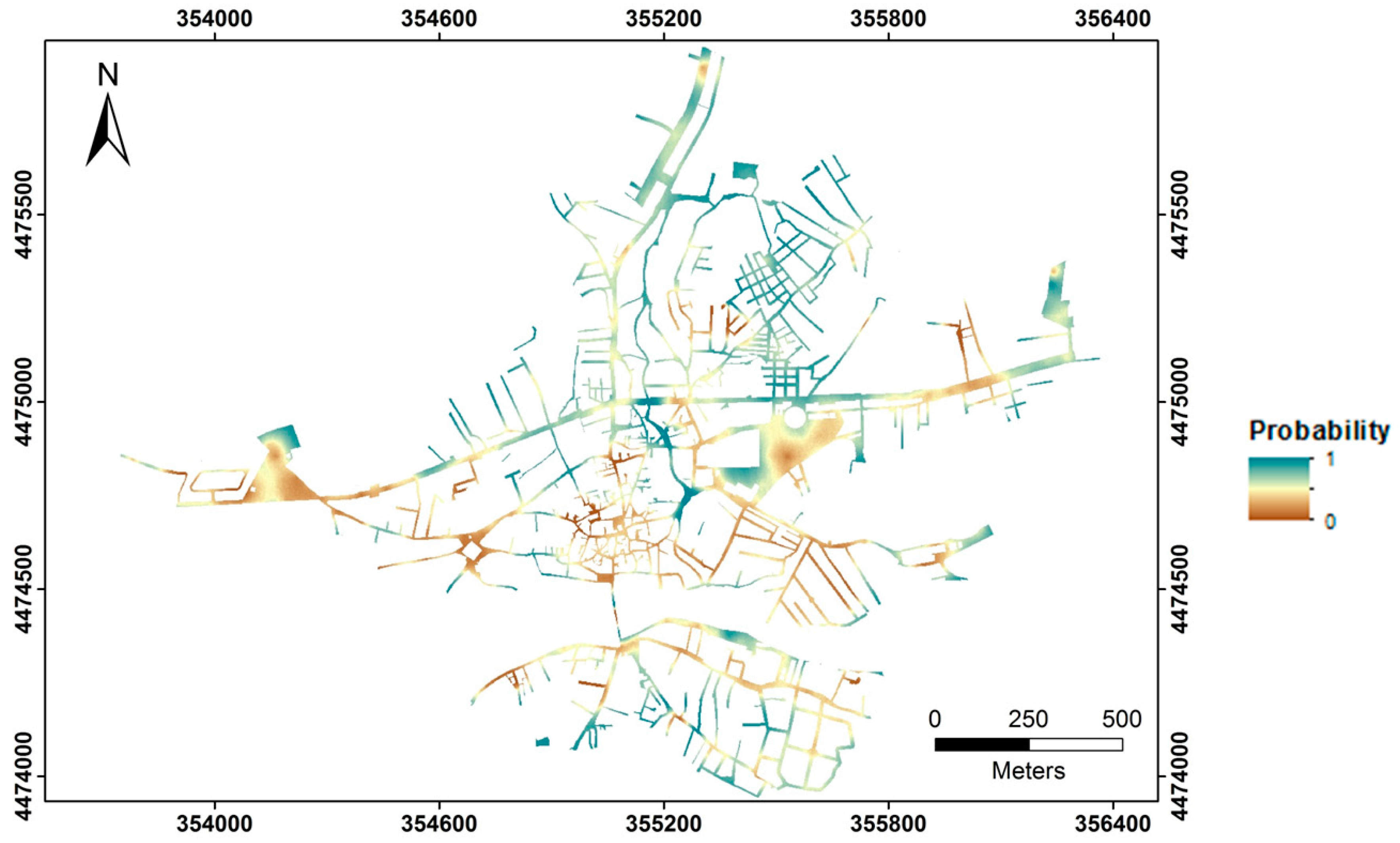
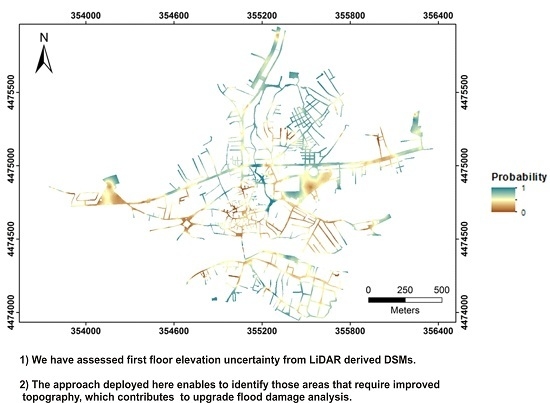
| Probability | Streets (Non-Prone to Be Flooded) | Streets (500-Year Flood Zone) | ||||
|---|---|---|---|---|---|---|
| Pixels | Area (m2) | Area (%) | Pixels | Area (m2) | Area (%) | |
| (0–0.10) | 1433 | 5732 | 1.42 | 450 | 1800 | 1.77 |
| (0.11–0.20) | 2660 | 10,640 | 2.64 | 690 | 2760 | 2.71 |
| (0.21–0.30) | 7027 | 28,108 | 6.96 | 2098 | 8392 | 8.25 |
| (0.31–0.40) | 12,067 | 48,268 | 11.96 | 4906 | 19,624 | 19.29 |
| (0.41–0.50) | 15,239 | 60,956 | 15.10 | 4640 | 18,560 | 18.25 |
| (0.51–0.60) | 14,917 | 59,668 | 14.78 | 4393 | 17,572 | 17.28 |
| (0.61–0.70) | 16,611 | 66,444 | 16.46 | 3135 | 12,540 | 12.33 |
| (0.71–0.80) | 14,111 | 56,444 | 13.98 | 1948 | 7792 | 7.66 |
| (0.81–0.90) | 12,224 | 48,896 | 12.11 | 1914 | 7656 | 7.53 |
| (0.91–1) | 4627 | 18,508 | 4.59 | 1253 | 5012 | 4.93 |
| Total | 100,916 | 403,664 | 100 | 25,427 | 101,708 | 100 |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bodoque, J.M.; Guardiola-Albert, C.; Aroca-Jiménez, E.; Eguibar, M.Á.; Martínez-Chenoll, M.L. Flood Damage Analysis: First Floor Elevation Uncertainty Resulting from LiDAR-Derived Digital Surface Models. Remote Sens. 2016, 8, 604. https://doi.org/10.3390/rs8070604
Bodoque JM, Guardiola-Albert C, Aroca-Jiménez E, Eguibar MÁ, Martínez-Chenoll ML. Flood Damage Analysis: First Floor Elevation Uncertainty Resulting from LiDAR-Derived Digital Surface Models. Remote Sensing. 2016; 8(7):604. https://doi.org/10.3390/rs8070604
Chicago/Turabian StyleBodoque, José María, Carolina Guardiola-Albert, Estefanía Aroca-Jiménez, Miguel Ángel Eguibar, and María Lorena Martínez-Chenoll. 2016. "Flood Damage Analysis: First Floor Elevation Uncertainty Resulting from LiDAR-Derived Digital Surface Models" Remote Sensing 8, no. 7: 604. https://doi.org/10.3390/rs8070604
APA StyleBodoque, J. M., Guardiola-Albert, C., Aroca-Jiménez, E., Eguibar, M. Á., & Martínez-Chenoll, M. L. (2016). Flood Damage Analysis: First Floor Elevation Uncertainty Resulting from LiDAR-Derived Digital Surface Models. Remote Sensing, 8(7), 604. https://doi.org/10.3390/rs8070604