Hyperspectral Unmixing with Robust Collaborative Sparse Regression
Abstract
:1. Introduction
2. Robust Collaborative Sparse Regression

3. Experiments
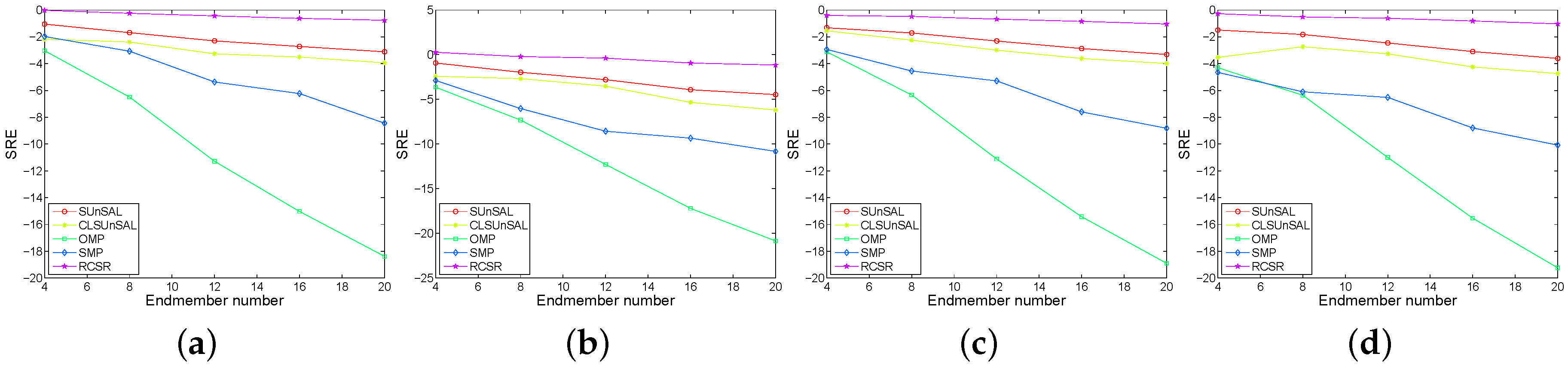
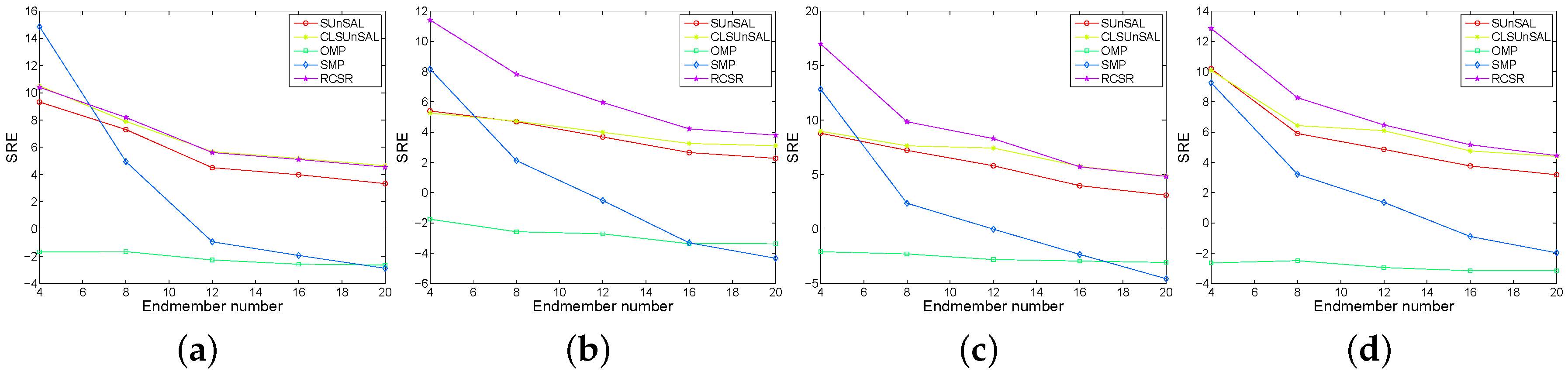
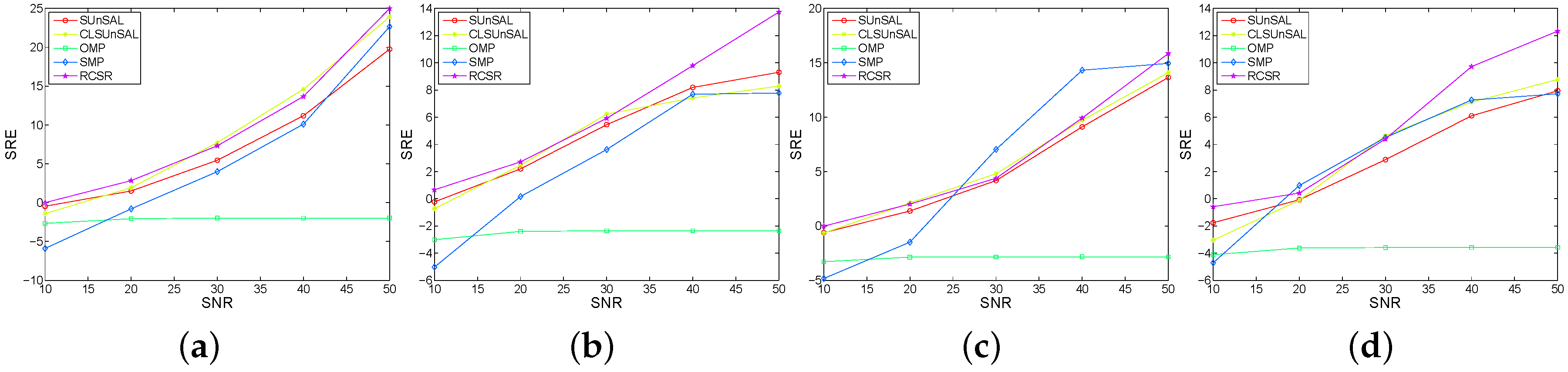
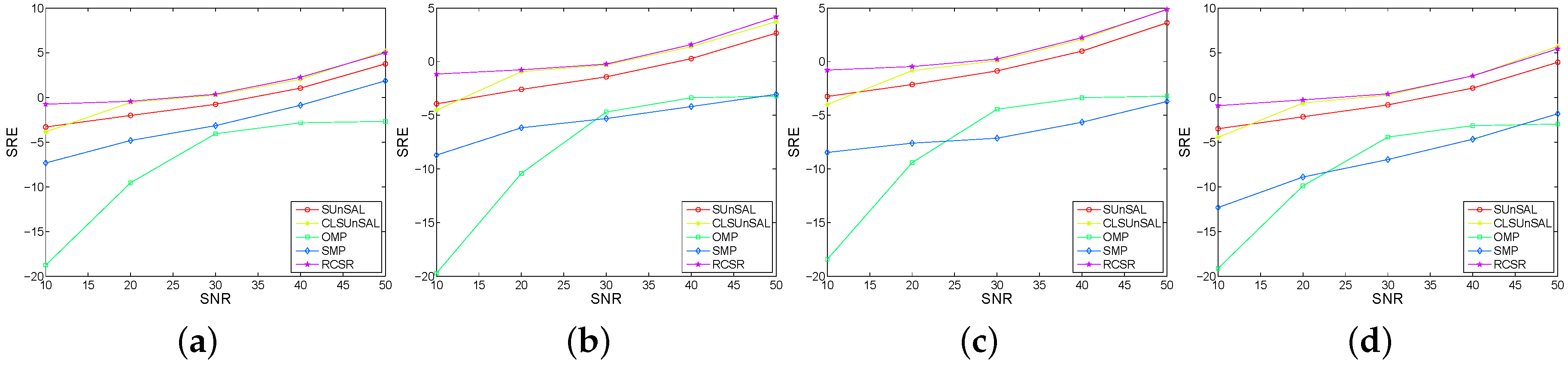
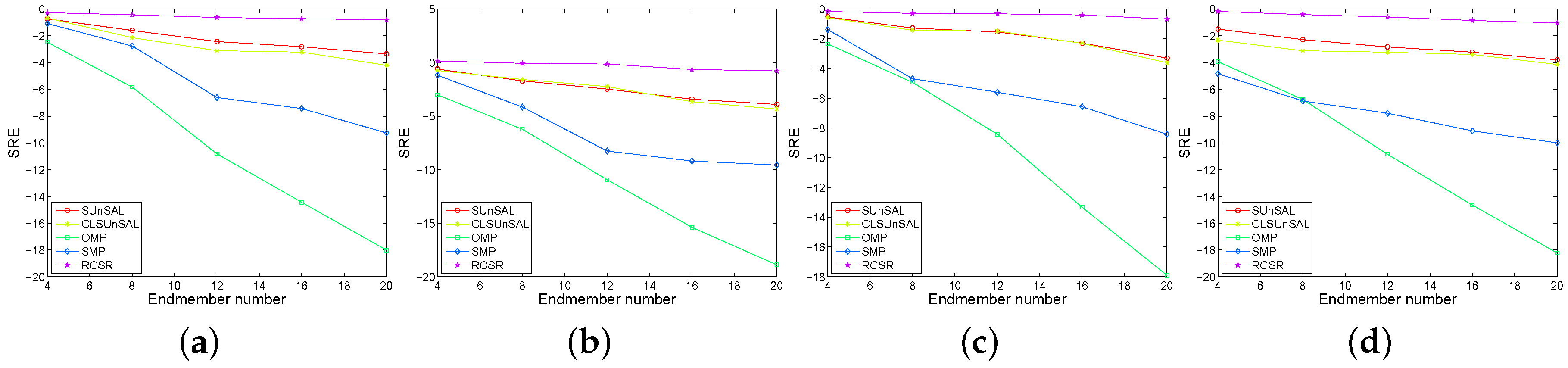
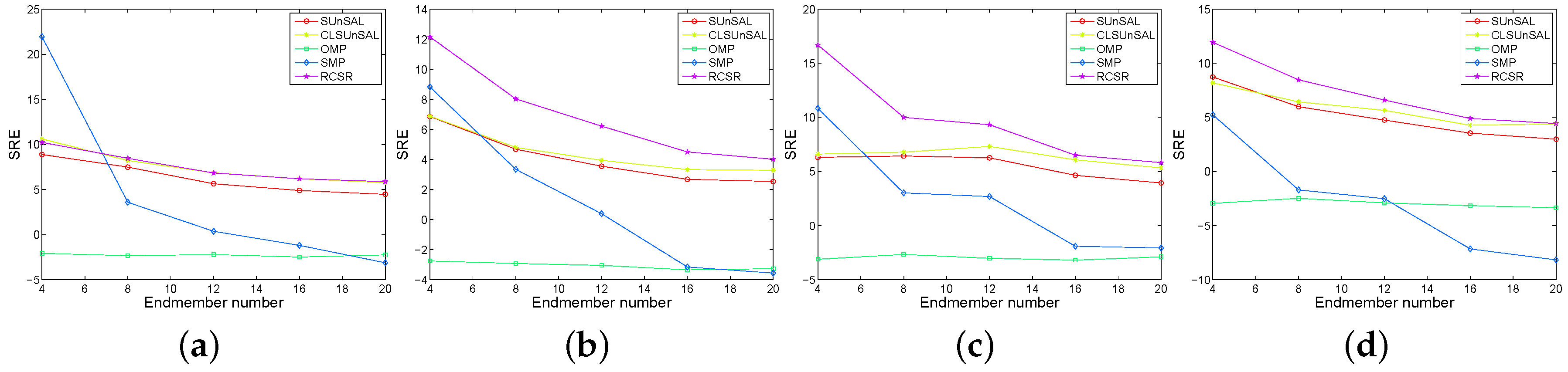
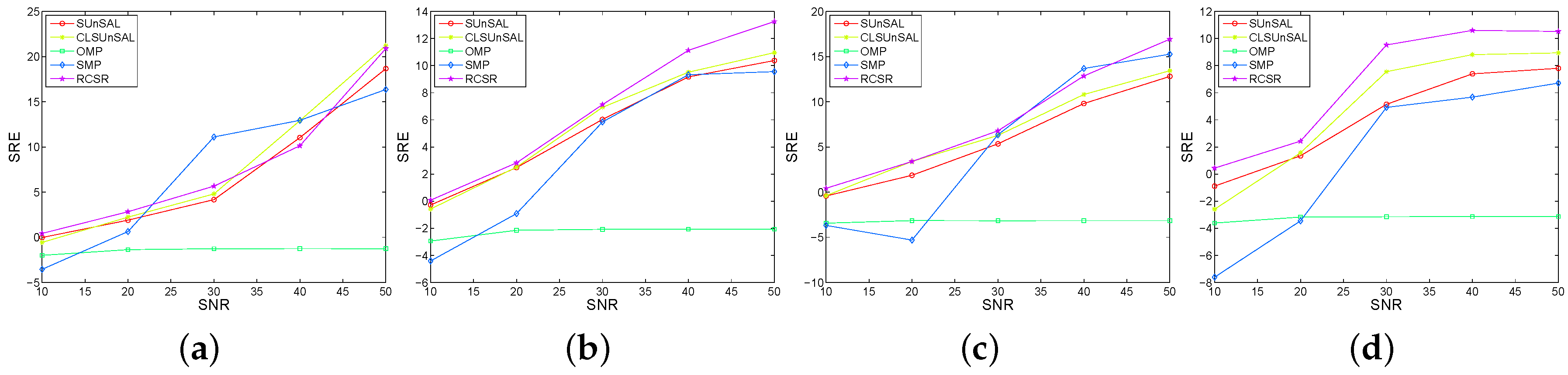
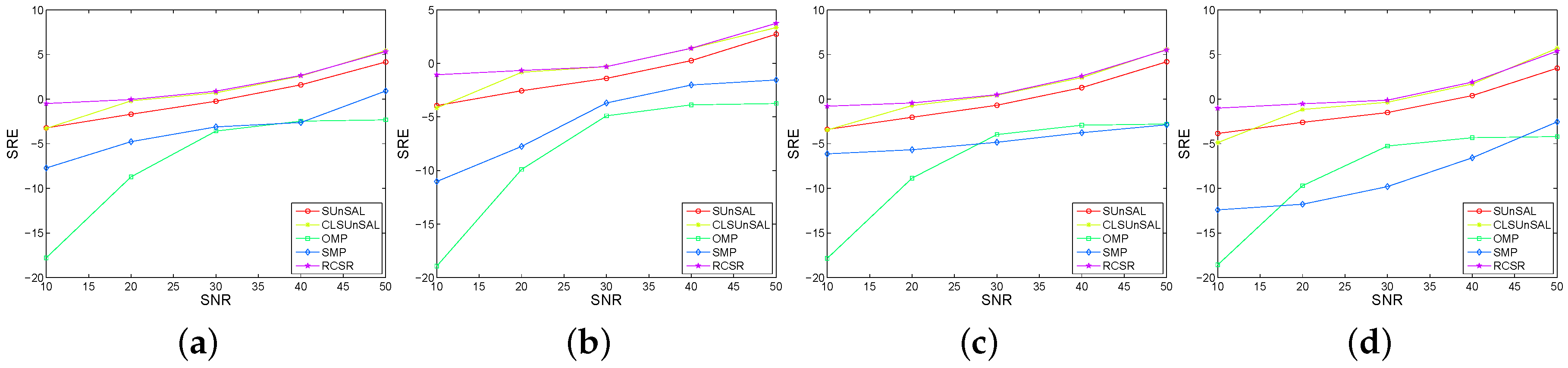
3.1. Experimental Results with Synthetic Data
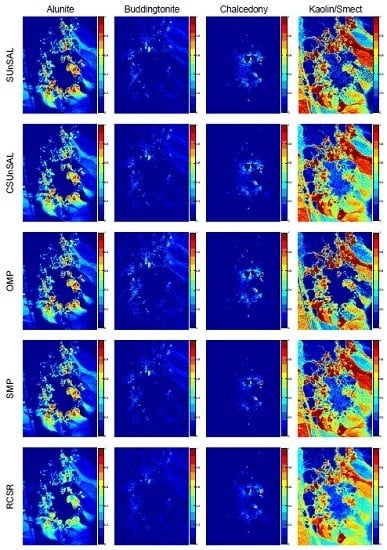
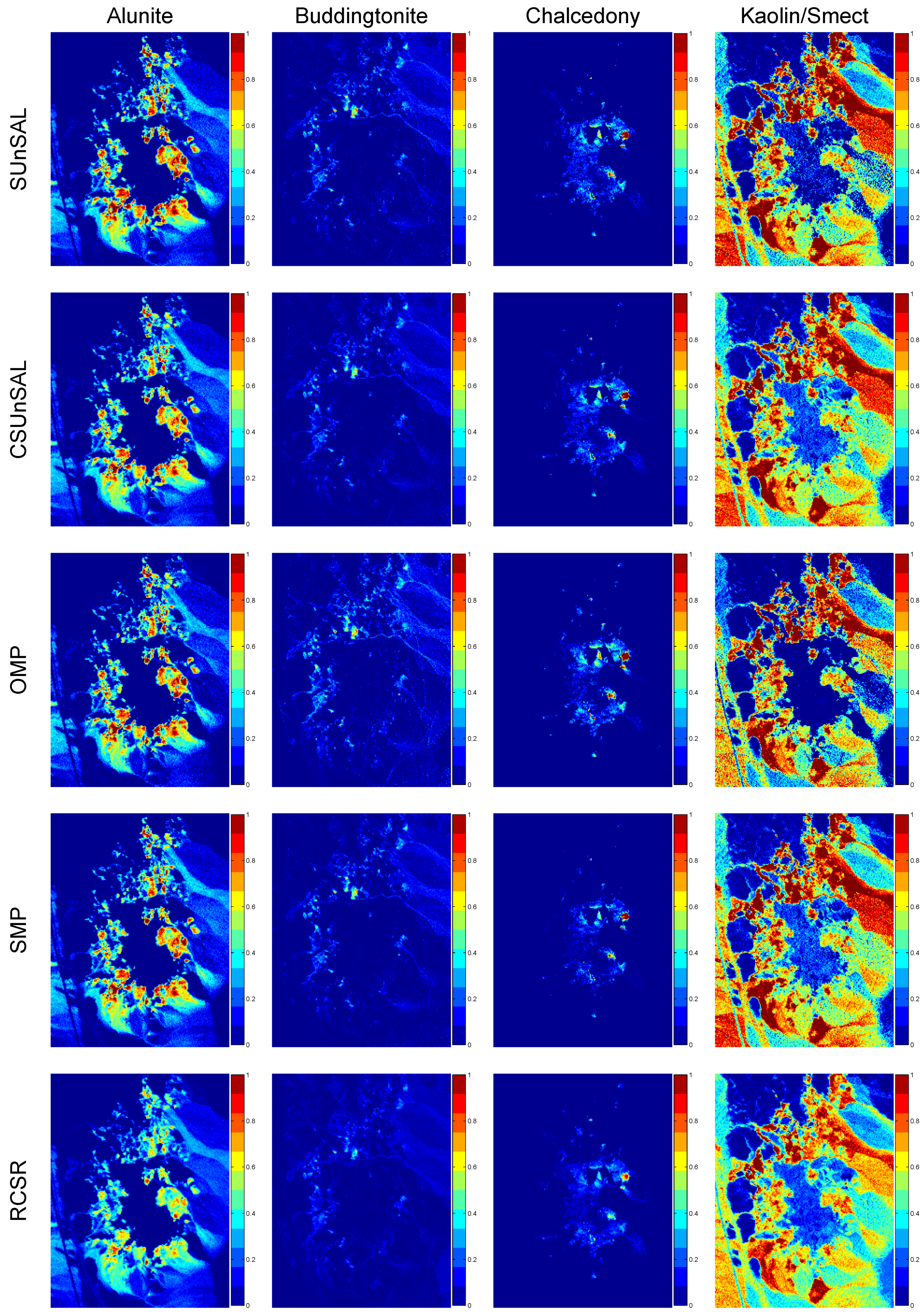
3.2. Experimental Results with Real Data
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Ma, L.; Crawford, M.M.; Yang, X.; Guo, Y. Local-manifold-learning-based graph construction for semisupervised hyperspectral image classification. IEEE Trans. Geosci. Remote Sens. 2015, 53, 2832–2844. [Google Scholar] [CrossRef]
- Ma, J.; Zhou, H.; Zhao, J.; Gao, Y.; Jiang, J.; Tian, J. Robust feature matching for remote sensing image registration via locally linear transforming. IEEE Trans. Geosci. Remote Sens. 2015, 53, 6469–6481. [Google Scholar] [CrossRef]
- Li, C.; Ma, Y.; Huang, J.; Mei, X.; Ma, J. Hyperspectral image denoising using the robust low-rank tensor recovery. JOSA A 2015, 32, 1604–1612. [Google Scholar] [CrossRef] [PubMed]
- Li, Y.; Tao, C.; Tan, Y.; Shang, K.; Tian, J. Unsupervised multilayer feature learning for satellite image scene classification. IEEE Geosci. Remote Sens. Lett. 2016, 13, 157–161. [Google Scholar] [CrossRef]
- Liu, H.; Liu, S.; Huang, T.; Zhang, Z.; Hu, Y.; Zhang, T. Infrared spectrum blind deconvolution algorithm via learned dictionaries and sparse representation. Appl. Opt. 2016, 55, 2813–2818. [Google Scholar] [CrossRef] [PubMed]
- Pu, H.; Chen, Z.; Wang, B.; Xia, W. Constrained least squares algorithms for nonlinear unmixing of hyperspectral imagery. IEEE Trans. Geosci. Remote Sens. 2015, 53, 1287–1303. [Google Scholar] [CrossRef]
- Stites, M.; Gunther, J.; Moon, T.; Williams, G. Using Physically-Modeled Synthetic data to assess hyperspectral unmixing approaches. Remote Sens. 2013, 5, 1974–1997. [Google Scholar] [CrossRef]
- Averbuch, A.; Zheludev, M. Two linear unmixing algorithms to recognize targets using supervised classification and orthogonal rotation in airborne hyperspectral images. Remote Sens. 2012, 4, 532–560. [Google Scholar] [CrossRef]
- Li, X.; Cui, J.; Zhao, L. Blind nonlinear hyperspectral unmixing based on constrained kernel nonnegative matrix factorization. Signal Image Video Process. 2014, 8, 1555–1567. [Google Scholar] [CrossRef]
- Zheng, C.Y.; Li, H.; Wang, Q.; Philip Chen, C. Reweighted sparse regression for hyperspectral unmixing. IEEE Trans. Geosci. Remote Sens. 2016, 54, 479–488. [Google Scholar] [CrossRef]
- Mei, S.; Du, Q.; He, M. Equivalent-sparse unmixing through spatial and spectral constrained endmember selection from an image-derived spectral library. IEEE J. Sel. Top. Appl. Earth Observ. Remote Sens. 2015, 8, 2665–2675. [Google Scholar] [CrossRef]
- Esmaeili Salehani, Y.; Gazor, S.; Kim, I.M.; Yousefi, S. L0-norm sparse hyperspectral unmixing using arctan smoothing. Remote Sens. 2016, 8, 187. [Google Scholar] [CrossRef]
- Ma, J.; Zhao, J.; Yuille, A.L. Non-rigid point set registration by preserving global and local structures. IEEE Trans. Image Process. 2016, 25, 53–64. [Google Scholar] [PubMed]
- Bioucas-Dias, J.M.; Figueiredo, M.A. Alternating direction algorithms for constrained sparse regression: Application to hyperspectral unmixing. In Proceedings of the IEEE Workshop on Hyperspectral Image and Signal Processing: Evolution in Remote Sensing, Reykjavik, Iceland, 14–16 June 2010; pp. 1–4.
- Iordache, M.D.; Bioucas-Dias, J.M.; Plaza, A. Total variation spatial regularization for sparse hyperspectral unmixing. IEEE Trans. Geosci. Remote Sens. 2012, 50, 4484–4502. [Google Scholar] [CrossRef]
- Iordache, M.D.; Bioucas-Dias, J.M.; Plaza, A. Sparse unmixing of hyperspectral data. IEEE Trans. Geosci. Remote Sens. 2011, 49, 2014–2039. [Google Scholar] [CrossRef]
- Shi, Z.; Tang, W.; Duren, Z.; Jiang, Z. Subspace matching pursuit for sparse unmixing of hyperspectral data. IEEE Trans. Geosci. Remote Sens. 2014, 52, 3256–3274. [Google Scholar] [CrossRef]
- Iordache, M.D.; Bioucas-Dias, J.M.; Plaza, A. Collaborative sparse regression for hyperspectral unmixing. IEEE Trans. Geosci. Remote Sens. 2014, 52, 341–354. [Google Scholar] [CrossRef]
- Heylen, R.; Parente, M.; Gader, P. A review of nonlinear hyperspectral unmixing methods. IEEE J. Sel. Topics Appl. Earth Observ. Remote Sens. 2014, 7, 1844–1868. [Google Scholar] [CrossRef]
- Li, C.; Ma, Y.; Huang, J.; Mei, X.; Liu, C.; Ma, J. GBM-based unmixing of hyperspectral data using bound projected optimal gradient method. IEEE Geosci. Remote Sens. Lett. 2016, 13, 952–956. [Google Scholar] [CrossRef]
- Dobigeon, N.; Tourneret, J.Y.; Richard, C.; Bermudez, J.; Mclaughlin, S.; Hero, A.O. Nonlinear unmixing of hyperspectral images: Models and algorithms. IEEE Signal Process. Mag. 2014, 31, 82–94. [Google Scholar] [CrossRef]
- Hapke, B. Bidirectional reflectance spectroscopy: 1. Theory. J. Geophys. Res. Solid Earth 1981, 86, 3039–3054. [Google Scholar] [CrossRef]
- Fan, W.; Hu, B.; Miller, J.; Li, M. Comparative study between a new nonlinear model and common linear model for analysing laboratory simulated-forest hyperspectral data. Int. J. Remote Sens. 2009, 30, 2951–2962. [Google Scholar] [CrossRef]
- Halimi, A.; Altmann, Y.; Dobigeon, N.; Tourneret, J.Y. Nonlinear unmixing of hyperspectral images using a generalized bilinear model. IEEE Trans. Geosci. Remote Sens. 2011, 49, 4153–4162. [Google Scholar] [CrossRef]
- Qu, Q.; Nasrabadi, N.M.; Tran, T.D. Abundance estimation for bilinear mixture models via joint sparse and low-rank representation. IEEE Trans. Geosci. Remote Sens. 2014, 52, 4404–4423. [Google Scholar]
- Heylen, R.; Scheunders, P. A multilinear mixing model for nonlinear spectral unmixing. IEEE Trans. Geosci. Remote Sens. 2016, 54, 240–251. [Google Scholar] [CrossRef]
- Licciardi, G.A.; Del Frate, F. Pixel unmixing in hyperspectral data by means of neural networks. IEEE Trans. Geosci. Remote Sens. 2011, 49, 4163–4172. [Google Scholar] [CrossRef]
- Chen, J.; Richard, C.; Honeine, P. Nonlinear unmixing of hyperspectral data based on a linear-mixture/ nonlinear-fluctuation model. IEEE Trans. Signal Process. 2013, 61, 480–492. [Google Scholar] [CrossRef]
- Chen, J.; Richard, C.; Honeine, P. Nonlinear estimation of material abundances in hyperspectral images with L1-norm spatial regularization. IEEE Trans. Geosci. Remote Sens. 2014, 52, 2654–2665. [Google Scholar] [CrossRef]
- Altmann, Y.; Dobigeon, N.; Tourneret, J.Y. Unsupervised post-nonlinear unmixing of hyperspectral images using a Hamiltonian Monte Carlo algorithm. IEEE Trans. Image Process. 2014, 23, 3968–3981. [Google Scholar] [CrossRef] [PubMed]
- Févotte, C.; Dobigeon, N. Nonlinear hyperspectral unmixing with robust nonnegative matrix factorization. IEEE Trans. Image Process. 2015, 24, 4810–4819. [Google Scholar] [CrossRef] [PubMed]
- Lin, Z.; Chen, M.; Ma, Y. The augmented lagrange multiplier method for exact recovery of corrupted low-rank matrices. arXiv 2010. [Google Scholar] [CrossRef]
- Guo, Z.; Wittman, T.; Osher, S. L1 unmixing and its application to hyperspectral image enhancement. Proc. SPIE 2009. [Google Scholar] [CrossRef]
- Eldar, Y.C.; Rauhut, H. Average case analysis of multichannel sparse recovery using convex relaxation. IEEE Trans. Inf. Theory 2010, 56, 505–519. [Google Scholar] [CrossRef]
- Ammanouil, R.; Ferrari, A.; Richard, C.; Mary, D. Blind and fully constrained unmixing of hyperspectral images. IEEE Trans. Image Process. 2014, 23, 5510–5518. [Google Scholar] [CrossRef] [PubMed]
- Mishali, M.; Eldar, Y.C. Reduce and boost: Recovering arbitrary sets of jointly sparse vectors. IEEE Trans. Signal Process. 2008, 56, 4692–4702. [Google Scholar] [CrossRef]
- Xu, H.; Caramanis, C.; Sanghavi, S. Robust PCA via outlier pursuit. IEEE Trans. Inf. Theory 2012, 58, 3047–3064. [Google Scholar] [CrossRef]
- Ma, J.; Chen, C.; Li, C.; Huang, J. Infrared and visible image fusion via gradient transfer and total variation minimization. Inf. Fusion 2016, 31, 100–109. [Google Scholar] [CrossRef]
- Wright, S.J.; Nowak, R.D.; Figueiredo, M.A. Sparse reconstruction by separable approximation. IEEE Trans. Signal Process. 2009, 57, 2479–2493. [Google Scholar] [CrossRef]
- Zhang, Y. Recent advances in alternating direction methods: Practice and theory. In IPAM Workshop: Numerical Methods for Continuous Optimization; UCLA: Los Angeles, CA, USA, 2010. [Google Scholar]
- Jiang, J.; Hu, R.; Wang, Z.; Han, Z. Noise robust face hallucination viaLocality-constrained representation. IEEE Trans. Multimedia 2014, 16, 1268–1281. [Google Scholar] [CrossRef]

© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, C.; Ma, Y.; Mei, X.; Liu, C.; Ma, J. Hyperspectral Unmixing with Robust Collaborative Sparse Regression. Remote Sens. 2016, 8, 588. https://doi.org/10.3390/rs8070588
Li C, Ma Y, Mei X, Liu C, Ma J. Hyperspectral Unmixing with Robust Collaborative Sparse Regression. Remote Sensing. 2016; 8(7):588. https://doi.org/10.3390/rs8070588
Chicago/Turabian StyleLi, Chang, Yong Ma, Xiaoguang Mei, Chengyin Liu, and Jiayi Ma. 2016. "Hyperspectral Unmixing with Robust Collaborative Sparse Regression" Remote Sensing 8, no. 7: 588. https://doi.org/10.3390/rs8070588
APA StyleLi, C., Ma, Y., Mei, X., Liu, C., & Ma, J. (2016). Hyperspectral Unmixing with Robust Collaborative Sparse Regression. Remote Sensing, 8(7), 588. https://doi.org/10.3390/rs8070588