Evaluating Biosphere Model Estimates of the Start of the Vegetation Active Season in Boreal Forests by Satellite Observations
Abstract
:1. Introduction
2. Materials and Methods
2.1. Study Area
2.2. Carbon Dioxide Flux Measurements
2.3. Phenological Observations of Bud Break of Birch
2.4. JSBACH Simulations
2.4.1. The JSBACH Model
2.4.2. Preparation of Meteorological Driving Data for Regional Runs
2.4.3. Regional JSBACH Runs
2.4.4. Site-Level JSBACH Runs
2.4.5. Model-Derived Indicators for the Start of Season
2.5. Remote Sensing Data
2.5.1. Pre-Processing of MODIS Time Series
2.5.2. Satellite-Observed Start of Season for JSBACH Model Evaluation
2.6. Evaluation of DBF_SOSsat against Bud Break Observations
2.7. Evaluation of JSBACH-Modelled Start of Season
3. Results
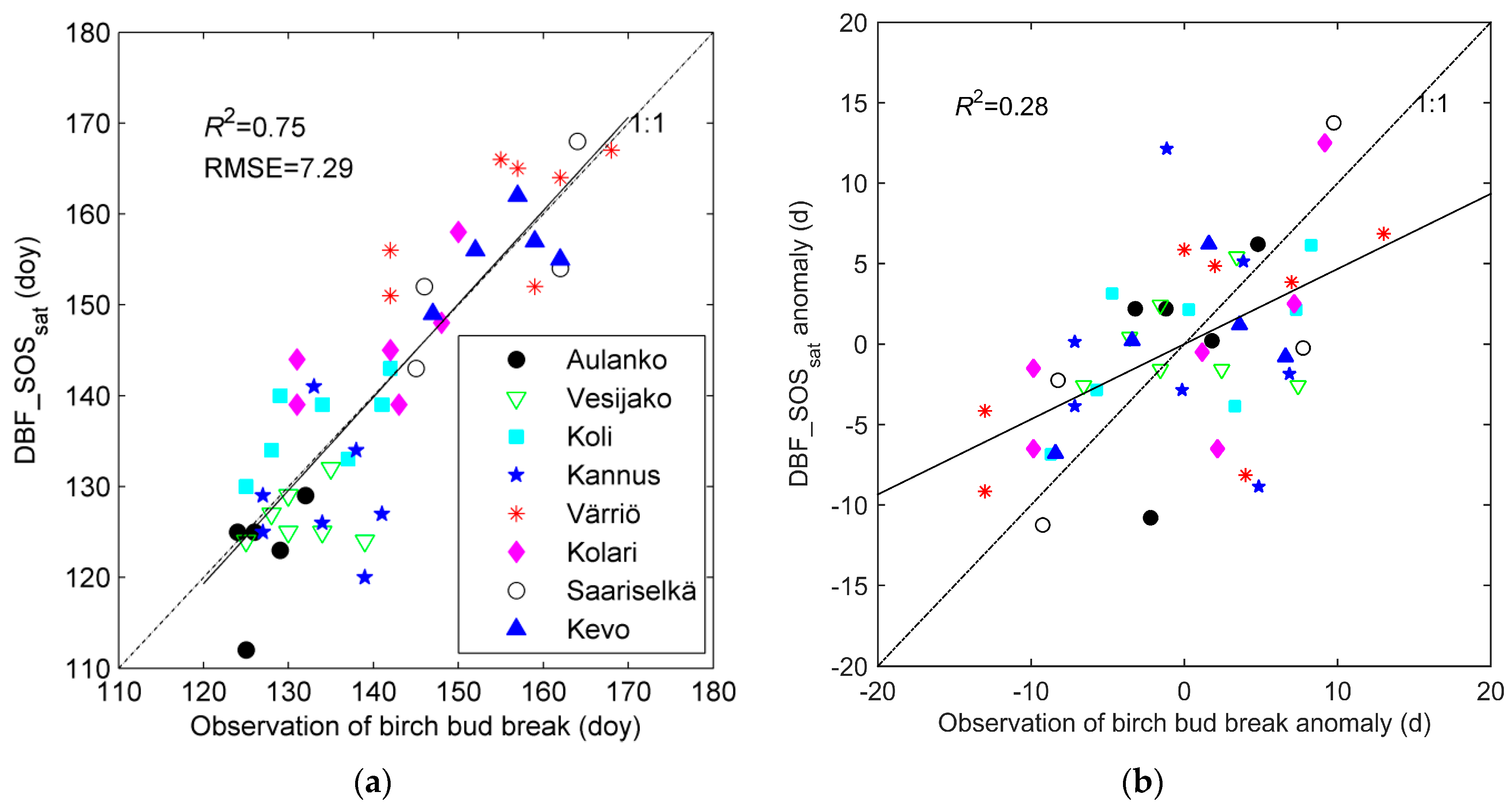
3.1. Evaluation of DBF_SOSsat with Phenological Observations of Bud Break
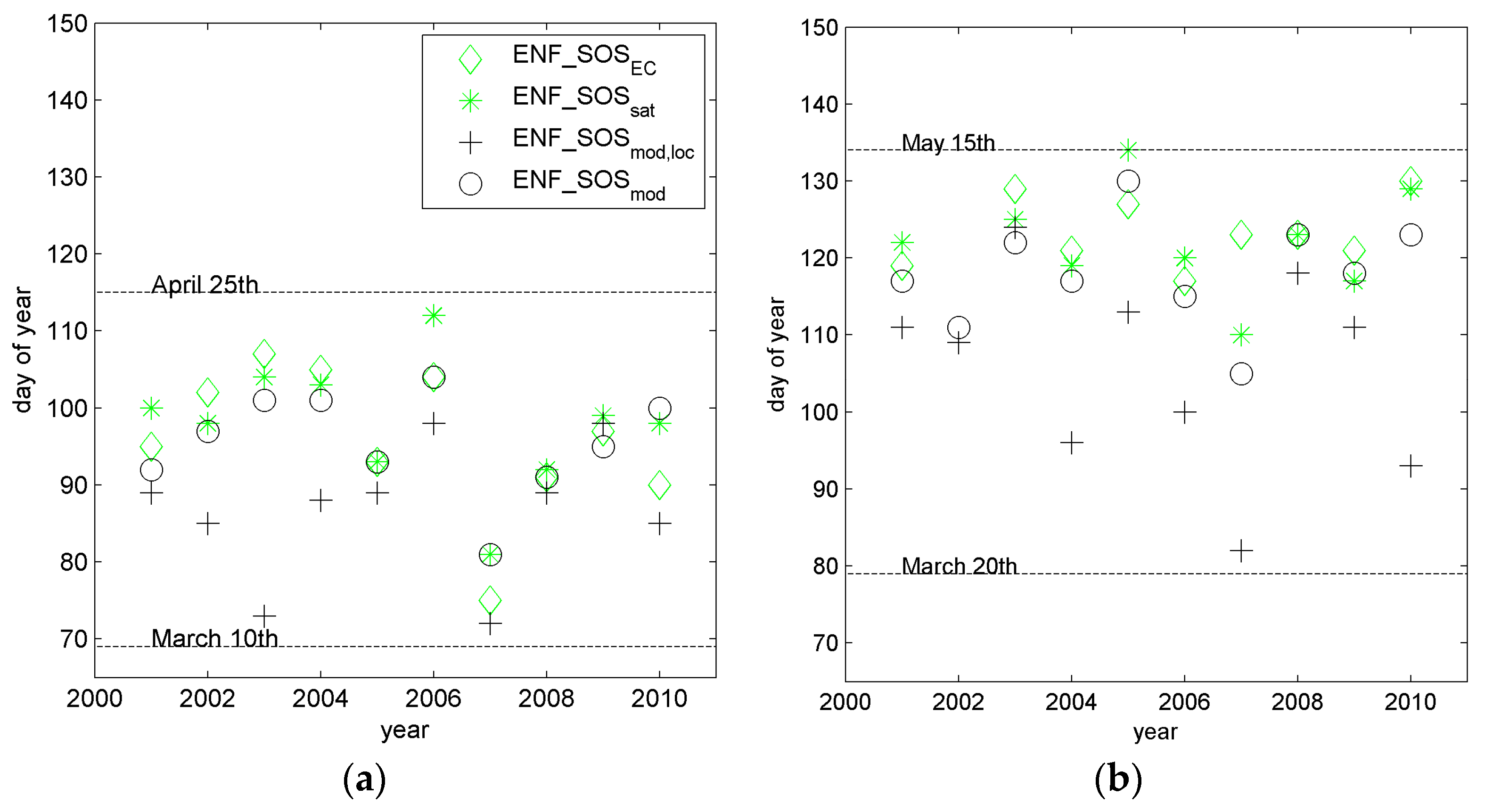
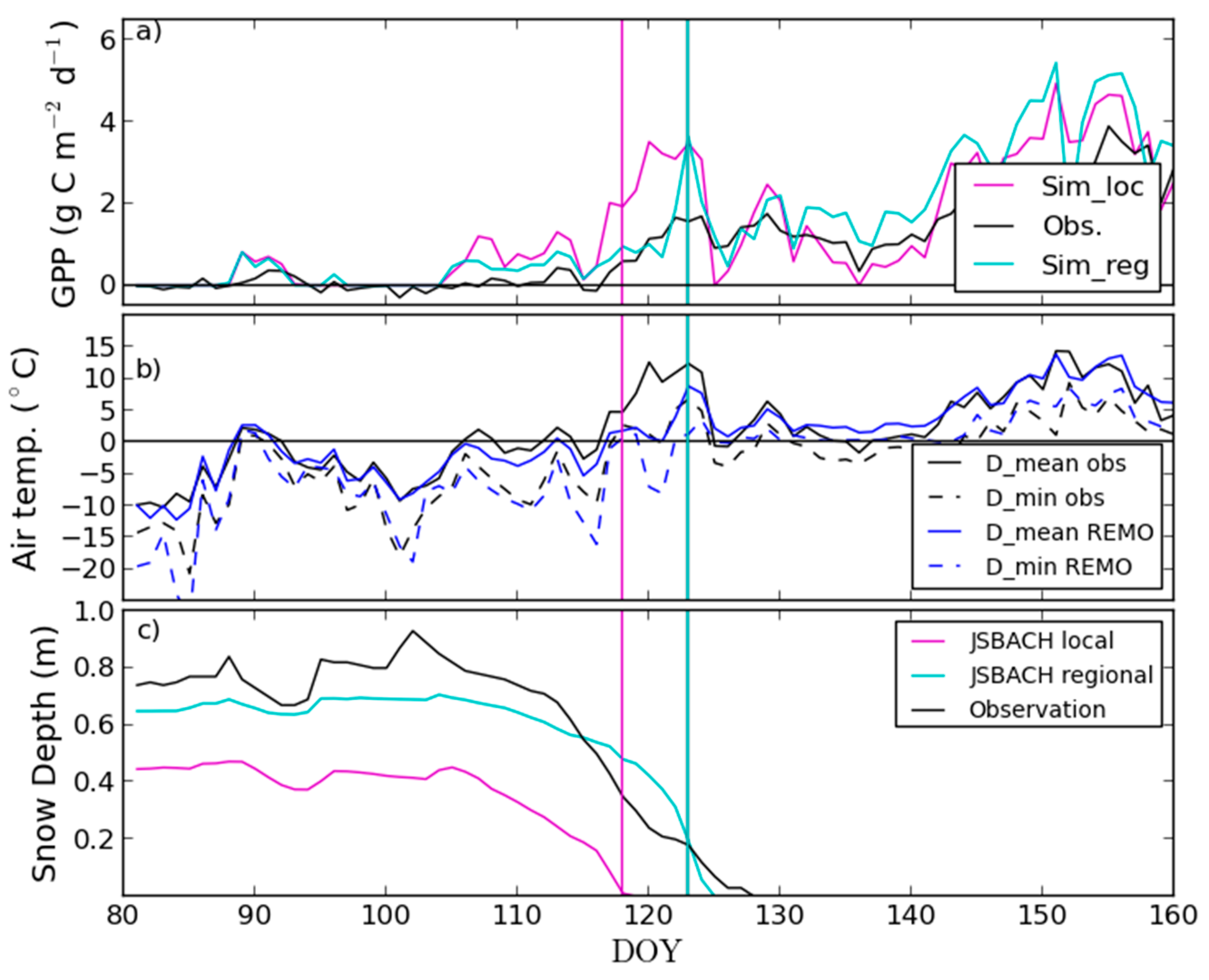
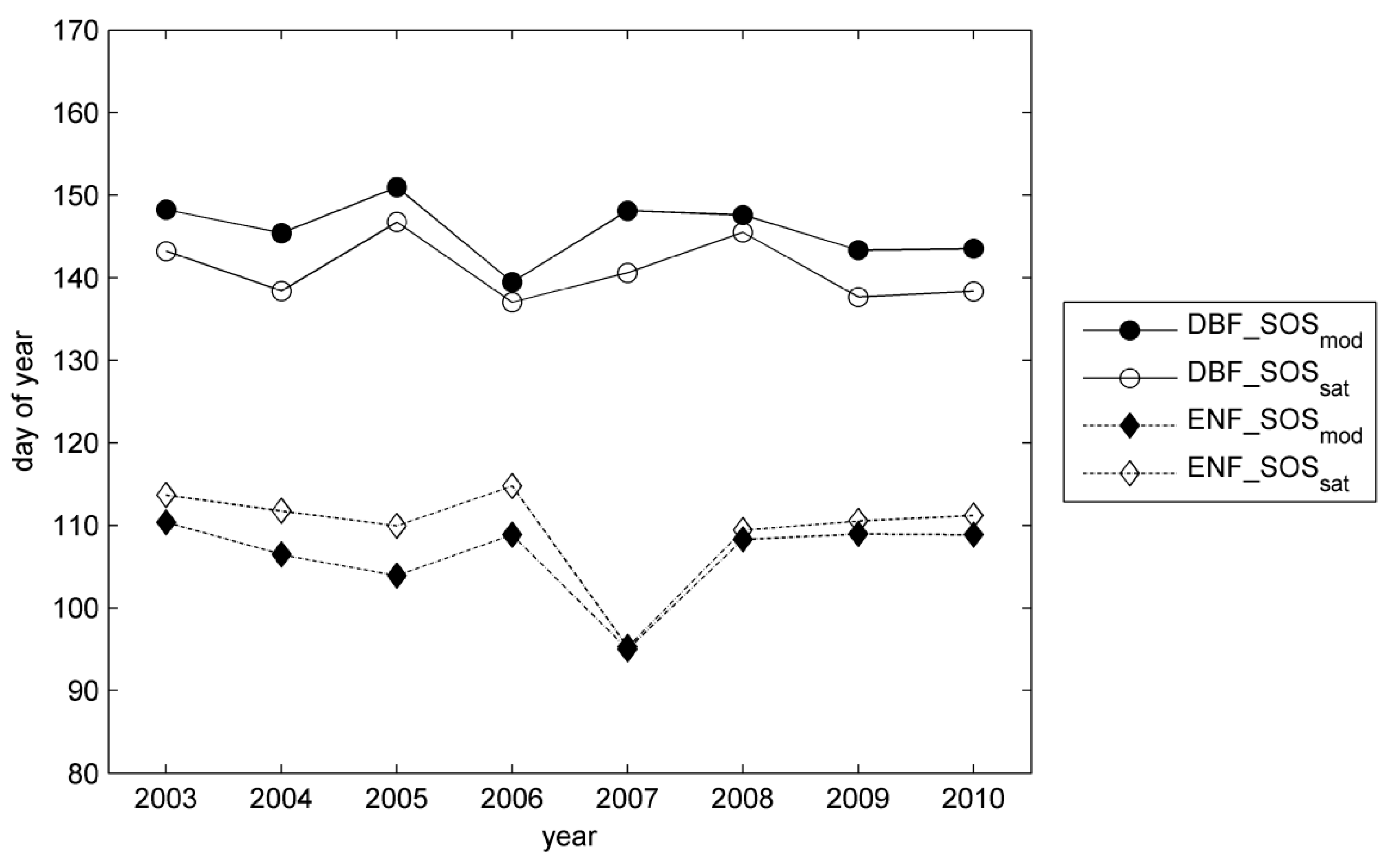
3.2. Site-Level Start of Season in Evergreen Needle-Leaf Forest
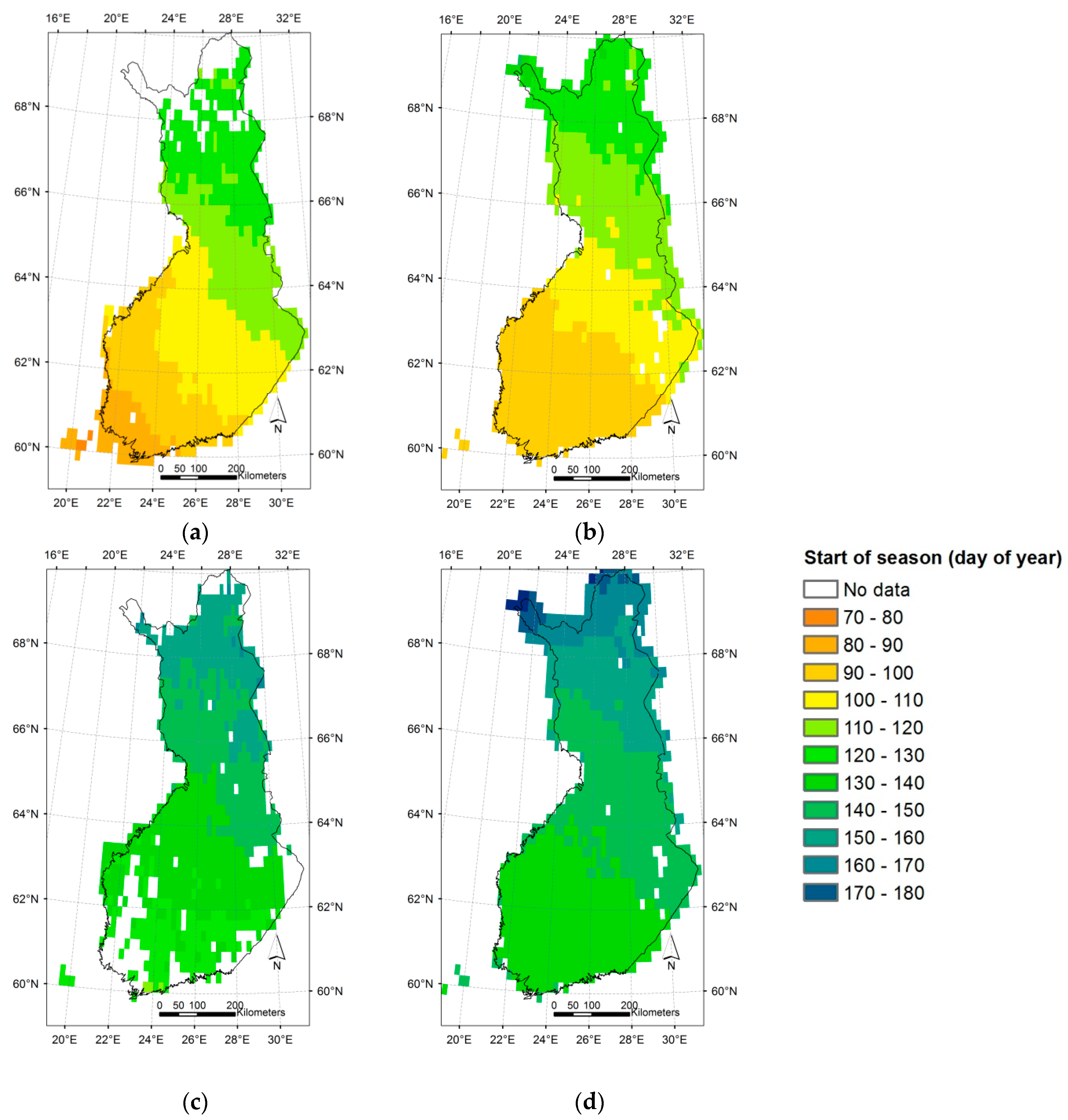
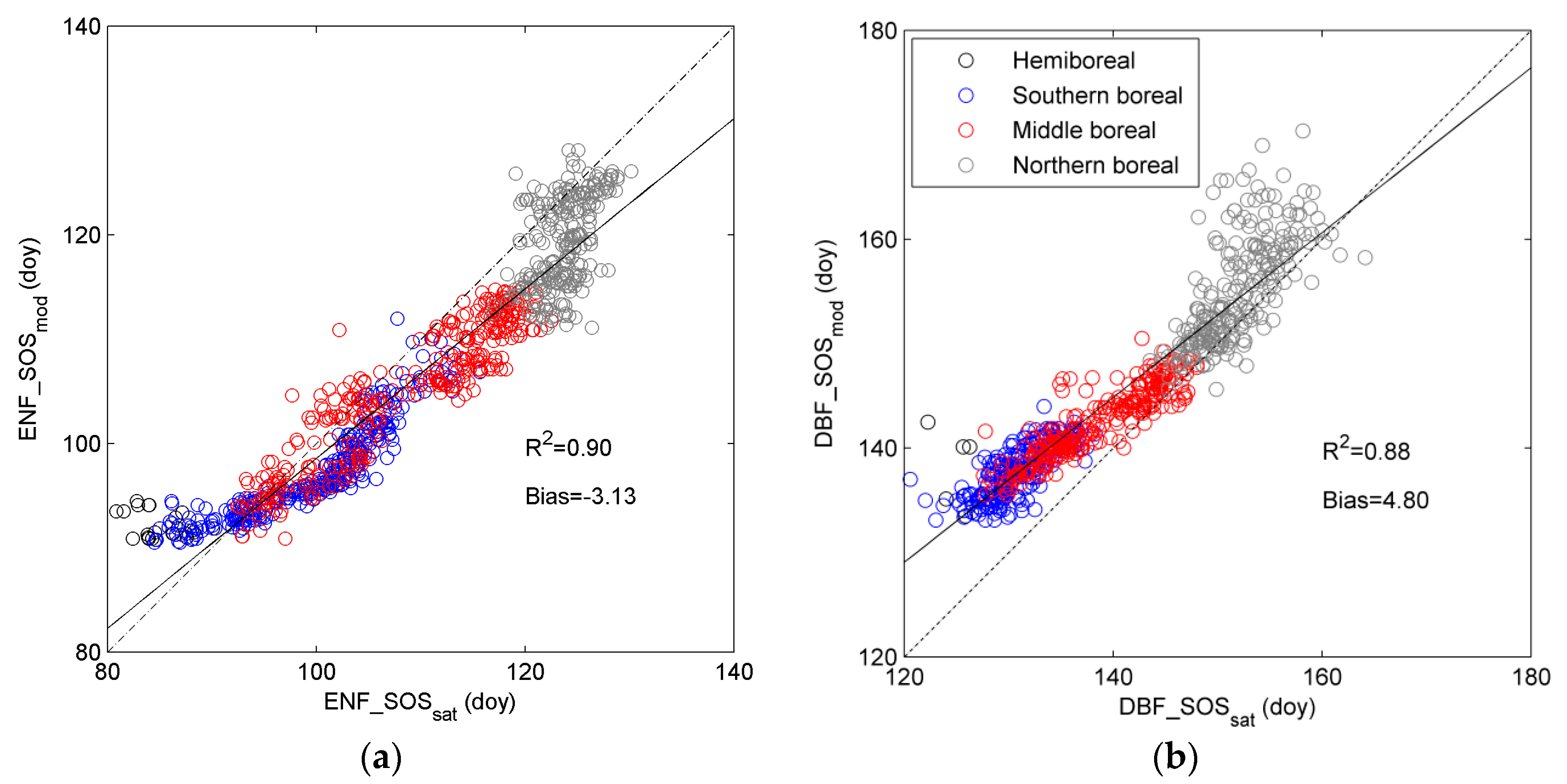
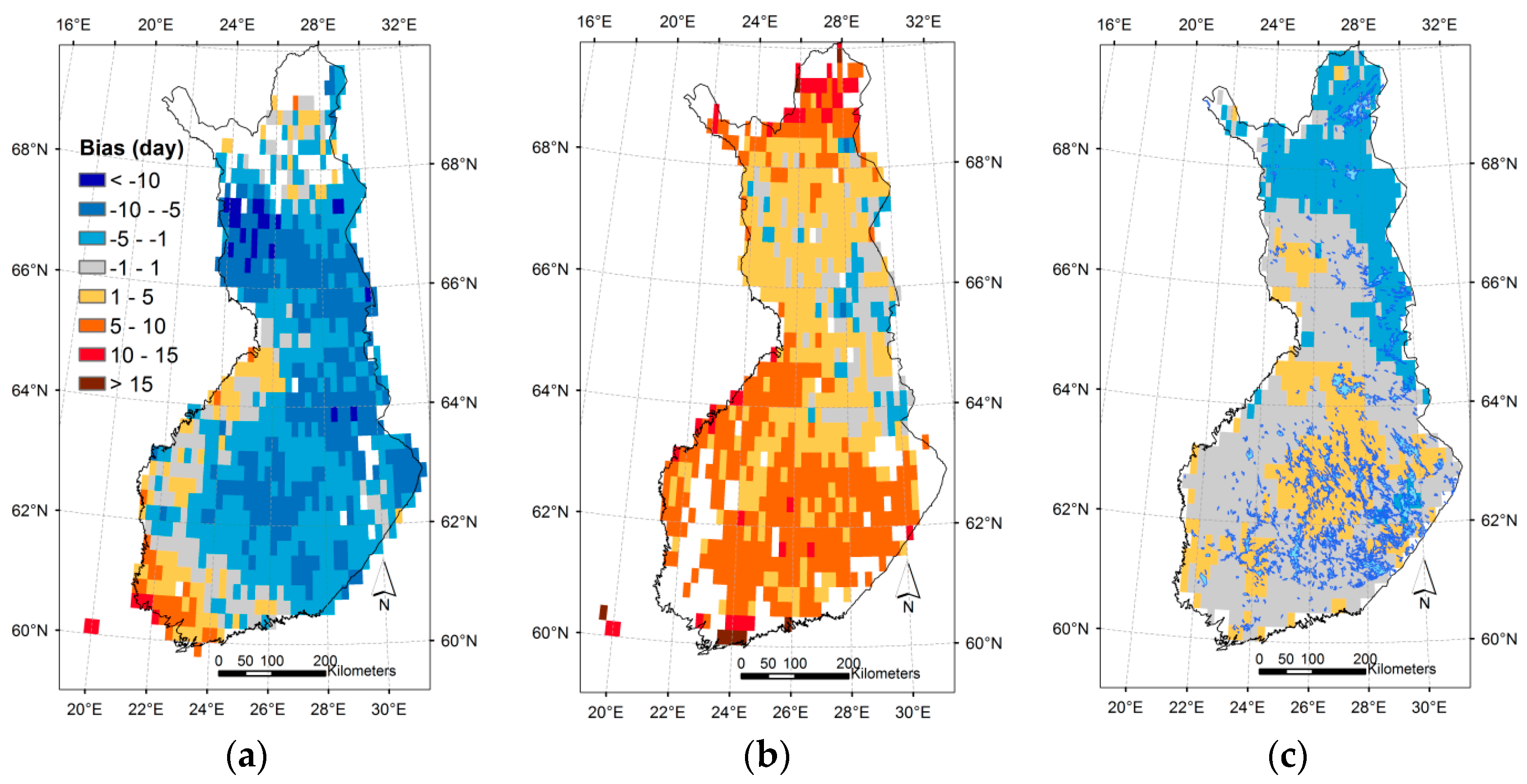
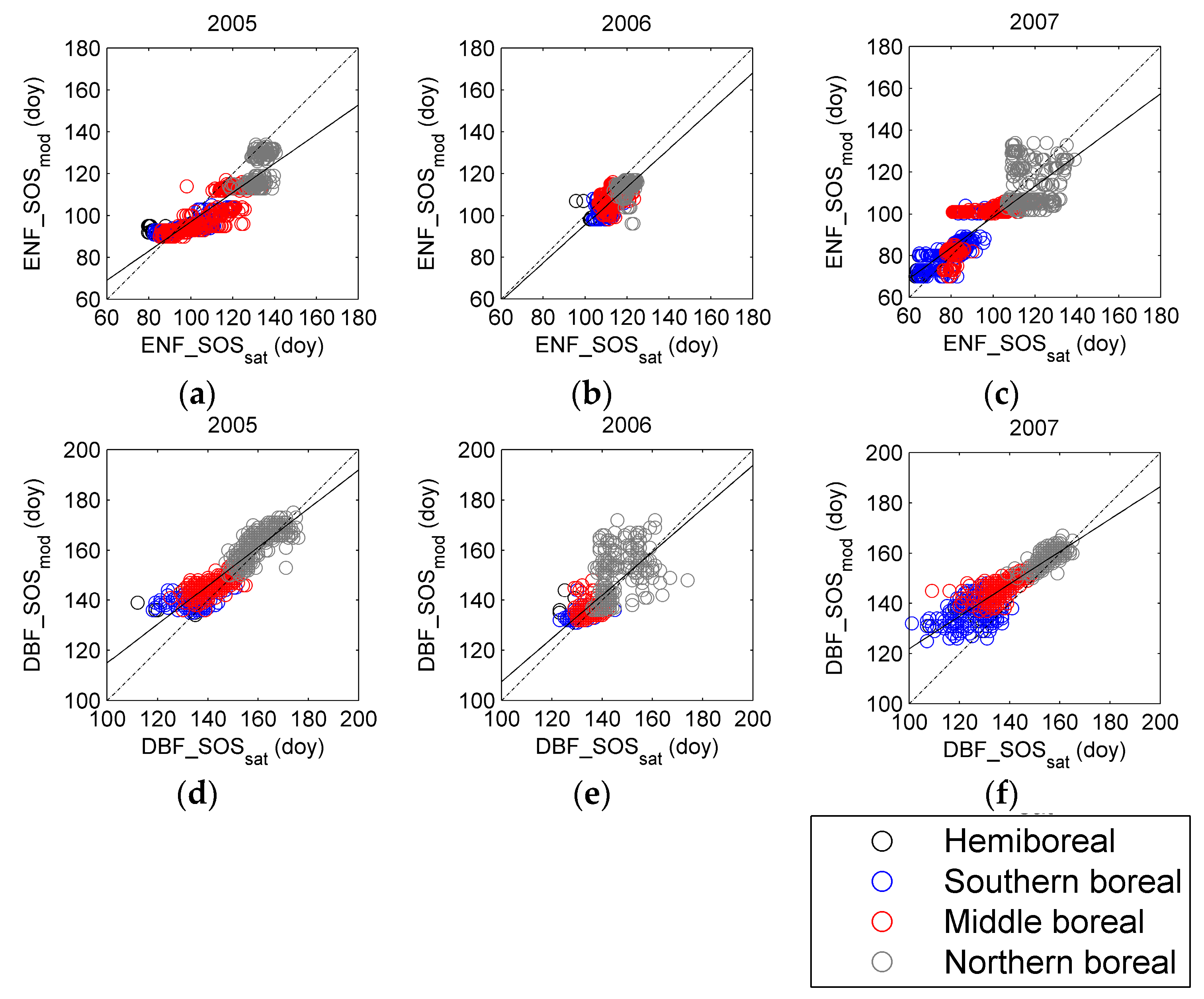
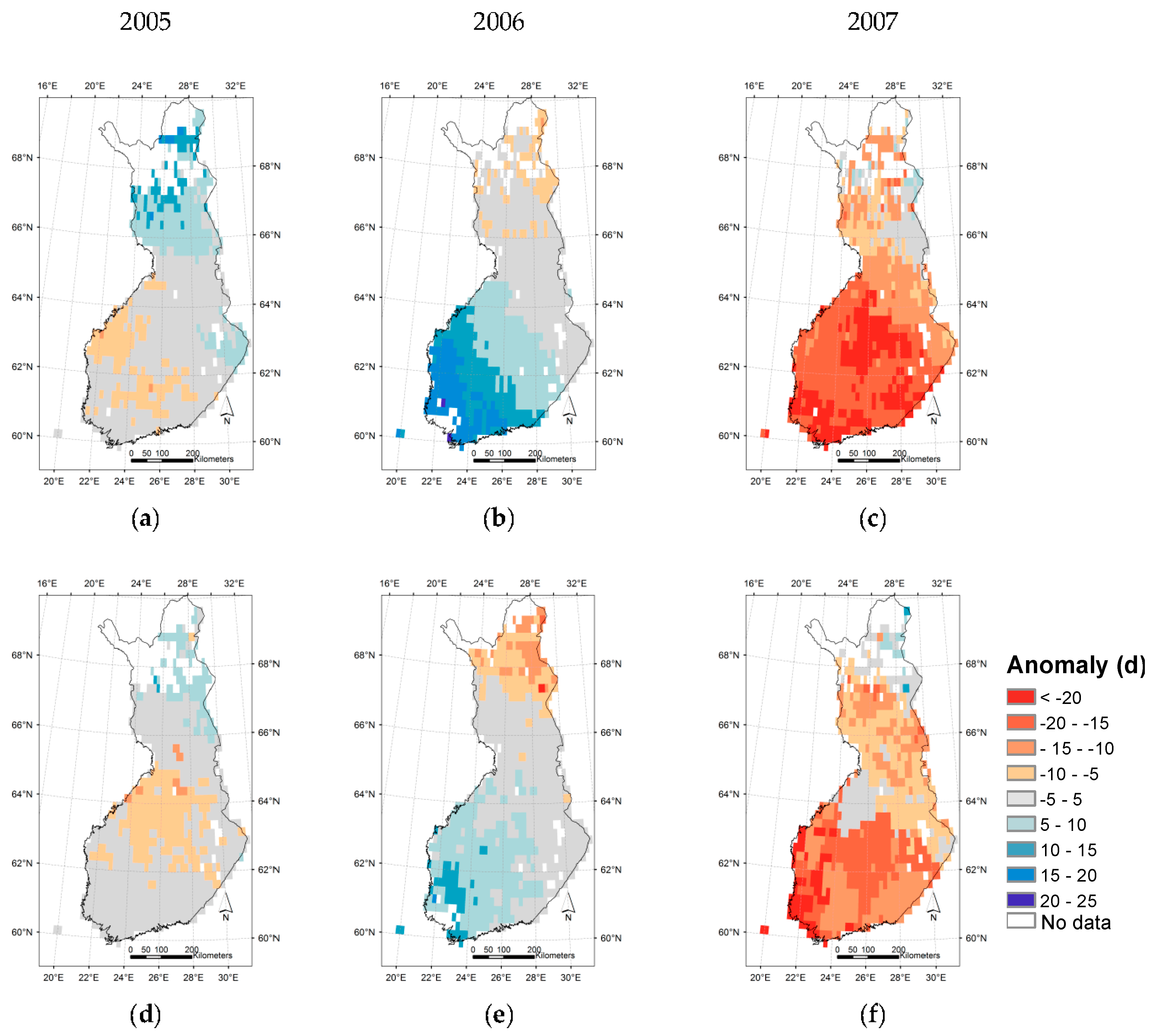
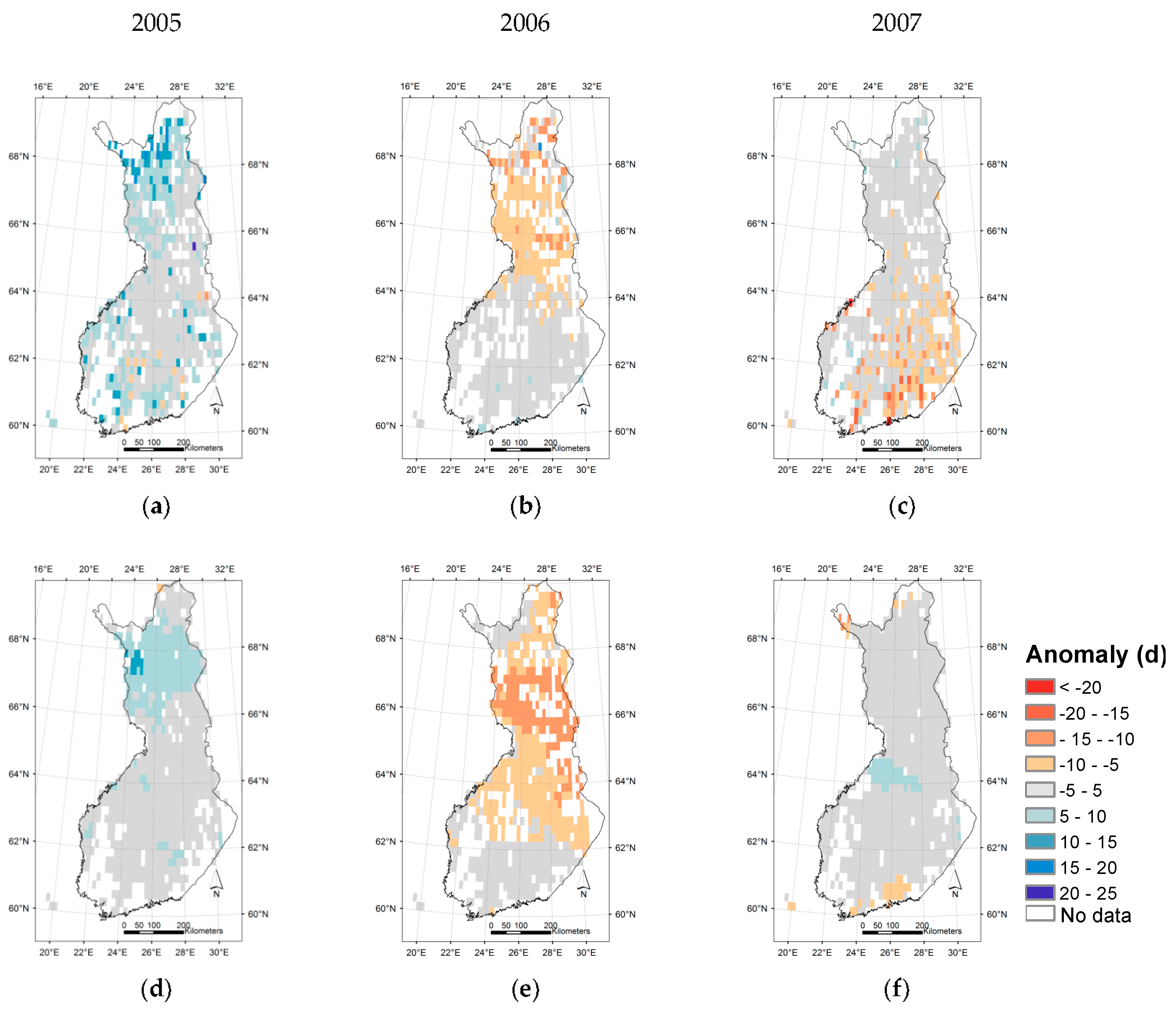
3.3. Regional Assessment of JSBACH-Modelled Start of Season against Satellite Observations
4. Discussion
4.1. Quality of Remote Sensing Observations of the Start of Season
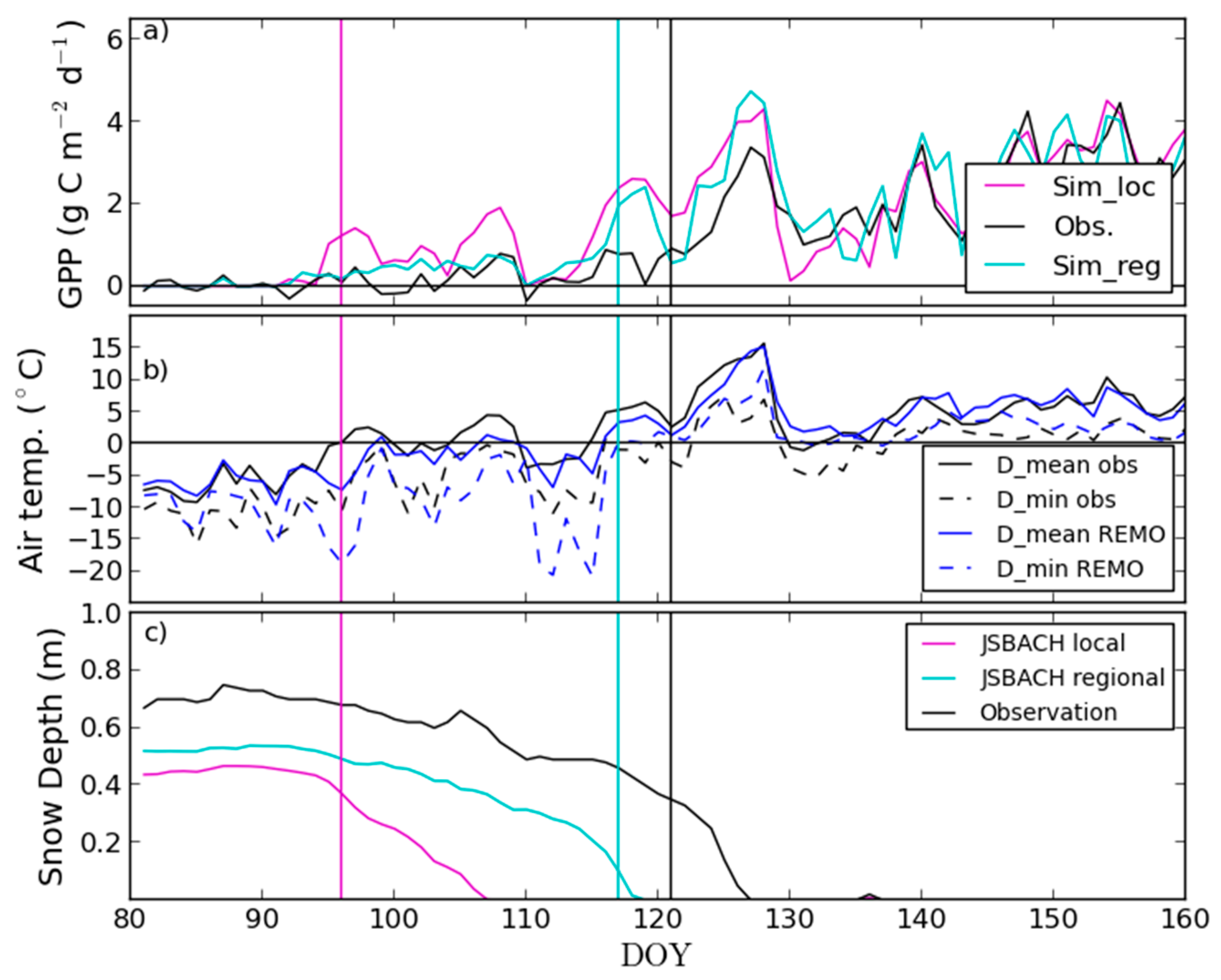
4.2. Modelling of Springtime Development and the Start of Season in JSBACH
5. Conclusions
Supplementary Materials
Acknowledgments
Author Contributions
Conflicts of Interest
Abbreviations
| 3D | Three-dimensional |
| CORINE | Coordinated Information on the European Environment |
| Decay parameter in the LoGro-P model | |
| DBF | Deciduous broad-leaf forest |
| DBF_SOS | Starting date of the vegetation active season of DBF |
| DBF_SOSmod | Starting date of the vegetation active season of DBF determined from JSBACH regional runs |
| DBF_SOSsat | Starting date of the vegetation active season of DBF determined from satellite observations |
| doy | Day of year |
| EC | Eddy covariance |
| ECMWF | European Centre for Medium-Range Weather Forecasts |
| ENF | Evergreen needle-leaf forest |
| ENF_SOS | Starting date of the vegetation active season in ENF |
| ENF_SOSEC | Starting date of the vegetation active season determined from continuous EC measurements |
| ENF_SOSmod,loc | Starting date of the vegetation active season of ENF determined from JSBACH local runs at CO2 flux measurement sites |
| ENF_SOSmod | Starting date of the vegetation active season of ENF determined from JSBACH regional runs |
| ENF_SOSsat | Starting date of the vegetation active season of ENF determined from satellite observations |
| fAPAR | Fraction of absorbed photosynthetically active radiation |
| FMI | Finnish Meteorological Institute |
| FSC | Fractional Snow Cover |
| GOME-2 | Global Ozone Monitoring Experiment |
| GOSAT | Greenhouse Gases Observing Satellite |
| GPP | Gross Primary Production |
| JSBACH | Jena Scheme for Biosphere–Atmosphere Hamburg |
| LAADS | Level-1 & Atmosphere Archive and Distribution System |
| LAI | Leaf Area Index |
| LoGro-P | Logistic Growth Phenology |
| MODIS | Moderate Resolution Imaging Spectrometer |
| MPI | Max Planck Institute |
| NASA | National Aeronautics and Space Administration |
| NDVI | Normalized Difference Vegetation Index |
| NDWI | Normalized Difference Water Index |
| NEE | Net ecosystem CO2 exchange |
| OCO-2 | Orbiting Carbon Observatory |
| N | Number of observations |
| p | Probability |
| PFT | Plant Functional Type |
| PPI | Plant Phenological Index |
| PRI | Photochemical Reflectance Index |
| R | Respiration |
| R2 | Coefficient of determination |
| REMO | Regional climate model |
| RMSE | Root mean square error |
| RMIR | Mid-infrared reflectance |
| RNIR | Near-infrared reflectance |
| SCAmod | Algorithm for the retrieval of FSC from optical satellite observations |
| Heat sum parameter in LoGro-P model | |
| Alternating temperature in LoGro-P model | |
| TOA | Top-of-Atmosphere |
Appendix A
A1. The JSBACH Phenology for Extra-Tropical Forests
A2. General Dynamics
A3. Evergreen Phenology
A4. Summer-Green Phenology
A5. Spring and Autumn Events
A6. The Spring Event
A7. The Autumn Event
A8. Calculation of Smoothed Air Temperature
A9. Parameter Values
| Parameter | Units | Summergreen | Evergreen |
|---|---|---|---|
| seed LAI | m2/m2 | 0.4 | 0.4 |
| d | 10 | 10 | |
| d−1 | 0.087 | 0.015 | |
| °C | 4.0 (2.0) | 4.0 | |
| °C | 10.0 (15.0) | - | |
| d·°C | 30 (30) | 10 | |
| d·°C | 200 | 150 | |
| d | 25 | 15 | |
| growth phase length | d | 60 | 60 |
| p (rest phase) | d−1 | 0.1 | 0.0008 |
| p (vegetative phase) | d−1 | 0.004 | - |
| PFT | |
|---|---|
| temperate broad-leaf evergreen trees | 6.0 |
| coniferous evergreen trees | 5.0 |
| temperate broad-leaf deciduous trees | 5.0 |
| coniferous deciduous trees | 5.0 |
Appendix B
| Statistical Measure | Equation |
|---|---|
| Root mean squared error | |
| Bias | |
| Coefficient of determination |
References
- Bonan, G.B. Forests and climate change: Forcings, feedbacks, and the climate benefits of forests. Science 2008, 320, 1444–1449. [Google Scholar] [CrossRef] [PubMed]
- Ruosteenoja, K.; Raisanen, J.; Pirinen, P. Projected changes in thermal seasons and the growing season in Finland. Int. J. Climatol. 2011, 31, 1473–1487. [Google Scholar] [CrossRef]
- Delpierre, N.; Soudani, K.; François, C.; Köstner, B.; Pontailler, J.Y.; Nikinmaa, E.; Misson, L.; Aubinet, M.; Bernhofer, C.; Granier, A.; et al. Exceptional carbon uptake in European forests during the warm spring of 2007: A data–model analysis. Glob. Chang. Biol. 2009, 15, 1455–1474. [Google Scholar] [CrossRef]
- Thum, T.; Aalto, T.; Laurila, T.; Aurela, M.; Hatakka, J.; Lindroth, A.; Vesala, T. Spring initiation and autumn cessation of boreal coniferous forest CO2 exchange assessed by meteorological and biological variables. Tellus B 2009, 61, 701–717. [Google Scholar] [CrossRef]
- Vesala, T.; Launiainen, S.; Kolari, P.; Pumpanen, J.; Sevanto, S.; Hari, P.; Nikinmaa, E.; Kaski, P.; Mannila, H.; Ukkonen, E.; et al. Autumn temperature and carbon balance of a boreal Scots pine forest in Southern Finland. Biogeosciences 2010, 7, 163–176. [Google Scholar] [CrossRef]
- Jylhä, K.; Ruosteenoja, K.; Räisänen, J.; Venäläinen, A.; Tuomenvirta, H.; Ruokolainen, L.; Saku, S.; Seitola, T. Arvioita Suomen Muuttuvasta Ilmastosta Sopeutumistutkimuksia Varten. ACCLIM-Hankkeen Raportti 2009 (Changing Climate in Finland: Estimates for Adaptation Studies. ACCLIM Project Report 2009); Finnish Meteorological Institute: Helsinki, Finland, 2009. [Google Scholar]
- Kaduk, J.; Los, S. Predicting the time of green up in temperate and boreal biomes. Clim. Chang. 2011, 107, 277–304. [Google Scholar] [CrossRef]
- Räisänen, J.; Eklund, J. 21st Century changes in snow climate in Northern Europe: A high-resolution view from ENSEMBLES regional climate models. Clim. Dyn. 2012, 38, 2575–2591. [Google Scholar]
- Rammig, A.; Jönsson, A.M.; Hickler, T.; Smith, B.; Bärring, L.; Sykes, M.T. Impacts of changing frost regimes on Swedish forests: Incorporating cold hardiness in a regional ecosystem model. Ecol. Modell. 2010, 221, 303–313. [Google Scholar] [CrossRef]
- Ensminger, I.; Sveshnikov, D.; Campbell, D.A.; Funk, C.; Jansson, S.; Lloyd, J.; Shibistova, O.; Öquist, G. Intermittent low temperatures constrain spring recovery of photosynthesis in boreal Scots pine forests. Glob. Chang. Biol. 2004, 10, 995–1008. [Google Scholar] [CrossRef]
- Jylhä, K.; Fronzek, S.; Tuomenvirta, H.; Carter, T.; Ruosteenoja, K. Changes in frost, snow and Baltic sea ice by the end of the twenty-first century based on climate model projections for Europe. Clim. Chang. 2008, 86, 441–462. [Google Scholar] [CrossRef]
- Picard, G.; Quegan, S.; Delbart, N.; Lomas, M.R.; Le Toan, T.; Woodward, F.I. Bud-burst modelling in Siberia and its impact on quantifying the carbon budget. Glob. Chang. Biol. 2005, 11, 2164–2176. [Google Scholar] [CrossRef]
- Jeong, S.-J.; Medvigy, D.; Shevliakova, E.; Malyshev, S. Uncertainties in terrestrial carbon budgets related to spring phenology. J. Geophys. Res.: Biogeosci. 2012, 117, G01030. [Google Scholar] [CrossRef]
- Richardson, A.D.; Anderson, R.S.; Arain, M.A.; Barr, A.G.; Bohrer, G.; Chen, G.; Chen, J.M.; Ciais, P.; Davis, K.J.; Desai, A.R.; et al. Terrestrial biosphere models need better representation of vegetation phenology: results from the North American Carbon Program Site Synthesis. Glob. Chang. Biol. 2012, 18, 566–584. [Google Scholar] [CrossRef]
- Mahowald, N.; Lo, F.; Zheng, Y.; Harrison, L.; Funk, C.; Lombardozzi, D. Leaf area index in earth system models: Evaluation and projections. Earth Syst. Dyn. Discuss. 2015, 6, 761–818. [Google Scholar] [CrossRef]
- Melaas, E.K.; Richardson, A.D.; Friedl, M.A.; Dragoni, D.; Gough, C.M.; Herbst, M.; Montagnani, L.; Moors, E. Using FLUXNET data to improve models of springtime vegetation activity onset in forest ecosystems. Agric. For. Meteorol. 2013, 171–172, 46–56. [Google Scholar] [CrossRef]
- Baldocchi, D.; Falge, E.; Gu, L.; Olson, R.; Hollinger, D.; Running, S.; Anthoni, P.; Bernhofer, C.; Davis, K.; Evans, R.; et al. FLUXNET: A new tool to study the temporal and spatial variability of ecosystem–scale carbon dioxide, water vapor, and energy flux densities. Bull. Am. Meteorol. Soc. 2001, 82, 2415–2434. [Google Scholar] [CrossRef]
- Suni, T.; Berninger, F.; Vesala, T.; Markkanen, T.; Hari, P.; Mäkelä, A.; Ilvesniemi, H.; Hänninen, H.; Nikinmaa, E.; Huttula, T.; et al. Air temperature triggers the recovery of evergreen boreal forest photosynthesis in spring. Glob. Chang. Biol. 2003, 9, 1410–1426. [Google Scholar]
- Yang, X.; Mustard, J.F.; Tang, J.; Xu, H. Regional-scale phenology modeling based on meteorological records and remote sensing observations. J. Geophys. Res.: Biogeosci. 2012, 117, G3. [Google Scholar] [CrossRef]
- Luo, Y.Q.; Randerson, J.T.; Abramowitz, G.; Bacour, C.; Blyth, E.; Carvalhais, N.; Ciais, P.; Dalmonech, D.; Fisher, J.B.; Fisher, R.; et al. A framework for benchmarking land models. Biogeosciences 2012, 9, 3857–3874. [Google Scholar] [CrossRef]
- Dalmonech, D.; Zaehle, S. Towards a more objective evaluation of modelled land-carbon trends using atmospheric CO2 and satellite-based vegetation activity observations. Biogeosciences 2013, 10, 4189–4210. [Google Scholar] [CrossRef]
- Beck, P.S.A.; Atzberger, C.; Høgda, K.A.; Johansen, B.; Skidmore, A.K. Improved monitoring of vegetation dynamics at very high latitudes: A new method using MODIS NDVI. Remote Sens. Environ. 2006, 100, 321–334. [Google Scholar] [CrossRef]
- Shen, M.; Tang, Y.; Desai, A.R.; Gough, C.; Chen, J. Can EVI-derived land-surface phenology be used as a surrogate for phenology of canopy photosynthesis? Int. J. Remote Sens. 2014, 35, 1162–1174. [Google Scholar] [CrossRef]
- Baldocchi, D.D.; Black, T.A.; Curtis, P.S.; Falge, E.; Fuentes, J.D.; Granier, A.; Gu, L.; Knohl, A.; Pilegaard, K.; Schmid, H.P.; et al. Predicting the onset of net carbon uptake by deciduous forests with soil temperature and climate data: A synthesis of FLUXNET data. Int. J. Biometeorol. 2005, 49, 377–387. [Google Scholar] [CrossRef] [PubMed]
- Wong, C.Y.S.; Gamon, J.A. The photochemical reflectance index provides an optical indicator of spring photosynthetic activation in evergreen conifers. New Phytol. 2015, 206, 196–208. [Google Scholar] [CrossRef] [PubMed]
- Walther, S.; Voigt, M.; Thum, T.; Gonsamo, A.; Zhang, Y.; Koehler, P.; Jung, M.; Varlagin, A.; Guanter, L. Satellite chlorophyll fluorescence measurements reveal large-scale decoupling of photosynthesis and greenness dynamics in boreal evergreen forests. Glob. Chang. Biol. 2015. [Google Scholar] [CrossRef] [PubMed]
- Delbart, N.; Kergoat, L.; Le Toan, T.; L’Hermitte, J.; Picard, G. Determination of phenological dates in boreal regions using normalized difference water index. Remote Sens. Environ. 2005, 97, 26–38. [Google Scholar] [CrossRef]
- Karlsen, S.R.; Tolvanen, A.; Kubin, E.; Poikolainen, J.; Høgda, K.A.; Johansen, B.; Danks, F.S.; Aspholm, P.; Wielgolaski, F.E.; Makarova, O. MODIS-NDVI-based mapping of the length of the growing season in northern Fennoscandia. Int. J. Appl. Earth Observ. Geoinf. 2008, 10, 253–266. [Google Scholar] [CrossRef]
- Gonsamo, A.; Chen, J.M.; Price, D.T.; Kurz, W.A.; Wu, C. Land surface phenology from optical satellite measurement and CO2 eddy covariance technique. J. Geophys. Res. 2012, 117, G3. [Google Scholar] [CrossRef]
- Beck, P.S.A.; Jönsson, P.; Høgda, K.-A.; Karlsen, S.R.; Eklundh, L.; Skidmore, A.K. A ground-validated NDVI dataset for monitoring vegetation dynamics and mapping phenology in Fennoscandia and the Kola Peninsula. Int. J. Remote Sens. 2007, 28, 4311–4330. [Google Scholar] [CrossRef]
- Richardson, A.D.; Black, A.T.; Ciais, P.; Delbart, N.; Friedl, M.A.; Gobron, N.; Hollinger, D.Y.; Kutsch, W.L.; Longdoz, B.; Luyssaert, S.; et al. Influence of spring and autumn phenological transitions on forest ecosystem productivity. Philos. Trans. R. Soc. B: Biol. Sci. 2010, 365, 3227–3246. [Google Scholar] [CrossRef] [PubMed]
- Dahlke, C.; Loew, A.; Reick, C. Robust identification of global greening phase patterns from remote sensing vegetation products. J. Clim. 2012, 25, 8289–8307. [Google Scholar] [CrossRef]
- Böttcher, K.; Aurela, M.; Kervinen, M.; Markkanen, T.; Mattila, O.-P.; Kolari, P.; Metsämäki, S.; Aalto, T.; Arslan, A.N.; Pulliainen, J. MODIS time-series-derived indicators for the beginning of the growing season in boreal coniferous forest—A comparison with CO2 flux measurements and phenological observations in Finland. Remote Sens. Environ. 2014, 140, 625–638. [Google Scholar] [CrossRef]
- Raddatz, T.J.; Reick, C.H.; Knorr, W.; Kattge, J.; Roeckner, E.; Schnur, R.; Schnitzler, K.G.; Wetzel, P.; Jungclaus, J. Will the tropical land biosphere dominate the climate-carbon cycle feedback during the twenty-first century? Clim. Dyn. 2007, 29, 565–574. [Google Scholar] [CrossRef]
- Pirinen, P.; Simola, H.; Aalto, J.; Kaukoranta, J.-P.; Karlsson, P.; Ruuhela, R. Tilastoja Suomen Ilmastosta 1981–2010 (Climatological Statistics of Finland 1981–2010); Finnish Meteorological Insitute: Helsinki, Finland, 2012. [Google Scholar]
- Ahti, T.; Hämet-Ahti, L.; Jalas, J. Vegetation zones and their sections on northwestern Europe. Ann. Bot. Fennica 1968, 5, 169–211. [Google Scholar]
- Parviainen, J.; Västilä, S. 5a/2011 State of Finland´s Forests 2011 Based on the Criteria and Indicators of Sustainable Forest Management; Ministry of Agriculture and Forestry: Helsinki, Finlandia, 2011.
- Baldocchi, D.D. Assessing the eddy covariance technique for evaluating carbon dioxide exchange rates of ecosystems: Past, present and future. Glob. Chang. Biol. 2003, 9, 479–492. [Google Scholar] [CrossRef]
- Kolari, P.; Kulmala, L.; Pumpanen, J.; Launiainen, S.; Ilvesniemi, H.; Hari, P.; Nikinmaa, E. CO2 exchange and component CO2 fluxes of a boreal Scots pine forest. Boreal Environ. Res. 2009, 14, 761–783. [Google Scholar]
- Reichstein, M.; Falge, E.; Baldocchi, D.; Papale, D.; Aubinet, M.; Berbigier, P.; Bernhofer, C.; Buchmann, N.; Gilmanov, T.; Granier, A.; et al. On the separation of net ecosystem exchange into assimilation and ecosystem respiration: Review and improved algorithm. Glob. Chang. Biol. 2005, 11, 1424–1439. [Google Scholar] [CrossRef]
- Thum, T.; Aalto, T.; Laurila, T.; Aurela, M.; Kolari, P.; Hari, P. Parametrization of two photosynthesis models at the canopy scale in a northern boreal Scots pine forest. Tellus B 2007, 59, 874–890. [Google Scholar] [CrossRef]
- Vesala, T.; Suni, T.; Rannik, Ü.; Keronen, P.; Markkanen, T.; Sevanto, S.; Grönholm, T.; Smolander, S.; Kulmala, M.; Ilvesniemi, H.; et al. Effect of thinning on surface fluxes in a boreal forest. Glob. Biogeochem. Cycles 2005, 19, GB2001. [Google Scholar] [CrossRef]
- Kubin, E.; Kotilainen, E.; Poikolainen, J.; Hokkanen, T.; Nevalainen, S.; Pouttu, A.; Karhu, J.; Pasanen, J. Fenologisen Havaintoverkon Seurantaohjeet; Finnish Forest Research Institute: Muhos, Finland, 2007. [Google Scholar]
- Reick, C.H.; Raddatz, T.; Brovkin, V.; Gayler, V. Representation of natural and anthropogenic land cover change in MPI-ESM. J. Adv. Model. Earth Syst. 2013, 5, 459–482. [Google Scholar] [CrossRef]
- Stevens, B.; Giorgetta, M.; Esch, M.; Mauritsen, T.; Crueger, T.; Rast, S.; Salzmann, M.; Schmidt, H.; Bader, J.; Block, K.; et al. Atmospheric component of the MPI-M Earth System Model: ECHAM6. J. Adv. Model. Earth Syst. 2013, 5, 146–172. [Google Scholar] [CrossRef]
- Beer, C.; Weber, U.; Tomelleri, E.; Carvalhais, N.; Mahecha, M.; Reichstein, M. Harmonized European Long-Term Climate Data for Assessing the Effect of Changing Temporal Variability on Land-Atmosphere CO2 Fluxes. J. Clim. 2014, 27, 4815–4834. [Google Scholar] [CrossRef]
- Van Oijen, M.; Balkovič, J.; Beer, C.; Cameron, D.; Ciais, P.; Cramer, W.; Kato, T.; Kuhnert, M.; Martin, R.; Myneni, R.; et al. Impact of droughts on the C-cycle in European vegetation: A probabilistic risk analysis using six vegetation models. Biogeosci. Discuss. 2014, 11, 8325–8371. [Google Scholar] [CrossRef]
- Peltoniemi, M.; Markkanen, T.; Härkönen, S.; Muukkonen, P.; Thum, T.; Aalto, T.; Mäkelä, A. Consistent estimates of gross primary production of Finnish forests—Comparison of estimates of two process models. Boreal Environ. Res. 2015, 20, 196–212. [Google Scholar]
- Gao, Y.; Markkanen, T.; Thum, T.; Aurela, M.; Lohila, A.; Mammarella, I.; Kämäräinen, M.; Hagemann, S.; Aalto, T. Assessing various drought indicators in representing summer drought in boreal forests in Finland. Hydrol. Earth Syst. Sci. 2016, 20, 175–191. [Google Scholar] [CrossRef]
- Murray, M.B.; Cannell, G.R.; Smith, R.I. Date of budburst of fifteen tree species in Britain following climate warming. J. Appl. Ecol. 1989, 26, 693–700. [Google Scholar] [CrossRef]
- Farquhar, G.D.; Caemmerer, S.; Berry, J.A. A biochemical model of photosynthetic CO2 assimilation in leaves of C3 species. Planta 1980, 149, 78–90. [Google Scholar] [CrossRef] [PubMed]
- Knorr, W. Annual and interannual CO2 exchanges of the terrestrial biosphere: Process-based simulations and uncertainties. Glob. Ecol. Biogeogr. 2000, 9, 225–252. [Google Scholar] [CrossRef]
- Roesch, A.; Wild, M.; Gilgen, H.; Ohmura, A. A new snow cover fraction parametrization for the ECHAM4 GCM. Clim. Dyn. 2001, 17, 933–946. [Google Scholar] [CrossRef]
- Jacob, D.; Podzun, R. Sensitivity studies with the regional climate model REMO. Meteorol. Atmos. Phys. 1997, 63, 119–129. [Google Scholar] [CrossRef]
- Jacob, D. A note to the simulation of the annual and inter-annual variability of the water budget over the Baltic Sea drainage basin. Meteorol. Atmos. Phys. 2001, 77, 61–73. [Google Scholar] [CrossRef]
- Gao, Y.; Weiher, S.; Markkanen, T.; Pietikäinen, J.-P.; Gregow, H.; Henttonen, H.M.; Jacob, D.; Laaksonen, A. Implementation of the CORINE land use classification in the regional climate model REMO. Boreal Environ. Res. 2015, 20, 261–282. [Google Scholar]
- Simmons, A.J.; Burridge, D.M. An Energy and angular-momentum conserving vertical finite-difference scheme and hybrid vertical coordinates. Mon. Weather Rev. 1981, 109, 758–766. [Google Scholar] [CrossRef]
- Dee, D.P.; Uppala, S.M.; Simmons, A.J.; Berrisford, P.; Poli, P.; Kobayashi, S.; Andrae, U.; Balmaseda, M.A.; Balsamo, G.; Bauer, P.; et al. The ERA-Interim reanalysis: Configuration and performance of the data assimilation system. Q. J. R. Meteorol. Soc. 2011, 137, 553–597. [Google Scholar] [CrossRef]
- Christensen, J.H.; Boberg, F.; Christensen, O.B.; Lucas-Picher, P. On the need for bias correction of regional climate change projections of temperature and precipitation. Geophys. Res. Lett. 2008, 35, L20709. [Google Scholar] [CrossRef]
- Teutschbein, C.; Seibert, J. Bias correction of regional climate model simulations for hydrological climate-change impact studies: Review and evaluation of different methods. J. Hydrol. 2012, 456–457, 12–29. [Google Scholar] [CrossRef]
- Pietikäinen, J.P.; O’Donnell, D.; Teichmann, C.; Karstens, U.; Pfeifer, S.; Kazil, J.; Podzun, R.; Fiedler, S.; Kokkola, H.; Birmili, W.; et al. The regional aerosol-climate model REMO-HAM. Geosci. Model Dev. 2012, 5, 1323–1339. [Google Scholar] [CrossRef]
- Aalto, J.; Pirinen, P.; Heikkinen, J.; Venalainen, A. Spatial interpolation of monthly climate data for Finland: Comparing the performance of kriging and generalized additive models. Theor. Appl. Climatol. 2013, 112, 99–111. [Google Scholar] [CrossRef]
- Räisänen, J.; Räty, O. Projections of daily mean temperature variability in the future: Cross-validation tests with ENSEMBLES regional climate simulations. Clim. Dyn. 2013, 41, 1553–1568. [Google Scholar] [CrossRef]
- Räty, O.; Räisanen, J.; Ylhäsi, J.S. Evaluation of delta change and bias correction methods for future daily precipitation: Intermodel cross-validation using ENSEMBLES simulations. Clim. Dyn. 2014, 42, 2287–2303. [Google Scholar] [CrossRef]
- Metsämäki, S.J.; Anttila, S.T.; Markus, H.J.; Vepsäläinen, J.M. A feasible method for fractional snow cover mapping in boreal zone based on a reflectance model. Remote Sens. Environ. 2005, 95, 77–95. [Google Scholar] [CrossRef]
- Metsämäki, S.; Mattila, O.-P.; Pulliainen, J.; Niemi, K.; Luojus, K.; Böttcher, K. An optical reflectance model-based method for fractional snow cover mapping applicable to continental scale. Remote Sens. Environ. 2012, 123, 508–521. [Google Scholar] [CrossRef]
- Badeck, F.-W.; Bondeau, A.; Böttcher, K.; Doktor, D.; Lucht, W.; Schaber, J.; Sitch, S. Responses of spring phenology to climate change. New Phytol. 2004, 162, 295–309. [Google Scholar] [CrossRef]
- Doktor, D.; Bondeau, A.; Koslowski, D.; Badeck, F.-W. Influence of heterogeneous landscapes on computed green-up dates based on daily AVHRR NDVI observations. Remote Sens. Environ. 2009, 113, 2618–2632. [Google Scholar] [CrossRef]
- Härmä, P.; Teiniranta, R.; Törmä, M.; Repo, R.; Järvenpää, E.; Kallio, E. CLC2000 Finland: Final Report; Finnish Environment Institute, Geoinformatics and Land Use Division: Helsinki, Finland, 2005. [Google Scholar]
- Delbart, N.; Le Toan, T.; Kergoat, L.; Fedotova, V. Remote sensing of spring phenology in boreal regions: A free of snow-effect method using NOAA-AVHRR and SPOT-VGT data (1982–2004). Remote Sens. Environ. 2006, 101, 52–62. [Google Scholar] [CrossRef]
- Moulin, S.; Kergoat, L.; Viovy, N.; Dedieu, G. Global-scale assessment of vegetation phenology using NOAA/AVHRR satellite measurements. J. Clim. 1997, 10, 1154–1155. [Google Scholar] [CrossRef]
- Jönsson, A.M.; Eklundh, L.; Hellström, M.; Bärring, L.; Jönsson, P. Annual changes in MODIS vegetation indices of Swedish coniferous forests in relation to snow dynamics and tree phenology. Remote Sens. Environ. 2010, 114, 2719–2730. [Google Scholar] [CrossRef]
- Delbart, N.; Picard, G.; Le Toan, T.; Kergoat, L.; Quegan, S.; Woodward, I.A.N.; Dye, D.; Fedotova, V. Spring phenology in boreal Eurasia over a nearly century time scale. Glob. Chang. Biol. 2008, 14, 603–614. [Google Scholar] [CrossRef]
- Savitzky, A.; Golay, M.J.E. Smoothing and differentiation of data by simplified least squares procedures. Anal. Chem. 1964, 36, 1627–1639. [Google Scholar] [CrossRef]
- Chen, J.; Jönsson, P.; Tamura, M.; Gu, Z.; Matsushita, B.; Eklundh, L. A simple method for reconstructing a high-quality NDVI time-series data set based on the Savitzky-Golay filter. Remote Sens. Environ. 2004, 91, 332–344. [Google Scholar] [CrossRef]
- Jönsson, P.; Eklundh, L. TIMESAT-a program for analyzing time-series of satellite sensor data. Comput. Geosci. 2004, 30, 833–845. [Google Scholar] [CrossRef]
- Karlsen, S.; Solheim, I.; Beck, P.; Høgda, K.; Wielgolaski, F.; Tømmervik, H. Variability of the start of the growing season in Fennoscandia, 1982–2002. Int. J. Biometeorol. 2007, 51, 513–524. [Google Scholar] [CrossRef] [PubMed]
- Karlsen, S.R.; Elvebakk, A.; Høgda, K.A.; Johansen, B. Satellite-based mapping of the growing season and bioclimatic zones in Fennoscandia. Glob. Ecol. Biogeogr. 2006, 15, 416–430. [Google Scholar] [CrossRef]
- Rousi, M.; Heinonen, J. Temperature sum accumulation effects on within-population variation and long-term trends in date of bud burst of European white birch (Betula pendula). Tree Physiol. 2007, 27, 1019–1025. [Google Scholar] [CrossRef] [PubMed]
- Drolet, G.G.; Huemmrich, K.F.; Hall, F.G.; Middleton, E.M.; Black, T.A.; Barr, A.G.; Margolis, H.A. A MODIS-derived photochemical reflectance index to detect inter-annual variations in the photosynthetic light-use efficiency of a boreal deciduous forest. Remote Sens. Environ. 2005, 98, 212–224. [Google Scholar] [CrossRef]
- Jin, H.; Eklundh, L. A physically based vegetation index for improved monitoring of plant phenology. Remote Sens. Environ. 2014, 152, 512–525. [Google Scholar] [CrossRef]
- Houborg, R.; Fisher, J.B.; Skidmore, A.K. Advances in remote sensing of vegetation function and traits. Int. J. Appl. Earth Observ. Geoinf. 2015, 43, 1–6. [Google Scholar] [CrossRef]
- Joiner, J.; Yoshida, Y.; Vasilkov, A.P.; Schaefer, K.; Jung, M.; Guanter, L.; Zhang, Y.; Garrity, S.; Middleton, E.M.; Huemmrich, K.F.; et al. The seasonal cycle of satellite chlorophyll fluorescence observations and its relationship to vegetation phenology and ecosystem atmosphere carbon exchange. Remote Sens. Environ. 2014, 152, 375–391. [Google Scholar] [CrossRef]
- Poggio, L.; Gimona, A.; Brown, I. Spatio-temporal MODIS EVI gap filling under cloud cover: An example in Scotland. ISPRS J. Photogr. Remote Sens. 2012, 72, 56–72. [Google Scholar] [CrossRef]
- Weiss, D.J.; Atkinson, P.M.; Bhatt, S.; Mappin, B.; Hay, S.I.; Gething, P.W. An effective approach for gap-filling continental scale remotely sensed time-series. ISPRS J. Photogr. Remote Sens. 2014, 98, 106–118. [Google Scholar] [CrossRef] [PubMed]
- Zhang, C.; Li, W.; Travis, D.J. Restoration of clouded pixels in multispectral remotely sensed imagery with cokriging. Int. J. Remote Sens. 2009, 30, 2173–2195. [Google Scholar] [CrossRef]
- Jones, M.O.; Jones, L.A.; Kimball, J.S.; McDonald, K.C. Satellite passive microwave remote sensing for monitoring global land surface phenology. Remote Sens. Environ. 2011, 115, 1102–1114. [Google Scholar] [CrossRef]
- Finnish Meteorological Institute. GlobSnow. Available online: http://www.globsnow.info (accessed on 5 July 2016).
- Kolari, P.; Chan, T.; Porcar-Castell, A.; Bäck, J.; Nikinmaa, E.; Juurola, E. Field and controlled environment measurements show strong seasonal acclimation in photosynthesis and respiration potential in boreal Scots pine. Front. Plant Sci. 2014, 5. [Google Scholar] [CrossRef] [PubMed]
- Thum, T.; Aalto, T.; Laurila, T.; Aurela, M.; Lindroth, A.; Vesala, T. Assessing seasonality of biochemical CO2 exchange model parameters from micrometeorological flux observations at boreal coniferous forest. Biogeosciences 2008, 5, 1625–1639. [Google Scholar] [CrossRef]
- Robakowski, P. Susceptibility to low-temperature photoinhibition in three conifers differing in successional status. Tree Physiol. 2005, 25, 1151–1160. [Google Scholar] [CrossRef] [PubMed]
- Sevanto, S.; Suni, T.; Pumpanen, J.; Grönholm, T.; Kolari, P.; Nikinmaa, E.; Hari, P.; Vesala, T. Wintertime photosynthesis and water uptake in a boreal forest. Tree Physiol. 2006, 26, 749–757. [Google Scholar] [CrossRef] [PubMed]
- Ekici, A.; Beer, C.; Hagemann, S.; Boike, J.; Langer, M.; Hauck, C. Simulating high-latitude permafrost regions by the JSBACH terrestrial ecosystem model. Geosci. Model Dev. 2014, 7, 631–647. [Google Scholar] [CrossRef]
- Pudas, E.; Leppälä, M.; Tolvanen, A.; Poikolainen, J.; Venäläinen, A.; Kubin, E. Trends in phenology of Betula pubescens across the boreal zone in Finland. Int. J. Biometeorol. 2008, 52, 251–259. [Google Scholar] [CrossRef] [PubMed]
- Bennie, J.; Kubin, E.; Wiltshire, A.; Huntley, B.; Baxter, R. Predicting spatial and temporal patterns of bud-burst and spring frost risk in north-west Europe: The implications of local adaptation to climate. Glob. Chang. Biol. 2010, 16, 1503–1514. [Google Scholar] [CrossRef]
- Linkosalo, T.; Lappalainen, H.K.; Hari, P. A comparison of phenological models of leaf bud burst and flowering of boreal trees using independent observations. Tree Physiol. 2008, 28, 1873–1882. [Google Scholar] [CrossRef] [PubMed]
- Botta, A.; Viovy, N.; Ciais, P.; Friedlingstein, P.; Monfray, P. A global prognostic scheme of leaf onset using satellite data. Glob. Chang. Biol. 2000, 6, 709–725. [Google Scholar] [CrossRef]
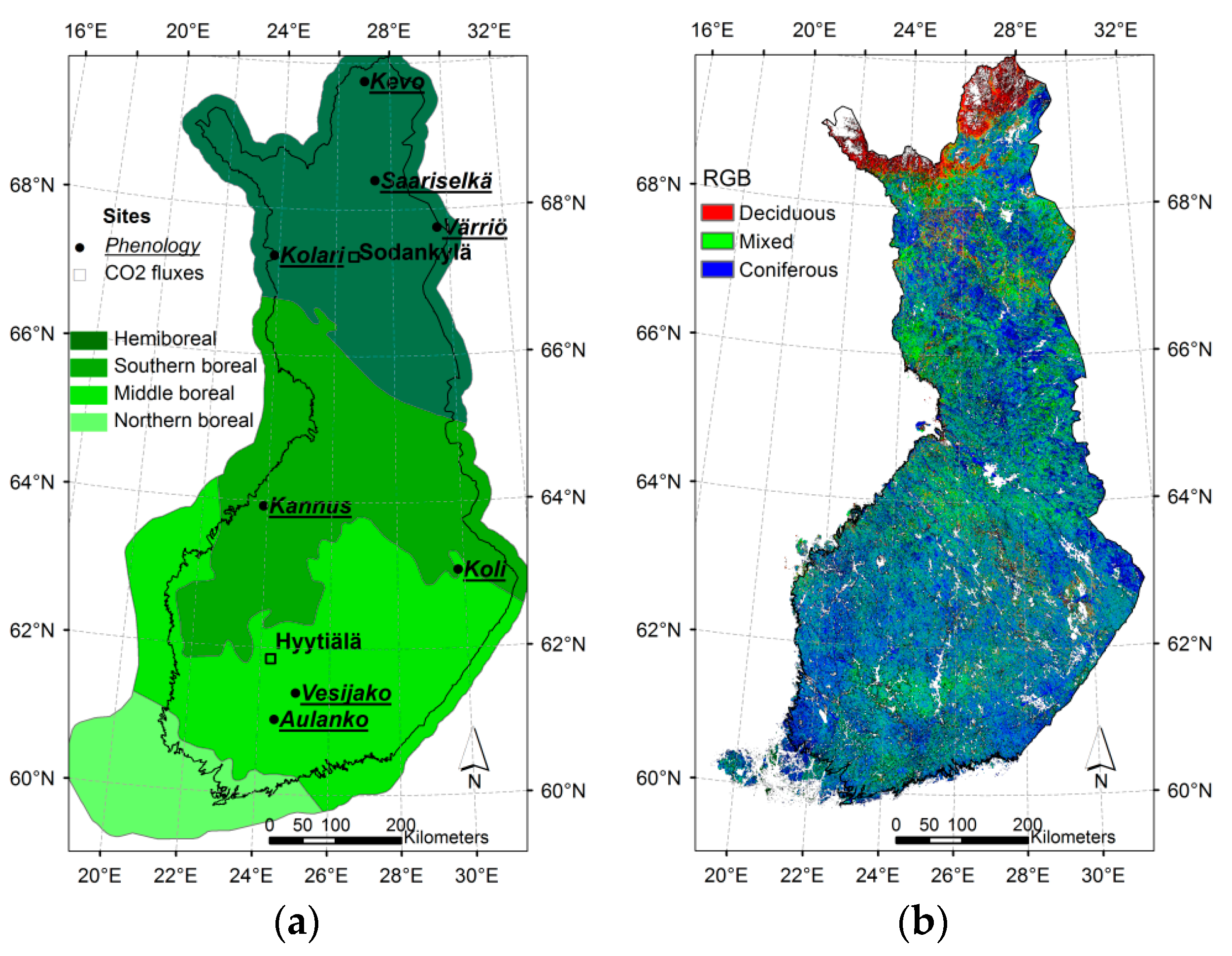
| Site Name | Location | Phytogeographical Zone | Altitude m a.s.l. | Number of Pixels 1 | |||
|---|---|---|---|---|---|---|---|
| Site | Median for Pixels 2 | SD 3 | |||||
| Aulanko | 61°01’N | 24°27’E | Southern boreal | 145 | 99.8 | 20.5 | 10 |
| Vesijako | 61°23’N | 25°03’E | Southern boreal | 110 | 109.6 | 9.3 | 12 |
| Koli | 63°06’N | 29°49’E | Southern boreal | 135 | 139.1 | 56.1 | 17 |
| Kannus | 63°54’N | 23°57’E | Middle boreal | 40 | 43.7 | 2.8 | 12 |
| Värriö | 67°45’N | 29°37’E | Northern boreal | 350 | 382.9 | 39.4 | 62 |
| Kolari | 67°21’N | 23°50’E | Northern boreal | 150 | 151.5 | 4.9 | 26 |
| Saariselkä | 68°24’N | 27°23’E | Northern boreal | 300 | 303.4 | 27.4 | 38 |
| Kevo | 69°45’N | 27°01’E | Northern boreal | 100 | 130.5 | 52.6 | 41 |
| Site Name | Number of Observations | Mean Bud Break (Doy) | Mean DBF_SOSsat (Doy) | R2 | p | RMSE (d) | Bias (d) |
|---|---|---|---|---|---|---|---|
| Aulanko | 5 | 127.2 | 122.8 | 0.28 | 0.362 | 6.6 | −4.4 |
| Vesijako | 7 | 131.6 | 126.6 | 0.01 | 0.807 | 7.0 | −5.0 |
| Koli | 7 | 133.7 | 136.8 | 0.40 | 0.127 | 5.7 | 3.1 |
| Kannus | 7 | 134.1 | 128.9 | 0.01 | 0.832 | 10.1 | −5.3 |
| Värriö | 7 | 155.0 | 160.1 | 0.43 | 0.111 | 8.6 | 5.1 |
| Kolari | 6 | 140.8 | 145.5 | 0.46 | 0.137 | 7.3 | 4.7 |
| Saariselkä | 4 | 154.3 | 154.3 | 0.66 | 0.191 | 5.5 | 0.0 |
| Kevo | 5 | 155.4 | 155.8 | 0.35 | 0.294 | 4.4 | −0.4 |
| Site-means | 8 | 141.5 | 141.4 | 0.94 | 0.001 | 4.4 | 0.2 |
| Site | Number of Years | ENF_SOSEC | ENF_SOSmod,loc | ENF_SOSmod | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Mean (Doy) | Mean (Doy) | R2 | p | Bias (d) | Mean (Doy) | R2 | p | Bias (d) | ||
| Hyytiälä | 10 | 95.9 | 86.6 | 0.11 | 0.336 | −9.3 | 95.5 | 0.75 | 0.001 | −0.4 |
| Sodankylä | 9 1 | 123.3 | 105.3 | 0.02 | 0.696 | −18.0 | 118.9 | 0.27 | 0.153 | −4.4 |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Böttcher, K.; Markkanen, T.; Thum, T.; Aalto, T.; Aurela, M.; Reick, C.H.; Kolari, P.; Arslan, A.N.; Pulliainen, J. Evaluating Biosphere Model Estimates of the Start of the Vegetation Active Season in Boreal Forests by Satellite Observations. Remote Sens. 2016, 8, 580. https://doi.org/10.3390/rs8070580
Böttcher K, Markkanen T, Thum T, Aalto T, Aurela M, Reick CH, Kolari P, Arslan AN, Pulliainen J. Evaluating Biosphere Model Estimates of the Start of the Vegetation Active Season in Boreal Forests by Satellite Observations. Remote Sensing. 2016; 8(7):580. https://doi.org/10.3390/rs8070580
Chicago/Turabian StyleBöttcher, Kristin, Tiina Markkanen, Tea Thum, Tuula Aalto, Mika Aurela, Christian H. Reick, Pasi Kolari, Ali N. Arslan, and Jouni Pulliainen. 2016. "Evaluating Biosphere Model Estimates of the Start of the Vegetation Active Season in Boreal Forests by Satellite Observations" Remote Sensing 8, no. 7: 580. https://doi.org/10.3390/rs8070580
APA StyleBöttcher, K., Markkanen, T., Thum, T., Aalto, T., Aurela, M., Reick, C. H., Kolari, P., Arslan, A. N., & Pulliainen, J. (2016). Evaluating Biosphere Model Estimates of the Start of the Vegetation Active Season in Boreal Forests by Satellite Observations. Remote Sensing, 8(7), 580. https://doi.org/10.3390/rs8070580








