Estimation of Water Quality Parameters in Lake Erie from MERIS Using Linear Mixed Effect Models
Abstract
:1. Introduction
2. Materials and Methods
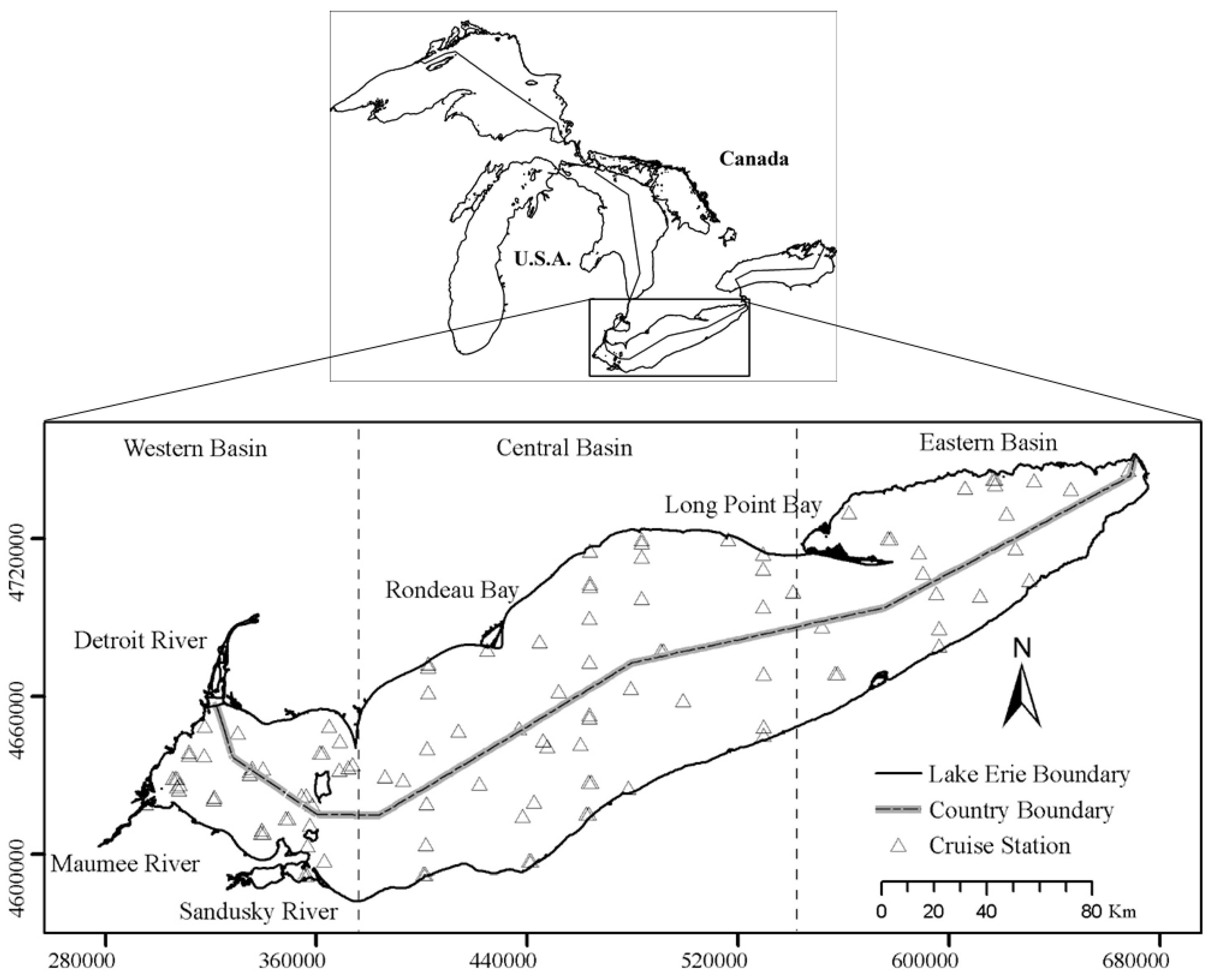
2.1. Study Site
2.2. Field Measurements of Water Quality Parameters
2.3. Satellite Data and Processing
2.4. Water Quality Parameters Algorithms
2.5. Accuracy Assessment
3. Results
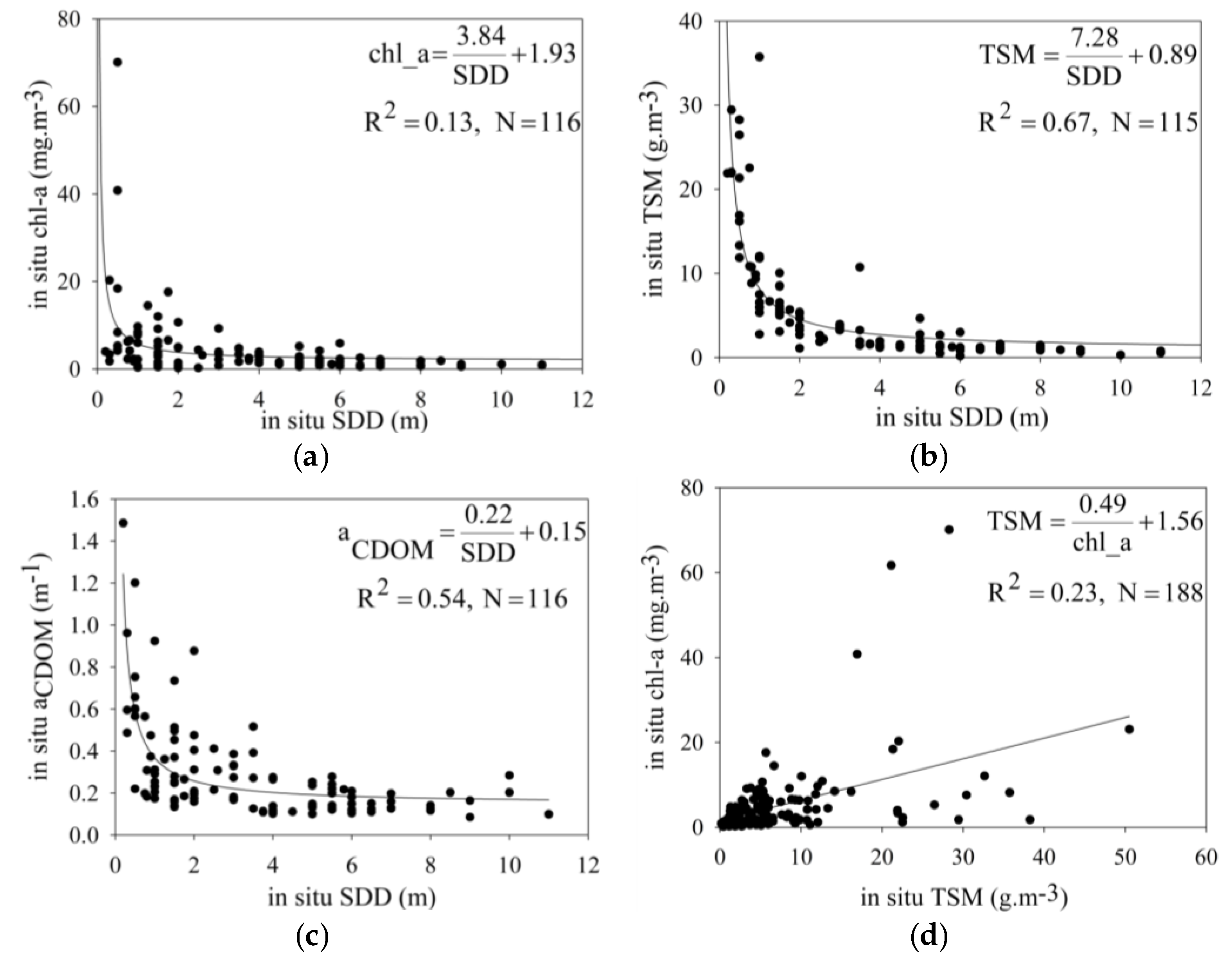
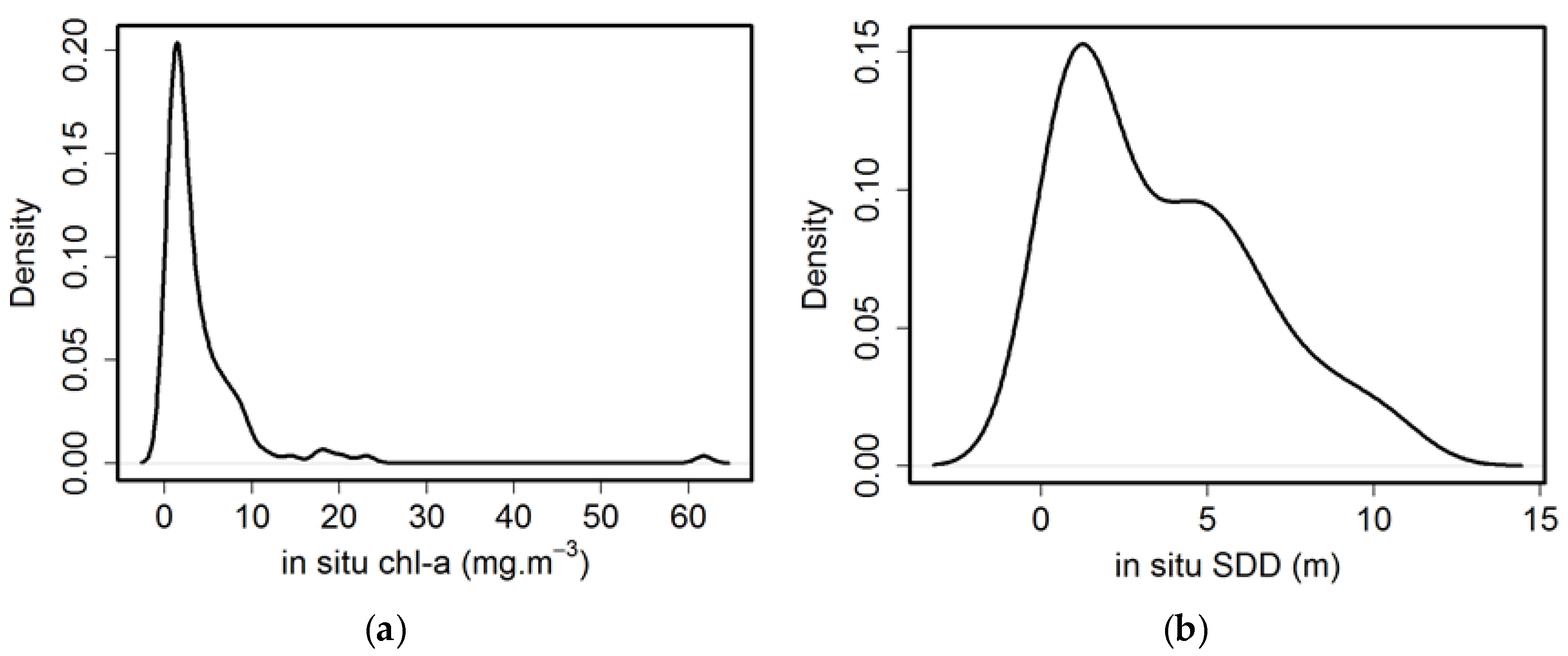
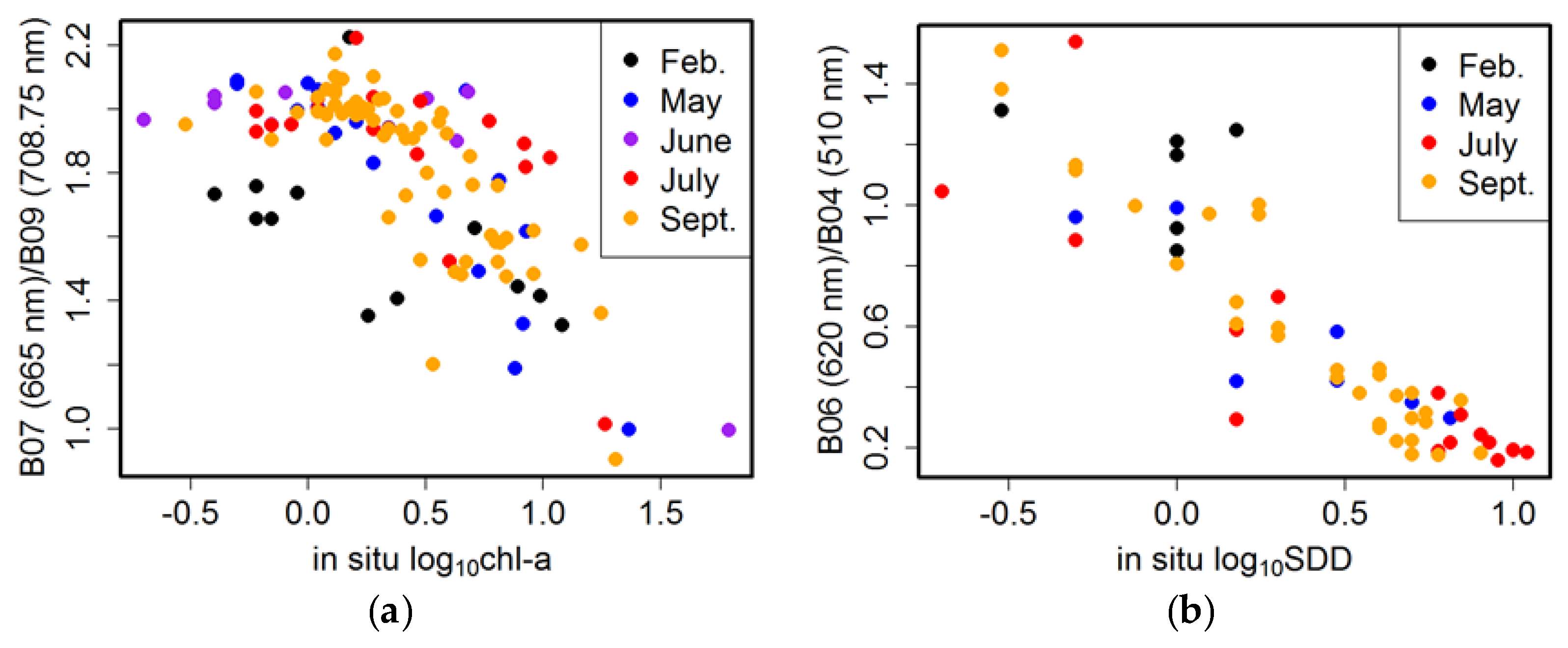
3.1. Lake Erie Optical Properties
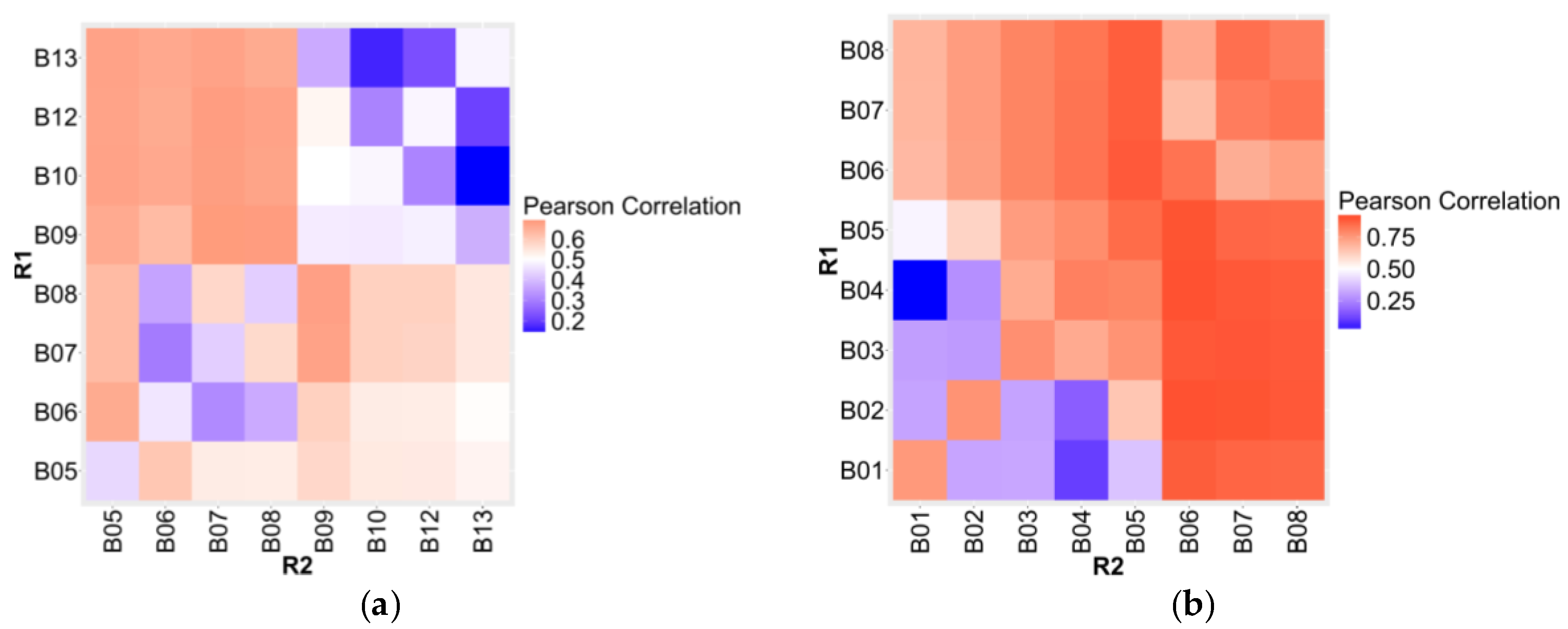
3.2. Linear Mixed Effect Models Calibration
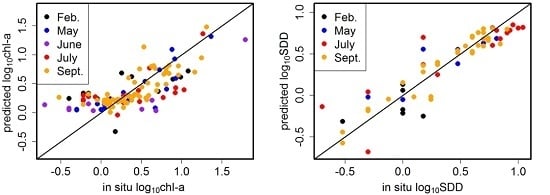
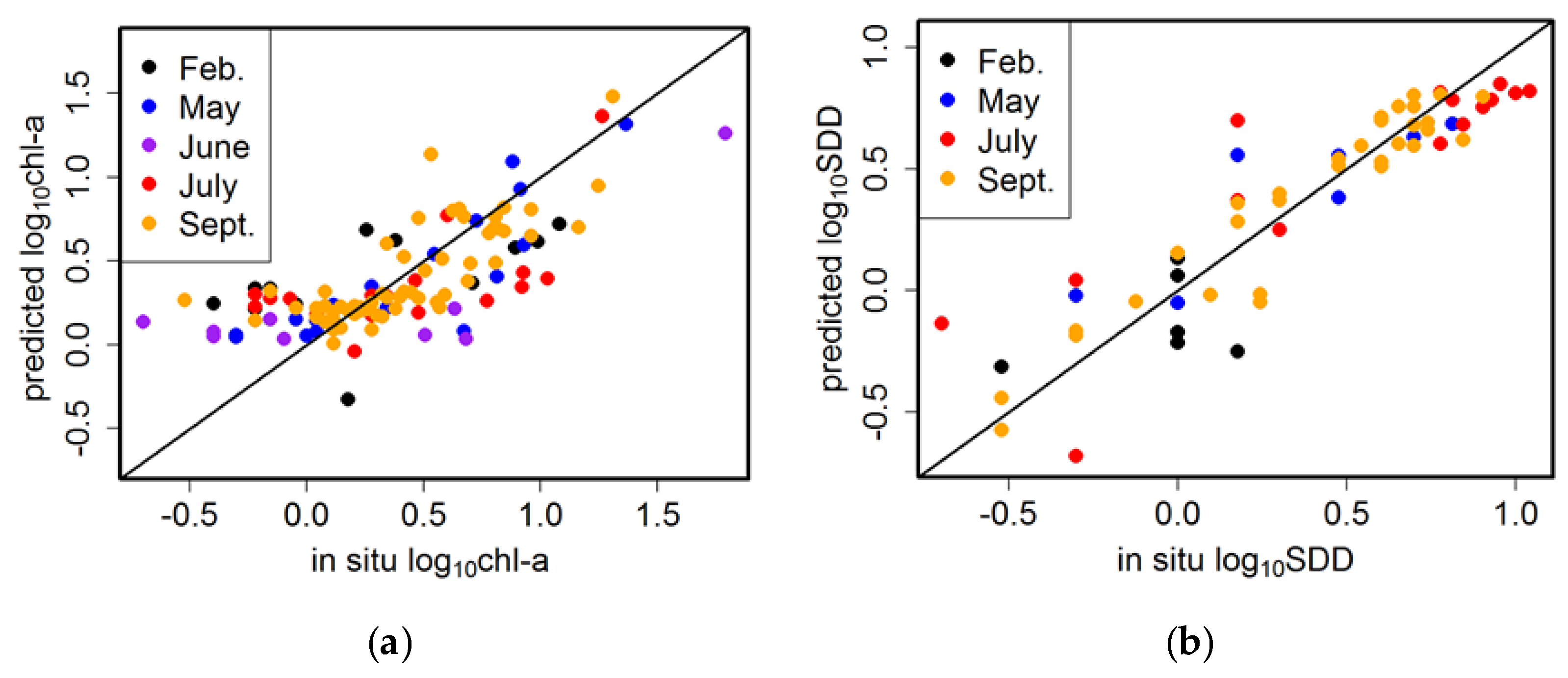
3.3. Evaluation of Linear Mixed Effect Models
3.4. Spatial and Temporal Variations of Chl-a and SDD
4. Discussion
4.1. Linear Mixed Effect Model Results
4.2. Interpretation of Spatial and Temporal Variations in Chl-a and SDD
4.3. Limitations and Uncertainties of the Applied Linear Mixed Effect Model on MERIS
5. Conclusions
Acknowledgments
Conflicts of Interest
Abbreviations
| BEAM | Basic ERS & ENVISAT (A)ATSR MERIS |
| CC | CoastColour |
| CDOM | Colored Dissolved Organic Matters |
| Chl-a | Chlorophyll-a |
| CPA | Color-Producing Agent |
| ESA | European Space Agency |
| IOP | Inherent Optical Property |
| LME | Linear Mixed Effect |
| MBE | Mean Bias Error |
| MCI | Maximum Chlorophyll Index |
| MERIS | Medium Resolution Imaging Spectrometer |
| MODIS | Moderate-resolution Imaging Spectrometer |
| NLET | National Laboratory for Environmental Testing |
| OLCI | Ocean and Land Colour Instrument |
| RMSE | Root Mean Square Error |
| SDD | Secchi Disk Depth |
| TSM | Total Suspended Matters |
References
- Binding, C.E.; Greenberg, T.A.; Bukata, R.P. An analysis of MODIS-derived algal and mineral turbidity in Lake Erie. J. Gt. Lakes Res. 2012, 38, 107–116. [Google Scholar] [CrossRef]
- Daher, S. Lake Erie LAMP Status Report; Environment Canada: Burlington, ON, Canada, 1999. [Google Scholar]
- Morel, A.; Prieur, L. Analysis of variations in ocean color. Limnol. Oceanogr. 1977, 22, 709–722. [Google Scholar] [CrossRef]
- Zhao, D.; Cai, Y.; Jiang, H.; Xu, D.; Zhang, W.; An, S. Estimation of water clarity in Taihu Lake and surrounding rivers using Landsat imagery. Adv. Water Resour. 2011, 34, 165–173. [Google Scholar] [CrossRef]
- McCullough, I.M.; Loftin, C.S.; Sader, S.A. Combining lake and watershed characteristics with Landsat TM data for remote estimation of regional lake clarity. Remote Sens. Environ. 2012, 123, 109–115. [Google Scholar] [CrossRef]
- Tebbs, E.J.; Remedios, J.J.; Harper, D.M. Remote sensing of chlorophyll-a as a measure of cyanobacterial biomass in Lake Bogoria, a hypertrophic, saline–alkaline, flamingo lake, using Landsat ETM+. Remote Sens. Environ. 2013, 135, 92–106. [Google Scholar] [CrossRef]
- Binding, C.E.; Greenberg, T.A.; Bukata, R.P. Time series analysis of algal blooms in Lake of the Woods using the MERIS maximum chlorophyll index. J. Plankton Res. 2011, 33, 1847–1852. [Google Scholar] [CrossRef]
- McCullough, I.M.; Loftin, C.S.; Sader, S.A. High-frequency remote monitoring of large lakes with MODIS 500 m imagery. Remote Sens. Environ. 2012, 124, 234–241. [Google Scholar] [CrossRef]
- Saulquin, B.; Hamdi, A.; Gohin, F.; Populus, J.; Mangin, A.; D’Andon, O.F. Estimation of the diffuse attenuation coefficient kdPAR using MERIS and application to seabed habitat mapping. Remote Sens. Environ. 2013, 128, 224–233. [Google Scholar] [CrossRef]
- Odermatt, D.; Pomati, F.; Pitarch, J.; Carpenter, J.; Kawka, M.; Schaepman, M.; Wüest, A. MERIS observations of phytoplankton blooms in a stratified eutrophic lake. Remote Sens. Environ. 2012, 126, 232–239. [Google Scholar] [CrossRef]
- Duan, H.; Ma, R.; Xu, J.; Zhang, Y.; Zhang, B. Comparison of different semi-empirical algorithms to estimate chlorophyll-a concentration in inland lake water. Environ. Monit. Assess. 2010, 170, 231–244. [Google Scholar] [CrossRef] [PubMed]
- Bresciani, M.; Giardino, C. Retrospective analysis of spatial and temporal variability of chlorophyll-a in the Curonian Lagoon. J. Coast. Conserv. 2012, 16, 511–519. [Google Scholar] [CrossRef]
- Matthews, M.W.; Bernard, S.; Winter, K. Remote sensing of cyanobacteria-dominant algal blooms and water quality parameters in Zeekoevlei, a small hypertrophic lake, using MERIS. Remote Sens. Environ. 2010, 114, 2070–2087. [Google Scholar] [CrossRef]
- Wu, G.; Leeuw, J.D.; Skidmore, A.K.; Prins, H.H.T.; Liu, Y. Comparison of MODIS and Landsat TM5 images for mapping tempo–spatial dynamics of secchi disk depths in Poyang Lake national nature reserve, China. Int. J. Remote Sens. 2008, 29, 2183–2198. [Google Scholar] [CrossRef]
- Kratzer, S.; Brockmann, C.; Moore, G. Using MERIS full resolution data to monitor coastal waters—A case study from Himmerfjärden, a fjord-like bay in the Northwestern Baltic Sea. Remote Sens. Environ. 2008, 112, 2284–2300. [Google Scholar] [CrossRef]
- Pinheiro, J.; Bates, D.; DebRoy, S.; Sarkar, D. Linear and Nonlinear Mixed Effects Models. Available online ftp://ftp.uni-bayreuth.de/pub/math/statlib/R/CRAN/doc/packages/nlme.pdf (accessed on 16 May 2016).
- Ruescas, A.; Brockmann, C.; Stelzer, K.; Tilstone, G.H.; Beltrán-Abaunza, J.M. DUE CoastColour Final Report, Version 1; Brockmann Consult: Geesthacht, Germany, 2014. [Google Scholar]
- Moore, T.S.; Dowell, M.D.; Bradt, S.; Ruiz-Verdu, A. An optical water type framework for selecting and blending retrievals from bio-optical algorithms in lakes and coastal waters. Remote Sens. Environ. 2014, 143, 97–111. [Google Scholar] [CrossRef] [PubMed]
- Kratzer, S.; Håkansson, B.; Sahlin, C. Assessing secchi and photic zone depth in the Baltic Sea from satellite data. AMBIO 2003, 32, 577–585. [Google Scholar] [CrossRef] [PubMed]
- Fleming-Lehtinen, V.; Laamanen, M. Long-term changes in secchi depth and the role of phytoplankton in explaining light attenuation in the Baltic Sea. Estuar. Coast. Shelf Sci. 2012, 102–103, 1–10. [Google Scholar] [CrossRef]
- Michalak, A.M.; Anderson, E.J.; Beletsky, D.; Boland, S.; Bosch, N.S.; Bridgeman, T.B.; Chaffin, J.D.; Cho, K.; Confesor, R.; Daloglu, I.; et al. Record-setting algal bloom in Lake Erie caused by agricultural and meteorological trends consistent with expected future conditions. Proc. Natl. Acad. Sci. USA 2013, 110, 6448–6452. [Google Scholar] [CrossRef] [PubMed]
- Bootsma, H.A.; Hecky, R.E. A comparative introduction to the biology and limnology of the African Great Lakes. J. Gt. Lakes Res. 2003, 29, 3–18. [Google Scholar] [CrossRef]
- Lake Erie LaMP Work Group. Lake Erie Lakewide Action and Management Plans (LAMPs); US Environmental Protection Agency: Chicago, IL, USA, 2000.
- International Joint Commission Canada and United States. Lake Erie Ecosystems Priority, Scientific Findings and Policy: Recommendations to Reduce Nutrient Loadings and Harmful Algal Blooms; International Joint Commission: Washington, DC, USA, 2013. [Google Scholar]
- UNESCO. Determination of Photosynthetic Pigments in Sea-Water; UNESCO Monographs on Oceanographic Methodology: Paris, France, 1966. [Google Scholar]
- Environment Canada. Manual of Analytical Methods; Environmental Conservation Service—ECD; Canadian Communications Group: Toronto, ON, Canada, 1997. [Google Scholar]
- Effler, S. Secchi disk transparency and turbidity. J. Environ. Eng. 1988, 114, 1436–1447. [Google Scholar] [CrossRef]
- Civera, J.I.; Miró, N.L.; Breijo, E.G.; Peris, R.M. Secchi depth and water quality control: Measurement of sunlight extinction. In Mediterranean Sea: Ecosystems, Economic Importance and Environmental Threats; Hughes, T.B., Ed.; Nova Science: New York, NY, USA, 2013; pp. 91–114. [Google Scholar]
- Mueller, J.L.; Bidigare, R.R.; Trees, C.; Balch, W.M.; Dore, J.; Drapeau, D.T.; Karl, D.; Heukelem, L.V.; Perl, J. Biogeochemical and bio-optical measurements and data analysis protocols. In Ocean Optics Protocols for Satellite Ocean Color Sensor Validation; Mueller, J.L., Fargion, G.S., Mcclain, C.R., Eds.; National Aeronautical and Space Administration: Washington, DC, USA, 2003. [Google Scholar]
- Pegau, S.; Zaneveld, J.R.V.; Mitchell, B.G.; Mueller, J.L.; Kahru, M.; Wieland, J.; Stramska, M. Inherent optical properties: Instruments, characterizations, field measurements and data analysis protocols. In Ocean Optics Protocols for Satellite Ocean Color Sensor Validation; Mueller, J.L., Fargion, G.S., McClain, C.R., Eds.; National Aeronautical and Space Administration: Washington, DC, USA, 2002. [Google Scholar]
- Doerffer, R.; Schiller, H. The MERIS Case 2 water algorithm. Int. J. Remote Sens. 2007, 28, 517–535. [Google Scholar] [CrossRef]
- Heim, B.; Abramova, E.; Doerffer, R.; Günther, F.; Hölemann, J.; Kraberg, A.; Lantuit, H.; Loginova, A.; Martynov, F.; Overduin, P.P.; et al. Ocean colour remote sensing in the Southern Laptev Sea: Evaluation and applications. Biogeosciences 2014, 11, 4191–4210. [Google Scholar] [CrossRef] [Green Version]
- Campbell, J.W. The lognormal distribution as a model for bio-optical variability in the sea. J. Geophys. Res. 1995, 100, 13237–13254. [Google Scholar] [CrossRef]
- Szeto, M.; Werdell, P.J.; Moore, T.S.; Campbell, J.W. Are the world’s oceans optically different? J. Geophys. Res. 2011, 116. [Google Scholar] [CrossRef]
- R Development Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2015. [Google Scholar]
- Branco, A.B.; Kremer, J.N. The relative importance of chlorophyll and colored dissolved organic matter (CDOM) to the prediction of the diffuse attenuation coefficient in shallow estuaries. Estuaries 2005, 28, 643–652. [Google Scholar] [CrossRef]
- Kemp, A.L.W.; MacInnis, G.A.; Harper, N.S. Sedimentation rates and a revised sediment budget for Lake Erie. Gt. Lakes Res. 1977, 3, 221–233. [Google Scholar] [CrossRef]
- Shi, K.; Zhang, Y.; Liu, X.; Wang, M.; Qin, B. Remote sensing of diffuse attenuation coefficient of photosynthetically active radiation in Lake Taihu using MERIS data. Remote Sens. Environ. 2014, 140, 365–377. [Google Scholar] [CrossRef]
- Dall’Olmo, G.; Gitelson, A.A. Effect of bio-optical parameter variability and uncertainties in reflectance measurements on the remote estimation of chlorophyll-a concentration in turbid productive waters: Modeling results. Appl. Opt. 2006, 44, 412–422. [Google Scholar] [CrossRef]
- Gitelson, A.; Schalles, J.; Hladik, C. Remote chlorophyll-a retrieval in turbid, productive estuaries: Chesapeake Bay case study. Remote Sens. Environ. 2007, 109, 464–472. [Google Scholar] [CrossRef]
- Hicks, B.J.; Stichbury, G.A.; Brabyn, L.K.; Allan, M.G.; Ashraf, S. Hindcasting water clarity from Landsat satellite images of unmonitored shallow lakes in the Waikato region, New Zealand. Environ. Monit. Assess. 2013, 185, 7245–7261. [Google Scholar] [CrossRef] [PubMed]
- Binding, C.E.; Greenberg, T.A.; Bukata, R.P. The MERIS maximum chlorophyll index; its merits and limitations for inland water algal bloom monitoring. J. Gt. Lakes Res. 2013, 39, 100–107. [Google Scholar] [CrossRef]
- Ali, K.A.; Witter, D.; Ortiz, J.D. Application of empirical and semi-analytical algorithms to MERIS data for estimating chlorophyll-a in Case 2 waters of Lake Erie. Environ. Earth Sci. 2014, 71, 4209–4220. [Google Scholar] [CrossRef]
- Witter, D.L.; Ortiz, J.D.; Palm, S.; Heath, R.T.; Budd, J.W. Assessing the application of SeaWiFS ocean color algorithms to Lake Erie. J. Gt. Lakes Res. 2009, 35, 361–370. [Google Scholar] [CrossRef]
- Sá, C.; D’Alimonte, D.; Brito, A.C.; Kajiyama, T.; Mendes, C.R.; Vitorino, J.; Oliveira, P.B.; da Silva, J.C.B.; Brotas, V. Validation of standard and alternative satellite ocean-color chlorophyll products off Western Iberia. Remote Sens. Environ. 2015, 168, 403–419. [Google Scholar] [CrossRef]
- Bolsenga, S.J.; Herdendorf, C.E. Lake Erie and Lake St. Clair Handbook; Wayne State University Press: Detroit, MI, USA, 1993. [Google Scholar]
- Morang, A.; Mohr, M.C.; Forgette, C.M. Longshore sediment movement and supply along the U.S. Shoreline of Lake Erie. J. Coast. Res. 2011, 27, 619–635. [Google Scholar] [CrossRef]
- Marvin, C.H.; Charlton, M.N.; Reiner, E.J.; Kolic, T.; MacPherson, K.; Stern, G.A.; Braekevelt, E.; Estenik, J.F.; Thiessen, L.; Painter, S. Surficial sediment contamination in Lakes Erie and Ontario: A comparative analysis. J. Gt. Lakes Res. 2002, 28, 437–450. [Google Scholar] [CrossRef]
- Dolan, D.M. Point source loadings of phosphorus to Lake Erie: 1986–1990. J. Gt. Lakes Res. 1993, 19, 212–223. [Google Scholar] [CrossRef]
- Binding, C.E.; Jerome, J.H.; Bukata, R.P.; Booty, W.G. Suspended particulate matter in Lake Erie derived from MODIS aquatic colour imagery. Int. J. Remote Sens. 2010, 31, 5239–5255. [Google Scholar] [CrossRef]
- Ortiz, J.D.; Witter, D.L.; Ali, K.A.; Fela, N.; Duff, M.; Mills, L. Evaluating multiple colour-producing agents in Case II waters from Lake Erie. Int. J. Remote Sens. 2013, 34, 8854–8880. [Google Scholar] [CrossRef]
- Carter, C.H. Sediment–Load Measurements along the United States Shore of Lake Erie; Ohio Division of Geological Survey: Columbus, OH, USA, 1977. [Google Scholar]
- Zhang, Y.; Shi, K.; Zhou, Y.; Liu, X.; Qin, B. Monitoring the river plume induced by heavy rainfall events in large, shallow, Lake Taihu using MODIS 250 imagery. Remote Sens. Environ. 2016, 173, 109–121. [Google Scholar] [CrossRef]
- Winder, M.; Sommer, U. Phytoplankton response to a changing climate. Hydrobiologia 2012, 698, 5–16. [Google Scholar] [CrossRef]
- Bukata, R.P.; Jerome, J.H.; Kondratyev, A.S.; Pozdnyakov, D.V. Optical Properties and Remote Sensing of Inland and Coastal Waters; CRC Press: Boca Raton, FL, USA, 1995. [Google Scholar]
- Wardell, P.J.; Bailey, S.W. An improved in-situ bio-optical data set for ocean color algorithm developement and satellite data product validation. Remote Sens. Environ. 2005, 98, 122–140. [Google Scholar] [CrossRef]
- Arar, J.E. Determination of Chlorophylls-a and b and Identification of Other Pigments of Interest in Marine and Freshwater Algae Using High Performance Liquid Chromatography with Visible Wavelength Detection; EPA: Cincinnati, OH, USA, 1997; pp. 1–20. [Google Scholar]
- Arar, J.E. Determination of Chlorophylls-a, b, c 1c and Pheopigments in Marine and Freshwater Algae by Visible Spectrophotometry; EPA: Cincinnati, OH, USA, 1997; pp. 1–26. [Google Scholar]
- Arar, J.E.; Collins, G.B. Determination of Chlorophyll-a and Pheophytin a in Marine and Freshwater Algae by Fluorescence; EPA: Cincinnati, OH, USA, 1997; pp. 1–22. [Google Scholar]
- DosSantos, A.C.A.; Calijuri, M.C.; Moraes, E.M.; Adorno, M.A.T.; Falco, P.B.; Carvalho, D.P.; Deberdt, G.L.B.; Benassi, S.F. Comparison of three methods for chlorophyll determination: Spectrophotometry and fluorimetry in samples containing pigment mixtures and spectrophotometry in samples with separate pigments through High Performance Liquid Chromatography. Acta Limnol. Bras. 2003, 15, 7–18. [Google Scholar]
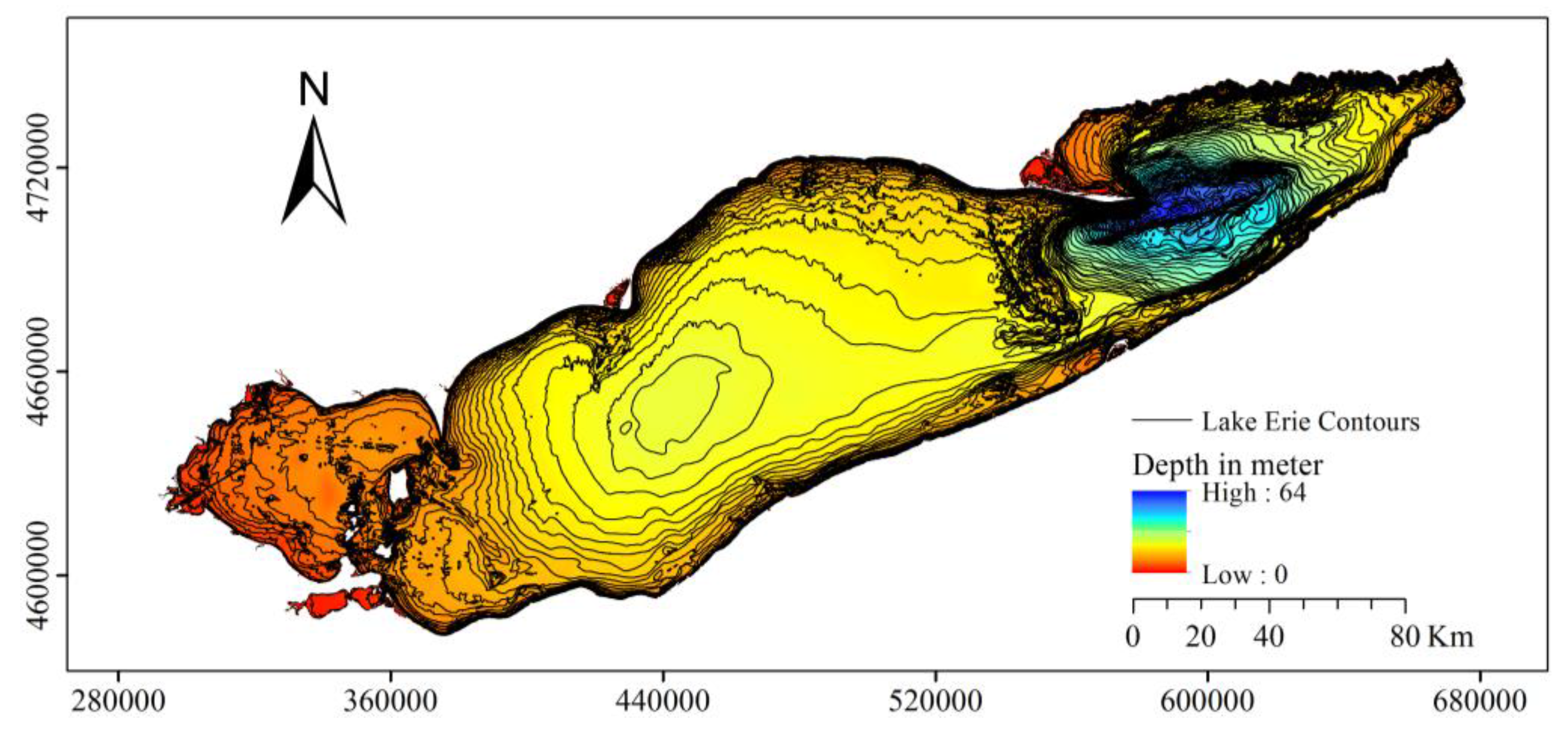
| Lake Erie | Mean Depth (m) | Maximum Depth (m) |
|---|---|---|
| West Basin | 7.4 | 19 |
| Central Basin | 18.3 | 25 |
| East Basin | 25 | 64 |
| Level 1 | Level 1P | Level 2 |
|---|---|---|
| Glint_risk | Land | AOT560_OOR (Aerosol optical thickness at 550 nm out of the training range) |
| Suspect | Cloud | TOA_OOR (Top of atmosphere reflectance in band 13 out of the training range) |
| Land_ocean | Cloud_ambigious | TOSA_OOR (Top of standard atmosphere reflectance in band 13 out of the training range) |
| Bright | Cloud_buffer | Solzen (Large solar zenith angle) |
| Coastline | Cloud_shadow | |
| Invalid | Snow_ice | |
| MixedPixel |
| N | Min | Max | Mean | St. dev. | |
|---|---|---|---|---|---|
| Chl-a | 190 | 0.20 | 70.10 | 4.27 | 7.82 |
| TSM | 190 | 0.18 | 50.50 | 5.75 | 8.00 |
| aCDOM | 160 | 0.04 | 2.36 | 0.31 | 0.33 |
| SDD | 117 | 0.20 | 11.00 | 3.69 | 2.68 |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zolfaghari, K.; Duguay, C.R. Estimation of Water Quality Parameters in Lake Erie from MERIS Using Linear Mixed Effect Models. Remote Sens. 2016, 8, 473. https://doi.org/10.3390/rs8060473
Zolfaghari K, Duguay CR. Estimation of Water Quality Parameters in Lake Erie from MERIS Using Linear Mixed Effect Models. Remote Sensing. 2016; 8(6):473. https://doi.org/10.3390/rs8060473
Chicago/Turabian StyleZolfaghari, Kiana, and Claude R. Duguay. 2016. "Estimation of Water Quality Parameters in Lake Erie from MERIS Using Linear Mixed Effect Models" Remote Sensing 8, no. 6: 473. https://doi.org/10.3390/rs8060473
APA StyleZolfaghari, K., & Duguay, C. R. (2016). Estimation of Water Quality Parameters in Lake Erie from MERIS Using Linear Mixed Effect Models. Remote Sensing, 8(6), 473. https://doi.org/10.3390/rs8060473