Hierarchical Coding Vectors for Scene Level Land-Use Classification
Abstract
:1. Introduction
- We devise the Hierarchical Coding Vectors (HCV) by organizing off-the-shelf coding methods into a hierarchical architecture and evaluate the parameters of HCV for land-use classification on the LU database.
- The HCV achieves excellent performance for land-use classification. Further, combining HCV with standard FV, our method (FV + HCV) outperforms the state-of-the-art performance reported on the LU and RSSCN7 databases.
2. Related Work
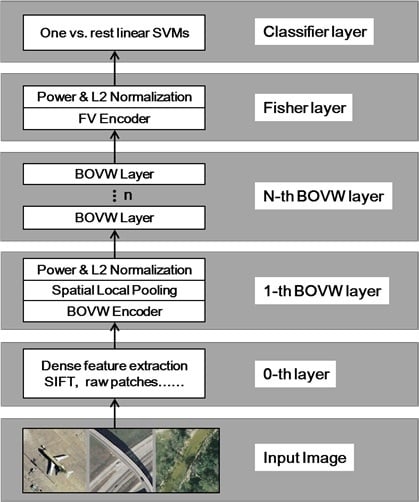
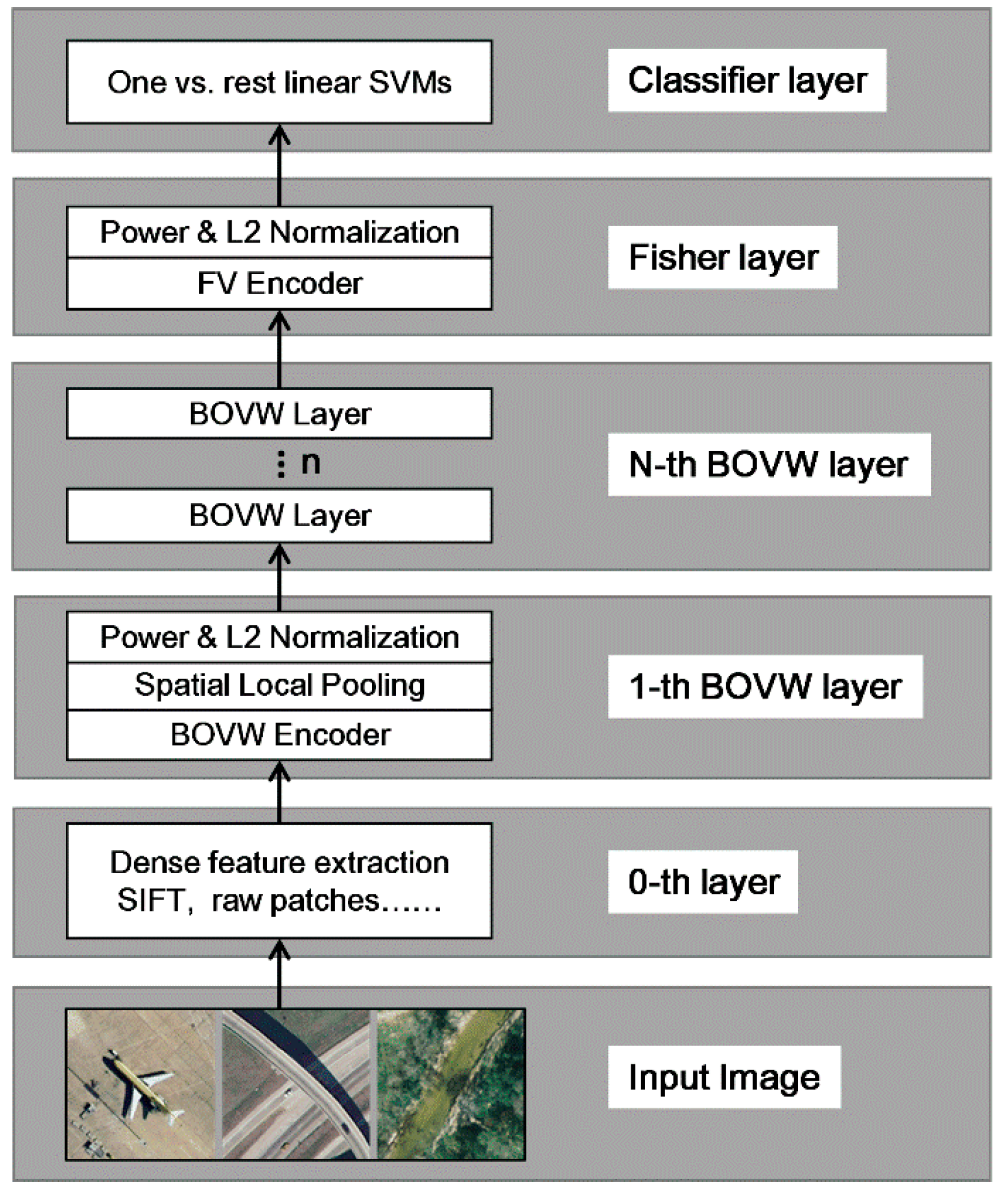
3. Hierarchical Coding Vector
3.1. The BOVW Coding Layer
3.1.1. BOVW Coding
3.1.2. Spatial Local Pooling
3.1.3. Normalization
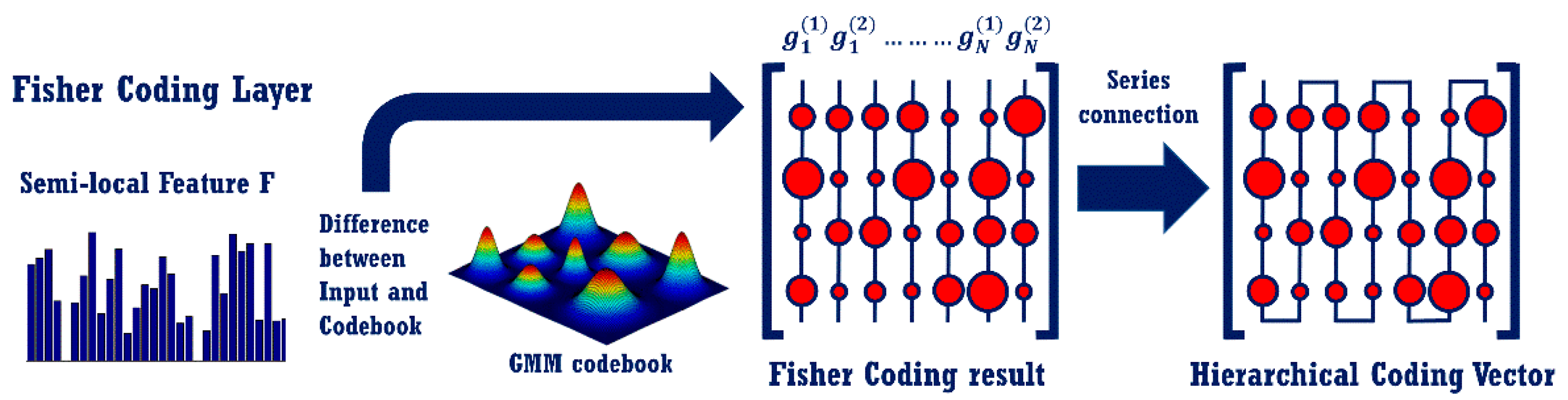
3.2. The Fisher Coding Layer
4. Experiment
4.1. Experimental Data and Setup
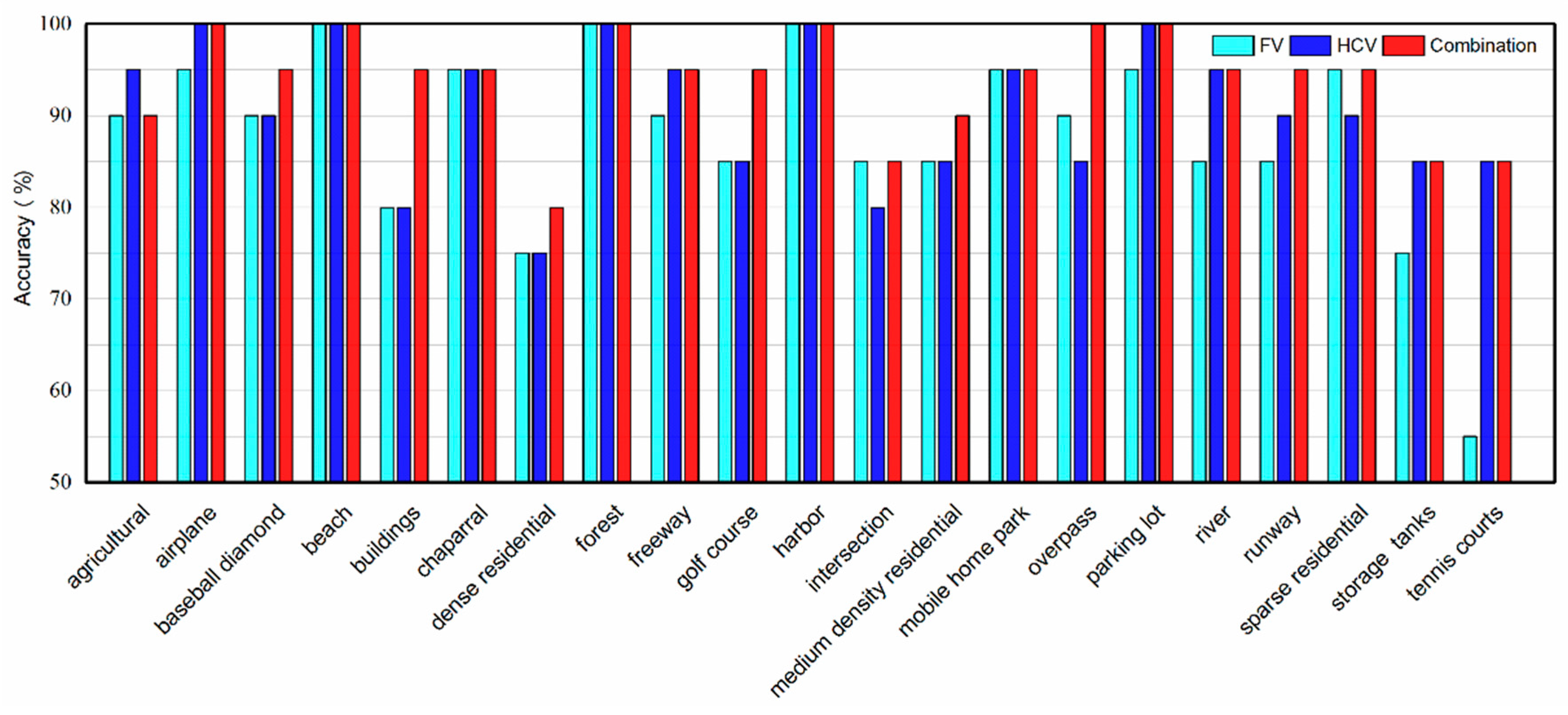
4.2. Experimental Results
4.3. Evaluation of the Parameters in HCV
4.3.1. The Effect of Different Codebook Size
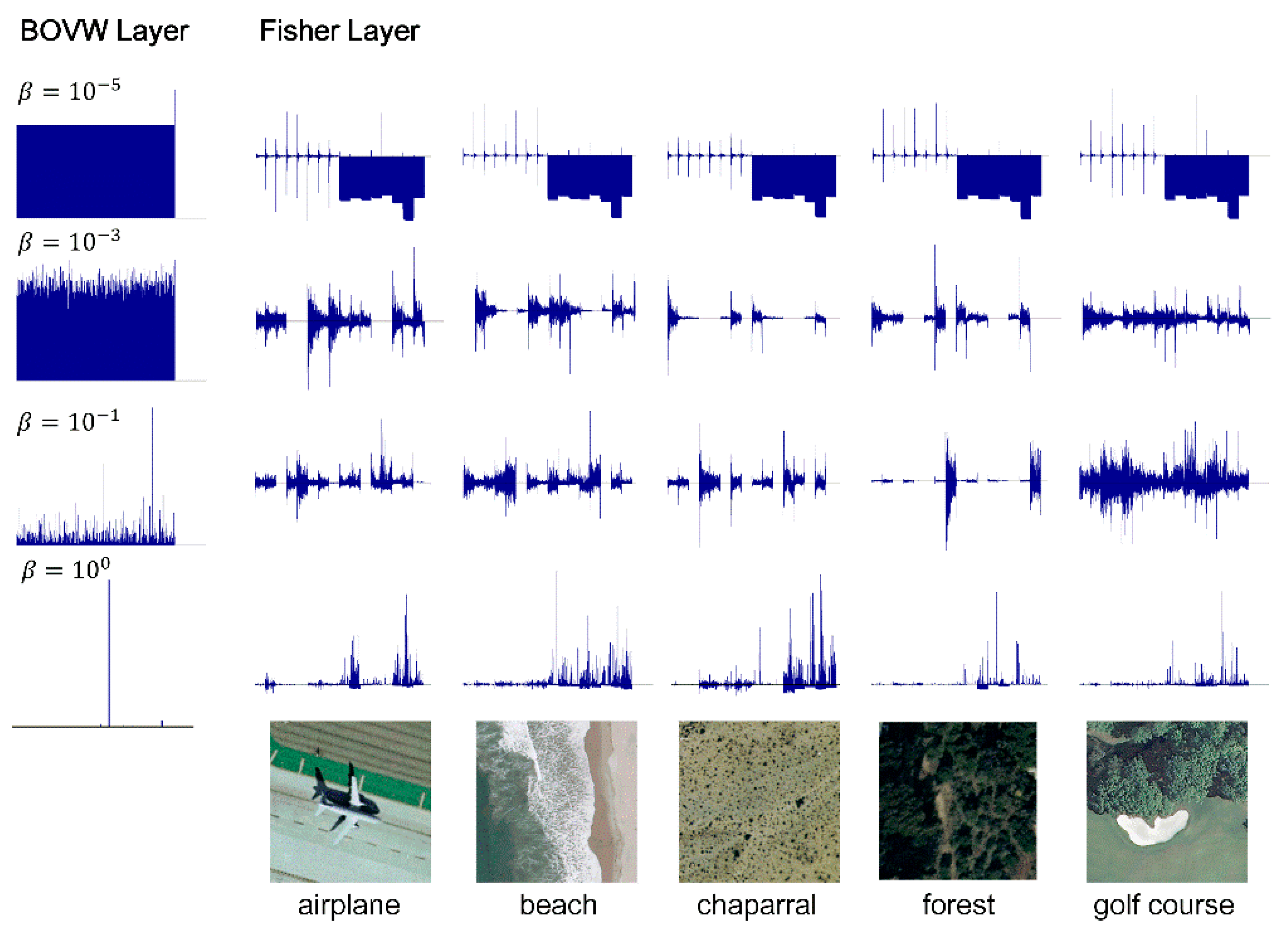
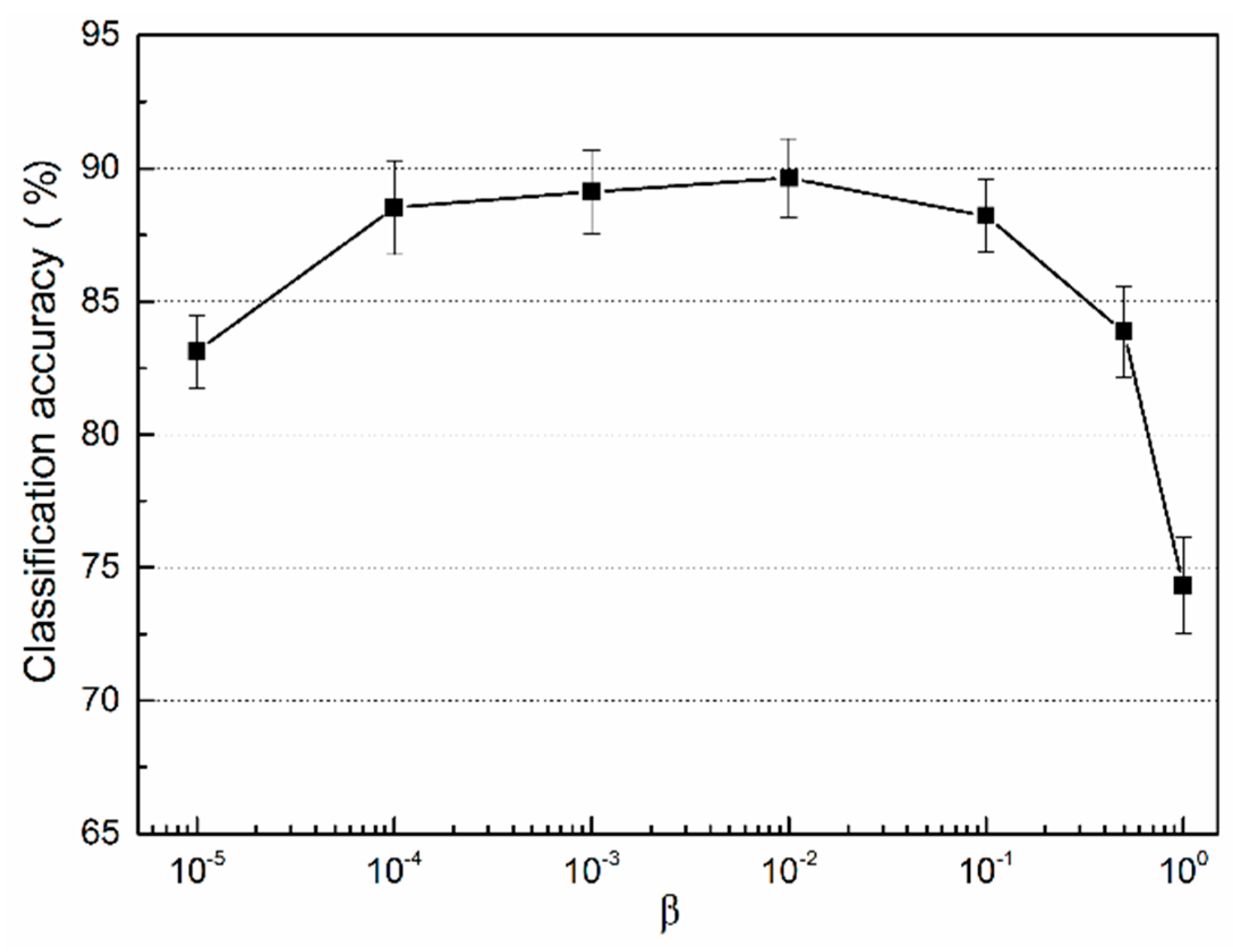
4.3.2. The Key Parameter in the SA Coding Method
4.3.3. The Effect of Different Spatial Structures in Local Pooling
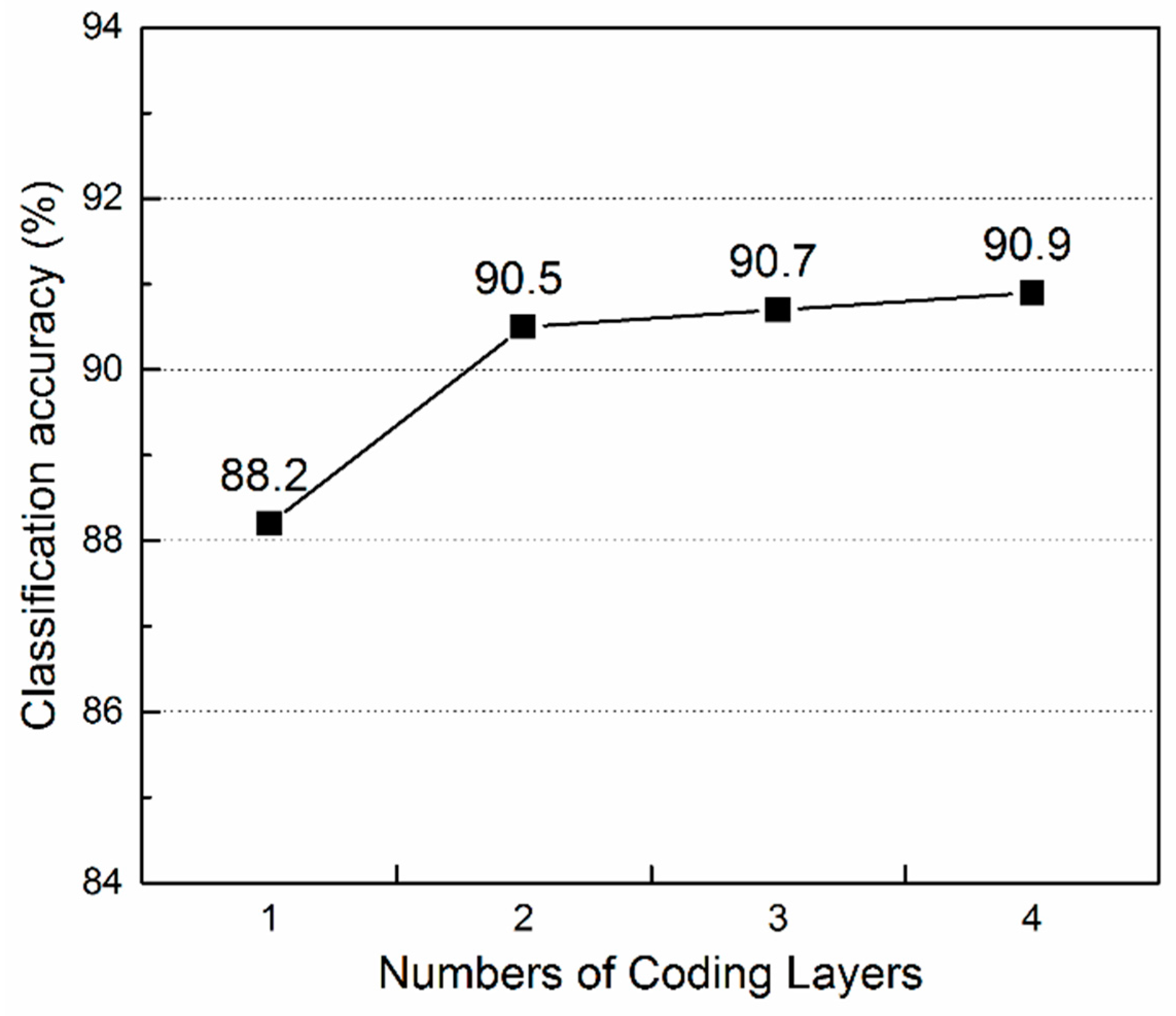
4.3.4. The Effect of the Number of Coding Layers
4.4. Comparison with the State-of-the-Art Methods
4.5. Computational Complexity
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Abbreviations
| HCV | Hierarchical Coding Vector |
| BOVW | Bag of Visual Words |
| HOG | Histogram of Oriented Gradient |
| LBP | Local Binary Pattern |
| SA | Soft Assignment |
| FV | Fisher Vectors |
| VLAD | Vector of Locally Aggregated Descriptors |
| LU | 21-Class Land Use |
| GMM | Gaussian Mixture Model |
| DNN | Deep Neural Network |
| SIFT | Scale Invariant Feature Transformation |
| SPCK | Spatial Pyramid Co-occurrence Kernel |
| CLBP | Completed Local Binary Pattern |
| HA | Hard Assignment |
| LCC | Local Coordinate Coding |
| LLC | Locality-constrained Linear Coding |
| SVC | Super Vector Coding |
| UCMCVL | University of California at Merced Computer Vision Lab |
| SVM | Support Vector Machine |
| ELM | Extreme Learning Machine |
| RBF | Radial Basis Function |
| DBN | Deep Belief Networks |
References
- Yang, Y.; Newsam, S. Bag-of-visual-words and spatial extensions for land-use classification. In Proceedings of the 18th SIGSPATIAL International Conference on Advances in Geographic Information Systems, San Jose, CA, USA, 3–5 November 2010.
- Zhao, L.-J.; Tang, P.; Huo, L.-Z. Land-use scene classification using a concentric circle-structured multiscale bag-of-visual-words model. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 7, 4620–4631. [Google Scholar] [CrossRef]
- Chen, S.; Tian, Y. Pyramid of spatial relatons for scene-level land use classification. IEEE Trans. Geosci. Remote Sens. 2015, 53, 1947–1957. [Google Scholar] [CrossRef]
- Yang, Y.; Newsam, S. Spatial pyramid co-occurrence for image classification. In Proceedings of the 2011 IEEE International Conference on Computer Vision (ICCV), Barcelona, Spain, 6–13 November 2011.
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. Imagenet classification with deep convolutional neural networks. In Proceedings of the Advances in Neural Information Processing Systems, Lake Tahoe, NV, USA, 3–8 December 2012; pp. 1097–1105.
- Liu, L.; Wang, L.; Liu, X. Defense of soft-assignment coding. In Proceedings of the 2011 IEEE International Conference on Computer Vision (ICCV), Barcelona, Spain, 6–13 November 2011.
- Sánchez, J.; Perronnin, F.; Mensink, T.; Verbeek, J. Image classification with the fisher vector: Theory and practice. Int. J. Comput. Vis. 2013, 105, 222–245. [Google Scholar] [CrossRef]
- Lowe, D.G. Distinctive image features from scale-invariant keypoints. Int. J. Comput. Vis. 2004, 60, 91–110. [Google Scholar] [CrossRef]
- Dalal, N.; Triggs, B. Histograms of oriented gradients for human detection. In Proceedings of the 2005 IEEE Computer Society Conference on Computer Vision and Pattern Recognition (CVPR), San Diego, CA, USA, 20–25 June 2005.
- Oliva, A.; Torralba, A. Modeling the shape of the scene: A holistic representation of the spatial envelope. Int. J. Comput. Vis. 2001, 42, 145–175. [Google Scholar] [CrossRef]
- Ojala, T.; Pietikäinen, M.; Harwood, D. A comparative study of texture measures with classification based on featured distributions. Pattern Recognit. 1996, 29, 51–59. [Google Scholar] [CrossRef]
- Peng, X.; Wang, L.; Wang, X.; Qiao, Y. Bag of Visual Words and Fusion Methods for Action Recognition: Comprehensive Study and Good Practice. Available online: http://arxiv.org/abs/1405.4506 (accessed on 18 May 2016).
- Yu, K.; Zhang, T.; Gong, Y. Nonlinear learning using local coordinate coding. In Proceedings of the Advances in Neural Information Processing Systems, Vancouver, BC, Canada, 6–10 December 2009; pp. 2223–2231.
- Wang, J.; Yang, J.; Yu, K.; Lv, F.; Huang, T.; Gong, Y. Locality-constrained linear coding for image classification. In Proceedings of the 2010 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), San Francisco, CA, USA, 13–18 June 2010.
- Jégou, H.; Perronnin, F.; Douze, M.; Sanchez, J.; Perez, P.; Schmid, C. Aggregating local image descriptors into compact codes. IEEE Trans. Pattern Anal. Mach. Intell. 2012, 34, 1704–1716. [Google Scholar] [CrossRef] [PubMed]
- Lin, C.J.; Hsu, C.-W.; Chang, C.-C. A Practical Guide to Support Vector Classification. Available online: https://www.cs.sfu.ca/people/Faculty/teaching/726/spring11/svmguide.pdf (accessed on 18 May 2016).
- Huang, G.-B.; Zhu, Q.-Y.; Siew, C.-K. Extreme learning machine: Theory and applications. Neurocomputing 2006, 70, 489–501. [Google Scholar] [CrossRef]
- Jaakkola, T.S.; Haussler, D. Exploiting generative models in discriminative classifiers. Adv. Neural Inf. Process. Syst. 1999, 487–493. [Google Scholar]
- Dai, D.; Yang, W. Satellite image classification via two-layer sparse coding with biased image representation. IEEE Geosci. Remote Sens. Lett. 2011, 8, 173–176. [Google Scholar] [CrossRef]
- Peng, X.; Zou, C.; Qiao, Y.; Peng, Q. Action recognition with stacked fisher vectors. Comput. Vis. 2014, 8693, 581–595. [Google Scholar]
- Arthur, D.; Vassilvitskii, S. K-means++: The advantages of careful seeding. In Proceedings of the Eighteenth Annual ACM-SIAM Symposium on Discrete Algorithms, New Orleans, LA, USA, 7–9 January 2007.
- Murray, N.; Perronnin, F. Generalized max pooling. In Proceedings of the 2014 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Columbus, OH, USA, 23–28 January 2014.
- Chatfield, K.; Lempitsky, V.S.; Vedaldi, A.; Zisserman, A. The devil is in the details: An evaluation of recent feature encoding methods. In Proceedings of the BMVC, Dundee, UK, 29 August–2 September 2011; p. 8.
- Perronnin, F.; Sánchez, J.; Mensink, T. Improving the fisher kernel for large-scale image classification. Comput. Vis. 2010, 6314, 143–156. [Google Scholar]
- Simonyan, K.; Vedaldi, A.; Zisserman, A. Deep fisher networks for large-scale image classification. In Proceedings of the Advances in Neural Information Processing Systems, Lake Tahoe, NV, USA, 5–10 December 2013; pp. 163–171.
- Zou, Q.; Ni, L.; Zhang, T.; Wang, Q. Deep learning based feature selection for remote sensing scene classification. IEEE Geosci. Remote Sens. Lett. 2015, 12, 2321–2325. [Google Scholar] [CrossRef]
- Chen, C.; Zhang, B.; Su, H.; Li, W.; Wang, L. Land-use scene classification using multi-scale completed local binary patterns. Signal Image Video Process. 2016, 4, 745–752. [Google Scholar] [CrossRef]
- Mekhalfi, M.L.; Melgani, F.; Bazi, Y.; Alajlan, N. Land-use classification with compressive sensing multifeature fusion. IEEE Geosci. Remote Sens. Lett. 2015, 12, 2155–2159. [Google Scholar] [CrossRef]
- Zhao, L.; Tang, P.; Huo, L. A 2-D wavelet decomposition-based bag-of-visual-words model for land-use scene classification. Int. J. Remote Sens. 2014, 35, 2296–2310. [Google Scholar]
- Simonyan, K.; Parkhi, O.M.; Vedaldi, A.; Zisserman, A. Fisher vector faces in the wild. In Proceedings of the BMVC, Bristol, UK, 9–13 September 2013.
- Gehler, P.; Nowozin, S. On feature combination for multiclass object classification. In Proceedings of the 2009 IEEE 12th International Conference on Computer Vision, Kyoto, Japan, 27 September–4 October 2009.
- Mandel, J. The Statistical Analysis of Experimental Data; Courier Corporation: New York, NY, USA, 2012. [Google Scholar]
- Risojević, V.; Babić, Z. Aerial image classification using structural texture similarity. In Proceedings of the 2011 IEEE International Symposium on Signal Processing and Information Technology (ISSPIT), 2011, 14–17 December 2011; IEEE: Bilbao, Spain.
- Cheriyadat, A.M. Unsupervised feature learning for aerial scene classification. IEEE Trans. Geosci. Remote Sens. 2014, 52, 439–451. [Google Scholar] [CrossRef]
- Zhang, F.; Du, B.; Zhang, L. Saliency-guided unsupervised feature learning for scene classification. IEEE Trans. Geosci. Remote Sens. 2015, 53, 2175–2184. [Google Scholar] [CrossRef]
- Shao, W.; Yang, W.; Xia, G.-S.; Liu, G. A hierarchical scheme of multiple feature fusion for high-resolution satellite scene categorization. Comput. Vis. Syst. 2013, 7963, 324–333. [Google Scholar]





| Parameter | Dim. | Definition |
|---|---|---|
| X | E × K | Low-level descriptors |
| B1 | E × M | K-means codebook |
| D | M × K | Coding result of BOVW coding layer |
| F | M × T | Semi-local features |
| B2 | M × N | Gaussian mixture model (GMM) codebook |
| G | M × 2N | Hierarchical coding Vector |
| xk | E | The k-th low-level descriptor |
| dk | M | The k-th coding result in D |
| bm | E | The m-th codeword in B1 |
| bn | M | The n-th codeword in B2 |
| ft | M | The t-th semi-local feature |
| M | Gaussian mean difference | |
| M | Gaussian variance difference | |
| E | 1 | Dimension of low-level descriptors |
| T | 1 | Number of semi-local features |
| M | 1 | Size of K-means codebook |
| N | 1 | Size of GMM codebook |
| K | 1 | Number of low-level descriptors |
| P | - | Local pooling region |
| 1 | Euclidean distance between xk and bm | |
| 1 | Smoothing factor in SA coding | |
| 1 | Smoothing factor in Power-normalization | |
| 1 | Soft assignment weight of ft to bn | |
| 1 | Mixture weights of bn | |
| 1 | Means of bn | |
| 1 | Diagonal covariance of bn |
| K-means/GMM | 2 | 4 | 8 | 16 | 32 |
|---|---|---|---|---|---|
| 50 | 71.55 | 76.98 | 81.62 | 84.33 | 87.62 |
| 100 | 77.05 | 82.02 | 85.79 | 85.98 | 87.93 |
| 200 | 83.00 | 84.74 | 87.31 | 88.10 | 88.21 |
| 600 | 86.86 | 88.69 | 89.50 | 89.45 | 88.81 |
| 1000 | 88.36 | 89.29 | 90.00 | 88.57 | 88.40 |
| 1400 | 88.26 | 89.76 | 89.17 | 88.49 | 88.36 |
| Method | Accuracy (%) |
|---|---|
| BOVW [1] | 76.8 |
| SPM [1] | 75.3 |
| BOVW + spatial co-occurrence kernel [1] | 77.7 |
| Color Gabor [1] | 80.5 |
| Color histogram [1] | 81.2 |
| SPCK [4] | 73.1 |
| SPCK + BOW [4] | 76.1 |
| SPCK + SPM [4] | 77.4 |
| Structural texture similarity [33] | 86.0 |
| Wavelet BOVW [29] | 87.4 ± 1.3 |
| Unsupervised feature learning [34] | 81.1 ± 1.2 |
| Saliency-guided feature learning [35] | 82.7 ± 1.2 |
| Concentric circle-structured BOVW [2] | 86.6 ± 0.8 |
| Multifeature concatenation [36] | 89.5 ± 0.8 |
| Pyramid-of-spatial-relations [3] | 89.1 |
| CLBP [27] | 85.5 ± 1.9 |
| MS-CLBP [27] | 90.6 ± 1.4 |
| HCV | 90.5 ± 1.1 |
| Our method | 91.8 ± 1.3 |
| Method | Accuracy (%) |
|---|---|
| GIST * | 69.5 ± 0.9 |
| Color histogram * | 70.9 ± 0.8 |
| BOVW * | 73.1 ± 1.1 |
| LBP * | 75.3 ± 1.0 |
| DBN based feature selection [26] | 77.0 |
| HCV | 84.7 ± 0.7 |
| Our method | 86.4 ± 0.7 |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, H.; Liu, B.; Su, W.; Zhang, W.; Sun, J. Hierarchical Coding Vectors for Scene Level Land-Use Classification. Remote Sens. 2016, 8, 436. https://doi.org/10.3390/rs8050436
Wu H, Liu B, Su W, Zhang W, Sun J. Hierarchical Coding Vectors for Scene Level Land-Use Classification. Remote Sensing. 2016; 8(5):436. https://doi.org/10.3390/rs8050436
Chicago/Turabian StyleWu, Hang, Baozhen Liu, Weihua Su, Wenchang Zhang, and Jinggong Sun. 2016. "Hierarchical Coding Vectors for Scene Level Land-Use Classification" Remote Sensing 8, no. 5: 436. https://doi.org/10.3390/rs8050436
APA StyleWu, H., Liu, B., Su, W., Zhang, W., & Sun, J. (2016). Hierarchical Coding Vectors for Scene Level Land-Use Classification. Remote Sensing, 8(5), 436. https://doi.org/10.3390/rs8050436