Computationally Inexpensive Landsat 8 Operational Land Imager (OLI) Pansharpening
Abstract
:1. Introduction
- (i)
- a band intensity image at the multispectral band resolution, typically as a weighted linear combination of the multispectral band values;
- (ii)
- a pan spatial resolution spatial detail image by subtracting the intensity image from the panchromatic band;
- (iii)
- a pan spatial resolution modulated spatial detail image for each multispectral band as the product of the pan spatial detail image and a locally adaptive, or fixed, scalar modulation coefficient;
- (iv)
- for each multispectral band a pansharpened equivalent by adding the multispectral band to the band’s modulated spatial detail image.
2. Data
2.1. Landsat 8 Data
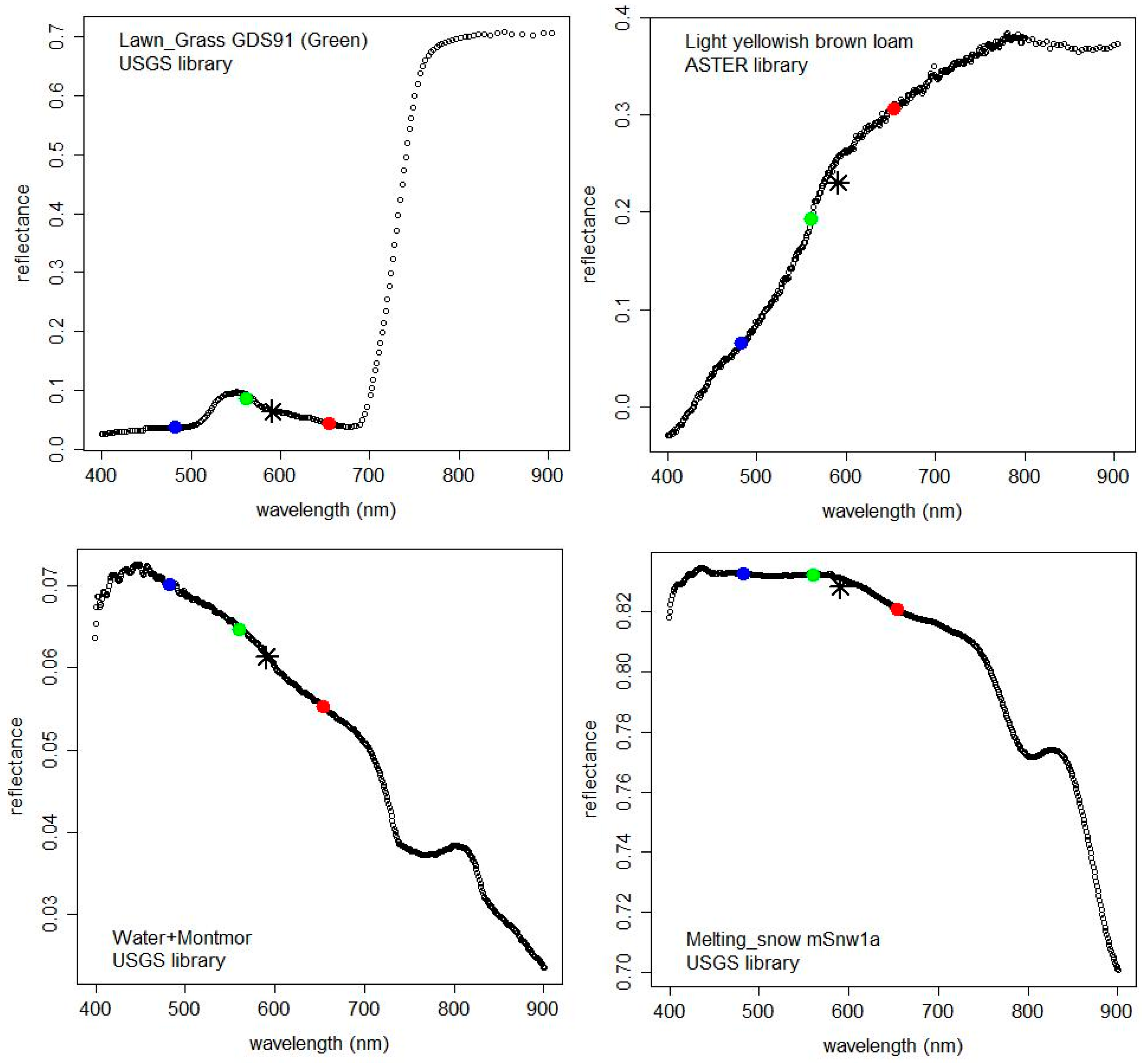
2.2. Spectral Library Data
3. Methods
3.1. Single Band Intensity Image Derivation
3.1.1. Equal Spectral Weights
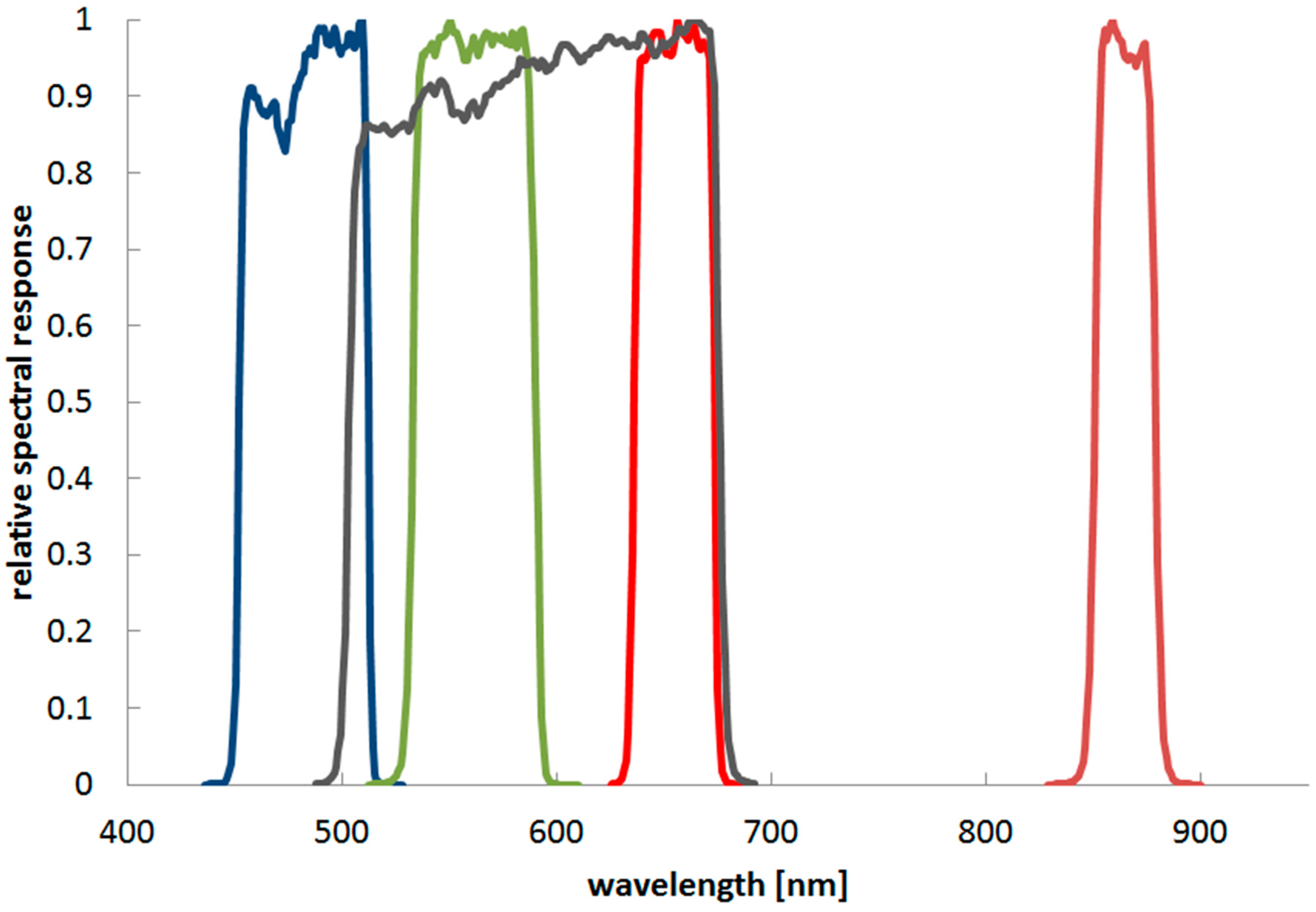
3.1.2. Spectral Response Function Based (SRFB) Spectral Weights
3.1.3. Image Specific Spectral Weights
3.2. Resampling Landsat 8 30 m Multispectral Bands to 15 m Panchromatic Pixel Grid
3.3. Pansharpening
3.3.1. Brovey Pansharpening
3.3.2. Context Adaptive Gram Schmidt Pansharpening
3.4. Evaluation
3.4.1. Evaluation of Spectral Response Function Based (SRFB) Spectral Weights
3.4.2. Evaluation of Intensity Image Derivation
3.4.3. Pansharpening Evaluation
3.4.4. Computational Efficiency Evaluation
4. Results
4.1. Evaluation of Spectral Response Function Based (SRFB) Spectral Weights
4.2. Evaluation of Intensity Image Derivation
4.3. Pansharpening Results and Evaluation
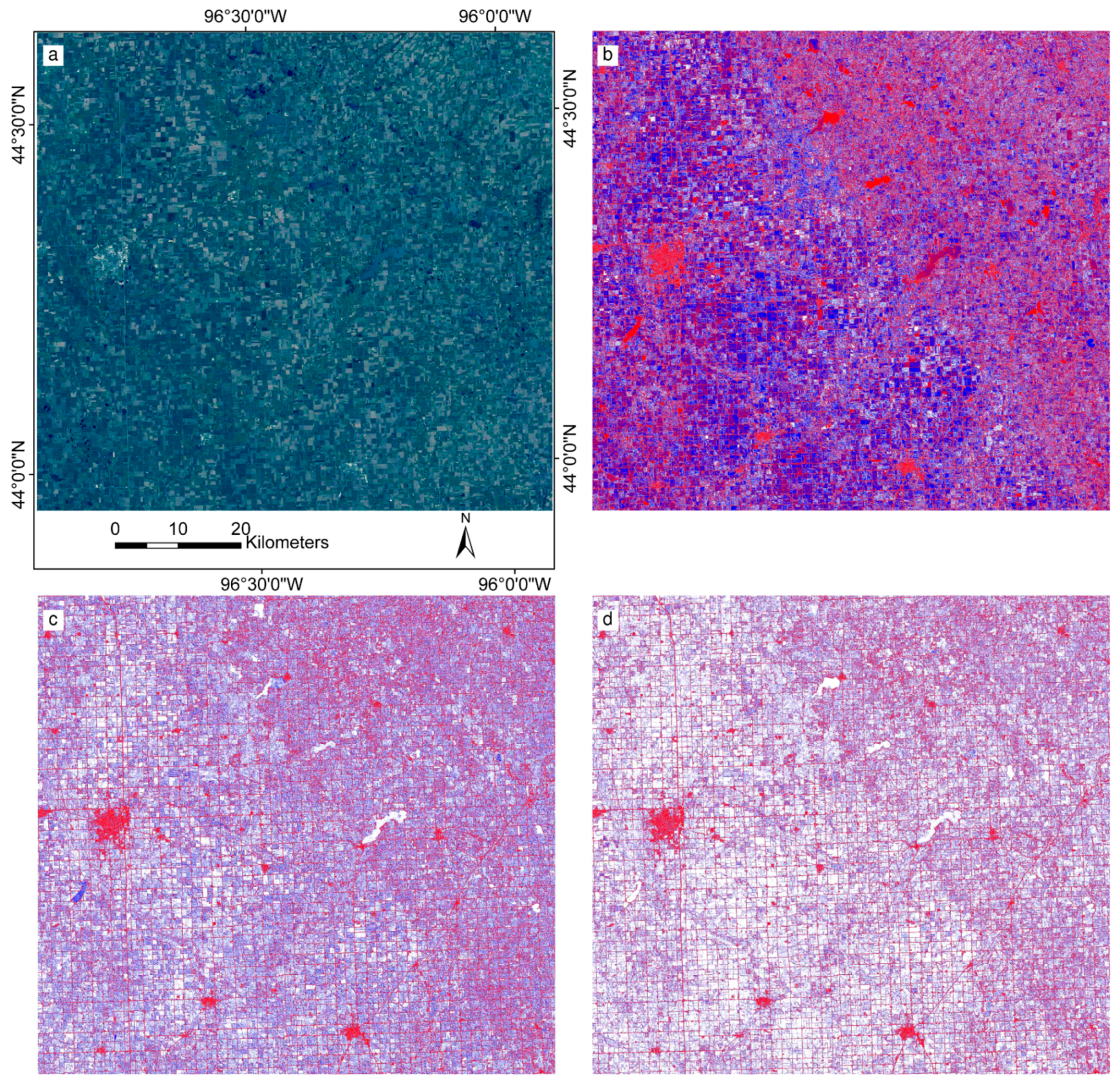
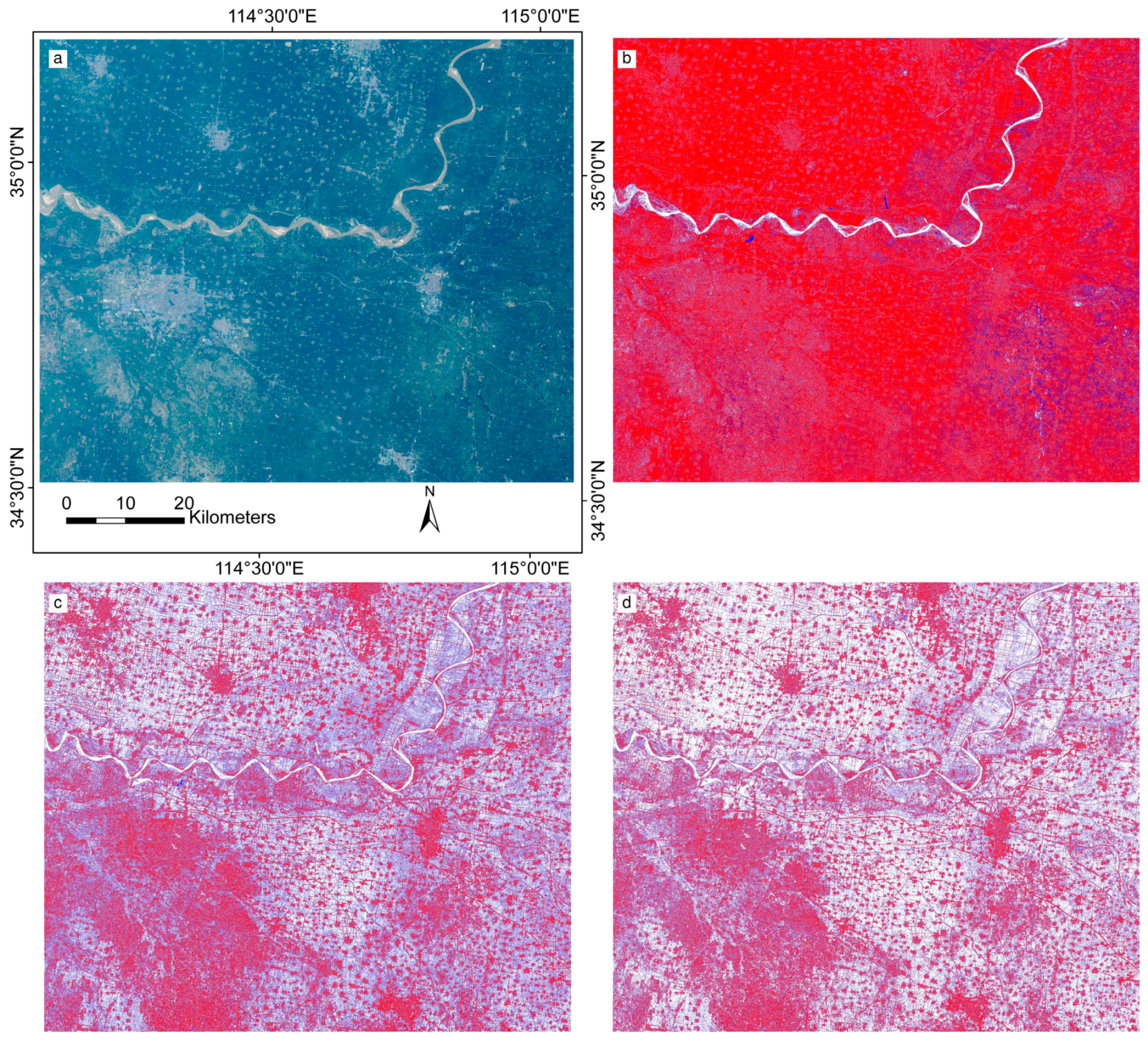
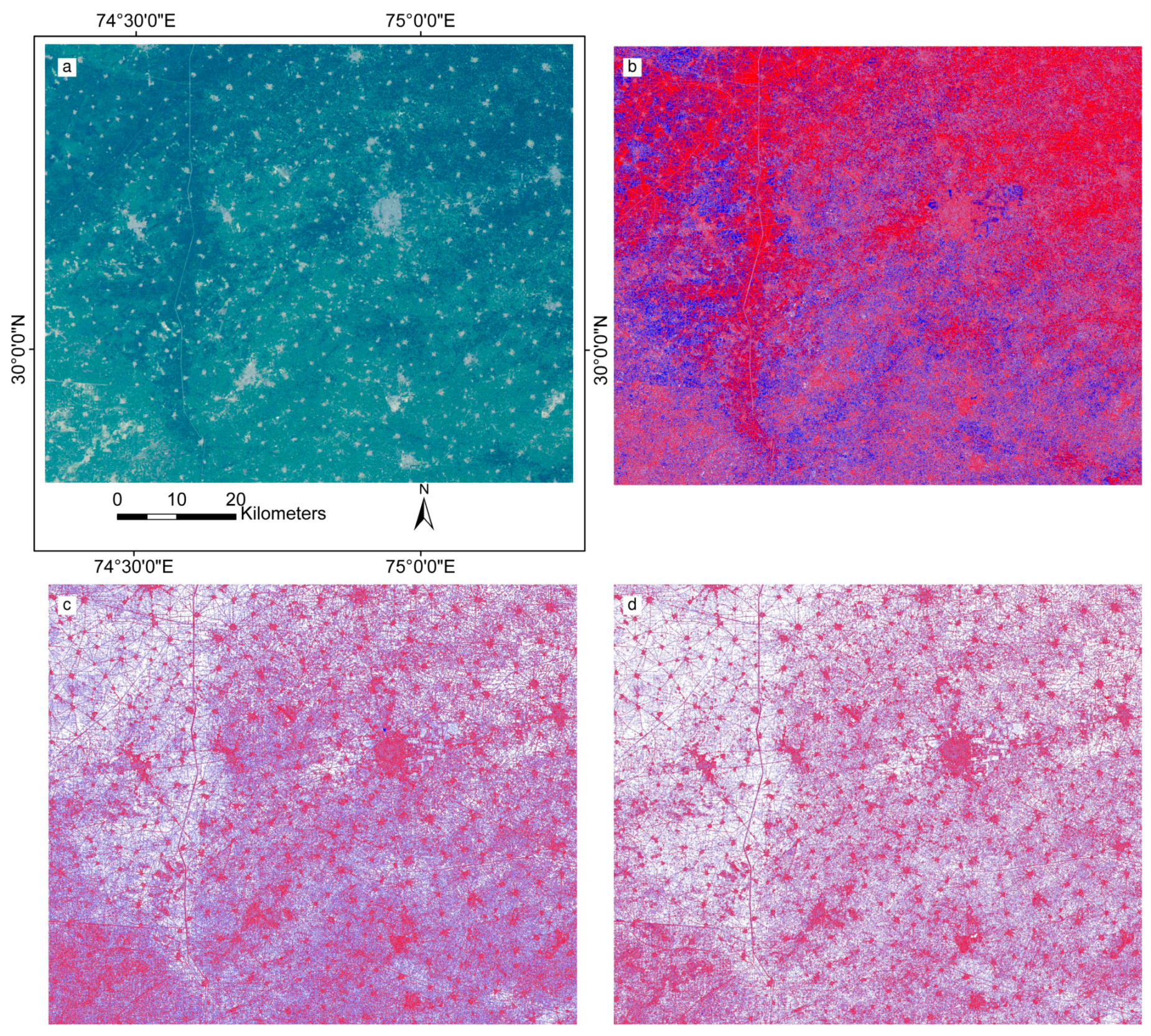
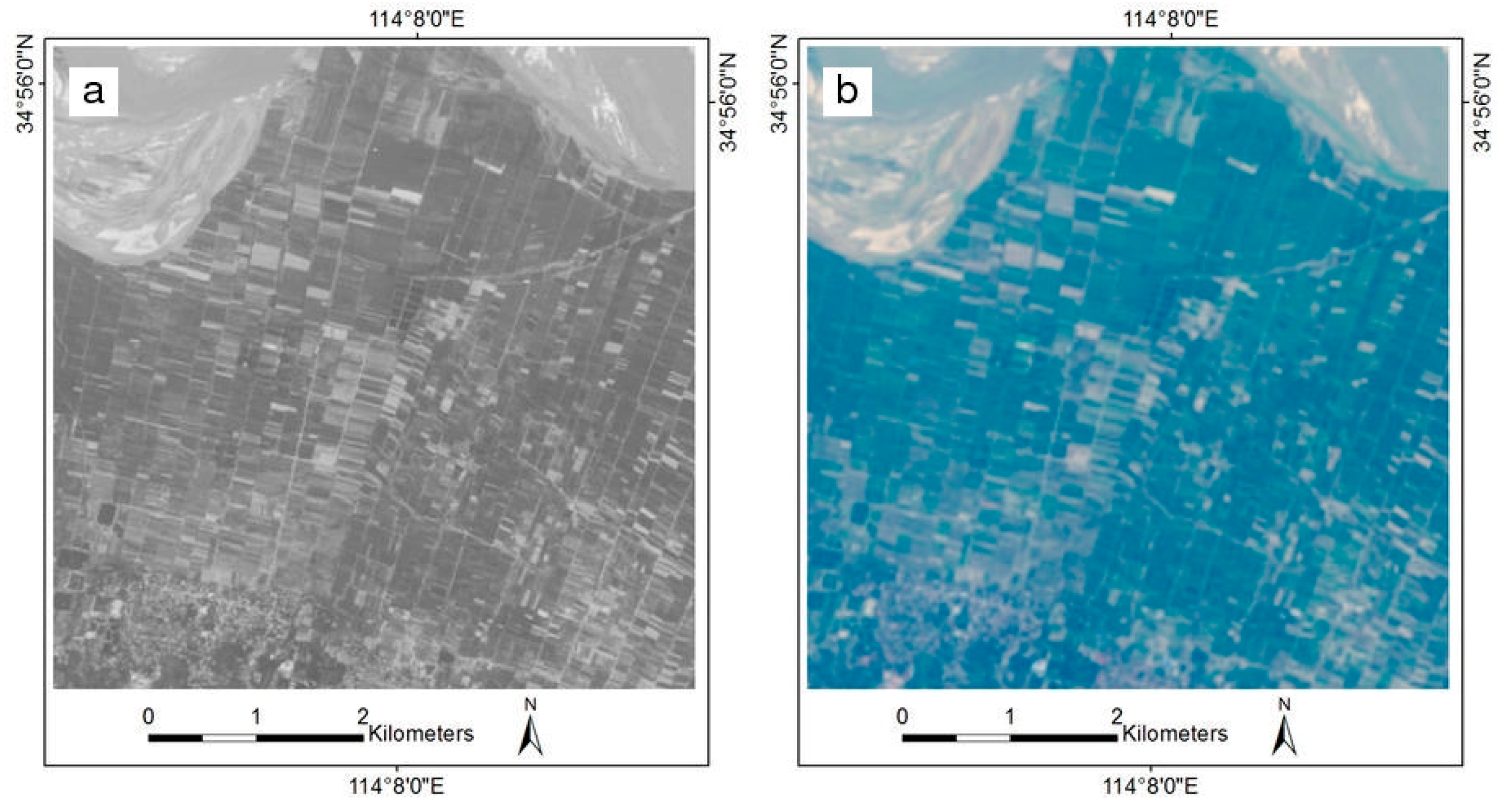
4.3.1. Qualitative Evaluation
4.3.2. Quantitative Evaluation
4.4. Computational Efficiency Evaluation
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Wald, L.; Ranchin, T.; Mangolini, M. Fusion of satellite images of different spatial resolutions: Assessing the quality of resulting images. Photogramm. Eng. Remote Sens. 1997, 63, 691–699. [Google Scholar]
- Pohl, C.; van Genderen, J.L. Multisensor image fusion in remote sensing: Concepts, methods and applications. Int. J. Remote Sens. 1998, 19, 823–854. [Google Scholar] [CrossRef]
- Tu, T.-M.; Su, S.-C.; Shyu, H.-C.; Huang, P.S. A new look at IHS-like image fusion methods. Inf. Fusion 2001, 2, 177–186. [Google Scholar] [CrossRef]
- Zhang, Y. Understanding image fusion. Photogramm. Eng. Remote Sens. 2004, 70, 657–661. [Google Scholar]
- Vivone, G.; Alparone, L.; Chanussot, J.; Dalla Mura, M.; Garzelli, A.; Licciardi, G.A.; Restaino, R.; Wald, L. A critical comparison among pansharpening algorithms. IEEE Trans. Geosci. Remote Sens. 2015, 53, 2565–2586. [Google Scholar] [CrossRef]
- Garzelli, A. Pansharpening of multispectral images based on nonlocal parameter optimization. IEEE Trans. Geosci. Remote Sens. 2015, 53, 2096–2107. [Google Scholar] [CrossRef]
- Loveland, T.R.; Dwyer, J.L. Landsat: Building a strong future. Remote Sens Environ. 2012, 122, 22–29. [Google Scholar] [CrossRef]
- Wulder, M.A.; White, J.C.; Loveland, T.R.; Woodcock, C.E.; Belward, A.S.; Cohen, W.B.; Fosnight, G.; Shaw, J.; Masek, J.G.; Roy, D.P. The global Landsat archive: Status, consolidation, and direction. Remote Sens. Environ. 2016. [Google Scholar] [CrossRef]
- Roy, D.P.; Ju, J.; Kline, K.; Scaramuzza, P.L.; Kovalskyy, V.; Hansen, M.; Loveland, T.R.; Vermote, E.; Zhang, C. Web-enabled Landsat data (WELD): Landsat ETM+ composited mosaics of the conterminous United States. Remote Sens. Environ. 2010, 114, 35–49. [Google Scholar] [CrossRef]
- Gong, P.; Wang, J.; Yu, L.; Zhao, Y.; Zhao, Y.; Liang, L.; Niu, Z.; Huang, X.; Fu, H.; Liu, S. Finer resolution observation and monitoring of global land cover: First mapping results with Landsat TM and ETM+ data. Int. J. Remote Sens. 2013, 34, 2607–2654. [Google Scholar] [CrossRef]
- Hansen, M.C.; Potapov, P.V.; Moore, R.; Hancher, M.; Turubanova, S.; Tyukavina, A.; Thau, D.; Stehman, S.; Goetz, S.; Loveland, T. High-resolution global maps of 21st-century forest cover change. Science 2013, 342, 850–853. [Google Scholar] [CrossRef] [PubMed]
- Vivone, G.; Simões, M.; Dalla Mura, M.; Restaino, R.; Bioucas-Dias, J.M.; Licciardi, G.A.; Chanussot, J. Pansharpening based on semiblind deconvolution. IEEE Trans. Geosci. Remote Sens. 2015, 53, 1997–2010. [Google Scholar] [CrossRef]
- Verpoorter, C.; Kutser, T.; Seekell, D.A.; Tranvik, L.J. A global Inventory of lakes based on high-resolution satellite imagery. Geophys. Res. Lett. 2014. 2014GL060641. [Google Scholar]
- Roy, D.P.; Wulder, M.A.; Loveland, T.R.; Woodcock, C.E.; Allen, R.G.; Anderson, M.C.; Helder, D.; Irons, J.R.; Johnson, D.M.; Kennedy, R.; et al. Landsat-8: Science and product vision for terrestrial global change research. Remote Sens. Environ. 2014, 145, 154–172. [Google Scholar] [CrossRef]
- Irons, J.R.; Dwyer, J.L.; Barsi, J.A. The next Landsat satellite: The Landsat data continuity mission. Remote Sens. Environ. 2012, 122, 11–21. [Google Scholar] [CrossRef]
- Ranchin, T.; Wald, L. Fusion of high spatial and spectral resolution images: The ARSIS concept and its implementation. Photogramm. Eng. Remote Sens. 2000, 66, 49–61. [Google Scholar]
- Thomas, C.; Ranchin, T.; Wald, L.; Chanussot, J. Synthesis of multispectral images to high spatial resolution: A critical review of fusion methods based on remote sensing physics. IEEE Trans. Geosci. Remote Sens. 2008, 46, 1301–1312. [Google Scholar] [CrossRef]
- Aiazzi, B.; Baronti, S.; Lotti, F.; Selva, M. A comparison between global and context-adaptive pansharpening of multispectral images. IEEE Geosci. Remote Sens. Lett. 2009, 6, 302–306. [Google Scholar] [CrossRef]
- Zhang, H.K.; Huang, B. A new look at image fusion methods from a bayesian perspective. Remote Sens. 2015, 7, 6828–6861. [Google Scholar] [CrossRef]
- Baronti, S.; Aiazzi, B.; Selva, M.; Garzelli, A.; Alparone, L. A theoretical analysis of the effects of aliasing and misregistration on pansharpened imagery. IEEE J. Sel. Top. Signal. Process. 2011, 5, 446–453. [Google Scholar] [CrossRef]
- Xu, Q.; Li, B.; Zhang, Y.; Ding, L. High-fidelity component substitution pansharpening by the fitting of substitution data. IEEE Trans. Geosci. Remote Sens. 2014, 52, 7380–7392. [Google Scholar]
- Shah, V.P.; Younan, N.H.; King, R.L. An efficient pan-sharpening method via a combined adaptive PCA approach and contourlets. IEEE Trans. Geosci. Remote 2008, 46, 1323–1335. [Google Scholar] [CrossRef]
- Gillespie, A.R.; Kahle, A.B.; Walker, R.E. Color enhancement of highly correlated images. II. Channel ratio and “chromaticity” transformation techniques. Remote Sens. Environ. 1987, 22, 343–365. [Google Scholar] [CrossRef]
- Aiazzi, B.; Baronti, S.; Selva, M. Improving component substitution pansharpening through multivariate regression of MS plus Pan data. IEEE Trans. Geosci. Remote Sens. 2007, 45, 3230–3239. [Google Scholar] [CrossRef]
- Barsi, J.A.; Markham, B.L.; Pedelty, J.A. The operational land imager: spectral response and spectral uniformity. Proc. SPIE 2011. [Google Scholar] [CrossRef]
- NASA Landsat Science. Spectral Response of the Operational Land Imager In-Band, Band-Average Relative Spectral Response. 2014. Available online: http://landsat.gsfc.nasa.gov/?p=5779 (accessed on 17 September 2014). [Google Scholar]
- Arvidson, T.; Gasch, J.; Goward, S.N. Landsat 7's long-term acquisition plan—An innovative approach to building a global imagery archive. Remote Sens. Environ. 2001, 78, 13–26. [Google Scholar] [CrossRef]
- Yan, L.; Roy, D.P. Automated crop field extraction from multi-temporal Web Enabled Landsat Data. Remote Sens. Environ. 2014, 144, 42–64. [Google Scholar] [CrossRef]
- Fan, S.G.; Chan-Kang, C. Is small beautiful? Farm size, productivity, and poverty in Asian agriculture. Agric. Econ. Blackwell. 2005, 32, 135–146. [Google Scholar] [CrossRef]
- Long, H.; Zou, J.; Pykett, J.; Li, Y. Analysis of rural transformation development in China since the turn of the new millennium. Appl. Geogr. 2011, 31, 1094–1105. [Google Scholar] [CrossRef]
- White, E.V.; Roy, D.P. A contemporary decennial examination of changing agricultural field sizes using Landsat time series data. Geo: Geogr. Environ. 2015, 2, 33–54. [Google Scholar] [CrossRef]
- Kalubarme, A.H.; Potdar, M.B.; Manjunath, K.R.; Mahey, R.K.; Siddhu, S.S. Growth profile based crop yield models: A case study of large area wheat yield modelling and its extendibility using atmospheric corrected NOAA AVHRR data. Int. J. Remote Sens. 2003, 24, 2037–2054. [Google Scholar] [CrossRef]
- Joint Agricultural Weather Facility, World Agricultural Outlook Board, United States Department of Agriculture. Major World Crop Areas and Climatic Profiles; Agricultural Handbook No. 664; United States Department of Agriculture: Washington, DC, USA, 1992.
- Chauhan, B.S.; Mahajan, G.; Sardana, V.; Timsina, J.; Jat, M.L. Productivity and sustainability of the rice-wheat cropping system in the Indo-Gangetic Plains of the Indian subcontinent: Problems, opportunities, and strategies. In Advances in Agronomy; Donald, L.S., Ed.; Academic Press: Waltham, MA, USA, 2012; pp. 315–369. [Google Scholar]
- Clark, R.L.; Swayze, G.A.; Wise, R.; Livo, K.E.; Hoefen, T.; Kokaly, R.F.; Sutley, S.J. USGS Digital Spectral Library splib06a. U.S. Geological Survey, 2007. Available online: http://speclab.cr.usgs.gov/spectral.lib06 (accessed on 19 September 2014). [Google Scholar]
- Baldridge, A.M.; Hook, S.J.; Grove, C.I.; Rivera, G. The ASTER spectral library version 2.0. Remote Sens. Environ. 2009, 113, 711–715. [Google Scholar] [CrossRef]
- ENVI. ENVI 5.1 spectral library readme files. Assessed in the installation directory of ENVI 5.1. 2013. [Google Scholar]
- Ju, J.; Roy, D.P.; Vermote, E.; Masek, J.; Kovalskyy, V. Continental-scale validation of MODIS-based and LEDAPS Landsat ETM+ atmospheric correction methods. Remote Sens. Environ. 2012, 122, 175–184. [Google Scholar] [CrossRef]
- Roy, D.P.; Qin, Y.; Kovalskyy, V.; Vermote, E.F.; Ju, J.; Egorov, A.; Hansen, M.C.; Kommareddy, I.; Yan, L. Conterminous United States demonstration and characterization of MODIS-based Landsat ETM+ atmospheric correction. Remote Sens Environ. 2014, 140, 433–449. [Google Scholar] [CrossRef]
- Steven, M.D.; Malthus, T.J.; Baret, F.; Xu, H.; Chopping, M.J. Intercalibration of vegetation indices from different sensor systems. Remote Sens. Environ. 2003, 88, 412–422. [Google Scholar] [CrossRef]
- Ouaidrari, H.; Vermote, E.F. Operational atmospheric correction of Landsat TM data. Remote Sens. Environ. 1999, 70, 4–15. [Google Scholar] [CrossRef]
- Reichenbach, S.E.; Koehler, D.E.; Strelow, D.W. Restoration and reconstruction of AVHRR images. IEEE Trans. Geosci. Remote Sens. 1995, 33, 997–1007. [Google Scholar] [CrossRef]
- Roy, D.P. The impact of misregistration upon composited wide field of view satellite data and implications for change detection. IEEE Trans. Geosci. Remote Sens. 2000, 38, 2017–2032. [Google Scholar] [CrossRef]
- Tanre, D.; Herman, M.; Deschamps, P. Influence of the background contribution upon space measurements of ground reflectance. Appl. Opt. 1981, 20, 3676–3684. [Google Scholar] [CrossRef] [PubMed]
- Aiazzi, B.; Alparone, L.; Baronti, S.; Garzelli, A.; Selva, M. MTF-tailored multiscale fusion of high-resolution MS and pan imagery. Photogramm. Eng. Remote Sens. 2006, 72, 591–596. [Google Scholar] [CrossRef]
- Shlien, S. Geometric correction, registration and resampling of Landsat imagery. Can. J. Remote Sens. 1979, 5, 75–89. [Google Scholar] [CrossRef]
- Park, S.K.; Schowengerdt, R.A. Image reconstruction by parametric cubic convolution. Comput. Vis. Gr. Image Process. 1983, 23, 258–272. [Google Scholar] [CrossRef]
- Keys, R. Cubic convolution interpolation for digital image processing. IEEE Trans. Acoust. Speech Signal. Process. 1981, 29, 1153–1160. [Google Scholar] [CrossRef]
- Dikshit, O.; Roy, D.P. An empirical investigation of image resampling effects upon the spectral and textural supervised classification of a high spatial resolution multispectral image. Photogramm. Eng. Remote Sens. 1996, 62, 1085–1092. [Google Scholar]
- Aiazzi, B.; Baronti, S.; Selva, M.; Alparone, L. Bi-cubic interpolation for shift-free pan-sharpening. ISPRS J. Photogramm. Remote Sens. 2013, 86, 65–76. [Google Scholar] [CrossRef]
- Kalpoma, K.A.; Kawano, K.; Kudoh, J. IKONOS image fusion process using steepest descent method with bi-linear interpolation. Int. J. Remote Sens. 2013, 34, 505–518. [Google Scholar] [CrossRef]
- Laben, C.A.; Brower, B.V. Process for Enhancing the Spatial Resolution of Multispectral Imagery Using Pan-Sharpening. U.S. Patent 6,011,875, 2000. [Google Scholar]
- Alparone, L.; Wald, L.; Chanussot, J.; Thomas, C.; Gamba, P.; Bruce, L.M. Comparison of pansharpening algorithms: Outcome of the 2006 GRS-S data-fusion contest. IEEE Trans. Geosci. Remote Sens. 2007, 45, 3012–3021. [Google Scholar] [CrossRef]
- Alparone, L.; Baronti, S.; Garzelli, A.; Nencini, F. A global quality measurement of pan-sharpened multispectral imagery. IEEE Geosci. Remote Sens. Lett. 2004, 1, 313–317. [Google Scholar] [CrossRef]
- Kruse, F.A.; Lefkoff, A.B.; Boardman, J.W.; Heidebrecht, K.B.; Shapiro, A.T.; Barloon, P.J.; Goetz, A.F.H. The spectral image-processing system (SIPS)—interactive visualization and analysis of imaging spectrometer data. Remote Sens. Environ. 1993, 44, 145–163. [Google Scholar] [CrossRef]
- Keshava, N. Distance metrics and band selection in hyperspectral processing with applications to material identification and spectral libraries. IEEE Transs. Geosci. Remote Sens. 2004, 42, 1552–1565. [Google Scholar] [CrossRef]
- Wald, L. Data Fusion: Definitions and Architectures—Fusion of Images of Different Spatial Resolutions; Les Presses: Paris, France, 2002. [Google Scholar]
- Wang, Z.; Bovik, A.C. A universal image quality index. IEEE Signal. Process. Lett. 2002, 9, 81–84. [Google Scholar] [CrossRef]
- Painter, T.H.; Rittger, K.; McKenzie, C.; Slaughter, P.; Davis, R.E.; Dozier, J. Retrieval of subpixel snow covered area, grain size, and albedo from MODIS. Remote Sens. Environ. 2009, 113, 868–879. [Google Scholar] [CrossRef]
- Ustin, S.L.; Roberts, D.A.; Pinzón, J.; Jacquemoud, S.; Gardner, M.; Scheer, G.; Castañeda, C.M.; Palacios-Orueta, A. Estimating canopy water content of chaparral shrubs using optical methods. Remote Sens. Environ. 1998, 65, 280–291. [Google Scholar] [CrossRef]
- Czapla-Myers, J.S.; Anderson, N.J.; Biggar, S.F. Early ground-based vicarious calibration results for Landsat 8 OLI. Proc. SPIE 2013. [Google Scholar] [CrossRef]
- Markham, B.L.; Storey, J.C.; Irons, J.R. Landsat data continuity mission, now Landsat-8: Six months on-orbit. Proc. SPIE 2013. [Google Scholar] [CrossRef]
- Yang, J.; Zhang, J.; Huang, G. A parallel computing paradigm for pan-sharpening algorithms of remotely sensed images on a multi-core computer. Remote Sens. 2014, 6, 6039–6063. [Google Scholar] [CrossRef]





| Spectra Cover Types | wred | wgreen | wblue | n | R2 | ||
|---|---|---|---|---|---|---|---|
| Vegetation | 0.3951 | 0.5197 | 0.0863 | 270 | 0.9999 | 0.00077 | 0.00865 |
| Soil | 0.3830 | 0.5588 | 0.0586 | 34 | 1.0000 | 0.00069 | 0.00409 |
| Water | 0.4072 | 0.5207 | 0.0709 | 10 | 1.0000 | 0.00036 | 0.00998 |
| Ice and snow | 0.4095 | 0.5166 | 0.0748 | 21 | 1.0000 | 0.00023 | 0.00051 |
| All (bootstrapped) | 0.4030 | 0.5177 | 0.0802 | 99 | 1.0000 | 0.00059 | 0.00530 |
| Spectra Cover Types | wred | wgreen | n | R2 | ||
|---|---|---|---|---|---|---|
| Vegetation | 0.4151 | 0.5626 | 270 | 0.9996 | 0.00157 | 0.01680 |
| Soil | 0.3357 | 0.6582 | 34 | 1.0000 | 0.00090 | 0.00484 |
| Water | 0.3616 | 0.6244 | 10 | 1.0000 | 0.00075 | 0.01740 |
| Ice and snow | 0.4984 | 0.5036 | 21 | 1.0000 | 0.00049 | 0.00101 |
| All (bootstrapped) | 0.3518 | 0.6448 | 99 | 0.9999 | 0.00211 | 0.01962 |
| Study Area | Pansharpening Method | ERGAS Value | SAM Value | Q4 Value | Algorithm Run Time (s) |
|---|---|---|---|---|---|
| South Dakota 2734 × 2532 30 m pixels | Cubic convolution (no pansharpening) | 2.016 | 1.876 | 0.902 | 0.17 |
| Brovey equal weights | 2.669 | 1.876 | 0.806 | 0.76 | |
| Brovey SRFB weights | 2.191 | 1.876 | 0.815 | 0.78 | |
| Brovey image specific weights | 1.989 | 1.876 | 0.819 | 133.54 | |
| CA-GS equal weights | 1.728 | 1.734 | 0.918 | 583.61 | |
| CA-GS SRFB weights | 1.513 | 1.580 | 0.917 | 575.05 | |
| CA-GS image specific weights | 1.491 | 1.602 | 0.916 | 719.93 | |
| China 2976 × 2520 30 m pixels | Cubic convolution (no pansharpening) | 1.741 | 1.731 | 0.843 | 0.16 |
| Brovey equal weights | 2.730 | 1.731 | 0.758 | 0.78 | |
| Brovey SRFB weights | 1.800 | 1.731 | 0.763 | 0.77 | |
| Brovey image specific weights | 1.686 | 1.731 | 0.764 | 142.75 | |
| CA-GS equal weights | 1.735 | 1.786 | 0.876 | 621.75 | |
| CA-GS SRFB weights | 1.372 | 1.491 | 0.876 | 614.83 | |
| CA-GS image specific weights | 1.346 | 1.461 | 0.874 | 756.97 | |
| India 2970 × 2470 30 m pixels | Cubic convolution (no pansharpening) | 1.543 | 1.471 | 0.854 | 0.15 |
| Brovey equal weights | 2.021 | 1.471 | 0.740 | 0.78 | |
| Brovey SRFB weights | 1.608 | 1.471 | 0.737 | 0.77 | |
| Brovey image specific weights | 1.499 | 1.471 | 0.738 | 139.93 | |
| CA-GS equal weights | 1.377 | 1.333 | 0.883 | 610.39 | |
| CA-GS SRFB weights | 1.109 | 1.151 | 0.883 | 605.76 | |
| CA-GS image specific weights | 1.093 | 1.156 | 0.881 | 747.57 |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons by Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, H.K.; Roy, D.P. Computationally Inexpensive Landsat 8 Operational Land Imager (OLI) Pansharpening. Remote Sens. 2016, 8, 180. https://doi.org/10.3390/rs8030180
Zhang HK, Roy DP. Computationally Inexpensive Landsat 8 Operational Land Imager (OLI) Pansharpening. Remote Sensing. 2016; 8(3):180. https://doi.org/10.3390/rs8030180
Chicago/Turabian StyleZhang, Hankui K., and David P. Roy. 2016. "Computationally Inexpensive Landsat 8 Operational Land Imager (OLI) Pansharpening" Remote Sensing 8, no. 3: 180. https://doi.org/10.3390/rs8030180
APA StyleZhang, H. K., & Roy, D. P. (2016). Computationally Inexpensive Landsat 8 Operational Land Imager (OLI) Pansharpening. Remote Sensing, 8(3), 180. https://doi.org/10.3390/rs8030180








