Classification of Small-Scale Eucalyptus Plantations Based on NDVI Time Series Obtained from Multiple High-Resolution Datasets

Abstract

Eucalyptus, a short-rotation plantation, has been expanding rapidly in southeast China in recent years owing to its short growth cycle and high yield of wood. Effective identification of eucalyptus, therefore, is important for monitoring land use changes and investigating environmental quality. For this article, we used remote sensing images over 15 years (one per year) with a 30-m spatial resolution, including Landsat 5 thematic mapper images, Landsat 7-enhanced thematic mapper images, and HJ 1A/1B images. These data were used to construct a 15-year Normalized Difference Vegetation Index (NDVI) time series for several cities in Guangdong Province, China. Eucalyptus reference NDVI time series sub-sequences were acquired, including one-year-long and two-year-long growing periods, using invested eucalyptus samples in the study region. In order to compensate for the discontinuity of the NDVI time series that is a consequence of the relatively coarse temporal resolution, we developed an inverted triangle area methodology. Using this methodology, the images were classified on the basis of the matching degree of the NDVI time series and two reference NDVI time series sub-sequences during the growing period of the eucalyptus rotations. Three additional methodologies (Bounding Envelope, City Block, and Standardized Euclidian Distance) were also tested and used as a comparison group. Threshold coefficients for the algorithms were adjusted using commission–omission error criteria. The results show that the triangle area methodology out-performed the other methodologies in classifying eucalyptus plantations. Threshold coefficients and an optimal discriminant function were determined using a mosaic photograph that had been taken by an unmanned aerial vehicle platform. Good stability was found as we performed further validation using multiple-year data from the high-resolution Gaofen Satellite 1 (GF-1) observations of larger regions. Eucalyptus planting dates were also estimated using invested eucalyptus samples and the Root Mean Square Error (RMSE) of the estimation was 84 days. This novel and reliable method for classifying short-rotation plantations at small scales is the focus of this study.

1. Introduction

As remote sensing technology advances, it plays an ever greater role in monitoring global land cover changes, since this approach yields faster results, better coverage and lower cost when compared with ground-based investigations [1,2,3]. For classification research, one objective, naturally, is to separate original images into different classes [4,5]; other researchers may be interested in extracting certain objects of interest from the images (crops, plantations, building, water, etc.) [6,7,8,9].

Awareness of the need to protect the environment has significantly increased in China. While a considerable number of researchers have focused on deforestation, few have considered the complementary problem of excessive plantation. A problematic crop in this regard is eucalyptus, which has a short growth period and is highly efficient for the production of wood [10]. In recent years, as urbanization has accelerated in the cities on China’s southeast coast, more and more of land that was once covered by virgin forests or crops has been cultivated with eucalyptus in order to meet the increasing demand for wood. A number of researchers have found that the planting of eucalyptus for economic benefit can reduce biodiversity [11,12]. Therefore, the ability to classify regions of eucalyptus accurately and efficiently is of great importance for environment monitoring and protection. Because there are many methodologies that may be used for the classification of remote sensing images, the choice of the best methodology for eucalyptus classification is an important concern.

Decision tree classification [13], neutral network classification [14], and support vector machine [8] are classifiers that are commonly applied to remote sensing images. In most cases, these methodologies are based on the spectral and textural features of the relevant classes [15,16]. However, in some cases, the spectral features of a target class are quite similar to those of other classes, so that other features of the target class are of primary importance, among which are multi-temporal features. The most commonly used multi-temporal feature for extracting vegetation is a time series of vegetation indices, such as the Normalized Difference Vegetation Index (NDVI) [17,18] and the Enhanced Vegetation Index (EVI) [19,20]. These indices not only distinguish vegetation from other classes, but, to some extent, can also indicate the growth condition of the vegetation.

Previous studies have led to the creation of a large-scale eucalyptus map using low-to-medium resolution images [21]. The high temporal resolution of the data makes it possible to create successive time series for analysis. In doing so, however, a compromise was made with regard to high spatial resolution. Thus, once a study region becomes sufficiently small, at the level of counties or even villages, low-to-medium spatial resolution is no longer sufficient to achieve the desired outcome. The only solution is to enhance the spatial resolution, though this approach may potentially lead to a loss of temporal resolution [22]. For this study, we accordingly used multiple high-resolution datasets and classification methodologies were adjusted for the loss of temporal resolution.

The main objectives of this study are: (1) to develop a methodology using high spatial resolution remote sensing images to map eucalyptus plantations in the Guangdong Province of China; (2) to compare the performance of the newly-created methodology with existing methodologies; and (3) to estimate eucalyptus plantation dates.

2. Experimental Section

2.1. Eucalyptus Plantations

Although the spatial resolution of the images used in this study was improved compared to that of the Moderate Resolution Imaging Spectroradiometer (MODIS) NDVI product, it remained impractical to map eucalyptus plantations efficiently based on spectral or textural features with a spatial resolution of, for example, 30 m. As an artificial forest, eucalyptus has a unique growth cycle: the wood is harvested and trees are replanted for another growth period every several years. This marked difference between artificial and natural forests makes it possible to classify the two kinds of forests by analyzing their changing features over time.

As alluded to above, among the most reliable indicators for classification of vegetation are such indices as the commonly used NDVI. As shown in Equation (1), the formula of the NDVI consists of red and infrared reflectance [23,24,25].

$$NDVI=\frac{{\rho }_{NIR}-{\rho }_R}{{\rho }_{NIR}+{\rho }_R},$$

(1)

where ${\rho }_{\mathrm{NIR}}$ and ${\rho }_{\mathrm{R}}$ are the reflectance values for the near infrared and red wavelengths, respectively. For vegetation, reflectance is high in the near-infrared band and low in the red band, resulting in relatively high NDVI values, compared to other features. Therefore, the NDVI can both distinguish vegetation from other features and indicate the health of the vegetation [26,27].

Planted eucalyptus has fairly regular growth rotations [21,28]. Each rotation usually lasts four to six years, though the exact duration varies. In a rotation, when a eucalyptus tree grows to maturity, the wood is harvested and rest of the tree is burned, after which the land is left fallow for a time. Several months later, new eucalyptus trees are replanted. The trees grow rapidly for about one year, faster than at any other time during their growth cycle, until they reach a high NDVI level. The trees then remain at this level for several years until they are harvested. Therefore, a low ebb of NDVI (as shown in Figure 1) is generated at the beginning of each rotation.

Figure 1. Conceptual diagram of the NDVI trend at the low ebb between two eucalyptus successive rotations, derived from related references and the experience of forest managers in Xinfeng County, Guangdong Province. The numbers 1 and 5 represent the mature periods of eucalyptus rotations when the NDVI is stable and at a high level. The number 2 represents the sudden drop that occurs when eucalyptus trees are cut down and burned at the end of the previous rotation. The number 3 represents the fallow time when the NDVI is at a low level, and the number 4 represents the period of rapid growth after the trees are replanted during the present rotation. The actual NDVI trend may not be linear since a number of small increases and decreases may occur during each period. This diagram is intended only to indicate the approximate change of NDVI between eucalyptus rotations. The dotted arrows indicate the potential acquisition time for remote sensing images, which will be discussed in Section 2.3.2.

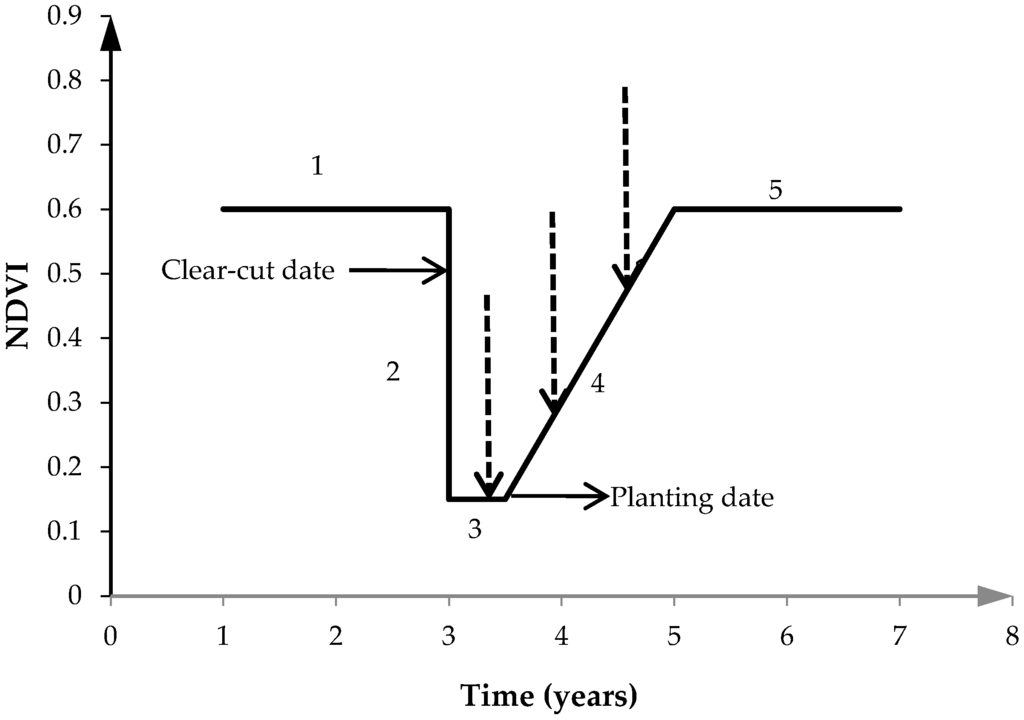
Figure 1. Conceptual diagram of the NDVI trend at the low ebb between two eucalyptus successive rotations, derived from related references and the experience of forest managers in Xinfeng County, Guangdong Province. The numbers 1 and 5 represent the mature periods of eucalyptus rotations when the NDVI is stable and at a high level. The number 2 represents the sudden drop that occurs when eucalyptus trees are cut down and burned at the end of the previous rotation. The number 3 represents the fallow time when the NDVI is at a low level, and the number 4 represents the period of rapid growth after the trees are replanted during the present rotation. The actual NDVI trend may not be linear since a number of small increases and decreases may occur during each period. This diagram is intended only to indicate the approximate change of NDVI between eucalyptus rotations. The dotted arrows indicate the potential acquisition time for remote sensing images, which will be discussed in Section 2.3.2.

The crucial point of extracting eucalyptus trees from the images was to search for a methodology that accurately describes the low ebb. In previous studies by le Maire, Dupuy, Nouvellon, Loos, and Hakarnada [21], the MODIS NDVI product (with a temporal resolution of 16 days) was used to acquire a successive NDVI time series. In this study, however, the temporal resolution was limited to about one year in order to allow for a sufficiently high spatial resolution so that eucalyptus plantations could be studied at the scale of countries. As mentioned, it is impractical to acquire such a successive NDVI time series. For this reason, traditional methodologies were deemed inefficient, and we worked to develop a new method for classifying eucalyptus trees.

2.2. Study Area and Construction of the NDVI Time Series

The study area covered three cities in the Guangdong Province of China: Shaoguan City, Heyuan City, and Ganzhou City. The area lies between 113°7′3.65′′E–114°3′16.34′′E and 23°9′1.14′′N–24°9′7.8′′N, as shown in Figure 2. We collected and downloaded the thematic mapper images of Landsat 5 (TM 5), the enhanced thematic mapper images of Landsat 7 ETM 7+ and HJ-1A/B Charge-coupled Device (CCD) images (HJ images) for the year 2000 through 2014 in one-year increments. Originally, we had planned to only use TM images to create the NDVI time series, but TM images for some months or years were not available due to cloud cover or were missing. The ETM 7+ and HJ images were therefore acquired in order to complete the NDVI time series. The spatial resolution of the three datasets was 30 m. Table 1 and Table 2 show the information of images used.

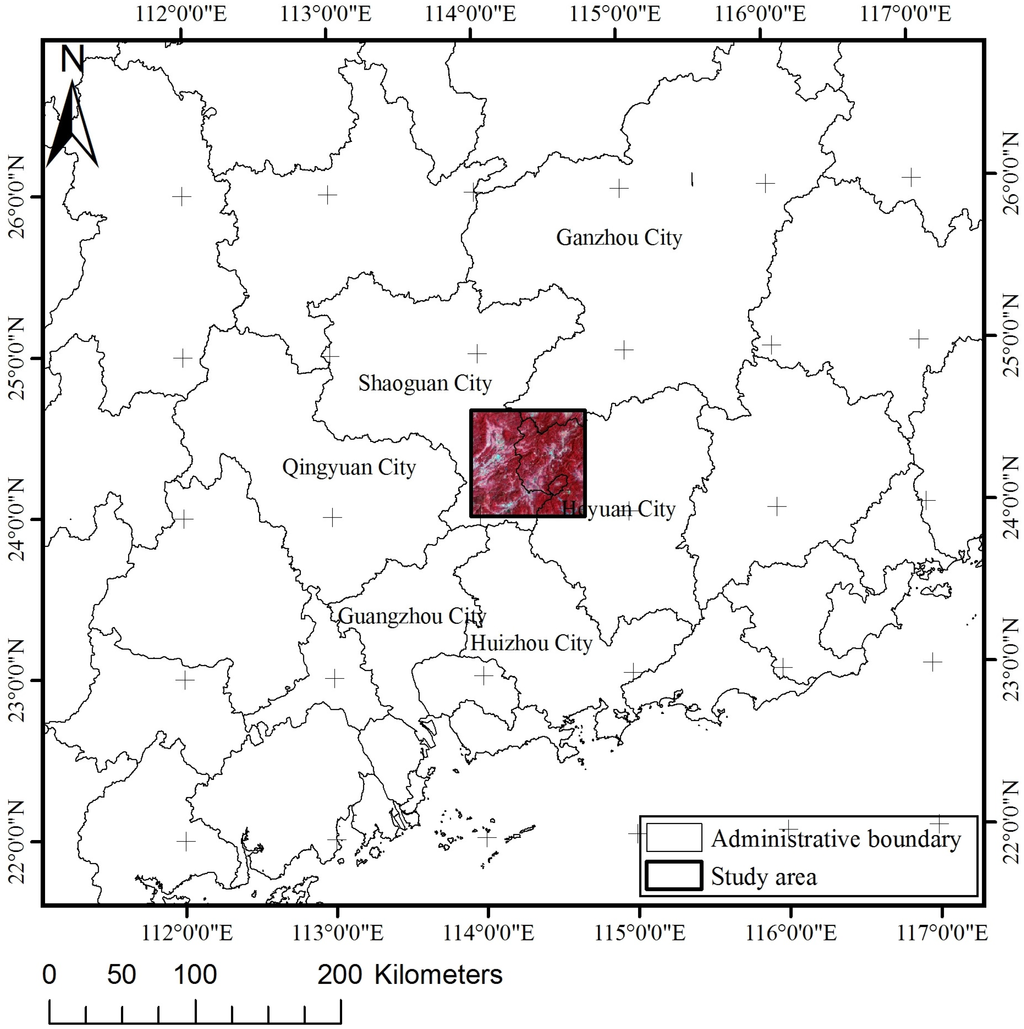
Figure 2. Location of the study area. The false color composite image displayed in the picture is one of the images used to build the NDVI time series, which was acquired on 14 September 2000.

Figure 2. Location of the study area. The false color composite image displayed in the picture is one of the images used to build the NDVI time series, which was acquired on 14 September 2000.

Before the acquired data were used, each pixel was preprocessed for radiation correction, atmospheric correction, and registration. The radiation and atmospheric correction were made in accordance with the Radiometric Calibration and Fast Line-of-Sight Atmospheric Analysis of Hypercubes (FLAASH) function modules in ENVI version 5.0. In terms of registration, we took the TM images as the base images, selected over 30 ground control points each time and used a first-order polynomial transformation method. It should be mentioned that the ETM+ images acquired after 2003 contained un-scanned areas due to a sensor fault. Although we avoided selecting those images in which large regions of vegetation were covered by the gaps, it was still necessary to preprocess these data with the extra step of filling the gaps [29,30]. The principle of the gap filling is assigning the missing pixels values obtained from statistics of their surrounding pixels.

Table 1. Images used in this study to build the Normalized Difference Vegetation Index (NDVI) time series.

	Sensor Type	Acquisition Date (Year/Day)		Sensor Type	Acquisition Date
1	ETM 7+	2000/258	9	TM 5	2008/320
2	TM 5	2001/251	10	TM 5	2009/290
3	ETM 7+	2002/311	11	HJ-1A CCD1	2010/278
4	TM 5	2003/338	12	HJ-1B CCD2	2011/296
5	TM 5	2004/325	13	HJ-1B CCD2	2012/274
6	TM 5	2005/346	14	HJ-1A CCD2	2013/287
7	TM 5	2006/266	15	HJ-1A CCD2	2014/285
8	ETM 7+	2007/293

Table 1. Images used in this study to build the Normalized Difference Vegetation Index (NDVI) time series.

	Sensor Type	Acquisition Date (Year/Day)		Sensor Type	Acquisition Date
1	ETM 7+	2000/258	9	TM 5	2008/320
2	TM 5	2001/251	10	TM 5	2009/290
3	ETM 7+	2002/311	11	HJ-1A CCD1	2010/278
4	TM 5	2003/338	12	HJ-1B CCD2	2011/296
5	TM 5	2004/325	13	HJ-1B CCD2	2012/274
6	TM 5	2005/346	14	HJ-1A CCD2	2013/287
7	TM 5	2006/266	15	HJ-1A CCD2	2014/285
8	ETM 7+	2007/293

Table 2. Information regarding the ETM 7+, TM 5, and HJ images. NDVI were calculated on the basis of the red and near infrared bands (the third and fourth bands of ETM 7+/TM 5, HJ images).

Sensor Type	Path/Row	Band Setting (μm)	Spatial Resolution	Map Projection
ETM 7+/TM 5	122/43	0.45~0.52, 0.52~0.60, 0.63~0.69, 0.76~0.90, 1.55~1.75, 10.4~12.5, 2.08~2.35, (0.5~0.9, ETM 7+ only)	30 m	UTM 49N, Datum WGS84
HJ-1A/B CCD1/CCD2	895/164	0.43~0.52, 0.52~0.60, 0.63~0.69, 0.76~0.90	30 m	UTM 50N, Datum WGS84

Table 2. Information regarding the ETM 7+, TM 5, and HJ images. NDVI were calculated on the basis of the red and near infrared bands (the third and fourth bands of ETM 7+/TM 5, HJ images).

Sensor Type	Path/Row	Band Setting (μm)	Spatial Resolution	Map Projection
ETM 7+/TM 5	122/43	0.45~0.52, 0.52~0.60, 0.63~0.69, 0.76~0.90, 1.55~1.75, 10.4~12.5, 2.08~2.35, (0.5~0.9, ETM 7+ only)	30 m	UTM 49N, Datum WGS84
HJ-1A/B CCD1/CCD2	895/164	0.43~0.52, 0.52~0.60, 0.63~0.69, 0.76~0.90	30 m	UTM 50N, Datum WGS84

Although these data were through radiation correction, effects of the mixing sensors may still existed. For the same area of vegetation, NDVI obtained from different sensors may vary, mostly because of their different spectral response in the red band [31]. Hao et al. [32] performed similar evaluations for TM 5 and HJ-1 CCD NDVI and found that NDVI obtained from the two different sensors has a linear correlation of over 0.98, which means that, in this study, NDVI from ETM 7+/TM 5, HJ-1A/B CCD were intercomparable and could be directly used to build the NDVI time series.

This handling method was on the basis of the consideration that the difference between NDVI from TM 5 and HJ-1 CCD was small, compared with the sharp NDVI decrease and increase during the low ebb of eucalyptus rotations. In general, however, it will be necessary to normalize NDVI if the datasets vary.

2.3. Eucalyptus Classification Methodology

2.3.1. Eucalyptus Classification Steps

In this study, the goal of the classification methodology was to identify the NDVI low ebb in the rotation and to ascertain the presence of eucalyptus trees using a suitable classification algorithm. The first step was to construct a reference sub-sequence of the NDVI time series, describing the typical NDVI low ebb of a eucalyptus rotation. Next, the NDVI time series of a given pixel had to be compared with the reference sub-sequence time series using the classification algorithm. Finally, the decision regarding whether a given pixel should be classified as eucalyptus was made on the basis of the similarity between the two time series mentioned above.

2.3.2. Building a Reference NDVI Time Series Sub-Sequence

Ground investigation were performed in order to build a typical and reliable reference sub-sequence time series. During the investigation, we made an effort to include eucalyptus trees in different sub-regions and with different planting dates in order to guarantee that the reference NDVI time series sub-sequence would be representative and universal. In the end, 270 scattered pixels were acquired, together with their planting dates (accurate to the month), and 135 of these were purely randomly selected to build the reference sub-sequence time series. The remaining pixels were used for the validation of eucalyptus planting dates (Section 3.3). As shown above, the low ebb in a eucalyptus rotation lasts between two and three years and the temporal resolution of the images was one year. Therefore, because many details may be omitted, the shape of the NDVI time series may not be consistent with the actual growth tendency of a eucalyptus plantation. In Figure 1, the dotted arrows represent potential acquisition times of images during a low ebb. For a given eucalyptus pixel at the low ebb of its rotation, the Earliest Acquisition Time (EAT) of images during this rotation differed. Generally speaking, there were two possible outcomes or cases. Case 1: when the EAT was shortly after the plantation in a rotation, there might be three time steps during the low ebb, which would result in a two-year-long growing period (the second low ebb in Figure 3). Case 2: when the EAT was long after the plantation in a rotation, there might be only two time steps during the low ebb, which would result in a one-year-long growing period (the first low ebb in Figure 3).

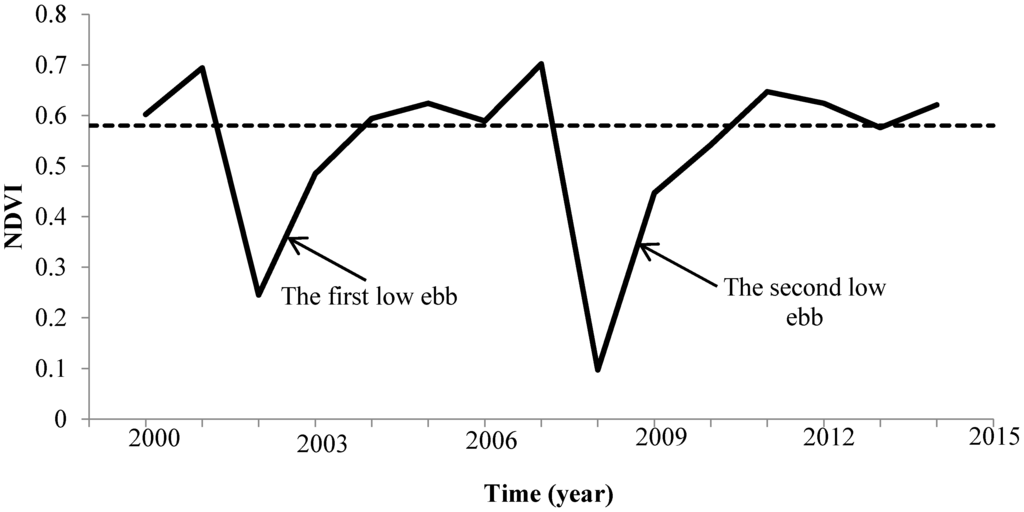
Figure 3. Example of the NDVI time series of a eucalyptus pixel, selected from the 135 pixels investigated. The two low ebbs of the curve represent the two cases with different EATs described above. The first low ebb represents Case 2, in which NDVI values of 2002 and 2003 were below the dashed line; the second low ebb represents Case 1, in which NDVI of 2008, 2009 and 2010 were below the dashed line. The dashed line represents the average NDVI high level in a eucalyptus rotation, calculated as the average value of the high NDVI values of the 135 pixels acquired over 15 years.

Figure 3. Example of the NDVI time series of a eucalyptus pixel, selected from the 135 pixels investigated. The two low ebbs of the curve represent the two cases with different EATs described above. The first low ebb represents Case 2, in which NDVI values of 2002 and 2003 were below the dashed line; the second low ebb represents Case 1, in which NDVI of 2008, 2009 and 2010 were below the dashed line. The dashed line represents the average NDVI high level in a eucalyptus rotation, calculated as the average value of the high NDVI values of the 135 pixels acquired over 15 years.

For these reasons, the low ebbs were subdivided into the two cases on the basis of the number of NDVI values they exhibited. Among the 15-year NDVI time series of the 135 eucalyptus pixels that were investigated, some pixels consisted of low ebbs of only either the first or second case, while others consisted of low ebbs of both cases. Of the 203 low ebb samples obtained from the NDVI time series of the 135 selected pixels, 110 belonged to Case 1 and 93 belonged to Case 2. Based on these findings, two reference sub-sequence time series were calculated by averaging the time series of the 110 first-case samples and the 93 second-case samples. The two sub-sequences are shown in Figure 4.

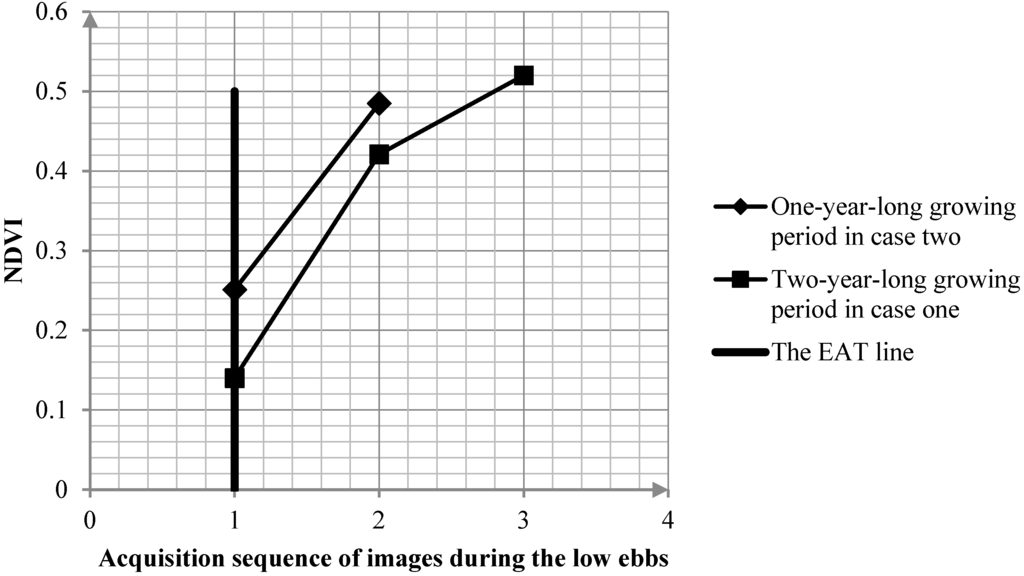
Figure 4. The two reference NDVI time series sub-sequences describing the growing periods during the low ebbs. Because the EAT of Case 1 occurred earlier in the rotations than that of Case 2, the NDVI value of Case 1 at EAT was lower than that of Case 2.

Figure 4. The two reference NDVI time series sub-sequences describing the growing periods during the low ebbs. Because the EAT of Case 1 occurred earlier in the rotations than that of Case 2, the NDVI value of Case 1 at EAT was lower than that of Case 2.

2.3.3. Eucalyptus Classification Algorithm

After the reference NDVI time series sub-sequences had been created, the next step was to search for a proper classification algorithm. With the proper algorithm, the NDVI time series of all pixels in the images could be traversed and the distance result could be calculated in order to judge whether a pixel was a eucalyptus pixel and, if so, when it had been planted.

The coarse temporal resolution (at intervals of approximately one year) made it impossible to acquire an NDVI time series, which was as successive as MODIS NDVI time series (at an interval of sixteen days). In addition, the EATs of different pixels acquired during a eucalyptus rotation differed with an amplitude of about one year. This situation led to a significant difference among the various pixels in an NDVI time series of the growing periods, regardless of which case, 1 or 2, was present. Traditional algorithms therefore may not be effective enough to describe the complicated and diversified growing periods of eucalyptus plantations.

To overcome this problem, we developed a new algorithm to build the discriminant function, which we termed the Inverted Triangle Area (ITA) algorithm. The ITA algorithm avoids the variability of different NDVI times during the growing period and instead takes advantage of the relatively stable area of an inverted triangle that is generated by vertical and horizontal auxiliary lines and the NDVI curves for the growing periods. As shown in Figure 5, we used Case 1 as an example (Case 2 performed in the same way). Altogether, there were three gradually increasing NDVI values for one eucalyptus pixel during its growing period in the low ebb. Therefore, as earlier, the EAT corresponded with lower values for all three NDVI. The area of the inverted triangle, however, remained much more stable than did the NDVI time series. In Figure 6, the NDVI values of two samples have an average NDVI difference of more than 0.1, the same order of magnitude as the NDVI itself. In contrast, the area values of the two inverted triangles only show a difference of two orders of magnitude smaller than that of the inverted triangle area itself. For a “not eucalyptus” pixel (whether it represented natural or other planted forest), such inverted triangles would not be generated. However, even if an inverted triangle were generated, its area value would differ significantly from the eucalyptus reference triangle owing to the unique growth pattern of the eucalyptus.

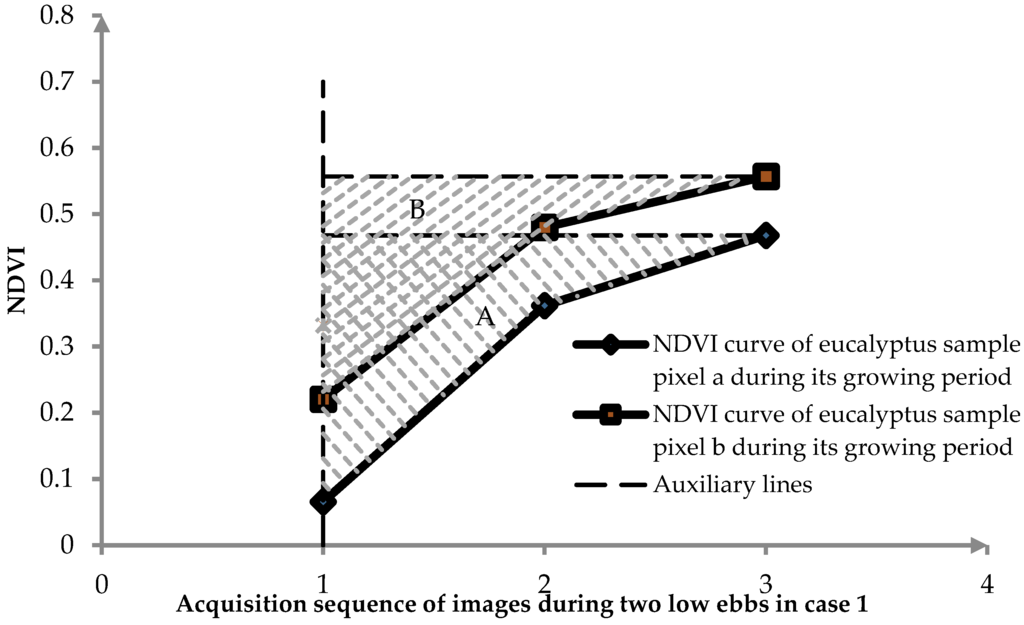
Figure 5. NDVI time series sub-sequences of two eucalyptus sample pixels during their growing periods for Case 1. Sections A and B, filled with diagonal lines, represent the areas of the two triangles, as generated by auxiliary vertical and horizontal lines and the NDVI times series sub-sequences of the two samples. The EAT (the earliest acquisition time of images) for both samples was October 2009, which was six months after Sample A was planted and 10 months after Sample B was planted.

Figure 5. NDVI time series sub-sequences of two eucalyptus sample pixels during their growing periods for Case 1. Sections A and B, filled with diagonal lines, represent the areas of the two triangles, as generated by auxiliary vertical and horizontal lines and the NDVI times series sub-sequences of the two samples. The EAT (the earliest acquisition time of images) for both samples was October 2009, which was six months after Sample A was planted and 10 months after Sample B was planted.

Figure 6. Mosaic photograph of the sub-region, assembled from 88 visible and infrared sub-photographs.

Figure 6. Mosaic photograph of the sub-region, assembled from 88 visible and infrared sub-photographs.

For a given discriminant function, the commission and omission errors of eucalyptus classification are greatly dependent on the threshold coefficients T1 and T2 (T1 for Case 1 and T2 for Case 2). In general, if these coefficients are assigned overly large values, many eucalyptus pixels would be classified as “not-eucalyptus”, which would result in high producer accuracy and low user accuracy. On the other hand, if they are assigned overly small values, many not-eucalyptus pixels would be classified as “eucalyptus”, which would result in low producer accuracy and high producer accuracy. Because producer and user accuracies always show opposite inverse trends, it is crucial to maintain a balance between them.

2.3.4. Estimation of the Presence and Planting Date of Eucalyptus Plantations

As shown in Table 1, the intervals of acquisition date of images were not strictly yearly owing to a deficiency of images; that is, some intervals were less than one year and some were greater, while our plan was to build an annual NDVI time series. In order to make the actual NDVI times series comparable with the two annual references, an “offset process” had to be done prior to the classification. The offset process involved the following, taking Case 1 as an example. When applying the ITA algorithm to the NDVI time series, NDVI values of three years were involved. The first NDVI value remained unchanged; the second and third were adjusted as shown in Equation (2):

$$NDV{I}_{offset}=NDV{I}_{in}+\frac{NDV{I}_{in}-NDV{I}_{prev}}{N_{in}-N_{prev}}\times \left(365-N_{in}+N_{prev}\right),$$

(2)

where NDVI_offset was the adjusted NDVI value, NDVI_in and NDVI_prev were respectively the initial NDVI values of the year in question and the previous year, N_in and N_prev were the acquisition day numbers of images in the year in question and the previous years, which were listed in Table 1. In this process, NDVI values were naturally assumed to be changing in a linear fashion during the offset days. This process was designed to make the NDVI time series of “potential” eucalyptus pixels during the growing period comparable over the time. There is the possibility that the assumption to some extent misrepresented the actual changing tendency of NDVI, which could have led to a small bias from the actual NDVI values. However, in consideration of the offset time length (several days or more), it was determined that such a bias was tolerated.

For a given pixel, the first step for estimating the presence and planting date of a eucalyptus plantation was to traverse its NDVI time series using the ITA discriminant function. Next, two distance time series were calculated for each pixel, one for Case 1 and one for Case 2. To examine the presence of a low ebb for one pixel in a given year, the two distance time series and two respective threshold coefficients (discussed in Section 3.1.1) were subtracted from each other.

The ITA discriminant functions were calculated from the beginning of the NDVI time series for a given pixel to the end of the series. For a given year, if the distance of any case (1 or 2) was less than its corresponding threshold coefficient, the particular pixel was classified as a eucalyptus pixel. If the distance was greater, it was classified as a not-eucalyptus pixel. When performing the classification, we also considered exceptions. For a few natural forest pixels, although the NDVI remained relatively high over several years, there were nevertheless some years when the NDVI was lower than normal values owing to the phenological changes. For example, if the NDVI value of a natural forest pixel was 0.5 in the previous year, while in the following year it rose back up to 0.7, the result would be a signal similar to the low ebb of a plantation eucalyptus pixel. In this case, a natural forest pixel would end up being classified as a eucalyptus pixel. To avoid such errors, we added the extra criterion of determining whether NDVI values during a low ebb were all lower than 0.58 (for this threshold, see the legend of Figure 3). If the values were lower than 0.58, the pixel was classified as a eucalyptus pixel, if not, it was excluded. In addition, for Case 2, only two NDVI time steps existed in a low ebb, which made the low ebb similar with that of some other plantation species (bamboo, acacia, pines, etc.). To distinguish eucalyptus of Case 2 from these species, we made full use of the unique growth period (4–6 years for eucalyptus). Even if a pixel were to meet the above conditions but its interval of adjoining rotations were less than four years or more than six years, it would be classified as a not-eucalyptus pixel.

Once the presence of a eucalyptus pixel was identified, its approximate planting date could also be calculated. Since the temporal resolution of the images used in this study was relatively coarse, the eucalyptus planting date could not, however, be accurately established to the day or month. Nevertheless, we still attempted to estimate the approximate planting date. As discussed in Section 2.3.2, the different EATs of the images resulted in the two different cases. If the EAT of a pixel was early in the interval of one year, the pixel was more likely to perform as Case 1. If the EAT was late, it behaved as Case 2. Accordingly, it was possible to estimate whether the planting date was during the first or second half of the interval year based on the two acquisition times of the images.

2.4. Comparison with Three Other Classification Algorithms Using a High-Resolution Photograph

2.4.1. Acquisition of the Validation Photograph

In general, images or maps used for validation should be more accurate and have a higher spatial resolution than the classified results to be validated. In this study, the spatial resolution of the remote sensing images used is 30m, which is relatively high for eucalyptus classification. For validation of the NDVI observations, we chose to use photographs taken in the study region. Although the classification result was a time series of binary values collected over 15 years, it was impractical to acquire validation photographs for each of these years. Therefore, we had to select the classification results of only some of the years for validation.

We chose to use an unmanned aerial vehicle (UAV) platform equipped with cameras to take photographs in sub-regions because of its suitability and low expense. Two SONY Alpha 5100 compact interchangeable lens digital cameras (which detect red, green and blue bands) were carried on an Avian-P Aerial Photography UAV platform. Our flight plan was implemented from 10:00–10:55 local time (the time at which the Landsat satellite passed over the area) on 17 December, 2014, when the weather and light conditions were suitable for the flight. The photographs covered one sub-region of the NDVI images, where the terrain was flat and surface features were complicated. The pose and trajectory of the UAV were pre-programmed before the flight. While the UAV was in the air, the cameras captured photographs during each of the passes, which were executed serially in parallel flight lines until the view of cameras had covered the entire targeted sub-region. The UAV was flown at an average elevation of 300 m.

The acquired images were processed to form a mosaic photograph that covered the entire sub-region. During the flight, the orientation of cameras kept changing within a small range because of slight shaking of the UAV. Accordingly, the first step was to perform image orthorectification on each of the photographs. Using ground control points, the images were re-projected and converted from the relative coordinate system to the WGS 84 coordinate system. Next, they went through a registration process using the overlaps between contiguous photographs. The last step was to fuse the images to form a mosaic photograph. As shown in Figure 6, the mosaic photograph covers an area of 1.2 × 1.5 km and has a spatial resolution of 0.1 m per pixel, so that even details of a single tree could be identified.

Using the high-resolution composite photograph, eucalyptus plantations could be identified easily and accurately, but for validation, we also needed to know the planting date. We invited the forest managers of the corresponding regions to interpret the photographs and labeled the eucalyptus plantations with planting dates that were accurate to the month.

2.4.2. Comparison of Four Discriminant Functions

To understand the classification performance of our algorithm better, we compared our results with three other algorithms. Several algorithms commonly used for time series analysis were tested. The City Block Algorithm (CTB) uses the average of reference time series sub-sequences, while the Standardized Euclidian Distance (SED) algorithm uses the average and standard deviations of reference time series sub-sequences [33]. Of particular interest to us was the Bounding Envelope (BE) algorithm developed by le Maire et al. [21], which had been originally used to warp dynamic time but later was adopted as a means to classify eucalyptus plantations using MOD13Q1 NDVI products. The authors built a reference NDVI time series with average NDVI values of control points and two bounding time series, one Upper Bounding (UB) time series and one Lower Bounding (LB) time series, which were calculated by adding or subtracting the standard deviation from the average value. Next, the distance was calculated by the summation of all distance values between the NDVI time series of a given pixel and the long, narrow channel generated by the UB and LB. Because there are two cases of reference NDVI time series sub-sequences during each growing period, all four algorithms are described in two forms (listed in Table 3), one for Case 1 and the other for Case 2.

Table 3. Discriminant functions used to compute the similarity between two sub-sequences of the reference and NDVI time series of a given pixel. Here, N_t is the NDVI value of the time series at time t. A(t)_1,2 and Aref_1,2 are the areas of the respective inverted triangles, generated by the NDVI time series sub-sequence of a given pixel starting at t and the reference NDVI time series sub-sequence for Cases 1 and 2; m is the length of the sub-sequence NDVI time series, which is three for Case 1 and two for Case 2.

Discriminant Functions	Formulas
ITA: Inverted Triangle Area	$ITA{\left(t\right)}_{1,2}=\left|A{\left(t\right)}_{1,2}-A_{ref1,2}\right|$; $A{\left(t\right)}_1=\frac{N_{t+1}-N_t}{2}+\frac{N_{t+2}-N_{t+1}}{2}+(N_{t+2}-N_{t+1})$; $A{\left(t\right)}_2=\frac{N_{t+1}-N_t}{2}$, $A{\left(t\right)}_1$ and $A{\left(t\right)}_2$ are the respective ITAs for case one and two.
CTB: City Block	$CTB(t)={\displaystyle \sum _{i=1}^m}|N_{t+i-1}-{\mu }_i|$ ${\mu }_i$ was NDVI average value of the ith time step of reference NDVI time series (the same below).
SED: Standardized Euclidian Distance	$SED(t)=\sqrt{{\displaystyle \sum _{i=1}^m}\frac{{(N_{t+i-1}-{\mu }_i)}^2}{{{\sigma }_i}^2}}$
BE: Bounding Envelope	$BE(t)=\sqrt{\frac{1}{m}{\displaystyle \sum _{i=1}^m}\Delta {N_{t+i-1}}^2}$; $\Delta N_{t+i-1}=N_{t+i-1}-U{B}_i$, if $N_{t+i-1}\ge U{B}_i$; $\Delta N_{t+i-1}=N_{t+i-1}-L{B}_i$, if $N_{t+i-1}\le L{B}_i$; $\Delta N_{t+i-1}-0$, elseif

Table 3. Discriminant functions used to compute the similarity between two sub-sequences of the reference and NDVI time series of a given pixel. Here, N_t is the NDVI value of the time series at time t. A(t)_1,2 and Aref_1,2 are the areas of the respective inverted triangles, generated by the NDVI time series sub-sequence of a given pixel starting at t and the reference NDVI time series sub-sequence for Cases 1 and 2; m is the length of the sub-sequence NDVI time series, which is three for Case 1 and two for Case 2.

Discriminant Functions	Formulas
ITA: Inverted Triangle Area	$ITA{\left(t\right)}_{1,2}=\left|A{\left(t\right)}_{1,2}-A_{ref1,2}\right|$; $A{\left(t\right)}_1=\frac{N_{t+1}-N_t}{2}+\frac{N_{t+2}-N_{t+1}}{2}+(N_{t+2}-N_{t+1})$; $A{\left(t\right)}_2=\frac{N_{t+1}-N_t}{2}$, $A{\left(t\right)}_1$ and $A{\left(t\right)}_2$ are the respective ITAs for case one and two.
CTB: City Block	$CTB(t)={\displaystyle \sum _{i=1}^m}|N_{t+i-1}-{\mu }_i|$ ${\mu }_i$ was NDVI average value of the ith time step of reference NDVI time series (the same below).
SED: Standardized Euclidian Distance	$SED(t)=\sqrt{{\displaystyle \sum _{i=1}^m}\frac{{(N_{t+i-1}-{\mu }_i)}^2}{{{\sigma }_i}^2}}$
BE: Bounding Envelope	$BE(t)=\sqrt{\frac{1}{m}{\displaystyle \sum _{i=1}^m}\Delta {N_{t+i-1}}^2}$; $\Delta N_{t+i-1}=N_{t+i-1}-U{B}_i$, if $N_{t+i-1}\ge U{B}_i$; $\Delta N_{t+i-1}=N_{t+i-1}-L{B}_i$, if $N_{t+i-1}\le L{B}_i$; $\Delta N_{t+i-1}-0$, elseif

2.5. Validation of Eucalyptus Classification Results

The comparison of the ITA to the other three algorithms was carried out using a UAV photograph (see Section 2.4.1). The UAV photograph had a very high resolution for validation of the eucalyptus classification results, but its limited area, 1.2 × 1.5 km, was insufficient to allow for a performance assessment of the ITA methodology. Further validation on a larger sub-regional scale and over more years was therefore necessary, so we downloaded GF-1 Particle Measuring System 2 (PMS2) data [34] acquired on 25 December 2014 for further validation. This image had a very high spatial resolution of 8 m per pixel. As representative sub-regions, two areas of 16 × 16 km were selected as validation sub-regions. In these sub-regions, other man-made forests (such as bamboo and fruit trees) and natural forests existed, making identification of eucalyptus plantations difficult. In addition, ground investigation was carried out in the region and for the month of image acquisition, dense control points were collected.

Compared to TM, ETM 7+, and HJ data, the spatial resolution of the GF-1 data was much higher, which made it possible to distinguish eucalyptus from other features. Based on the control points, we employed a supervision classification to identify eucalyptus in the image. The control points were randomly divided into two groups, with one being used as training samples and the other for the classification validation. The maximum likelihood method was chosen as the most suitable decision algorithm. The overall accuracy of the HJ-1 image classification is 91.67%, with a Kappa coefficient of up to 0.78, which indicates a “very good” classification level. Thus, using the eucalyptus map created from the HJ-1 image classification, the eucalyptus classification using the ITA methodology could be validated.

3. Results and Discussion

3.1. Comparison of the Four Different Classification Algorithms

3.1.1. Determination of two Threshold Coefficients

Following the approach of Boschetti et al. [35], we selected the eucalyptus classification distance result for the year 2009 in order to adjust the two threshold coefficients (T1 and T2) for the ITA algorithm as well as for the three other algorithms described above. For comparison, we extracted the eucalyptus trees planted during September 2008 and October 2009 from the eucalyptus map using the mosaic photograph.

The two curves shown in Figure 7 clearly display the changing trends of the four indices used for the ITA classification results. Uniquely in this study, two threshold coefficients needed to be adjusted. To understand the impact of these coefficients on the classification results better, we used the control variable method: we adjusted one threshold coefficient while keeping the other fixed and computed a loop until all potential values for T1 and T2 (T1 ranging from 0 to 1 and T2 ranging from 0 to 0.2) had been tried. Finally, T1 and T2 were determined to be 0.2 and 0.075, respectively, when the ITA classification was optimized, not only for relatively high producer–user accuracy and low commission–omission errors but also for an acceptable balance between these parameters.

Figure 7. ITA producer–user accuracy and commission–omission error trends with T1 and T2 ranging within their potential values. The two curves were modified using the value points. When one threshold coefficient was fixed and the other increased, producer accuracy and commission error increased, while user accuracy and omission error decreased. The two curves intersect at two points, at the optimal values for T1 and T2 and at their end points.

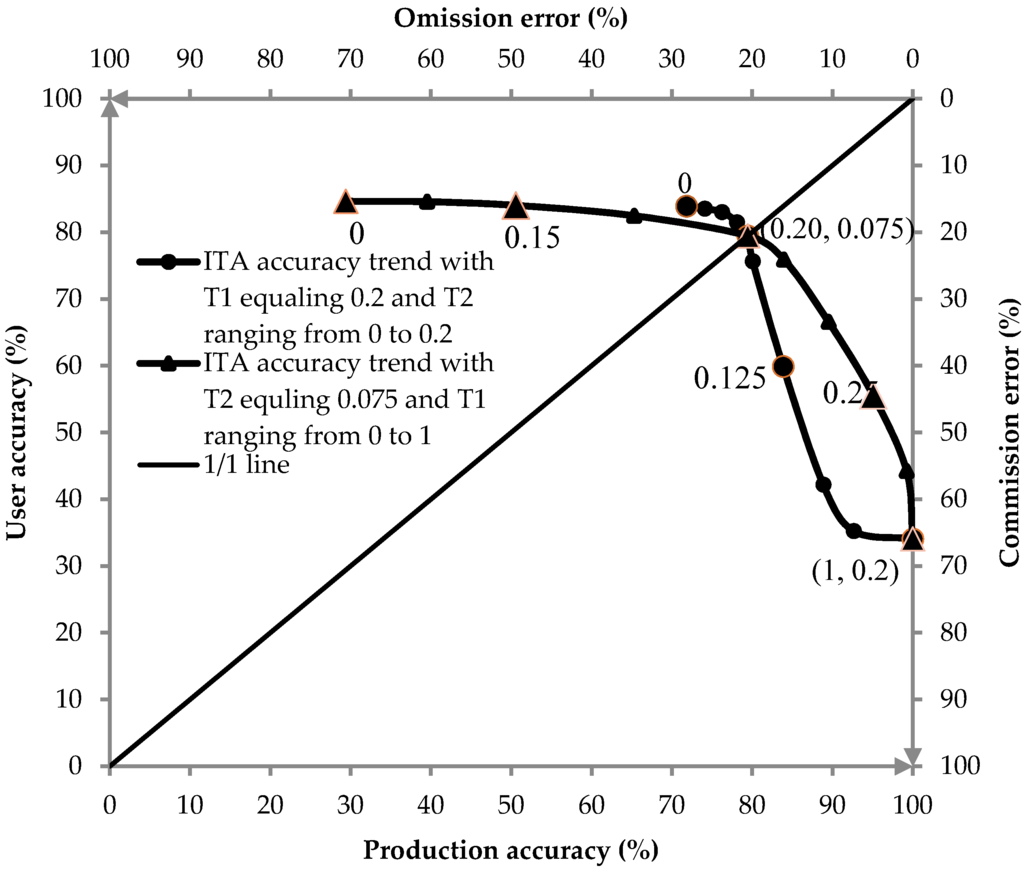
Figure 7. ITA producer–user accuracy and commission–omission error trends with T1 and T2 ranging within their potential values. The two curves were modified using the value points. When one threshold coefficient was fixed and the other increased, producer accuracy and commission error increased, while user accuracy and omission error decreased. The two curves intersect at two points, at the optimal values for T1 and T2 and at their end points.

3.1.2. Comparison of Our Results with the Other Classification Algorithms

The commission–omission error method was adopted to determine the threshold coefficients for the three other discriminant functions. As shown in Table 4, among the three algorithms, the BE performed best but still had a quite low producer–user accuracy of less than 60%. The other two algorithms (SED and CTB), yielded similar results with a producer–user accuracy less than 50%. The ITA methodology performed much better in classifying eucalyptus in this sub-region.

Table 4. Confusion matrix between classification results and interpreted photographs using the four discriminant functions and their optimal threshold coefficients.

		Truth Class (from the Mosaic Photograph)		User Accuracy
		Eucalyptus Pixels (Case 1/Case 2)	Not-Eucalyptus Pixels (Case 1/Case 2)
ITA discriminant function	Eucalyptus pixels	126/106	35/25	79%
	Not-eucalyptus pixels	60	926	94%
	Producer accuracy	79%	94%	Overall acc. 91%
BE discriminant function	Eucalyptus pixels	169	123	58%
	Not-eucalyptus pixels	123	863	88%
	Producer accuracy	58%	88%	Overall acc. 81%
SED discriminant function	Eucalyptus pixels	145	147	50%
	Not-eucalyptus pixels	147	839	85%
	Producer accuracy	50%	85%	Overall acc. 77%
CTB discriminant function	Eucalyptus pixels	143	149	49%
	Not-eucalyptus pixels	149	837	85%
	Producer accuracy	49%	85%	Overall acc. 77%

Table 4. Confusion matrix between classification results and interpreted photographs using the four discriminant functions and their optimal threshold coefficients.

		Truth Class (from the Mosaic Photograph)		User Accuracy
		Eucalyptus Pixels (Case 1/Case 2)	Not-Eucalyptus Pixels (Case 1/Case 2)
ITA discriminant function	Eucalyptus pixels	126/106	35/25	79%
	Not-eucalyptus pixels	60	926	94%
	Producer accuracy	79%	94%	Overall acc. 91%
BE discriminant function	Eucalyptus pixels	169	123	58%
	Not-eucalyptus pixels	123	863	88%
	Producer accuracy	58%	88%	Overall acc. 81%
SED discriminant function	Eucalyptus pixels	145	147	50%
	Not-eucalyptus pixels	147	839	85%
	Producer accuracy	50%	85%	Overall acc. 77%
CTB discriminant function	Eucalyptus pixels	143	149	49%
	Not-eucalyptus pixels	149	837	85%
	Producer accuracy	49%	85%	Overall acc. 77%

3.2. Further Validation of the Classification Results Using a High-Resolution GF Image

Although it was determined that the ITA methodology performed best in the region of mosaic photograph, it could not yet be concluded that the ITA methodology was suitable for classifying eucalyptus at small scales with a spatial resolution of 30 m and a temporal resolution of one year. Further validation in different regions and different years was still necessary.

A GF-1 PMS2 image was acquired on 25 December 2014, and two areas of 16 × 16 km were selected as sub-regions (A and B) for further validation. Eucalyptus plantations normally have a normal growing period of five to six years, so it could be assumed that the eucalyptus class shown in the GF image from 2014 had been growing for the past five to six years, and that eucalyptus planted in 2014 had not grown enough to register in the image. With these considerations in mind, we added the classified eucalyptus plantations planted from 2009, 2010, 2011, 2012 and 2013 and compared the result with the eucalyptus class derived from the GF image of 2014. The comparison is shown in Table 5 and Figure 8. Both the accuracies for both producers and users in the two sub-regions are between 75 and 80%, which is close to the values discussed in Section 3.1.2. The Kappa coefficients were 0.66 and 0.70, indicating a “good” level of classification. From Figure 8b,c, it is clear that the majority of classification errors occur at the borders of eucalyptus plantations. Because these border areas contain different features, the classification there is more likely to be effected by mixed pixels.

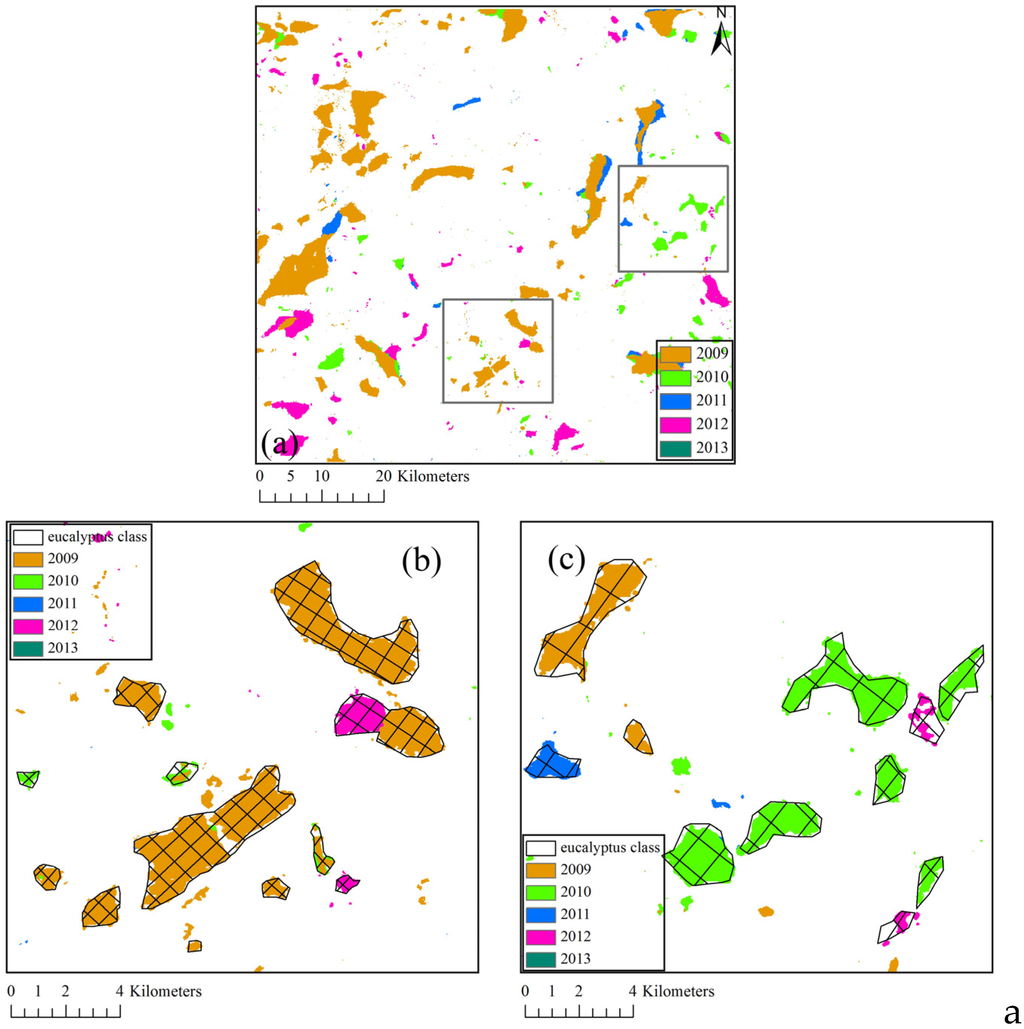
Figure 8. Further validation of the classification results using the GF-1 PMS2 image. (a) Eucalyptus map, generated by combining eucalyptus classifications from 2009 to 2013. Squares indicate positions of two sub-regions selected for validation; (b) and (c) show a comparison of classification results for sub-regions A and B and the eucalyptus class determined from the GF-1 image. The cross-hatching represents the eucalyptus class from GF-1 image.

Figure 8. Further validation of the classification results using the GF-1 PMS2 image. (a) Eucalyptus map, generated by combining eucalyptus classifications from 2009 to 2013. Squares indicate positions of two sub-regions selected for validation; (b) and (c) show a comparison of classification results for sub-regions A and B and the eucalyptus class determined from the GF-1 image. The cross-hatching represents the eucalyptus class from GF-1 image.

Table 5. Confusion matrix for classification results and the truth class interpreted from the GF-1 Particle Measuring System 2 (PMS2) image. The Kappa coefficients for sub-regions A and B are 0.66 and 0.70, respectively.

		Truth Class (Interpreted from GF-1 Image)		User Accuracy
		Eucalyptus Pixels	Not-Eucalyptus Pixels
Classification result of sub-region A	Eucalyptus pixels	62636	20198	75.62%
	Not-eucalyptus pixels	19141	182114	90.49%
	Producer accuracy	76.59%	90.02%	Overall acc 86.15%
Classification result of sub-region B	Eucalyptus pixels	51319	14756	77.67%
	Not-eucalyptus pixels	15623	202391	92.83%
	Producer accuracy	76.66%	93.20%	Overall acc.89.31%

Table 5. Confusion matrix for classification results and the truth class interpreted from the GF-1 Particle Measuring System 2 (PMS2) image. The Kappa coefficients for sub-regions A and B are 0.66 and 0.70, respectively.

		Truth Class (Interpreted from GF-1 Image)		User Accuracy
		Eucalyptus Pixels	Not-Eucalyptus Pixels
Classification result of sub-region A	Eucalyptus pixels	62636	20198	75.62%
	Not-eucalyptus pixels	19141	182114	90.49%
	Producer accuracy	76.59%	90.02%	Overall acc 86.15%
Classification result of sub-region B	Eucalyptus pixels	51319	14756	77.67%
	Not-eucalyptus pixels	15623	202391	92.83%
	Producer accuracy	76.66%	93.20%	Overall acc.89.31%

3.3. Estimation of the Eucalyptus Planting Date

The temporal resolution of the NDVI time series used in this study is about one year, so the estimated planting date of eucalyptus plantations cannot be accurate to the month. As explained in Section 2.3.2, differing EATs result in two different cases of low ebb. If Case 1 applies, the EAT occurred shortly after the planting of the eucalyptus; if Case 2 applies, the EAT occurred long after the eucalyptus was planted. In other words, the planting date was always some time earlier than the EAT. Since the EAT was known, then the accurate “some time” (delta T) would be sufficient to determine the planting date. Here we assigned delta T an initial value, three months for Case 1 and nine months for Case 2. Next, the planting dates were calculated according to Equation (3):

$$T_{plan}=T_{EAT}-\Delta t_{1,2},$$

(3)

where T_plan was the estimated planting date of eucalyptus, T_EAT was the EAT of the pixel in a certain rotation and Δt_1,2 was the delta T.

As discussed in Section 2.3.2, among the 270 pixels, 135 pixels were purely randomly selected to build the reference NDVI time series sub-sequence, and the remaining 135 were used to estimate the eucalyptus planting dates, as shown in Figure 9. The slope of the linear regression is 0.9880 and ${\mathrm{R}}^2$ reaches 94.0%. The greatest difference between estimated and real planting dates is seven months, and the average estimated planting date was only 48 days later than the actual date. To improve the estimation accuracy, we performed a correction by adjusting the delta T (three months and nine months) by adding 48 days. After the correction, the RMSE of the planting date estimation decreased to 95 days. With a temporal resolution of one year, such an estimation accuracy is ideal.

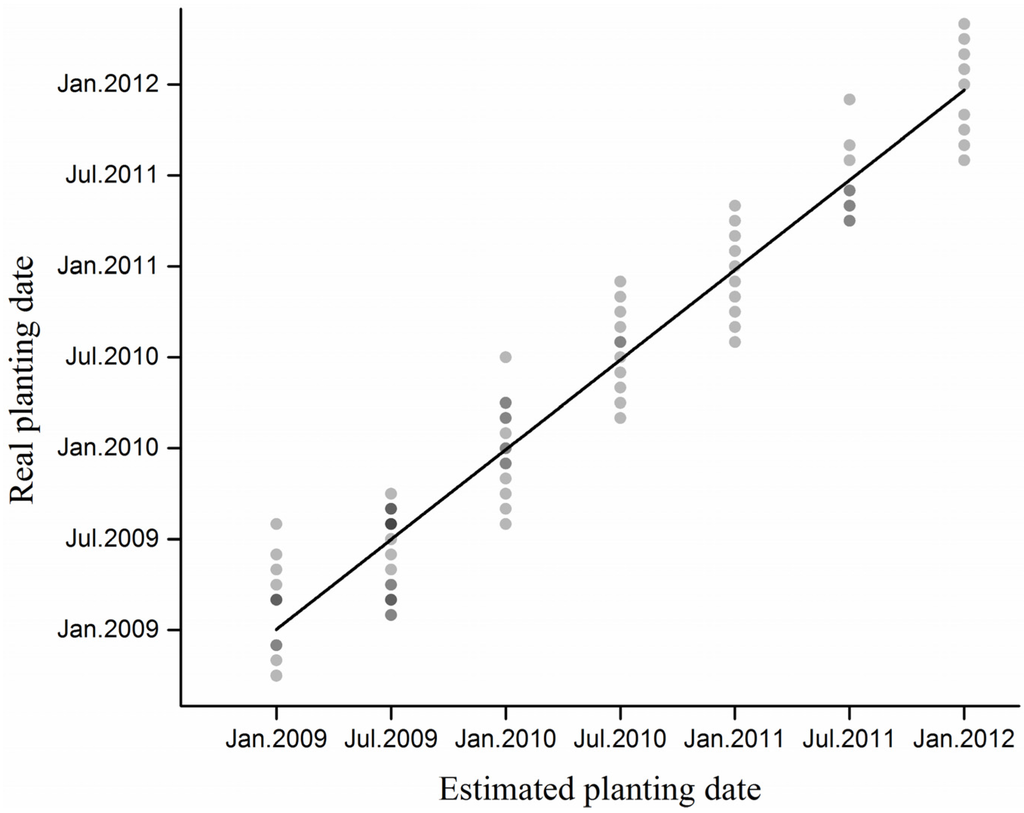
Figure 9. Validation of estimated eucalyptus planting dates. Estimated planting dates were calculated by pushing the EAT forward by delta T, so that the points form parallel lines and the different tones of points represent numbers of points (samples).

Figure 9. Validation of estimated eucalyptus planting dates. Estimated planting dates were calculated by pushing the EAT forward by delta T, so that the points form parallel lines and the different tones of points represent numbers of points (samples).

3.4. Eucalyptus Plantation Map Classified with the ITA Algorithm

After the eucalyptus plantation distribution and its planting date were determined with the ITA algorithm, the final map could be drawn. Figure 10 shows the eucalyptus plantation distribution in the study area over the past 14 years. On the basis of this distribution, the planting area was calculated. As shown in Figure 11, from 2000 to 2005, several increases and decreases are indicated, but the area remained relatively stable. Beginning in 2006, eucalyptus plantations increased gradually and they peaked in 2008. After 2008, the area returned to pre-2000 planting levels.

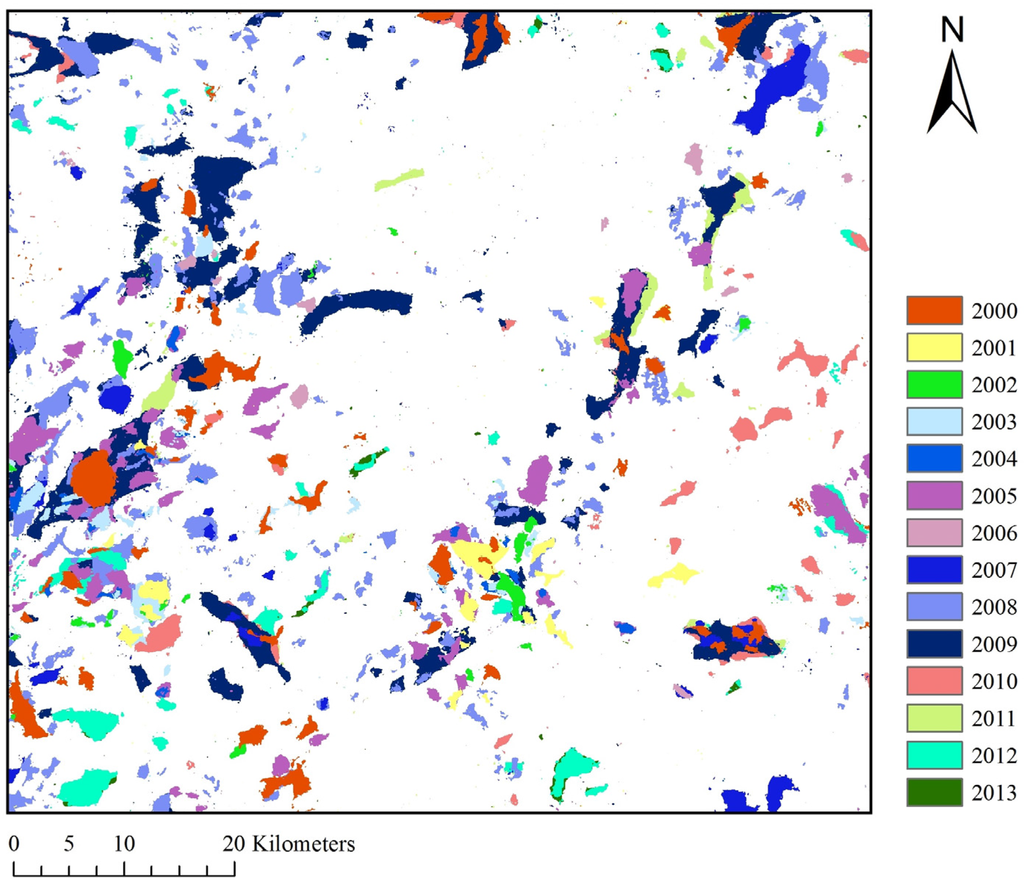
Figure 10. Eucalyptus plantation distribution in the study area over the past 14 years shown as a combination of classified eucalyptus plantations for 2000 to 2013.

Figure 10. Eucalyptus plantation distribution in the study area over the past 14 years shown as a combination of classified eucalyptus plantations for 2000 to 2013.

Figure 11. Variation of eucalyptus planting area over the past 14 years.

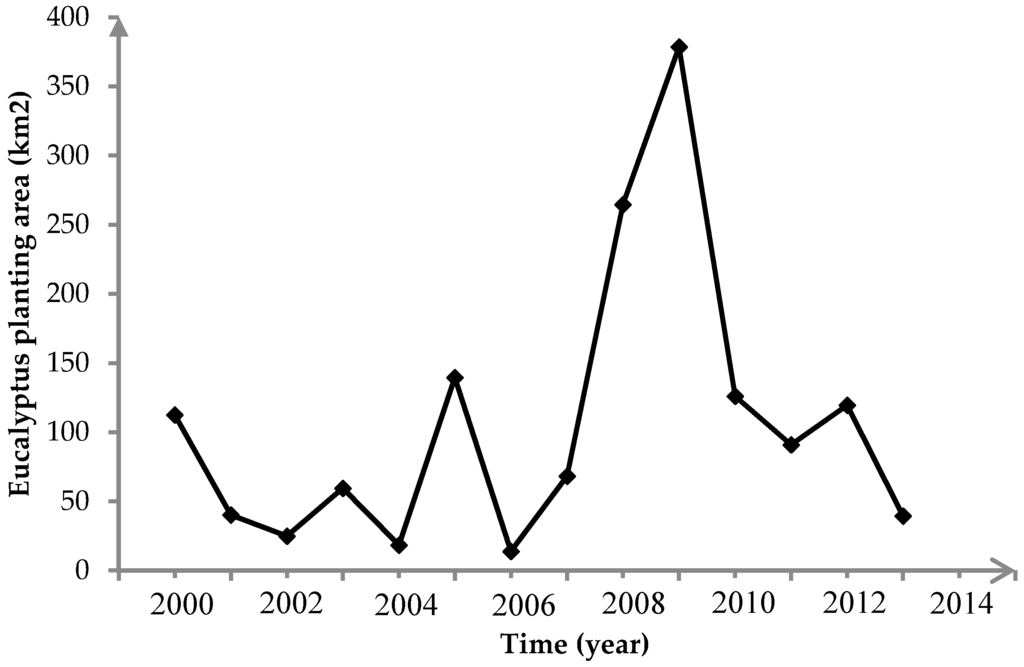
Figure 11. Variation of eucalyptus planting area over the past 14 years.

3.5. Assessment of Eucalyptus Classification

For this study of eucalyptus growing conditions at the county scale, we adopted images with high spatial resolution of 30 m, but with coarse temporal resolution of about one year. Given this temporal resolution, a successive NDVI time series (e.g., with a temporal resolution of one month) could not be acquired, for which reason traditional analytical methods (e.g., BE, SED, CTB) were rendered ineffective. We therefore created the ITA methodology as a way to analyze the characteristics of the NDVI time series. As shown in Section 3.1.1, this methodology has producer and user accuracies of 79%, which are relatively high compared with the other analytical methods. During an interval of up to one year in the NDVI time series, the planting date can be positioned at any point, resulting in a significant difference in the NDVI time series sub-sequence during the growing period. Accordingly, for the BE, SED and CTB methods, large threshold coefficients are needed to classify actual eucalyptus plantations as eucalyptus pixels, and these coefficients bring with them a high commission error. By contrast, the triangle areas generated by our method remained stable and relatively low threshold coefficients are needed for classification, so high commission errors are avoided.

Even though the ITA methodology performed better in classifying eucalyptus plantations at high spatial and coarse temporal resolution, accuracy is still limited for the following reasons:

(1)

Errors due to different data sources. When building the NDVI time series, we used NDVI from ETM 7+/TM 5 from 2000 to 2009 and NDVI from HJ-1A/B from 2010 to 2014. Although the difference of NDVI from these three sensors was so small (as discussed in Section 2.2) that a process of normalizing NDVI was left out, the classification accuracy of 2008, 2009, 2010 and 2011 (the biggest length of the reference NDVI time series sub-sequence was three time steps) was likely somewhat lower due to the lack of normalization between sensors. For validation, we used the UAV photographs and the GF-1 image. Although all images were pre-processed, many errors, especially those caused by different flight angles and attitudes of satellites could not be avoided [36,37].

(2)

Errors due to mixed pixels. In the application of remote sensing data, one pixel necessarily includes information from many different features in addition to the one of interest [6,38]. For example, on the borders of eucalyptus plantations, a eucalyptus pixel may be classified as a not-eucalyptus pixel because of interference from extraneous features (water, bamboo, etc.), thereby decreasing accuracy in these areas. As shown in Figure 8, within the eucalyptus class, numerous vacant regions existed, where the coverage of eucalyptus plantations was low and even some bare soil was exposed, resulting in mixed pixels. Therefore, although the spatial resolution was high in this study, errors from the effect of mixed pixels could not be avoided.

(3)

Errors caused by the determination of the reference NDVI time series sub-sequence and threshold coefficients. The reference NDVI time series sub-sequence and threshold coefficients are the basis of the classification algorithms. When determining these coefficients, we considered as many significant factors as we could to build a representative reference time series. However, artificial and systemic factors still existed. We selected a mosaic photograph region to determine threshold coefficients and worked to balance commission and omission errors. Nevertheless, as further validation showed, there remained a small difference between these errors. Our study area was relatively small, so the same threshold coefficients could be shared. Larger study areas will require additional investigations and the adjustment of threshold coefficients for different sub-regions.

3.6. Potential of the ITA Methodology

3.6.1. Potential Improvement of the ITA Methodology

As shown above, with different EATs for eucalyptus growing periods, there are two different growing periods displayed in the NDVI time series, specifically one-year-long and two-year-long growing periods. Although the triangle area determined by the ITA remains relatively constant, it still varies to a small degree owing to the differing EATs. For example, a triangle area generated when the EAT occurs two months after the planting date is likely to be different from one created when the EAT occurs six months later, although both would indicate the same case (Case 1). If the change of the triangle area were to be studied on the basis of more samples and if the cases could be classified into more than two types, the estimation accuracy of the planting date would significantly improve.

The collection of at least two images per year, as originally planned, would result in a more accurate description of the growing period of eucalyptus plantations than the one that we were actually able to generate. However, because of image deficiencies and cloud coverage in some years, the temporal resolution available for this study was only up to one year. Our findings suggest that, if the temporal resolution were increased, the NDVI time series would show more details, which would improve the accuracy of the classification and of the estimation of the planting date.

3.6.2. Application Potential of the ITA Methodology

The biggest advantage of the images used in this study was the high spatial resolution, which made it possible to estimate the eucalyptus plantation area at the scale of counties. As mentioned in the introduction, eucalyptus cultivation in southeast China has been expanding rapidly in recent years as a source of wood. With the ability to estimate planting dates, the extent of eucalyptus expansion can be determined, including expansion areas and dates. Accordingly, a “gain” or “loss” condition for eucalyptus plantations could be mapped out, which would be of great benefit for the eucalyptus monitoring and environmental protection that are the concerns of governmental departments and research institutions.

4. Conclusions

The goal of this study was to classify eucalyptus plantations at the fine scale of counties in three cities of Guangdong Province, China, using multiple data sources (TM 5, ETM 7+, and HJ images), with high spatial resolution of 30 m and low temporal resolution of one year over the past 15 years. Because the NDVI time series was discontinuous, we created the ITA discriminant function to classify eucalyptus plantations, and this algorithm out-performed the BE, SED, and CTB discriminant functions. In a validation using a mosaic high-resolution photograph, the producer and user accuracies reached up to 79% and further validation, using an interpreted high-resolution GF-1 PMS2 image, also indicated good stability. Based on this classification, we were able to estimate the eucalyptus planting date, with an accuracy of three months, which is acceptable considering the coarse temporal resolution of one year. To be true, classification accuracy remains limited owing to errors that arise from multiple data sources, mixed pixels, and other artifacts. Nevertheless, considering the profound effect of eucalyptus expansion on the ecosystem, these classification results could be of great significance for eucalyptus monitoring and ecosystem protection. We suggest that such a methodology may also be suitable for small-scale classification of other short-rotation plantations, though more validation work needs to be done.