Analysis of the Effects of Drought on Vegetation Cover in a Mediterranean Region through the Use of SPOT-VGT and TERRA-MODIS Long Time Series
Abstract
:1. Introduction
2. Database
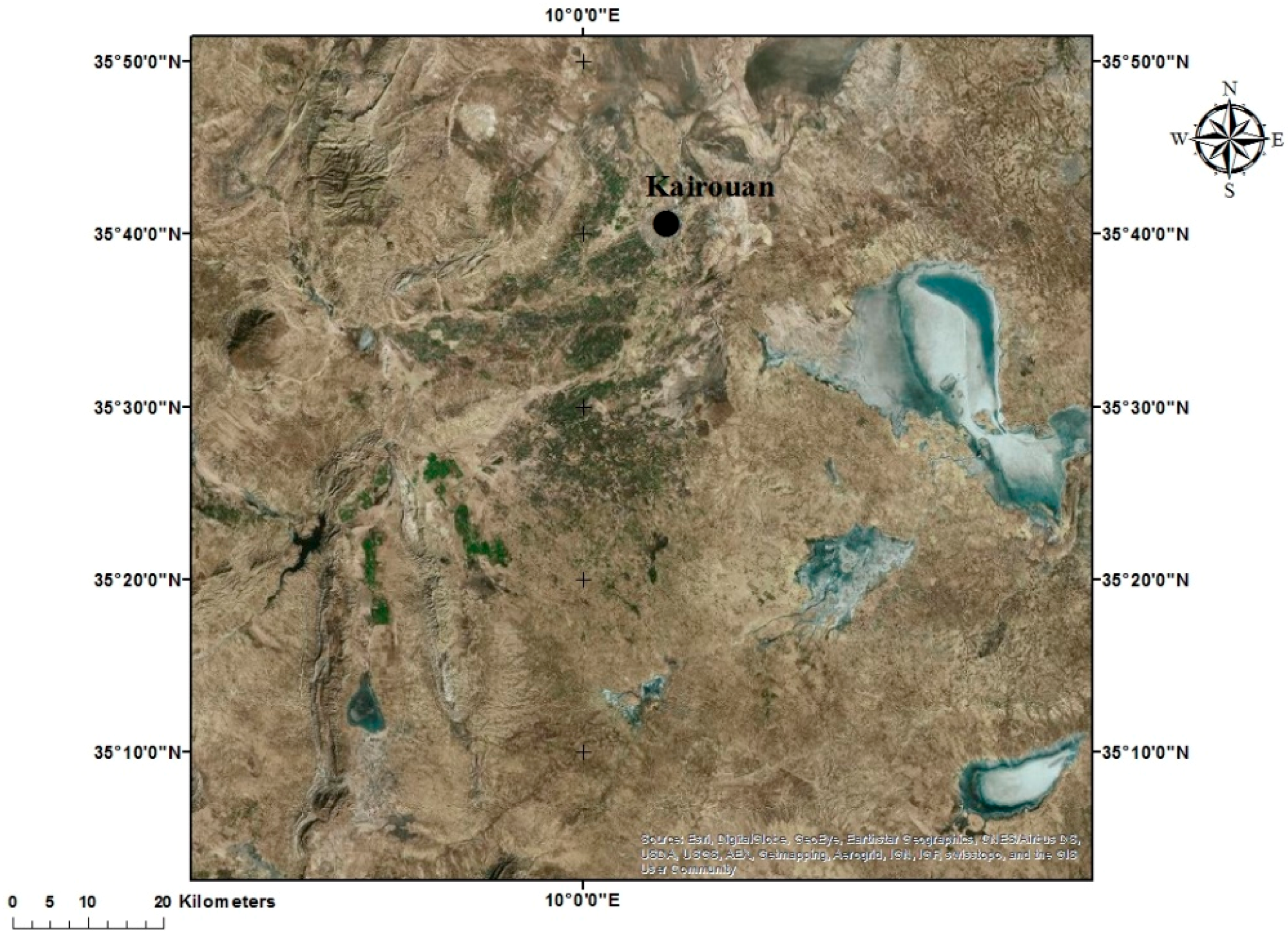
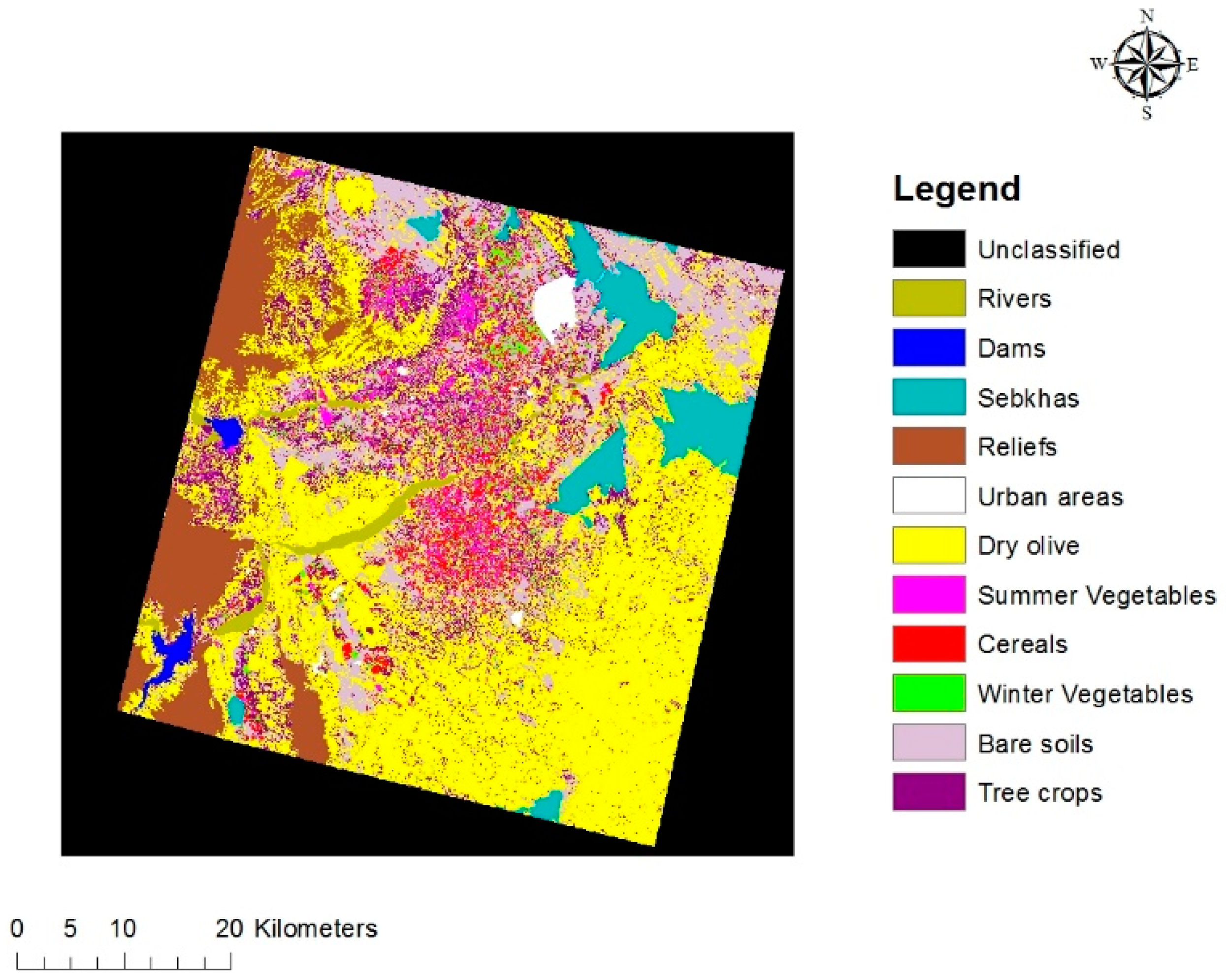
2.1. Studied Site
2.2. Satellite Data
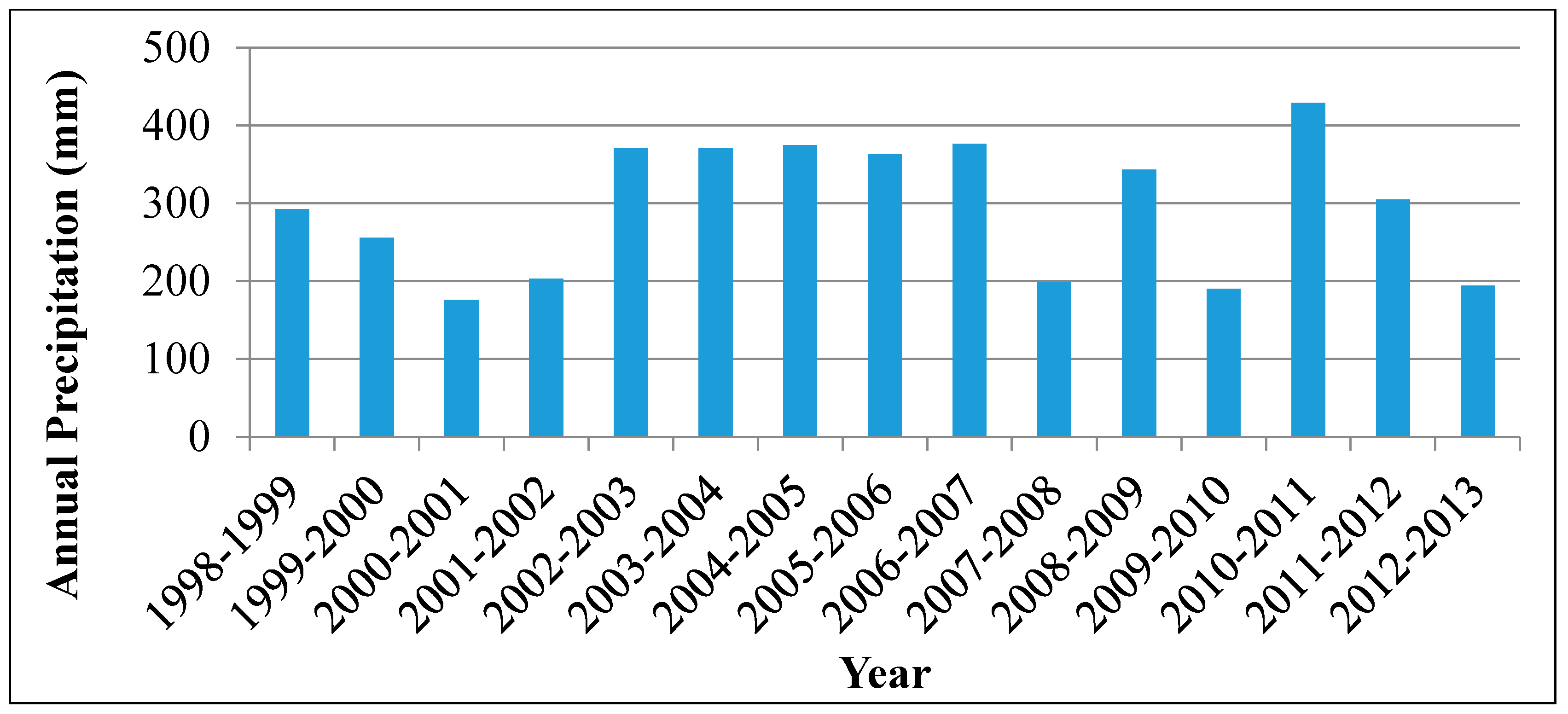
2.3. Precipitation
2.4. NDVI Temporal Series
3. Analysis of Vegetation Dynamics with SPOT-VGT and TERRA-MODIS NDVI Products
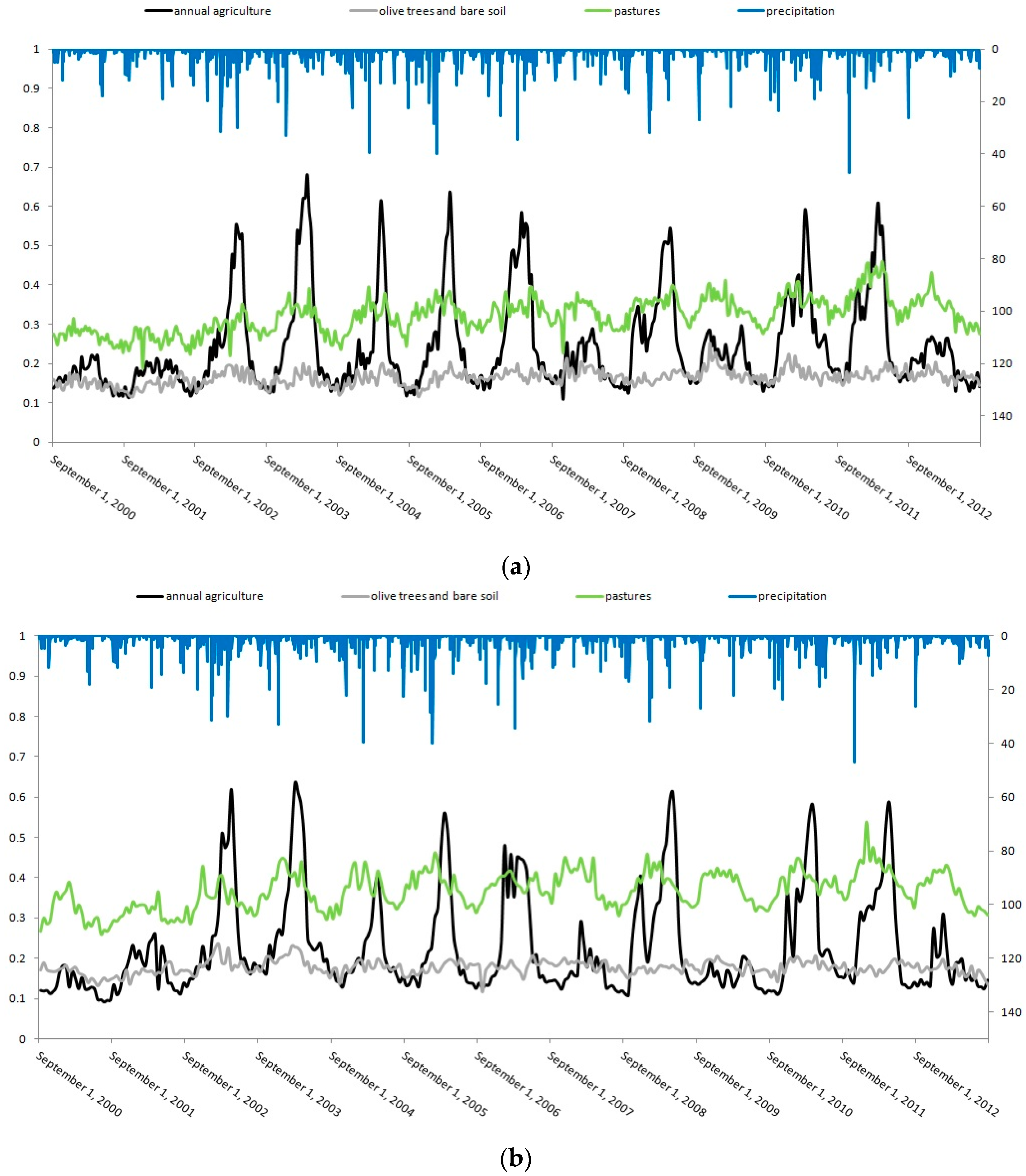
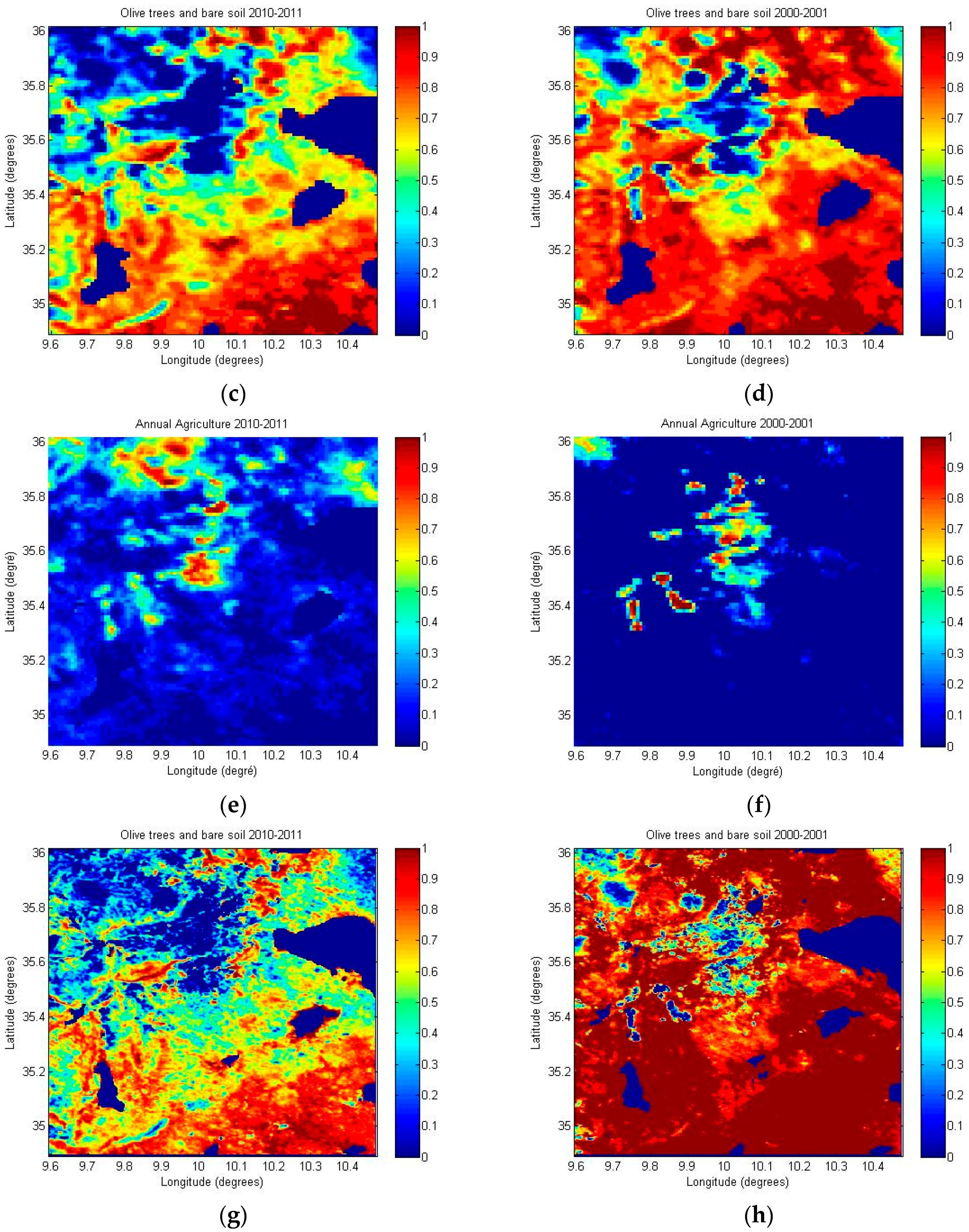
3.1. Temporal Dynamics of Land Use Mapping
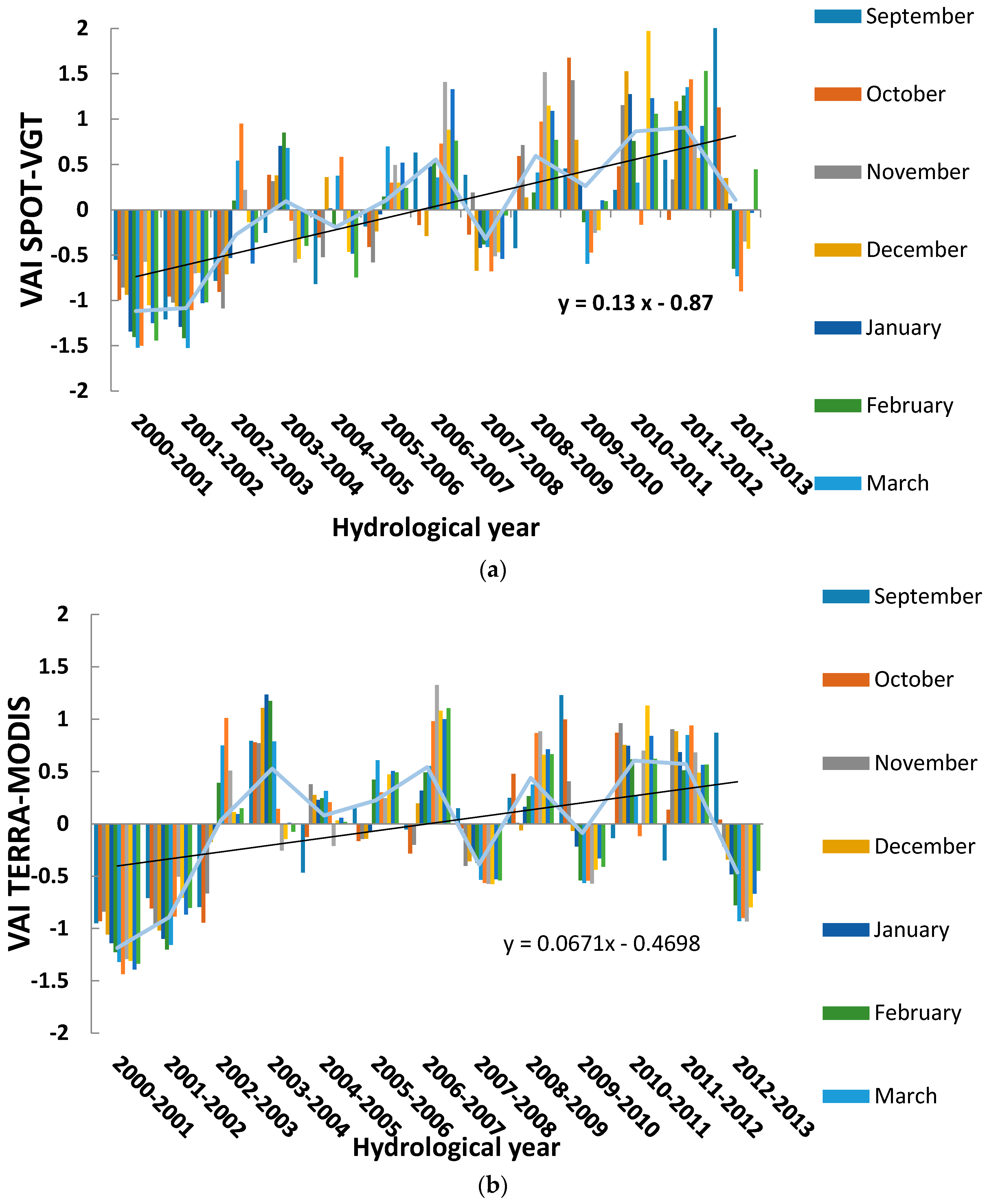
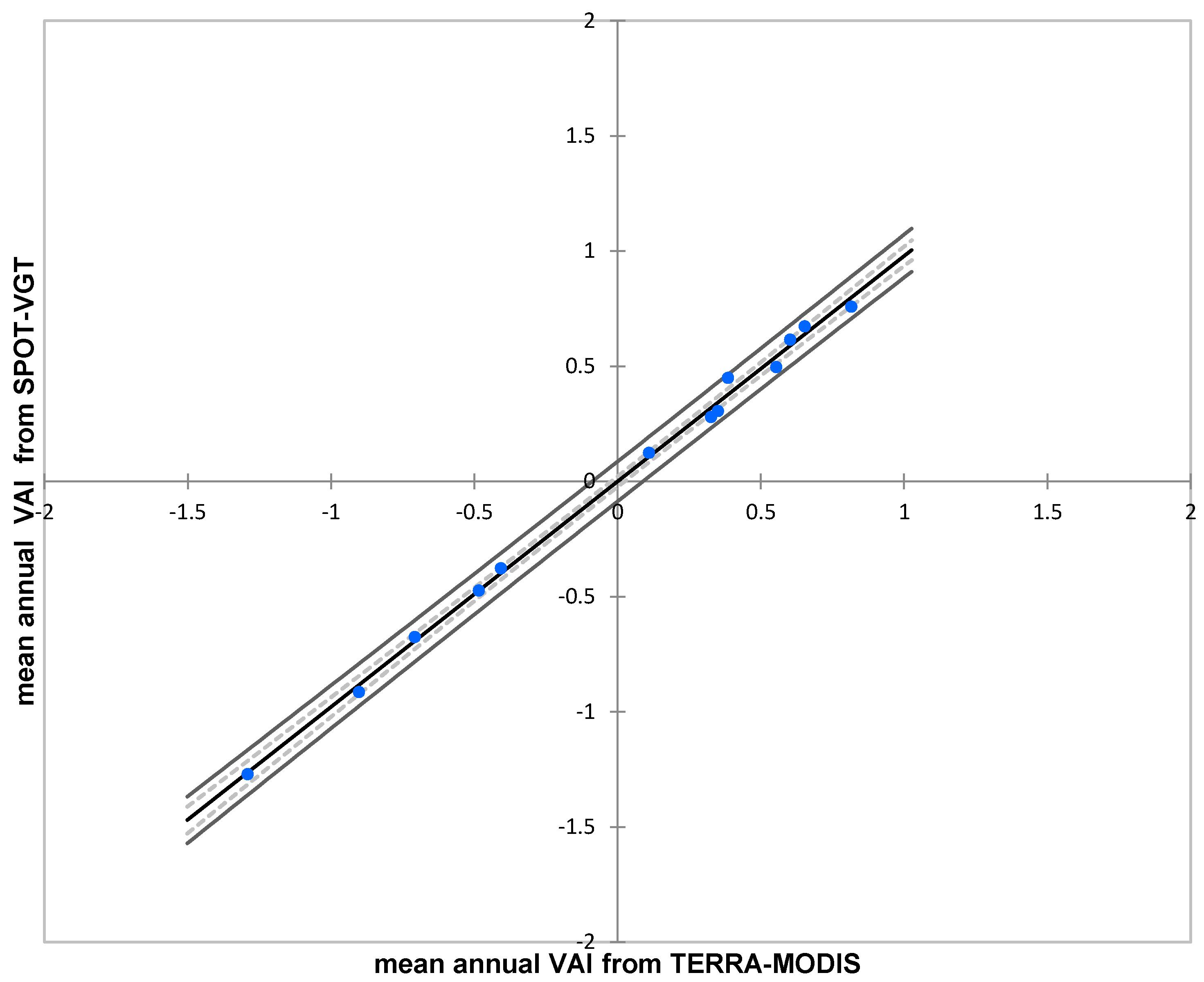
3.2. Discussion of NDVI Anomalies with TERRA-MODIS and SPOT-VGT Data
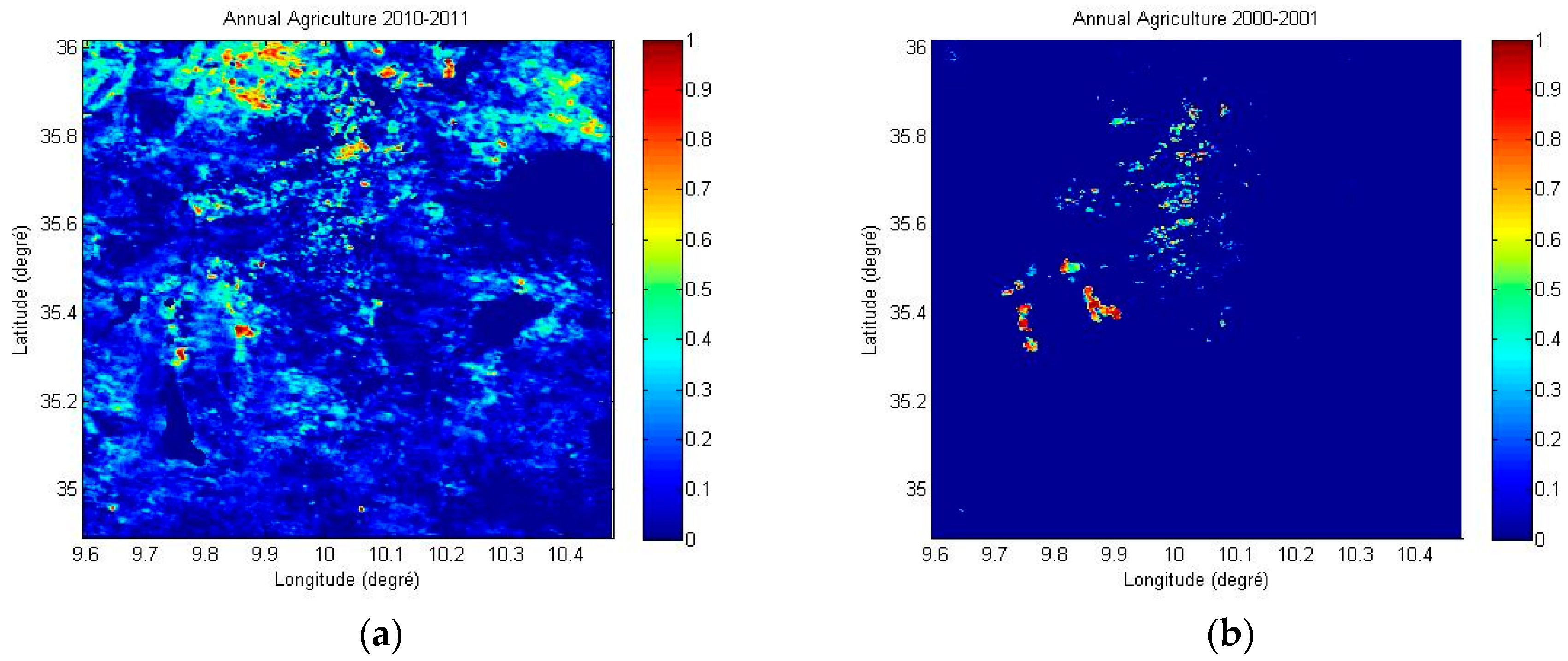
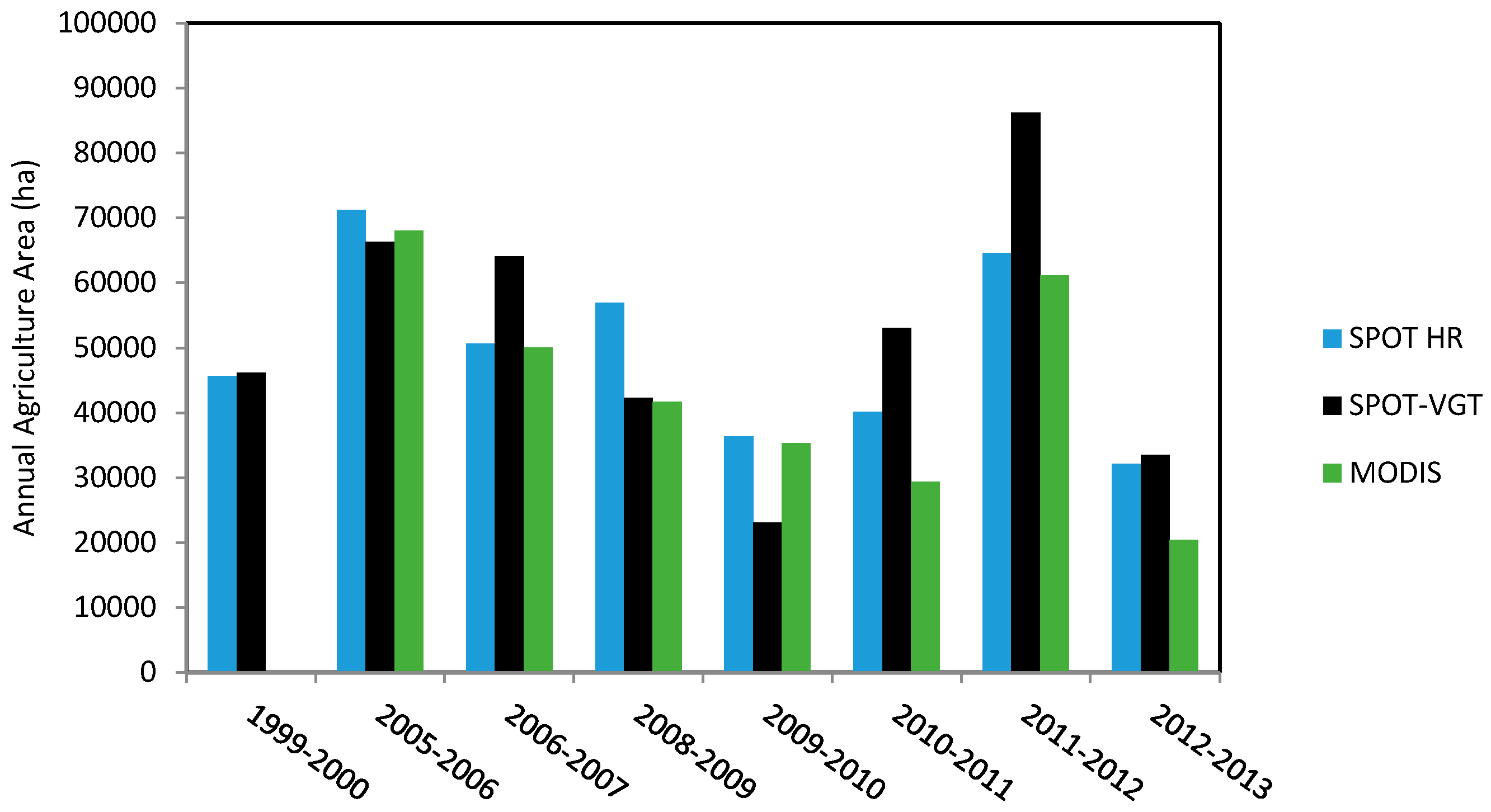
4. Dynamics of the Area Used for Annual Agriculture
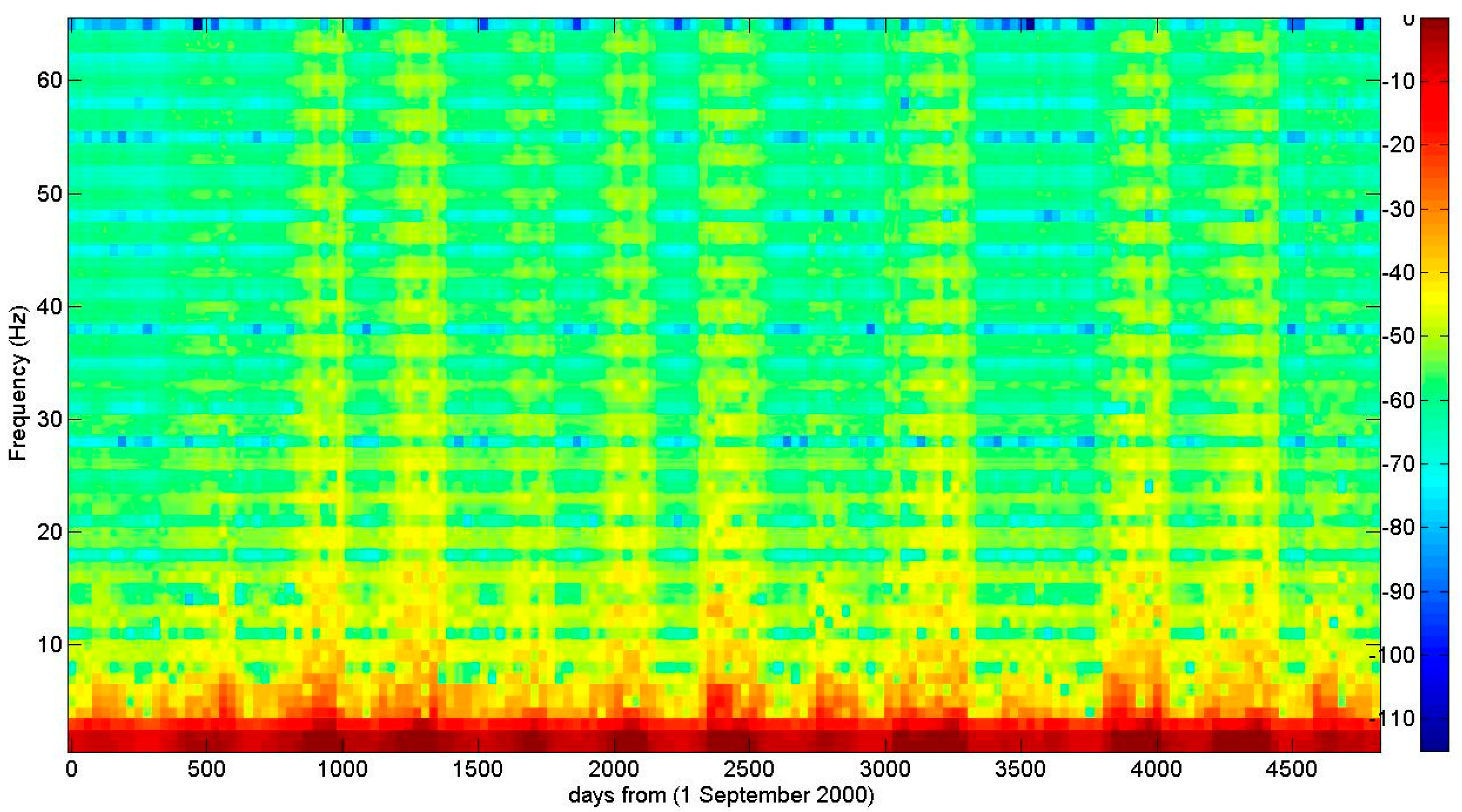
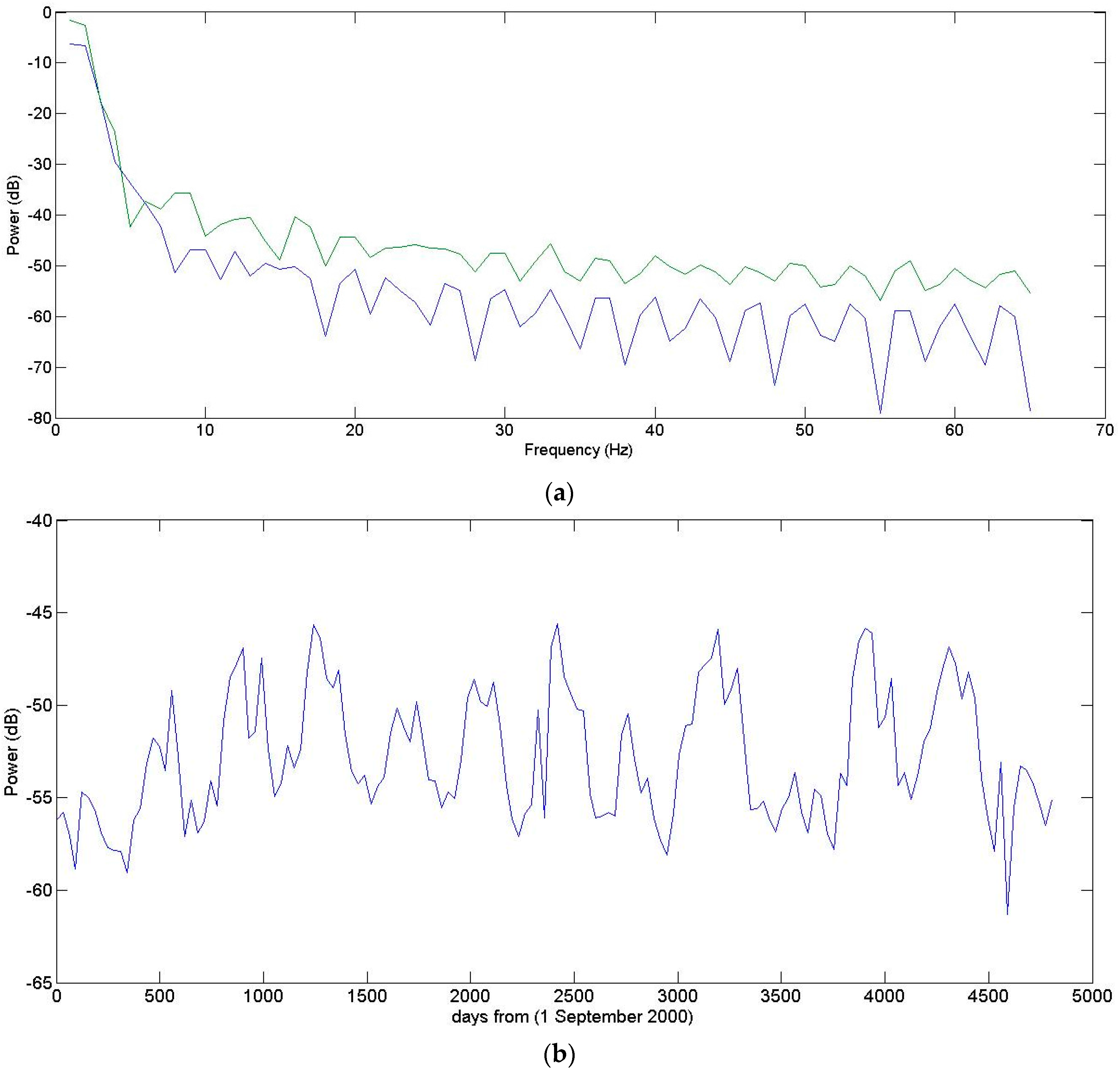
4.1. Analysis of the Vegetation Using a Windowed Fourier Transform
4.2. Monitoring of Bare Soils in Agricultural Areas
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Heim, R.R. A review of twentieth-century drought indices used in the United States. Bull. Am. Meteorol. Soc. 2002, 84, 1149–1165. [Google Scholar]
- Quiring, S.M. Developing objective operational definitions for monitoring drought. J. Appl. Meteorol. Climatol. 2009, 48, 1217–1229. [Google Scholar] [CrossRef]
- Gommes, R.; Petrassi, F. Rainfall variability and drought in Sub-Saharan Africa since 1960. In Agro-Meteorology Series Working; Version 9; Food and Agriculture Organization: Rome, Italy, 1994. [Google Scholar]
- Vicente-Serrano, S.M.; Beguería, S.; López-Moreno, J.I. A Multi-scalar drought index sensitive to global warming: The standardized precipitation evapotranspiration index—SPEI. J. Clim. 2010, 23, 1696–1718. [Google Scholar] [CrossRef]
- Palmer, W.C. Meteorologic Drought; Research Paper; U.S. Department of Commerce, Weather Bureau: Washington, DC, USA, 1965.
- McKee, T.B.; Doesken, N.J.; Kleist, J. The relationship of drought frequency and duration to time scales. In Proceedings of the 8th Conference on Applied Climatology of American Meteorological Society, Anaheim, CA, USA, 7–22 January 1993.
- McKee, T.B.; Doesken, N.J.; Kleist, J. Drought monitoring with multiple time scales. In Proceedings of the 9th Conference on Applied Climatology of American Meteorological Society, Dallas, TX, USA, 15–20 January 1995.
- Kogan, F.N. Application of vegetation index and brightness temperature for drought detection. Adv. Space Res. 1995, 15, 91–100. [Google Scholar] [CrossRef]
- Ji, L.; Peters, A. Assessing vegetation response to drought in the northern Great Plains using vegetation and drought indices. Remote Sens. Environ. 2003, 87, 85–89. [Google Scholar] [CrossRef]
- Singh, R.P.; Roy, S.; Kogan, F.N. Vegetation and temperature condition indices from NOAA AVHRR data for drought monitoring over India. Int. J. Remote Sens. 2003, 24, 4393–4402. [Google Scholar] [CrossRef]
- Amri, R.; Zribi, M.; Lili-Chabaane, Z.; Wagner, W.; Hauesner, S. Analysis of ASCAT-C band scatterometer estimations derived over a semi-arid region. IEEE Trans. Geosic. Remote Sens. 2012, 50, 2630–2638. [Google Scholar] [CrossRef]
- Kogan, F.N. Global drought watch from space. Bull. Am. Meteorol. Soc. 1997, 78, 621–636. [Google Scholar] [CrossRef]
- Gu, Y.; Brown, J.F.; Verdin, J.P.; Wardlow, B. A five-year analysis of MODIS NDVI and NDWI for grassland drought assessment over the central Great Plains of the United States. Geophys. Res. Lett. 2007, 34. [Google Scholar] [CrossRef]
- Amri, R.; Zribi, M.; Duchemin, B.; Lili-Chabaane, Z.; Gruhier, C.; Chebouni, A. Analysis of vegetation behavior in a semi-arid region, using SPOT-VEGETATION NDVI data. Remote Sens. 2011, 3, 2568–2590. [Google Scholar] [CrossRef]
- Paris Anguela, T.; Zribi, M.; Habets, F.; Hasenauer, S.; Loumagne, C. Analysis of surface and root soil moisture dynamics with ERS scatterometer and the hydrometeorological model SAFRAN-ISBA-MODCOU at Grand Morin watershed (France). Hydrol. Earth Syst. Sci. 2008, 5, 1903–1926. [Google Scholar] [CrossRef]
- Albergel, C.; Zakharova, E.; Calvet, J.C.; Zribi, M.; Pardé, M.; Wigneron, J.P.; Novello, N.; Kerr, Y.; Mialon, A.; Nour-ed-Dine, F. A first assessment of the SMOS data in southwestern France using in situ and airborne soil moisture estimates: The CAROLS airborne campaign. Remote Sens. Environ. 2011, 115, 2718–2728. [Google Scholar] [CrossRef]
- Zribi, M.; Pardé, M.; Boutin, J.; Fanise, P.; Hauser, D.; Dechambre, M.; Kerr, Y.; Leduc-Leballeur, M.; Reverdin, G.; Skou, N.; et al. CAROLS: A new airborne l-band radiometer for ocean surface and land observations. Sensors 2011, 11, 719–742. [Google Scholar] [CrossRef] [PubMed]
- Sellers, P.J. Canopy reflectance, photosynthesis and transpiration. Int. J. Remote Sens. 1985, 6, 1335–1372. [Google Scholar] [CrossRef]
- Myneni, R.B.; Los, S.O.; Asrar, G. Potential gross primary productivity of terrestrial vegetation from 1982 to 1990. Geophys. Res. Lett. 1995, 22, 2617–2620. [Google Scholar] [CrossRef]
- Propastin, P.; Kappas, M. Modeling net ecosystem exchange for grassland in Central Kazakhstan by combining remote sensing and field data. Remote Sens. 2009, 1, 159–183. [Google Scholar] [CrossRef]
- Seiler, R.A.; Kogan, F.; Wei, G. Monitoring weather impact and crop yield from NOAA AVHRR data in Argentina. Adv. Space Res. 2000, 26, 1177–1185. [Google Scholar] [CrossRef]
- Quiring, S.M.; Ganesh, S. Evaluating the utility of the Vegetation Condition Index (VCI) formonitoring meteorological drought in Texas. Agric. For. Meteorol. 2010, 150, 330–339. [Google Scholar] [CrossRef]
- Gitelson, A.A.; Kogan, F.N.; Zakarin, E.; Spivak, L.; Lebed, L. Using AVHRR data for quantitative estimation of vegetation conditions: Calibration and validation. Adv. Space Res. 1998, 22, 673–676. [Google Scholar] [CrossRef]
- Fensholt, R.; Proud, S.R. Evaluation of Earth Observation based global long term vegetation trends-Comparing GIMMS and MODIS global NDVI time series. Remote Sens. Environ. 2012, 119, 131–147. [Google Scholar] [CrossRef]
- Zribi, M.; Chahbi, A.; Lili, Z.; Duchemin, B.; Baghdadi, N.; Amri, R.; Chehbouni, A. Soil surface moisture estimation over a semi-arid region using ENVISAT ASAR radar data for soil evaporation evaluation. Hydrol. Earth Syst. Sci. 2011, 15, 345–358. [Google Scholar] [CrossRef]
- Shepard, D. A tow dimensional interpolation function for regularly spaced data. In Proceedings of the 23rd ACM National Conference of the Association for Computing Machinery, Princeton, NJ, USA, 27–29 August 1968.
- Orvos, P.I.; Homonnai, V.; Várai, A.; Bozóki, Z.; Jánosi, I.M. Trend analysis of a new MODIS drought severity index with emphasis on the Carpathian Basin. Q. J. Hung. Meteorol. Serv. 2014, 118, 323–333. [Google Scholar]
- Shabou, M.; Zribi, M.; Lili-chabaane, Z.; Amri, R.; Selmi, A. Evolution de l’occupation du sol sur le site semi-aride de Merguellil (Tunisie centrale), en utilisant des données optiques de hautes résolutions (SPOT/HRV, Landsat). In Proceedings of the International Workshop: Water Resources in Kairouan Plain: Natural Constraints and Social Developments, Tunis, Tunisia, 16–17 November 2011.
- Settle, J.J.; Drake, N.A. Linear mixing and the estimation of ground cover proportions. Int. J. Remote Sens. 1993, 14, 1159–1177. [Google Scholar] [CrossRef]

| Agricultural Year | Date of Acquisition | Satellites |
|---|---|---|
| 1999/2000 | 5 January 2000 | SPOT 2 |
| 13 March 2000 | ||
| 9 July 200 | ||
| 2005/2006 | 16 November 2005 | SPOT 2 |
| 26 March 2006 | ||
| 22 July 2006 | ||
| 2006/2007 | 21 December 2006 | SPOT 2/LANDSAT |
| 25 March 2007 | ||
| 27 July 2007 | ||
| 2008/2009 | 21 December 2008 | SPOT 5 |
| 14 April 2009 | ||
| 20 May 2009 | ||
| 17 July 2009 | ||
| 2009/2010 | 8 October 2009 | SPOT 5 |
| 30 December 2009 | ||
| 28 March 2010 | ||
| 24 June 2010 | ||
| 2010/2011 | 24 December 2010 | SPOT 5 |
| 29 January 2011 | ||
| 17 March 2011 | ||
| 03 July 2011 | ||
| 2011/2012 | 6 November 2011 | SPOT 5 |
| 13 January 2012 | ||
| 31 March 2012 | ||
| 6 July 2012 | ||
| 2012/2013 | 26 December 2012 | SPOT 5 |
| 21 January 2013 | ||
| 19 March 2013 | ||
| 11 July 2013 |
| Month | α | β |
|---|---|---|
| September | 0.78 | 0.0075 |
| October | 1.05 | 0.01 |
| November | 0.88 | 0.03 |
| December | 0.96 | 0.06 |
| January | 1.02 | 0.02 |
| February | 0.99 | −0.02 |
| March | 1.08 | −0.05 |
| April | 1.07 | 0.0028 |
| May | 0.87 | 0.1 |
| June | 1.04 | 0.066 |
| July | 1.07 | 0.07 |
| August | 0.96 | 0.06 |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zribi, M.; Dridi, G.; Amri, R.; Lili-Chabaane, Z. Analysis of the Effects of Drought on Vegetation Cover in a Mediterranean Region through the Use of SPOT-VGT and TERRA-MODIS Long Time Series. Remote Sens. 2016, 8, 992. https://doi.org/10.3390/rs8120992
Zribi M, Dridi G, Amri R, Lili-Chabaane Z. Analysis of the Effects of Drought on Vegetation Cover in a Mediterranean Region through the Use of SPOT-VGT and TERRA-MODIS Long Time Series. Remote Sensing. 2016; 8(12):992. https://doi.org/10.3390/rs8120992
Chicago/Turabian StyleZribi, Mehrez, Ghofrane Dridi, Rim Amri, and Zohra Lili-Chabaane. 2016. "Analysis of the Effects of Drought on Vegetation Cover in a Mediterranean Region through the Use of SPOT-VGT and TERRA-MODIS Long Time Series" Remote Sensing 8, no. 12: 992. https://doi.org/10.3390/rs8120992
APA StyleZribi, M., Dridi, G., Amri, R., & Lili-Chabaane, Z. (2016). Analysis of the Effects of Drought on Vegetation Cover in a Mediterranean Region through the Use of SPOT-VGT and TERRA-MODIS Long Time Series. Remote Sensing, 8(12), 992. https://doi.org/10.3390/rs8120992








