2.1. Two Component Decomposition of HH/VV Data
Working with coherent HH/VV-polarized data, information of both channels HH and VV may be expressed by the coherency matrix
. The matrix is derived by multiplying the two component target Pauli vector
(Equation (1)) with its conjugate transpose
(Equation (2)).
is a Hermitian matrix with two by two elements (Equation (3)) and represents the upper square sub-matrix of the full 3 × 3 coherency matrix of a quad-polarized measurement. The matrix elements are linear combinations of the complex HH- and VV-channels, based on the Pauli spin matrices [
2] (Equation (4)).
can be used to exploit the phase difference of HH and VV channels: This relation is known to be a crucial discriminator for the characterization of the type of backscattering [
1,
31]; more precisely the discrimination between odd- and even-bounce scattering.
In the formulas
denotes the complex conjugate,
the conjugate transpose, and
refers to the spatial averaging. Yamaguchi et al. [
29] introduced a modified four component scattering model for quad-polarized data based on the decomposition concept of Freeman and Durden [
32]. The approach of Yamaguchi et al. [
29] is decomposing the full 3 × 3 coherency matrix into four signal components of surface scattering, double bounce, volume, and helix scattering (so-called power components). The method utilizes the model for the Bragg scattering via reflection coefficients that rely on the co-polarized information alone. The coefficients of
and
are defined as stated in the original approach of Yamaguchi et al. [
29] and display the orientation and characteristic of the scattered wave [
5], thus these coefficients contain the “polarimetric information” and are called the “scattering mechanisms”. The decomposition model of Yamaguchi et al. [
29] can be realized as a three component model, which is the more frequently applied approach. The model then decomposes the full 3 × 3 coherency matrix
into the features surface, double bounce, and volume scattering. A straight forward adaption of this approach for HH/VV-polarized SAR data is the decomposition of the span into the scattering power components of surface (
) and double bounce (
) scattering neglecting volume scattering: The estimation of these parameters is based on the co-polarized information alone. Such a two component decomposition model can be designed assuming no contribution of the cross-polarized channels on the respective co-polarized channels as shown in Equations (5) and (6).
The definition of the model leads to the three equations shown in Equations (5)–(7). The equation system has four unknowns
,
,
, and
, and is therewith underdetermined. The unknowns
and
are the intensity components of the two scattering components to be determined [
29]. The left hand side is given by the measured values of
,
,
, and
of the HH/VV-polarized Coherency Matrix
.
Two cases can be distinguished to simplify the equation system in order to be uniquely solvable; Case 1 with dominant surface scattering (
) and Case 2, with dominant double bounce scattering (
), where the non-dominant scattering contribution is set to zero [
5]. These definitions are identical to the original models of Yamaguchi and Freeman-Durden. The unknowns
,
,
or
are then defined by Equations (8)–(10) for Case 1 and by Equations (11)–(13) for Case 2.
Case 1:
:
Case 2:
:
The scattering power components
and
can be derived via Equations (14) and (15) consistently for both cases:
The differences between the decomposition features of this two component model and of the three component model of [
29] are the assumption of the absence of a significant volume scattering contribution and a volume-induced depolarization, respectively. This means the cross-polarized information will be ignored and is not measured for dual-polarimetric T. For real world applications one should take into account that a zero contribution of the cross-polarized channels—respectively an observation of
in terms of quad-polarized coherency matrix—is not a likely situation for radar observations of natural surfaces [
1]. Furthermore, zero elements in the off-diagonal positions
and
of quad-polarized coherency matrices are only observable when no coherence between cross- and co-polarized channels is present [
1] due to reflection symmetry for example. Nevertheless, this is a quite frequently applied symmetry assumption for natural media [
5,
29].
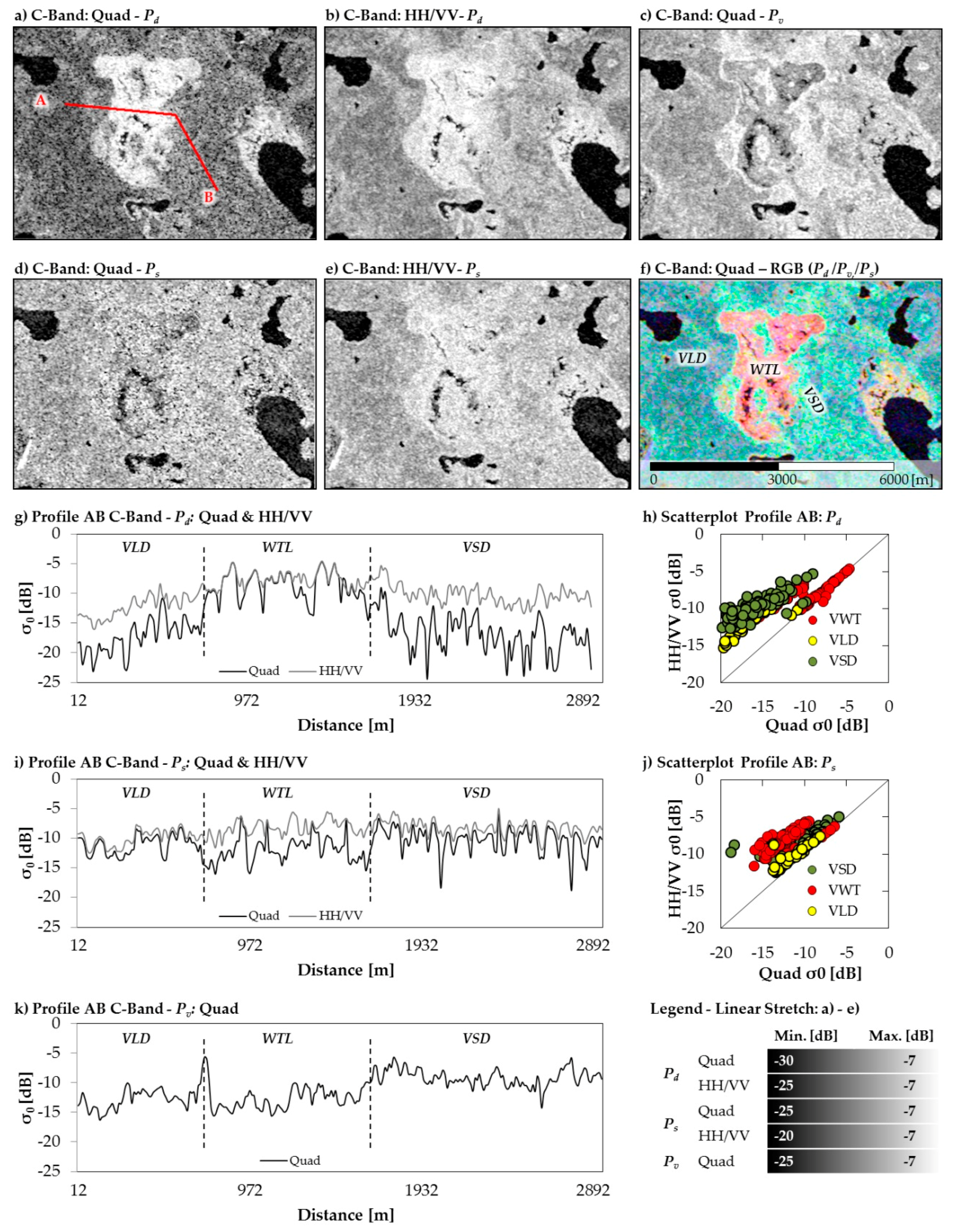
Accordingly, the correlations of and between the two and three component decomposition models is expected to be high for land cover types, e.g., bare or sparsely vegetated ground, that show no significant volume scattering with respect to the used wavelength and the spatial resolution. Contrary, the differences will be maximized for urban areas and for densely vegetated ground like forests: for such land cover types the contribution of volume scattering is usually high and not negligible at all. In comparison to the simple Pauli decomposition the discrimination between double-bounce (or even bounce in Pauli’s definition) and surface scattering (or odd bounce in the Pauli notation) is enhanced by introducing the polarimetric scattering mechanisms and in Equations (14) and (15). The idea is to understand both, the intensity (, ) and the scattering mechanisms (, ) by using also the coherent nature of the data and not only the incoherent channel intensities (like for the Pauli decomposition of multi-looked images). Moreover, the Pauli decomposition would only distinguish between odd and even bounce scattering (multiple bounces) and not directly between surface and double-bounce scattering. So higher order scattering is actually not expected for tundra and just pure surface or dihedral scattering should be present, as the vegetation is low and comparably simple in structure. Thus, land cover discrimination and PolSAR signal interpretation is expected to be easier than using just the simple elements of the Coherency matrix.
2.3. In Situ Data
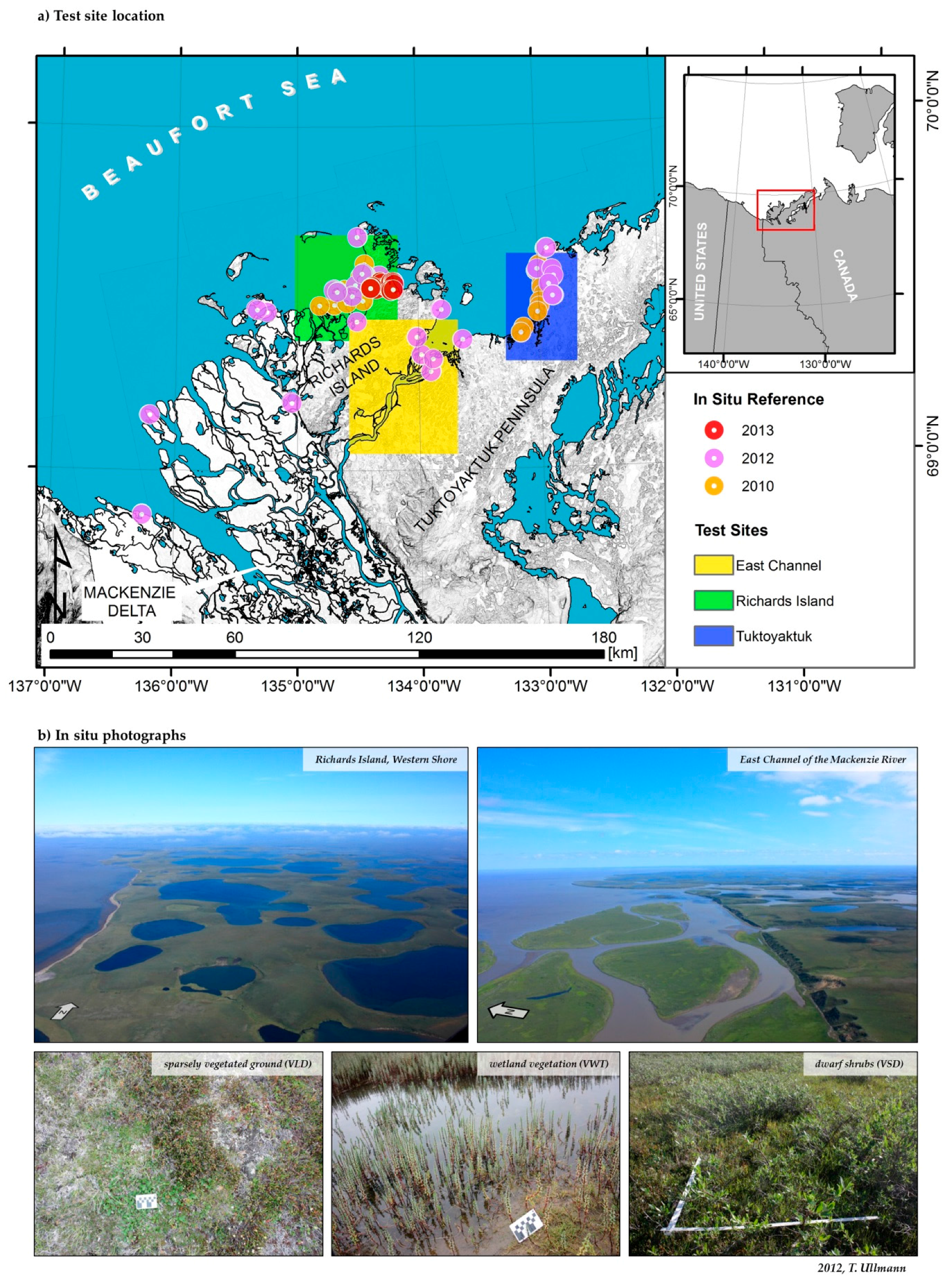
Additionally, in situ ground truth data on the land cover were recorded in the summers of the years 2010, 2012, and 2013. The location of the investigated sites is drawn in
Figure 1. In 2010 the field work was conducted by the NWRC (National Wildlife Research Centre, Ottawa, ON, Canada). The field work in 2012 and 2013 was conducted by the Carleton University Ottawa, the NWRC, and the University of Wuerzburg. More than forty locations inside the region were visited and surface properties were documented. The number of reference samples was increased afterwards using high resolution aerial ortho-photos provided by Hartmann and Sachs [
34] and NWT-Geomatics [
35]. After this operation the set of land cover reference data comprised more than 1700 individual polygons and a minimum of 200 polygons per land cover class. A set of 1000 points per class was then chosen randomly for each test site.
Six land cover classes were distinguished qualitatively in the field (
Table 2) and in dependence on the classification systems of Corns [
36] and the Land Cover Classification LCC-2000-V provided by the authorities of the Natural Resources Canada (
geogratis.gc.ca): Water, Bare Ground (NBG), Low/Sparsely Vegetated Tundra (VLD), Medium/Mixed Tundra (VMD), High/Shrub-Dominated Tundra (VSD), and Wetlands (VWT). The main cut-off criteria for the categorization of the land cover classes were the estimated height of the vegetation and the occurrence/density of the shrubs.
Table 2 draws the main parameters and a scheme of these generalized land cover classes. The sorting of the classes from NBG to VLD to VMD to VSD corresponds to increasing vegetation height and shrub density on an ordinal scale. Photographs of the classes VLD, VWT, and VSD are provided in
Figure 1.
2.4. Correlation Analysis
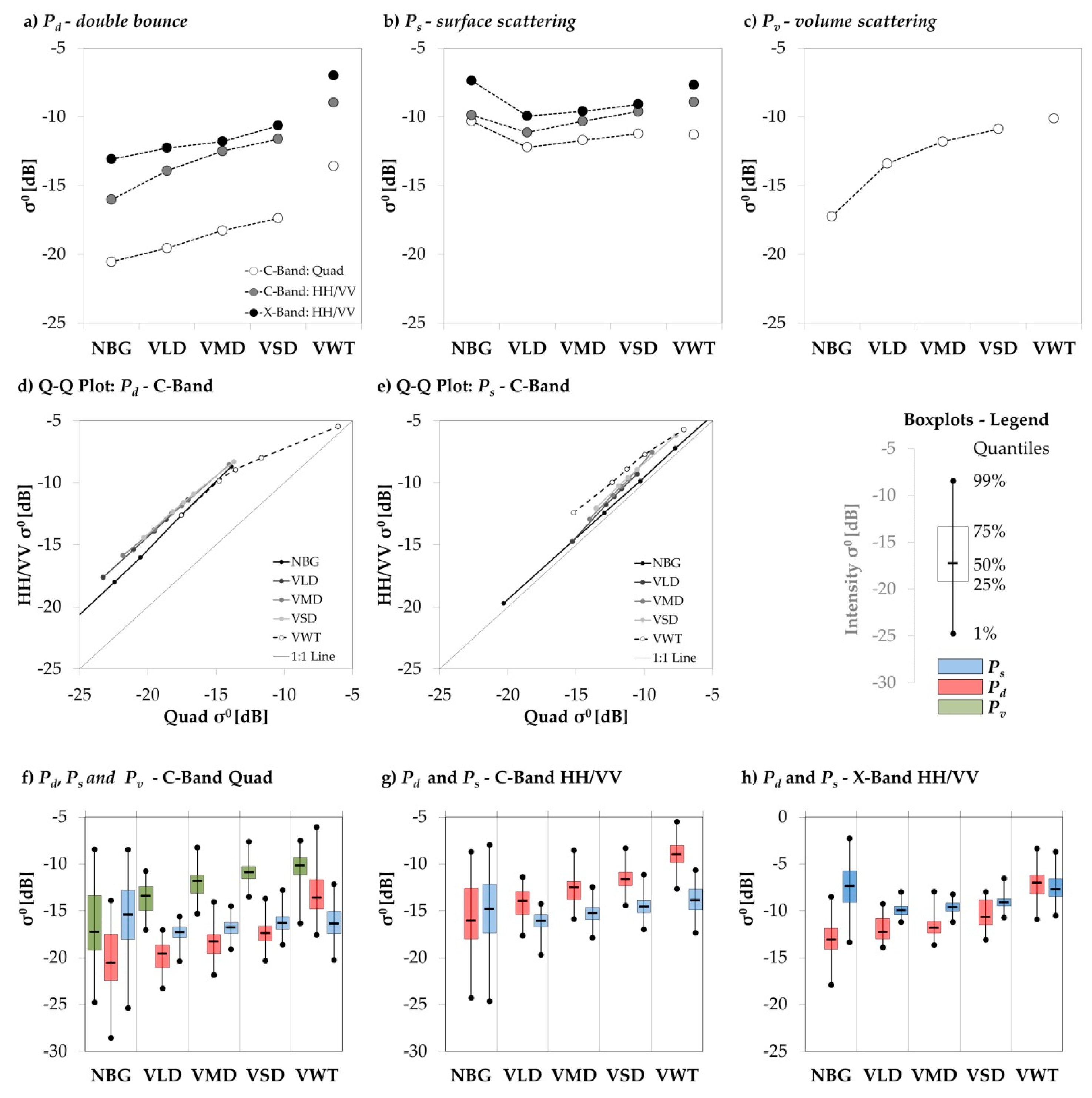
The relationships and dependencies between the features of the two and three component decomposition were investigated for the C-Band and X-Band datasets using correlation analysis. The two component decomposition features P
s and P
d were processed for C-Band HH/VV-polarized data and X-Band HH/VV-polarized data. The three component decomposition features P
s, P
d, and P
v were processed using the C-Band quad-polarized data. The alterations between the C-Band two and three component decomposition features P
s (P
d) were then connected to the differences of the models and not to changes caused by temporal variations, since pseudo HH/VV-polarized data were derived from quad-polarized data.
Table 3 provides an overview of the investigated features.
Prior to the analysis, a random stratification was applied to the land cover reference dataset to avoid auto-correlation: For each land cover class and each test site a set of 1000 pixels was chosen randomly (see
Section 2.3 in situ Data)
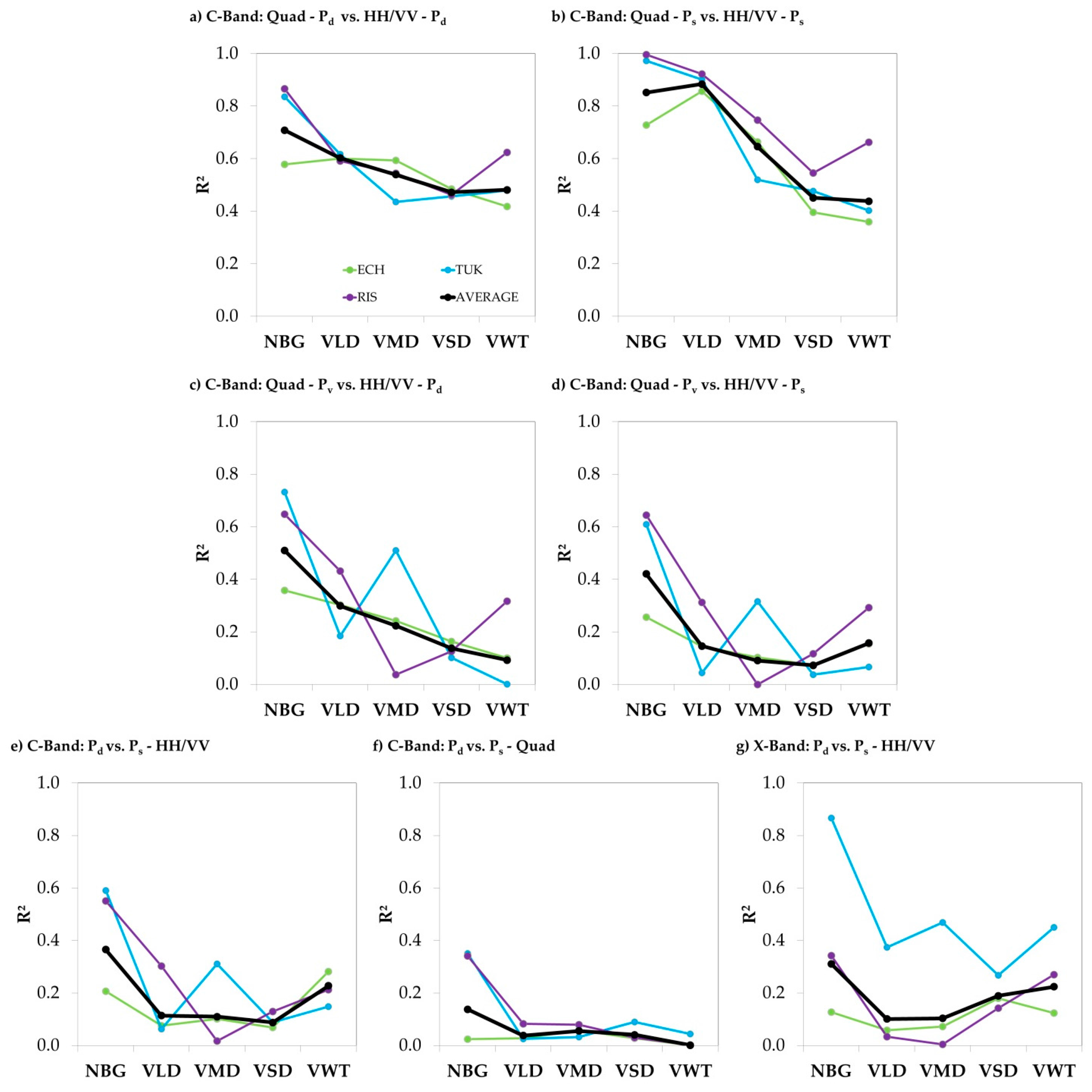
.The correlations between the decomposition features were investigated using the intensity values of the sigma nought calibrated data. The linear Pearson Correlation Coefficient (R), the squared linear Pearson Correlation Coefficient (R
2), and the Spearman’s Rank Correlation Coefficient (
) were processed for all of the features for each land cover class of each test site using the reference data. The coefficient
is defined as the ratio between the covariance (
Cov) of two variables (
i,
j) and the product of the individual standard deviations of these two variables (SD) (16) and (17). Similar,
is defined as the ratio between the covariance (
Cov) of two ranked variables (
) and the product of the individual standard deviations of these two ranked variables (
) (18).
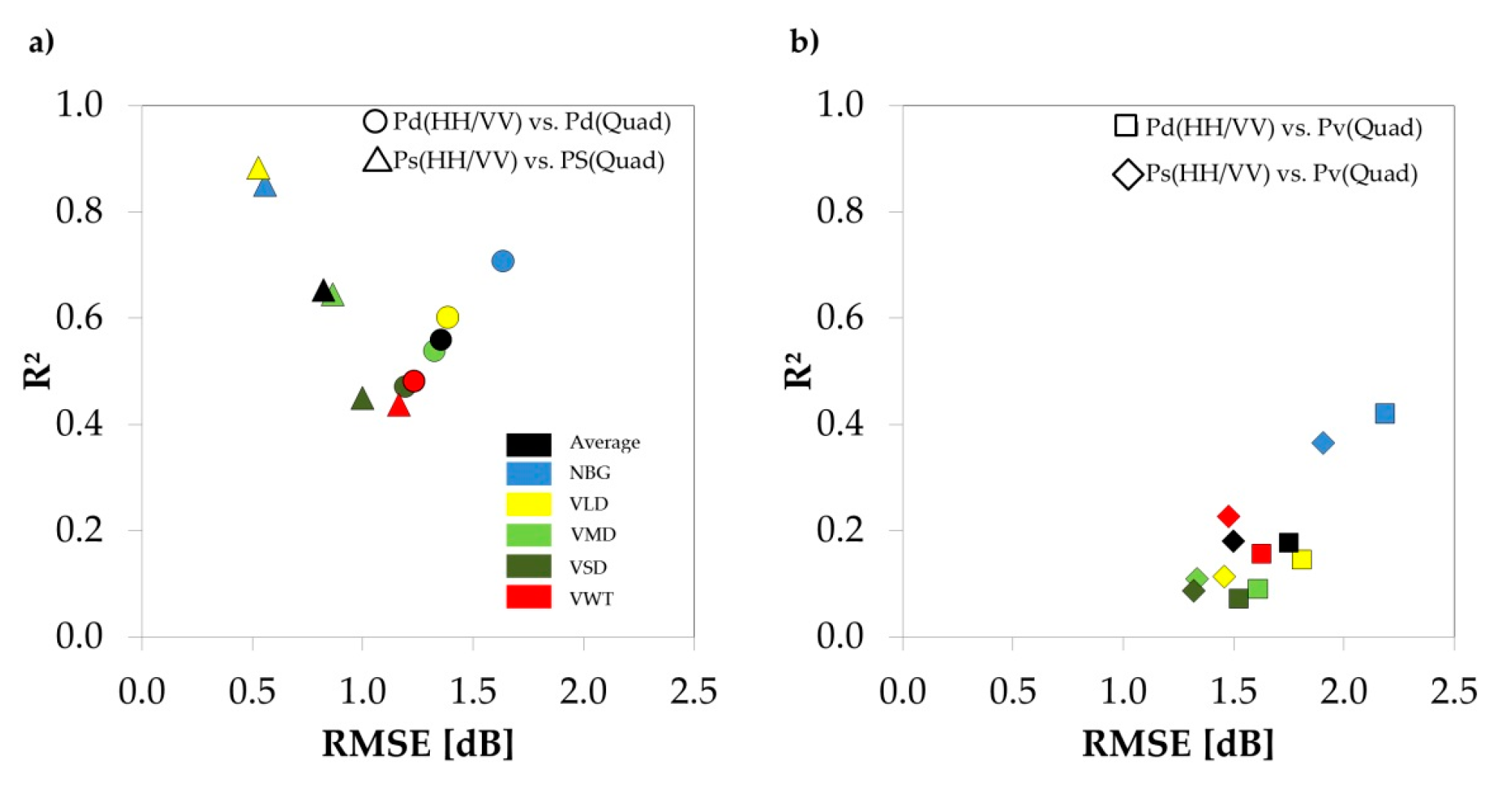
The coefficients R and are relative and dimensionless and therefore show the linear (R) or monotonic () correlations among the features, respectively the degree of determination (R2). The values of R and R2 range from zero to one, where a value of one (zero) indicates perfect (no) linear correlation and a maximum (minimum) determination, which is 100% (0%) of the explained variance. The values of range from −1 to +1, where −1/+1 indicate perfect monotonic properties, thus one variable is a function of the other. R and were investigated to examine the linear and monotonic dependencies among the features. The X-Band data acted as a control variable in this study: A positive correlation between C- and X-Band is expected due to the similar wavelengths of 5 cm and 3 cm, respectively. However; this relationship should be less significant compared to the correlation among the C-Band features due to the temporal decorrelation, the differences in the speckle characteristics, and the differences in absolute radiometric calibration. Therefore it is more statistically reliable to compare C-Band quad-polarized with C-Band synthesized dual-polarized data.
2.5. Regression Analysis
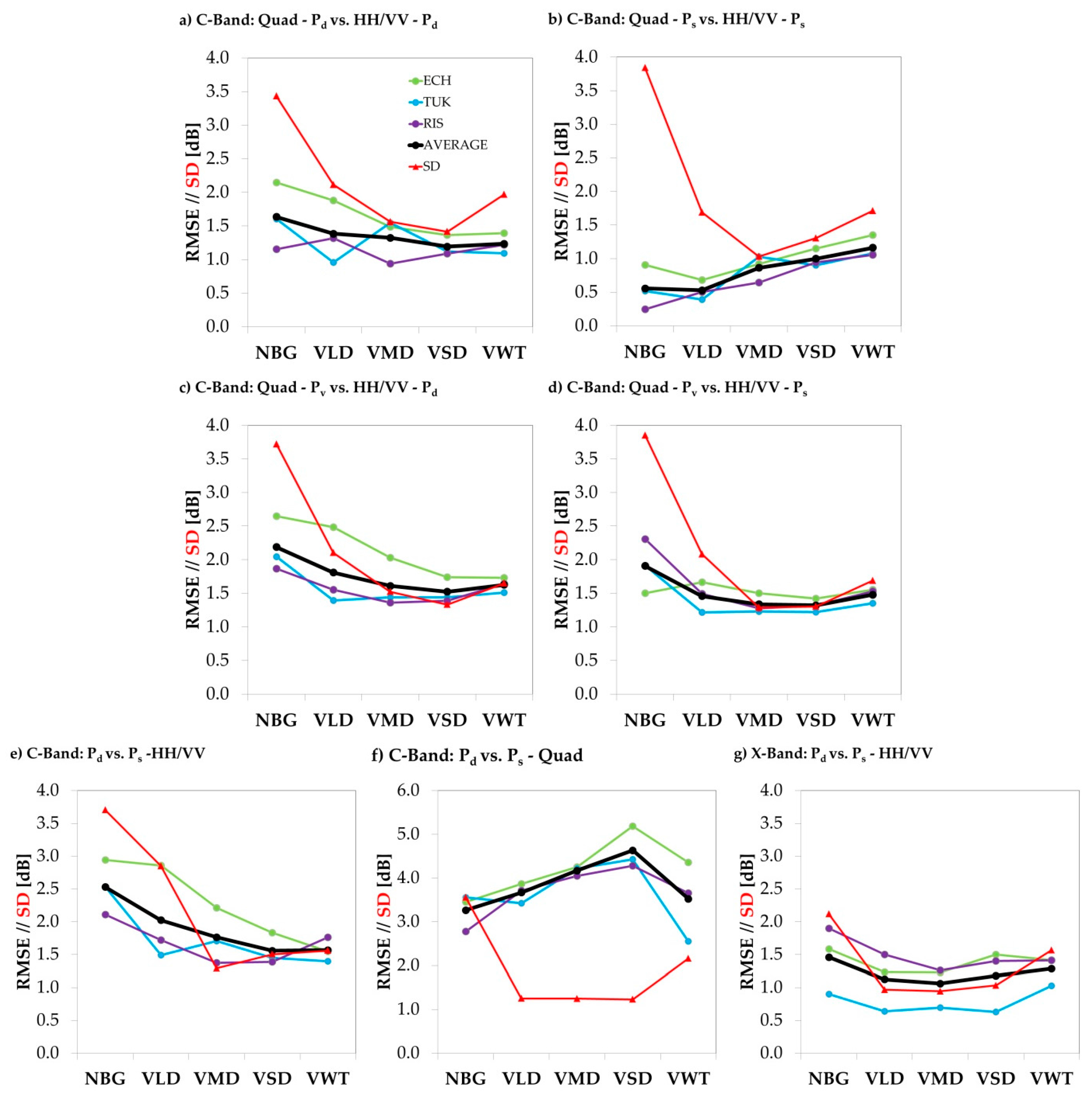
Along with the correlation coefficients, the parameters of the linear regression models were processed for all of the features for each land cover class of each test site using the reference data. The linear model
y =
ax +
b was assumed for the modelling. The two linear model parameters are the slope (coefficient
a) and the axis intercept (coefficient
b). The differences between the predictions (
y) and the true observations (
y’) can be expressed via the Root Mean Square Error (RMSE). The RMSE (Equation (19)) is an absolute measurement of the mean deviation of the model and processed for a sample
n. It is therefore measured in the unit of the input variables—decibel (dB) in our case, since the scattering power components were investigated. The RMSE is a frequently used measure to assess the absolute variation of the model prediction, which is often interpreted as the “absolute error” of the model.
RMSE is not adjusted to the variances of the two samples (SD) and it should therefore be interpreted along with a relative correlation coefficient, or with a feature that displays the variations of the features (e.g., ). A low (high) coefficient of determination (R2) does not necessarily infer a high (low) RMSE, e.g., in the case that the classes’ standard deviations are low (high).
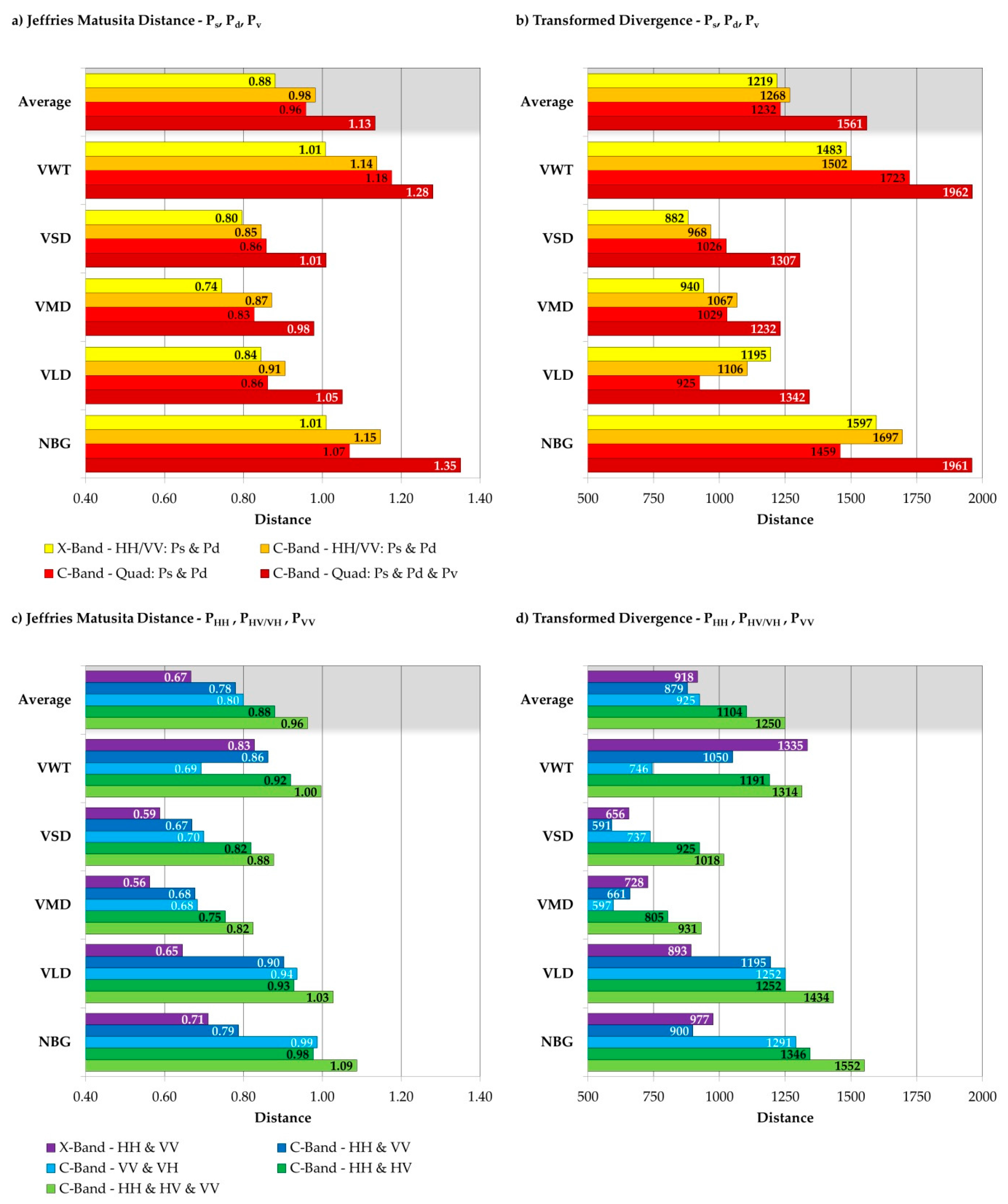
2.6. Separability Analysis
The separability features Jeffries Matusita Distance (JD) and Transformed Divergence (TD) [
37,
38] were further investigated to examine the differences between C- and X-Band, between the two and three component decomposition features and to examine if PolSAR decomposition offers better class separation compared to the “pure” intensities of the polarimetric channels. The values of the dimensionless JD range from 0.0 to
. The values of the dimensionless Transformed Divergence range usually from 0 to 2000. The higher the value of a separability feature the higher is the estimated separation of the classes in the feature space and the expected classification accuracy. JD and TD require that the values of the classes are normally distributed. This is usually not the case; however a common assumption for natural targets and media for simplicity reasons. JD and TD then estimate the overlap between the multivariate normal distributions of two classes of interest in a given feature space. Less (more) overlap indicates better (worse) separability and therefore the classification accuracy is expected to be higher (lower).
The TD between two classes
c and
d is defined by Equation (20) using the classes’ mean vectors
M and the classes’ covariances
V for a given set of features, with two features required as minimum. In the formula
tr denotes the trace of a matrix and
T refers to the matrix/vector transpose.
C is a 3 × 3 matrix and
M a three-element vector for the case that three features are investigated [
37].
The JD between two classes
c and
d is defined by (21) and (22) using the classes’ mean vectors
M and the classes’ covariances
V for a given set of features, with two features required as minimum. The calculation of JD is based on the Bhattacharyya Distance (BD) (21). In the formula
det denotes the determinant of a matrix. Both features are based on the Mahalanobis Distance, which estimates the distance between a point and a distribution [
37].
JD and TD were shown to act as authentic predictors for the accuracy of supervised classifications, when the classifier relies on normal distribution parametrization [
37,
38,
39], e.g., the relationship between JM and supervised classification accuracy obtained from Maximum Likelihood Classification (based on the Mahalanobis Distance). However, the saturation behavior of both features is different and thus it is meaningful to compute and to interpret both in the separability analysis. For this study the land cover reference data were used to define the classes’ statistics. The feature spaces examined were the intensities of C-Band pseudo dual-polarized data (HH/HV; VV/VH; HH/VV), C-Band quad-polarized data (HH/HV/VV), X-Band dual-polarized data (HH/VV), C-Band Three Component Decomposition Features (P
s/P
d/P
v), C-Band Three Component Decomposition Features without the volume scattering (P
s/P
d), C-Band Two Component Decomposition Features (P
s/P
d), and the X-Band Two Component Decomposition Features (P
s/P
d) (
Table 3). The analysis was conducted for the none-water land cover classes (NBG, VLD, VMD, VSD, VWT) to avoid an overestimation of the average separability; the class water is comparably easy to be classified with PolSAR data [
31] and a high separability of this class might artificially enhance the results.