L-Band Relative Permittivity of Organic Soil Surface Layers—A New Dataset of Resonant Cavity Measurements and Model Evaluation
Abstract
:1. Introduction
2. Materials and Methods
2.1. Description of Study Sites and Soil Samples
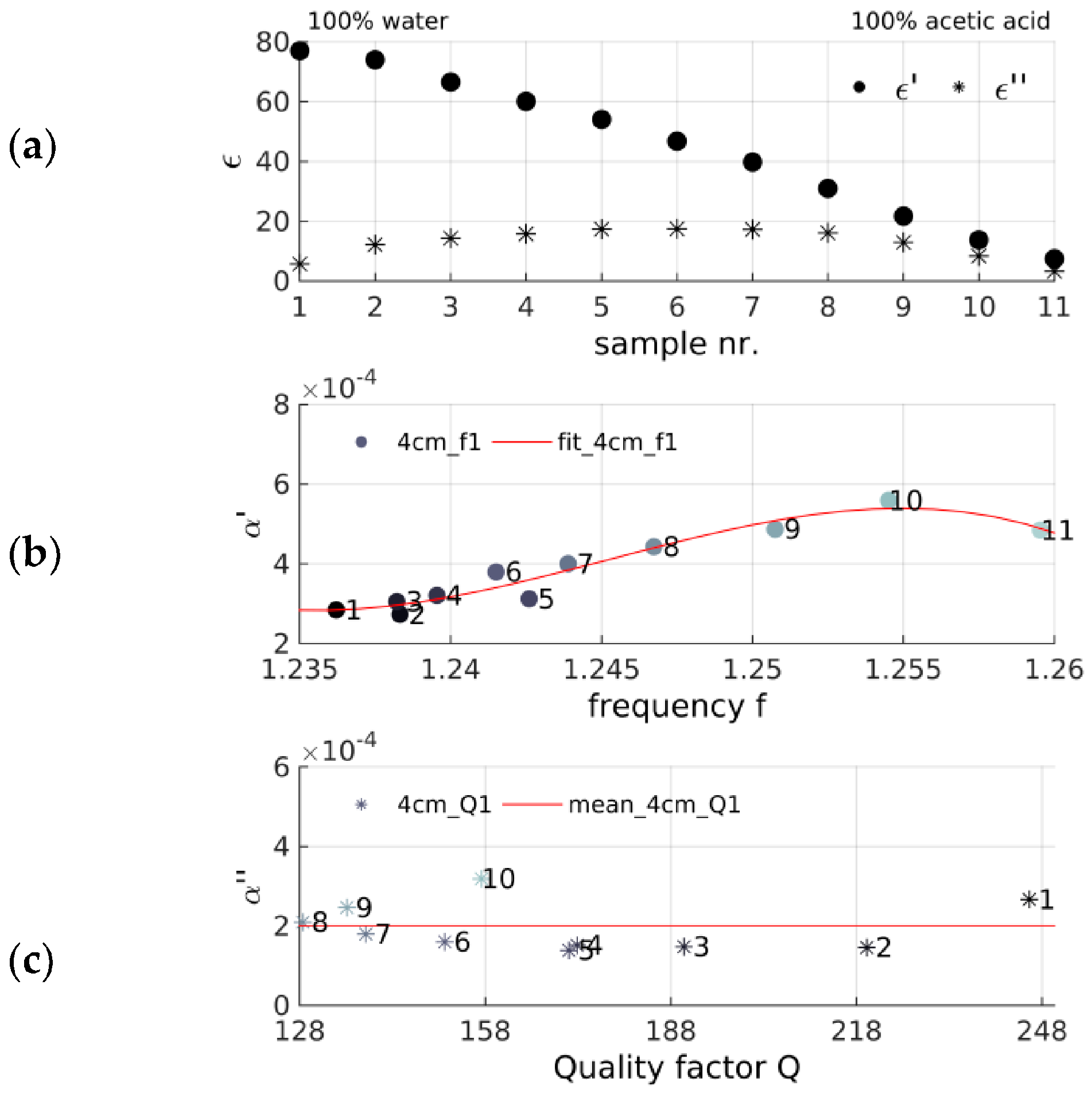
2.2. Resonant Cavity Using Weak Perturbation Method
2.2.1. α-Factor Calibration for Adjusted Tube Length
2.2.2. Sample Preparation
2.2.3. Measurement Procedure and Data Processing
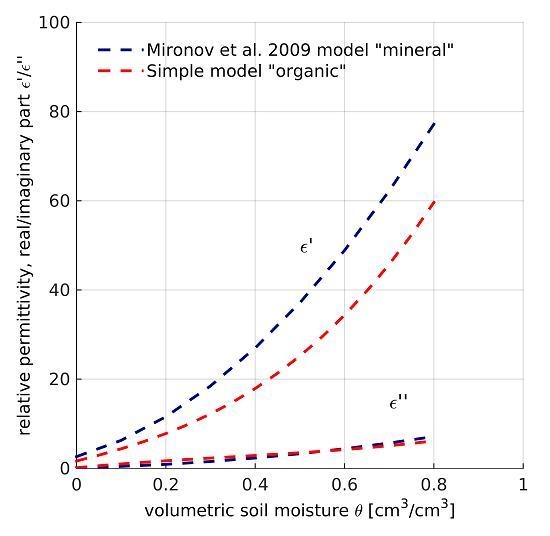
2.3. Derivation of Simple Empirical Models and Evaluation of Existing Dielectric Models
3. Results
4. Discussion
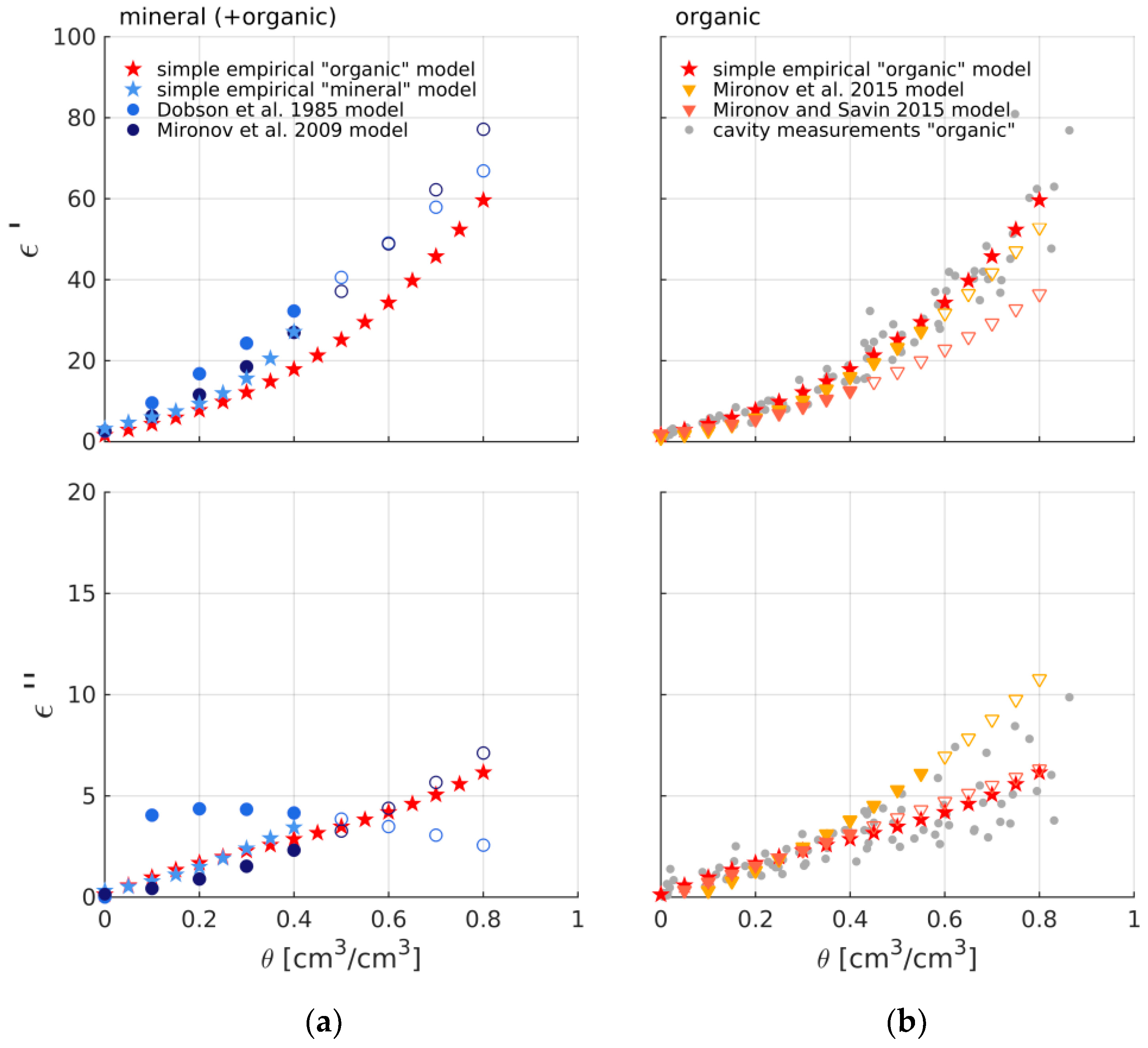
4.1. Measured Resonant Cavity Dataset and Derived Simple Empirical Models
4.2. Evaluation of Existing Dielectric Models by Means of Measured Resonant Cavity Dataset and Derived Simple Empirical Models
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Zimov, S.A.; Schuur, E.; Chapin, F. Climate change: Permafrost and the global carbon budget. Science 2006, 312, 1612–1613. [Google Scholar] [CrossRef] [PubMed]
- Tarnocai, C.; Canadell, J.G.; Schuur, E.A.G.; Kuhry, P.; Mazhitova, G.; Zimov, S. Soil organic carbon pools in the northern circumpolar permafrost region: Soil organic carbon pools. Glob. Biogeochem. Cycles 2009, 23. [Google Scholar] [CrossRef]
- Hansen, J.; Sato, M.; Ruedy, R.; Lo, K.; Lea, D.W.; Medina-Elizade, M. Global temperature change. Proc. Natl. Acad. Sci. USA 2006, 103, 14288–14293. [Google Scholar] [CrossRef] [PubMed]
- Collins, M.; Knutti, R.; Arblaster, J.; Dufresne, T.; Fichefet, T.; Friedlingstein, P.; Gao, X.; Gutowski, W.J.; Johns, T.; Krinner, G.; et al. Long-term climate change: Projections, commitments and irreversibility. In Climate Change 2013: The Physical Science Basis. Contribution of Working Group I to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change; Stocker, T.F., Qin, D., Plattner, G.-K., Tignor, M., Allen, S.K., Boschung, J., Nauels, A., Xia, Y., Bex, V., Midgley, P.M., Eds.; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2013. [Google Scholar]
- Stokstad, E. Defrosting the carbon freezer of the North. Science 2004, 304, 1618. [Google Scholar] [CrossRef] [PubMed]
- Schuur, E.A.G.; Bockheim, J.; Canadell, J.G.; Euskirchen, E.; Field, C.B.; Goryachkin, S.V.; Hagemann, S.; Kuhry, P.; Lafleur, P.M.; Lee, H.; et al. Vulnerability of permafrost carbon to climate change: Implications for the global carbon cycle. BioScience 2008, 58, 701. [Google Scholar] [CrossRef]
- Schuur, E.A.G.; Abbott, B. Climate change: High risk of permafrost thaw. Nature 2011, 480, 32–33. [Google Scholar] [CrossRef] [PubMed]
- Davidson, E.A.; Janssens, I.A. Temperature sensitivity of soil carbon decomposition and feedbacks to climate change. Nature 2006, 440, 165–173. [Google Scholar] [CrossRef] [PubMed]
- Kerr, Y.H.; Waldteufel, P.; Wigneron, J.-P.; Martinuzzi, J.; Font, J.; Berger, M. Soil moisture retrieval from space: The Soil Moisture and Ocean Salinity (SMOS) mission. IEEE Trans. Geosci. Remote Sens. 2001, 39, 1729–1735. [Google Scholar] [CrossRef]
- Kerr, Y.H.; Waldteufel, P.; Wigneron, J.-P.; Delwart, S.; Cabot, F.; Boutin, J.; Escorihuela, M.-J.; Font, J.; Reul, N.; Gruhier, C.; et al. The SMOS mission: New tool for monitoring key elements ofthe global water cycle. Proc. IEEE 2010, 98, 666–687. [Google Scholar] [CrossRef]
- Wagner, W.; Blöschl, G.; Pampaloni, P.; Calvet, J.-C.; Bizzarri, B.; Wigneron, J.-P.; Kerr, Y. Operational readiness of microwave remote sensing of soil moisture for hydrologic applications. Hydrol. Res. 2007, 38, 1–20. [Google Scholar] [CrossRef]
- Lagerloef, G.; Colomb, F.R.; Le Vine, D.; Wentz, F.; Yueh, S.; Ruf, C.; Lilly, J.; Gunn, J.; Chao, Y.; deCharon, A.; et al. The aquarius/SAC-D mission: Designed to meet the salinity remote-sensing challenge. Oceanography 2008, 21, 68–81. [Google Scholar] [CrossRef]
- Entekhabi, D.; Njoku, E.G.; O’Neill, P.E.; Kellogg, K.H.; Crow, W.T.; Edelstein, W.N.; Entin, J.K.; Goodman, S.D.; Jackson, T.J.; Johnson, J.; et al. The Soil Moisture Active Passive (SMAP) mission. Proc. IEEE 2010, 98, 704–716. [Google Scholar] [CrossRef]
- Mo, T.; Choudhury, B.J.; Schmugge, T.J.; Wang, J.R.; Jackson, T.J. A model for microwave emission from vegetation-covered fields. J. Geophys. Res. 1982, 87, 11229. [Google Scholar] [CrossRef]
- Wigneron, J.-P.; Chanzy, A.; Calvet, J.-C.; Bruguier, N. A simple algorithm to retrieve soil moisture and vegetation biomass using passive microwave measurements over crop fields. Remote Sens. Environ. 1995, 51, 331–341. [Google Scholar] [CrossRef]
- Dobson, M.; Ulaby, F.; Hallikainen, M.; El-Rayes, M. Microwave dielectric behavior of wet soil-Part II: Dielectric mixing models. IEEE Trans. Geosci. Remote Sens. 1985, GE-23, 35–46. [Google Scholar] [CrossRef]
- Peplinski, N.R.; Ulaby, F.T.; Dobson, M.C. Dielectric properties of soils in the 0.3–1.3-GHz range. IEEE Trans. Geosci. Remote Sens. 1995, 33, 803–807. [Google Scholar] [CrossRef]
- Mironov, V.L.; Dobson, M.C.; Kaupp, V.H.; Komarov, S.A.; Kleshchenko, V.N. Generalized refractive mixing dielectric model for moist soils. IEEE Trans. Geosci. Remote Sens. 2004, 42, 773–785. [Google Scholar] [CrossRef]
- Mironov, V.L.; Kosolapova, L.G.; Fomin, S.V. Physically and mineralogically based spectroscopic dielectric model for moist soils. IEEE Trans. Geosci. Remote Sens. 2009, 47, 2059–2070. [Google Scholar] [CrossRef]
- Mironov, V.; Kerr, Y.; Wigneron, J.-P.; Kosolapova, L.; Demontoux, F. Temperature- and texture-dependent dielectric model for moist soils at 1.4 GHz. IEEE Geosci. Remote Sens. Lett. 2013, 10, 419–423. [Google Scholar] [CrossRef]
- Mironov, V.L.; Fomin, S.V. Temperature and mineralogy dependable model for microwave dielectric spectra of moist soils. PIERS Online 2009, 5, 411–415. [Google Scholar] [CrossRef]
- Kerr, Y.; Waldteufel, P.; Richaume, P.; Ferrazzoli, P.; Wigneron, J.-P. SMOS Level 2 Processor for Soil Moisture Algorithm Theoretical Basis Document (ATBD) V4.a; SM-ESL (CBSA): Toulouse, France, 2015; p. 131. [Google Scholar]
- Mialon, A.; Richaume, P.; Leroux, D.; Bircher, S.; Bitar, A.A.; Pellarin, T.; Wigneron, J.-P.; Kerr, Y.H. Comparison of dobson and mironov dielectric models in the SMOS soil moisture retrieval algorithm. IEEE Trans. Geosci. Remote Sens. 2015, 53, 3084–3094. [Google Scholar] [CrossRef]
- Bircher, S.; Balling, J.E.; Skou, N.; Kerr, Y.H. Validation of SMOS brightness temperatures during the HOBE airborne campaign, Western Denmark. IEEE Trans. Geosci. Remote Sens. 2012, 50, 1468–1482. [Google Scholar] [CrossRef]
- Srivastava, P.K.; O’Neill, P.; Cosh, M.; Kurum, M.; Lang, R.; Joseph, A. Evaluation of dielectric mixing models for passive microwave soil moisture retrieval using data from ComRAD ground-based SMAP simulator. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2015, 8, 4345–4354. [Google Scholar] [CrossRef]
- Kellner, E.; Lundin, L.-C. Calibration of time domain reflectometry for water content in peat soil. Hydrol. Res. 2001, 32, 315–332. [Google Scholar]
- Li, H.; Parent, L.E.; Karam, A.; Tremblay, C. Potential of sphagnum peat for improving soil organic matter, water holding capacity, bulk density and potato yield in a sandy soil. Plant Soil 2004, 265, 355–365. [Google Scholar] [CrossRef]
- Jones, S.B.; Wraith, J.M.; Or, D. Time domain reflectometry measurement principles and applications. Hydrol. Process. 2002, 16, 141–153. [Google Scholar] [CrossRef]
- Mironov, V.L.; De Roo, R.D.; Savin, I.V. Temperature-dependable microwave dielectric model for an arctic soil. IEEE Trans. Geosci. Remote Sens. 2010, 48, 2544–2556. [Google Scholar] [CrossRef]
- Mironov, V.L.; Kerr, Y.H.; Kosolapova, L.G.; Savin, I.V.; Muzalevskiy, K.V. A temperature-dependent dielectric model for thawed and frozen organic soil at 1.4 GHz. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2015, 8, 4470–4477. [Google Scholar] [CrossRef]
- Mironov, V.; Savin, I. A temperature-dependent multi-relaxation spectroscopic dielectric model for thawed and frozen organic soil at 0.05–15 GHz. Phys. Chem. Earth Parts ABC 2015, 83–84, 57–64. [Google Scholar] [CrossRef]
- Bircher, S.; Kerr, Y.H.; Wigneron, J.-P. SMOSHiLat—Microwave L-Band Emissions from Organic-Rich Soils in the Northern Cold Climate Zone and Their Impact on the SMOS Soil Moisture Product; Support to Science Element—Changing Earth Science Network; ESA-ESRIN: Frascati, Italy, 2015; p. 71. [Google Scholar]
- Jensen, K.H.; Illangasekare, T.H. HOBE: A hydrological observatory. Vadose Zone J. 2011, 10, 1. [Google Scholar] [CrossRef]
- Bircher, S.; Skou, N.; Jensen, K.H.; Walker, J.P.; Rasmussen, L. A soil moisture and temperature network for SMOS validation in Western Denmark. Hydrol. Earth Syst. Sci. 2012, 16, 1445–1463. [Google Scholar] [CrossRef]
- Ikonen, J.; Vehviläinen, J.; Rautiainen, K.; Smolander, T.; Lemmetyinen, J.; Bircher, S.; Pulliainen, J. The Sodankylä in situ soil moisture observation network: An example application of ESA CCI soil moisture product evaluation. Geosci. Instrum. Methods Data Syst. 2016, 5, 95–108. [Google Scholar] [CrossRef]
- Zanella, A.; Jabiol, B.; Ponge, J.-F.; Sartori, G.; De Waal, R.; Van Delft, B.; Graefe, U.; Cools, N.; Katzensteiner, K.; Hager, H.; et al. European Humus Forms Reference Base. Available online: http://hal.archives-ouvertes.fr/hal-00541496 (accessed on 8 April 2016).
- Ball, D.F. Loss-on-ignition as an estimate of organic matter and organic carbon in non-calcareous soils. J. Soil Sci. 1964, 15, 84–92. [Google Scholar] [CrossRef]
- Heiri, O.; Lotter, A.F.; Lemcke, G. Loss on ignition as a method for estimating organic and carbonate content in sediments: Reproducibility and comparability of results. J. Paleolimnol. 2001, 25, 101–110. [Google Scholar] [CrossRef]
- Boudouris, G. Validité de la méthode de perturbation appliquée aux cavités résonnantes pour la mesure de la perméabilité et de la permittivité des petits échantillons. Ann. Télécommun. 1964, 19, 63–80. [Google Scholar]
- Demontoux, F.; Razafindratsima, S.; Bircher, S.; Ruffié, G.; Bonnaudin, G.; Jonard, F.; Wigneron, J.-P.; Sbartai, M.; Kerr, Y. Efficiency of end effect probes for in-situ permittivity measurements in the 0.5–6 GHz frequency range and their application for organic soil horizons study. Sens. Actuators A Phys. 2016. accepted. [Google Scholar] [CrossRef]
- O’Kelly, B.C. Accurate determination of moisture content of organic soils using the oven drying method. Dry. Technol. 2004, 22, 1767–1776. [Google Scholar] [CrossRef]
- Schaap, M.G.; de Lange, L.; Heimovaara, T.J. TDR calibration of organic forest floor media. Soil Technol. 1997, 11, 205–217. [Google Scholar] [CrossRef]
- Pumpanen, J.; Ilvesniemi, H. Calibration of time domain reflectometry for forest soil humus layers. Boreal Environ. Res. 2005, 10, 589–595. [Google Scholar]
- Bircher, S.; Andreasen, M.; Vuollet, J.; Vehviläinen, J.; Rautiainen, K.; Jonard, F.; Weihermüller, L.; Zakharova, E.; Wigneron, J.-P.; Kerr, Y.H. Soil moisture sensor calibration for organic soil surface layers. Geosci. Instrum. Methods Data Syst. 2016, 5, 109–125. [Google Scholar] [CrossRef]
- National Aeronautics and Space Administration (NASA). Global Land Data Assimilation Systems (GLDAS) Land Surface Parameters. Available online: http://ldas.gsfc.nasa.gov/gldas/GLDASsoils.php (accessed on 12 August 2016).



| Type | Sample Name | Location | Land Cover | Layer Depth (cm) | OM (%) | Sand/Silt/Clay (%) | Density (g/cm3) | Water Regime | Form and Biotype | Horizons | θ Range (cm3/cm3) |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Organic | FMI_Spruce_2013_O | Sodankylä, FI | Forest | 0–5 | 89.73 | 0.13 | T | Terro Mor | OF | Excluded | |
| FMI_Elbara_2013_O | Sodankylä, FI | Heath | 0–3 | 51.27 | 0.28 | T | Enti Mor | OL-OF-OH | 0.00–0.75 | ||
| HOBE_heath_2013_O1 | Gludsted, DK | Heath | 0–4 | 91.22 | 0.18 | T | Terro Moder | OL-OF | 0.00–0.85 | ||
| HOBE_heath_2013_O2 | Gludsted, DK | Heath | 4–6 | 64.95 | 0.81 | T | Terro Moder | OH | 0.10–0.80 | ||
| HOBE_forest_2013_O1 | Gludsted, DK | Forest | 0–4 | 83.19 | 0.16 | T | Terro Mor | OL-OF | 0.00–0.85 | ||
| HOBE_forest_2013_O2 | Gludsted, DK | Forest | 4–10 | 22.27 | 0.79 | T | Terro Mor | OH | 0.05–0.65 1 | ||
| Islay_peat1_2013_O1 | Islay, GB | Bog | 0–5 | 95.22 | 0.04 | ST | Histo Mor | hf | 0.00–0.60 2 | ||
| Islay_peat1_2013_O2 | Islay, GB | Bog | 5–10 | 91.65 | 0.12 | ST | Histo Mor | hm | 0.00–0.45 | ||
| Islay_peat2_2013_O | Islay, GB | Bog | 0-10 | 95.65 | 0.24 | ST | Histo Mor | hf(-hm) | 0.00–0.80 | ||
| siberia_tundra_2012_O | Siberia, RU | Tundra | 0–10 | 95.23 | 0.13 | ST | Hydro Mor | (OLg)-OFg-(OHg) | 0.00–0.85 | ||
| siberia_bog_2013_O | Siberia, RU | Bog | 0–10 | 97.98 | 0.03 | ST | Histo Mor | hf | 0.00–0.70 | ||
| siberia_forest_2013_O | Siberia, RU | Forest | 0–10 | 72.98 | 0.1 | T | Terro Mor | OL-OF-OH | 0.00–0.60 | ||
| Mineral | FMI_Spruce_2013_S | Sodankylä, FI | Forest | 10–15 | 9.44 | 84.8/0.2/0.0 | 1.06 | OH-A | 0.00–0.40 | ||
| FMI_Elbara_2013_S1 | Sodankylä, FI | Heath | 3–6 | 3.78 | 91.5/1.4/0.3 | 1.00 | A | 0.00–0.15 | |||
| FMI_Elbara_2013_S2 | Sodankylä, FI | Heath | 6–12 | 3.66 | 92.4/2.6/0.0 | 1.50 | A | 0.00–0.35 | |||
| HOBE_heath_2013_S | Gludsted, DK | Heath | 6–12 | 10.69 | 84.7/13.9/1.4 | 1.26 | OH-A | 0.10–0.50 | |||
| HOBE_nw_avg_S | Brande, DK | Cropland | 0–5 | 4.86 | 87.3/7.3/4.9 | 1.22 | A | 0.00–0.30 |
| Parameter | Description | Dobson Mineral Model | Mironov Mineral Model |
|---|---|---|---|
| T (°C) | Temperature | 20 | 20 |
| Sand (%) | Sand fraction | 88 | - |
| Clay (%) | Clay fraction | 1.3 | 1.3 |
| Rhob (g/cm3) | Dry soil bulk density | 1.27 | - |
| Rhos (g/cm3) | Dry solid soil particle density | 2.66 | - |
| Type | c1 | c2 | c3 | c4 | |
|---|---|---|---|---|---|
| Organic | ε′ | 50.69 | 18.81 | 25 | 1.636 |
| ε″ | 10.61 | −11.08 | 9.613 | 0.1211 | |
| Mineral | ε′ | 404.3 | −98.4 | 34.54 | 3.183 |
| ε″ | −7.946 | 14.51 | 3.29 | 0.3185 |
| Type | Model | N | R | Bias | UbRMSD | |
|---|---|---|---|---|---|---|
| Organic | Simple empirical model based on cavity measurements | ε′ | 87 | 0.96 | 2.80 × 10−15 | 4.8 |
| ε″ | 87 | 0.86 | 5.46 × 10−16 | 1.0 | ||
| Mironov et al. [30] | ε′ | 87 | 0.96 | 2.4 | 5.1 | |
| ε″ | 87 | 0.86 | −1.2 | 2.0 | ||
| Mironov and Savin [31] | ε′ | 87 | 0.96 | 7.1 | 8.4 | |
| ε″ | 87 | 0.86 | -0.1 | 1.0 | ||
| Mineral | Simple empirical model based on cavity measurements | ε′ | 20 | 0.98 | −5.33 × 10−15 | 1.8 |
| ε″ | 20 | 0.96 | 7.11 × 10−16 | 0.3 | ||
| Dobson et al. [16] | ε′ | 20 | 0.93 | −4.5 | 3.9 | |
| ε″ | 20 | 0.86 | −1.6 | 0.6 | ||
| Mironov et al. [18,19,20]/Mironov and Fomin [21] | ε′ | 20 | 0.96 | −0.6 | 2.7 | |
| ε″ | 20 | 0.96 | 0.6 | 0.5 | ||
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bircher, S.; Demontoux, F.; Razafindratsima, S.; Zakharova, E.; Drusch, M.; Wigneron, J.-P.; Kerr, Y.H. L-Band Relative Permittivity of Organic Soil Surface Layers—A New Dataset of Resonant Cavity Measurements and Model Evaluation. Remote Sens. 2016, 8, 1024. https://doi.org/10.3390/rs8121024
Bircher S, Demontoux F, Razafindratsima S, Zakharova E, Drusch M, Wigneron J-P, Kerr YH. L-Band Relative Permittivity of Organic Soil Surface Layers—A New Dataset of Resonant Cavity Measurements and Model Evaluation. Remote Sensing. 2016; 8(12):1024. https://doi.org/10.3390/rs8121024
Chicago/Turabian StyleBircher, Simone, François Demontoux, Stephen Razafindratsima, Elena Zakharova, Matthias Drusch, Jean-Pierre Wigneron, and Yann H. Kerr. 2016. "L-Band Relative Permittivity of Organic Soil Surface Layers—A New Dataset of Resonant Cavity Measurements and Model Evaluation" Remote Sensing 8, no. 12: 1024. https://doi.org/10.3390/rs8121024
APA StyleBircher, S., Demontoux, F., Razafindratsima, S., Zakharova, E., Drusch, M., Wigneron, J.-P., & Kerr, Y. H. (2016). L-Band Relative Permittivity of Organic Soil Surface Layers—A New Dataset of Resonant Cavity Measurements and Model Evaluation. Remote Sensing, 8(12), 1024. https://doi.org/10.3390/rs8121024