Automatic Sun Glint Removal of Multispectral High-Resolution Worldview-2 Imagery for Retrieving Coastal Shallow Water Parameters
Abstract
:1. Introduction
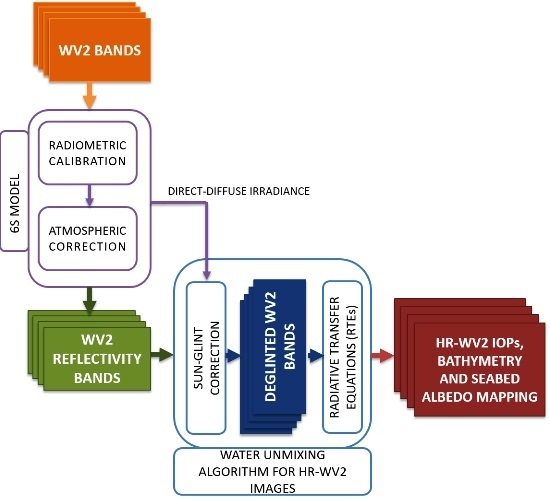
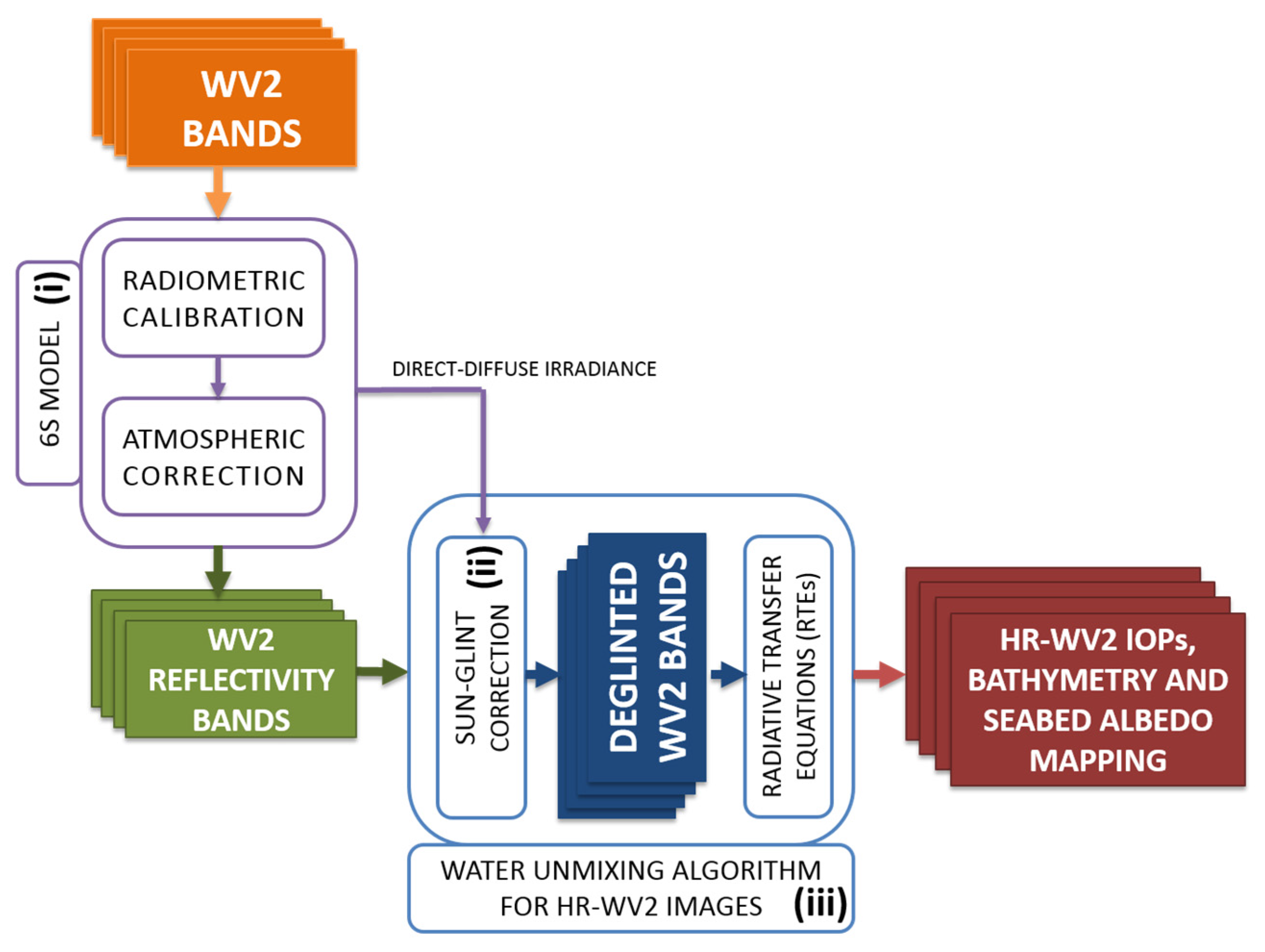
2. Methodology
- (i)
- A radiometric calibration and optimal atmospheric correction model.
- (ii)
- A novel automatic algorithm for sun glint removal based on physical modeling.
- (iii)
- A multichannel physics-based algorithm which integrates the new deglinting technique and the Radiative Transfer Equations for monitoring and mapping coastal shallow water parameters: Inherent Optical Properties, water depth and bottom reflectance.
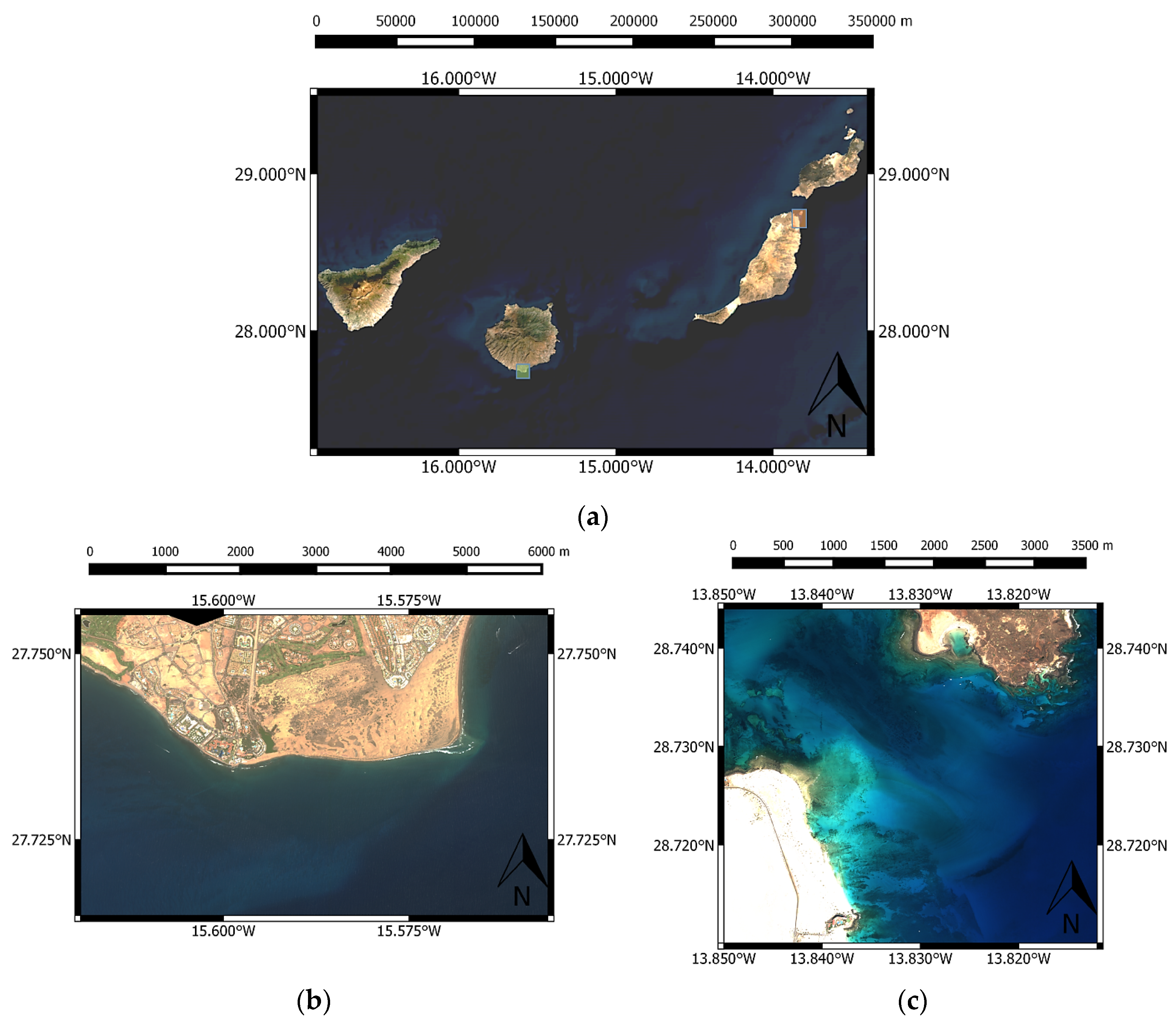
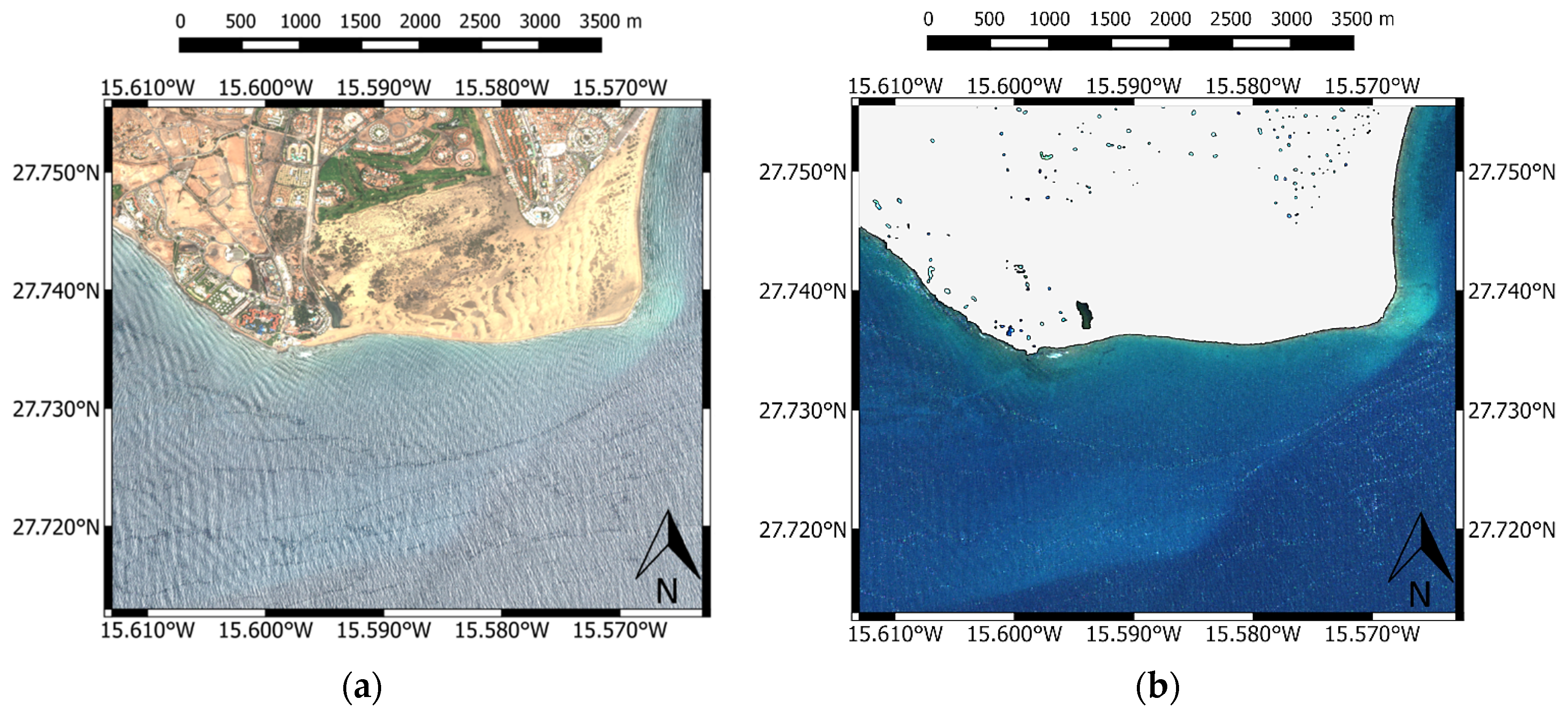
2.1. WorldView-2 Multispectral Imagery and Study Area
2.2. Atmospheric Correction Algorithm
2.3. Sun Glint Multispectral Data Correction Algorithm
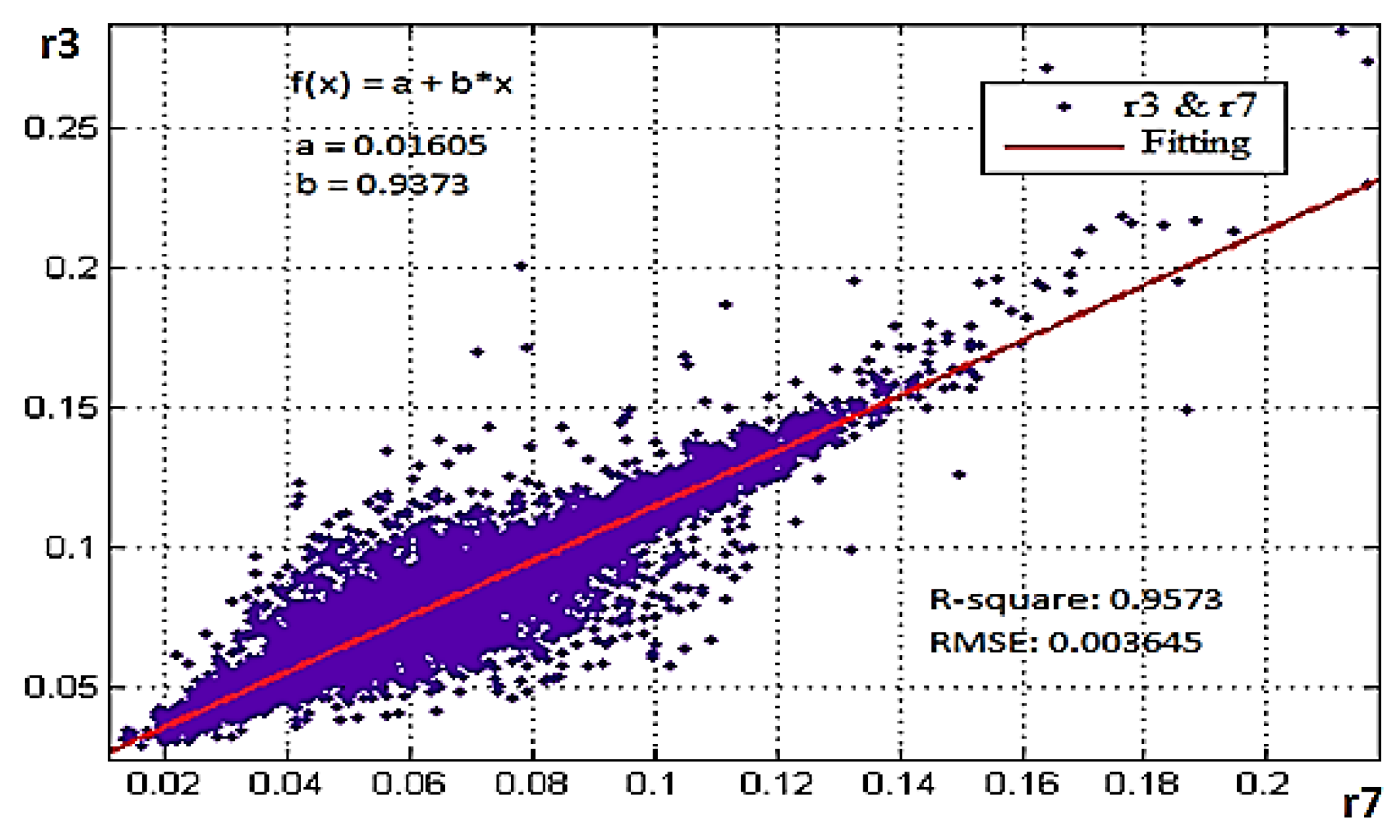
| R7 | R8 | R2 | a | b | min (ρTOC (NIR)) | |
|---|---|---|---|---|---|---|
| R1 | X | 0.8513 | 0.04074 | 0.7854 | 0.0064 | |
| R2 | X | 0.9561 | 0.03918 | 0.8943 | 0.0082 | |
| R3 | X | 0.9373 | 0.01605 | 0.9673 | 0.0082 | |
| R4 | X | 0.8836 | 0.01434 | 0.9848 | 0.0064 | |
| R5 | X | 0.9582 | 0.006162 | 1.003 | 0.0082 | |
| R6 | X | 0.7946 | 0.004212 | 1.007 | 0.0064 |
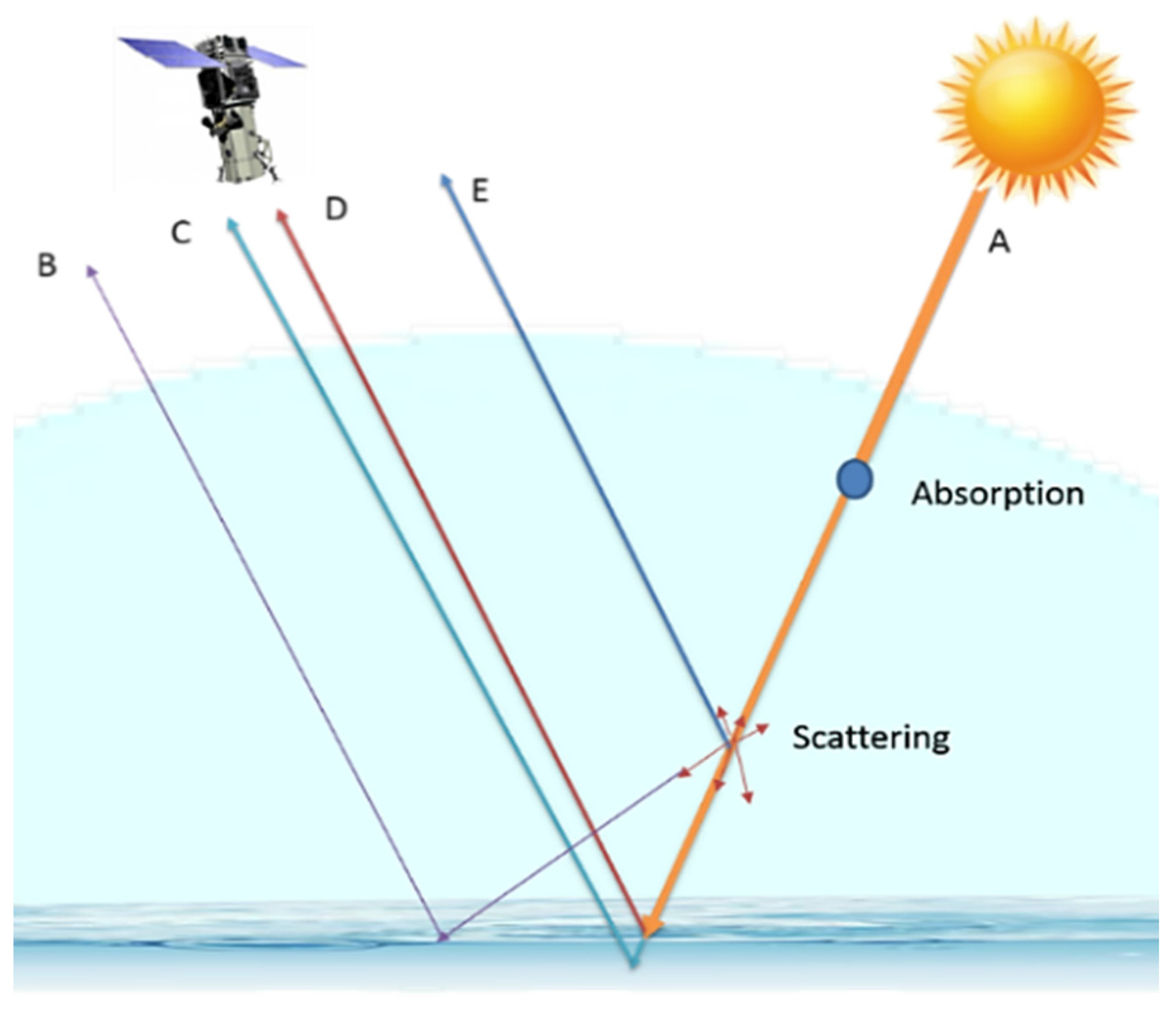
- ▪
- A-route is the down directed sun beam.
- ▪
- B-route is the scattering of the atmosphere to the water surface and then reflected to the satellite (sky-glint).
- ▪
- C-route is the water-leaving reflectance transmitted through the atmosphere and the air-water surface.
- ▪
- D-route is the specular reflection of the water surface (sun glint).
- ▪
- E-route is the single or multiple backscattering of the atmosphere (Rayleigh and aerosol).

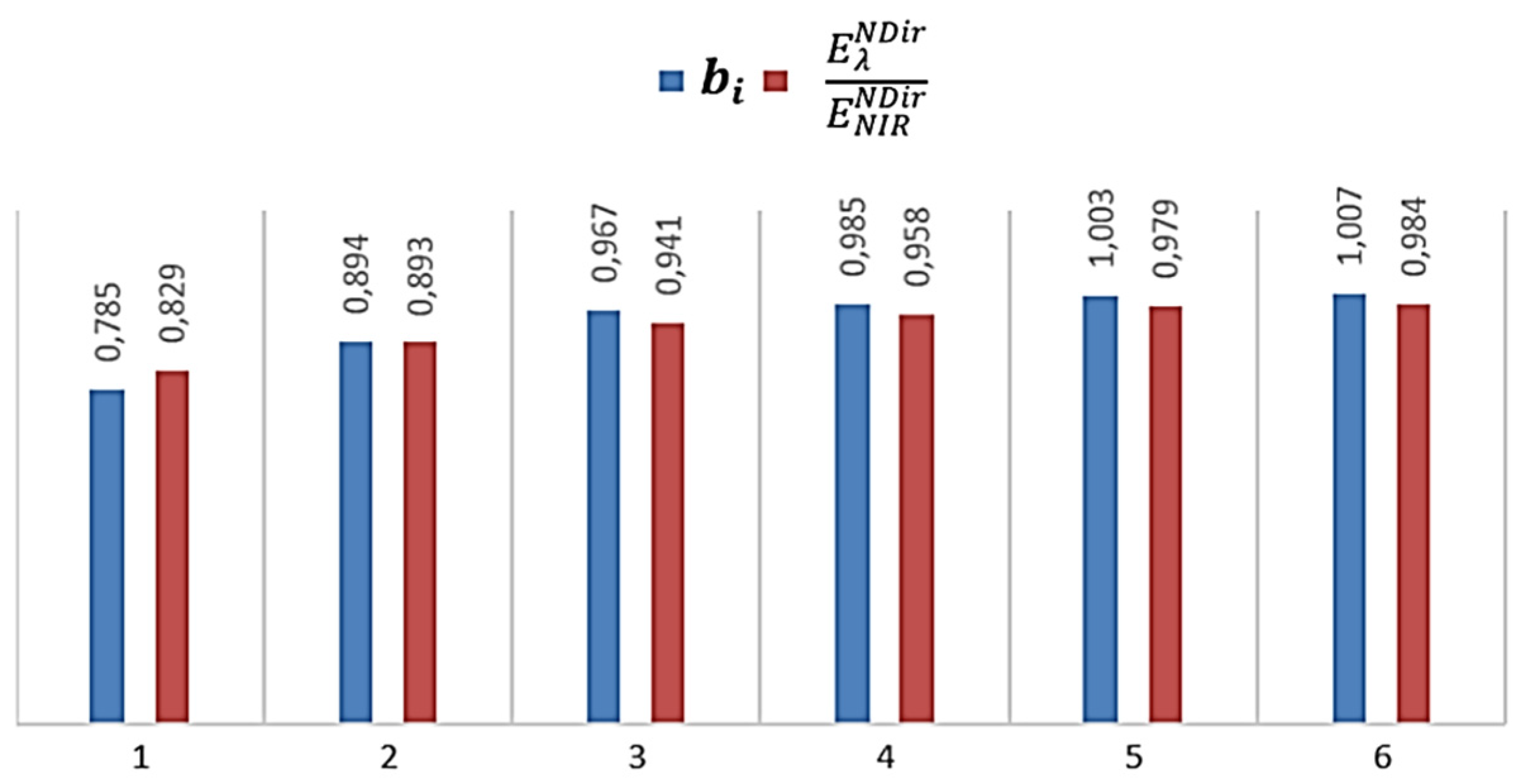
| R1 | R2 | R3 | R4 | R5 | R6 | R7 | R8 | |
|---|---|---|---|---|---|---|---|---|
| 0.214 | 0.158 | 0.114 | 0.091 | 0.077 | 0.067 | 0.058 | 0.052 | |
| 0.786 | 0.842 | 0.886 | 0.909 | 0.923 | 0.933 | 0.942 | 0.948 | |
| 0.829 | 0.893 | 0.941 | 0.958 | 0.979 | 0.984 | - | - |
2.4. Deglinting Algorithm Integrated into the Radiative Transfer Modeling (RTM)
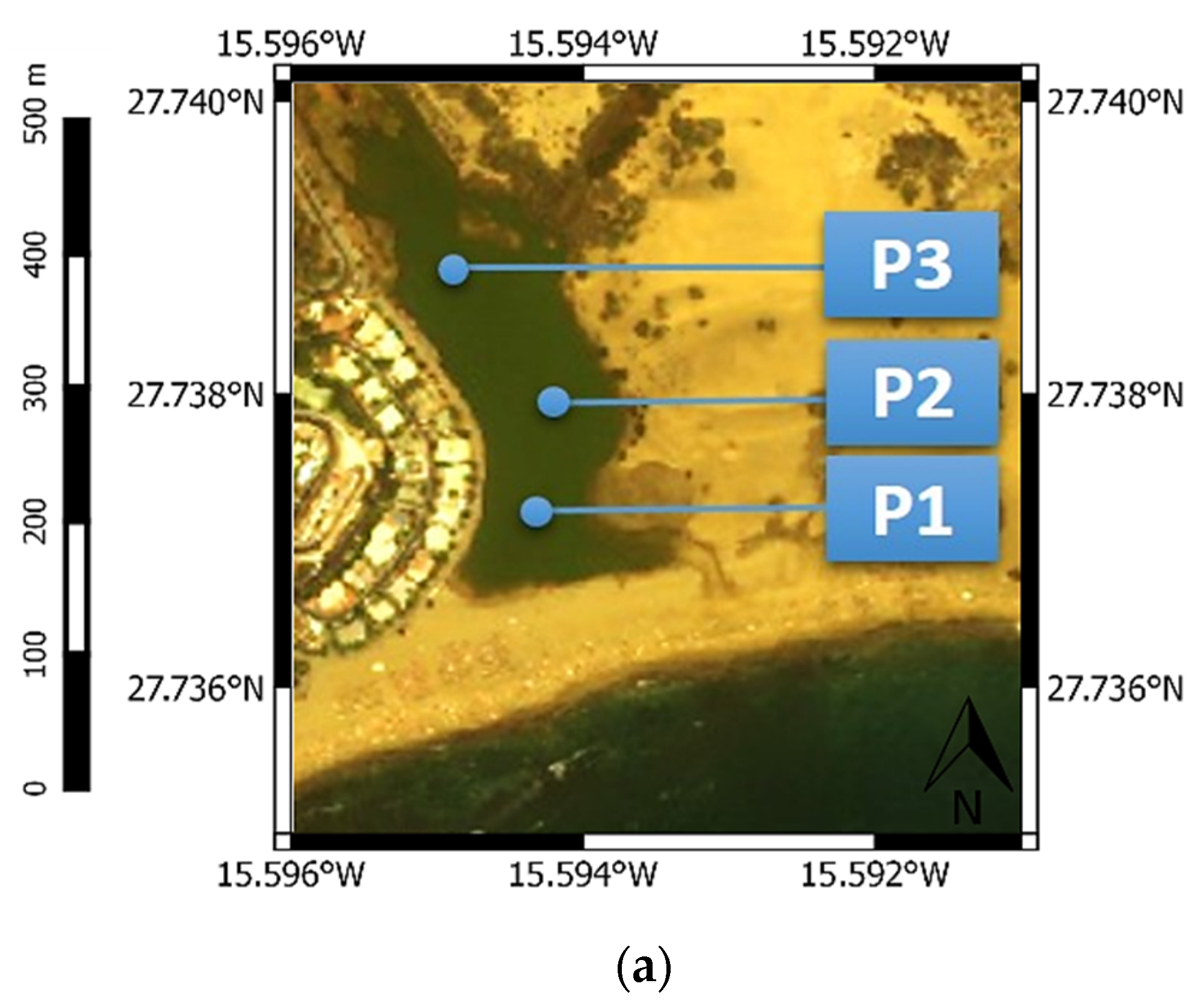
3. Results and Discussion
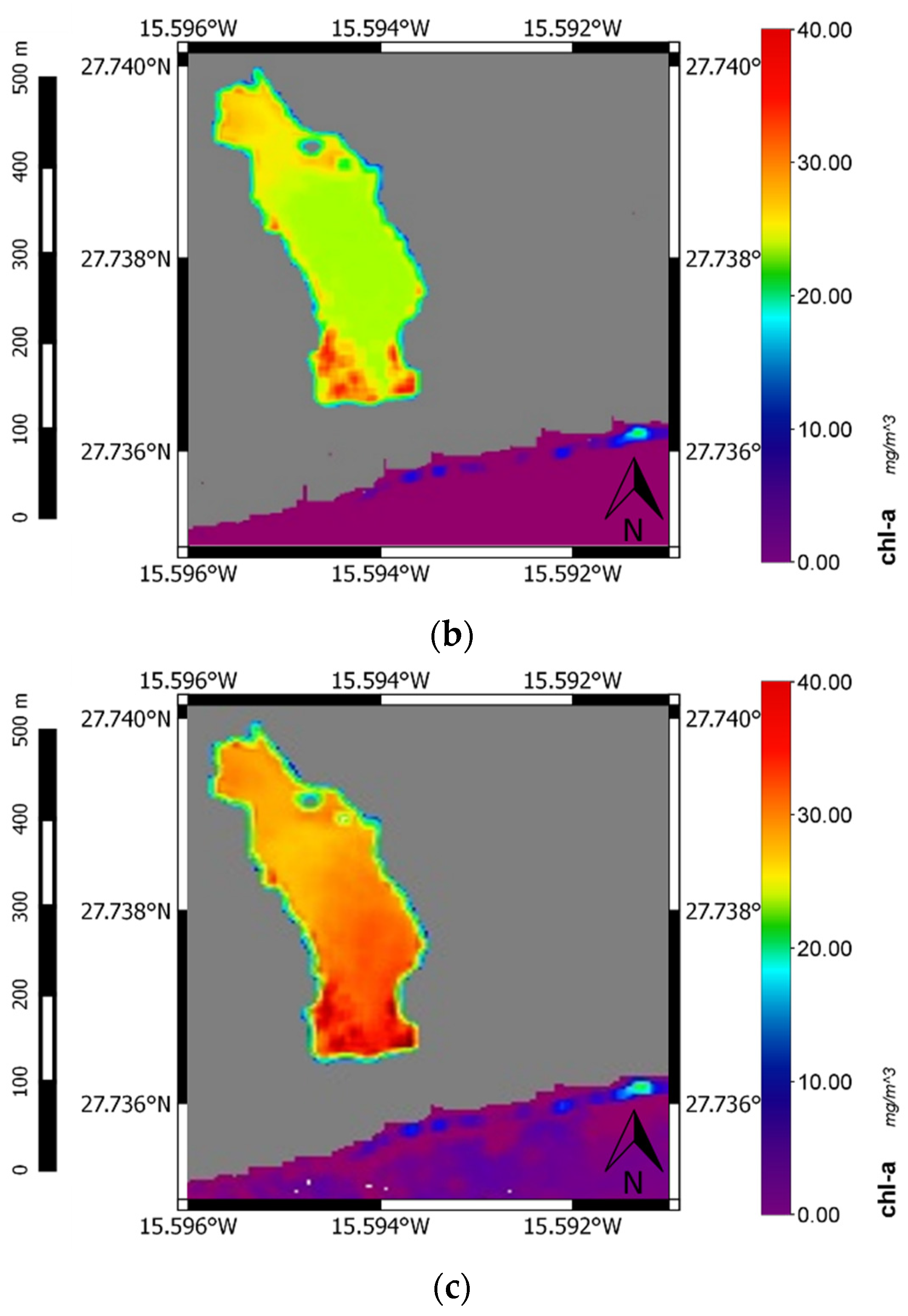
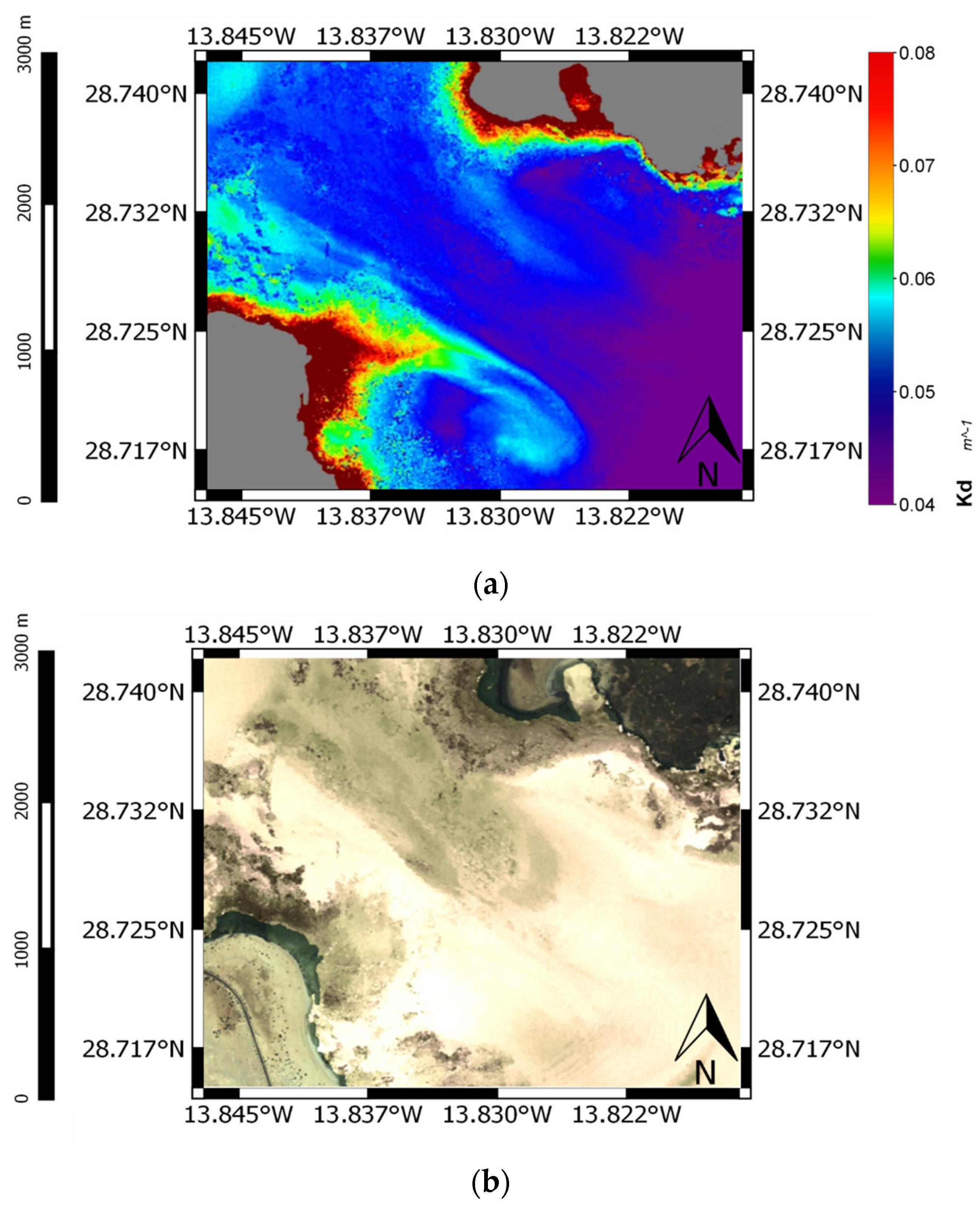
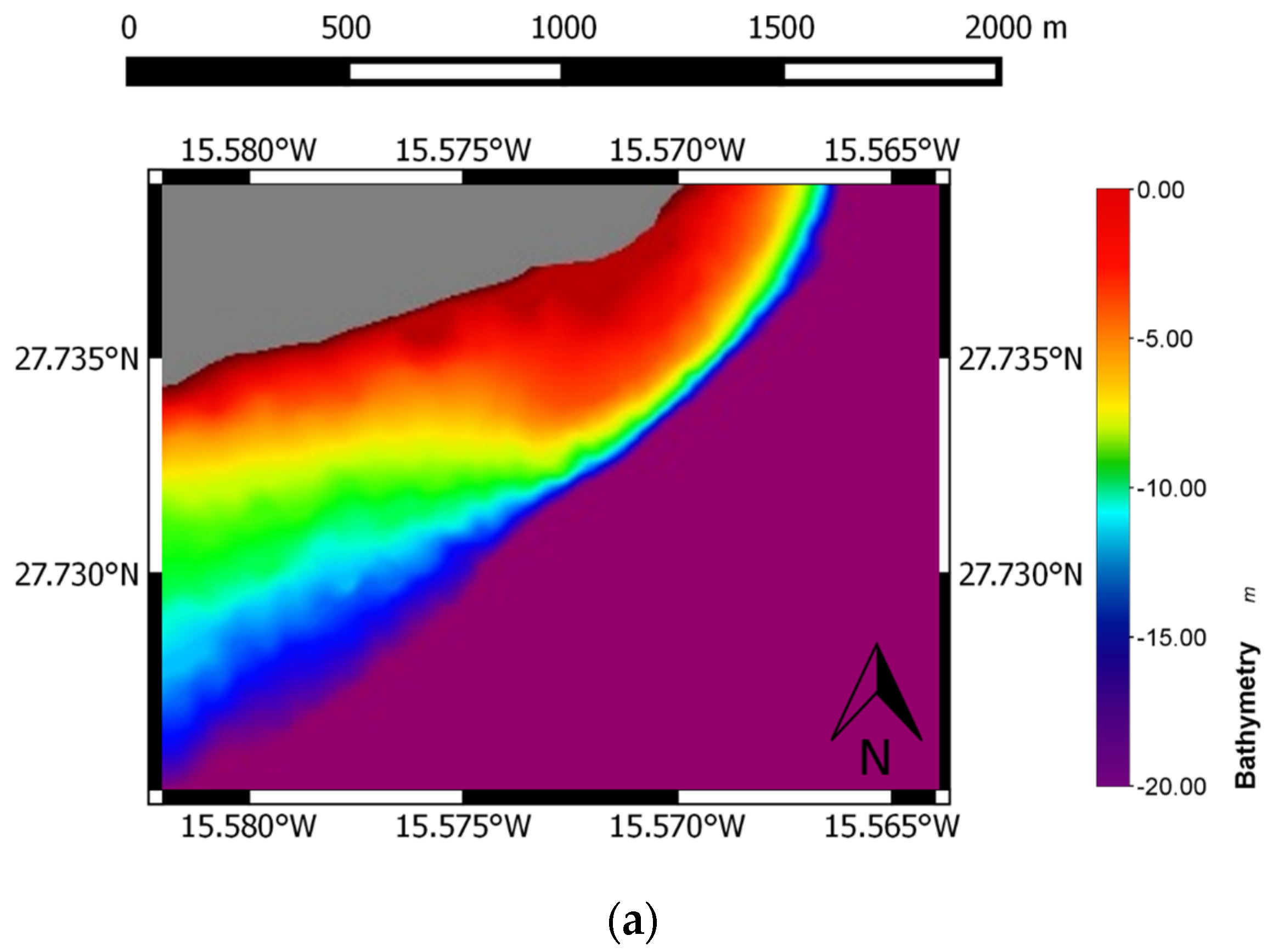

4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Richards, J.A. Remote Sensing Digital Image Analysis; Springer: Berlin, Germany, 2013. [Google Scholar]
- Miller, R.L.; del Castillo, C.; McKee, B. Remote Sensing of Coastal Aquatic Environments; Springer: Berlin, Germany, 2005. [Google Scholar]
- Abdolrassoul, S.; Mahiny, B.; Turner, J. A comparison of four common atmospheric correction methods. Photogramm. Eng. Remote Sens. 2007, 73, 361–368. [Google Scholar]
- Eugenio, F.; Marcello, J.; Martin, J. High-resolution maps of bathymetry and benthic habitats in shallow-water environments using multispectral remote sensing imagery. IEEE Trans. Geosci. Remote Sens. 2015, 53, 3539–3549. [Google Scholar] [CrossRef]
- Kay, S.; Hedley, J.; Lavender, S. Sun glint correction of high and low spatial resolution images of aquatic scenes: A review of methods for visible and near-infrared wavelengths. Remote Sens. 2009, 1, 697–730. [Google Scholar] [CrossRef]
- Adler-Golden, S.M.; Acharya, P.A.; Berk, A.; Matthew, M.; Gorodetzky, D. Remote bathymetry of the littoral zone from AVIRIS, LASH and QuickBird imagery. IEEE Trans. Geosci. Remote Sens. 2005, 43, 337–347. [Google Scholar] [CrossRef]
- Morel, A. Optical modeling of the upper ocean in relation to its biogenous matter content (case I waters). J. Geophys. Res. Oceans 1988, 93, 10749–10768. [Google Scholar] [CrossRef]
- Vermote, E.; Tanré, D.; Deuzé, J.L.; Herman, M.; Morcrette, J.J.; Kotchenova, S.Y. Second Simulation of a Satellite Signal in the Solar Spectrum-Vector (6SV). Available online: http://6s.ltdri.org/files/tutorial/6S_Manual_Part_1.pdf (accessed on 21 December 2015).
- Svetlana, Y.; Kotchenova, E.; Vermote, F.; Raffaella, M.; Klemm, F.J., Jr. Validation of vector version of 6s radiative transfer code for atmospheric correction of satellite data. Part I. Parth radiance. Appl. Opt. 2006, 45, 6762–6774. [Google Scholar]
- Mobley, C.D. Hydrolight 4.0 Users Guide; Sequoia Scientific Inc.: Mercer Island, WA, USA, 1998. [Google Scholar]
- Sokoletsky, L.G.; Fang, S. Optical closure for remote-sensing reflectance based on accurate radiative transfer approximations: The case of the Changjiang (Yangtze) River Estuary and its adjacent coastal area, China. Int. J. Remote Sens. 2014, 35, 4193–4224. [Google Scholar] [CrossRef]
- DigitalGlobe, Inc. Radiometric Use of WorldView-2 Imagery: Technical Note 2010. Available online: http://global.digitalglobe.com/sites/default/files/Radiometric_Use_of_WorldView-2_Imagery%20%281%29.pdf (accessed on 1 December 2015).
- Doxani, G.; Papadopoulou, M.; Lafazani, M.; Tsakiri-Strati, M.; Mavridou, E. Sun Glint Correction of Very High Spatial Resolution Images. Available online: https://www.researchgate.net/publication/258843930_Sun_glint_correction_of_very_high_spatial_resolution_images (accessed on 21 December 2015).
- Cornette, W.M.; Shanks, J. Physically reasonable analytic expression for the single-scattering phase function. Appl. Opt. 1992, 31, 3152–3160. [Google Scholar] [CrossRef] [PubMed]
- Cavalli, R.M.; Pignatti, S.; Zappitelli, E. Correction of sun glint effect on MIVIS data of the Sicily campaign in July 2000. Ann. Geophys. 2006, 49. [Google Scholar] [CrossRef]
- Cox, C.; Munk, W. Slopes of the Sea Surface Deduced from Photographs of Sun Glitter; Scripps Institution of Oceanography: San Diego, CA, USA, 1956. [Google Scholar]
- Garaba, S.P.; Zielinski, O. Methods in reducing surface reflected glint for shipborne above-water remote sensing. J. Eur. Opt. Soc. Rapid Publ. 2013, 8. [Google Scholar] [CrossRef]
- Maritorena, S.; Morel, A.; Gentilly, B. Diffuse reflectance of oceanic shallow waters: Influence of water depth and bottom albedo. Limn. Ocean. 1994, 39, 1689–1703. [Google Scholar] [CrossRef]
- Zhonping, L. Hyperspectral remote sensing for shallow waters: 2. Deriving bottom depths and water properties by optimization. Appl. Opt. 1999, 38, 3831–3843. [Google Scholar]
- Kokhanovsky, A.; Sokoletsky, L.G. Reflection of light from semi-infinite absorbing turbid media. Part 1: Spherical albedo. Color Res. Appl. 2006, 31, 491–497. [Google Scholar] [CrossRef]
- Reynolds, R.A.; Stramski, D.; Mitchell, B.G. A chlorophyll-dependent semianalytical reflectance model derived from field measurements of absorption and backscattering coefficients within the Southern Ocean. J. Geophys. Res. 2001, 106, 7125–7138. [Google Scholar] [CrossRef]
- Loisel, H.; Stramski, D.; Greg Mitchell, B.; Fell, F.; Fournier-Sicre, V.; Lemasle, B.; Babin, M. Comparison of the ocean inherent optical properties obtained from measurements and inverse modeling. Appl. Opt. 2001, 40, 2384–2397. [Google Scholar] [CrossRef] [PubMed]
- Gavin, H.P. The Levenberg-Marquardt Method for Nonlinear Least Squares Curve-Fitting Problems. Available online: http://people.duke.edu/~hpgavin/ce281/lm.pdf (accessed on 30 December 2015).
- Camacho, M.A. Depth Analysis of Midway Atoll Using QuickBird Multi-Spectral Imaging over Variable Substrates. Ph.D. Thesis, Naval Postgraduate School, Monterey, CA, USA, 2006. [Google Scholar]
- Marcello, J.; Eugenio, F.; Estrada-Allis, S.; Sangrà, P. Segmentation and tracking of anticyclonic eddies during a submarine volcanic eruption using ocean colour imagery. Sensors 2015, 15, 8732–8748. [Google Scholar] [CrossRef] [PubMed]
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons by Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Martin, J.; Eugenio, F.; Marcello, J.; Medina, A. Automatic Sun Glint Removal of Multispectral High-Resolution Worldview-2 Imagery for Retrieving Coastal Shallow Water Parameters. Remote Sens. 2016, 8, 37. https://doi.org/10.3390/rs8010037
Martin J, Eugenio F, Marcello J, Medina A. Automatic Sun Glint Removal of Multispectral High-Resolution Worldview-2 Imagery for Retrieving Coastal Shallow Water Parameters. Remote Sensing. 2016; 8(1):37. https://doi.org/10.3390/rs8010037
Chicago/Turabian StyleMartin, Javier, Francisco Eugenio, Javier Marcello, and Anabella Medina. 2016. "Automatic Sun Glint Removal of Multispectral High-Resolution Worldview-2 Imagery for Retrieving Coastal Shallow Water Parameters" Remote Sensing 8, no. 1: 37. https://doi.org/10.3390/rs8010037
APA StyleMartin, J., Eugenio, F., Marcello, J., & Medina, A. (2016). Automatic Sun Glint Removal of Multispectral High-Resolution Worldview-2 Imagery for Retrieving Coastal Shallow Water Parameters. Remote Sensing, 8(1), 37. https://doi.org/10.3390/rs8010037