Sensor Capability and Atmospheric Correction in Ocean Colour Remote Sensing
Abstract
:1. Introduction
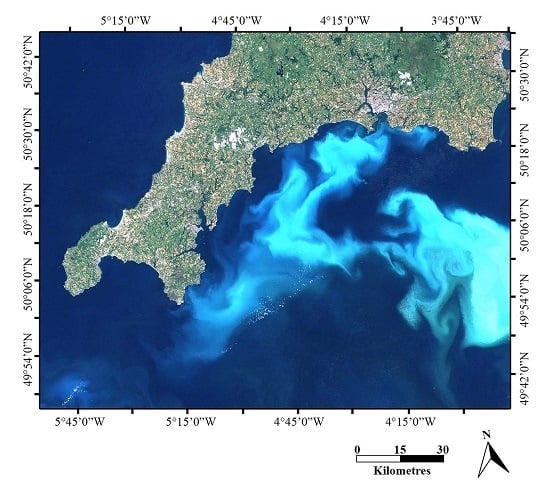
2. Ground-Based Sensors
2.1. Land-Based Sensors
2.2. Sea-Based Sensors
3. Remote Sensors
3.1. Sensor Resolutions
| Ref. | Sensor | No. of Bands | Spectral Range (nm) | Spatial Res. (m) | Coverage (km) | Orbit | Revisit (Days) | Location | Origin | Launch |
|---|---|---|---|---|---|---|---|---|---|---|
| [14] | CZCS | 5 and 1 | 433–800 and 10,000–12,500 | 825 | 1556 | Sun-sync | 6 | Nimbus 7 | USA | 1978 |
| [74] | AVIRIS | 224 | 410–2500 | N/A | N/A | N/A | N/A | Airborne | USA | 1987 |
| [75] | OCTS | 8 and 4 | 402–885 and 3550–12,700 | 700 | 1400 | Sun-sync | 41 | ADEOS | Japan | 1996 |
| [76] | SeaWiFS | 8 | 402–885 | 1100 | 2801 | Sun-sync | 1 | OrbView-2 | USA | 1997 |
| [77] | ETM+ | 8 | 450–2350 | 30/60 | 185 | Sun-sync | 16 | Landsat 7 | USA | 1999 |
| [78] | Hyperion | 220 | 400–2500 | 30 | 7.5 × 100 | Sun-sync | 16 | EO-1 | USA | 2000 |
| [79] | CHRIS | 19/63 | 415–1050 | 18/36 | 14 | Sun-sync | 7 | Proba-1 | EU | 2001 |
| [80] | MERIS | 15 | 390–1040 | 300/1200 | 1150 | Polar | 3 | Envisat-1 | EU | 2002 |
| [81] | MODIS Aqua | 19 and 16 | 405–2155 and 3660–14,385 | 250/500/1000 | 2330 | Sun-sync | 1–2 | EOS-PM | USA | 2002 |
| [82] | POLDER 3 | 15 | 443–1020 | 6000 | 2400 | Sun-sync | — | PARASOL | France | 2004 |
| [83] | AVIRIS-NG | 426 | 380–2510 | N/A | N/A | N/A | N/A | Airborne | USA | 2009 |
| [18] | HICO | 128 | 380–960 | 90 | ∼42 × 192 | ISS orbit | ∼10 | International Space Station | USA | 2009 |
| [84] | GOCI | 8 | 412–865 | 500 | 2500 | Geostationary | 1/24 | COMS | S. Korea | 2010 |
| [85] | VIIRS | 15 and 7 | 402–2280 and 3550–12,490 | 375/750 | 3000 | Sun-sync | 1 | S-NPP and JPSS | USA | 2011 |
| [86] | PRISM | 202 | 350–1050 and 1240, 1610 | N/A | N/A | N/A | N/A | Airborne | USA | 2012 |
| [77] | OLI/TIRS | 9 and 2 | 435–2294 and 10,600–12,510 | 30/60 | 185 | Sun-sync | 16 | Landsat 8 | USA | 2013 |
| [87] | SGLI | 19 | 380–865 | 250 | 1150 | Sun-sync | 1–3 | GCOM-C1 | Japan | 2017 |
| [88] | OLCI | 21 | 400–1020 | 300/1200 | 1270 | Sun-sync | ∼2 | Sentinel-3 | Europe | 2015 |
| [19] | HISUI (MSS) | 4 | 485–835 | 5 | 90 | Sun-sync | 60 | ALOS-3 | Japan | 2015 |
| [19] | HISUI (HSS) | 185 | 400–2500 | 30 | 30 | Sun-sync | 60 | ALOS-3 | Japan | 2015 |
| [20] | PRISMA | 237 | 400–2505 | 30 | 30 | Sun-sync | 3.5 | PRISMA | Italy | 2015 |
| [89] | EnMAP | 244 | 420–2450 | 30 | 30 | Sun-sync | 4 | EnMAP | Germany | 2017 |
| [91] | OCI | — | — | — | — | Polar | — | PACE | USA | 2018 |
| [92] | GOCI-II | 13 | 360–900 | 250 | 2500 | Geostationary | 1/48 | GeoKompsat2B | S. Korea | 2018 |
| [90] | OES | — | — | — | — | Polar | — | ACE | USA | >2020 |
| [93] | — | — | — | — | — | Geostationary | — | GEO-CAPE | USA | >2022 |
| [21] | HyspIRI | 212 | 380–2500 and 4000, 7500–12,000 | 30 | 185 | Sun-sync | 16 | HyspIRI | USA | >2022 |
3.2. Other Sensors
4. Sensors: Outlook
4.1. Sensor Resolutions
4.2. Other Sensors
5. Contributions to the Top-of-Atmosphere Signal

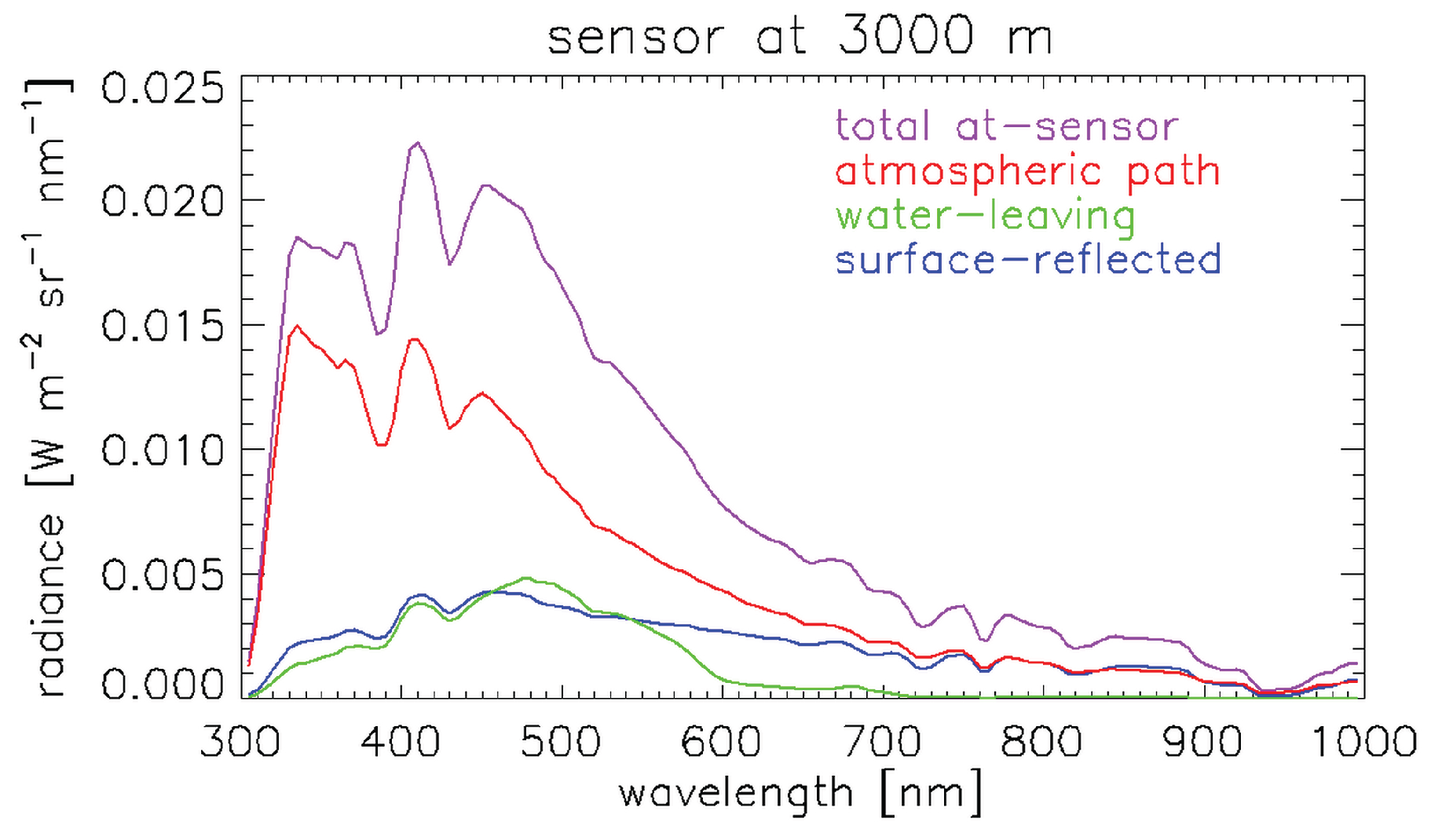
5.1. Atmospheric Contributions
5.2. Water Surface Effects
5.3. Clouds and Adjacency Effects
6. Multispectral Approaches for Atmospheric Correction
6.1. Black Pixel Approaches
| Ref. | Bands | Conditions | Comments |
|---|---|---|---|
| [205] | NIR | — | Optical model estimates normalised water-leaving radiance in the NIR bands |
| [110,206] | NIR | — | Assumes a spatial homogeneity exists in the ratios of two NIR bands |
| [150] | NIR | — | Based on a regional (Western Pacific) empirical relationship between the water-leaving radiance in the NIR and the diffuse attenuation coefficient at 490 nm |
| [207] | NIR | — | Improves performance by building upon the advantages of three methods [150,205,206] (e.g., aerosol reflectance ratios between two NIR bands are locally derived) |
| [39,208] | SWIR | TW | Resolves the black pixel assumption issue for atmospheric correction over turbid coastal and inland waters; limited by low SNR in SWIR bands of current sensors |
| [216] | SWIR | TW | Spatially averaged (5 × 5 grid) SWIR data improves MODIS SWIR SNR performance |
| [217] | SWIR | TW | Cross-calibration process uses a 5 × 5 grid of pixels from less turbid waters to calculate aerosol reflectance and type |
| [219] | SWIR | AA | Estimate of water-leaving radiance in the 412-nm channel of SeaWiFS constrains the aerosol retrieval model |
| [220] | NIR/SWIR | TW/AA | Uses pre-atmospheric correction step to find pixels corresponding to turbid waters or absorbing aerosols |
6.2. Spectral Inversion Approaches
6.3. Absorbing Aerosols
6.4. Multi-Purpose Approaches
7. Hyperspectral Approaches for Atmospheric Correction
7.1. Spectral Inversion Approaches
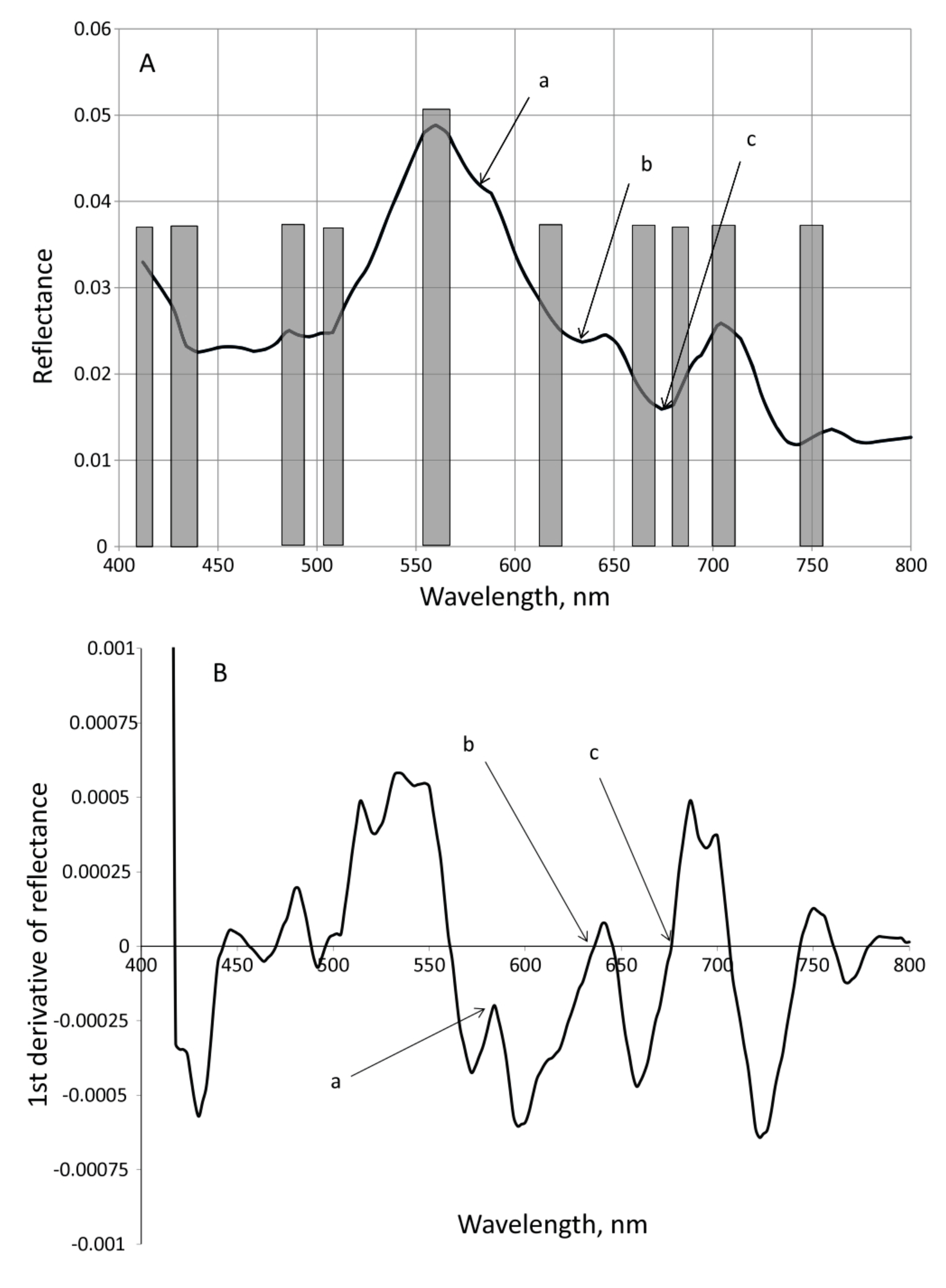
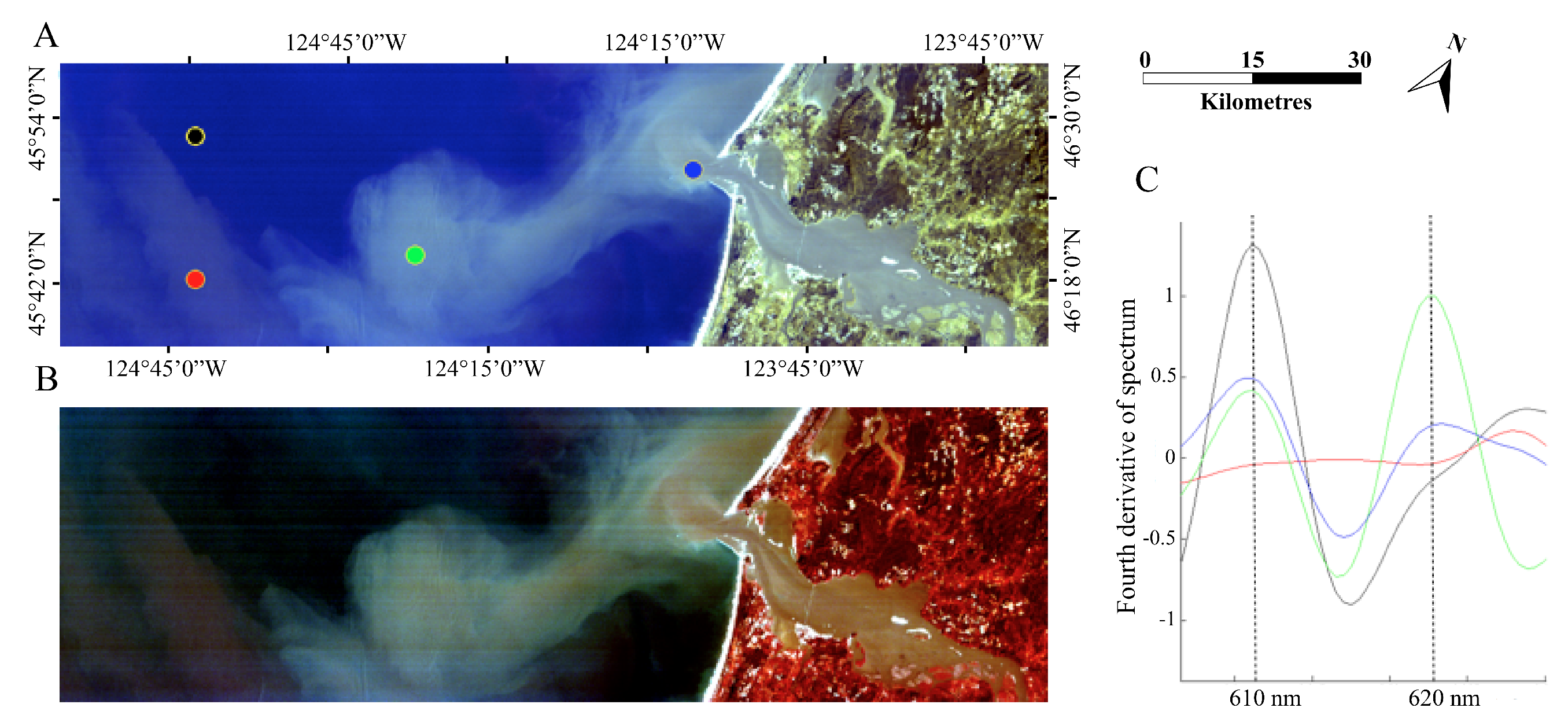
7.2. Derivative Spectroscopy
8. Conclusions
Acknowledgements
Author Contributions
Conflicts of Interest
References
- Goetz, A.F. Three decades of hyperspectral remote sensing of the Earth: A personal view. Remote Sens. Environ. 2009, 113, S5–S16. [Google Scholar] [CrossRef]
- Gordon, H.R.; Clark, D.K.; Mueller, J.L.; Hovis, W.A. Phytoplankton pigments from the Nimbus-7 Coastal Zone Color Scanner: comparisons with surface measurements. Science 1980, 210, 63–66. [Google Scholar] [CrossRef]
- McClain, C.R. A decade of satellite ocean color observations. Ann. Rev. Mar. Sci. 2009, 1, 19–42. [Google Scholar] [CrossRef]
- Aumann, H.H.; Gregorich, D.T.; Broberg, S.E.; Elliott, D.A. Seasonal correlations of SST, water vapor, and convective activity in tropical oceans: A new hyperspectral data set for climate model testing. Geophys. Res. Lett. 2007, 34, L15813. [Google Scholar] [CrossRef]
- Nagendra, H.; Lucas, R.; Honrado, J.P.; Jongman, R.H.; Tarantino, C.; Adamo, M.; Mairota, P. Remote sensing for conservation monitoring: Assessing protected areas, habitat extent, habitat condition, species diversity, and threats. Ecol. Indic. 2012, 33, 45–59. [Google Scholar] [CrossRef]
- Hochberg, E.J.; Atkinson, M.J.; Apprill, A.; Andrefouet, S. Spectral reflectance of coral. Coral Reefs 2004, 23, 84–95. [Google Scholar] [CrossRef]
- Stephens, F.C.; Louchard, E.M.; Reid, R.P.; Maffione, R.A. Effects of microalgal communities on reflectance spectra of carbonate sediments in subtidal optically shallow marine environments. Limnol. Oceanogr. 2003, 48, 535–546. [Google Scholar] [CrossRef]
- Corson, M.R.; Lucke, R.L.; Davis, C.O.; Bowles, J.H.; Chen, D.T.; Gao, B.C.; Snyder, W.A. The Hyperspectral Imager for the Coastal Ocean (HICO) environmental littoral imaging from the International Space Station. In Proceedings of the IEEE Geoscience and Remote Sensing Symposium, Honolulu, HI, USA, 25–30 July 2010; pp. 3752–3755.
- Shi, W.; Wang, M. Satellite views of the Bohai Sea, Yellow Sea, and East China Sea. Prog. Oceanogr. 2012, 104, 30–45. [Google Scholar] [CrossRef]
- Wang, M.; Shi, W.; Tang, J. Water property monitoring and assessment for China’s inland Lake Taihu from MODIS-Aqua measurements. Remote Sens. Environ. 2011, 115, 841–854. [Google Scholar] [CrossRef]
- Emmerson, P.; Ross, H. Colour constancy with change of viewing distance under water. Perception 1985, 14, 349–358. [Google Scholar] [CrossRef] [PubMed]
- Skorupski, P.; Chittka, L. Is colour cognitive? Opt. Laser Technol. 2011, 43, 251–260. [Google Scholar] [CrossRef]
- Schaepman, M.E.; Ustin, S.L.; Plaza, A.J.; Painter, T.H.; Verrelst, J.; Liang, S. Earth system science related imaging spectroscopy—An assessment. Remote Sens. Environ. 2009, 113, S123–S137. [Google Scholar] [CrossRef]
- Hovis, W.A.; Clark, D.K.; Anderson, F.; Austin, R.W.; Wilson, W.H.; Baker, E.T.; Ball, D.; Gordon, H.R.; Mueller, J.L.; El-Sayed, S.Z.; et al. Nimbus-7 Coastal Zone Color Scanner: system description and initial imagery. Science 1980, 210, 60–63. [Google Scholar] [CrossRef] [PubMed]
- McClain, C.R.; Feldman, G.C.; Hooker, S.B. An overview of the SeaWiFS project and strategies for producing a climate research quality global ocean bio-optical time series. Deep Sea Res. Pt. II: Top. Stud. Oceanogr. 2004, 51, 5–42. [Google Scholar] [CrossRef]
- Rast, M.; Bezy, J.L.; Bruzzi, S. The ESA Medium Resolution Imaging Spectrometer MERIS a review of the instrument and its mission. Int. J. Remote Sens. 1999, 20, 1681–1702. [Google Scholar] [CrossRef]
- Wang, M.; Liu, X.; Tan, L.; Jiang, L.; Son, S.; Shi, W.; Rausch, K.; Voss, K. Impact of VIIRS SDR performance on ocean color products. J. Geophys. Res. Atmos. 2013, 118, 10347–10360. [Google Scholar] [CrossRef]
- HICO. Available online: http://hico.coas.oregonstate.edu/ (accessed on 14 August 2015).
- HISUI. Available online: https://directory.eoportal.org/web/eoportal/satellite-missions/a/alos-3 (accessed on 14 August 2015).
- PRISMA. Available online: https://directory.eoportal.org/web/eoportal/satellite-missions/p/prisma-hyperspectral (accessed on 14 August 2015).
- HyspIRI. Available online: http://hyspiri.jpl.nasa.gov/ (accessed on 14 August 2015).
- Tsai, F.; Philpot, W. Derivative analysis of hyperspectral data. Remote Sens. Environ. 1998, 66, 41–51. [Google Scholar] [CrossRef]
- Gitelson, A.A.; Gao, B.C.; Li, R.R.; Berdnikov, S.; Saprygin, V. Estimation of chlorophyll-a concentration in productive turbid waters using a Hyperspectral Imager for the Coastal Ocean—The Azov Sea case study. Environ. Res. Lett. 2011, 6. [Google Scholar] [CrossRef]
- Matthews, M.W. A current review of empirical procedures of remote sensing in inland and near-coastal transitional waters. Int. J. Remote Sens. 2011, 32, 6855–6899. [Google Scholar] [CrossRef]
- Odermatt, D.; Gitelson, A.; Brando, V.E.; Schaepman, M. Review of constituent retrieval in optically deep and complex waters from satellite imagery. Remote Sens. Environ. 2012, 118, 116–126. [Google Scholar] [CrossRef] [Green Version]
- Hestir, E.L.; Brando, V.E.; Bresciani, M.; Giardino, C.; Matta, E.; Villa, P.; Dekker, A.G. Measuring freshwater aquatic ecosystems: The need for a hyperspectral global mapping satellite mission. Remote Sens. Environ. 2015, 167, 181–195. [Google Scholar] [CrossRef]
- Gordon, H.R.; Wang, M. Retrieval of water-leaving radiance and aerosol optical thickness over the oceans with SeaWiFS: A preliminary algorithm. Appl. Opt. 1994, 33, 443–452. [Google Scholar] [CrossRef] [PubMed]
- Mobley, C. Light and Water: Radiative Transfer in Natural Waters; Academic Press: San Diego, CA, USA, 1994. [Google Scholar]
- Wang, M. Remote sensing of the ocean contributions from ultraviolet to near-infrared using the shortwave infrared bands: Simulations. Appl. Opt. 2007, 46, 1535–1547. [Google Scholar] [CrossRef] [PubMed]
- IOCCG. Atmospheric Correction for Remotely-Sensed Ocean-Colour Products (Reports of the International Ocean-Colour Coordinating Group, No. 10); Technical Report; Wang, M., Ed.; IOCCG Project Office: Dartmouth, NS, Canada, 2010. [Google Scholar]
- O’Reilly, J.E.; Maritorena, S.; Mitchell, B.G.; Siegel, D.A.; Carder, K.L.; Garver, S.A.; Kahru, M.; McClain, C. Ocean color chlorophyll algorithms for SeaWiFS. J. Geophys. Res. Oceans (1978–2012) 1998, 103, 24937–24953. [Google Scholar] [CrossRef]
- Miller, R.L.; McKee, B. Using MODIS Terra 250 m imagery to map concentrations of total suspended matter in coastal waters. Remote Sens. Environ. 2004, 93, 259–266. [Google Scholar] [CrossRef]
- Son, S.; Wang, M. Water properties in Chesapeake Bay from MODIS-Aqua measurements. Remote Sens. Environ. 2012, 123, 163–174. [Google Scholar] [CrossRef]
- Zhang, M.; Tang, J.; Dong, Q.; Song, Q.; Ding, J. Retrieval of total suspended matter concentration in the Yellow and East China Seas from MODIS imagery. Remote Sens. Environ. 2010, 114, 392–403. [Google Scholar] [CrossRef]
- Lee, Z.; Carder, K.L.; Arnone, R.A. Deriving inherent optical properties from water color: A multiband quasi-analytical algorithm for optically deep waters. Appl. Opt. 2002, 41, 5755–5772. [Google Scholar] [CrossRef] [PubMed]
- Maritorena, S.; Siegel, D.A.; Peterson, A.R. Optimization of a semianalytical ocean color model for global-scale applications. Appl. Opt. 2002, 41, 2705–2714. [Google Scholar] [CrossRef] [PubMed]
- Groom, S. Landsat 7 False Colour Image; NERC EO Data Acquisition and Analysis Service: Plymouth, UK, 1999. [Google Scholar]
- Chang, G.; Mahoney, K.; Briggs-Whitmire, A.; Kohler, D.; Mobley, C.; Lewis, M.; Moline, M.; Boss, E.; Kim, M.; Philpot, W.; et al. The new age of hyperspectral oceanography. Oceanography 2004, 17, 22–29. [Google Scholar] [CrossRef]
- Shi, W.; Wang, M. An assessment of the black ocean pixel assumption for MODIS SWIR bands. Remote Sens. Environ. 2009, 113, 1587–1597. [Google Scholar] [CrossRef]
- Wang, M.; Son, S.; Shi, W. Evaluation of MODIS SWIR and NIR-SWIR atmospheric correction algorithm using SeaBASS data. Remote Sens. Environ. 2009, 113, 635–644. [Google Scholar] [CrossRef]
- Jamet, C.; Loisel, H.; Kuchinke, C.P.; Ruddick, K.; Zibordi, G.; Feng, H. Comparison of three SeaWiFS atmospheric correction algorithms for turbid waters using AERONET-OC measurements. Remote Sens. Environ. 2011, 115, 1955–1965. [Google Scholar] [CrossRef]
- Goyens, C.; Jamet, C.; Schroeder, T. Evaluation of four atmospheric correction algorithms for MODIS-Aqua images over contrasted coastal waters. Remote Sens. Environ. 2013, 131, 63–75. [Google Scholar] [CrossRef]
- Wang, M.; Shi, W. Estimation of ocean contribution at the MODIS near-infrared wavelengths along the east coast of the U.S.: Two case studies. Geophys. Res. Lett. 2005, 32, L13606. [Google Scholar] [CrossRef]
- Wang, M.; Shi, W. The NIR-SWIR combined atmospheric correction approach for MODIS ocean color data processing. Opt. Express 2007, 15, 15722–15733. [Google Scholar] [CrossRef] [PubMed]
- Loisel, H.; Vantrepotte, V.; Jamet, C.; Dat, D.N. Challenges and new advances in ocean color remote sensing of coastal waters. In Topics in Oceanography; Zambianchi, E., Ed.; InTechOpen: Rijeka, Croatia, 2013. [Google Scholar]
- Mouw, C.B.; Greb, S.; Aurin, D.; DiGiacomo, P.M.; Lee, Z.; Twardowski, M.; Binding, C.; Hu, C.; Ma, R.; Moore, T.; et al. Aquatic color radiometry remote sensing of coastal and inland waters: Challenges and recommendations for future satellite missions. Remote Sens. Environ. 2015, 160, 15–30. [Google Scholar] [CrossRef]
- Zibordi, G.; Mélin, F.; Berthon, J.F.; Holben, B.; Slutsker, I.; Giles, D.; D’Alimonte, D.; Vandemark, D.; Feng, H.; Schuster, G.; et al. AERONET-OC: A network for the validation of ocean color primary products. J. Atmos. Oceanic Technol. 2009, 26, 1634–1651. [Google Scholar] [CrossRef]
- Gordon, H.R. In-orbit calibration strategy for ocean color sensors. Remote Sens. Environ. 1998, 63, 265–278. [Google Scholar] [CrossRef]
- Wang, M.; Gordon, H.R. Calibration of ocean color scanners: How much error is acceptable in the near-infrared. Remote Sens. Environ. 2002, 82, 497–504. [Google Scholar] [CrossRef]
- Franz, B.A.; Bailey, S.W.; Werdell, P.J.; McClain, C.R. Sensor-independent approach to the vicarious calibration of satellite ocean color radiometry. Appl. Opt. 2007, 46, 5068–5082. [Google Scholar] [CrossRef]
- Lewis, D.; Gould, R.W., Jr.; Ladner, S.D.; Lawson, T.A.; Martinolich, P. Vicarious Calibration of the Hyperspectral Imager for Coastal Oceans (HICO) Using MOBY and AERONET-OC Data; Technical Report, NRL/PP/7330–12–1391; Naval Research Lab, Stennis Detachment, Stennis Space Center: Hancock County, MS, USA, 2012. [Google Scholar]
- Clark, D.K.; Gordon, H.R.; Voss, K.J.; Ge, Y.; Broenkow, W.; Trees, C. Validation of atmospheric correction over the ocean. J. Geophys. Res. Atmos. (1984–2012) 1997, 102, 17209–17217. [Google Scholar] [CrossRef]
- Clark, D.K.; Yarbrough, M.A.; Feinholz, M.; Flora, S.; Broenkow, W.; Kim, Y.S.; Johnson, B.C.; Brown, S.W.; Yuen, M.; Mueller, J.L. MOBY, A Radiometric Buoy for Performance Monitoring and Vicarious Calibration of Satellite Ocean Color Sensors: Measurement and Data Analysis Protocols; Technical Report, NASA/TM–2003–211621/Rev4–Vol. IV; NASA Goddard Space Flight Center: Greenbelt, MD, USA, 2002. [Google Scholar]
- Holben, B.N.; Eck, T.F.; Slutsker, I.; Tanre, D.; Buis, J.P.; Setzer, A.; Smirnov, A. AERONET—A federated instrument network and data archive for aerosol characterization. Remote Sens. Environ. 1998, 66, 1–16. [Google Scholar] [CrossRef]
- AERONET-OC. Available online: http://aeronet.gsfc.nasa.gov/new_web/ocean_color.html (accessed on 14 August 2015).
- Smirnov, A.; Holben, B.N.; Slutsker, I.; Giles, D.M.; McClain, C.R.; Eck, T.F.; Sakerin, S.M.; Macke, A.; Croot, P.; Zibordi, G.; et al. Maritime aerosol network as a component of aerosol robotic network. J. Geophys. Res. Atmos. (1984–2012) 2009, 114, D06204. [Google Scholar] [CrossRef]
- Kleidman, R.G.; Smirnov, A.; Levy, R.C.; Mattoo, S.; Tanre, D. Evaluation and wind speed dependence of MODIS aerosol retrievals over open oceans. IEEE Trans. Geosci. Remote Sens. 2012, 50, 429–435. [Google Scholar] [CrossRef]
- Antoine, D.; Guevel, P.; Deste, J.F.; Becu, G.; Louis, F.; Scott, A.J.; Bardey, P. The “BOUSSOLE” buoy-a new transparent-to-swell taut mooring dedicated to marine optics: Design, tests, and performance at sea. J. Atmos. Oceanic Technol. 2008, 25, 968–989. [Google Scholar] [CrossRef]
- Clark, D.K.; Feinholz, M.; Yarbrough, M.; Johnson, B.C.; Brown, S.W.; Kim, Y.S.; Barnes, R.A. Overview of the radiometric calibration of MOBY. Proc. SPIE 2002, 4483, 64–76. [Google Scholar]
- MOBY. Available online: http://moby.mlml.calstate.edu/MOBY-data (accessed on 14 August 2015).
- Eplee, R.E., Jr.; Robinson, W.D.; Bailey, S.W.; Clark, D.K.; Werdell, P.J.; Wang, M.; Barnes, R.A.; McClain, C.R. Calibration of SeaWiFS. II: Vicarious techniques. Appl. Opt. 2001, 40, 6701–6718. [Google Scholar] [CrossRef] [PubMed]
- Wang, M.; Isaacman, A.; Franz, B.A.; McClain, C.R. Ocean color optical property data derived from the Japanese Ocean Color and Temperature Scanner and the French Polarization and Directionality of the Earth’s Reflectances: A comparison study. Appl. Opt. 2002, 41, 974–990. [Google Scholar] [CrossRef]
- CoastWatch. Available online: http://coastwatch.noaa.gov/moby/ (accessed on 14 August 2015).
- Wang, M.; Shi, W.; Jiang, L.; Liu, X.; Son, S.; Voss, K. Technique for monitoring performance of VIIRS reflective solar bands for ocean color data processing. Opt. Express 2015, 23, 14446–14460. [Google Scholar] [CrossRef]
- Zibordi, G.; Melin, F.; Voss, K.; Johnson, B.C.; Franz, B.A.; Kwiatkowska, E.; Huot, J.P.; Wang, M.; Antoine, D. System vicarious calibration for ocean color climate change applications: Requirements for in situ data. Remote Sens. Environ. 2015, 159, 361–369. [Google Scholar] [CrossRef]
- Argo. Available online: http://www.argo.ucsd.edu (accessed on 14 August 2015).
- IOCCG. Bio-Optical Sensors on Argo Floats (Reports of the International Ocean-Colour Coordinating Group, No. 11); Technical Report; IOCCG Project Office: Dartmouth, NS, Canada, 2011. [Google Scholar]
- Xing, X.; Claustre, H.; Wang, H.; Poteau, A.; D’Ortenzio, F. Seasonal dynamics in colored dissolved organic matter in the Mediterranean Sea: Patterns and drivers. Deep Sea Res. Pt. I: Oceanogr. Res. Pap. 2014, 83, 93–101. [Google Scholar] [CrossRef]
- Mignot, A.; Claustre, H.; Uitz, J.; Poteau, A.; D’Ortenzio, F.; Xing, X. Understanding the seasonal dynamics of phytoplankton biomass and the deep chlorophyll maximum in oligotrophic environments: A Bio-Argo float investigation. Global Biogeochem. Cycles 2014, 28, 856–876. [Google Scholar] [CrossRef]
- Xing, X.; Claustre, H.; Uitz, J.; Mignot, A.; Poteau, A.; Wang, H. Seasonal variations of bio-optical properties and their interrelationships observed by Bio-Argo floats in the subpolar North Atlantic. J. Geophys. Res. Oceans 2014, 119, 7372–7388. [Google Scholar] [CrossRef]
- D’Ortenzio, F.; Lavigne, H.; Besson, F.; Claustre, H.; Coppola, L.; Garcia, N.; Laes-Huon, A.; Reste, S.L.; Malarde, D.; Migon, C.; et al. Observing mixed layer depth, nitrate and chlorophyll concentrations in the northwestern Mediterranean: A combined satellite and NO3 profiling floats experiment. Geophys. Res. Lett. 2014, 41, 6443–6451. [Google Scholar] [CrossRef]
- Blockstein, L.; Yadid-Pecht, O. Lensless miniature portable fluorometer for measurement of chlorophyll and CDOM in water using fluorescence contact imaging. IEEE Photon. J. 2014, 6, 1–16. [Google Scholar]
- Werdell, J. SeaWiFS Bio—Optical Archive and Storage System (SeaBASS). Available online: http://seabass.gsfc.nasa.gov (accessed on 14 August 2015).
- AVIRIS. Available online: http://aviris.jpl.nasa.gov/ (accessed on 14 August 2015).
- OCTS. Available online: http://oceancolor.gsfc.nasa.gov/cms/data/octs (accessed on 14 August 2015).
- SeaWiFS. Available online: http://oceancolor.gsfc.nasa.gov/SeaWiFS/ (accessed on 14 August 2015).
- Landsat. Available online: http://landsat.gsfc.nasa.gov/ (accessed on 14 August 2015).
- Hyperion. Available online: http://eo1.usgs.gov/sensors/hyperion (accessed on 14 August 2015).
- CHRIS. Available online: https://earth.esa.int/web/guest/missions/esa-operational-eo-missions/proba/instruments/chris (accessed on 14 August 2015).
- MERIS. Available online: https://earth.esa.int/web/guest/missions/esa-operational-eo-missions/envisat/instruments/meris (accessed on 14 August 2015).
- MODIS. Available online: http://modis.gsfc.nasa.gov/ (accessed on 14 August 2015).
- POLDER. Available online: http://smsc.cnes.fr/PARASOL/ (accessed on 14 August 2015).
- AVIRIS-NG. Available online: http://avirisng.jpl.nasa.gov/ (accessed on 14 August 2015).
- GOCI. Available online: http://kosc.kiost.ac/kosc_eng/main/ (accessed on 14 August 2015).
- Cao, C.; De Luccia, F.J.; Xiong, X.; Wolfe, R.; Weng, F. Early on-orbit performance of the Visible Infrared Imaging Radiometer Suite onboard the Suomi National Polar-Orbiting Partnership (S-NPP) satellites. IEEE Trans. Geosci. Remote Sens. 2014, 52, 1142–1156. [Google Scholar] [CrossRef]
- PRISM. Available online: http://prism.jpl.nasa.gov/index.html (accessed on 14 August 2015).
- Imaoka, K.; Kachi, M.; Fujii, H.; Murakami, H.; Hori, M.; Ono, A.; Igarashi, T.; Nakagawa, K.; Oki, T.; Honda, Y.; et al. Global Change Observation Mission (GCOM) for monitoring carbon, water cycles, and climate change. Proc. IEEE 2010, 98, 717–734. [Google Scholar] [CrossRef]
- OLCI. Available online: https://earth.esa.int/web/guest/missions/esa-future-missions/sentinel-3 (accessed on 14 August 2015).
- EnMap. Available online: http://www.enmap.org/ (accessed on 14 August 2015).
- ACE. Available online: http://neptune.gsfc.nasa.gov/osb/index.php?section=241 (accessed on 14 August 2015).
- PACE. Pre-Aerosol, Clouds, and Ocean Ecosystem (PACE) Mission Science Definition Team Report; Technical Report; NASA Goddard Space Flight Center: Greenbelt, MD, USA, 2012. [Google Scholar]
- GOCI-II. Available online: http://www.wmo-sat.info/oscar/instruments/view/674 (accessed on 14 August 2015).
- GEO-CAPE. Available online: http://geo-cape.larc.nasa.gov/ (accessed on 14 August 2015).
- Suomalainen, J.; Anders, N.; Iqbal, S.; Roerink, G.; Franke, J.P.; Wenting, P.; Hunniger, D.; Bartholomeus, H.; Becker, R.; Kooistra, L. A lightweight hyperspectral mapping system and photogrammetric processing chain for Unmanned Aerial Vehicles. Remote Sens. 2014, 6, 11013–11030. [Google Scholar] [CrossRef]
- Bissett, W.P.; Arnone, R.A.; Davis, C.O.; Dickey, T.D.; Dye, D.; Kohler, D.D.; Gould, R.W. From meters to milometers: A look at ocean-color scales of variability, spatial coherence, and the need for fine-scale remote sensing in coastal ocean optics. Oceanography 2004, 17, 32–42. [Google Scholar] [CrossRef] [Green Version]
- Davis, C.O.; Kavanaugh, M.; Letelier, R.; Bissett, W.P.; Kohler, D. Spatial and spectral resolution considerations for imaging coastal waters. Proc. SPIE 2007, 6680. [Google Scholar] [CrossRef] [Green Version]
- Chen, J.; Fu, J.; Zhang, M. An atmospheric correction algorithm for Landsat/TM imagery basing on inverse distance spatial interpolation algorithm: A case study in Taihu Lake. IEEE J. Sel. Top. Appl. Earth Observ. 2012, 4, 882–889. [Google Scholar] [CrossRef]
- Hu, C.; Muller-Karger, F.E.; Andrefouet, S.; Carder, K.L. Atmospheric correction and cross-calibration of LANDSAT-7/ETM+ imagery over aquatic environments: A multiplatform approach using SeaWiFS/MODIS. Remote Sens. Environ. 2001, 78, 99–107. [Google Scholar] [CrossRef]
- Vanhellemont, Q.; Ruddick, K. Turbid wakes associated with offshore wind turbines observed with Landsat 8. Remote Sens. Environ. 2014, 145, 105–115. [Google Scholar] [CrossRef]
- Guanter, L.; Segl, K.; Kaufmann, H. Simulation of optical remote-sensing scenes with application to the EnMAP hyperspectral mission. IEEE Trans. Geosci. Remote Sens. 2009, 47, 2340–2351. [Google Scholar] [CrossRef]
- Hu, C.; Feng, L.; Lee, Z.; Davis, C.O.; Mannino, A.; McClain, C.R.; Franz, B.A. Dynamic range and sensitivity requirements of satellite ocean color sensors: Learning from the past. Appl. Opt. 2012, 51, 6045–6062. [Google Scholar] [CrossRef]
- Moses, W.J.; Gitelson, A.A.; Berdnikov, S.; Bowles, J.H.; Povazhnyi, V.; Saprygin, V.; Wagner, E.J.; Patterson, K.W. HICO-based NIR-red models for estimating chlorophyll-concentration in productive coastal waters. IEEE Geosci. Remote Sens. Lett. 2014, 11, 1111–1115. [Google Scholar] [CrossRef]
- Mallinis, G.; Galidaki, G.; Gitas, I. A comparative analysis of EO-1 Hyperion, Quickbird and Landsat TM imagery for fuel type mapping of a typical Mediterranean landscape. Remote Sens. 2014, 6, 1684–1704. [Google Scholar] [CrossRef]
- Gao, B.C.; Li, R.R. Removal of thin cirrus scattering effects for remote sensing of ocean color from space. IEEE Geosci. Remote Sens. Lett. 2012, 9, 972–976. [Google Scholar]
- Moses, W.J.; Gitelson, A.A.; Perk, R.L.; Gurlin, D.; Rundquist, D.C.; Leavitt, B.C.; Barrow, T.M.; Brakhage, P. Estimation of chlorophyll-a concentration in turbid productive waters using airborne hyperspectral data. Water Res. 2012, 46, 993–1004. [Google Scholar] [CrossRef] [PubMed]
- Ryan, J.P.; Davis, C.O.; Tufillaro, N.B.; Kudela, R.M.; Gao, B.C. Application of the Hyperspectral Imager for the Coastal Ocean to phytoplankton ecology studies in Monterey Bay, CA, USA. Remote Sens. 2014, 6, 1007–1025. [Google Scholar] [CrossRef]
- Braga, F.; Giardino, C.; Bassani, C.; Matta, E.; Candiani, G.; Strömbeck, N.; Adamo, M.; Bresciani, M. Assessing water quality in the northern Adriatic Sea from HICO data. Remote Sens. Lett. 2013, 4, 1028–1037. [Google Scholar] [CrossRef]
- Cho, H.J.; Ogashawara, I.; Mishra, D.; White, J.; Kamerosky, A.; Morris, L.; Clarke, C.; Simpson, A.; Banisakher, D. Evaluating Hyperspectral Imager for the Coastal Ocean (HICO) data for seagrass mapping in Indian River Lagoon, FL. GISci. Remote Sens. 2014, 51, 120–138. [Google Scholar] [CrossRef]
- Gao, B. C.; Montes, M. J.; Ahmad, Z.; Davis, C. O. Atmospheric correction algorithm for hyperspectral remote sensing of ocean color from space. Appl. Opt. 2000, 39, 887–896. [Google Scholar] [CrossRef] [PubMed]
- Ruddick, K.G.; Ovidio, F.; Rijkeboer, M. Atmospheric correction of SeaWiFS imagery for turbid coastal and inland waters. Appl. Opt. 2000, 39, 897–912. [Google Scholar] [CrossRef] [PubMed]
- Siegel, D.A.; Wang, M.; Maritorena, S.; Robinson, W. Atmospheric correction of satellite ocean color imagery: The black pixel assumption. Appl. Opt. 2000, 39, 3582–3591. [Google Scholar] [CrossRef] [PubMed]
- Patterson, K.W.; Lamela, G. Influence of aerosol estimation on coastal water products retrieved from HICO images. Proc. SPIE 2011, 8030, 25–28. [Google Scholar]
- Bassani, C.; Manzo, C.; Braga, F.; Bresciani, M.; Giardino, C.; Alberotanza, L. Impact of the aerosol type on HICO atmospheric correction in coastal waters. Atmos. Meas. Tech. Discuss. 2014, 7, 5147–5172. [Google Scholar] [CrossRef]
- Devred, E.; Turpie, K.R.; Moses, W.; Klemas, V.V.; Moisan, T.; Babin, M.; Toro-Farmer, G.; Forget, M.; Jo, Y.H. Future retrievals of water column bio-optical properties using the hyperspectral infrared imager (HyspIRI). Remote Sens. 2013, 5, 6812–6837. [Google Scholar] [CrossRef]
- Lucke, R. L.; Corson, M.; McGlothlin, N. R.; Butcher, S. D.; Wood, D. L.; Korwan, D. R.; Li, R. R.; Snyder, W. A.; Davis, C. O.; Chen, D. T. Hyperspectral imager for the coastal ocean: Instrument description and first images. Appl. Opt. 2011, 50, 1501–1516. [Google Scholar] [CrossRef] [PubMed]
- Cho, S.; Ahn, Y.H.; Ryu, J.H.; Kang, G.; Youn, H. Development of geostationary ocean color imager (GOCI). Korean J. Remote Sens. 2010, 26, 157–165. [Google Scholar]
- Choi, J.K.; Park, Y.J.; Ahn, J.H.; Lim, H.S.; Eom, J.; Ryu, J.H. GOCI, the world’s first geostationary ocean color observation satellite, for the monitoring of temporal variability in coastal water turbidity. J. Geophys. Res. Oceans (1984–2012) 2012, 117, C09004. [Google Scholar] [CrossRef]
- Ryu, J.H.; Choi, J.K.; Eom, J.; Ahn, J.H. Temporal variation in Korean coastal waters using Geostationary Ocean Color Imager. J. Coast. Res. 2011, 64, 1731–1735. [Google Scholar]
- Wang, M.; Ahn, J.H.; Jiang, L.; Shi, W.; Son, S.; Park, Y.J.; Ryu, J.H. Ocean color products from the Korean Geostationary Ocean Color Imager (GOCI). Opt. Express 2013, 21, 3835–3849. [Google Scholar] [CrossRef] [PubMed]
- Kahn, R.A.; Gaitley, B.J.; Martonchik, J.V.; Diner, D.J.; Crean, K.A.; Holben, B. Multiangle Imaging SpectroRadiometer (MISR) global aerosol optical depth validation based on 2 years of coincident Aerosol Robotic Network (AERONET) observations. J. Geophys. Res. Atmos. (1984–2012) 2005, 110, D10S04. [Google Scholar] [CrossRef]
- Kahn, R.A.; Garay, M.J.; Nelson, D.L.; Yau, K.K.; Bull, M.A.; Gaitley, B.J.; Martonchik, J.V.; Levy, R.C. Satellite-derived aerosol optical depth over dark water from MISR and MODIS: Comparisons with AERONET and implications for climatological studies. J. Geophys. Res. Atmos. (1984–2012) 2007, 112, D18205. [Google Scholar] [CrossRef]
- Kahn, R.A.; Nelson, D.L.; Garay, M.J.; Levy, R.C.; Bull, M.A.; Diner, D.J.; Martonchik, J.V.; Paradise, S.R.; Hansen, E.G.; Remer, L.A. MISR aerosol product attributes and statistical comparisons with MODIS. IEEE Trans. Geosci. Remote Sens. 2009, 47, 4095–4114. [Google Scholar] [CrossRef]
- Kahn, R.A.; Gaitley, B.J.; Garay, M.J.; Diner, D.J.; Eck, T.F.; Smirnov, A.; Holben, B.N. Multiangle Imaging SpectroRadiometer global aerosol product assessment by comparison with the Aerosol Robotic Network. J. Geophys. Res. Atmos. (1984–2012) 2010, 115, D23209. [Google Scholar] [CrossRef]
- Bevan, S.L.; North, P.R.; Los, S.O.; Grey, W.M. A global dataset of atmospheric aerosol optical depth and surface reflectance from AATSR. Remote Sens. Environ. 2012, 116, 199–210. [Google Scholar] [CrossRef]
- Harmel, T.; Chami, M. Influence of polarimetric satellite data measured in the visible region on aerosol detection and on the performance of atmospheric correction procedure over open ocean waters. Opt. Express 2011, 19, 20960–20983. [Google Scholar] [CrossRef] [PubMed]
- He, X.; Pan, D.; Bai, Y.; Wang, D.; Hao, Z. A new simple concept for ocean colour remote sensing using parallel polarisation radiance. Sci. Rep. 2014, 4. [Google Scholar] [CrossRef]
- Meister, G.; McClain, C.R.; Ahmad, Z.; Bailey, S.W.; Barnes, R.A.; Brown, S.; Eplee, R.E.; Franz, B.; Holmes, A.; Monosmith, W.B.; et al. Requirements for an Advanced Ocean Radiometer; Technical Report; NASA Goddard Space Flight Center: Greenbelt, MD, USA, 2011. [Google Scholar]
- IOCCG. Mission Requirements for Future Ocean-Colour Sensors (Reports of the International Ocean-Colour Coordinating Group, No. 13); Technical Report; IOCCG Project Office: Dartmouth, Canada, 2012. [Google Scholar]
- Iwasaki, A.; Ohgi, N.; Tanii, J.; Kawashima, T.; Inada, H. Hyperspectral Imager Suite (HISUI)-Japanese hyper-multi spectral radiometer. In Proceedings of the IEEE Geoscience and Remote Sensing Symposium, Vancouver, BC, Canada, 24–29 July 2011; pp. 1025–1028.
- Galeazzi, C.; Sacchetti, A.; Cisbani, A.; Babini, G. The PRISMA program. In Proceedings of the IEEE Geoscience and Remote Sensing Symposium, Boston, MA, USA, 7–11 July 2008; Volume 4, pp. 105–108.
- McClain, C.R. The Ocean Radiometer for Carbon Assessment (ORCA); Technical Report; NASA Goddard Space Flight Center: Greenbelt, MD, USA, 2010. [Google Scholar]
- Amin, R.; Lewis, D.; Gould, R.W.; Hou, W.; Lawson, A.; Ondrusek, M.; Arnone, R. Assessing the application of cloud–shadow atmospheric correction algorithm on HICO. IEEE Trans. Geosci. Remote Sens. 2014, 52, 2646–2653. [Google Scholar] [CrossRef]
- Bracchini, L.; Tognazzi, A.; Dattilo, A.M.; Decembrini, F.; Rossi, C.; Loiselle, S.A. Sensitivity analysis of CDOM spectral slope in artificial and natural samples: An application in the central eastern Mediterranean Basin. Aquat. Sci. 2010, 72, 485–498. [Google Scholar] [CrossRef]
- Helms, J.R.; Stubbins, A.; Ritchie, J.D.; Minor, E.C.; Kieber, D.J.; Mopper, K. Absorption spectral slopes and slope ratios as indicators of molecular weight, source, and photobleaching of chromophoric dissolved organic matter. Limnol. Oceanogr. 2008, 53, 955–969. [Google Scholar] [CrossRef]
- He, X.; Bai, Y.; Pan, D.; Tang, J.; Wang, D. Atmospheric correction of satellite ocean color imagery using the ultraviolet wavelength for highly turbid waters. Opt. Express 2012, 20, 20754–20770. [Google Scholar] [CrossRef]
- Kudela, R.M.; Palacios, S.L.; Austerberry, D.C.; Accorsi, E.K.; Guild, L.S.; Torres-Perez, J. Application of hyperspectral remote sensing to cyanobacterial blooms in inland waters. Remote Sens. Environ. 2015, 167, 196–205. [Google Scholar] [CrossRef]
- Mouroulis, P.; Gorp, B.V.; Green, R.O.; Dierssen, H.; Wilson, D.W.; Eastwood, M.; Boardman, J.; Gao, B.C.; Cohen, D.; Franklin, B.; et al. Portable Remote Imaging Spectrometer coastal ocean sensor: Design, characteristics, and first flight results. Appl. Opt. 2014, 53, 1363–1380. [Google Scholar] [CrossRef]
- Palacios, S.L.; Kudela, R.M.; Guild, L.S.; Negrey, K.H.; Torres-Perez, J.; Broughton, J. Remote sensing of phytoplankton functional types in the coastal ocean from the HyspIRI Preparatory Flight Campaign. Remote Sens. Environ. 2015, 167, 269–280. [Google Scholar] [CrossRef]
- Dierssen, H.M.; Chlus, A.; Russell, B. Hyperspectral discrimination of floating mats of seagrass wrack and the macroalgae Sargassum in coastal waters of Greater Florida Bay using airborne remote sensing. Remote Sens. Environ. 2015, 167, 247–258. [Google Scholar] [CrossRef]
- Hochberg, E.J.; Roberts, D.A.; Dennison, P.E.; Hulley, G.C. Special issue on the Hyperspectral Infrared Imager (HyspIRI): Emerging science in terrestrial and aquatic ecology, radiation balance and hazards. Remote Sens. Environ. 2015, 167, 1–5. [Google Scholar] [CrossRef]
- Bell, T.W.; Cavanaugh, K.C.; Siegel, D.A. Remote monitoring of giant kelp biomass and physiological condition: An evaluation of the potential for the Hyperspectral Infrared Imager (HyspIRI) mission. Remote Sens. Environ. 2015, 167, 218–228. [Google Scholar] [CrossRef]
- Hu, C.; Feng, L.; Hardy, R.F.; Hochberg, E.J. Spectral and spatial requirements of remote measurements of pelagic Sargassum macroalgae. Remote Sens. Environ. 2015, 167, 229–246. [Google Scholar] [CrossRef]
- Lorenzoni, L.; Toro-Farmer, G.; Varela, R.; Guzman, L.; Rojas, J.; Montes, E.; Muller-Karger, F. Characterization of phytoplankton variability in the Cariaco Basin using spectral absorption, taxonomic and pigment data. Remote Sens. Environ. 2015, 167, 259–268. [Google Scholar] [CrossRef]
- Thompson, D.R.; Gao, B.C.; Green, R.O.; Roberts, D.A.; Dennison, P.E.; Lundeen, S.R. Atmospheric correction for global mapping spectroscopy: ATREM advances for the HyspIRI preparatory campaign. Remote Sens. Environ. 2015, 167, 64–77. [Google Scholar] [CrossRef]
- Kutser, T. Quantitative detection of chlorophyll in cyanobacterial blooms by satellite remote sensing. Limnol. Oceanogr. 2004, 49, 2179–2189. [Google Scholar] [CrossRef]
- Cavanaugh, K.C.; Siegel, D.A.; Raimondi, P.T.; Alberto, F. Patch definition in metapopulation analysis: A graph theory approach to solve the mega-patch problem. Ecology 2014, 95, 316–328. [Google Scholar] [CrossRef] [PubMed]
- IOCCG. Phytoplankton Functional Types from Space; Technical Report of the International Ocean-Colour Coordinating Group, No. 15; Sathyendranath, S., Ed.; IOCCG Project Office: Dartmouth, NS, Canada, 2014. [Google Scholar]
- Gao, B.C.; Heidebrecht, K.B.; Goetz, A.F.H. Atmosphere Removal Program (ATREM) Version 2.0 Users Guide; Technical Report; Center for the Study of Earth from Space/CIRES, University of Colorado: Boulder, CO, USA, 1996. [Google Scholar]
- Fishman, J.; Iraci, L.T.; Al-Saadi, J.; Chance, K.; Chavez, F.; Chin, M.; Coble, P.; Davis, C.; DiGiacomo, P.M.; Eldering, A.; et al. The United States’ next generation of atmospheric composition and coastal ecosystem measurements: NASA’s geostationary coastal and air pollution events (GEO-CAPE) missions. Bull. Am. Meteor. Soc. 2012, 93, 1547–1566. [Google Scholar] [CrossRef]
- Wang, M.; Shi, W.; Jiang, L. Atmospheric correction using near-infrared bands for satellite ocean color data processing in the turbid western Pacific region. Opt. Express 2012, 20, 741–753. [Google Scholar] [CrossRef] [PubMed]
- Mobley, C.; Boss, E.; Roesler, C. Ocean Optics Web Book. Available online: http://www.oceanopticsbook.info (accessed on 14 August 2015).
- Gordon, H.R. Atmospheric correction of ocean color imagery in the Earth Observing System era. J. Geophys. Res. Atmos. (1984–2012) 1997, 102, 17081–17106. [Google Scholar] [CrossRef]
- Griffin, M.K.; Burke, H.H.K. Compensation of hyperspectral data for atmospheric effects. Linc. Lab. J. 2003, 14, 29–54. [Google Scholar]
- Gordon, H.R.; Brown, J.W.; Evans, R.H. Exact Rayleigh scattering calculations for use with the Nimbus-7 Coastal Zone Color Scanner. Appl. Opt. 1988, 27, 862–871. [Google Scholar] [CrossRef] [PubMed]
- Gordon, H.R.; Wang, M. Surface roughness considerations for atmospheric correction of ocean color sensors. 1: The Rayleigh scattering component. Appl. Opt. 1992, 31, 4247–4260. [Google Scholar] [CrossRef]
- Wang, M. The Rayleigh lookup tables for the SeaWiFS data processing: Accounting for the effects of ocean surface roughness. Int. J. Remote Sens. 2002, 23, 2693–2702. [Google Scholar] [CrossRef]
- Wang, M. A refinement for the Rayleigh radiance computation with variation of the atmospheric pressure. Int. J. Remote Sens. 2005, 26, 5651–5663. [Google Scholar] [CrossRef]
- Ahmad, Z.; Franz, B.A.; McClain, C.R.; Kwiatkowska, E.J.; Werdell, J.; Shettle, E.P.; Holben, B.N. New aerosol models for the retrieval of aerosol optical thickness and normalized water-leaving radiances from the SeaWiFS and MODIS sensors over coastal regions and open oceans. Appl. Opt. 2010, 49, 5545–5560. [Google Scholar] [CrossRef]
- Shettle, E.P.; Fenn, R.W. Models for the Aerosols of the Lower Atmosphere and the Effects of Humidity Variations on Their Optical Properties; Technical Report; AFGL–TR–79–0214; Air Force Geophysics Lab: Hanscom AFB, MA, USA, 1979. [Google Scholar]
- Moulin, C.; Gordon, H.R.; Banzon, V.F.; Evans, R.H. Assessment of Saharan dust absorption in the visible from SeaWiFS imagery. J. Geophys. Res. Atmos. (1984–2012) 2001, 106, 18239–18249. [Google Scholar] [CrossRef]
- Dubovik, O.; Sinyuk, A.; Lapyonok, T.; Holben, B.N.; Mishchenko, M.; Yang, P.; Eck, T.; Volten, H.; Munoz, O.; Veihelmann, B.; et al. Application of spheroid models to account for aerosol particle nonsphericity in remote sensing of desert dust. J. Geophys. Res. Atmos. (1984–2012) 2006, 111, 2156–2202. [Google Scholar] [CrossRef]
- Steinmetz, F.; Deschamps, P.Y.; Ramon, D. Atmospheric correction in presence of sun glint: Application to MERIS. Opt. Express 2011, 19, 9783–9800. [Google Scholar] [CrossRef] [PubMed]
- Chomko, R.M.; Gordon, H.R. Atmospheric correction of ocean color imagery: Use of the Junge power-law aerosol size distribution with variable refractive index to handle aerosol absorption. Appl. Opt. 1998, 37, 5560–5572. [Google Scholar] [CrossRef] [PubMed]
- Chomko, R.M.; Gordon, H.R.; Maritorena, S.; Siegel, D.A. Simultaneous retrieval of oceanic and atmospheric parameters for ocean color imagery by spectral optimization: A validation. Remote Sens. Environ. 2003, 84, 208–220. [Google Scholar] [CrossRef]
- Brajard, J.; Jamet, C.; Moulin, C.; Thiria, S. Use of a neuro-variational inversion for retrieving oceanic and atmospheric constituents from satellite ocean colour sensor: Application to absorbing aerosols. Neural. Netw. 2006, 19, 178–185. [Google Scholar] [CrossRef] [PubMed]
- Brajard, J.; Moulin, C.; Thiria, S. Atmospheric correction of SeaWiFS ocean color imagery in the presence of absorbing aerosols off the Indian coast using a neuro-variational methods. Geophys. Res. Lett. 2008, 35, 1944–8007. [Google Scholar] [CrossRef]
- Frouin, R.; Schwindling, M.; Deschamps, P.Y. Spectral reflectance of sea foam in the visible and near-infrared: In situ measurements and remote sensing implications. J. Geophys. Res. Oceans (1978–2012) 1996, 101, 14361–14371. [Google Scholar]
- Koepke, P. Effective reflectance of oceanic whitecaps. Appl. Opt. 1984, 23, 1816–1824. [Google Scholar] [CrossRef]
- Moore, K.D.; Voss, K.J.; Gordon, H.R. Spectral reflectance of whitecaps: Their contribution to water-leaving radiances. J. Geophys. Res. Oceans (1978–2012) 2000, 105, 6493–6499. [Google Scholar] [CrossRef]
- Gordon, H.R.; Wang, M. Influence of oceanic whitecaps on atmospheric correction of ocean-color sensor. Appl. Opt. 1994, 33, 7754–7763. [Google Scholar] [CrossRef]
- Cox, C.; Munk, W. Measurement of the roughness of the sea surface from photographs of the sun’s glitter. J. Opt. Soc. Am 1954, 44, 838–850. [Google Scholar] [CrossRef]
- NCEP. Available online: http://oceancolor.gsfc.nasa.gov/cms/ancillary (accessed on 14 August 2015).
- Fore, A.G.; Yueh, S.H.; Tang, W.; Hayashi, A.K.; Lagerloef, G.S. Aquarius wind speed products: Algorithms and validation. IEEE Trans. Geosci. Remote Sens. 2014, 52, 2920–2927. [Google Scholar] [CrossRef]
- Wang, M.; Bailey, S. Correction of the sun glint contamination on the SeaWiFS ocean and atmosphere products. Appl. Opt. 2001, 40, 4790–4798. [Google Scholar] [CrossRef] [PubMed]
- Zhang, H.; Wang, M. Evaluation of sun glint models using MODIS measurements. J. Quant. Spectrosc. Radiat. Transf. 2010, 111, 492–506. [Google Scholar] [CrossRef]
- Garaba, S.P.; Zielinski, O. Methods in reducing surface reflected glint for shipborne above-water remote sensing. J. Eur. Opt. Soc. 2013, 8. [Google Scholar] [CrossRef]
- Van Mol, B.; Ruddick, K. The Compact High Resolution Imaging Spectrometer (CHRIS): the future of hyperspectral satellite sensors. Imagery of Oostende coastal and inland waters. In Proceedings of the Airborne Imaging Spectroscopy workshop, Bruges, Belgium, 8 October 2004.
- Montes, M.J.; Gao, B.; Davis, C.O. Hyperspectral remote sensing of ocean colour: A comparison of Hyperion and AVIRIS. In Proceedings of the 13th JPL Airborne Earth Science Workshop, Pasadena, CA, USA, 31 March–2 April 2004; pp. 175–180.
- Harmel, T.; Chami, M. Estimation of the sunglint radiance field from optical satellite imagery over open ocean: Multidirectional approach and polarization aspects. J. Geophys. Res. Oceans 2013, 118, 76–90. [Google Scholar] [CrossRef]
- Hooker, S.B.; Lazin, G.; Zibordi, G.; McLean, S. An evaluation of above-and in-water methods for determining water-leaving radiances. J. Atmos. Oceanic Technol. 2002, 19, 486–514. [Google Scholar] [CrossRef]
- Shanmugam, P. CAAS: An atmospheric correction algorithm for the remote sensing of complex waters. Ann. Geophys. 2012, 30, 203–220. [Google Scholar] [CrossRef]
- Gao, B.C.; Kaufman, Y.J. Water vapor retrievals using Moderate Resolution Imaging Spectroradiometer (MODIS) near-infrared channels. J. Geophys. Res. Atmos. (1984–2012) 2003, 108. [Google Scholar] [CrossRef]
- Kaufman, Y.J.; Martins, J.V.; Remer, L.A.; Schoeberl, M.R.; Yamasoe, M.A. Satellite retrieval of aerosol absorption over the oceans using sunglint. Geophys. Res. Lett. 2002, 29. [Google Scholar] [CrossRef]
- Hagolle, O.; Nicolas, J.M.; Fougnie, B.; Cabot, F.; Henry, P. Absolute calibration of VEGETATION derived from an interband method based on the sun glint over ocean. IEEE Trans. Geosci. Remote Sens. 2004, 42, 1472–1481. [Google Scholar] [CrossRef]
- Robinson, W.D.; Franz, B.A.; Patt, F.S.; Bailey, S.W.; Werdell, P.J. Masks and flags updates, SeaWiFS Postlaunch Technical Report Series, Vol. 22; Technical Report, NASA/TM–2003–206892; Hooker, S.B., Firestone, E.R., Eds.; NASA Goddard Space Flight Center: Greenbelt, MD, USA, 2003. [Google Scholar]
- Wang, M.; Shi, W. Cloud masking for ocean color data processing in the coastal regions. IEEE Trans. Geosci. Remote Sens. 2006, 44, 3196–3205. [Google Scholar] [CrossRef]
- Zhao, G.; Girolamo, L.D.; Dey, S.; Jones, A.L.; Bull, M. Examination of direct cumulus contamination on MISR-retrieved aerosol optical depth and Angstrom coefficient over ocean. Geophys. Res. Lett. 2009, 36, L13811. [Google Scholar] [CrossRef]
- Nordkvist, K.; Loisel, H.; Gaurier, L.D. Cloud masking of SeaWiFS images over coastal waters using spectral variability. Opt. Express 2009, 17, 12246–12258. [Google Scholar] [CrossRef] [PubMed]
- Amato, U.; Antoniadis, A.; Cuomo, V.; Cutillo, L.; Franzese, M.; Murino, L.; Serio, C. Statistical cloud detection from SEVIRI multispectral images. Remote Sens. Environ. 2008, 112, 750–766. [Google Scholar] [CrossRef]
- Lee, Y.; Wahba, G.; Ackerman, S.A. Cloud classification of satellite radiance data by multicategory support vector machines. J. Atmos. Oceanic Technol. 2004, 21, 159–169. [Google Scholar] [CrossRef]
- Tian, B.; Shaikh, M.A.; Azimi-Sadjadi, M.R.; Haar, T.H.V.; Reinke, D.L. A study of cloud classification with neural networks using spectral and textural features. IEEE Trans. Neural Netw. 1999, 10, 138–151. [Google Scholar] [CrossRef]
- Gomez-Chova, L.; Camps-Valls, G.; Calpe-Maravilla, J.; Guanter, L.; Moreno, J. Cloud-screening algorithm for ENVISAT/MERIS multispectral images. IEEE Trans. Geosci. Remote Sens. 2007, 45, 4105–4118. [Google Scholar] [CrossRef]
- King, N.; Vaughan, G. Vertical profile retrievals of marine stratocumulus from passive remote sensing: An assessment of information content and the potential for improved retrievals from hyperspectral measurements. In Proceedings of the EGU General Assembly Conference Abstracts, Vienna, Austria, 22–27 April 2012; p. 5454.
- Purdom, J.F.W. Geostationary hyperspectral imaging and sounding: A revolutionary breakthrough in satellite derived cloud motion vectors. In Proceedings of the Chairperson of Session VI: Research Methods and Applications; 7th International Winds Workshop, Helsinki, Finland, 14–17 June 2004.
- Gomez-Chova, L.; Camps-Valls, G.; Amorós-López, J.; Calpe, J.; Guanter, L.; Alonso, L.; Fortea, J.C.; Moreno, J. Cloud Probability Mask for PROBA/CHRIS Hyperspectral Images. In Proceedings of the IV CHRIS/Proba Workshop, Frascati, Italy, 19–21 September 2006.
- Anderson, G.P.; Pukall, B.; Allred, C.L.; Jeong, L.S.; Hoke, M.A.H.M.; Chetwynd, J.H.; Adler-Golden, S.M.; Berk, A.; Bernstein, L.S.; et al. FLAASH and MODTRAN4: state-of-the-art atmospheric correction for hyperspectral data. In Proceedings of the IEEE Aerospace Conference, Aspen, CO, USA, 7 March 1999; pp. 177–181.
- Richter, R.; Schlapfer, D. Atmospheric/Topographic Correction for Airborne Imagery: ATCOR-4 User Guide; Technical Report; DLR: Wessling, Germany, 2008. [Google Scholar]
- Arai, K. Adjacency effect of layered clouds estimated with Monte Carlo simulations. Adv. Space Res. 2002, 29, 1807–1812. [Google Scholar] [CrossRef]
- Burazerovic, D.; Heylen, R.; Geens, B.; Sterckx, S.; Scheunders, P. Detecting the adjacency effect in hyperspectral imagery with spectral unmixing techniques. IEEE J. Sel. Topics Appl. Earth Observ. 2013, 6, 1070–1078. [Google Scholar] [CrossRef]
- Santer, R.; Sterckx, S. SIMEC-ICOL-ODESA processing MERIS (ISECA-A2); Technical Report for ADRINORD: Lille, France; VITO: Mol, Belgium, 2013. [Google Scholar]
- Kratzer, S.; Vinterhav, C. Improvement of MERIS level 2 products in Baltic Sea coastal areas by applying the Improved Contrast between Ocean and Land processor (ICOL)-data analysis and validation. Oceanologia 2010, 52, 211–236. [Google Scholar] [CrossRef]
- Sterckx, S.; Knaeps, S.; Kratzer, S.; Ruddick, K. SIMilarity Environment Correction (SIMEC) applied to MERIS data over inland and coastal waters. Remote Sens. Environ. 2014, 157, 96–110. [Google Scholar] [CrossRef]
- Sterckx, S.; Knaeps, E.; Ruddick, K. Detection and correction of adjacency effects in hyperspectral airborne data of coastal and inland waters: The use of the near infrared similarity spectrum. Int. J. Remote Sens. 2011, 32, 6479–6505. [Google Scholar] [CrossRef]
- Stumpf, R.P.; Arnone, R.A.; Gould, R.W.; Martinolich, P.M.; Ransibrahmanakul, V. A Partially Coupled Ocean-Atmosphere Model for Retrieval of Water-Leaving Radiance from SeaWiFS in Coastal Waters; Technical Report; NASA/TM–2003–206892; Hooker, S B., Firestone, E.R., Eds.; NASA Goddard Space Flight Center: Greenbelt, MD, USA, 2003. [Google Scholar]
- Bailey, S.W.; Franz, B.A.; Werdell, P.J. Estimation of near-infrared water-leaving reflectance for satellite ocean color data processing. Opt. Express 2010, 18, 7521–7527. [Google Scholar] [CrossRef] [PubMed]
- Ruddick, K.; Cauwer, V.D.; Park, Y.J.; Moore, G. Seaborne measurements of near infrared water-leaving reflectance: The similarity spectrum for turbid waters. Limnol. Oceanogr. 2006, 51, 1167–1179. [Google Scholar] [CrossRef]
- Jiang, L.; Wang, M. Improved near-infrared ocean reflectance correction algorithm for satellite ocean color data processing. Opt. Express 2014, 22, 21657–21678. [Google Scholar] [CrossRef] [PubMed]
- Li, R.R.; Kaufman, Y.J.; Gao, B.C.; Davis, C.O. Remote sensing of suspended sediments and shallow coastal waters. IEEE Trans. Geosci. Remote Sens. 2003, 41, 559–566. [Google Scholar]
- Shi, W.; Wang, M. Characterization of global ocean turbidity from Moderate Resolution Imaging Spectroradiometer ocean color observations. J. Geophys. Res. Oceans (1978–2012) 2010, 115, C11022. [Google Scholar] [CrossRef]
- Son, S.; Wang, M.; Harding, L.W., Jr. Satellite-measured net primary production in the Chesapeake Bay. Remote Sens. Environ. 2014, 144, 109–119. [Google Scholar] [CrossRef]
- Wang, M.; Nim, C.J.; Son, S.; Shi, W. Characterization of turbidity in Florida’s Lake Okeechobee and Caloosahatchee and St. Lucie estuaries using MODIS-Aqua measurements. Water Res. 2012, 46, 5410–5422. [Google Scholar] [CrossRef] [PubMed]
- Wang, M.; Son, S.; Zhang, Y.; Shi, W. Remote sensing of water optical property for China’s inland Lake Taihu using the SWIR atmospheric correction with 1640 and 2130 nm bands. IEEE J. Sel. Topics Appl. Earth Observ. 2013, 6, 2505–2516. [Google Scholar] [CrossRef]
- Wang, M.; Tang, J.; Shi, W. MODIS-derived ocean color products along the China east coastal region. Geophys. Res. Lett. 2007, 34, L06611. [Google Scholar] [CrossRef]
- Shi, W.; Wang, M. Ocean reflectance spectra at the red, near-infrared, and shortwave infrared from highly turbid waters: A study in the Bohai Sea, Yellow Sea, and East China Sea. Limnol. Oceanogr. 2014, 59, 427–444. [Google Scholar] [CrossRef]
- Shi, W.; Wang, M. Decadal changes of water properties in the Aral Sea observed by MODIS-Aqua. J. Geophys. Res. Oceans 2015, 120, 4687–4708. [Google Scholar] [CrossRef]
- Wang, M.; Shi, W. Sensor noise effects of the SWIR bands on MODIS-derived ocean color products. IEEE Trans. Geosci. Remote Sens. 2012, 50, 3280–3292. [Google Scholar] [CrossRef]
- Chen, J.; Cui, T.; Lin, C. An improved SWIR atmospheric correction model: A cross-calibration-based model. IEEE Trans. Geosci. Remote Sens. 2014, 52, 3959–3967. [Google Scholar] [CrossRef]
- Singh, R.K.; Shanmugam, P. A novel method for estimation of aerosol radiance and its extrapolation in the atmospheric correction of satellite data over optically complex oceanic waters. Remote Sens. Environ. 2014, 142, 188–206. [Google Scholar] [CrossRef]
- Oo, M.; Vargas, M.; Gilerson, A.; Gross, B.; Moshary, F.; Ahmed, S. Improving atmospheric correction for highly productive coastal waters using the short wave infrared retrieval algorithm with water-leaving reflectance constraints at 412 nm. Appl. Opt. 2008, 47, 3846–3859. [Google Scholar] [CrossRef]
- Shi, W.; Wang, M. Detection of turbid waters and absorbing aerosols for the MODIS ocean color data processing. Remote Sens. Environ. 2007, 110, 149–161. [Google Scholar] [CrossRef]
- Banzon, V.F.; Gordon, H.R.; Kuchinke, C.P.; Antoine, D.; Voss, K.J.; Evans, R.H. Validation of a SeaWiFS dust-correction methodology in the Mediterranean Sea: Identification of an algorithm-switching criterion. Remote Sens. Environ. 2009, 113, 2689–2700. [Google Scholar] [CrossRef]
- Kuchinke, C.P.; Gordon, H.R.; Harding, L.W., Jr.; Voss, K.J. Spectral optimization for constituent retrieval in Case 2 waters II: Validation study in the Chesapeake Bay. Remote Sens. Environ. 2009, 113, 610–621. [Google Scholar] [CrossRef]
- Kuchinke, C.P.; Gordon, H.R.; Franz, B.A. Spectral optimization for constituent retrieval in Case 2 waters I: Implementation and performance. Remote Sens. Environ. 2009, 113, 571–587. [Google Scholar] [CrossRef]
- Doerffer, R.; Helmut, S. Neural network for retrieval of concentrations of water constituents with the possibility of detecting exceptional out of scope spectra. In Proceedings of the IEEE Geoscience and Remote Sensing Symposium, Honolulu, HI, USA, 24–28 July 2000; pp. 714–717.
- Schiller, H.; Doerffer, R. Neural network for emulation of an inverse model operational derivation of Case II water properties from MERIS data. Int. J. Remote Sens. 1999, 20, 1735–1746. [Google Scholar] [CrossRef]
- Doerffer, R.; Schiller, H. MERIS Regional Coastal and Lake Case 2 Water Project Atmospheric Correction; Technical Report; Algorithm Theoretical Basis Document (ATBD); GKSS Research Center: Geesthacht, Germany, 2008. [Google Scholar]
- Vilas, L.G.; Spyrakos, E.; Palenzuela, J.M.T. Neural network estimation of chlorophyll a from MERIS full resolution data for the coastal waters of Galician rias (NW Spain). Remote Sens. Environ. 2011, 115, 524–535. [Google Scholar] [CrossRef]
- Brajard, J.; Jamet, C.; Moulin, C.; Thiria, S. Validation of a neuro-variational inversion of ocean colour images. Adv. Space Res. 2006, 38, 2169–2175. [Google Scholar] [CrossRef]
- Jamet, C.; Thiria, S.; Moulin, C.; Crépon, M. Use of a neurovariational inversion for retrieving oceanic and atmospheric constituents from ocean color imagery: A feasibility study. J. Atmos. Oceanic Technol. 2005, 22, 460–475. [Google Scholar] [CrossRef]
- Brajard, J.; Santer, R.; Crépon, M.; Thiria, S. Atmospheric correction of MERIS data for case-2 waters using a neuro-variational inversion. Remote Sens. Environ. 2012, 126, 51–61. [Google Scholar] [CrossRef]
- Kokhanovsky, A.A.; Deuzé, J.L.; Diner, D.J.; Dubovik, O.; Ducos, F.; Emde, C.; Garay, M.J.; Grainger, R.G.; Heckel, A.; Herman, M.; et al. The inter-comparison of major satellite aerosol retrieval algorithms using simulated intensity and polarization characteristics of reflected light. Atmos. Meas. Tech. 2010, 3, 909–932. [Google Scholar] [CrossRef]
- Omar, A.H.; Winker, D.M.; Kittaka, C.; Vaughan, M.A.; Liu, Z.; Hu, Y.; Hostetler, C.A.; Kittaka, C.; Rogers, R.R.; Kuehn, R.E.; et al. The CALIPSO automated aerosol classification and lidar ratio selection algorithm. J. Atmos. Oceanic Technol. 2009, 26, 1994–2014. [Google Scholar] [CrossRef]
- Winker, D.M.; Pelon, J.; Coakley, J.A.; Ackerman, S.A.; Charlson, R.J.; Colarco, P.R.; Flamant, P.; Fu, Q.; Hoff, R.M.; Kittaka, C.; et al. The CALIPSO Mission: A global 3D view of aerosols and clouds. Bull. Amer. Meteor. Soc. 2010, 91, 1211–1229. [Google Scholar] [CrossRef]
- Sun, G.; Niu, Z.; Gao, S.; Huang, W.; Wang, L.; Li, W.; Feng, M. 32-channel hyperspectral waveform LiDAR instrument to monitor vegetation: Design and initial performance trials. Proc. SPIE 2014, 9263. [Google Scholar] [CrossRef]
- Fukushima, H.; Toratani, M.; Murakami, H.; Deschamps, P.Y.; Frouin, R.; Tanaka, A. Evaluation of ADEOS-II GLI ocean color atmospheric correction using SIMBADA handheld radiometer data. J. Oceanogr. 2007, 63, 533–543. [Google Scholar] [CrossRef]
- Toratani, M.; Fukushima, H.; Murakami, H.; Tanaka, A. Atmospheric correction scheme for GLI with absorptive aerosol correction. J. Oceanogr. 2007, 63, 525–532. [Google Scholar] [CrossRef]
- Moore, G.F.; Aiken, J.; Lavender, S.J. The atmospheric correction of water colour and the quantitative retrieval of suspended particulate matter in Case II waters: Application to MERIS. Int. J. Remote Sens. 1999, 20, 1713–1733. [Google Scholar] [CrossRef]
- Mao, Z.; Chen, J.; Hao, Z.; Pan, D.; Tao, B.; Zhu, Q. A new approach to estimate the aerosol scattering ratios for the atmospheric correction of satellite remote sensing data in coastal regions. Remote Sens. Environ. 2013, 132, 186–194. [Google Scholar] [CrossRef]
- Ali, K.A.; Ortiz, J.D. Multivariate approach for chlorophyll-a and suspended matter retrievals in Case II type waters using hyperspectral data. Hydrolog. Sci. J. 2014. [Google Scholar] [CrossRef]
- Lee, Z.; Shang, S.; Hu, C.; Zibordi, G. Spectral interdependence of remote-sensing reflectance and its implications on the design of ocean color satellite sensors. Appl. Opt. 2014, 53, 3301–3310. [Google Scholar] [CrossRef] [PubMed]
- Lee, Z.; Carder, K.L. Effect of spectral band numbers on the retrieval of water column and bottom properties from ocean color data. Appl. Opt. 2002, 41, 2191–2201. [Google Scholar] [CrossRef] [PubMed]
- Lee, Z.P.; Rhea, W.J.; Arnone, R.; Goode, W. Absorption coefficients of marine waters: Expanding multiband information to hyperspectral data. IEEE Trans. Geosci. Remote Sens. 2005, 43, 118–124. [Google Scholar]
- Defoin-Platel, M.; Chami, M. How ambiguous is the inverse problem of ocean color in coastal waters? J. Geophys. Res. Oceans (1978–2012) 2007, 112, C03004. [Google Scholar] [CrossRef]
- IOCCG. Remote Sensing of Inherent Optical Properties: Fundamentals, Tests of Algorithms, and Applications (Reports of the International Ocean-Colour Coordinating Group, No. 5); Technical Report; IOCCG Project Office: Dartmouth, Canada, 2006. [Google Scholar]
- Brando, V.E.; Dekker, A.G.; Park, Y.J.; Schroeder, T. Adaptive semianalytical inversion of ocean color radiometry in optically complex waters. Appl. Opt. 2012, 51, 2808–2833. [Google Scholar] [CrossRef]
- Hoge, F.E.; Lyon, P.E. Spectral parameters of inherent optical property models: Method for satellite retrieval by matrix inversion of an oceanic radiance model. Appl. Opt. 1999, 38, 1657–1662. [Google Scholar] [CrossRef] [PubMed]
- Gordon, H.R.; Lewis, M.R.; McLean, S.D.; Twardowski, M.S.; Freeman, S.A.; Voss, K.J.; Boynton, G.C. Spectra of particulate backscattering in natural waters. Opt. Express 2009, 17, 16192–16208. [Google Scholar] [CrossRef] [PubMed]
- Gordon, H.R.; Morel, A.Y. Remote assessment of ocean color for interpretation of satellite visible imagery: A review. AGU 1983, 4, 1–114. [Google Scholar]
- Hu, C.; Lee, Z.; Franz, B.A. Chlorophyll a algorithms for oligotrophic oceans: A novel approach based on three-band reflectance difference. J. Geophys. Res. Oceans (1984–2012) 2012, 117, C01011. [Google Scholar]
- Huang, C.; Zou, J.; Li, Y.; Yang, H.; Shi, K.; Li, J.; Wang, Y.; Chena, X.; Zheng, F. Assessment of NIR-red algorithms for observation of chlorophyll-a in highly turbid inland waters in China. ISPRS J. Photogramm. Remote Sens. 2014, 93, 29–39. [Google Scholar] [CrossRef]
- Torrecilla, E.; Stramski, D.; Reynolds, R.A.; Millán-Núñez, E.; Piera, J. Cluster analysis of hyperspectral optical data for discriminating phytoplankton pigment assemblages in the open ocean. Remote Sens. Environ. 2011, 115, 2578–2593. [Google Scholar] [CrossRef] [Green Version]
- Hansell, R.A.; Tsay, S.C.; Pantina, P.; Lewis, J.R.; Ji, Q.; Herman, J.R. Spectral derivative analysis of solar spectroradiometric measurements: Theoretical basis. J. Geophys. Res. Atmos. 2014, 119, 8908–8924. [Google Scholar] [CrossRef]
- Philpot, W.D. The derivative ratio algorithm: Avoiding atmospheric effects in remote sensing. IEEE Trans. Geosci. Remote Sens. 1991, 29, 350–357. [Google Scholar] [CrossRef]
- Holden, H.; LeDrew, E. Spectral discrimination of healthy and non-healthy corals based on cluster analysis, principal components analysis, and derivative spectroscopy. Remote Sens. Environ. 1998, 65, 217–224. [Google Scholar] [CrossRef]
- Louchard, E.; Reid, R.; Stephens, C.; Davis, C.; Leathers, R.; Downes, T.; Maffione, R. Derivative analysis of absorption features in hyperspectral remote sensing data of carbonate sediments. Opt. Express 2002, 10, 1573–1584. [Google Scholar] [CrossRef] [PubMed]
- Lubac, B.; Loisel, H.; Guiselin, N.; Astoreca, R.; Artigas, L.F.; Mériaux, X. Hyperspectral and multispectral ocean color inversions to detect Phaeocystis globosa blooms in coastal waters. J. Geophys. Res. Oceans (1978–2012) 2008, 113, C06026. [Google Scholar]
- Hunter, P.D.; Tyler, A.N.; Présing, M.; Kovács, A.W.; Preston, T. Spectral discrimination of phytoplankton colour groups: The effect of suspended particulate matter and sensor spectral resolution. Remote Sens. Environ. 2008, 112, 1527–1544. [Google Scholar] [CrossRef]
- Ali, K.A. Prediction of Water Quality Parameters from VIS-NIR Radiometry: Using Lake Erie as a Natural Laboratory for Analysis of Case 2 Waters. Ph.D. Thesis, Kent State University, Kent, OH, USA, 2011. [Google Scholar]
- Tufillaro, N.B.; Davis, C.O. Derivative spectroscopy with HICO. In Proceedings of the Optical Remote Sensing of the Environment, Monterey, CA, USA, 24–28 June 2012.
- Turpie, K.R.; Klemas, V.V.; Byrd, K.; Kelly, M.; Jo, Y.H. Prospective HyspIRI global observations of tidal wetlands. Remote Sens. Environ. 2015, 167, 206–217. [Google Scholar] [CrossRef]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons by Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Emberton, S.; Chittka, L.; Cavallaro, A.; Wang, M. Sensor Capability and Atmospheric Correction in Ocean Colour Remote Sensing. Remote Sens. 2016, 8, 1. https://doi.org/10.3390/rs8010001
Emberton S, Chittka L, Cavallaro A, Wang M. Sensor Capability and Atmospheric Correction in Ocean Colour Remote Sensing. Remote Sensing. 2016; 8(1):1. https://doi.org/10.3390/rs8010001
Chicago/Turabian StyleEmberton, Simon, Lars Chittka, Andrea Cavallaro, and Menghua Wang. 2016. "Sensor Capability and Atmospheric Correction in Ocean Colour Remote Sensing" Remote Sensing 8, no. 1: 1. https://doi.org/10.3390/rs8010001
APA StyleEmberton, S., Chittka, L., Cavallaro, A., & Wang, M. (2016). Sensor Capability and Atmospheric Correction in Ocean Colour Remote Sensing. Remote Sensing, 8(1), 1. https://doi.org/10.3390/rs8010001