Mapping Forest Canopy Height Across Large Areas by Upscaling ALS Estimates with Freely Available Satellite Data
Abstract
:1. Introduction
2. Materials and Methods
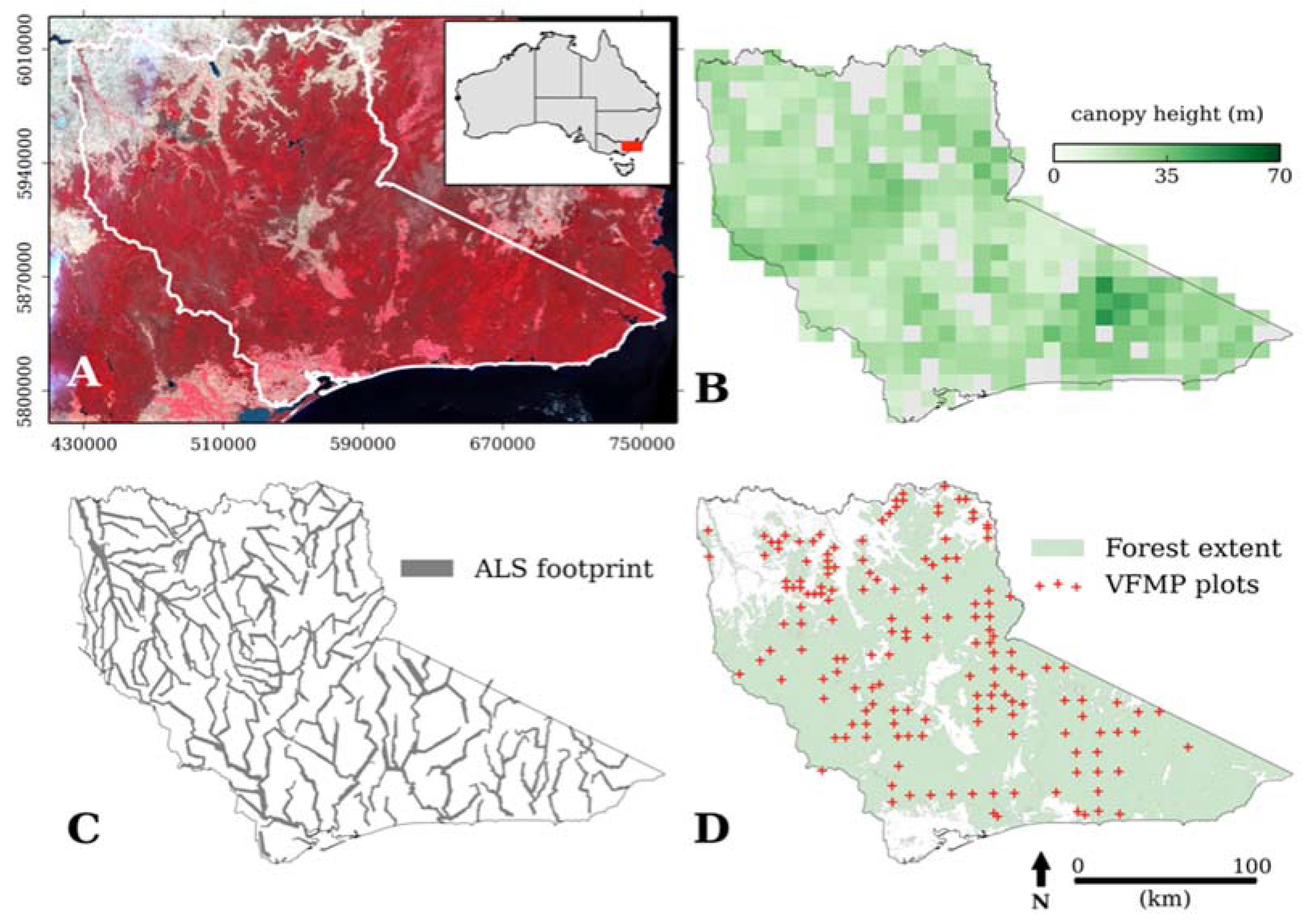
2.1. Study Area
2.2. Data Collection
2.2.1. Forest Inventory
2.2.2. Airborne Laser Scanning Data
| Specifications | |
|---|---|
| Capture specifications | |
| Date | December 2009–January 2011 |
| Flying height | 600–1500 m above ground level |
| Mean pulse density | 9.4 pl m−2 |
| Swath overlap | 20% |
| Absolute vertical accuracy | ± 20 cm |
| Absolute horizontal accuracy | ± 30 cm |
| Mean footprint diameter | ~35 cm |
| Instrument specifications | |
| Instrument | Leica ALS50-II and ALS60 (Heerbrugg, Switzerland) |
| Operating wavelength | 1064 nm |
| Max off-nadir scan angle | ± 15° |
| Outgoing pulse rate | 36.4 Hz |
2.2.3. Satellite Imagery and Ancillary Data
| Source | |
|---|---|
| Landsat TM (30 m) | MOD13Q1 (NDVI) time series (2001–2010) (250 m) |
| Tasselled Cap features and | Summer mean |
| NDVI | Summer standard deviation |
| Summer brightness | Summer coefficient of variation |
| Summer greenness | Summer linear regression slope coefficient |
| Summer wetness | Spring mean |
| Spring brightness | Spring standard deviation |
| Spring greenness | Spring coefficient of variation |
| Spring wetness | Spring linear regression slope coefficient |
| Summer NDVI | SRTM (~30 m) |
| Spring NDVI | Elevation |
| Aspect | |
| Image context/texture+ | Slope |
| Summer mean brightness | Climatic (1 km) [66] |
| Summer mean greenness | Total annual precipitation |
| Summer mean wetness | Mean annual temperature |
| Spring mean brightness | Soils |
| Spring mean greenness | Soil moisture (1 km) [67] |
| Spring mean wetness | Major soil type (vector) [68] |
| Summer brightness variance | Coordinates (MGA zone 55) (30 m) |
| Summer greenness variance | X location |
| Summer wetness variance | Y location |
| Spring brightness variance | |
| Spring greenness variance | |
| Spring wetness variance | |
2.3. Canopy Height Estimation with Random Forest
2.3.1. Random Forest Implementation
2.3.2. Selecting Predictor Variables
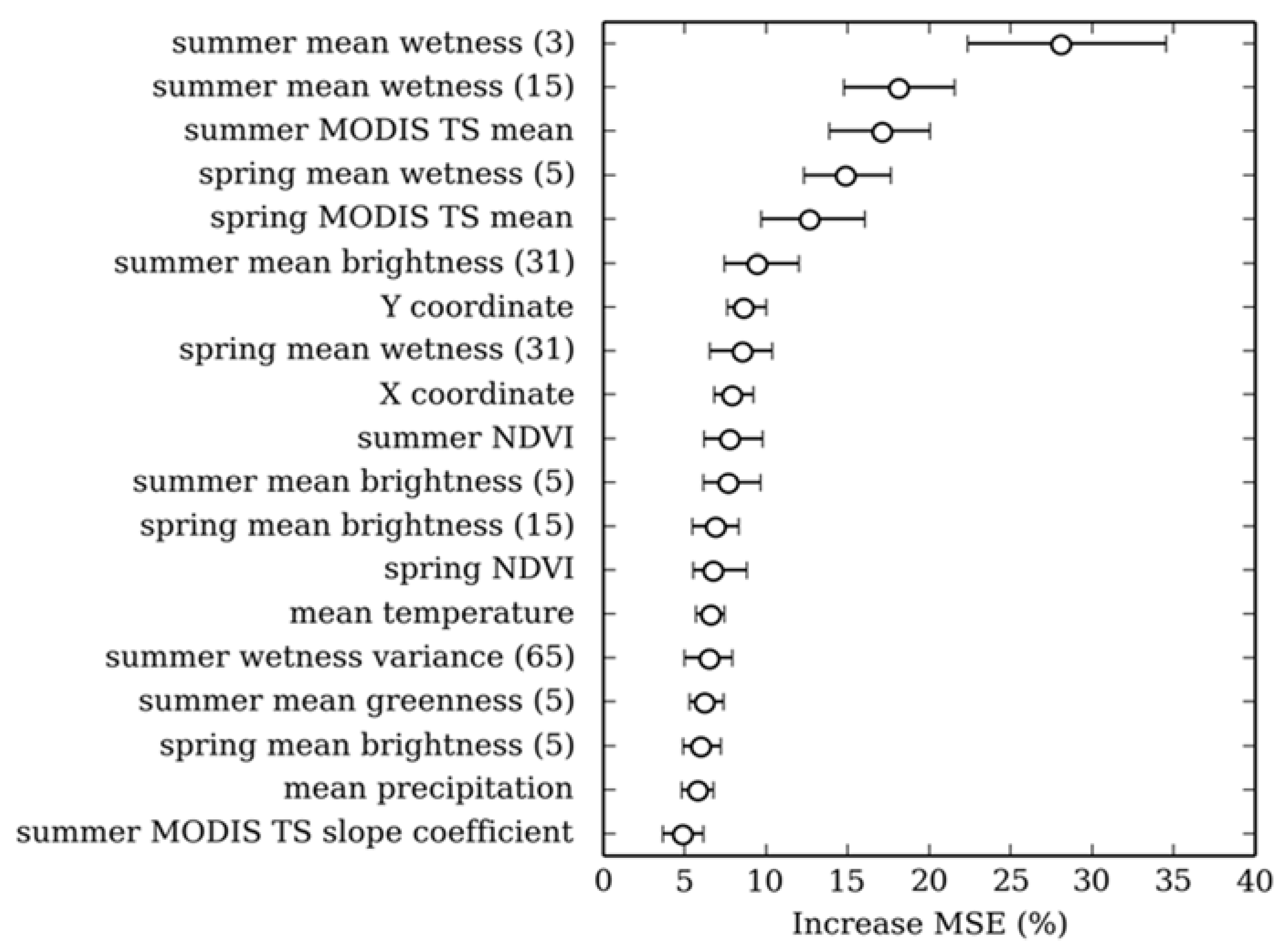
2.3.3. Systematic Error in Model Output
3. Results
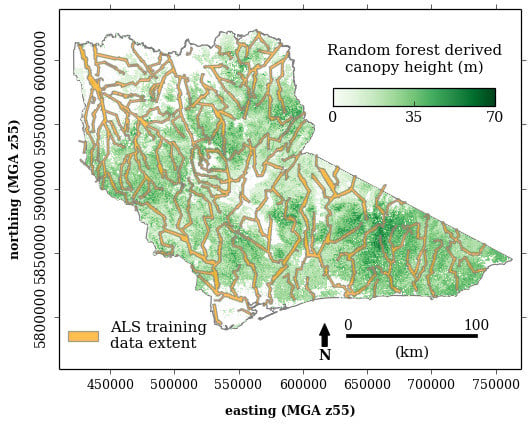
3.1. Canopy Height Estimation
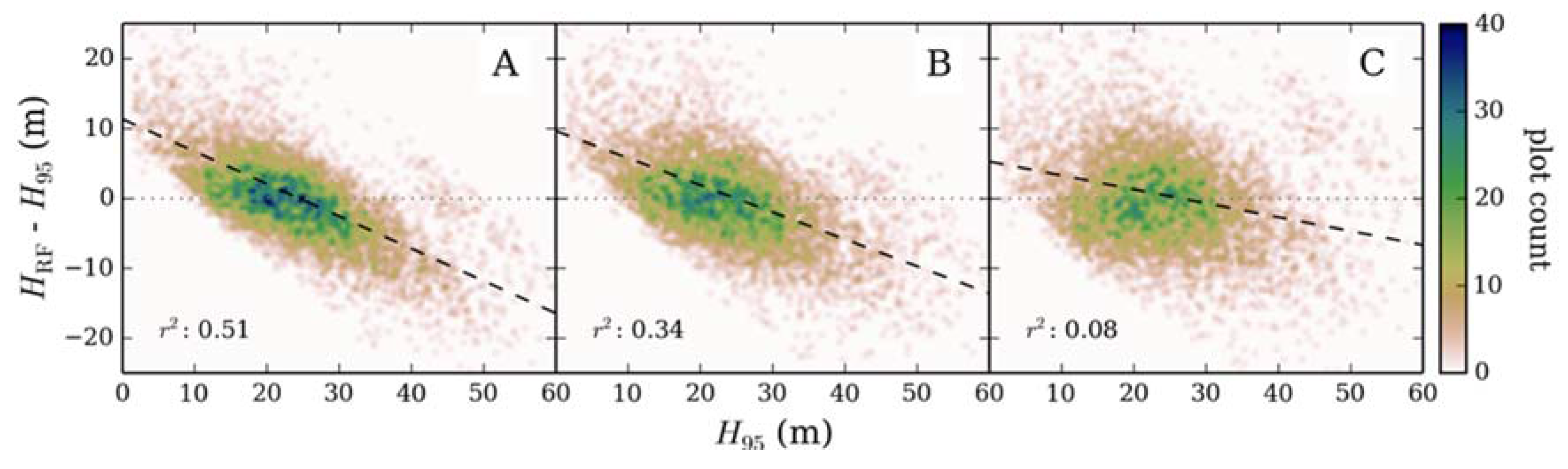
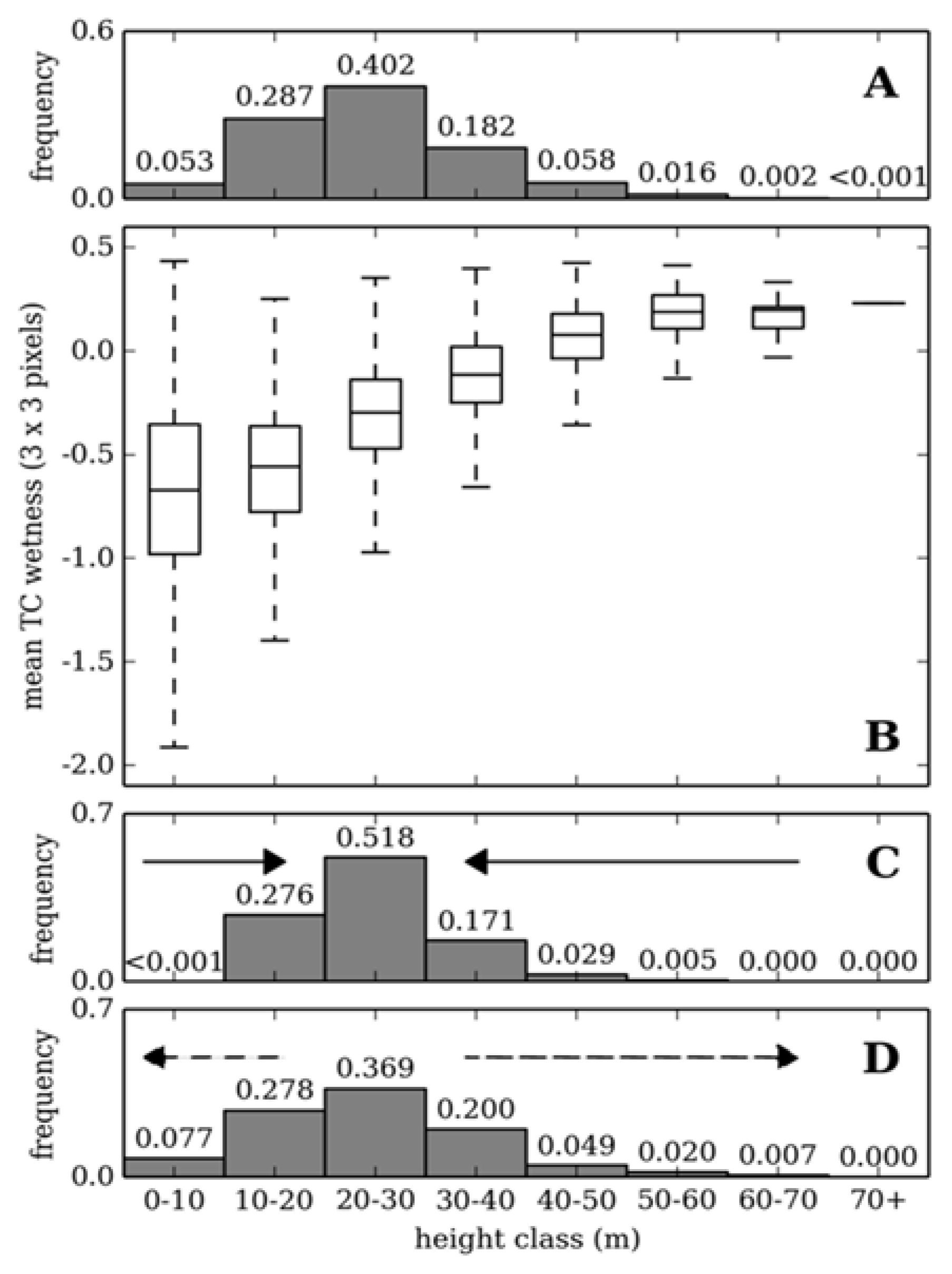
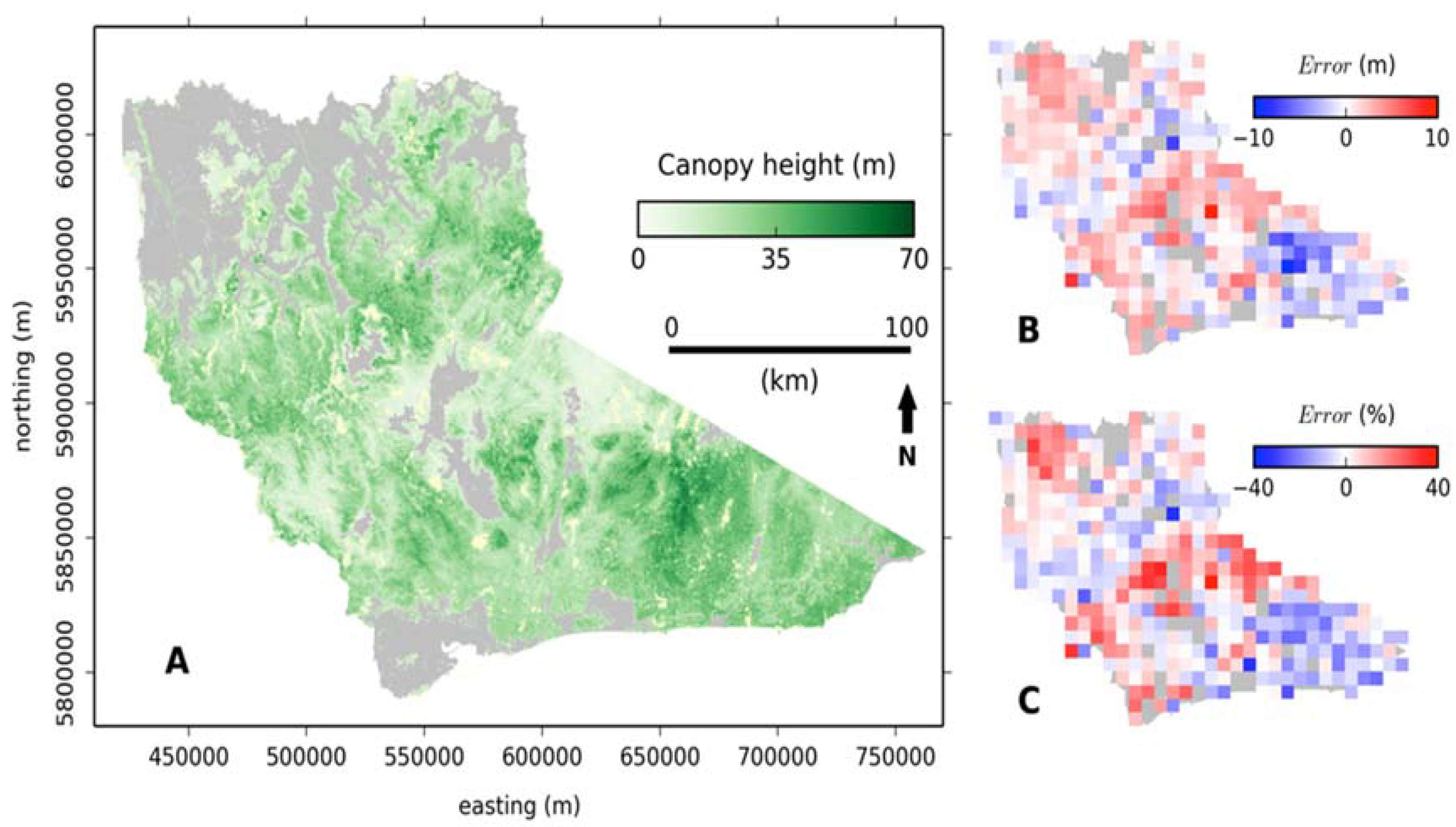
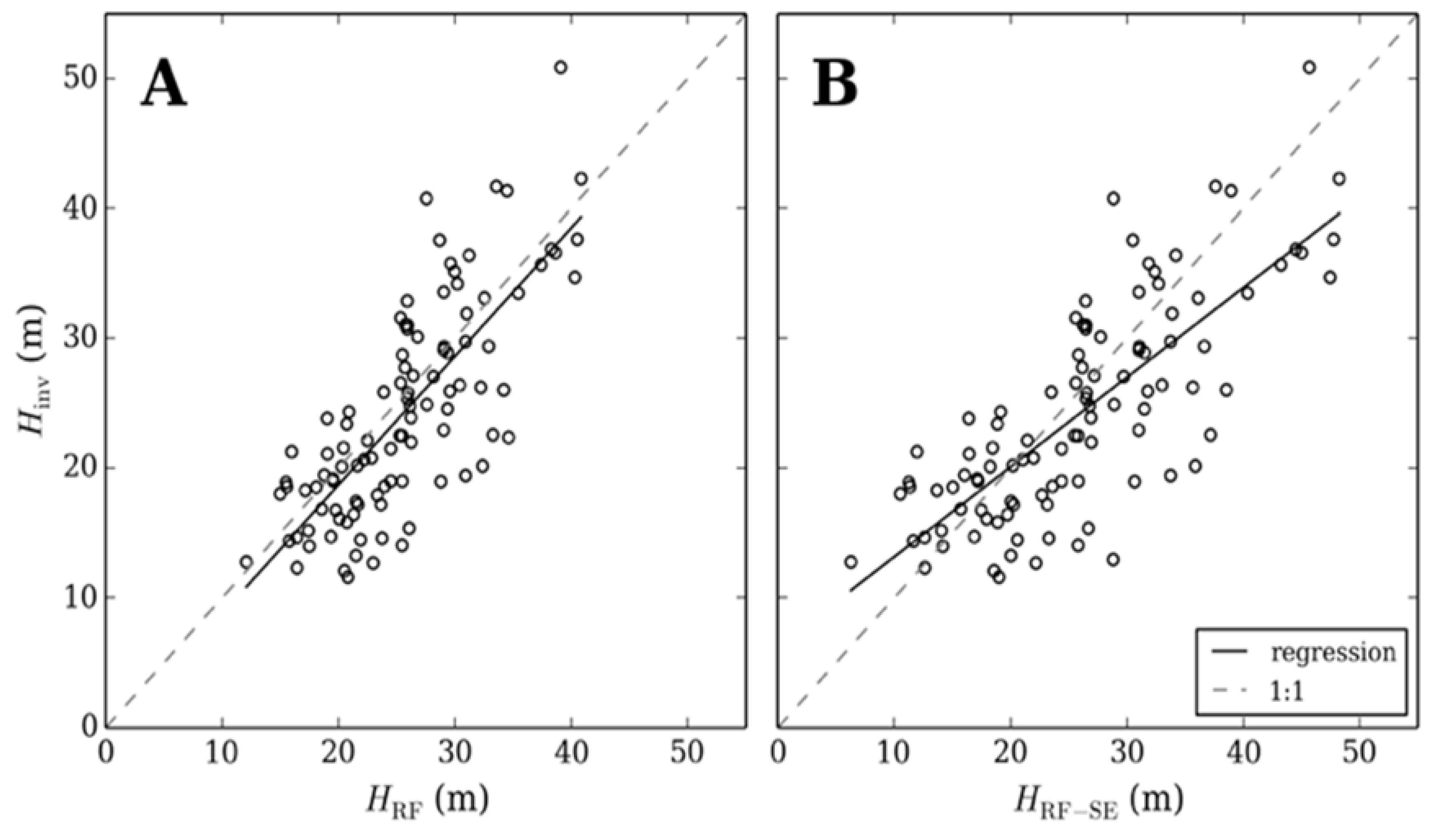
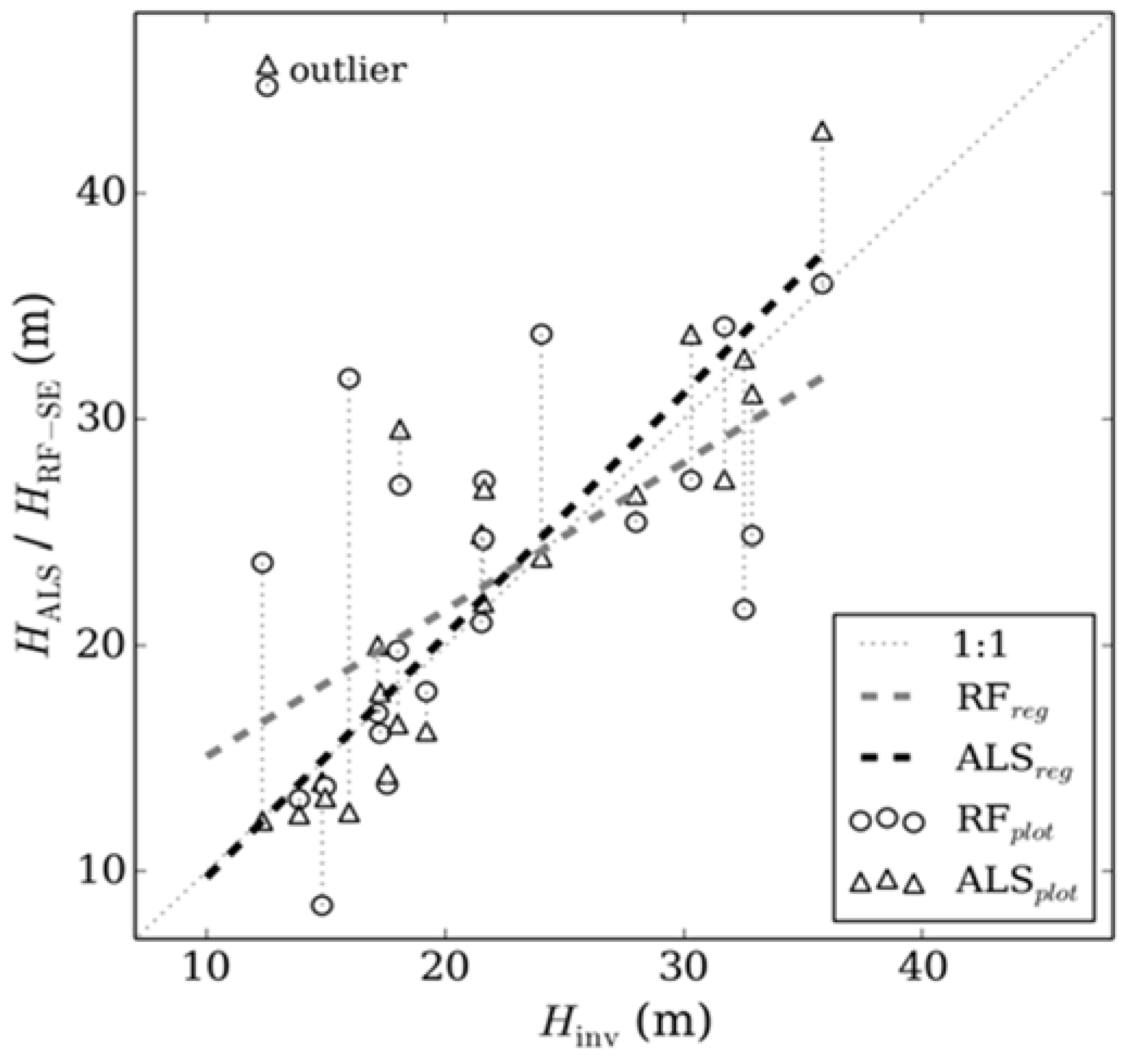
3.2. Validation with Inventory Data
3.3. Training and Validation of Random Forest Using Smaller Geographic Areas
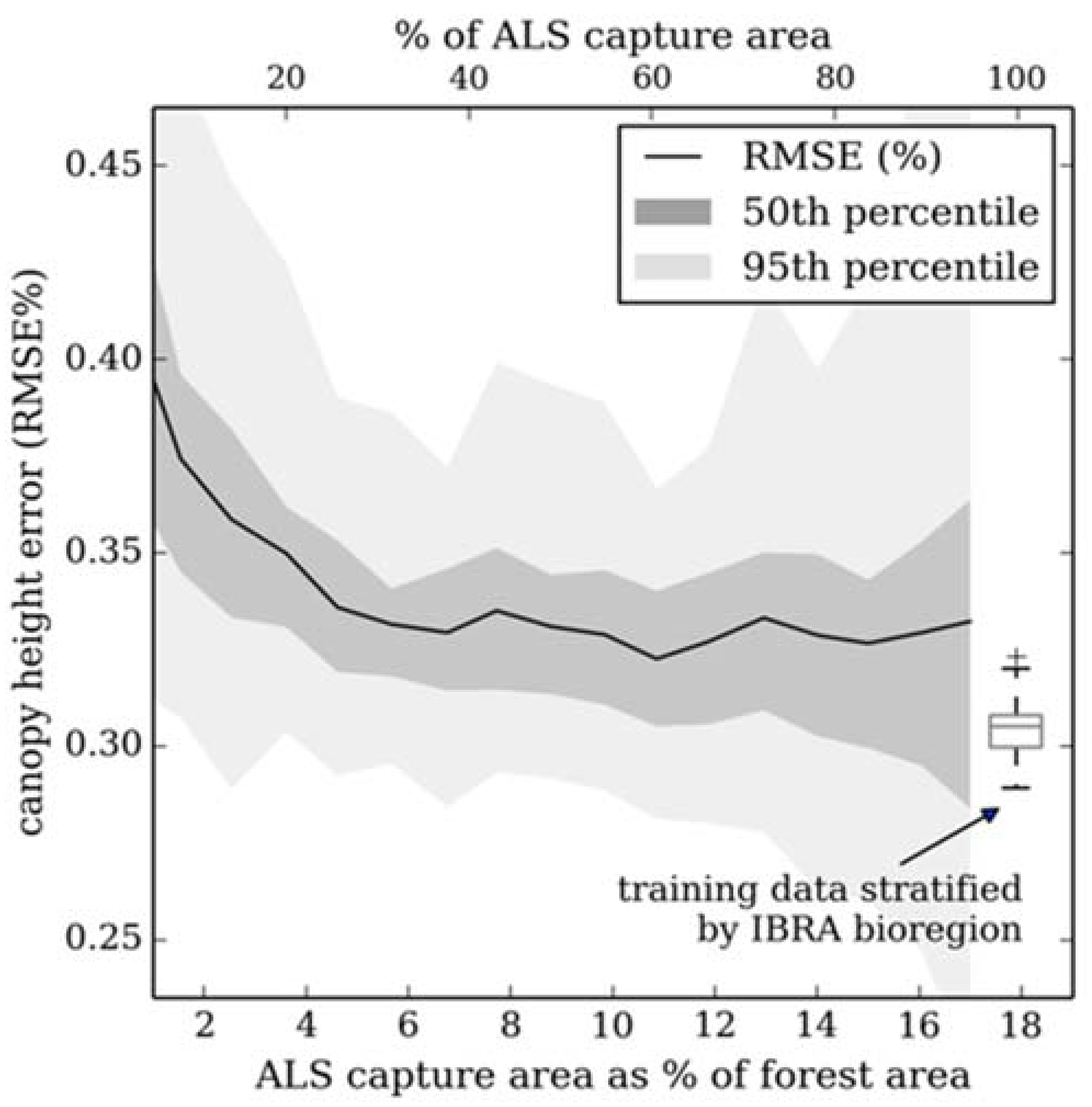
3.4. Simulating Disparate ALS Capture for Training a Random Forest
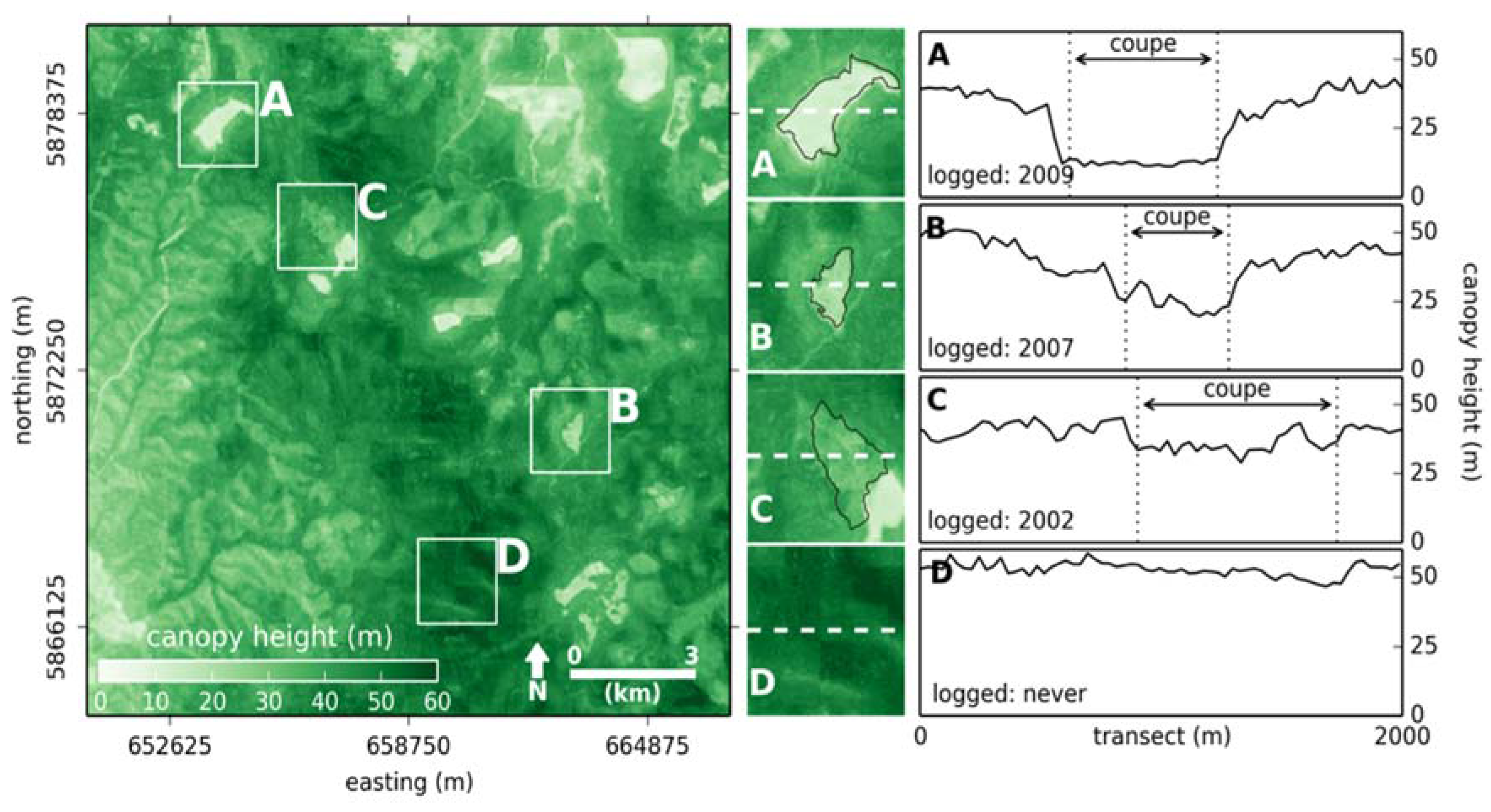
4. Discussion
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Wulder, M.A.; White, J.C.; Nelson, R.F.; Næsset, E.; Ørka, H.O.; Coops, N.C.; Hilker, T.; Bater, C.W.; Gobakken, T. LiDAR sampling for large-area forest characterization: A review. Remote Sens. Environ. 2012, 121, 196–209. [Google Scholar] [CrossRef]
- Wulder, M.A.; White, J.C.; Bater, C.W.; Coops, N.C.; Hopkinson, C.; Chen, G. Lidar plots—A new large-area data collection option: Context, concepts, and case study. Can. J. Remote Sens. 2012, 38, 600–618. [Google Scholar] [CrossRef]
- McRoberts, R.E.; Cohen, W.B.; Næsset, E.; Stehman, S.V.; Tomppo, E.O. Using remotely sensed data to construct and assess forest attribute maps and related spatial products. Scand. J. For. Res. 2010, 25, 340–367. [Google Scholar] [CrossRef]
- Wulder, M.A. Optical remote-sensing techniques for the assessment of forest inventory and biophysical parameters. Prog. Phys. Geogr. 1998, 22, 449–476. [Google Scholar] [CrossRef]
- Franklin, J.; Strahler, A.H. Invertible canopy reflectance modeling of vegetation structure in semiarid woodland. IEEE Trans. Geosci. Remote Sens. 1988, 26, 809–825. [Google Scholar] [CrossRef]
- Hansen, M.C.; Potapov, P.V.; Moore, R.; Hancher, M.; Turubanova, S.A.; Tyukavina, A.; Thau, D.; Stehman, S.V.; Goetz, S.J.; Loveland, T.R.; et al. High-resolution global maps of 21st-century forest cover change. Science 2013, 342, 850–853. [Google Scholar] [CrossRef] [PubMed]
- Armston, J.D.; Denham, R.J.; Danaher, T.J.; Scarth, P.; Moffiet, T.N. Prediction and validation of foliage projective cover from Landsat-5 TM and Landsat-7 ETM+ imagery. J. Appl. Remote Sens. 2009. [Google Scholar] [CrossRef]
- Cohen, W.B.; Spies, T.A. Estimating structural attributes of Douglas-fir/western hemlock forest stands from landsat and SPOT imagery. Remote Sens. Environ. 1992, 41, 1–17. [Google Scholar] [CrossRef]
- Lefsky, M.A.; Cohen, W.B.; Parker, G.G.; Harding, D.J. LiDAR remote sensing for ecosystem studies. Bioscience 2002, 52, 19–30. [Google Scholar] [CrossRef]
- Pasher, J.; King, D.J. Development of a forest structural complexity index based on multispectral airborne remote sensing and topographic data This article is one of a selection of papers from extending forest inventory and monitoring over space and time. Can. J. For. Res. 2011, 41, 44–58. [Google Scholar] [CrossRef]
- Holmgren, J.; Jonsson, T. Large scale airborne laser scanning of forest resources in Sweden. Arch. Photogramm. Remote Sens. Spat. Inf. Sic. 2004, 36, 157–160. [Google Scholar]
- Maltamo, M.; Eerikäinen, K.; Packalén, P.; Hyyppä, J. Estimation of stem volume using laser scanning-based canopy height metrics. Forestry 2006, 79, 217–229. [Google Scholar] [CrossRef]
- Torabzadeh, H.; Morsdorf, F.; Schaepman, M.E. Fusion of imaging spectroscopy and airborne laser scanning data for characterization of forest ecosystems—A review. ISPRS J. Photogramm. Remote Sens. 2014, 97, 25–35. [Google Scholar] [CrossRef]
- Quadros, N.; Frisina, R.; Wilson, P. Using airborne survey to map stream Form and Riparian Vegetation Characteristics across Victoria. In Proceedings of the SilviLaser, Hobart, Australia, 16–19 October 2011.
- Asner, G.P.; Powell, G.V.; Mascaro, J.; Knapp, D.E.; Clark, J.K.; Jacobson, J.; Kennedy-Bowdoin, T.; Balaji, A.; Paez-Acosta, G.; Victoria, E.; et al. High-resolution forest carbon stocks and emissions in the Amazon. Proc. Natl. Acad. Sci. 2010, 107, 16738–16742. [Google Scholar] [CrossRef] [PubMed]
- Gregoire, T.G.; Ståhl, G.; Næsset, E.; Gobakken, T.; Nelson, R.F.; Holm, S. Model-assisted estimation of biomass in a LiDAR sample survey in Hedmark County, Norway. Can. J. For. Res. 2011, 41, 83–95. [Google Scholar] [CrossRef]
- Hansen, A.J.; Phillips, L.B.; Dubayah, R.O.; Goetz, S.J.; Hofton, M.A. Regional-scale application of LiDAR: Variation in forest canopy structure across the southeastern US. For. Ecol. Manag. 2014, 329, 214–226. [Google Scholar] [CrossRef]
- Gobakken, T.; Næsset, E.; Nelson, R.; Bollandsås, O.M.; Gregoire, T.G.; Ståhl, G.; Holm, S.; Ørka, H.O.; Astrup, R. Estimating biomass in Hedmark County, Norway using national forest inventory field plots and airborne laser scanning. Remote Sens. Environ. 2012, 123, 443–456. [Google Scholar]
- Mora, B.; Wulder, M.A.; Hobart, G.W.; White, J.C.; Bater, C.W.; Gougeon, F.A.; Varhola, A.; Coops, N.C. Forest inventory stand height estimates from very high spatial resolution satellite imagery calibrated with LiDAR plots. Int. J. Remote Sens. 2013, 34, 4406–4424. [Google Scholar] [CrossRef]
- Hudak, A.T.; Lefsky, M.A.; Cohen, W.B.; Berterretche, M. Integration of LiDAR and Landsat ETM+ data for estimating and mapping forest canopy height. Remote Sens. Environ. 2002, 82, 397–416. [Google Scholar] [CrossRef]
- Ørka, H.O.; Wulder, M.A.; Gobakken, T.; Næsset, E. Integrating airborne laser scanner data and ancillary information for delineating the boreal-alpine transition zone in Hedmark County, Norway. In Proceedings of the SilviLaser 2010, Freiburg, Germany, 14–17 September 2010.
- Pascual, C.; García-Abril, A.; Cohen, W.B.; Martín-Fernández, S. Relationship between LiDAR-derived forest canopy height and Landsat images. Int. J. Remote Sens. 2010, 31, 1261–1280. [Google Scholar] [CrossRef]
- McInerney, D.O.; Suarez-Minguez, J.; Valbuena, R.; Nieuwenhuis, M. Forest canopy height retrieval using LiDAR data, medium-resolution satellite imagery and kNN estimation in Aberfoyle, Scotland. Forestry 2010, 83, 195–206. [Google Scholar] [CrossRef]
- Cartus, O.; Kellndorfer, J.M.; Rombach, M.; Walker, W. Mapping canopy height and growing stock volume using airborne LiDAR, ALOS PALSAR and Landsat ETM+. Remote Sens. 2012, 4, 3320–3345. [Google Scholar] [CrossRef]
- Wulder, M.A.; Seemann, D. Forest inventory height update through the integration of LiDAR data with segmented Landsat imagery. Can. J. Remote Sens. 2003, 29, 536–543. [Google Scholar] [CrossRef]
- Simard, M.; Pinto, N.; Fisher, J.B.; Baccini, A. Mapping forest canopy height globally with spaceborne LiDAR. J. Geophys. Res. 2011, 116, 1–12. [Google Scholar] [CrossRef]
- Lefsky, M.A. A global forest canopy height map from the Moderate Resolution Imaging Spectroradiometer and the Geoscience Laser Altimeter System. Geophys. Res. Lett. 2010, 37, 1–5. [Google Scholar] [CrossRef]
- Baccini, A.; Laporte, N.T.T.; Goetz, S.J.; Sun, M.; Dong, H. A first map of tropical Africa’s above-ground biomass derived from satellite imagery. Environ. Res. Lett. 2008, 3, 1–9. [Google Scholar] [CrossRef]
- Mellor, A.; Haywood, A.; Stone, C.; Jones, S. The performance of random forests in an operational setting for large area sclerophyll forest classification. Remote Sens. 2013, 5, 2838–2856. [Google Scholar] [CrossRef]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Breiman, L. Bagging predictors. Mach. Learn. 1996, 24, 123–140. [Google Scholar] [CrossRef]
- Rodriguez-Galiano, V.F.; Ghimire, B.; Rogan, J.; Chica-Olmo, M.; Rigol-Sanchez, J.P. An assessment of the effectiveness of a random forest classifier for land-cover classification. ISPRS J. Photogramm. Remote Sens. 2012, 67, 93–104. [Google Scholar] [CrossRef]
- Mascaro, J.; Asner, G.P.; Knapp, D.E.; Kennedy-Bowdoin, T.; Martin, R.E.; Anderson, C.; Higgins, M.; Chadwick, K.D. A tale of two “Forests”: Random Forest machine learning aids tropical Forest carbon mapping. PLoS ONE 2014, 9, 12–16. [Google Scholar] [CrossRef] [PubMed]
- Evans, J.S.; Cushman, S.A. Gradient modeling of conifer species using random forests. Landscape. Ecol. 2009, 24, 673–683. [Google Scholar] [CrossRef]
- Mellor, A.; Jones, S.D.; Haywood, A.; Wilkes, P. Using random forest decision tree classification for large area forest extent mapping with multi-source remote sensing and GIS data. In Proceedings of the 16th Australasian Remote Sensing and Photogrammetry Conference, Melbourne, Australia, 27–28 August 2012.
- Mellor, A.; Boukir, S.; Haywood, A.; Jones, S. Exploring issues of training data imbalance and mislabelling on random forest performance for large area land cover classification using the ensemble margin. ISPRS J. Photogramm. Remote Sens. 2015, 105, 155–168. [Google Scholar] [CrossRef]
- Johansen, K.; Phinn, S.; Witte, C. Mapping of riparian zone attributes using discrete return LiDAR, QuickBird and SPOT-5 imagery: Assessing accuracy and costs. Remote Sens. Environ. 2010, 114, 2679–2691. [Google Scholar] [CrossRef]
- Ahmed, O.S.; Franklin, S.E.; Wulder, M.A.; White, J.C. Characterizing stand-level forest canopy cover and height using Landsat time series, samples of airborne LiDAR, and the random forest algorithm. ISPRS J. Photogramm. Remote Sens. 2015, 101, 89–101. [Google Scholar] [CrossRef]
- Kellndorfer, J.M.; Walker, W.S.; LaPoint, E.; Kirsch, K.; Bishop, J.; Fiske, G. Statistical fusion of LiDAR, InSAR, and optical remote sensing data for forest stand height characterization: A regional-scale method based on LVIS, SRTM, Landsat ETM+, and ancillary data sets. J. Geophys. Res. Biogeosci. 2010. [Google Scholar] [CrossRef]
- Stojanova, D.; Panov, P.; Gjorgjioski, V.; Kobler, A.; Džeroski, S. Estimating vegetation height and canopy cover from remotely sensed data with machine learning. Ecol. Inform. 2010, 5, 256–266. [Google Scholar] [CrossRef]
- Peterson, B.; Nelson, K. Mapping forest height in Alaska using GLAS, Landsat composites, and airborne LiDAR. Remote Sens. 2014, 6, 12409–12426. [Google Scholar] [CrossRef]
- Turner, W.; Rondinini, C.; Pettorelli, N.; Mora, B.; Leidner, A.K.; Szantoi, Z.; Buchanan, G.; Dech, S.; Dwyer, J.; Herold, M.; et al. Free and open-access satellite data are key to biodiversity conservation. Biol. Conserv. 2015, 182, 173–176. [Google Scholar] [CrossRef]
- Rodriguez-Galiano, V.F.; Chica-Olmo, M.; Abarca-Hernandez, F.; Atkinson, P.M.; Jeganathan, C. Random forest classification of mediterranean land cover using multi-seasonal imagery and multi-seasonal texture. Remote Sens. Environ. 2012, 121, 93–107. [Google Scholar] [CrossRef]
- Coburn, C.; Roberts, A. A multiscale texture analysis procedure for improved forest stand classification. Int. J. Remote Sens. 2004, 25, 4287–4308. [Google Scholar] [CrossRef]
- Ghimire, B.; Rogan, J.; Miller, J. Contextual land-cover classification: incorporating spatial dependence in land-cover classification models using random forests and the Getis statistic. Remote Sens. Lett. 2010, 1, 45–54. [Google Scholar] [CrossRef]
- Franklin, S.E.; Wulder, M.A.; Gerylo, G.R. Texture analysis of IKONOS panchromatic data for Douglas-fir forest age class separability in British Columbia. Int. J. Remote Sens. 2001, 22, 2627–2632. [Google Scholar] [CrossRef]
- Lefsky, M.A.; Cohen, W.B.; Harding, D.J. LiDAR remote sensing of above ground biomass in three biomes. Int. Arch. Photogramm. Remote Sens. 2001, 34, 155–162. [Google Scholar] [CrossRef]
- Lucas, R.M.; Lee, A.C.; Bunting, P.J. Retrieving forest biomass through integration of CASI and LiDAR data. Int. J. Remote Sens. 2008, 29, 1553–1577. [Google Scholar] [CrossRef]
- Goetz, S.J.; Steinberg, D.; Dubayah, R.O.; Blair, B.J. Laser remote sensing of canopy habitat heterogeneity as a predictor of bird species richness in an eastern temperate forest, USA. Remote Sens. Environ. 2007, 108, 254–263. [Google Scholar] [CrossRef]
- Hyde, P.; Dubayah, R.O.; Walker, W.; Blair, B.J.; Hofton, M.A.; Hunsaker, C. Mapping forest structure for wildlife habitat analysis using multi-sensor (LiDAR, SAR/InSAR, ETM+, Quickbird) synergy. Remote Sens. Environ. 2006, 102, 63–73. [Google Scholar] [CrossRef]
- Næsset, E. Airborne laser scanning as a method in operational forest inventory: Status of accuracy assessments accomplished in Scandinavia. Scand. J. For. Res. 2007, 22, 433–442. [Google Scholar] [CrossRef]
- Næsset, E. Determination of mean tree height of forest stands using airborne laser scanner data. ISPRS J. Photogramm. Remote Sens. 1997, 52, 49–56. [Google Scholar] [CrossRef]
- Wulder, M.A.; Bater, C.W.; Coops, N.C.; Hilker, T.; White, J.C. The role of LiDAR in sustainable forest management. For. Chron. 2008, 84, 807–826. [Google Scholar] [CrossRef]
- Miles, P.D. Using biological criteria and indicators to address forest inventory data at the state level. For. Ecol. Manag. 2002, 155, 171–185. [Google Scholar] [CrossRef]
- National Forest Inventory. Australia’s State of the Forests Report 1998; National Forest Inventory, Bureau of Rural Sciences: Canberra, Australia, 1998.
- Department of Environment Australia’s bioregions (IBRA). Available online: http://www.environment.gov.au/land/nrs/science/ibra (accessed on 29 July 2015).
- Gellie, N.J.H. Native vegetation of the Southern Forests: South-east highlands, Australian alps, south-west slopes, and SE corner bioregions. Cunninghamia 2005, 9, 219–254. [Google Scholar]
- Van Dijk, A.I.J.M.; Beck, H.E.; Crosbie, R.S.; de Jeu, R.A.M.; Liu, Y.Y.; Podger, G.M.; Timbal, B.; Viney, N.R. The Millennium Drought in southeast Australia (2001–2009): Natural and human causes and implications for water resources, ecosystems, economy, and society. Water Resour. Res. 2013, 49, 1040–1057. [Google Scholar] [CrossRef]
- Semple, B.; Rankin, M.; Koen, T.; Geeves, G. A note on tree deaths during the current (2001–?) drought in South-eastern Australia. Aust. Geogr. 2010, 41, 391–401. [Google Scholar] [CrossRef]
- Jacobs, M.R. Growth Habits of the Eucalypts; Commonwealth Forestry and Timber Bureau: Canberra, Australia, 1955. [Google Scholar]
- Jenkins, R.B.; Coops, N.C. Landscape controls on structural variation in Eucalypt vegetation communities: Woronora Plateau, Australia. Aust. Geogr. 2011, 42, 1–17. [Google Scholar] [CrossRef]
- Department of Sustainability and Environment Victorian Forest Monitoring Program Guidelines for Ground Plot Measurement Standard Operating Procedure 13: Measuring a Large Tree Plot. Available online: http://www.depi.vic.gov.au/__data/assets/pdf_file/0013/226030/SOP13_v1.2.pdf (accessed on 29 July 2015).
- Lovell, J.L.; Jupp, D.L.; Culvenor, D.S.; Coops, N.C. Using airborne and ground-based ranging Lidar to measure canopy structure in Australian forests. Can. J. Remote Sens. 2003, 29, 607–622. [Google Scholar] [CrossRef]
- Wilkes, P.; Jones, S.D.; Suarez, L.; Haywood, A.; Mellor, A.; Woodgate, W.; Soto-berelov, M.; Skidmore, A.K. Understanding the effects of ALS pulse density for metric retrieval across diverse forest types. Photogramm. Eng. Remote Sens. 2015, 81, 625–635. [Google Scholar] [CrossRef]
- LAStools-Efficient Tools for LiDAR Processing 2012. Available online: http://rapidlasso.com/lastools/ (accessed 18 September 2015).
- Flood, N.; Danaher, T.; Gill, T.; Gillingham, S. An operational scheme for deriving standardised surface reflectance from landsat TM/ETM+ and SPOT HRG imagery for Eastern Australia. Remote Sens. 2013, 5, 83–109. [Google Scholar] [CrossRef]
- Crist, E.P.; Cicone, R.C. A physically-based transformation of Thematic Mapper data—The TM Tasseled Cap. IEEE Trans. Geosci. Remote Sens. 1984, 3, 256–263. [Google Scholar] [CrossRef]
- Wilkes, P.; Jones, S.D.; Suarez, L.; Haywood, A.; Mellor, A.; Woodgate, W.; Soto-Berelov, M.; Skidmore, A.K. Using discrete-return ALS to quantify number of canopy strata across diverse forest types. Methods Ecol. Evol. 2015, in press. [Google Scholar]
- Zhang, X.; Friedl, M.A.; Schaaf, C.B.; Strahler, A.H.; Hodges, J.C.F.; Gao, F.; Reed, B.C.; Huete, A. Monitoring vegetation phenology using MODIS. Remote Sens. Environ. 2003, 84, 471–475. [Google Scholar] [CrossRef]
- Austin, M.P. Models for the analysis of species’ response to environmental gradients. Vegetatio 1987, 69, 35–45. [Google Scholar] [CrossRef]
- Hijmans, R.J.; Cameron, S.E.; Parra, J.L.; Jones, P.G.; Jarvis, A. Very high resolution interpolated climate surfaces for global land areas. Int. J. Climatol. 2005, 25, 1965–1978. [Google Scholar] [CrossRef]
- Global Soil Water Balance Geospatial Database. CGIAR Consortium for Spatial Information. Available online: http://www.cgiar-csi.org (accessed on 29 July 2015).
- National Resource Information Centre Atlas of Australian Soils (digital version). Available online: http://gcmd.gsfc.nasa.gov/KeywordSearch/Metadata.do?Portal=idn_ceos&KeywordPath=[Keyword%3D%27NORTHCOTE+CLASSIFICATION%27]&EntryId=EARTH_LAND_AUS_NRIC_SOILS1&MetadataView=Full&MetadataType=0&lbnode=mdlb4 (accessed on 29 July 2015).
- McGarigal, K.; Tagil, S.; Cushman, S.A. Surface metrics: An alternative to patch metrics for the quantification of landscape structure. Landscape Ecol. 2009, 24, 433–450. [Google Scholar] [CrossRef]
- Lindenmayer, D.B.; Cunningham, R.; Donnelly, C.; Franklin, J.F. Structural features of old-growth Australian montane ash forests. For. Ecol. Manag. 2000, 134, 189–204. [Google Scholar] [CrossRef]
- ForestLAS Python packakge 2015. Available online: https://bitbucket.org/phil_wilkes/forestlas (accessed 18 September 2015).
- GRASS Development Team Geographic Resources Analysis Support System (GRASS) Software 2015. Available online: https://grass.osgeo.org (accessed on 29 July 2015).
- QGIS Development Team QGIS Geographic Information System. Open Source Geospatial Foundation Project 2015. Available online: http://www.qgis.org/en/site/ (accessed on 29 July 2015).
- Python Software Foundation Python 2015. Available online: https://www.python.org/psf-landing/ (accessed on 29 July 2015).
- R Development Core Team R: A Language and Environment for Statistical Computing 2014. Available online: http://www.R-project.org (accessed on 29 July 2015).
- Liaw, A.; Wiener, M. Package “randomForest”. 2013. Available online: https://cran.r-project.org/web/packages/RRF/RRF.pdf (accessed on 29 July 2015).
- Murphy, M.A.; Evans, J.S.; Strofer, A. Quantifying Bufo boreas connectivity in Yellowstone National Park with landscape genetics. Ecology 2010, 91, 252–261. [Google Scholar] [CrossRef] [PubMed]
- Svetnik, V.; Liaw, A.; Tong, C.; Wang, T. Application of Breiman’s random forest to modeling structure-activity relationships of pharmaceutical molecules. Mult. Classif. Syst. 2004. [Google Scholar] [CrossRef]
- Cutler, D.R.; Edwards, T.J.; Beard, K.; Cutler, A.; Hess, K.T.; Gibson, J.; Lawler, J.J. Random forests for classification in ecology. Ecology 2007, 88, 2783–2792. [Google Scholar] [CrossRef] [PubMed]
- Using Random Forest to Learn Imbalanced Data. Available online: http://statistics.berkeley.edu/sites/default/files/tech-reports/666.pdf (accessed on 29 July 2015).
- Seifert, F.; Scipal, K.; Quegan, S.; Le Toan, T. The Earth Explorer Biomass Mission—Status and preparatory activities. In Proceedings of the GOFC/GOLD Biomass workshop, Brisbane, Australia, 24–26 February 2015.
- McRoberts, R.E.; Tomppo, E.O. Remote sensing support for national forest inventories. Remote Sens. Environ. 2007, 110, 412–419. [Google Scholar] [CrossRef]
- Foody, G.M.; Boyd, D.S.; Cutler, M.E. Predictive relations of tropical forest biomass from Landsat TM data and their transferability between regions. Remote Sens. Environ. 2003, 85, 463–474. [Google Scholar] [CrossRef]
- Hudak, A.T.; Strand, E.K.; Vierling, L.A.; Byrne, J.C.; Eitel, J.U.; Martinuzzi, S.; Falkowski, M.J. Quantifying aboveground forest carbon pools and fluxes from repeat LiDAR surveys. Remote Sens. Environ. 2012, 123, 25–40. [Google Scholar] [CrossRef]
- Steininger, M.K. Satellite estimation of tropical secondary forest above-ground biomass: Data from Brazil and Bolivia. Int. J. Remote Sens. 2000, 21, 1139–1157. [Google Scholar] [CrossRef]
- Lindenmayer, D.B. Factors at multiple scales affecting distribution patterns and their implications for animal conservation—Leadbeater’s Possum as a case study. Biodivers. Conserv. 2000, 9, 15–35. [Google Scholar] [CrossRef]
- VicForests Operating Procedures Regulatory Handbook Version 2.1. 2014. Available online: www.vicforests.com.au/files/dbkixdmfrz/VicForests-Operating-Procedures---Regulatory-Handbook-v2.1.pdf (accessed on 29 July 2015).
- Dubayah, R.O.; Schaaf, C.B. Global ecosystem dynamics investigation. In Proceedings of the GOFC/GOLD Biomass workshop, Brisbane, Australia, 24–26 February 2015.
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wilkes, P.; Jones, S.D.; Suarez, L.; Mellor, A.; Woodgate, W.; Soto-Berelov, M.; Haywood, A.; Skidmore, A.K. Mapping Forest Canopy Height Across Large Areas by Upscaling ALS Estimates with Freely Available Satellite Data. Remote Sens. 2015, 7, 12563-12587. https://doi.org/10.3390/rs70912563
Wilkes P, Jones SD, Suarez L, Mellor A, Woodgate W, Soto-Berelov M, Haywood A, Skidmore AK. Mapping Forest Canopy Height Across Large Areas by Upscaling ALS Estimates with Freely Available Satellite Data. Remote Sensing. 2015; 7(9):12563-12587. https://doi.org/10.3390/rs70912563
Chicago/Turabian StyleWilkes, Phil, Simon D. Jones, Lola Suarez, Andrew Mellor, William Woodgate, Mariela Soto-Berelov, Andrew Haywood, and Andrew K. Skidmore. 2015. "Mapping Forest Canopy Height Across Large Areas by Upscaling ALS Estimates with Freely Available Satellite Data" Remote Sensing 7, no. 9: 12563-12587. https://doi.org/10.3390/rs70912563
APA StyleWilkes, P., Jones, S. D., Suarez, L., Mellor, A., Woodgate, W., Soto-Berelov, M., Haywood, A., & Skidmore, A. K. (2015). Mapping Forest Canopy Height Across Large Areas by Upscaling ALS Estimates with Freely Available Satellite Data. Remote Sensing, 7(9), 12563-12587. https://doi.org/10.3390/rs70912563