1. Introduction
Ground subsidence has gradually become one of the most common threats to lives and properties in the fast-booming mega-cities in China. Along with the rapid development of cities often comes the excessive withdrawal of underground resources and ceaseless new construction above and under the ground surface, all of which are potential risks that cause ground subsidence. Monitoring the stability over urban areas thus becomes very important for preventing ground subsidence and to ensure surface stability [
1,
2,
3,
4,
5].
Up to now, the most common approach for observing and measuring ground subsidence remains traditional ground leveling and GPS measurements. On the one hand, when combining with the advanced GPS technique and the precise coordinates of control point grids, ground leveling makes it possible to directly measure ground motion with quite high accuracy. On the other hand, however, as cities expand rapidly over time and space, the traditional methods are now facing many challenges, among which are the shortage in manpower, the cost required for performing more measurements, as well as the inability to get full coverage of time and space over large areas. To overcome these shortcomings, a new technique that calls for all-time, wide-area and high-accuracy ground monitoring is needed, and that is where synthetic aperture radar interferometry (InSAR) comes in.
Since its first illumination of the Earth from the 1980s, the InSAR technique has been successful drawing enormous attention from scholars and researchers in the field of geoscience. Nowadays, this technology has already been widely acknowledged for its ability to continuously monitor ground motions and to recover the digital elevation model (DEM) [
6,
7]. Furthermore, for the purpose of overcoming the two major limiting factors of InSAR, namely geometric and temporal decorrelation along with the atmospheric phase screen (APS) disturbance, the persistent scatterers interferometry (PSI) technique, also known as the multi-temporal InSAR (MTI) technique, was proposed and has since become the core concept in precisely measuring ground displacement from a stack of multi-SAR-images [
8,
9,
10]. Among many of the technique’s strengths, the most important is detecting displacement within millimeter to sub-millimeter accuracy. In the past, a number of projects were carried out to demonstrate the sensitivity of PSI technique under ideal circumstances. For example, the experiment carried out by Ferretti [
11], using two dihedral corner reflectors (CR) with a specifically-designed size and placed on the top of a building roof (so that a good signal-to-clutter ratio could be guaranteed), mounted on two sliding platforms controlled by a robust clamping system (so that the CR can be manually and precisely adjusted by the millimeter) and close to each other (so that the atmospheric effect can be neglected), demonstrated the sub-millimeter accuracy of the PSI technique with the C-band synthetic aperture radar (SAR) dataset. Other similar experiments also showed a similar conclusion [
12,
13].
However, in a real scenario, the accuracy of the PSI technique can vary with a blending of different factors, including the accuracy of the satellite’s spatial baseline, atmospheric conditions [
14], the physical nature of persistent scatterer (PS) points [
15], the coherence between adjacent PS points [
16],
etc. For example, our area of interest (AOI), Hong Kong, consists mostly of ocean, vegetation and dense skyscrapers, together with high humidity all year round. From the radar point of view, the complicated ground features make it very difficult to generate high quality interferograms with high spatial resolution and wide spatial coverage if using the conventional InSAR technique. Even applying the PSI technique, a large portion of the ocean, mountainous area and isolated islands can mean a low temporal/spatial coherence, bringing down the accuracy of PSI technique. In addition, the fact that skyscrapers usually look like a complex mix of point-wise targets, but vegetated areas absolutely lack these brings more challenges to PSI processing. From the atmospheric point of view, the humid subtropical climate of the city and extremely high water vapor density in the air result in a greater extent of water vapor delay than in general, causing significant distortion in detected ground displacement. To successfully apply the PSI technique, the atmospheric water vapor delay must be carefully estimated and removed [
1].
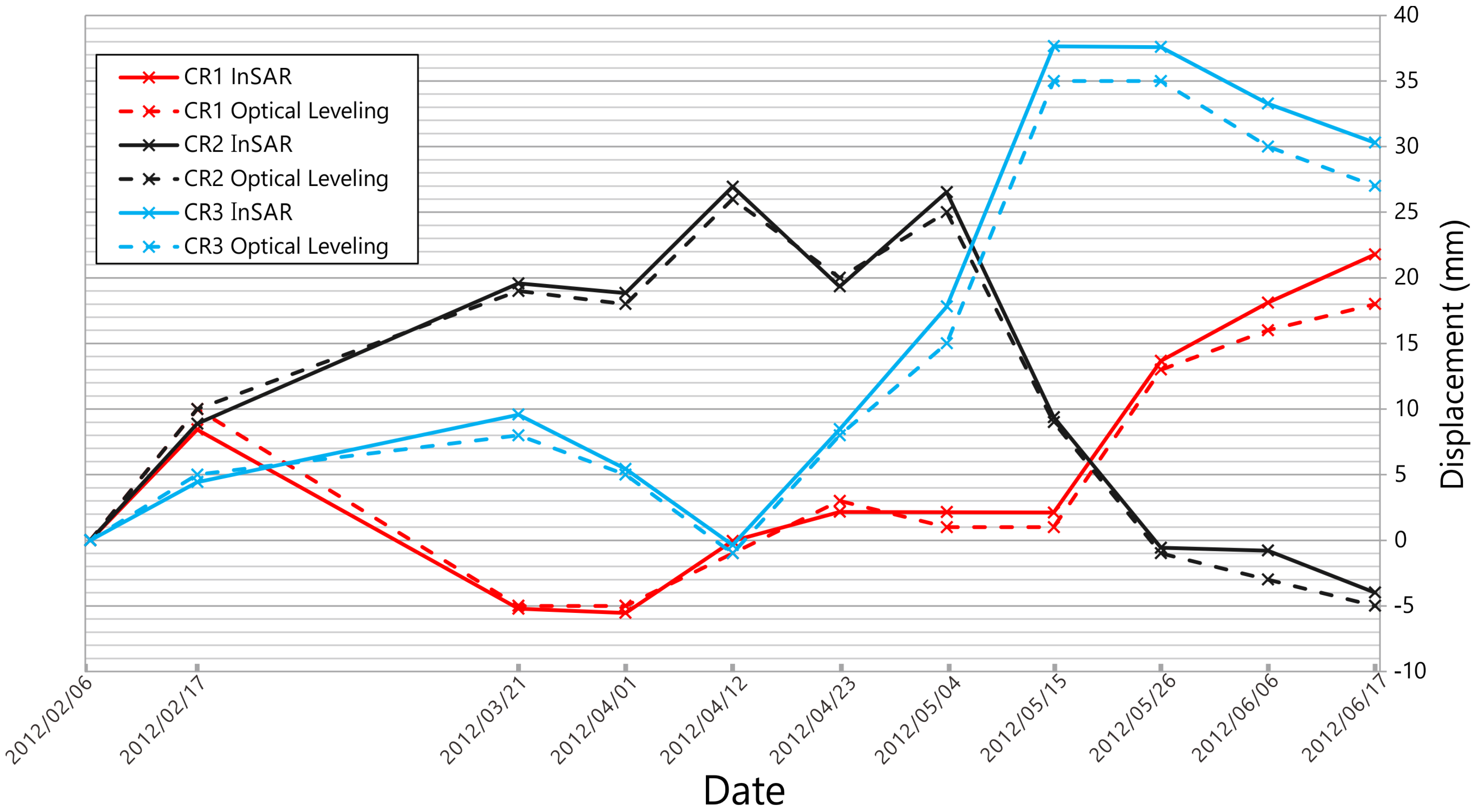
In this project, we try to carry out the experiment of generating a ground displacement map in the urban area of Hong Kong, China, with the PSI technique and compare the outcome with traditional survey methods so as to demonstrate the millimeter accuracy of PSI in practical applications. To prove the accuracy of the PSI technique, four corner reflectors (CR) were installed inside the AOI. In order to compare the deferential displacements of each CR with regard to the others, one CR was chosen as the reference and kept stable all of the time, while the others were either lifted or lowered manually to an extent of some millimeters, and their displacements were recorded by optical leveling. The accuracy of PSI would then be evaluated by comparing the displacement computed by PSI and recorded by optical leveling. The experiment, carried out in unideal conditions (since the CR validation test was located at a construction site on reclaimed land), nevertheless proved that millimeter accuracy can definitely be achieved. At last, the advantages and limitations of the PSI technique applied in this project were fully evaluated, aiming at providing some beneficial references for similar applications in the future.
This paper is organized as follows. Firstly, PSI processing over the Hong Kong urban area was carried out, bringing three outcomes: the reflectivity map, the 3D location of PS points with 1-m precision and the estimated millimeter displacement along the satellite line of sight (LOS) of PS points. For the second part, a set of CR was deployed for a time period of a half year for the purpose of validation testing, and the displacement values of CR from both ground leveling and PSI processing were compared. A discussion of the validation outcome and the assessment of the accuracy will follow at the end of the paper.
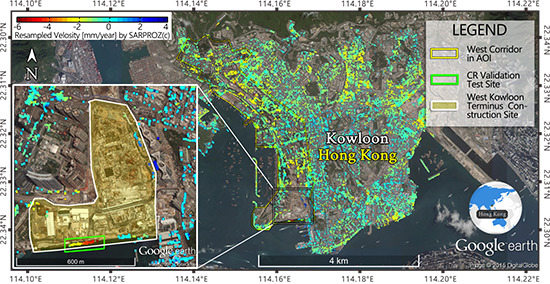
2. Study Area and Dataset
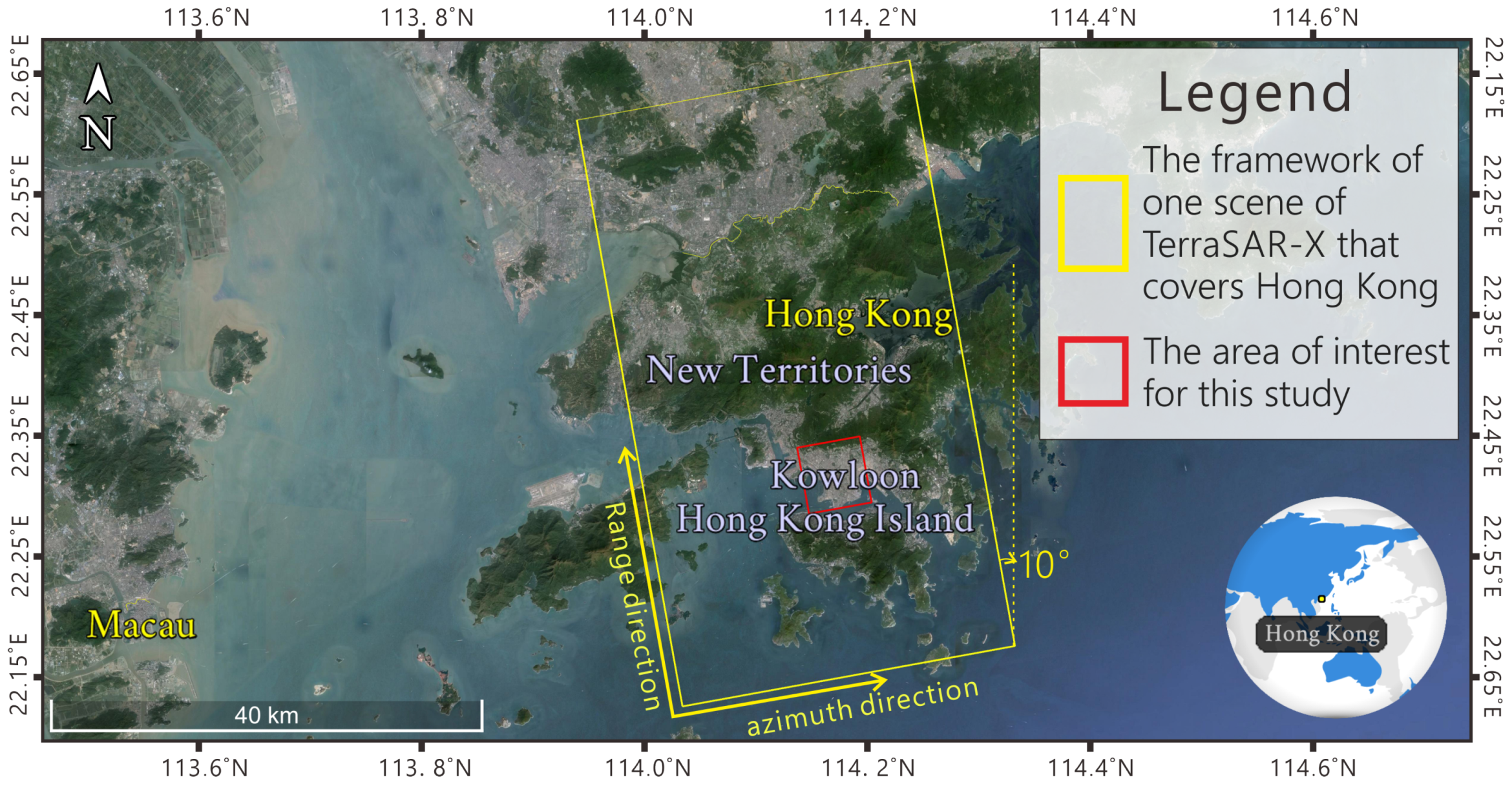
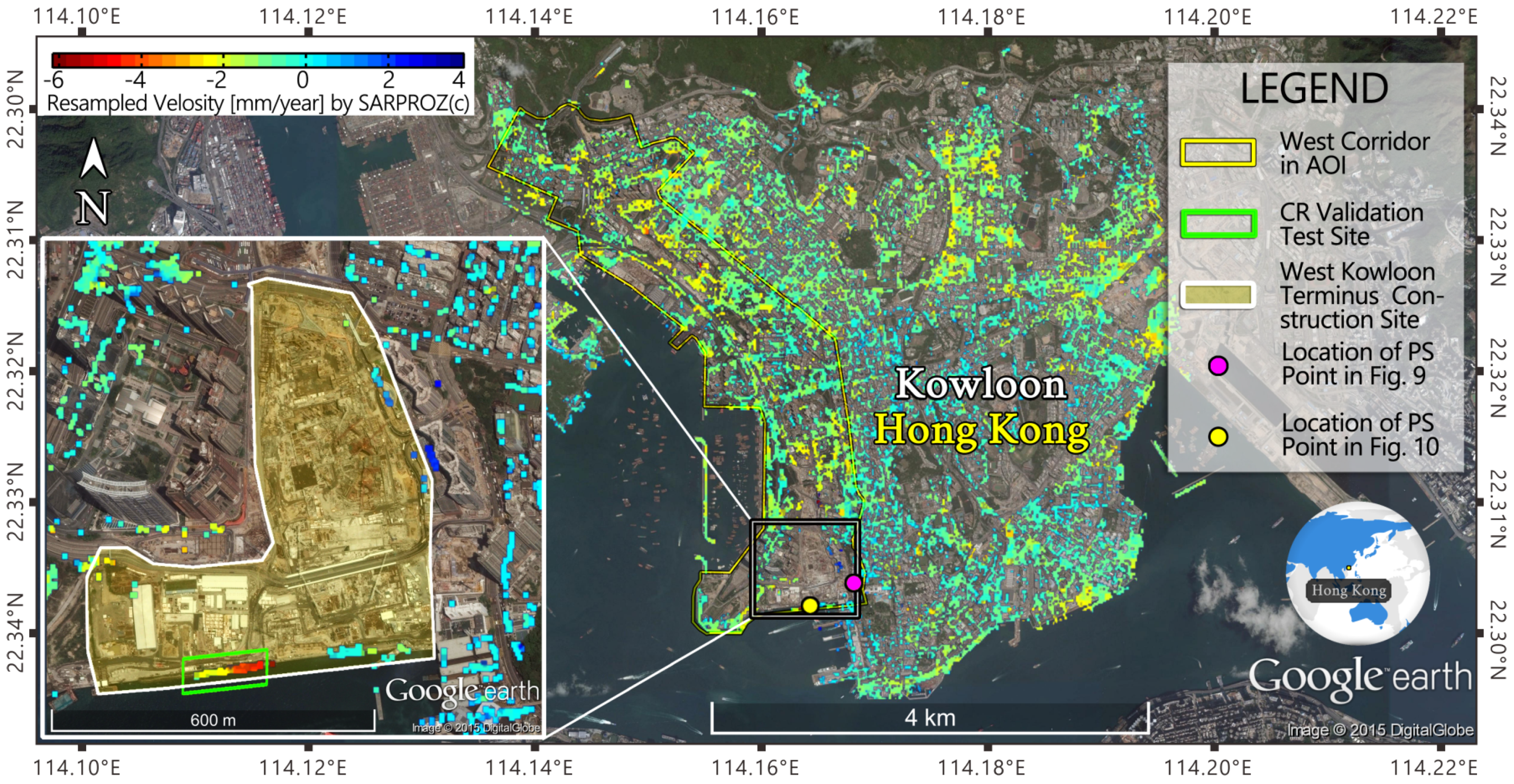
The study area of interest belongs to Kowloon, which is the majority region of urban Hong Kong, China. The area is marked with the red rectangle in
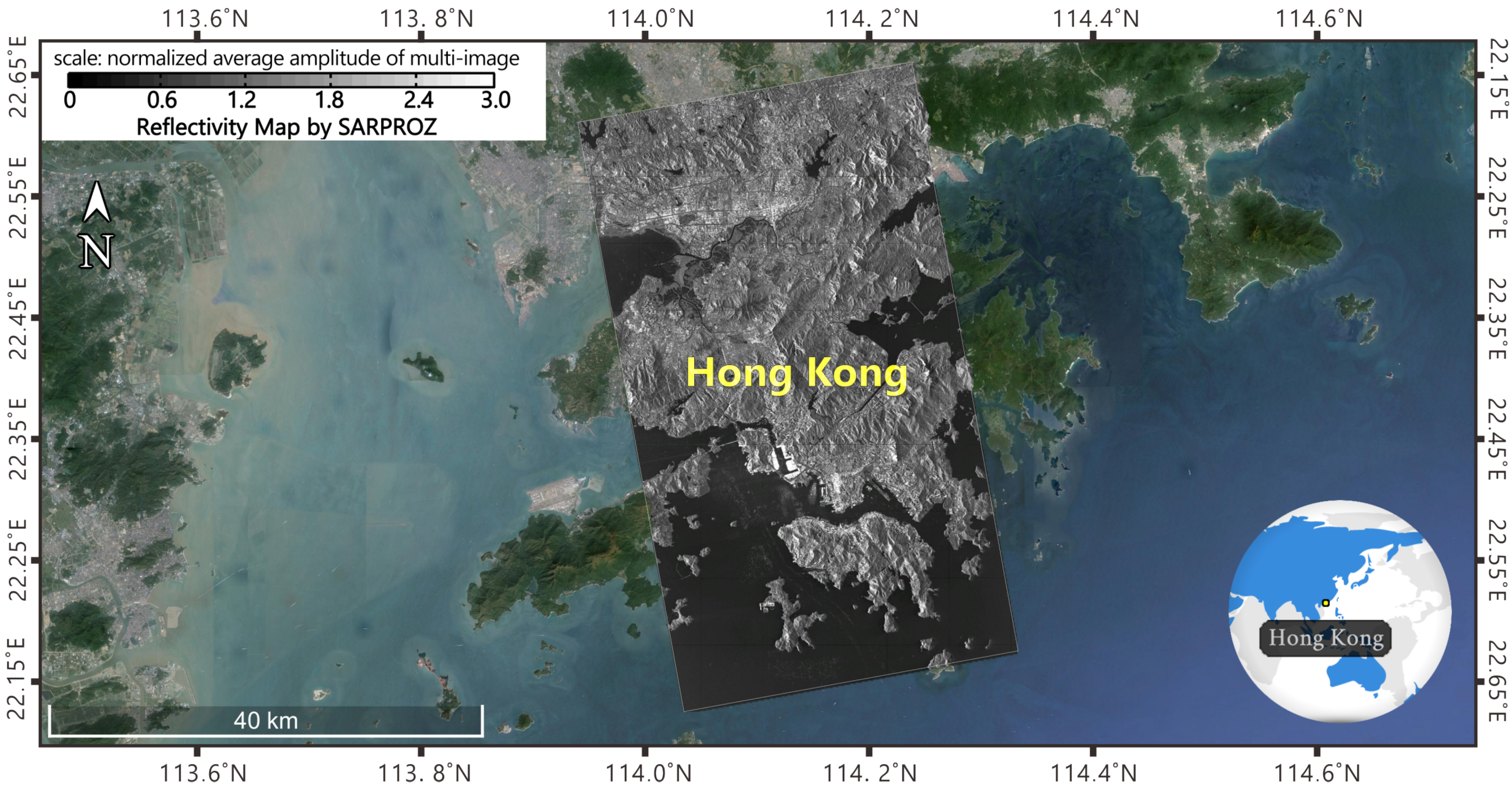
Figure 1. In this study, a total of 73 TerraSAR-X (TSX) and TanDEM-X (TDX) images acquired between October 2008 and September 2012 was used. The SAR images are in the X-band with a wavelength of 31 mm and a frequency of 9.6 GHz, with a resolution of up to 2 m. The minimum interval between the two successive acquisitions is 11 days. The images were acquired at about 6:25 pm each day, along an ascending orbit with an incidence angle of approximately 37°.
Figure 1.
The area of interest (AOI) for the study, which covers the majority of urban Hong Kong.
Figure 1.
The area of interest (AOI) for the study, which covers the majority of urban Hong Kong.
Figure 2.
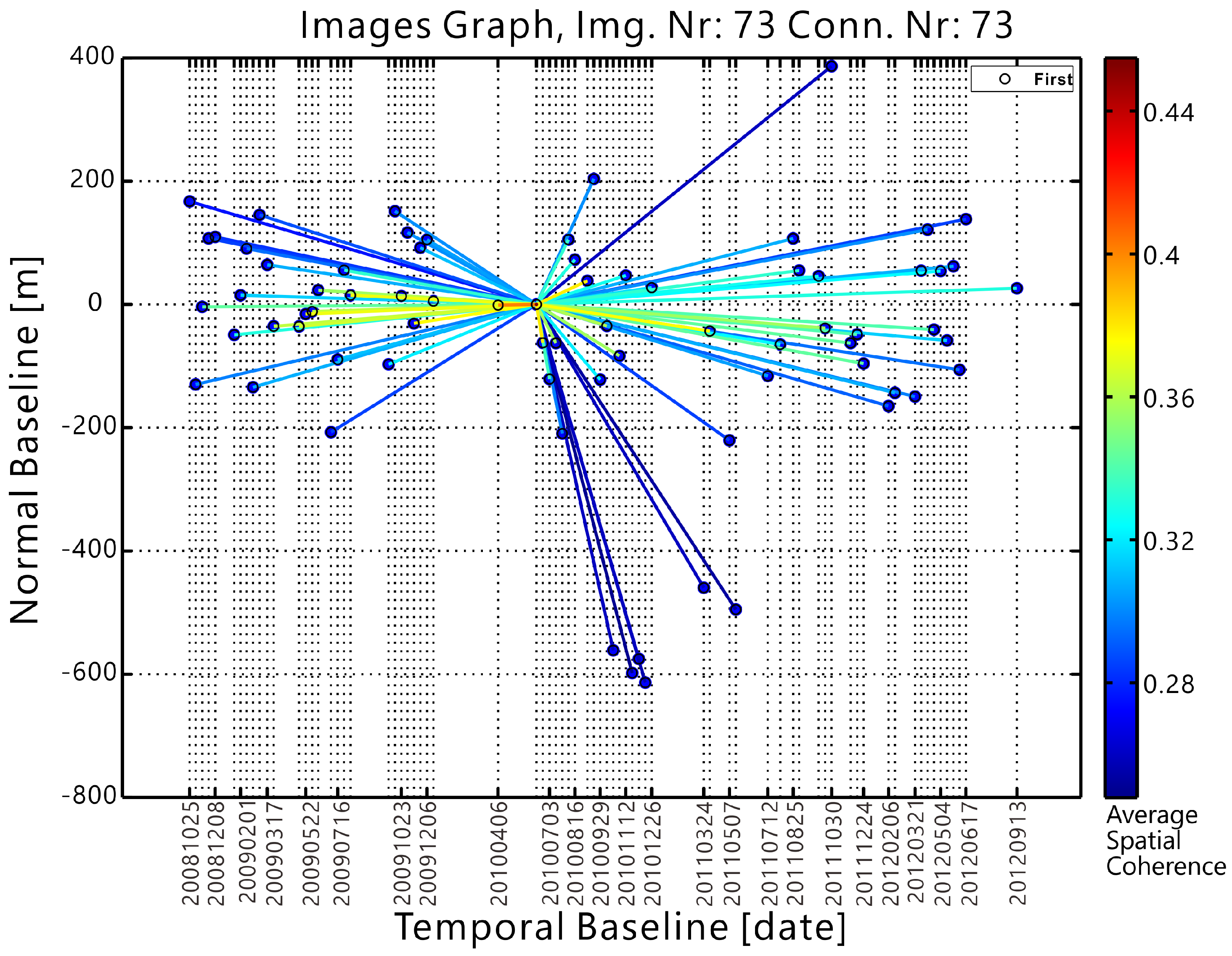
This is the figure showing TSX and TDX images used in our analysis, where the x-axis indicates the temporal baseline and the y-axis indicates the perpendicular baseline. It is worth noting that nearly all of the baselines for TSX images are precisely controlled to within a distance of about 200 m, with only a few exceptions that are mostly TDX images, which requires a larger baseline for its DEM mapping mission. The color bar indicates the average spatial coherence of the interferogram given one master and one slave image. It gives a general idea that with a smaller spatial/temporal baseline usually comes a higher spatial coherence.
Figure 2.
This is the figure showing TSX and TDX images used in our analysis, where the x-axis indicates the temporal baseline and the y-axis indicates the perpendicular baseline. It is worth noting that nearly all of the baselines for TSX images are precisely controlled to within a distance of about 200 m, with only a few exceptions that are mostly TDX images, which requires a larger baseline for its DEM mapping mission. The color bar indicates the average spatial coherence of the interferogram given one master and one slave image. It gives a general idea that with a smaller spatial/temporal baseline usually comes a higher spatial coherence.
In
Figure 2, the interferometric configuration is shown. Each dot in the image represents a SAR acquisition in the normal baseline
vs. the temporal baseline axis, and each line depicts one interferogram. The star-like graph is also usually the standard and optimized configuration for PSI processing. In this star-like connection, all images are referred to one master image taken on 11 June 2010. In general, the image acquired midway through the monitoring period will be selected as the master image. In general, the selected master will not impact the final output.
6. Discussion
6.1. Analysis of the Bias
From
Figure 11, we can see that the results retrieved from PSI and the ground survey in May and June were not matching as well as the previous months; the biases have a trend of growing bigger. However, the discrepancy between InSAR and leveling in May and June is not irregular, if we notice that PSI-derived data are always higher than ground survey data. In other words, the result appears shifted. This suggests that some factors occurred somehow and biased the results.
It is important to investigate the reasons for such biases. First of all, we can rule out the possibilities of precipitation and thermal expansion after some calculations. Hence, the most possible explanation is the movement of the ground where the CRs were located. As a matter of fact, we know that the area where the CRs were installed (which were located in the area of
Figure 10) was moving.
Here, we try to carry out a small area PSI process to investigate the differential velocity between the four CRs. During the process, we will choose a new reference point close to the test site with a high temporal coherence. Here, the temporal coherence of one PS point is defined as [
24]:
where
is the acquired interferometric phase,
is the elevation-dependent phase term,
is the deformation-dependent phase term,
N is the total number of scenes for PSI processing and
means the phase difference between the master image and the
i-th image for the selected point. Points with higher temporal coherence can be seen as potential PS candidates. In this case, when choosing a new reference point with a high temporal coherence, we can also observe a moving trend of the points around the CRs, including the reference reflector in May and June. In particular, by taking the four PS points closest to each of the four CRs with a high temporal coherence value, we calculate the annual velocity during the period of the validation test, and we can see from
Figure 13 that the reference CR4 has a very different velocity, −7.9 mm/year, compared to the rest, which all have a velocity close to 1 mm/year. The differential movement between the reference CR and the rest explains the biases we observed in
Figure 11.
Figure 13.
Here, we selected four PS points that were closest to each of the four CRs. The time series analysis of the four PS points shows a moving trend. In this case, since the vertical displacements were biased, this moving trend is very likely to be an eastward horizontal movement.
Figure 13.
Here, we selected four PS points that were closest to each of the four CRs. The time series analysis of the four PS points shows a moving trend. In this case, since the vertical displacements were biased, this moving trend is very likely to be an eastward horizontal movement.
Hence, a possible explanation here of the bias could be a horizontal west-east direction movement between the reference CR and the others, recorded by InSAR, but not by ground leveling. We will verify the assumption by using ground GPS records.
6.2. Verification of CR Movement
The coordinates of the four CRs were measured by GPS RTK with the help of a ground survey team at the beginning and end of the experiment. As shown in
Figure 5, the SAR system is more sensitive in the west-east direction movement and less sensitive in the north-south direction; hence, here, we only analyze the west-east movement. The west-east coordinates measured by GPS RTK are listed in
Table 3. According to
Table 3, the reference CR, CR4, was moving towards the other three, while the others remain relatively stable. This moving east is equivalent to a bias that will result in a larger displacement value than it should be. This explains why the SAR results are always higher than those of the ground survey, because the SAR results include this horizontal differential motion, while the ground survey’s measurement does not.
Table 3.
CRs’ reference mark coordinates in the east-west direction at the beginning and ending of the validation test.
Table 3.
CRs’ reference mark coordinates in the east-west direction at the beginning and ending of the validation test.
| | CR1 Easting (m) | CR2 Easting (m) | CR3 Easting (m) | CR4 Easting (m) |
|---|
| 2 June 2012 | 834,831.51 | 834,810.39 | 834,791.74 | 834,773.77 |
| 11 September 2012 | 834,831.50 | 834,810.39 | 834,791.74 | 834,773.81 |
| Δ(m) | −0.01 | 0.00 | 0.00 | 0.04 |
Since the accuracy of GPS RTK is far lower than PSI and only two sets of data were recorded, no quantitative analysis can be carried out. However, we can carry out the quantitative analysis in another way. If we neglect the reference CR in this case and take any other CR as the new reference CR, we can calculate the relative movement between the new reference CR and the rest using exactly the same method shown in
Figure 12. Since the other three CRs are relatively stable, the results between SAR measurement and ground survey measurement should be well matched.
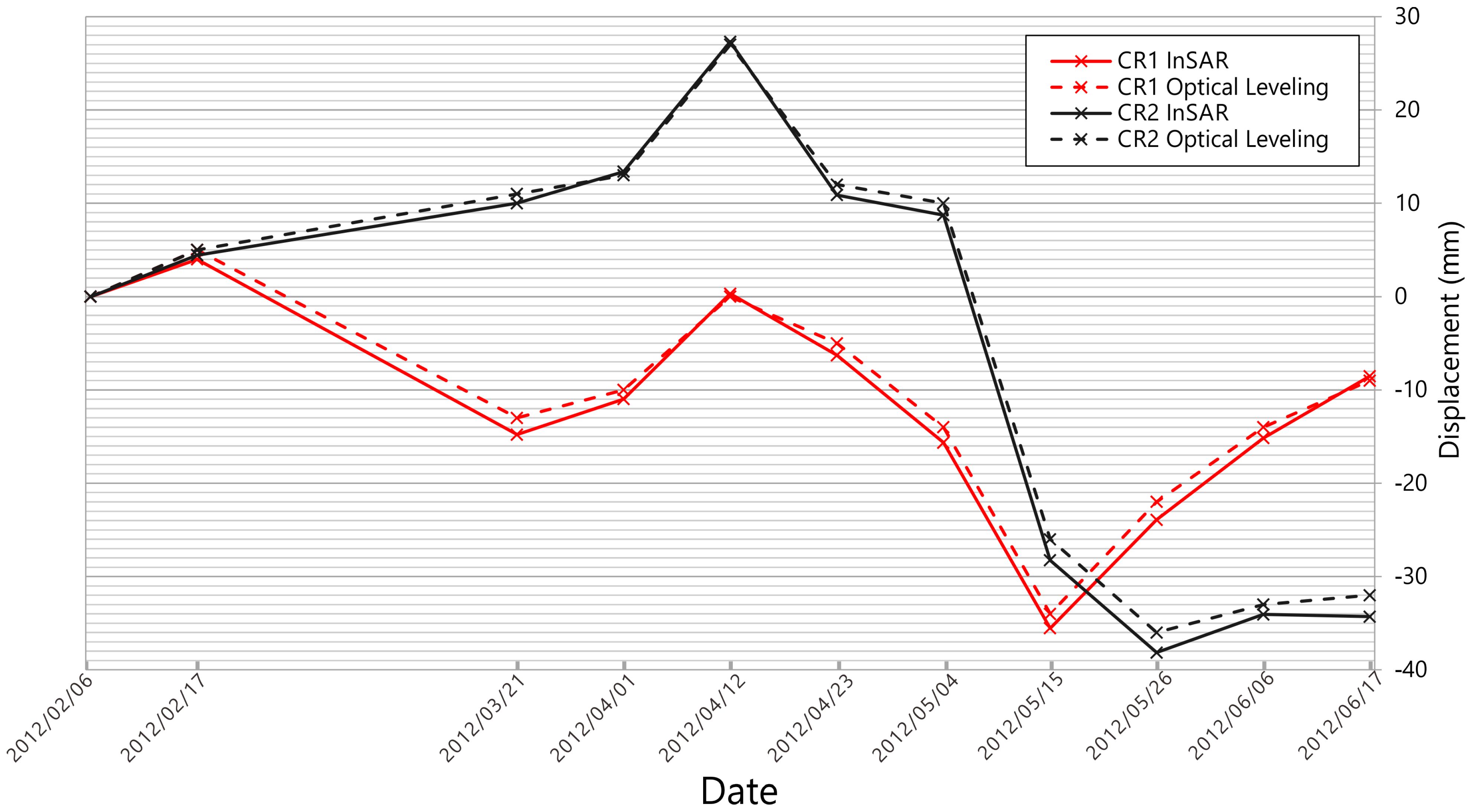
For example, if we take CR3 as the new reference, we can get the relative movement of the other two compared to the new reference. The result is illustrated in
Figure 14 and
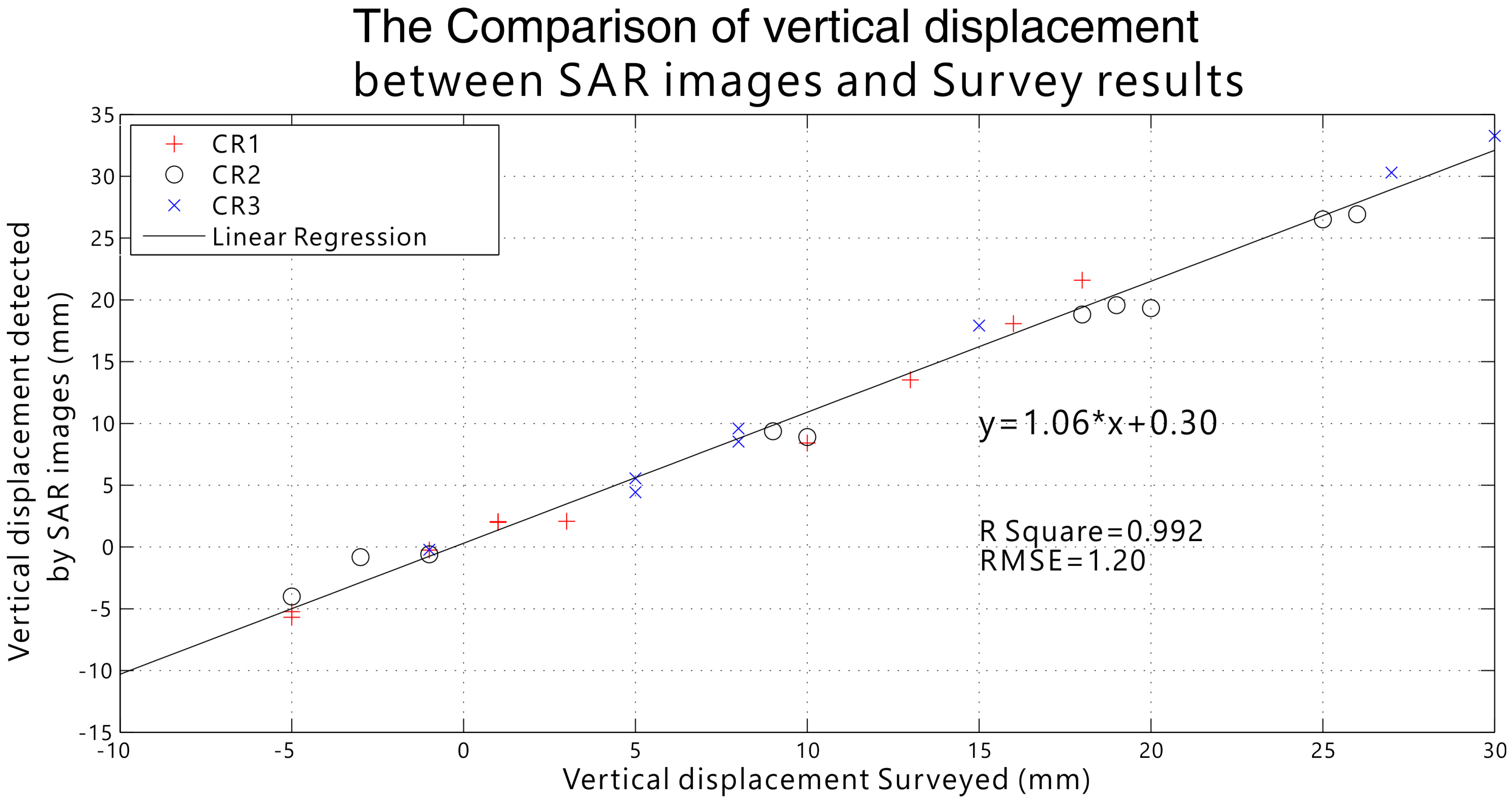
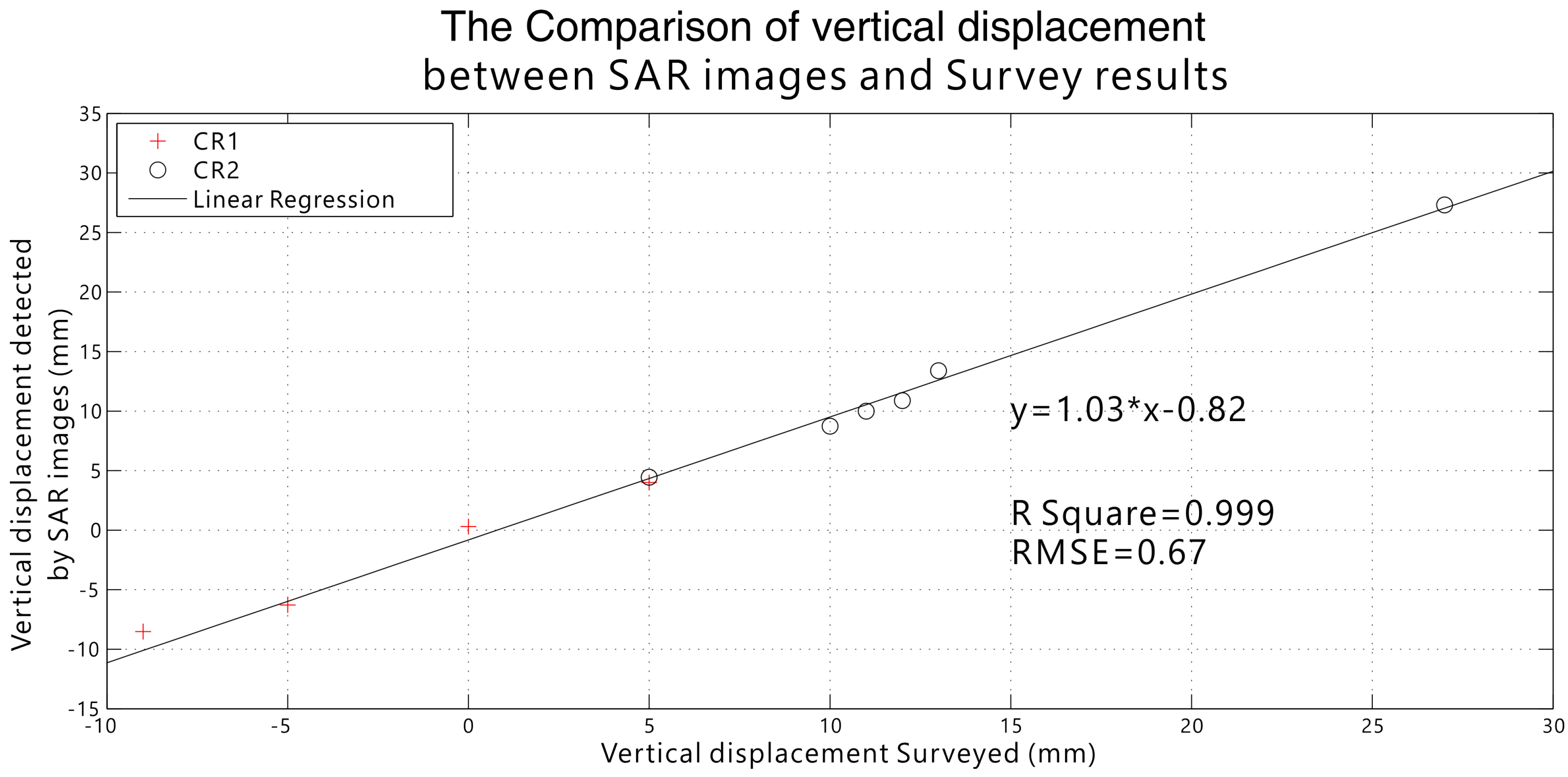
Figure 15, from which we can see that the PSI result and optical leveling result are better matching each other. A statistical analysis is also carried out. The outcome of the linear regression is:
It shows a bias of less than one millimeter and a deviation from the linear relation of about 3%. Comparing with
Figure 12, the new one shows a
of 0.999 and an RMSE of 0.67 mm, which is a great improvement. This new RMSE is significantly lower than 1 mm, meaning that the accuracy can even be better than 1 mm. This verifies the previous assumption that the default reference CR is not stable during the period of experiment with an eastward horizontal movement. Furthermore, by ruling out this bias, the PSI technique can indeed reach a millimeter to sub-millimeter level accuracy.
Figure 14.
The relative vertical displacements time series compared to CR3 retrieved by InSAR in comparison to the result retrieved by the leveling survey.
Figure 14.
The relative vertical displacements time series compared to CR3 retrieved by InSAR in comparison to the result retrieved by the leveling survey.
Figure 15.
The statistical analyses on the deviation between the displacement detected by InSAR and by the leveling survey measurement when CR3 is taken as the reference CR.
Figure 15.
The statistical analyses on the deviation between the displacement detected by InSAR and by the leveling survey measurement when CR3 is taken as the reference CR.
6.3. Strengths and Weaknesses of the PSI Technique
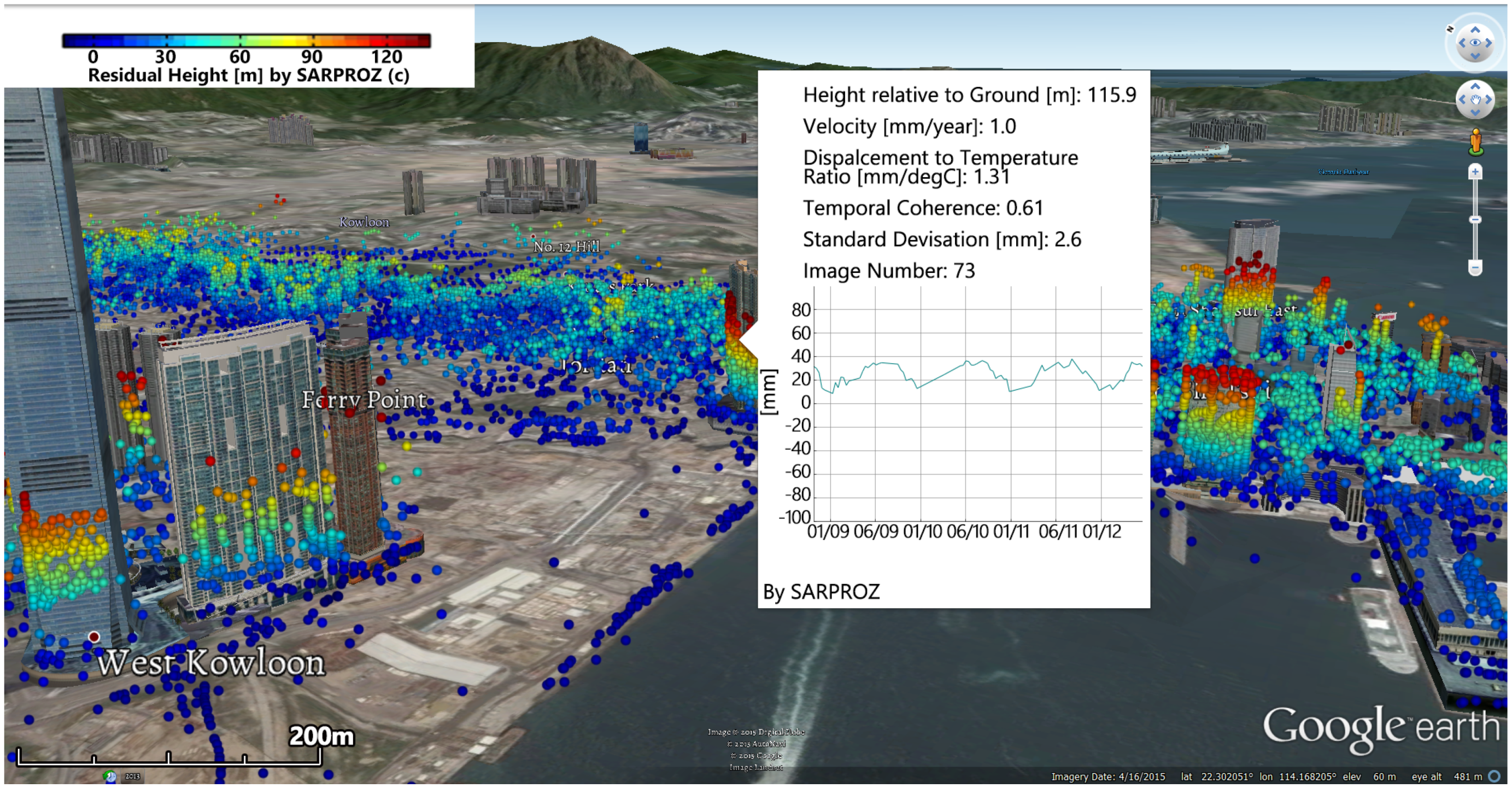
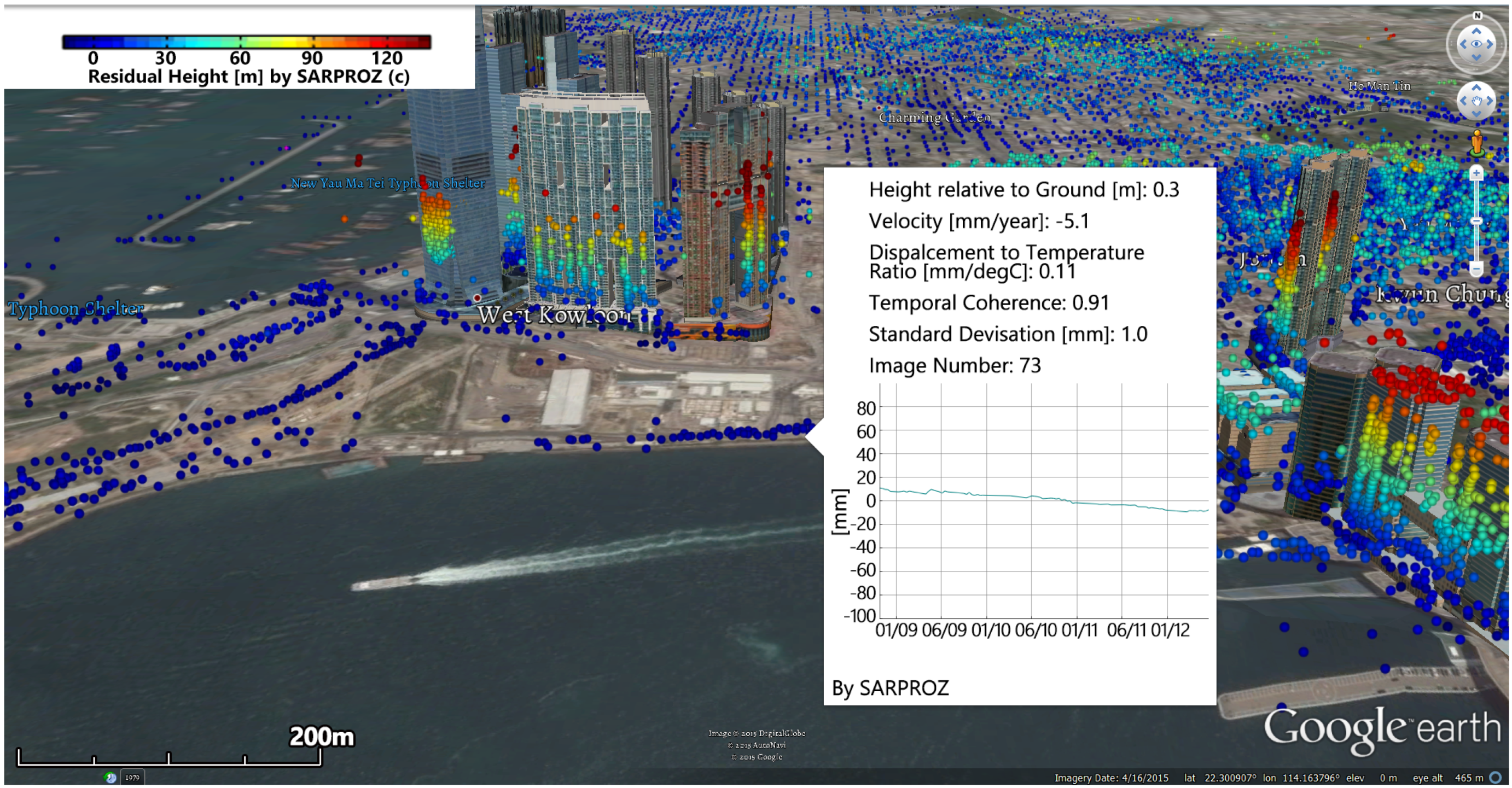
Here, we try to discuss some of the strengths and weaknesses of the PSI technique for monitoring urban areas that came out of this study. As demonstrated in the project, PSI is specialized in wide area monitoring. For example, for TerraSAR-X strip map mode, the image can cover a wide area of approximately 1500 km2. Besides, the PSI technique can derive the extremely high density of PSCs from images. Most importantly, PSI is capable of achieving the same level of accuracy of the ground survey, while being much more convenient for monitoring large areas.
However, there are still some limitations. In the first place, the method does not work with vegetated area. As shown in
Figure 7, there is no information in the vegetated area.
Secondly, even in non-vegetated areas, PS points are not everywhere. For example, no PS points can be found in the shadowed-by-skyscrapers area, which is often the case in Hong Kong. In order to overcome this problem, it is suggested to use both ascending and descending SAR images.
Thirdly, the continuity of the data relies on the stability of satellite acquisition. If the satellite fails to acquire data for a long period, then no information can be retrieved.
Moreover, if the monitoring area undergoes a subsidence greater than the length of one phase cycle, then PSI is unable to read this fast movement. The solution for this kind of problem in the future is to maintain stable and regular acquisition and to shorten the revisiting time to get more available data.
Last, but not the least, as already shown in
Figure 5, PSI is only sensitive along the LOS direction. With one single geometry, we cannot decompose vertical and horizontal movements. One way to solve the problem is again to use both ascending and descending track images.
In conclusion, PSI is a very powerful technique for wide areas and high accuracy monitoring tasks, where it is possible to reach millimeter accuracy in monitoring the displacement of millions of targets all at once. PSI can be extremely useful if used in collaboration with other techniques, so that the advantages can be highlighted and the drawbacks avoided. Future efforts should be spent to find the best way to combine PSI with other techniques for the purpose of monitoring ground displacement more accurately.
7. Conclusions
In this study, we analyzed the ground displacement over the Hong Kong urban area using the PSI technique. Seventy three TSX and TDX images spanning over a four-year time period are used for the data process. The PSI process generated a map of displacement annual velocity along the LOS direction that shows an overall velocity close to zero in most of the regions with partial regions varying from −10 mm/year to 5 mm/year. In particular, a number of spots inside the west corridor shown in
Figure 7 and the corner reflector validation test site (
Figure 10) are showing some displacement trends that exceed −5 mm/year; both of the sites stand on reclamation land and near ongoing underground/ground construction sites. It is likely that both the geological features of surface land and ongoing human activities resulted in ground displacement in these areas.
To validate if the accuracy of the PSI technique can indeed reach the millimeter level in this study, a corner reflector validation test was carried out. The reflectors were manually moved up or down, and their true values were compared to the value derived from the PSI process. A linear regression of the displacement between the surveyed value and the PSI-derived value was conducted, and the result shows a very high correlation between PSI processing and the ground leveling recorded value, with an RMSE of 1.20 mm, very close to 1 mm. The validation test presents the fact that the PSI technique can reach a millimeter-level accuracy.
As a further effort to the analysis and discarding a trend of bias between PSI and ground leveling that happened in the latter phase of the validation test, we carried out another small area PSI process to investigate the ground movement where the four corner reflectors were located. The analysis shows a horizontal moving trend between the reference reflector and the other three. The fact that the reference reflector was moving horizontally towards the other three explains the bias well, because ground leveling can only record vertical movement, while PSI records both horizontal and vertical movement. After this factor was ruled out in calculating the deviation of displacement between PSI and ground leveling, the new RMSE significantly dropped to 0.67 mm, far lower than 1 mm, showing that the PSI technique can indeed reach up to sub-millimeter level accuracy when no bias is introduced.