Multiple Stable States and Catastrophic Shifts in Coastal Wetlands: Progress, Challenges, and Opportunities in Validating Theory Using Remote Sensing and Other Methods
Abstract
:1. Introduction
1.1. Coastal Wetland Occurrence and Value
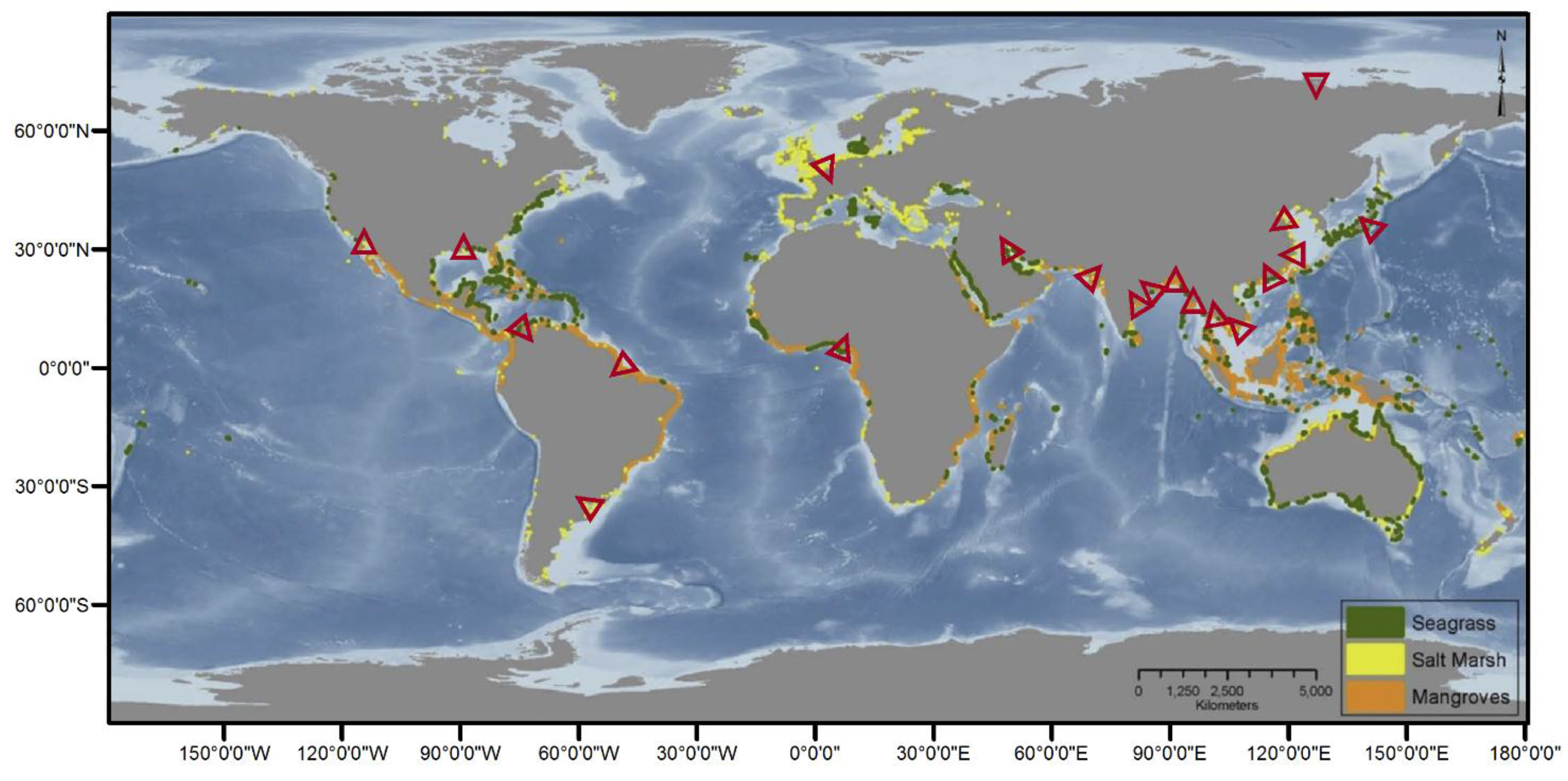
1.2. Invoking Multiple Stable State Theory
2. Background: Multiple Stable State Theory and Coastal Wetlands
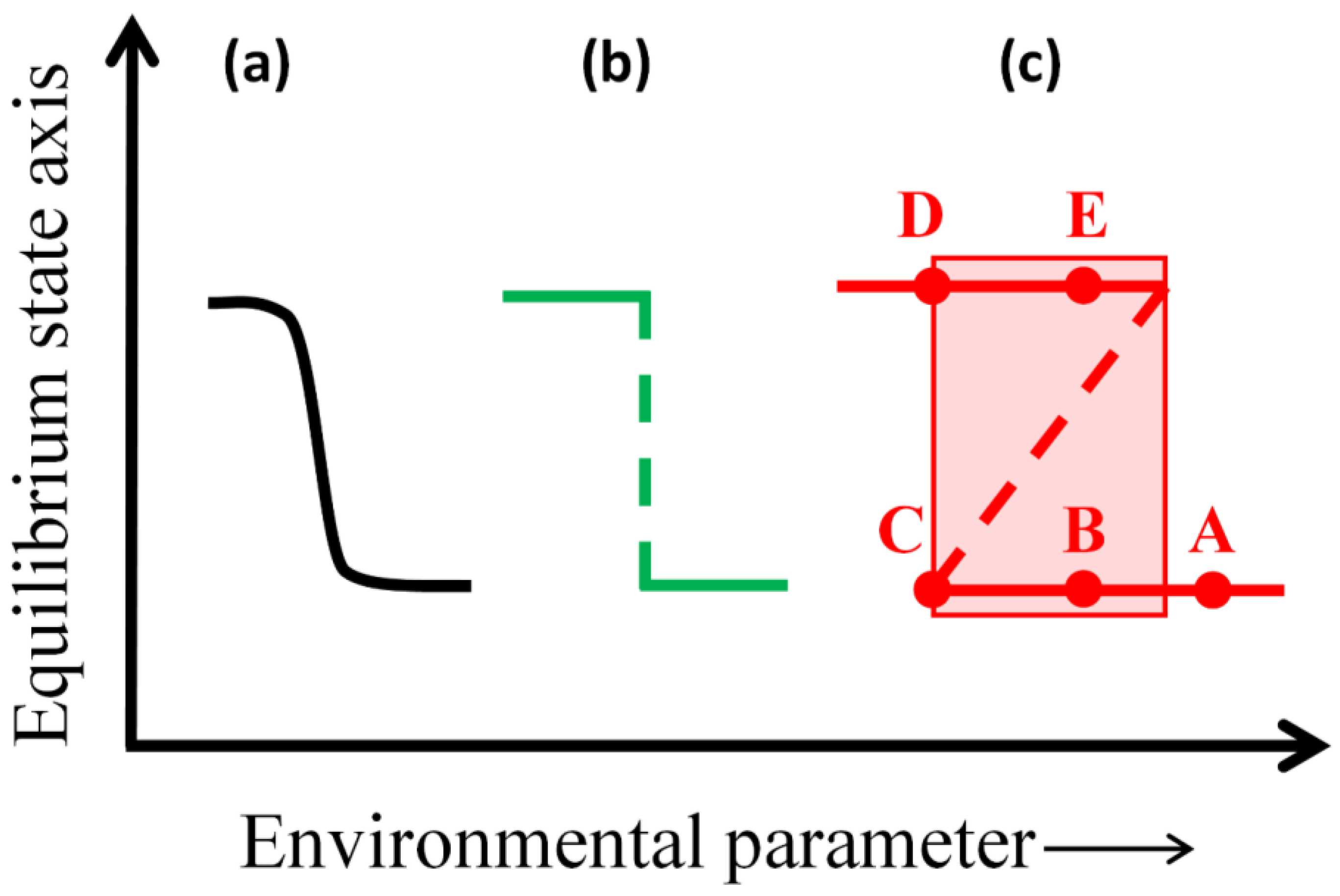
2.1. Theory of Multiple Stable Ecosystem States
- (1)
- A system is in a state of stable equilibrium if a small environmental perturbation that pushes the system away from equilibrium is dampened by negative feedbacks in the subsequent system dynamics, returning the system to the same stable equilibrium. Such stable states should be observationally identifiable as being continuously maintained over large areas and long times, often in sharp juxtaposition to alternative states observed adjacent in space or time (also see Section 2.2.).
- (2)
- In some cases, a system may be pushed, even by a small perturbation in environmental conditions, from a stable equilibrium into a transient, unstable equilibrium state. Upon briefly occupying the unstable equilibrium, the system then has a chance of either returning to the previous stable equilibrium via negative feedbacks (as in (1)) or else experiencing “runaway” positive feedback and a catastrophic shift to an alternative stable state. Unstable equilibrium states are likely to be local, transient, or observationally overlooked, disappearing upon perturbation; but catastrophic shifts should be observationally apparent given sufficient temporal resolution of data.
- (3)
- Alternatively, a system may exhibit gradual change in response to a small perturbation in environmental conditions, or may exhibit gradual change along a gradient of conditions in space or time (e.g., ecological succession), in which case the system dynamics do not conform to multiple-equilibrium state theory. Observationally, such systems are likely to grade into adjacent ecosystems rather than being juxtaposed across sharp ecosystem boundaries, and should exhibit continuous (and theoretically reversible) change over space and time.
2.2. Significance of Multiple Stable States in Observation and Management
2.3. Numerical Modeling of Multiple Stable States in Coastal Wetlands
3. Progress Testing Theory: Empirical Evidence of Multiple Stable States
3.1. Laboratory and Field Evidence
3.1.1. Salt Marshes
3.1.2. Freshwater Tidal Wetlands and Deltas

3.1.3. Mangroves
3.1.4. Seagrass Meadows

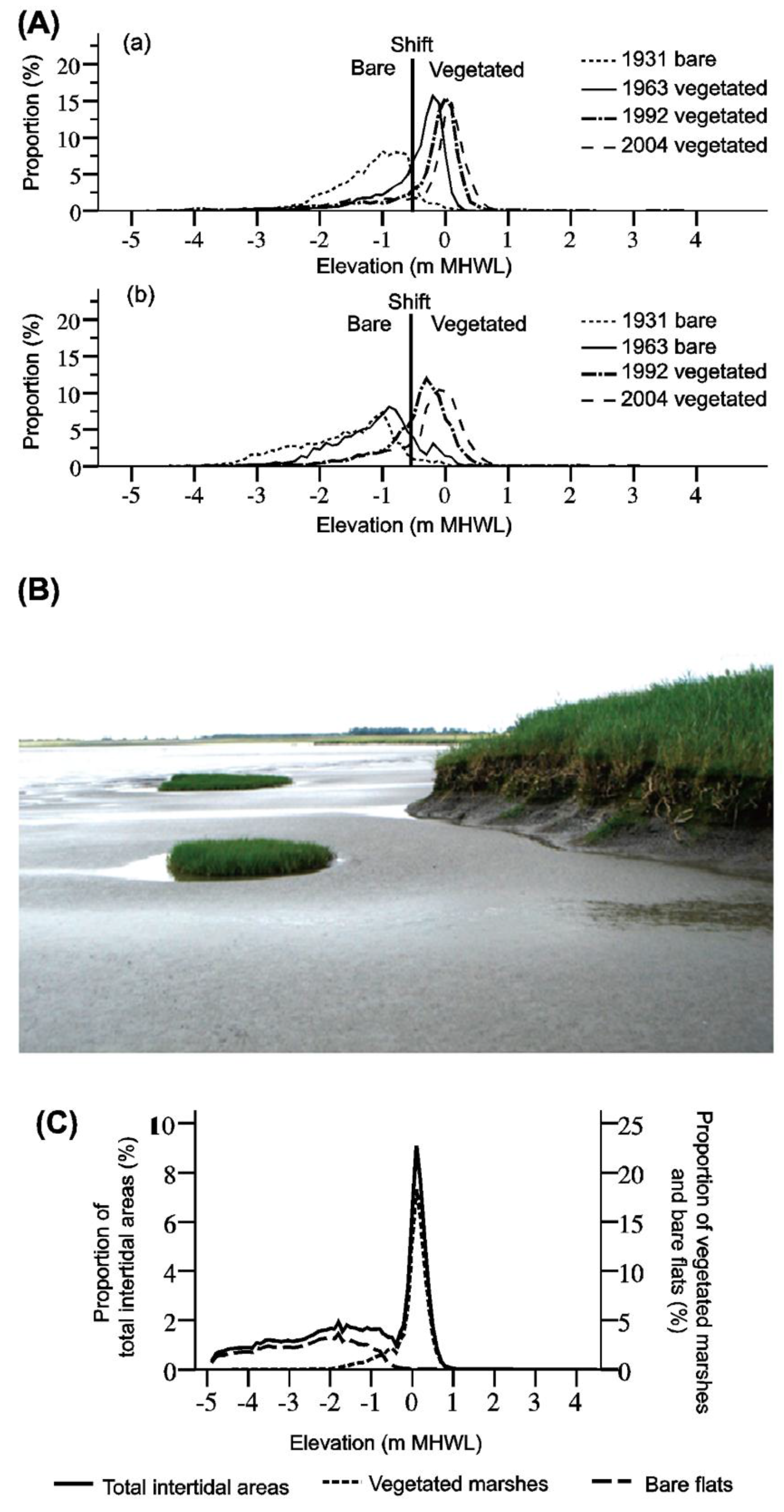
3.2. Remote Sensing Evidence
3.2.1. Salt Marshes
3.2.2. Freshwater Tidal Wetlands and Deltas
3.2.3. Mangroves
3.2.4. Seagrass Meadows
4. Examples of New Remote Sensing Applications Testing Theory
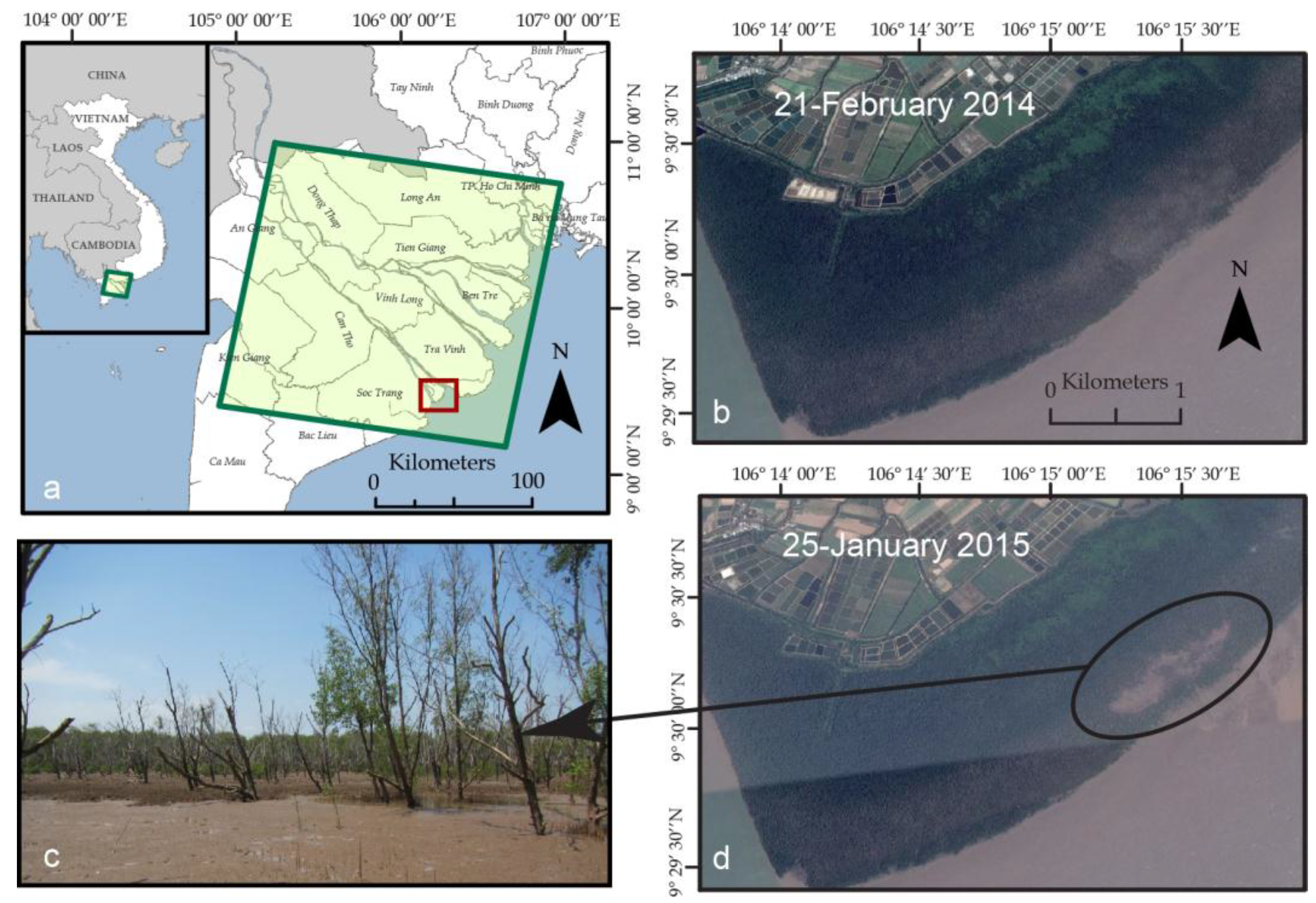
4.1. NDVI and SRTM Mapping of Patchy Mangrove Expansion in the Mekong Delta
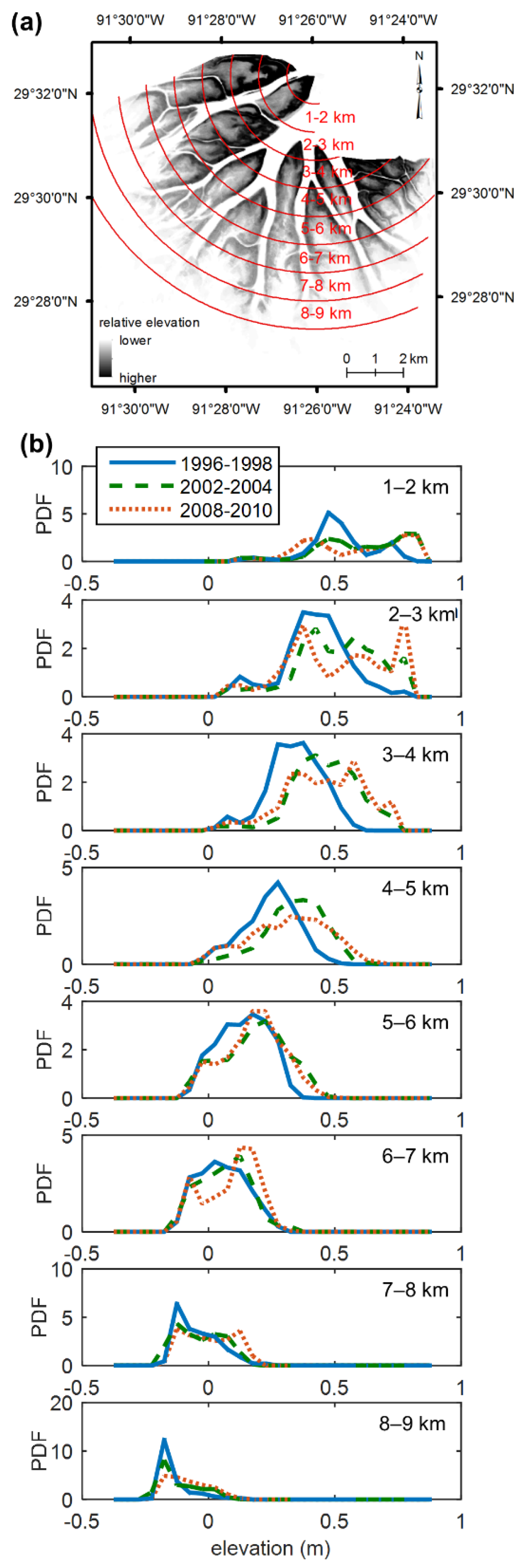
4.2. Landsat Records of Topographic State Bifurcation in the Wax Lake Delta
4.3. Orthophotos Capture Two States among Salt Marshes of San Francisco Bay

5. Further Research Needs and Opportunities
5.1. Theory and Models Need to Be Made Spatially Explicit and Species Explicit
5.2. The Relative Roles of Biotic vs. Abiotic Factors Need to Be Better Quantified
5.3. Multi-Species, Multi-State Dynamics Need to Be Tied to Specific Biological Interactions
5.4. Analysis Needs to Extend to Open Systems, with Differences and Similarities between Closed and Open Systems Appreciated
5.5. The Distinction between True Ecosystem Self-Organization, Reliant on Internal Feedbacks, and Other Causes of Complex Ecosystem Patterning Needs to Be Clarified and More Strictly and Critically Examined in Applications
5.6. The Scaling Relationships between Ecosystem Scale Processes and the Patch-Scale Processes Observable in Laboratories, Greenhouses, and Field Plots Need to Be Determined
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- USGS. Delta Research and Global Observation Network (DRAGON). Available online: http://deltas.usgs.gov/ (accessed on 24 April 2015).
- Pendleton, L.; Donato, D.C.; Murray, B.C.; Crooks, S.; Jenkins, W.A.; Sifleet, S.; Craft, C.; Fourqurean, J.W.; Kauffman, J.B.; Marbà, N.; et al. A. Estimating global “blue carbon” emissions from conversion and degradation of vegetated coastal ecosystems. PLoS ONE 2012, 7, e43542. [Google Scholar]
- IGPB. Deltas at Risk—IGBP. Available online: http://www.igbp.net/multimedia/multimedia/deltasatrisk.5.62dc35801456272b46d351.html (accessed on 24 April 2015).
- Kirwan, M.L.; Murray, A.B.; Donnelly, J.P.; Corbett, D.R. Rapid wetland expansion during European settlement and its implication for marsh survival under modern sediment delivery rates. Geology 2011, 39, 507–510. [Google Scholar]
- Coverdale, T.C.; Herrmann, N.C.; Altieri, A.H.; Bertness, M.D. Latent impacts: The role of historical human activity in coastal habitat loss. Front. Ecol. Environ. 2013, 11, 69–74. [Google Scholar]
- Creel, L. Ripple Effects: Population and Coastal Regions; Population Reference Bureau: Washington, DC, USA, 2003. [Google Scholar]
- Temmerman, S.; Meire, P.; Bouma, T.J.; Herman, P.M.J.; Ysebaert, T.; de Vriend, H.J. Ecosystem-based coastal defence in the face of global change. Nature 2013, 504, 79–83. [Google Scholar]
- Byrne, R.; Ingram, B.L.; Starratt, S.; Malamud-Roam, F.; Collins, J.N.; Conrad, M.E. Carbon-isotope, diatom, and pollen evidence for late holocene salinity change in a brackish marsh in the San Francisco estuary. Quat. Res. 2001, 55, 66–76. [Google Scholar]
- Malamud-Roam, F.; Lynn Ingram, B. Late Holocene δ13C and pollen records of paleosalinity from tidal marshes in the San Francisco Bay estuary, California. Quat. Res. 2004, 62, 134–145. [Google Scholar]
- Kemp, A.C.; Bernhardt, C.E.; Horton, B.P.; Kopp, R.E.; Vane, C.H.; Peltier, W.R.; Hawkes, A.D.; Donnelly, J.P.; Parnell, A.C.; Cahill, N. Late Holocene sea- and land-level change on the U.S. southeastern Atlantic coast. Mar. Geol. 2014, 357, 90–100. [Google Scholar]
- Bolshiyanov, D.; Makarov, A.; Savelieva, L. Lena River delta formation during the Holocene. Biogeosciences 2015, 12, 579–593. [Google Scholar] [CrossRef]
- Brain, M.J.; Kemp, A.C.; Horton, B.P.; Culver, S.J.; Parnell, A.C.; Cahill, N. Quantifying the contribution of sediment compaction to late Holocene salt-marsh sea-level reconstructions, North Carolina, USA. Quat. Res. 2015, 83, 41–51. [Google Scholar] [CrossRef]
- Stéphan, P.; Goslin, J.; Pailler, Y.; Manceau, R.; Suanez, S.; Van Vliet-Lanoë, B.; Hénaff, A.; Delacourt, C. Holocene salt-marsh sedimentary infilling and relative sea-level changes in West Brittany (France) using foraminifera-based transfer functions. Boreas 2015, 44, 153–177. [Google Scholar] [CrossRef]
- Simas, T.; Nunes, J.P.; Ferreira, J.G. Effects of global climate change on coastal salt marshes. Ecol. Model. 2001, 139, 1–15. [Google Scholar] [CrossRef]
- Cahoon, D.R.; Hensel, P.F.; Spencer, T.; Reed, D.J.; McKee, K.L.; Saintilan, N. Coastal wetland vulnerability to relative sea-level rise: Wetland elevation trends and process controls. In Wetlands and Natural Resource Management; Springer: Berlin, Germany, 2006; pp. 271–292. [Google Scholar]
- Blume, H.P.; Müller-Thomsen, U. A field experiment on the influence of the postulated global climatic change on coastal marshland soils. J. Plant Nutr. Soil Sci. 2007, 170, 145–156. [Google Scholar] [CrossRef]
- Day, J.W.; Christian, R.R.; Boesch, D.M.; Yáñez-Arancibia, A.; Morris, J.; Twilley, R.R.; Naylor, L.; Schaffner, L.; Stevenson, C. Consequences of Climate Change on the Ecogeomorphology of Coastal Wetlands. Estuaries Coasts 2008, 31, 477–491. [Google Scholar] [CrossRef]
- Kirwan, M.L.; Murray, A.B. Tidal marshes as disequilibrium landscapes? Lags between morphology and Holocene sea level change. Geophys. Res. Lett. 2008, 35. [Google Scholar] [CrossRef]
- Craft, C.; Clough, J.; Ehman, J.; Joye, S.; Park, R.; Pennings, S.; Guo, H.; Machmuller, M. Forecasting the effects of accelerated sea-level rise on tidal marsh ecosystem services. Front. Ecol. Environ. 2009, 7, 73–78. [Google Scholar] [CrossRef]
- Kirwan, M.L.; Guntenspergen, G.R.; D’Alpaos, A.; Morris, J.T.; Mudd, S.M.; Temmerman, S. Limits on the adaptability of coastal marshes to rising sea level. Geophys. Res. Lett. 2010, 37, L23401. [Google Scholar] [CrossRef]
- Kirwan, M.L.; Megonigal, J.P. Tidal wetland stability in the face of human impacts and sea-level rise. Nature 2013, 504, 53–60. [Google Scholar] [CrossRef] [PubMed]
- Costanza, R.; D’Arge, R.; de Groot, R.; Farber, S.; Grasso, M.; Hannon, B.; Limburg, K.; Naeem, S.; O’Neill, R.V.; Paruelo, J.; et al. The value of the world’s ecosystem services and natural capital. Nature 1997, 387, 253–260. [Google Scholar] [CrossRef]
- Woodward, R.T.; Wui, Y.S. The economic value of wetland services: A meta-analysis. Ecol. Econ. 2001, 37, 257–270. [Google Scholar] [CrossRef]
- Tol, R.S.J. The double trade-off between adaptation and mitigation for sea level rise: An application of FUND. Mitig. Adapt. Strateg. Glob. Change 2007, 12, 741–753. [Google Scholar] [CrossRef]
- Costanza, R.; Pérez-Maqueo, O.; Martinez, M.L.; Sutton, P.; Anderson, S.J.; Mulder, K. The value of coastal wetlands for hurricane protection. AMBIO J. Hum. Environ. 2008, 37, 241–248. [Google Scholar] [CrossRef]
- Gedan, K.B.; Kirwan, M.L.; Wolanski, E.; Barbier, E.B.; Silliman, B.R. The present and future role of coastal wetland vegetation in protecting shorelines: Answering recent challenges to the paradigm. Clim. Change 2011, 106, 7–29. [Google Scholar] [CrossRef]
- Möller, I.; Kudella, M.; Rupprecht, F.; Spencer, T.; Paul, M.; van Wesenbeeck, B.K.; Wolters, G.; Jensen, K.; Bouma, T.J.; Miranda-Lange, M.; et al. Wave attenuation over coastal salt marshes under storm surge conditions. Nat. Geosci. 2014, 7, 727–731. [Google Scholar] [CrossRef]
- Mcleod, E.; Chmura, G.L.; Bouillon, S.; Salm, R.; Björk, M.; Duarte, C.M.; Lovelock, C.E.; Schlesinger, W.H.; Silliman, B.R. A blueprint for blue carbon: Toward an improved understanding of the role of vegetated coastal habitats in sequestering CO2. Front. Ecol. Environ. 2011, 9, 552–560. [Google Scholar] [CrossRef]
- Bauer, J.E.; Cai, W.J.; Raymond, P.A.; Bianchi, T.S.; Hopkinson, C.S.; Regnier, P.A.G. The changing carbon cycle of the coastal ocean. Nature 2013, 504, 61–70. [Google Scholar] [CrossRef] [PubMed]
- Duarte, C.M.; Losada, I.J.; Hendriks, I.E.; Mazarrasa, I.; Marbà, N. The role of coastal plant communities for climate change mitigation and adaptation. Nat. Clim. Change 2013, 3, 961–968. [Google Scholar] [CrossRef]
- Mitsch, W.J.; Gosselink, J.G. Wetlands, 4th ed.; Wiley: Hoboken, NJ, USA, 2007. [Google Scholar]
- Yang, M.; Geng, X.; Grace, J.; Lu, C.; Zhu, Y.; Zhou, Y.; Lei, G. Spatial and Seasonal CH4 Flux in the Littoral Zone of Miyun Reservoir near Beijing: The Effects of Water Level and Its Fluctuation. PLoS ONE 2014, 9, e94275. [Google Scholar] [CrossRef] [PubMed]
- Poffenbarger, H.J.; Needelman, B.A.; Megonigal, J.P. Salinity Influence on Methane Emissions from Tidal Marshes. Wetlands 2011, 31, 831–842. [Google Scholar] [CrossRef]
- Kneib, R.T.; Wagner, S.L. Nekton use of vegetated marsh habitats at different stages of tidal inundation. Mar. Ecol. Prog. Ser. 1994, 106, 227–238. [Google Scholar] [CrossRef]
- Minello, T.J.; Rozas, L.P. Nekton in Gulf Coast wetlands: Fine-scale distributions, landscape patterns, and restoration implications. Ecol. Appl. 2002, 12, 441–455. [Google Scholar] [CrossRef]
- Bretsch, K.; Allen, D.M. Tidal migrations of nekton in salt marsh intertidal creeks. Estuaries Coasts 2006, 29, 474–486. [Google Scholar] [CrossRef]
- UNEP-WCMC. Ocean Data Viewer. Available online: http://data.unep-wcmc.org/ (accessed on 24 April 2015).
- US FWS. National Wetlands Inventory. Available online: http://www.fws.gov/wetlands/index.html (accessed on 24 April 2015).
- Kirwan, M.L.; Murray, A.B. A coupled geomorphic and ecological model of tidal marsh evolution. Proc. Natl. Acad. Sci. USA 2007, 104, 6118–6122. [Google Scholar] [CrossRef] [PubMed]
- Marani, M.; D’Alpaos, A.; Lanzoni, S.; Carniello, L.; Rinaldo, A. Biologically-controlled multiple equilibria of tidal landforms and the fate of the Venice lagoon. Geophys. Res. Lett. 2007, 34. [Google Scholar] [CrossRef]
- Marani, M.; D’Alpaos, A.; Lanzoni, S.; Carniello, L.; Rinaldo, A. The importance of being coupled: Stable states and catastrophic shifts in tidal biomorphodynamics. J. Geophys. Res. Earth Surf. 2010, 115, F04004. [Google Scholar] [CrossRef]
- Marani, M.; da Lio, C.; D’Alpaos, A. Vegetation engineers marsh morphology through multiple competing stable states. Proc. Natl. Acad. Sci. USA 2013, 110, 3259–3263. [Google Scholar] [CrossRef] [PubMed]
- Fagherazzi, S.; Kirwan, M.L.; Mudd, S.M.; Guntenspergen, G.R.; Temmerman, S.; D’Alpaos, A.; van de Koppel, J.; Rybczyk, J.M.; Reyes, E.; Craft, C.; et al. Numerical models of salt marsh evolution: Ecological, geomorphic, and climatic factors. Rev. Geophys. 2012, 50, RG1002. [Google Scholar] [CrossRef]
- Osman, R.W.; Munguia, P.; Zajac, R.N. Ecological thresholds in marine communities: Theory, experiments and mangement. Mar. Ecol. Prog. Ser. 2010, 413, 185–187. [Google Scholar] [CrossRef]
- Thrush, S.F.; Hewitt, J.E.; Lohrer, A.M. Interaction networks in coastal soft-sediments highlight the potential for change in ecological resilience. Ecol. Appl. 2012, 22, 1213–1223. [Google Scholar] [CrossRef] [PubMed]
- Williams, P.; Faber, P. Salt marsh restoration experience in San Francisco Bay. J. Coast. Res. 2001, 27, 203–211. [Google Scholar]
- Williams, P.B.; Orr, M.K. Physical evolution of restored breached levee salt marshes in the San Francisco Bay estuary. Restor. Ecol. 2002, 10, 527–542. [Google Scholar] [CrossRef]
- Hughes, R.G.; Paramor, O.A.L. On the loss of saltmarshes in south-east England and methods for their restoration. J. Appl. Ecol. 2004, 41, 440–448. [Google Scholar] [CrossRef]
- Palmer, M.A. Reforming watershed restoration: Science in need of application and applications in need of science. Estuaries Coasts 2008, 32, 1–17. [Google Scholar] [CrossRef]
- Ozesmi, S.L.; Bauer, M.E. Satellite remote sensing of wetlands. Wetl. Ecol. Manag. 2002, 10, 381–402. [Google Scholar] [CrossRef]
- Silva, T.S.F.; Costa, M.P.F.; Melack, J.M.; Novo, E.M.L.M. Remote sensing of aquatic vegetation: Theory and applications. Environ. Monit. Assess. 2007, 140, 131–145. [Google Scholar] [CrossRef] [PubMed]
- Xie, Y.; Sha, Z.; Yu, M. Remote sensing imagery in vegetation mapping: A review. J. Plant Ecol. 2008, 1, 9–23. [Google Scholar] [CrossRef]
- Klemas, V. Remote sensing techniques for studying coastal ecosystems: An overview. J. Coast. Res. 2010, 27, 2–17. [Google Scholar] [CrossRef]
- Bartlett, D.S.; Klemas, V. Quantitative assessment of tidal wetlands using remote sensing. Environ. Manag. 1980, 4, 337–345. [Google Scholar] [CrossRef]
- Bartlett, D.; Klemas, V. In situ spectral reflectance studies of tidal wetland grasses. Photogramm. Eng. Remote Sens. 1981, 47, 1695–1703. [Google Scholar]
- Silvestri, S.; Marani, M.; Marani, A. Hyperspectral remote sensing of salt marsh vegetation, morphology and soil topography. Phys. Chem. Earth Parts ABC 2003, 28, 15–25. [Google Scholar] [CrossRef]
- Ustin, S.L.; Roberts, D.A.; Gamon, J.A.; Asner, G.P.; Green, R.O. Using imaging spectroscopy to study ecosystem processes and properties. BioScience 2004, 54, 523–534. [Google Scholar] [CrossRef]
- Li, L.; Ustin, S.L.; Lay, M. Application of multiple endmember spectral mixture analysis (MESMA) to AVIRIS imagery for coastal salt marsh mapping: A case study in China Camp, CA, USA. Int. J. Remote Sens. 2005, 26, 5193–5207. [Google Scholar] [CrossRef]
- Rosso, P.H.; Ustin, S.L.; Hastings, A. Mapping marshland vegetation of San Francisco Bay, California, using hyperspectral data. Int. J. Remote Sens. 2005, 26, 5169–5191. [Google Scholar] [CrossRef]
- Artigas, F.J.; Yang, J. Spectral discrimination of marsh vegetation types in the New Jersey Meadowlands, USA. Wetlands 2006, 26, 271–277. [Google Scholar] [CrossRef]
- Gao, Z.G.; Zhang, L.Q. Multi-seasonal spectral characteristics analysis of coastal salt marsh vegetation in Shanghai, China. Estuar. Coast. Shelf Sci. 2006, 69, 217–224. [Google Scholar] [CrossRef]
- Judd, C.; Steinberg, S.; Shaughnessy, F.; Crawford, G. Mapping salt marsh vegetation using aerial hyperspectral imagery and linear unmixing in Humboldt Bay, California. Wetlands 2007, 27, 1144–1152. [Google Scholar] [CrossRef]
- Sadro, S.; Gastil-Buhl, M.; Melack, J. Characterizing patterns of plant distribution in a southern California salt marsh using remotely sensed topographic and hyperspectral data and local tidal fluctuations. Remote Sens. Environ. 2007, 110, 226–239. [Google Scholar] [CrossRef]
- Gilmore, M.S.; Wilson, E.H.; Barrett, N.; Civco, D.L.; Prisloe, S.; Hurd, J.D.; Chadwick, C. Integrating multi-temporal spectral and structural information to map wetland vegetation in a lower Connecticut River tidal marsh. Remote Sens. Environ. 2008, 112, 4048–4060. [Google Scholar] [CrossRef]
- Miyamoto, M.; Kushida, K.; Yoshino, K.; Nagano, T.; Sato, Y. Evaluation of multispatial scale measurements for monitoring wetland vegetation, Kushiro wetland, Japan: Application of SPOT images, CASI data, airborne CNIR video images and balloon aerial photography. IEEE Geosci. Remote Sens. Symp. 2003, 5, 3275–3277. [Google Scholar]
- Wang, L.; Sousa, W.P.; Gong, P.; Biging, G.S. Comparison of IKONOS and QuickBird images for mapping mangrove species on the Caribbean coast of Panama. Remote Sens. Environ. 2004, 91, 432–440. [Google Scholar] [CrossRef]
- Belluco, E.; Camuffo, M.; Ferrari, S.; Modenese, L.; Silvestri, S.; Marani, A.; Marani, M. Mapping salt-marsh vegetation by multispectral and hyperspectral remote sensing. Remote Sens. Environ. 2006, 105, 54–67. [Google Scholar] [CrossRef]
- Klemas, V. Airborne remote sensing of coastal features and processes: An overview. J. Coast. Res. 2012, 29, 239–255. [Google Scholar] [CrossRef]
- Moffett, K.B.; Gorelick, S.M. Distinguishing wetland vegetation and channel features with object-based image segmentation. Int. J. Remote Sens. 2013, 34, 1332–1354. [Google Scholar] [CrossRef]
- Wang, L.; Sousa, W.P.; Gong, P. Integration of object-based and pixel-based classification for mapping mangroves with IKONOS imagery. Int. J. Remote Sens. 2004, 25, 5655–5668. [Google Scholar] [CrossRef]
- Lathrop, R.G.; Montesano, P.; Haag, S. A multi-scale segmentation approach to mapping seagrass habitats using airborne digital camera imagery. Photogramm. Eng. Remote Sens. 2006, 72, 665–675. [Google Scholar] [CrossRef]
- Yu, Q.; Gong, P.; Clinton, N.; Biging, G.; Kelly, M.; Schirokauer, D. Object-based detailed vegetation classification with airborne high spatial resolution remote sensing imagery. Photogramm. Eng. Remote Sens. 2006, 72, 799–811. [Google Scholar] [CrossRef]
- Tian, B.; Zhou, Y.; Zhang, L.; Yuan, L. Analyzing the habitat suitability for migratory birds at the Chongming Dongtan Nature Reserve in Shanghai, China. Estuar. Coast. Shelf Sci. 2008, 80, 296–302. [Google Scholar] [CrossRef]
- Tuxen, K.; Kelly, M. Multi-scale functional mapping of tidal marsh vegetation using object-based image analysis. In Object-Based Image Analysis; Lecture Notes in Geoinformation and Cartography; Blaschke, T., Lang, S., Hay, G.J., Eds.; Springer: Berlin, Heidelberg, Germany, 2008; pp. 415–442. [Google Scholar]
- Rokitnicki-Wojcik, D.; Wei, A.; Chow-Fraser, P. Transferability of object-based rule sets for mapping coastal high marsh habitat among different regions in Georgian Bay, Canada. Wetl. Ecol. Manag. 2011, 19, 223–236. [Google Scholar] [CrossRef]
- Silvestri, S.; Marani, M.; Settle, J.; Benvenuto, F.; Marani, A. Salt marsh vegetation radiometry: Data analysis and scaling. Remote Sens. Environ. 2002, 80, 473–482. [Google Scholar] [CrossRef]
- Simard, M.; Rivera-Monroy, V.H.; Mancera-Pineda, J.E.; Castañeda-Moya, E.; Twilley, R.R. A systematic method for 3D mapping of mangrove forests based on Shuttle Radar Topography Mission elevation data, ICEsat/GLAS waveforms and field data: Application to Ciénaga Grande de Santa Marta, Colombia. Remote Sens. Environ. 2008, 112, 2131–2144. [Google Scholar] [CrossRef]
- Kim, M.; Warner, T.A.; Madden, M.; Atkinson, D.S. Multi-scale GEOBIA with very high spatial resolution digital aerial imagery: Scale, texture and image objects. Int. J. Remote Sens. 2011, 32, 2825–2850. [Google Scholar] [CrossRef]
- Klemas, V.; Daiber, F.; Bartlett, D.; Crichton, O.; Fornes, A. Inventory of Delawares Wetlands. Photogramm. Eng. Remote Sens. 1974, 40, 433–439. [Google Scholar]
- Hardisky, M.A.; Klemas, V. Tidal wetlands natural and human-made changes from 1973 to 1979 in Delaware: Mapping techniques and results. Environ. Manag. 1983, 7, 339–344. [Google Scholar] [CrossRef]
- Zharikov, Y.; Skilleter, G.A.; Loneragan, N.R.; Taranto, T.; Cameron, B.E. Mapping and characterising subtropical estuarine landscapes using aerial photography and GIS for potential application in wildlife conservation and management. Biol. Conserv. 2005, 125, 87–100. [Google Scholar] [CrossRef]
- Prigent, C.; Matthews, E.; Aires, F.; Rossow, W.B. Remote sensing of global wetland dynamics with multiple satellite data sets. Geophys. Res. Lett. 2001, 28, 4631–4634. [Google Scholar] [CrossRef]
- Prigent, C.; Papa, F.; Aires, F.; Rossow, W.B.; Matthews, E. Global inundation dynamics inferred from multiple satellite observations, 1993–2000. J. Geophys. Res. 2007, 112. [Google Scholar] [CrossRef]
- Feola, A. A geomorphic study of lagoonal landforms. Water Resour. Res. 2005, 41. [Google Scholar] [CrossRef]
- Klemas, V. Remote sensing of emergent and submerged wetlands: An overview. Int. J. Remote Sens. 2013, 34, 6286–6320. [Google Scholar] [CrossRef]
- Wang, C.; Temmerman, S. Does biogeomorphic feedback lead to abrupt shifts between alternative landscape states? An empirical study on intertidal flats and marshes. J. Geophys. Res. Earth Surf. 2013, 118, 229–240. [Google Scholar] [CrossRef]
- Zhang, M.; Ustin, S.L.; Rejmankova, E.; Sanderson, E.W. Monitoring Pacific coast salt marshes using remote sensing. Ecol. Appl. 1997, 7, 1039–1053. [Google Scholar] [CrossRef]
- Ustin, S.L.; Lay, M.C.; Li, L. Remote sensing of wetland conditions in West Coast salt marshes. SPIE Remote Sens. Model. Ecosyst. Sustain. 2004, 5544. [Google Scholar] [CrossRef]
- Wilson, M.D.; Ustin, S.L.; Rocke, D.M. Classification of contamination in salt marsh plants using hyperspectral reflectance. IEEE Trans. Geosci. Remote Sens. 2004, 42, 1088–1095. [Google Scholar] [CrossRef]
- Tilley, D.R.; Ahmed, M.; Son, J.H.; Badrinarayanan, H. Hyperspectral reflectance response of freshwater macrophytes to salinity in a brackish subtropical marsh. J. Environ. Qual. 2007, 36, 780–789. [Google Scholar] [CrossRef] [PubMed]
- Smith, G.M.; Spencer, T.; Murray, A.L.; French, J.R. Assessing seasonal vegetation change in coastal wetlands with airborne remote sensing: An outline methodology. Mangroves Salt Marshes 1998, 2, 15–28. [Google Scholar] [CrossRef]
- Krause, G.; Bock, M.; Weiers, S.; Braun, G. Mapping land-cover and mangrove structures with remote sensing techniques: A contribution to a synoptic GIS in support of coastal management in North Brazil. Environ. Manag. 2004, 34, 429–440. [Google Scholar] [CrossRef] [PubMed]
- Hilbert, K.W. Land cover change within the Grand Bay National Estuarine Research Reserve: 1974–2001. J. Coast. Res. 2006, 226, 1552–1557. [Google Scholar] [CrossRef]
- Jefferies, R.L.; Jano, A.P.; Abraham, K.F. A biotic agent promotes large-scale catastrophic change in the coastal marshes of Hudson Bay. J. Ecol. 2006, 94, 234–242. [Google Scholar] [CrossRef]
- Nielsen, E.M.; Prince, S.D.; Koeln, G.T. Wetland change mapping for the U.S. mid-Atlantic region using an outlier detection technique. Remote Sens. Environ. 2008, 112, 4061–4074. [Google Scholar] [CrossRef]
- Van der Wal, D.; Wielemaker-van den Dool, A.; Herman, P.M.J. Spatial patterns, rates and mechanisms of saltmarsh cycles (Westerschelde, The Netherlands). Estuar. Coast. Shelf Sci. 2008, 76, 357–368. [Google Scholar] [CrossRef]
- Kelly, M.; Tuxen, K.A.; Stralberg, D. Mapping changes to vegetation pattern in a restoring wetland: Finding pattern metrics that are consistent across spatial scale and time. Ecol. Indic. 2011, 11, 263–273. [Google Scholar] [CrossRef]
- Andrew, M.; Ustin, S. The role of environmental context in mapping invasive plants with hyperspectral image data. Remote Sens. Environ. 2008, 112, 4301–4317. [Google Scholar] [CrossRef]
- Peterson, C.H. Does a rigorous criterion for environmental identity preclude the existence of multiple stable points? Am. Nat. 1984, 127–133. [Google Scholar] [CrossRef]
- Schröder, A.; Persson, L.; de Roos, A.M. Direct experimental evidence for alternative stable states: A review. Oikos 2005, 110, 3–19. [Google Scholar]
- Dudgeon, S.R.; Aronson, R.B.; Bruno, J.F.; Precht, W.F. Phase shifts and stable states on coral reefs. Mar. Ecol. Prog. Ser. 2010, 413, 201–216. [Google Scholar]
- Aronson, R.B.; Macintyre, I.G.; Wapnick, C.M.; O’Neill, M.W. Phase shifts, alternative states, and the unprecedented convergence of two reef systems. Ecology 2004, 85, 1876–1891. [Google Scholar]
- Norstrm, A.V.; Nystrm, M.; Lokrantz, J.; Folke, C. Alternative states on coral reefs: Beyond coral—Macroalgal phase shifts. Mar. Ecol. Prog. Ser. 2009, 376, 295–306. [Google Scholar]
- Petraitis, P.S.; Hoffman, C. Multiple stable states and relationship between thresholds in processes and states. Mar. Ecol. Prog. Ser. 2010, 413, 189–200. [Google Scholar]
- Scheffer, M.; Carpenter, S.; Foley, J.A.; Folke, C.; Walker, B. Catastrophic shifts in ecosystems. Nature 2001, 413, 591–596. [Google Scholar] [PubMed]
- Scheffer, M.; Carpenter, S.R. Catastrophic regime shifts in ecosystems: Linking theory to observation. Trends Ecol. Evol. 2003, 18, 648–656. [Google Scholar]
- Rietkerk, M.; Dekker, S.C.; de Ruiter, P.C.; van de Koppel, J. Self-organized patchiness and catastrophic shifts in ecosystems. Science 2004, 305, 1926–1929. [Google Scholar] [CrossRef] [PubMed]
- Scheffer, M.; Bascompte, J.; Brock, W.A.; Brovkin, V.; Carpenter, S.R.; Dakos, V.; Held, H.; van Nes, E.H.; Rietkerk, M.; Sugihara, G. Early-warning signals for critical transitions. Nature 2009, 461, 53–59. [Google Scholar] [CrossRef] [PubMed]
- Dakos, V.; Kéfi, S.; Rietkerk, M.; Nes Scheffer, M. Slowing down in spatially patterned ecosystems at the brink of collapse. Am. Nat. 2011, 177, E153–E166. [Google Scholar] [CrossRef] [PubMed]
- May, R.M. Biological populations with nonoverlapping generations: Stable points, stable cycles, and chaos. Science 1974, 186, 645–647. [Google Scholar] [CrossRef] [PubMed]
- May, R.M. Thresholds and breakpoints in ecosystems with a multiplicity of stable states. Nature 1977, 269, 471–477. [Google Scholar] [CrossRef]
- May, R.M.; Oster, G.F. Bifurcations and dynamic complexity in simple ecological models. Am. Nat. 1976, 573–599. [Google Scholar] [CrossRef]
- Knowlton, N. Thresholds and multiple stable states in coral reef community dynamics. Am. Zool. 1992, 32, 674–682. [Google Scholar] [CrossRef]
- Turing, A.M. The chemical basis of morphogenesis. Philos. Trans. R. Soc. Lond. B Biol. Sci. 1952, 237, 37–72. [Google Scholar] [CrossRef]
- Cross, M.C.; Hohenberg, P.C. Pattern formation outside of equilibrium. Rev. Mod. Phys. 1993, 65, 851–1112. [Google Scholar] [CrossRef]
- Maini, P.K.; Painter, K.J.; Chau, H.N.P. Spatial pattern formation in chemical and biological systems. J. Chem. Soc. Faraday Trans. 1997, 93, 3601–3610. [Google Scholar] [CrossRef]
- Shnerb, N.M.; Sarah, P.; Lavee, H.; Solomon, S. Reactive glass and vegetation patterns. Phys. Rev. Lett. 2003, 90, 038101. [Google Scholar] [CrossRef] [PubMed]
- Meron, E.; Gilad, E.; von Hardenberg, J.; Shachak, M.; Zarmi, Y. Vegetation patterns along a rainfall gradient. Chaos Solitons Fractals 2004, 19, 367–376. [Google Scholar] [CrossRef]
- Manor, A.; Shnerb, N.M. Dynamical failure of Turing patterns. Europhys. Lett. EPL 2006, 74, 837–843. [Google Scholar] [CrossRef]
- Eppinga, M.B.; Rietkerk, M.; Borren, W.; Lapshina, E.D.; Bleuten, W.; Wassen, M.J. Regular surface patterning of peatlands: Confronting theory with field data. Ecosystems 2008, 11, 520–536. [Google Scholar] [CrossRef]
- Rietkerk, M.; van de Koppel, J. Regular pattern formation in real ecosystems. Trends Ecol. Evol. 2008, 23, 169–175. [Google Scholar] [CrossRef] [PubMed]
- Van de Koppel, J.; Gascoigne, J.C.; Theraulaz, G.; Rietkerk, M.; Mooij, W.M.; Herman, P.M.J. Experimental evidence for spatial self-organization and its emergent effects in mussel bed ecosystems. Science 2008, 322, 739–742. [Google Scholar] [CrossRef] [PubMed]
- Borgogno, F.; D’Odorico, P.; Laio, F.; Ridolfi, L. Mathematical models of vegetation pattern formation in ecohydrology. Rev. Geophys. 2009, 47, RG1005. [Google Scholar] [CrossRef]
- Lefever, R.; Barbier, N.; Couteron, P.; Lejeune, O. Deeply gapped vegetation patterns: On crown/root allometry, criticality and desertification. J. Theor. Biol. 2009, 261, 194–209. [Google Scholar] [CrossRef] [PubMed]
- Pastor, J.; Peckham, B.; Bridgham, S.; Weltzin, J.; Chen, J. Plant community dynamics, nutrient cycling, and alternative stable equilibria in peatlands. Am. Nat. 2002, 160, 553–568. [Google Scholar] [CrossRef] [PubMed]
- Baskett, M.L.; Salomon, A.K. Recruitment facilitation can drive alternative states on temperate reefs. Ecology 2010, 91, 1763–1773. [Google Scholar] [CrossRef] [PubMed]
- González-Rivero, M.; Yakob, L.; Mumby, P.J. The role of sponge competition on coral reef alternative steady states. Ecol. Model. 2011, 222, 1847–1853. [Google Scholar] [CrossRef]
- Fagherazzi, S.; Carniello, L.; D’Alpaos, L.; Defina, A. Critical bifurcation of shallow microtidal landforms in tidal flats and salt marshes. Proc. Natl. Acad. Sci. USA 2006, 103, 8337–8341. [Google Scholar] [CrossRef] [PubMed]
- Fagherazzi, S.; Palermo, C.; Rulli, M.C.; Carniello, L.; Defina, A. Wind waves in shallow microtidal basins and the dynamic equilibrium of tidal flats. J. Geophys. Res. Earth Surf. 2007, 112. [Google Scholar] [CrossRef]
- Defina, A.; Carniello, L.; Fagherazzi, S.; D’Alpaos, L. Self-organization of shallow basins in tidal flats and salt marshes. J. Geophys. Res. Earth Surf. 2007, 112. [Google Scholar] [CrossRef]
- Carniello, L.; Defina, A.; D’Alpaos, L. Morphological evolution of the Venice lagoon: Evidence from the past and trend for the future. J. Geophys. Res. Earth Surf. 2009, 114, F04002. [Google Scholar] [CrossRef]
- Mariotti, G.; Fagherazzi, S. A numerical model for the coupled long-term evolution of salt marshes and tidal flats. J. Geophys. Res. Earth Surf. 2010, 115. [Google Scholar] [CrossRef]
- Lefever, R.; Lejeune, O. On the origin of tiger bush. Bull. Math. Biol. 1997, 59, 263–294. [Google Scholar] [CrossRef]
- Couteron, P.; Lejeune, O. Periodic spotted patterns in semi-arid vegetation explained by a propagation-inhibition model. J. Ecol. 2001, 89, 616–628. [Google Scholar] [CrossRef]
- Hardenberg, J.; von Meron, E.; Shachak, M.; Zarmi, Y. Diversity of vegetation patterns and desertification. Phys. Rev. Lett. 2001, 87, 198101. [Google Scholar] [CrossRef]
- Van de Koppel, J.; Rietkerk, M. Spatial interactions and resilience in arid ecosystems. Am. Nat. 2004, 163, 113–121. [Google Scholar] [CrossRef] [PubMed]
- Sherratt, J.A. An analysis of vegetation stripe formation in semi-arid landscapes. J. Math. Biol. 2005, 51, 183–197. [Google Scholar] [CrossRef] [PubMed]
- Saco, P.M.; Willgoose, G.R.; Hancock, G.R. Eco-geomorphology of banded vegetation patterns in arid and semi-arid regions. Hydrol. Earth Syst. Sci. 2007, 11, 1717–1730. [Google Scholar] [CrossRef]
- Barbier, N.; Couteron, P.; Lefever, R.; Deblauwe, V.; Lejeune, O. Spatial decoupling of facilitation and competition at the origin of gapped vegetation patterns. Ecology 2008, 89, 1521–1531. [Google Scholar] [CrossRef] [PubMed]
- Deblauwe, V.; Barbier, N.; Couteron, P.; Lejeune, O.; Bogaert, J. The global biogeography of semi-arid periodic vegetation patterns. Glob. Ecol. Biogeogr. 2008, 17, 715–723. [Google Scholar] [CrossRef]
- Rietkerk, M.; Dekker, S.C.; Wassen, M.J.; Verkroost, A.W.M.; Bierkens, M.F.P. A putative mechanism for bog patterning. Am. Nat. 2004, 163, 699–708. [Google Scholar] [CrossRef] [PubMed]
- Couwenberg, J. A simulation model of mire patterning—Revisited. Ecography 2005, 28, 653–661. [Google Scholar] [CrossRef]
- Couwenberg, J.; Joosten, H. Self-organization in raised bog patterning: The origin of microtope zonation and mesotope diversity. J. Ecol. 2005, 93, 1238–1248. [Google Scholar] [CrossRef]
- Eppinga, M.B.; Ruiter, P.C.; de Wassen, M.J.; Rietkerk, M. Nutrients and hydrology indicate the driving mechanisms of peatland surface patterning. Am. Nat. 2009, 173, 803–818. [Google Scholar] [CrossRef] [PubMed]
- Temmerman, S.; Bouma, T.J.; Koppel, J.V.; de Wal, D.V.; der Vries, M.B.D.; Herman, P.M.J. Vegetation causes channel erosion in a tidal landscape. Geology 2007, 35, 631–634. [Google Scholar] [CrossRef]
- Van der Heide, T.; Bouma, T.J.; van Nes, E.H.; van de Koppel, J.; Scheffer, M.; Roelofs, J.G.M.; van Katwijk, M.M.; Smolders, A.J.P. Spatial self-organized patterning in seagrasses along a depth gradient of an intertidal ecosystem. Ecology 2010, 91, 362–369. [Google Scholar] [CrossRef] [PubMed]
- Weerman, E.J.; Koppel, J.; van de Eppinga, M.B.; Montserrat, F.; Liu, Q.; Herman, P.M.J. Spatial self-organization on intertidal mudflats through biophysical stress divergence. Am. Nat. 2010, 176, E15–E32. [Google Scholar] [CrossRef] [PubMed]
- Vandenbruwaene, W.; Temmerman, S.; Bouma, T.J.; Klaassen, P.C.; de Vries, M.B.; Callaghan, D.P.; van Steeg, P.; Dekker, F.; van Duren, L.A.; Martini, E.; et al. Flow interaction with dynamic vegetation patches: Implications for biogeomorphic evolution of a tidal landscape. J. Geophys. Res. Earth Surf. 2011, 116, F01008. [Google Scholar] [CrossRef]
- Foti, R.; del Jesus, M.; Rinaldo, A.; Rodriguez-Iturbe, I. Hydroperiod regime controls the organization of plant species in wetlands. Proc. Natl. Acad. Sci. USA 2012, 109, 19596–19600. [Google Scholar] [CrossRef] [PubMed]
- Van de Koppel, J.; van der Wal, D.; Bakker, J.P.; Herman, P.M. Self-organization and vegetation collapse in salt marsh ecosystems. Am. Nat. 2005, 165, E1–E12. [Google Scholar] [CrossRef] [PubMed]
- Scheffer, M.; Hosper, S.H.; Meijer, M.L.; Moss, B.; Jeppesen, E. Alternative equilibria in shallow lakes. Trends Ecol. Evol. 1993, 8, 275–279. [Google Scholar] [CrossRef]
- Seekell, D.A.; Cline, T.J.; Carpenter, S.R.; Pace, M.L. Evidence of alternate attractors from a whole-ecosystem regime shift experiment. Theor. Ecol. 2013, 6, 385–394. [Google Scholar] [CrossRef]
- Holling, C.S. Resilience and stability of ecological systems. Annu. Rev. Ecol. Syst. 1973, 4, 1–23. [Google Scholar] [CrossRef]
- Folke, C.; Carpenter, S.; Walker, B.; Scheffer, M.; Elmqvist, T.; Gunderson, L.; Holling, C.S. Regime shifts, resilience, and biodiversity in ecosystem management. Annu. Rev. Ecol. Evol. Syst. 2004, 35, 557–581. [Google Scholar] [CrossRef]
- Fagherazzi, S.; Mariotti, G.; Wiberg, P.L.; McGlathery, K.J. Marsh collapse does not require sea level rise. Oceanography 2013, 26, 70–77. [Google Scholar] [CrossRef]
- Van Wesenbeeck, B.K.; Koppel, J.; Herman, P.M.J.; Bertness, M.D.; Wal, D.; Bakker, J.P.; Bouma, T.J. Potential for sudden shifts in transient systems: Distinguishing between local and landscape-scale processes. Ecosystems 2008, 11, 1133–1141. [Google Scholar] [CrossRef]
- Mayer, A.L.; Rietkerk, M. The dynamic regime concept for ecosystem management and restoration. BioScience 2004, 54, 1013–1020. [Google Scholar] [CrossRef]
- Suding, K.N.; Gross, K.L.; Houseman, G.R. Alternative states and positive feedbacks in restoration ecology. Trends Ecol. Evol. 2004, 19, 46–53. [Google Scholar] [CrossRef] [PubMed]
- McGlathery, K.J.; Reidenbach, M.A.; D’Odorico, P.; Fagherazzi, S.; Pace, M.L.; Porter, J.H. Nonlinear dynamics and alternative stable states in shallow coastal systems. Oceanography 2013, 26, 220–231. [Google Scholar] [CrossRef]
- Viaroli, P.; Bartoli, M.; Giordani, G.; Naldi, M.; Orfanidis, S.; Zaldivar, J.M. Community shifts, alternative stable states, biogeochemical controls and feedbacks in eutrophic coastal lagoons: A brief overview. Aquat. Conserv. Mar. Freshw. Ecosyst. 2008, 18, S105–S117. [Google Scholar] [CrossRef]
- Fairweather, P.G.; Lester, R.E. Predicting future ecological degradation based on modelled thresholds. Mar. Ecol. Prog. Ser. 2010, 413, 291–304. [Google Scholar] [CrossRef]
- D’Alpaos, A.; da Lio, C.; Marani, M. Biogeomorphology of tidal landforms: Physical and biological processes shaping the tidal landscape. Ecohydrology 2012, 5, 550–562. [Google Scholar] [CrossRef]
- Jiang, J.; Gao, D.; DeAngelis, D.L. Towards a theory of ecotone resilience: Coastal vegetation on a salinity gradient. Theor. Popul. Biol. 2012, 82, 29–37. [Google Scholar] [CrossRef] [PubMed]
- Jiang, J.; DeAngelis, D.L.; Anderson, G.H.; Smith, T.J., III. Analysis and simulation of propagule dispersal and salinity intrusion from storm surge on the movement of a Marsh-Mangrove Ecotone in South Florida. Estuaries Coasts 2014, 37, 24–35. [Google Scholar] [CrossRef]
- Van Wesenbeeck, B.K.; van de Koppel, J.; Herman, P.M.J.; Bouma, T.J. Does scale-dependent feedback explain spatial complexity in salt-marsh ecosystems? Oikos 2008, 117, 152–159. [Google Scholar] [CrossRef]
- Bouma, T.J.; Friedrichs, M.; van Wesenbeeck, B.K.; Temmerman, S.; Graf, G.; Herman, P.M.J. Density-dependent linkage of scale-dependent feedbacks: A flume study on the intertidal macrophyte Spartina anglica. Oikos 2009, 118, 260–268. [Google Scholar] [CrossRef]
- Morris, J.T.; Sundareshwar, P.V.; Nietch, C.T.; Kjerfve, B.; Cahoon, D.R. Responses of coastal wetlands to rising sea level. Ecology 2002, 83, 2869–2877. [Google Scholar] [CrossRef]
- Bouma, T.J.; van Duren, L.A.; Temmerman, S.; Claverie, T.; Blanco-Garcia, A.; Ysebaert, T.; Herman, P.M.J. Spatial flow and sedimentation patterns within patches of epibenthic structures: Combining field, flume and modelling experiments. Cont. Shelf Res. 2007, 27, 1020–1045. [Google Scholar] [CrossRef]
- Nolte, S.; Koppenaal, E.C.; Esselink, P.; Dijkema, K.S.; Schuerch, M.; Groot, A.V.D.; Bakker, J.P.; Temmerman, S. Measuring sedimentation in tidal marshes: A review on methods and their applicability in biogeomorphological studies. J. Coast. Conserv. 2013, 17, 301–325. [Google Scholar] [CrossRef]
- Erwin, R.M.; Cahoon, D.R.; Prosser, D.J.; Sanders, G.M.; Hensel, P. Surface elevation dynamics in vegetated Spartina marshes vs. unvegetated tidal ponds along the Mid-Atlantic coast, USA, with implications to waterbirds. Estuaries Coasts 2006, 29, 96–106. [Google Scholar] [CrossRef]
- Du, Q.; Zhong, Q.C.; Wang, K.Y. Root effect of three vegetation types on shoreline stabilization of Chongming Island, Shanghai. Pedosphere 2010, 20, 692–701. [Google Scholar] [CrossRef]
- Hubble, T.C.T.; Docker, B.B.; Rutherfurd, I.D. The role of riparian trees in maintaining riverbank stability: A review of Australian experience and practice. Ecol. Eng. 2010, 36, 292–304. [Google Scholar] [CrossRef]
- Cahoon, D.R.; White, D.A.; Lynch, J.C. Sediment infilling and wetland formation dynamics in an active crevasse splay of the Mississippi River delta. Geomorphology 2011, 131, 57–68. [Google Scholar] [CrossRef]
- Ganthy, F.; Sottolichio, A.; Verney, R. The stability of vegetated tidal flats in a coastal lagoon through quasi in-situ measurements of sediment erodability. J. Coast. Res. 2011, SI 64, 1500–1504. [Google Scholar]
- Bouma, T.J.; Friedrichs, M.; Klaassen, P.; van Wesenbeeck, B.K.; Brun, F.G.; Temmerman, S.; van Katwijk, M.M.; Graf, G.; Herman, P.M.J. Effects of shoot stiffness, shoot size and current velocity on scouring sediment from around seedlings and propagules. Mar. Ecol. Prog. Ser. 2009, 388, 293–297. [Google Scholar] [CrossRef]
- Peralta, G.; van Duren, L.; Morris, E.; Bouma, T. Consequences of shoot density and stiffness for ecosystem engineering by benthic macrophytes in flow dominated areas: A hydrodynamic flume study. Mar. Ecol. Prog. Ser. 2008, 368, 103–115. [Google Scholar] [CrossRef]
- Temmerman, S.; Bouma, T.J.; Govers, G.; Lauwaet, D. Flow paths of water and sediment in a tidal marsh: Relations with marsh developmental stage and tidal inundation height. Estuaries Coasts 2005, 28, 338–352. [Google Scholar] [CrossRef]
- Temmerman, S.; Bouma, T.J.; Govers, G.; Wang, Z.B.; de Vries, M.B.; Herman, P.M.J. Impact of vegetation on flow routing and sedimentation patterns: Three-dimensional modeling for a tidal marsh. J. Geophys. Res. 2005, 110. [Google Scholar] [CrossRef]
- Bouma, T.J.; Temmerman, S.; van Duren, L.A.; Martini, E.; Vandenbruwaene, W.; Callaghan, D.P.; Balke, T.; Biermans, G.; Klaassen, P.C.; van Steeg, P.; et al. Organism traits determine the strength of scale-dependent bio-geomorphic feedbacks: A flume study on three intertidal plant species. Geomorphology 2013, 180–181, 57–65. [Google Scholar] [CrossRef]
- Temmerman, S.; Moonen, P.; Schoelynck, J.; Govers, G.; Bouma, T.J. Impact of vegetation die-off on spatial flow patterns over a tidal marsh. Geophys. Res. Lett. 2012, 39, L03406. [Google Scholar] [CrossRef]
- Wang, C.; Kirwan, M.L.; Belluco, E.; D’Alpaos, A.; Temmerman, S. Coastal marsh degradation and recovery: Critical geomorphic conditions for pool presence and revegetation. J. Geophys. Res. Earth Surf. 2015. in review. [Google Scholar]
- Handa, I.T.; Harmsen, R.; Jefferies, R.L. Patterns of vegetation change and the recovery potential of degraded areas in a coastal marsh system of the Hudson Bay Lowlands. J. Ecol. 2002, 90, 86–99. [Google Scholar] [CrossRef]
- Kotanen, P.M.; Abraham, K.F. Decadal changes in vegetation of a subarctic salt marsh used by lesser snow and Canada geese. Plant Ecol. 2013, 214, 409–422. [Google Scholar] [CrossRef]
- Follett, E.M.; Nepf, H.M. Sediment patterns near a model patch of reedy emergent vegetation. Geomorphology 2012, 179, 141–151. [Google Scholar] [CrossRef]
- Nepf, H.M. Hydrodynamics of vegetated channels. J. Hydraul. Res. 2012, 50, 262–279. [Google Scholar] [CrossRef]
- Ortiz, A.C.; Ashton, A.; Nepf, H. Mean and turbulent velocity fields near rigid and flexible plants and the implications for deposition. J. Geophys. Res. Earth Surf. 2013, 118, 2585–2599. [Google Scholar] [CrossRef]
- Wang, C.; Wang, Q.; Meire, D.; Ma, W.D.; Wu, C.Q.; Meng, Z.; van de Koppel, J.; Troch, P.; Verhoeven, R.; Mulder, T.D.; et al. Biogeomorphic feedback between plant growth and flooding cause alternative stable states in an experimental floodplain. Adv. Water Resour. 2015. [Google Scholar] [CrossRef]
- Smith, B.C. The Effects of Vegetation on Island Geomorphology in the Wax Lake Delta, Louisiana. Master’s Thesis, The University of Texas at Austin, Austin, TX, USA, 2014. [Google Scholar]
- Smith, B.C.; Moffett, K.B.; Mohrig, D. The effects of vegetation on island geomorphology in the Wax Lake Delta, Louisiana. Geomorphology 2015. in review. [Google Scholar]
- Brinkman, R.M. Wave Attenuation in Mangrove Forests: An Investigation through Field and Theoretical Studies. Ph.D. Thesis, James Cook University, North Queensland, Australia, 2006. [Google Scholar]
- Quartel, S.; Kroon, A.; Augustinus, P.G.E.F.; van Santen, P.; Tri, N.H. Wave attenuation in coastal mangroves in the Red River Delta, Vietnam. J. Asian Earth Sci. 2007, 29, 576–584. [Google Scholar] [CrossRef]
- Vo-Luong, P.; Massel, S. Energy dissipation in non-uniform mangrove forests of arbitrary depth. J. Mar. Syst. 2008, 74, 603–622. [Google Scholar] [CrossRef]
- Mazda, Y.; Wolanski, E.; King, B.; Sase, A.; Ohtsuka, D.; Magi, M. Drag force due to vegetation in mangrove swamps. Mangroves Salt Marshes 1997, 1, 193–199. [Google Scholar] [CrossRef]
- Ellison, J.C. Impacts of sediment burial on mangroves. Mar. Pollut. Bull. 1999, 37, 420–426. [Google Scholar] [CrossRef]
- Alongi, D.M. Mangrove forests: Resilience, protection from tsunamis, and responses to global climate change. Estuar. Coast. Shelf Sci. 2008, 76, 1–13. [Google Scholar] [CrossRef]
- Cahoon, D.R.; Hensel, P.; Rybczyk, J.; McKee, K.L.; Proffitt, C.E.; Perez, B.C. Mass tree mortality leads to mangrove peat collapse at Bay Islands, Honduras after Hurricane Mitch. J. Ecol. 2003, 91, 1093–1105. [Google Scholar] [CrossRef]
- Duke, N.C.; Jackes, B.R. A systematic revision of the mangrove genus Sonneratia (Sonneratiaceae) in Australasia. Blumea 1987, 32, 277–302. [Google Scholar]
- Thampanya, U.; Vermaat, J.E.; Terrados, J. The effect of increasing sediment accretion on the seedlings of three common Thai mangrove species. Aquat. Bot. 2002, 74, 315–325. [Google Scholar] [CrossRef]
- Yang, J.; Gao, J.; Cheung, A.; Liu, B.; Schwendenmann, L.; Costello, M.J. Vegetation and sediment characteristics in an expanding mangrove forest in New Zealand. Estuar. Coast. Shelf Sci. 2013, 134, 11–18. [Google Scholar] [CrossRef]
- Ball, M.C.; Pidsley, S.M. Growth responses to salinity in relation to distribution of two mangrove species, Sonneratia alba and S. lanceolata, in Northern Australia. Funct. Ecol. 1995, 9, 77–85. [Google Scholar] [CrossRef]
- Piou, C.; Berger, U.; Hildenbrandt, H.; Feller, I.C. Testing the intermediate disturbance hypothesis in species-poor systems: A simulation experiment for mangrove forests. J. Veg. Sci. 2008, 19, 417–424. [Google Scholar] [CrossRef]
- Harris, R.J.; Milbrandt, E.C.; Everham, M.E., III; Bovard, B.D. The effects of reduced tidal flushing on mangrove structure and function across a disturbance gradient. Estuaries Coasts 2010, 33, 1176–1185. [Google Scholar] [CrossRef]
- Vogt, J.; Piou, C.; Berger, U. Comparing the influence of large- and small-scale disturbances on forest heterogeneity: A simulation study for mangroves. Ecol. Complex. 2014, 20, 107–115. [Google Scholar] [CrossRef]
- Osland, M.J.; Enwright, N.; Day, R.H.; Doyle, T.W. Winter climate change and coastal wetland foundation species: Salt marshes vs. mangrove forests in the southeastern United States. Glob. Change Biol. 2013, 19, 1482–1494. [Google Scholar] [CrossRef] [PubMed]
- D’Odorico, P.; He, Y.; Collins, S.; de Wekker, S.F.J.; Engel, V.; Fuentes, J.D. Vegetation-microclimate feedbacks in woodland-grassland ecotones: Vegetation-microclimate feedbacks. Glob. Ecol. Biogeogr. 2013, 22, 364–379. [Google Scholar] [CrossRef]
- Semeniuk, C.A.; Semeniuk, V. The response of basin wetlands to climate changes: A review of case studies from the Swan Coastal Plain, South-Western Australia. Hydrobiologia 2013, 708, 45–67. [Google Scholar] [CrossRef]
- Osland, M.J.; Day, R.H.; Larriviere, J.C.; From, A.S. Aboveground allometric models for freeze-affected black mangroves (Avicennia germinans): Equations for a climate sensitive mangrove-marsh ecotone. PLoS ONE 2014, 9, e99604. [Google Scholar] [CrossRef] [PubMed]
- Alongi, D.M. The impact of climate change on mangrove forests. Curr. Clim. Change Rep. 2015, 1, 30–39. [Google Scholar] [CrossRef]
- Doyle, T.W.; Krauss, K.W.; Conner, W.H.; From, A.S. Predicting the retreat and migration of tidal forests along the northern Gulf of Mexico under sea-level rise. For. Ecol. Manag. 2010, 259, 770–777. [Google Scholar] [CrossRef]
- Krauss, K.W.; McKee, K.L.; Lovelock, C.E.; Cahoon, D.R.; Saintilan, N.; Reef, R.; Chen, L. How mangrove forests adjust to rising sea level. New Phytol. 2014, 202, 19–34. [Google Scholar] [CrossRef] [PubMed]
- Carr, J.; D’Odorico, P.; McGlathery, K.; Wiberg, P. Stability and bistability of seagrass ecosystems in shallow coastal lagoons: Role of feedbacks with sediment resuspension and light attenuation. J. Geophys. Res. Biogeosci. 2010, 115, G03011. [Google Scholar] [CrossRef]
- Carr, J.A.; D’Odorico, P.; McGlathery, K.J.; Wiberg, P.L. Modeling the effects of climate change on eelgrass stability and resilience: Future scenarios and leading indicators of collapse. Mar. Ecol. Prog. Ser. 2012, 448, 289–301. [Google Scholar] [CrossRef]
- Carr, J.A.; D’Odorico, P.; McGlathery, K.J.; Wiberg, P.L. Stability and resilience of seagrass meadows to seasonal and interannual dynamics and environmental stress. J. Geophys. Res. Biogeosci. 2012, 117, G01007. [Google Scholar] [CrossRef]
- McGlathery, K.J.; Reynolds, L.K.; Cole, L.W.; Orth, R.J.; Marion, S.R.; Schwarzschild, A. Recovery trajectories during state change from bare sediment to eelgrass dominance. Mar. Ecol. Prog. Ser. 2012, 448, 209–221. [Google Scholar] [CrossRef]
- MAV. In Monitoraggio Dell’ecosistema Lagunare (MELa2)—2° Stralcio Triennale. Linea A: “Rilievo Delle Fanerogame Marine in Laguna di Venezia con Taratura di un Sistema di Telerilevamento e Completamento Delle Conoscenze Sulle Macroalghe”. Rapporto di 2°Anno sui Risultati Della Mappatura; Technical Report; Consorzio Venezia Nuova. Esecutore SELC: Venice, Italy, 2004.
- Carniello, L.; Silvestri, S.; Marani, M.; D’Alpaos, A.; Volpe, V.; Defina, A. Sediment dynamics in shallow tidal basins: In situ observations, satellite retrievals, and numerical modeling in the Venice Lagoon. J. Geophys. Res. Earth Surf. 2014, 119. [Google Scholar] [CrossRef]
- Kim, J.H.; Kang, E.J.; Kim, K.; Jeong, H.J.; Lee, K.; Edwards, M.S.; Park, M.G.; Lee, B.G.; Kim, K.Y. Evaluation of carbon flux in vegetative bay based on ecosystem production and CO2 exchange driven by coastal autotrophs. Algae 2015, 30, 121–137. [Google Scholar] [CrossRef]
- Nepf, H.M. Flow and transport in regions with aquatic vegetation. Annu. Rev. Fluid Mech. 2012, 44, 123–142. [Google Scholar] [CrossRef]
- Folkard, A.M. Hydrodynamics of model Posidonia oceanica patches in shallow water. Limnol. Oceanogr. 2005, 50, 1592–1600. [Google Scholar] [CrossRef]
- Morris, J.T.; Porter, D.; Neet, M.; Noble, P.A.; Schmidt, L.; Lapine, L.A.; Jensen, J.R. Integrating LiDAR elevation data, multi-spectral imagery and neural network modelling for marsh characterization. Int. J. Remote Sens. 2005, 26, 5221–5234. [Google Scholar] [CrossRef]
- Marani, M.; Zillio, T.; Belluco, E.; Silvestri, S.; Maritan, A. Non-neutral vegetation dynamics. PLoS ONE 2006, 1, e78. [Google Scholar] [CrossRef] [PubMed]
- Wang, C.; Menenti, M.; Stoll, M.-P.; Feola, A.; Belluco, E.; Marani, M. Separation of ground and low vegetation signatures in LiDAR measurements of salt-marsh environments. IEEE Trans. Geosci. Remote Sens. 2009, 47, 2014–2023. [Google Scholar] [CrossRef]
- Jano, A.P.; Jefferies, R.L.; Rockwell, R.F. The detection of vegetational change by multitemporal analysis of LANDSAT data: The effects of goose foraging. J. Ecol. 1998, 86, 93–99. [Google Scholar] [CrossRef]
- Carle, M.V.; Wang, L.; Sasser, C.E. Mapping freshwater marsh species distributions using WorldView-2 high-resolution multispectral satellite imagery. Int. J. Remote Sens. 2014, 35, 4698–4716. [Google Scholar] [CrossRef]
- Nardin, W.; Edmonds, D.A. Optimum vegetation height and density for inorganic sedimentation in deltaic marshes. Nat. Geosci. 2014, 7, 722–726. [Google Scholar] [CrossRef]
- Rosen, T.; Xu, Y.J. Recent decadal growth of the Atchafalaya River Delta complex: Effects of variable riverine sediment input and vegetation succession. Geomorphology 2013, 194, 108–120. [Google Scholar] [CrossRef]
- Mason, D.C.; Davenport, I.J.; Robinson, G.J.; Flather, R.A.; McCartney, B.S. Construction of an inter-tidal digital elevation model by the “Water-Line” Method. Geophys. Res. Lett. 1995, 22, 3187–3190. [Google Scholar] [CrossRef]
- Mason, D.C.; Scott, T.R.; Dance, S.L. Remote sensing of intertidal morphological change in Morecambe Bay, U.K., between 1991 and 2007. Estuar. Coast. Shelf Sci. 2010, 87, 487–496. [Google Scholar] [CrossRef]
- Ryu, J.H.; Kim, C.H.; Lee, Y.K.; Won, J.S.; Chun, S.S.; Lee, S. Detecting the intertidal morphologic change using satellite data. Estuar. Coast. Shelf Sci. 2008, 78, 623–632. [Google Scholar] [CrossRef]
- Kuenzer, C.; Bluemel, A.; Gebhardt, S.; Quoc, T.V.; Dech, S. Remote sensing of mangrove ecosystems: A review. Remote Sens. 2011, 3, 878–928. [Google Scholar] [CrossRef]
- Lugo, A.E. Mangrove ecosystems: successional or steady state? Biotropica 1980, 12, 65–72. [Google Scholar] [CrossRef]
- Balke, T. Establishment of Biogeomorphic Ecosystems: A Study on Mangrove and Salt Marsh Pioneer Vegetation. Ph.D. Thesis, Radboud University, Nijmegen, The Netherlands, 2013. [Google Scholar]
- Twilley, R.R.; Rivera-Monroy, V.H.; Chen, R.; Botero, L. Adapting an ecological mangrove model to simulate trajectories in restoration ecology. Mar. Pollut. Bull. 1999, 37, 404–419. [Google Scholar] [CrossRef]
- Ramsey, E.W., III; Jensen, J.R. Remote sensing of mangrove wetlands: Relating canopy spectra to site-specific data. Photogramm. Eng. Remote Sens. 1996, 62, 939–948. [Google Scholar]
- Wang, L.; Silván-Cárdenas, J.L.; Sousa, W.P. Neural network classification of mangrove species from multi-seasonal Ikonos imagery. Photogramm. Eng. Remote Sens. 2008, 74, 921–927. [Google Scholar] [CrossRef]
- Green, E.P.; Clark, C.D.; Mumby, P.J.; Edwards, A.J.; Ellis, A.C. Remote sensing techniques for mangrove mapping. Int. J. Remote Sens. 1998, 19, 935–956. [Google Scholar] [CrossRef]
- Tong, P.H. S.; Auda, Y.; Populus, J.; Aizpuru, M.; Habshi, A.A.; Blasco, F. Assessment from space of mangroves evolution in the Mekong Delta, in relation to extensive shrimp farming. Int. J. Remote Sens. 2004, 25, 4795–4812. [Google Scholar] [CrossRef]
- Lee, T.M.; Yeh, H.C. Applying remote sensing techniques to monitor shifting wetland vegetation: A case study of Danshui River estuary mangrove communities, Taiwan. Ecol. Eng. 2009, 35, 487–496. [Google Scholar] [CrossRef]
- Muttitanon, W.; Tripathi, N.K. Land use/land cover changes in the coastal zone of Ban Don Bay, Thailand using Landsat 5 TM data. Int. J. Remote Sens. 2005, 26, 2311–2323. [Google Scholar] [CrossRef]
- Giri, C.; Pengra, B.; Zhu, Z.; Singh, A.; Tieszen, L.L. Monitoring mangrove forest dynamics of the Sundarbans in Bangladesh and India using multi-temporal satellite data from 1973 to 2000. Estuar. Coast. Shelf Sci. 2007, 73, 91–100. [Google Scholar] [CrossRef]
- Rovai, A.S.; Soriano-Sierra, E.J.; Pagliosa, P.R.; Cintrón, G.; Schaeffer-Novelli, Y.; Menghini, R.P.; Coelho, C., Jr.; Horta, P.A.; Lewis, R.R., III; Simonassi, J.C.; et al. Secondary succession impairment in restored mangroves. Wetl. Ecol. Manag. 2012, 20, 447–459. [Google Scholar] [CrossRef]
- Lovelock, C.E.; Sorrell, B.K.; Hancock, N.; Hua, Q.; Swales, A. Mangrove forest and soil development on a rapidly accreting shore in New Zealand. Ecosystems 2010, 13, 437–451. [Google Scholar] [CrossRef]
- Ferguson, R.L.; Korfmacher, K. Remote sensing and GIS analysis of seagrass meadows in North Carolina, USA. Aquat. Bot. 1997, 58, 241–258. [Google Scholar] [CrossRef]
- Mumby, P.J.; Green, E.P.; Edwards, A.J.; Clark, C.D. Measurement of seagrass standing crop using satellite and digital airborne remote sensing. Mar. Ecol. Prog. Ser. 1997, 159, 51–60. [Google Scholar] [CrossRef]
- Dahdouh-Guebas, F.; Coppejans, E.; Speybroeck, D.V. Remote sensing and zonation of seagrasses and algae along the Kenyan coast. Hydrobiologia 1999, 400, 63–73. [Google Scholar] [CrossRef]
- Lundén, B.; Gullström, M. Satellite remote sensing for monitoring of vanishing seagrass in Swedish coastal waters. Nor. Geogr. Tidsskr. Nor. J. Geogr. 2003, 57, 121–124. [Google Scholar] [CrossRef]
- Phinn, S.; Roelfsema, C.; Dekker, A.; Brando, V.; Anstee, J. Mapping seagrass species, cover and biomass in shallow waters: An assessment of satellite multi-spectral and airborne hyper-spectral imaging systems in Moreton Bay (Australia). Remote Sens. Environ. 2008, 112, 3413–3425. [Google Scholar] [CrossRef]
- Phinn, S.R.; Roelfsema, C.M.; Mumby, P.J. Multi-scale, object-based image analysis for mapping geomorphic and ecological zones on coral reefs. Int. J. Remote Sens. 2012, 33, 3768–3797. [Google Scholar] [CrossRef]
- Roelfsema, C.M.; Phinn, S.R.; Udy, N.; Maxwell, P. An integrated field and remote sensing approach for mapping seagrass cover, Moreton Bay, Australia. J. Spat. Sci. 2009, 54, 45–62. [Google Scholar] [CrossRef]
- Roelfsema, C. Integrating field data with high spatial resolution multispectral satellite imagery for calibration and validation of coral reef benthic community maps. J. Appl. Remote Sens. 2010, 4, 043527. [Google Scholar] [CrossRef]
- Dekker, A.G.; Phinn, S.R.; Anstee, J.; Bissett, P.; Brando, V.E.; Casey, B.; Fearns, P.; Hedley, J.; Klonowski, W.; Lee, Z.P. Others Intercomparison of shallow water bathymetry, hydro-optics, and benthos mapping techniques in Australian and Caribbean coastal environments. Limnol. Oceanogr. Methods 2011, 9, 396–425. [Google Scholar] [CrossRef]
- Gullström, M.; Lundén, B.; Bodin, M.; Kangwe, J.; Öhman, M.C.; Mtolera, M.S.P.; Björk, M. Assessment of changes in the seagrass-dominated submerged vegetation of tropical Chwaka Bay (Zanzibar) using satellite remote sensing. Estuar. Coast. Shelf Sci. 2006, 67, 399–408. [Google Scholar] [CrossRef]
- Yang, D.; Yang, C. Detection of seagrass distribution changes from 1991 to 2006 in Xincun Bay, Hainan, with satellite remote sensing. Sensors 2009, 9, 830–844. [Google Scholar] [CrossRef] [PubMed]
- Barillé, L.; Robin, M.; Harin, N.; Bargain, A.; Launeau, P. Increase in seagrass distribution at Bourgneuf Bay (France) detected by spatial remote sensing. Aquat. Bot. 2010, 92, 185–194. [Google Scholar] [CrossRef]
- Lyons, M.; Phinn, S.; Roelfsema, C. Integrating Quickbird multi-spectral satellite and field data: mapping bathymetry, seagrass cover, seagrass species and change in Moreton Bay, Australia in 2004 and 2007. Remote Sens. 2011, 3, 42–64. [Google Scholar] [CrossRef]
- Lyons, M.B.; Phinn, S.R.; Roelfsema, C.M. Long term land cover and seagrass mapping using Landsat and object-based image analysis from 1972 to 2010 in the coastal environment of South East Queensland, Australia. ISPRS J. Photogramm. Remote Sens. 2012, 71, 34–46. [Google Scholar] [CrossRef]
- Lyons, M.B.; Roelfsema, C.M.; Phinn, S.R. Towards understanding temporal and spatial dynamics of seagrass landscapes using time-series remote sensing. Estuar. Coast. Shelf Sci. 2013, 120, 42–53. [Google Scholar] [CrossRef]
- Kim, K.; Choi, J.K.; Ryu, J.H.; Jeong, H.J.; Lee, K.; Park, M.G.; Kim, K.Y. Observation of typhoon-induced seagrass die-off using remote sensing. Estuar. Coast. Shelf Sci. 2015, 154, 111–121. [Google Scholar] [CrossRef]
- Saunders, M.I.; Bayraktarov, E.; Roelfsema, C.M.; Leon, J.X.; Samper-Villarreal, J.; Phinn, S.R.; Lovelock, C.E.; Mumby, P.J. Spatial and temporal variability of seagrass at Lizard Island, Great Barrier Reef. Bot. Mar. 2015, 58, 35–49. [Google Scholar] [CrossRef]
- Ward, D.H.; Markon, C.J.; Douglas, D.C. Distribution and stability of eelgrass beds at Izembek Lagoon, Alaska. Aquat. Bot. 1997, 58, 229–240. [Google Scholar] [CrossRef]
- Howari, F.M.; Jordan, B.R.; Bouhouche, N.; Wyllie-Echeverria, S. Field and remote-sensing assessment of mangrove forests and seagrass beds in the northwestern part of the United Arab Emirates. J. Coast. Res. 2009, 48–56. [Google Scholar] [CrossRef]
- Blasco, F.; Aizpuru, M.; Gers, C. Depletion of the mangroves of Continental Asia. Wetl. Ecol. Manag. 2001, 9, 255–266. [Google Scholar] [CrossRef]
- Thu, P.M.; Populus, J. Status and changes of mangrove forest in Mekong Delta: Case study in Tra Vinh, Vietnam. Estuar. Coast. Shelf Sci. 2007, 71, 98–109. [Google Scholar] [CrossRef]
- Nardin, W.; Locatelli, S.; Pasquarella, V.; Rulli, M.C.; Woodcock, C.E.; Fagherazzi, S. Dynamics of a fringe mangrove forest detected by Landsat images in the Mekong delta, Vietnam. Earth Surf. Process. Landf. 2015. in review. [Google Scholar]
- O’Connor, M.T.; Moffett, K.B. Groundwater dynamics and surface water-groundwater interactions in a prograding delta island, Louisiana, USA. J. Hydrol. 2015, 524, 15–29. [Google Scholar] [CrossRef]
- Geleynse, N.; Hiatt, M.; Sangireddy, H.; Passalacqua, P. Identifying environmental controls on the shoreline of a natural river delta. J. Geophys. Res. Earth Surf. 2015. [Google Scholar] [CrossRef]
- Carle, M.V.; Sasser, C.E.; Roberts, H.H. Accretion and vegetation community change in the Wax Lake Delta following the historic 2011 Mississippi River flood. J. Coast. Res. 2013, 31, 596–587. [Google Scholar] [CrossRef]
- Pickett, S.T.A. Space-for-time substitution as an alternative to long-term studies. In Long-Term Studies in Ecology; Likens, G.E., Ed.; Springer: New York, NY, USA, 1989; pp. 110–135. [Google Scholar]
- Walker, L.R.; Wardle, D.A.; Bardgett, R.D.; Clarkson, B.D. The use of chronosequences in studies of ecological succession and soil development. J. Ecol. 2010, 98, 725–736. [Google Scholar] [CrossRef]
- EarthData International. ADS-40 Digital Imagery Acquisition of San Francisco-Oakland, California; EarthData International of Maryland, LLC: Frederick, MD, USA, 2004. [Google Scholar]
- SFEI. Modern view of South Bay Subregion CA. 1997. In Bay Area EcoAtlas Version 1.50pr5; San Francisco Estuary Institute: Oakland, CA, USA, 1997. [Google Scholar]
- WWR. Wetlands Inventory Maps: Wetlands Projects, Completed and Planned Projects in theSan Francisco Estuary, California; Wetlands and Water Resources, Inc.: San Francisco, CA, USA. Available online: http://www.swampthing.org/projects/regional-planning/item/120-south-bay-wetlands-inventory-map, http://swampthing.org/esa/projects/regional-planning/item/118-north-bay-wetland-inventory-map, and http://swampthing.org/esa/projects/regional-planning/item/123-suisun-science-advisor (accessed on 8 July 2006).
- Adema, E.B.; van de Koppel, J.; Meijer, H.A.J.; Grootjans, A.P. Enhanced nitrogen loss may explain alternative stable states in dune slack succession. Oikos 2005, 109, 374–386. [Google Scholar] [CrossRef]
- Balke, T.; Herman, P.M.J.; Bouma, T.J. Critical transitions in disturbance-driven ecosystems: Identifying windows of opportunity for recovery. J. Ecol. 2014, 102, 700–708. [Google Scholar] [CrossRef]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Moffett, K.B.; Nardin, W.; Silvestri, S.; Wang, C.; Temmerman, S. Multiple Stable States and Catastrophic Shifts in Coastal Wetlands: Progress, Challenges, and Opportunities in Validating Theory Using Remote Sensing and Other Methods. Remote Sens. 2015, 7, 10184-10226. https://doi.org/10.3390/rs70810184
Moffett KB, Nardin W, Silvestri S, Wang C, Temmerman S. Multiple Stable States and Catastrophic Shifts in Coastal Wetlands: Progress, Challenges, and Opportunities in Validating Theory Using Remote Sensing and Other Methods. Remote Sensing. 2015; 7(8):10184-10226. https://doi.org/10.3390/rs70810184
Chicago/Turabian StyleMoffett, Kevan B., William Nardin, Sonia Silvestri, Chen Wang, and Stijn Temmerman. 2015. "Multiple Stable States and Catastrophic Shifts in Coastal Wetlands: Progress, Challenges, and Opportunities in Validating Theory Using Remote Sensing and Other Methods" Remote Sensing 7, no. 8: 10184-10226. https://doi.org/10.3390/rs70810184
APA StyleMoffett, K. B., Nardin, W., Silvestri, S., Wang, C., & Temmerman, S. (2015). Multiple Stable States and Catastrophic Shifts in Coastal Wetlands: Progress, Challenges, and Opportunities in Validating Theory Using Remote Sensing and Other Methods. Remote Sensing, 7(8), 10184-10226. https://doi.org/10.3390/rs70810184