Airborne LiDAR Detects Selectively Logged Tropical Forest Even in an Advanced Stage of Recovery
Abstract
:1. Introduction
2. Experimental Section
2.1. Study Area
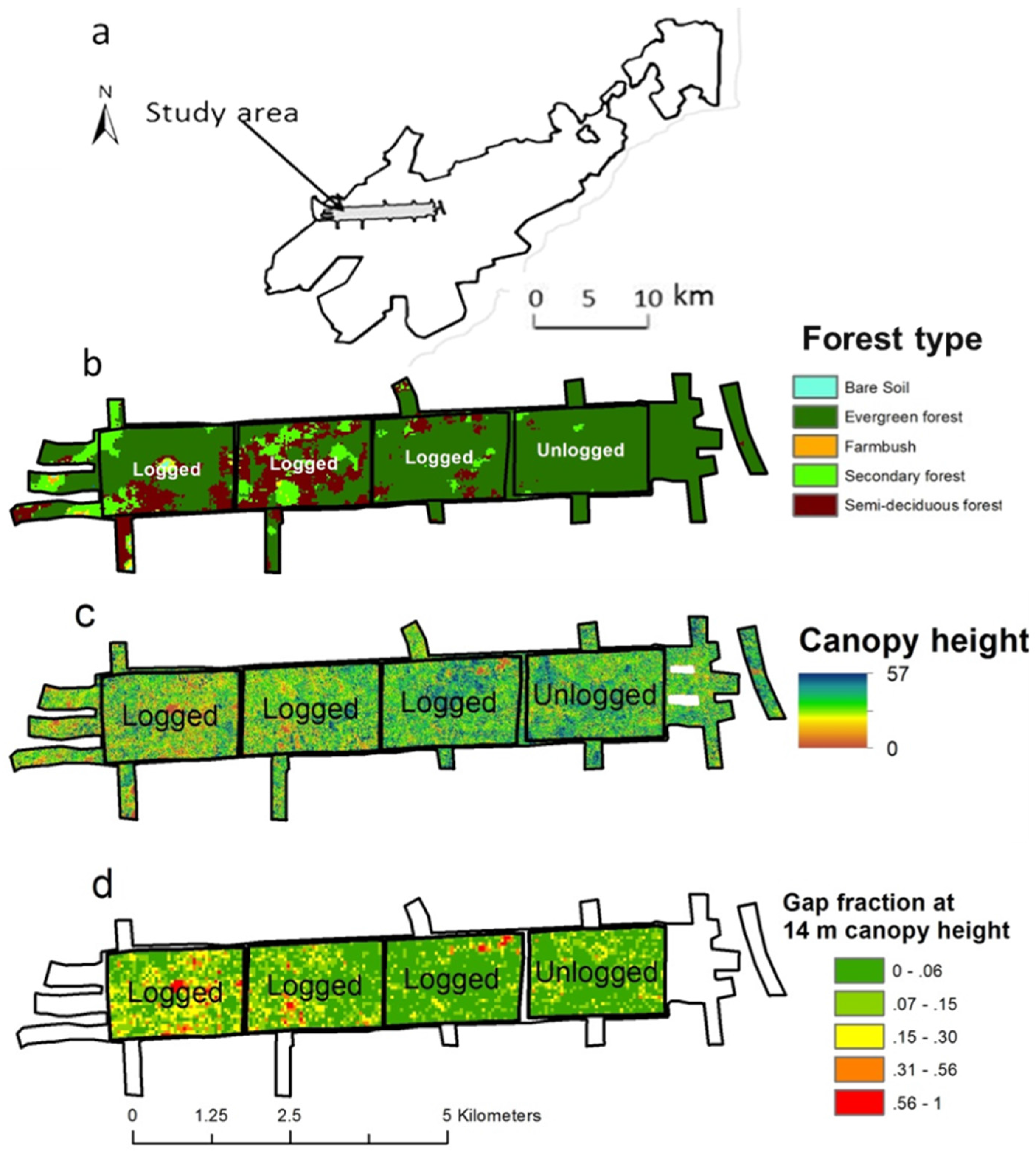
2.2. LiDAR Data
2.2.1. Canopy Surface Height
2.2.2. Gap Size Distribution

2.3. Canopy Height and Gap Fraction Estimates from Ground Sampling Plots
| Variable | Data Source | Variable Description |
|---|---|---|
| LiDAR Canopy surface height | LiDAR | The mean height of the canopy as extracted from the first returns of the LiDAR point cloud over the entire 3 km2 blocks, at 1 m2 resolution |
| Field Canopy surface height | Field plots [44] | The heights and crown areas of all tagged trees within a plot were estimated from diameters using site- and species-specific allometries [57]. The height of each tree was weighted by its proportional contribution to the total crown area when calculating mean canopy surface height |
| LiDAR Gap fraction | LiDAR | Total area of gaps per height tier in the canopy height model, divided by block area (3 km2) |
| Field Gap fraction | Field plots [34] | Evaluation of gap fraction in the field plots, by summing crown areas of all trees in the plot, and subtracting it from plot size |
| Gap size distribution parameters | LiDAR | The scaling exponent (λ) and quadratic modifier (β) of the gap size frequency distribution, estimated using an MCMC sampling procedure |
3. Results and Discussion
3.1. Results
3.1.1. Canopy Height
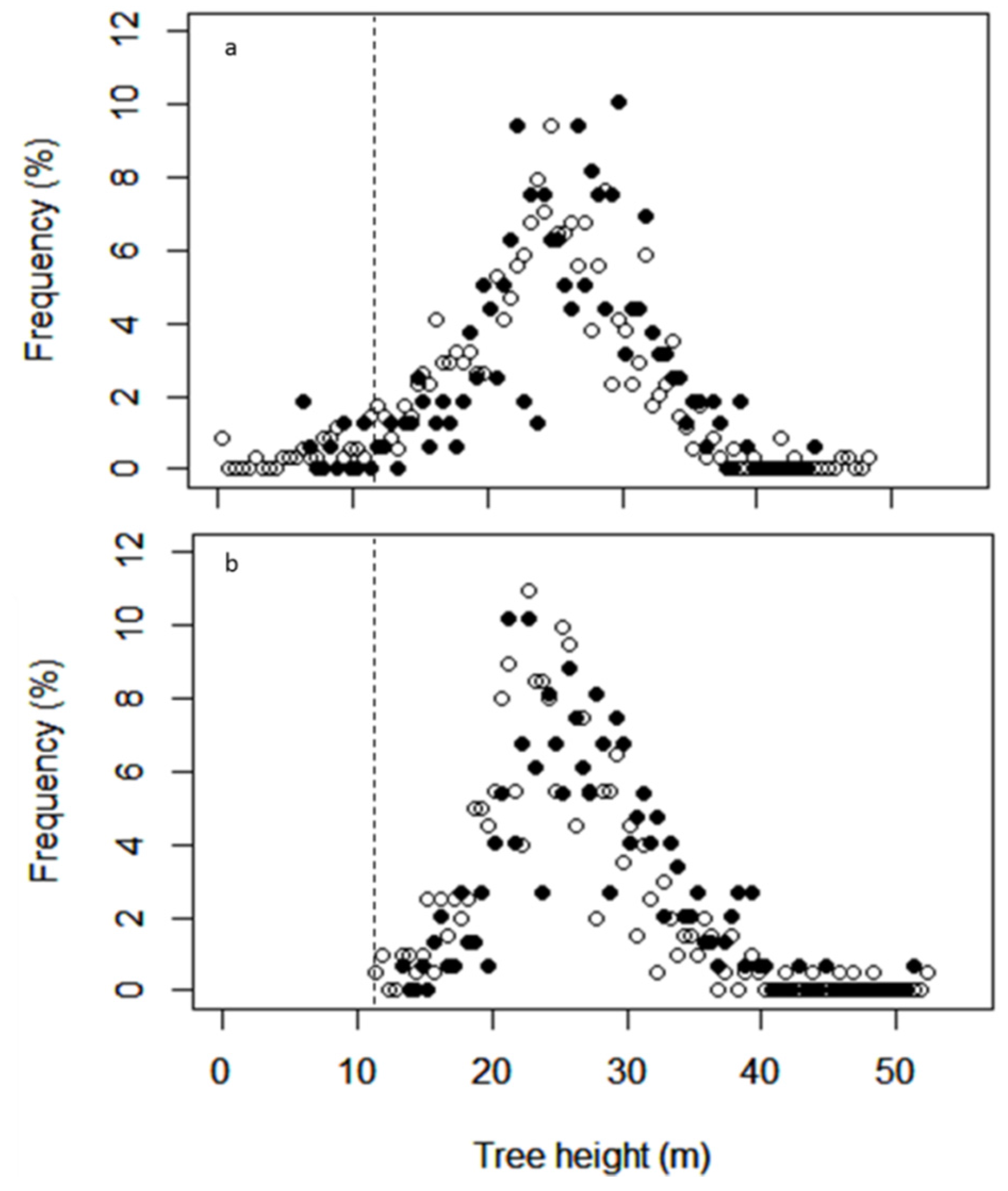
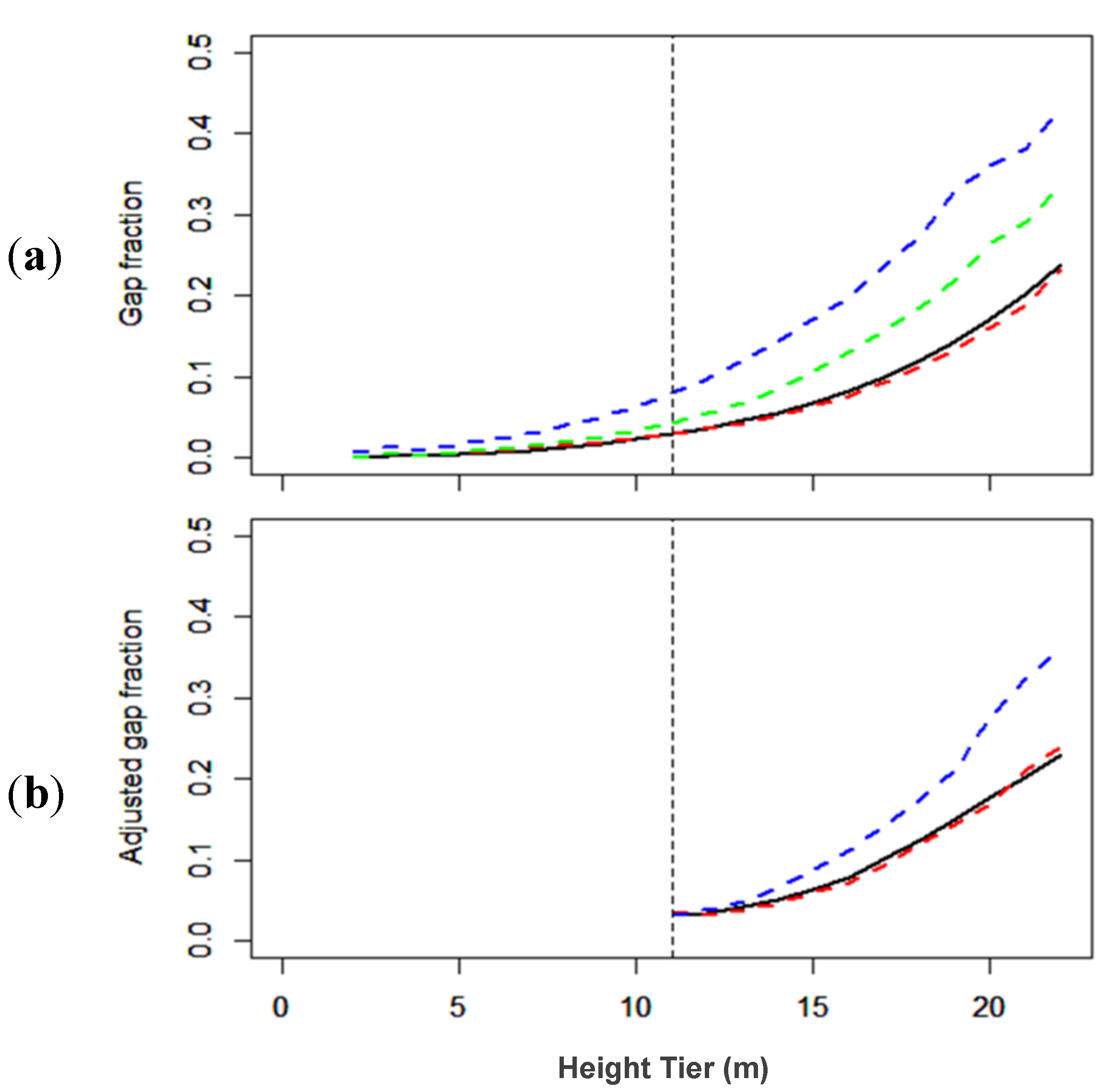
3.1.2. Gap Fraction
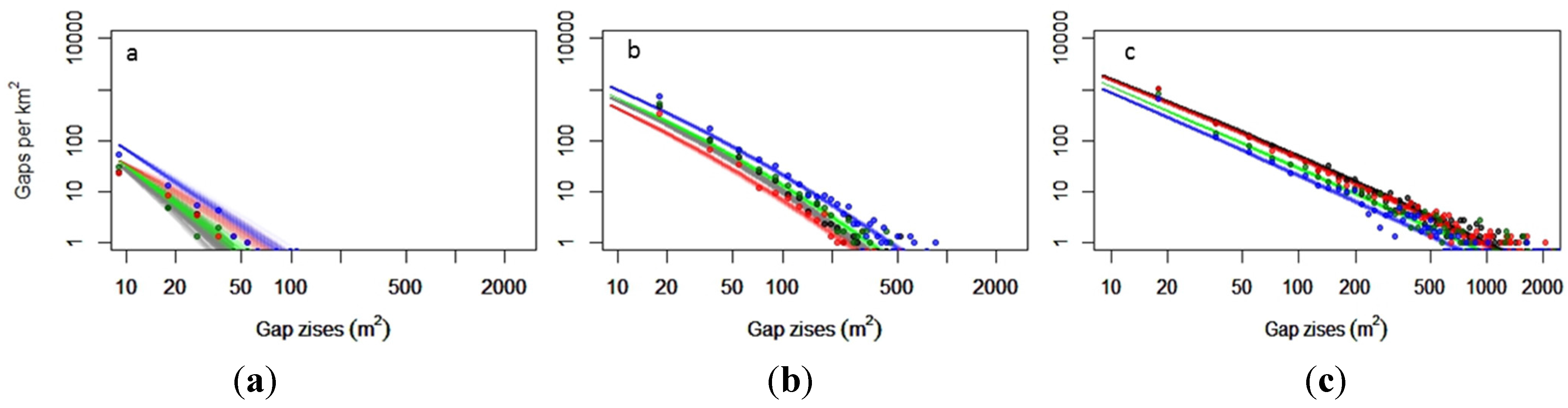
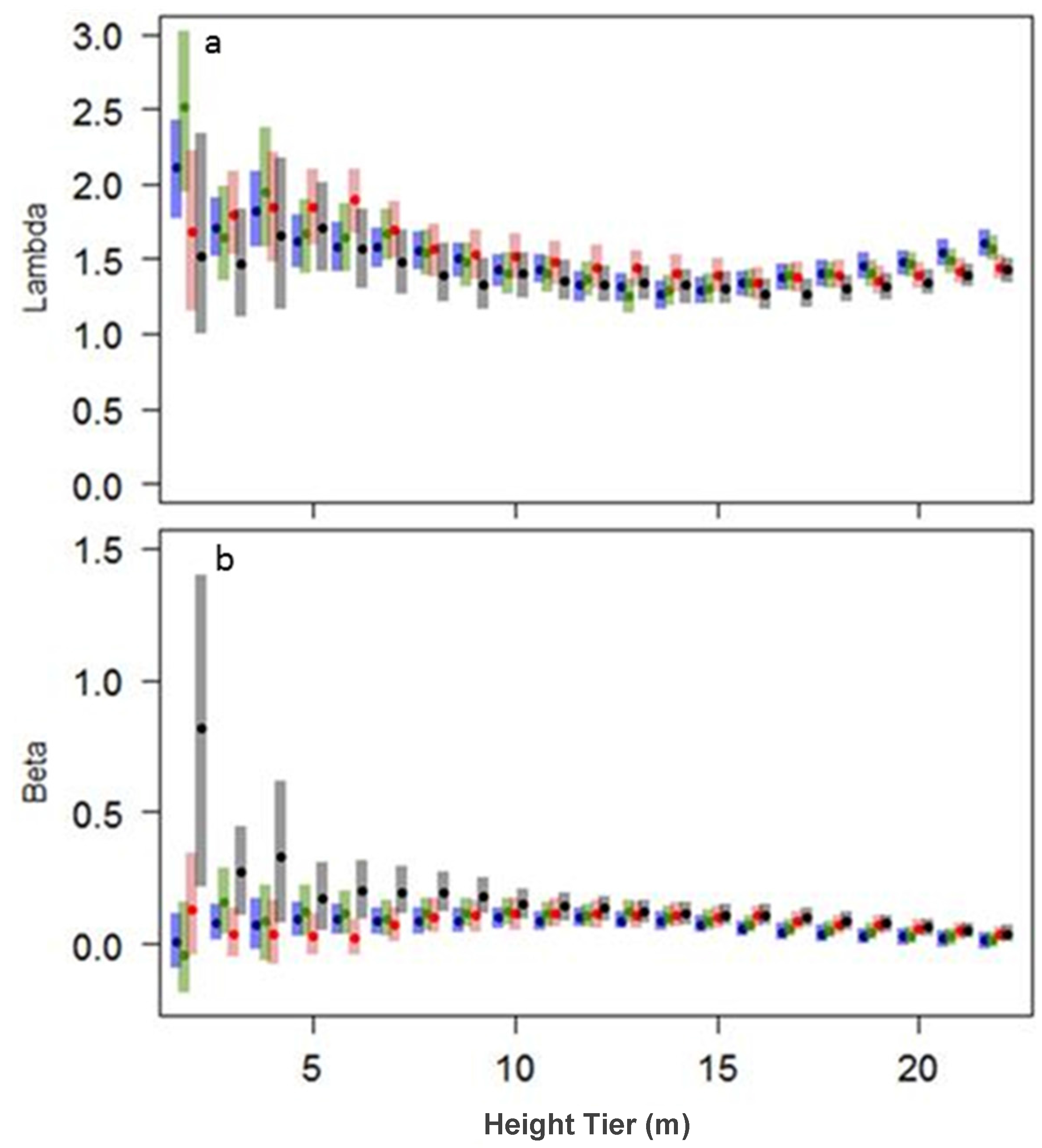
3.1.3. Gap-Size Distributions
3.1.4. Mapping Areas of Forest Recovering from Disturbance
3.2. Discussion
3.2.1. Canopy Height
3.2.2. Gap Fractions
3.2.3. Gap Size Distributions
4. Conclusions
Supplementary Files
Supplementary File 1Acknowledgments
Author Contributions
Conflicts of Interest
References
- Chazdon, R.L. Tropical forest recovery: Legacies of human impact and natural disturbances. Perspect. Plant Ecol. Evol. Syst. 2003, 6, 51–71. [Google Scholar] [CrossRef]
- Gibson, L.; Lee, T.M.; Koh, L.P.; Brook, B.W.; Gardner, T.A.; Barlow, J.; Peres, C.A.; Bradshaw, C.J.A.; Laurance, W.F.; Lovejoy, T.E.; et al. Primary forests are irreplaceable for sustaining tropical biodiversity. Nature 2011, 478, 378–381. [Google Scholar] [CrossRef] [PubMed]
- International Tropical Timber Organization. ITTO Guidelines for the Restoration, Management and Rehabilitation of Degraded and Secondary Tropical Forests; International Tropical Timber Organization: Yokohama, Japan, 2002. [Google Scholar]
- FAO The State of The World’s Forests. Available online: http://www.fao.org/forestry/sofo/en/ (accessed on 19 June 2015).
- Wright, S.J.; Muller-Landau, H.C. The future of tropical forest species. Biotropica 2006, 38, 287–301. [Google Scholar] [CrossRef]
- Cannon, C.H.; Peart, D.R.; Leighton, M. Tree species diversity in commercially logged bornean rainforest. Science 1998, 281, 1366–1368. [Google Scholar] [CrossRef] [PubMed]
- Barlow, J.; Gardner, T.A.; Araujo, I.S.; Avila-Pires, T.C.; Bonaldo, A.B.; Costa, J.E.; Esposito, M.C.; Ferreira, L.V.; Hawes, J.; Hernandez, M.I.M.; et al. Quantifying the biodiversity value of tropical primary, secondary, and plantation forests. Proc. Natl. Acad. Sci. USA 2007, 104, 18555–18560. [Google Scholar] [CrossRef] [PubMed]
- Berry, N.J.; Phillips, O.L.; Lewis, S.L.; Hill, J.K.; Edwards, D.P.; Tawatao, N.B.; Ahmad, N.; Magintan, D.; Khen, C.V.; Maryati, M.; et al. The high value of logged tropical forests: Lessons from northern Borneo. Biodivers. Conserv. 2010, 19, 985–997. [Google Scholar] [CrossRef]
- Putz, F.E.; Zuidema, P.A.; Synnott, T.; Peña-Claros, M.; Pinard, M.A.; Sheil, D.; Vanclay, J.K.; Sist, P.; Gourlet-Fleury, S.; Griscom, B.; et al. Sustaining conservation values in selectively logged tropical forests: The attained and the attainable. Conserv. Lett. 2012, 5, 296–303. [Google Scholar] [CrossRef]
- Silver, W.L.; Ostertag, R.; Lugo, A.E. The potential for carbon sequestration through reforestation of abandoned tropical agricultural and pasture lands. Restor. Ecol. 2000, 8, 394–407. [Google Scholar] [CrossRef]
- Hooker, T.D.; Compton, J.E. Forest ecosystem carbon and nitrogen accumulation during the first century after agricultural abandonment. Ecol. Appl. 2003, 13, 299–313. [Google Scholar] [CrossRef]
- Martin, P.A.; Newton, A.C.; Bullock, J.M. Carbon pools recover more quickly than plant biodiversity in tropical secondary forests. Proc. R. Soc. B 2013. [Google Scholar] [CrossRef] [PubMed]
- Letcher, S.G.; Chazdon, R.L. Rapid recovery of biomass, species richness, and species composition in a forest chronosequence in northeastern Costa Rica. Biotropica 2009, 41, 608–617. [Google Scholar] [CrossRef]
- Pereira, R.; Zweede, J.; Asner, G.P.; Keller, M. Forest canopy damage and recovery in reduced-impact and conventional selective logging in eastern Para, Brazil. For. Ecol. Manage. 2002, 168, 77–89. [Google Scholar] [CrossRef]
- Bugmann, H. A review of forest gap models. Clim. Change 2001, 51, 259–305. [Google Scholar] [CrossRef]
- Asner, G.P.; Keller, M.; Silva, J.N.M. Spatial and temporal dynamics of forest canopy gaps following selective logging in the eastern Amazon. Glob. Chang. Biol. 2004, 10, 765–783. [Google Scholar] [CrossRef]
- Anderson, L.O.; Shimabukuro, Y.E.; Defries, R.S.; Morton, D. Assessment of deforestation in near real time over the Brazilian Amazon using multitemporal fraction images derived from Terra MODIS. IEEE Geosci. Remote Sens. Lett. 2005, 2, 315–318. [Google Scholar] [CrossRef]
- Gibbs, H.K.; Brown, S.; Niles, J.O.; Foley, J.A. Monitoring and estimating tropical forest carbon stocks: making REDD a reality. Environ. Res. Lett. 2007, 2, 045023. [Google Scholar] [CrossRef]
- Asner, G.P.; Knapp, D.E.; Broadbent, E.N.; Oliveira, P.J.C.; Keller, M.; Silva, J.N. Selective logging in the Brazilian Amazon. Science 2005, 310, 480–482. [Google Scholar] [CrossRef] [PubMed]
- Baker, P.J.; Bunyavejchewin, S.; Oliver, C.D.; Ashton, P.S. Disturbance history and historical stanf dynamics of a seasonal tropical forest in Western Thailand. Ecol. Monogr. 2005, 75, 317–343. [Google Scholar] [CrossRef]
- Asner, G.P.; Broadbent, E.N.; Oliveira, P.J.C.; Keller, M.; Knapp, D.E.; Silva, J.N.M. Condition and fate of logged forests in the Brazilian Amazon. Proc. Natl. Acad. Sci. USA 2006, 103, 12947–12950. [Google Scholar] [CrossRef] [PubMed]
- Brokaw, N.; Busing, R. Niche versus chance and tree diversity in forest gaps. Trends Ecol. Evol. 2000, 15, 183–188. [Google Scholar] [CrossRef]
- Schnitzer, S.A.; Dalling, J.W.; Carson, W.P. The impact of lianas on tree regeneration in tropical forest canopy gaps: Evidence for an alternative pathway of gap-phase regeneration. J. Ecol. 2000, 88, 655–666. [Google Scholar] [CrossRef]
- Alvarez, J.; Willig, M.R. Effects of treefall gaps on the density of land snails in the Luquillo Experimental Forest of Puerto Ricol. Biotropica 1993, 25, 100–110. [Google Scholar] [CrossRef]
- Simonson, W.D.; Allen, H.D.; Coomes, D.A. Use of an airborne LiDAR system to model plant species composition and diversity of Mediterranean oak forests. Conserv. Biol. 2012, 26, 840–850. [Google Scholar] [CrossRef] [PubMed]
- Murdiyarso, D.; Skutsch, M.; Guariguata, M.; Kanninen, M. Measuring and Monitoring Forest Degradation for REDD: Implications of Country Circumstances; CIFOR Infobrief no. 16; CIFOR: Bogor, Indonesia, 2008. [Google Scholar]
- Kellner, J.R.; Asner, G.P. Convergent structural responses of tropical forests to diverse disturbance regimes. Ecol. Lett. 2009, 12, 887–897. [Google Scholar] [CrossRef] [PubMed]
- Asner, G.P.; Kellner, J.R.; Kennedy-Bowdoin, T.; Knapp, D.E.; Anderson, C.; Martin, R.E. Forest canopy gap distributions in the southern Peruvian Amazon. PLoS ONE 2013, 8. [Google Scholar] [CrossRef] [PubMed]
- Lobo, E.; Dalling, J.W. Effects of topography, soil type and forest age on the frequency and size distribution of canopy gap disturbances in a tropical forest. Biogeosci. Discuss. 2013, 10, 7103–7133. [Google Scholar] [CrossRef]
- Palace, M.W.; Sullivan, F.B.; Ducey, M.J.; Treuhaft, R.N.; Herrick, C.; Shimbo, J.Z.; Mota-E-Silva, J. Estimating forest structure in a tropical forest using field measurements, a synthetic model and discrete return LiDAR data. Remote Sens. Environ. 2015, 161, 1–11. [Google Scholar] [CrossRef]
- Armston, J.; Disney, M.; Lewis, P.; Scarth, P.; Phinn, S.; Lucas, R.; Bunting, P.; Goodwin, N. Direct retrieval of canopy gap probability using airborne waveform LiDAR. Remote Sens. Environ. 2013, 134, 24–38. [Google Scholar] [CrossRef]
- Brokaw, N.V.L. The definition of treefall gap and its effect on measures of forest dynamics. Biotropica 1982, 14, 158–160. [Google Scholar] [CrossRef]
- Strahler, A.H.; Jupp, D.L.B.; Woodcock, C.E.; Schaaf, C.B.; Yao, T.; Zhao, F.; Yang, X.; Lovell, J.; Culvenor, D.; Newnham, G.; et al. Retrieval of forest structural parameters using a ground-based LiDAR instrument (Echidna). Can. J. Remote Sens. 2008, 34 (S2), S426–S440. [Google Scholar] [CrossRef]
- Yao, T.; Yang, X.; Zhao, F.; Wang, Z.; Zhang, Q.; Jupp, D.; Lovell, J.; Culvenor, D.; Newnham, G.; Ni-Meister, W.; Schaaf, C.; Woodcock, C.; Wang, J.; Li, X.; Strahler, A. Measuring forest structure and biomass in New England forest stands using Echidna ground-based LiDAR. Remote Sens. Environ. 2011, 115, 2965–2974. [Google Scholar] [CrossRef]
- Hilker, T.; van Leeuwen, M.; Coops, N.C.; Wulder, M.A.; Newnham, G.J.; Jupp, D.L.B.; Culvenor, D.S. Comparing canopy metrics derived from terrestrial and airborne laser scanning in a Douglas-fir dominated forest stand. Trees - Struct. Funct. 2010, 24, 819–832. [Google Scholar] [CrossRef]
- Chen, Q.; Gong, P.; Baldocchi, D.; Tian, Y.Q. Estimating basal area and stem volume for individual trees from LiDAR data. Photogramm. Eng. Remote Sens. 2007, 73, 1355–1365. [Google Scholar] [CrossRef]
- Kankare, V.; Vastaranta, M.; Holopainen, M.; Räty, M.; Yu, X.; Hyyppä, J.; Hyyppä, H.; Alho, P.; Viitala, R. Retrieval of forest aboveground biomass and stem volume with airborne scanning LiDAR. Remote Sens. 2013, 5, 2257–2274. [Google Scholar] [CrossRef] [Green Version]
- Lindberg, E.; Hollaus, M. Comparison of methods for estimation of stem volume, stem number and basal area from airborne laser scanning data in a hemi-boreal forest. Remote Sens. 2012, 4, 1004–1023. [Google Scholar] [CrossRef]
- Tang, H.; Dubayah, R.; Swatantran, A.; Hofton, M.; Sheldon, S.; Clark, D.B.; Blair, B. Retrieval of vertical LAI profiles over tropical rain forests using waveform LiDAR at La Selva, Costa Rica. Remote Sens. Environ. 2012, 124, 242–250. [Google Scholar] [CrossRef]
- Dubayah, R.O.; Sheldon, S.L.; Clark, D.B.; Hofton, M.A.; Blair, J.B.; Hurtt, G.C.; Chazdon, R.L. Estimation of tropical forest height and biomass dynamics using LiDAR remote sensing at La Selva, Costa Rica. J. Geophys. Res. 2010, 115, G00E09. [Google Scholar] [CrossRef]
- Nelson, R.; Ranson, K.J.; Sun, G.; Kimes, D.S.; Kharuk, V.; Montesano, P. Estimating Siberian timber volume using MODIS and ICESat/GLAS. Remote Sens. Environ. 2009, 113, 691–701. [Google Scholar] [CrossRef]
- Splechtna, B.E.; Gratzer, G. Natural disturbances in Central European forests: Approaches and preliminary results from Rothwald, Austria. For. snow Landsc. Res. 2005, 67, 57–67. [Google Scholar]
- Verbesselt, J.; Kalomenopoulos, M.; Souza, C.; Herold, M. Near real-time deforestation monitoring in tropical ecosystems using satellite image time series. In IGRASS; IEEE: Munich, Germany, 2012; pp. 2020–2023. [Google Scholar]
- Lindsell, J.A.; Klop, E. Spatial and temporal variation of carbon stocks in a lowland tropical forest in West Africa. For. Ecol. Manage. 2013, 289, 10–17. [Google Scholar] [CrossRef]
- Lindsell, J.A.; Klop, E.; Siaka, A.M. The impact of civil war on forest wildlife in West Africa: mammals in Gola Forest, Sierra Leone. Oryx 2011, 45, 69–77. [Google Scholar] [CrossRef]
- Vaglio, G.; Chan, J.C.; Chen, Q.; Lindsell, J.A.; Coomes, D.A. Biodiversity mapping in a tropical West African forest with airborne hyperspectral data. PLoS One 2014, 9. [Google Scholar] [CrossRef]
- Ramage, B.S.; Sheil, D.; Salim, H.M.W.; Fletcher, C.; Mustafa, N.-Z.A.; Luruthusamay, J.C.; Harrison, R.D.; Butod, E.; Dzulkiply, A.D.; Kassim, A.R.; Potts, M.D. Pseudoreplication in tropical forests and the resulting effects on biodiversity conservation. Conserv. Biol. 2013, 27, 364–372. [Google Scholar] [CrossRef] [PubMed]
- Chen, Q.; Gong, P.; Baldocchi, D.; Tian, Y.Q. Airborne LiDAR data processing and information extraction. Photogramm. Eng. Remote Sens. 2007, 73, 109–112. [Google Scholar]
- ESRI ArcView GIS Version 10; Environmental Systems Research Institute: Redlands, CA, USA, 2011.
- Jenness, J.; Brost, B.; Beier, P. Land Facet Corridor Designer: Extension for ArcGIS. Available online: http://www.jennessent.com/arcgis/land_facets.htm (accessed on 8 July 2013).
- R Core Team. R: A Language and Environment for Statistical Computing. R Foundation for Statisical Computing,. 2010. Available online: http://www.r-project.org/ (accessed on 19 June 2015).
- Gaulton, R.; Malthus, T. LiDAR mapping of canopy gaps in continuous cover forests: A comparison of canopy height model and point cloud based techniques. Int. J. Remote Sens. 2010, 31, 1193–1211. [Google Scholar] [CrossRef]
- Coomes, D.A.; Duncan, R.P.; Allen, R.B.; Truscott, J. Disturbances prevent stem size-density distributions in natural forests from following scaling relationships. Ecol. Lett. 2003, 6, 980–989. [Google Scholar] [CrossRef]
- Purves, D.; Lyutsarev, V. Filzbach User Guide. 2012. Available at http://research.microsoft.com/en-us/um/cambridge/groups/science/tools/filzbach/filzbach.htm (accessed on 23 June 2015).
- Clauset, A.; Shalizi, C.R.; Newman, M.E.J. Power-law distributions in empirical data. SIAM Rev. 2009, 51, 661–703. [Google Scholar] [CrossRef]
- Frazer, G.; Magnussen, S.; Wulder, M.; Niemann, K. Simulated impact of sample plot size and co-registration error on the accuracy and uncertainty of LiDAR-derived estimates of forest stand biomass. Remote Sens. Environ. 2011, 115, 636–649. [Google Scholar] [CrossRef]
- Small, D. Some Ecological and Vegetational Studies in the Gola Forest Reserve, Sierra Leone. Master’s Thesis, Queen’s University of Belfast, Belfast, UK, 1953. [Google Scholar]
- Spriggs, R.; Vanderwel, M.; Jones, T.; Caspersen, J.; Coomes, D. A simple area-based model for predicting airborne LiDAR first returns from stem diameter distributions: An example study in an uneven aged, mixed temperate forest. Can. J. For. Res. 2015. [Google Scholar] [CrossRef]
- Osunkoya, O.; Omar-Ali, K.; Amit, N.; Dayan, J.; Daud, D.; Sheng, T. Comparative height crown allometry and mechanical design in 22 tree species of Kuala Belalong Rainforest, Brunei, Borneo. Am. J. Bot. 2007, 94, 1951–1962. [Google Scholar] [CrossRef] [PubMed]
- Burnham, K.P.; Anderson, D.R. Model Selection and Multimodel Inference, 2nd ed.; Springer: New York, NY, USA, 2002. [Google Scholar]
- Anderson, K.J.; Allen, A.P.; Gillooly, J.F.; Brown, J.H. Temperature-dependence of biomass accumulation rates during secondary succession. Ecol. Lett. 2006, 9, 673–682. [Google Scholar] [CrossRef] [PubMed]
- Cole, L.E.S.; Bhagwat, S.A.; Willis, K.J. Recovery and resilience of tropical forests after disturbance. Nat. Commun. 2014, 5. [Google Scholar] [CrossRef] [PubMed]
- Villela, D.M.; Nascimento, M.T.; Aragao, L.E.O.C.; da Gama, D.M. Effect of selective logging on forest structure and nutrient cycling in a seasonally dry Brazilian Atlantic forest. J. Biogeogr. 2006, 33, 506–516. [Google Scholar] [CrossRef]
- Okuda, T.; Suzuki, M.; Adachi, N.; Quah, E.S.; Hussein, N.A.; Manokaran, N. Effect of selective logging on canopy and stand structure and tree species composition in a lowland dipterocarp forest in peninsular Malaysia. For. Ecol. Manage. 2003, 175, 297–320. [Google Scholar] [CrossRef]
- Brearley, F.Q.; Prajadinata, S.; Kidd, P.S.; Proctor, J. Structure and floristics of an old secondary rain forest in Central Kalimantan, Indonesia, and a comparison with adjacent primary forest. For. Ecol. Manage. 2004, 195, 385–397. [Google Scholar] [CrossRef]
- Pinagé, E.R.; Matricardi, E.A.T.; Osako, L.S.; Gomes, A.R. Gap fraction estimates over selectively logged forests in Western Amazon. Nat. Resour. 2014, 5, 969–980. [Google Scholar] [CrossRef]
- Beckage, B.; Clark, J.S.; Clinton, B.D.; Haines, B.L. A long-term study of tree seedling recruitment in southern Appalachian forests: The effects of canopy gaps and shrub understories. Can. J. For. Res. 2000, 30, 1617–1631. [Google Scholar] [CrossRef]
- Royo, A.A.; Carson, W.P. On the formation of dense understory layers in forests worldwide: consequences and implications for forest dynamics, biodiversity and succession. Can. J. For. Res. 2006, 36, 1345–1362. [Google Scholar] [CrossRef]
- Bak, P.; Chen, K.; Tang, C. A forest-fire model and some thoughts on turbulence. Phys. Lett. A 1990, 147, 297–300. [Google Scholar] [CrossRef]
- Reed, W.J.; McKelvey, K.S. Power-law behaviour and parametric models for the size-distribution of forest fires. Ecol. Modell. 2002, 150, 239–254. [Google Scholar] [CrossRef]
- Cui, W.; Perera, A.H. What do we know about forest fire size distribution, and why is this knowledge useful for forest management? Int. J. Wildl. Fire 2008, 17, 234–244. [Google Scholar] [CrossRef]
- Lieberman, M.; Lieberman, D.; Peralta, R. Forest are not just Swiss cheeese: Canopy steregeometry of non-gaps in tropical forests. Ecology 1989, 70, 550–552. [Google Scholar] [CrossRef]
- Tanaka, H.; Nakashizuka, T. Fifteen years of canopy dynamics analyzed by aerial photographs in a temperate deciduous forest, Japan. Ecology 1997, 78, 612–620. [Google Scholar] [CrossRef]
- Swaine, M.D.; Lieberman, D.; Putz, F.E. The dynamics of tree populations in tropical forest: A review. J. Trop. Ecol. 1987, 3, 359–366. [Google Scholar] [CrossRef]
- Espírito-Santo, F.D.B.; Keller, M.M.; Linder, E.; Oliveira Junior, R.C.; Pereira, C.; Oliveira, C.G. Gap formation and carbon cycling in the Brazilian Amazon: measurement using high-resolution optical remote sensing and studies in large forest plots. Plant Ecol. Divers. 2013. [Google Scholar] [CrossRef]
- Chambers, J.Q.; Negron-Juarez, R.I.; Marra, D.M.; Di Vittorio, A.; Tews, J.; Roberts, D.; Ribeiro, G.H.P.M.; Trumbore, S.E.; Higuchi, N. The steady-state mosaic of disturbance and succession across an old-growth Central Amazon forest landscape. Proc. Natl. Acad. Sci. USA 2013, 110, 3949–3954. [Google Scholar] [CrossRef] [PubMed]
- Gloor, M.; Phillips, O.L.; Lloyd, J.J.; Lewis, S.L.; Malhi, Y.; Baker, T.R.; Lopez-Gonzalez, G.; Peacock, J.; Almeida, S.; Alves de Oliveira, A.C.; et al. Does the disturbance hypothesis explain the biomass increase in basin-wide Amazon forest plot data? Glob. Chang. Biol. 2009, 15, 2418–2430. [Google Scholar] [CrossRef] [Green Version]
- Nelson, B.W.; Kapos, V.; Adams, J.B.; Oliveira, W.J.; Oscar, P.G. Forest Disturbance by Large Blowdowns in the Brazilian Amazon. Ecology 1994, 75, 853–858. [Google Scholar] [CrossRef]
- Espírito-Santo, F.D.B.; Gloor, M.; Keller, M.; Malhi, Y.; Saatchi, S.; Nelson, B.; Junior, R.C.O.; Pereira, C.; Lloyd, J.; Frolking, S.; et al. Size and frequency of natural forest disturbances and the Amazon forest carbon balance. Nat. Commun. 2014. [Google Scholar] [CrossRef] [PubMed]
- Birnbaum, P. Canopy surface topography in a French Guiana forest and the folded forest theory. Plant Ecol. 2001, 153, 293–300. [Google Scholar] [CrossRef]
- Berenguer, E.; Ferreira, J.; Gardner, T.A.; Aragão, L.E.O.C.; De Camargo, P.B.; Cerri, C.E.; Durigan, M.; Cosme De Oliveira Junior, R.; Vieira, I.C.G.; Barlow, J. A large-scale field assessment of carbon stocks in human-modified tropical forests. Glob. Chang. Biol. 2014, 20, 3713–3726. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hawthorne, W.D.; Sheil, D.; Agyeman, V.K.; Abu Juam, M.; Marshall, C.A.M. Logging scars in Ghanaian high forest: Towards improved models for sustainable production. For. Ecol. Manage. 2012, 271, 27–36. [Google Scholar] [CrossRef]
- Lefsky, M.A.; Cohen, W.B.; Acker, S.A.; Parker, G.G.; Spies, T.A.; Harding, D. Lidar remote sensing of the canopy structure and biophysical properties of douglas-fir western hemlock forests. Remote Sens. Environ. 1999, 70, 339–361. [Google Scholar] [CrossRef]
- Vaglio, G.; Chen, Q.; Lindsell, J.A.; Coomes, D.A.; Del, F.; Guerriero, L.; Pirotti, F.; Valentini, R. Above ground biomass estimation in an African tropical forest with LiDAR and hyperspectral data. ISPRS J. Photogramm. Remote Sens. 2014, 89, 49–58. [Google Scholar] [CrossRef]
- Pirotti, F.; Laurin, G.; Vettore, A.; Masiero, A.; Valentini, R. Small footprint full-waveform metrics contribution to the prediction of biomass in tropical forests. Remote Sens. 2014, 6, 9576–9599. [Google Scholar] [CrossRef]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kent, R.; Lindsell, J.A.; Laurin, G.V.; Valentini, R.; Coomes, D.A. Airborne LiDAR Detects Selectively Logged Tropical Forest Even in an Advanced Stage of Recovery. Remote Sens. 2015, 7, 8348-8367. https://doi.org/10.3390/rs70708348
Kent R, Lindsell JA, Laurin GV, Valentini R, Coomes DA. Airborne LiDAR Detects Selectively Logged Tropical Forest Even in an Advanced Stage of Recovery. Remote Sensing. 2015; 7(7):8348-8367. https://doi.org/10.3390/rs70708348
Chicago/Turabian StyleKent, Rafi, Jeremy A. Lindsell, Gaia Vaglio Laurin, Riccardo Valentini, and David A. Coomes. 2015. "Airborne LiDAR Detects Selectively Logged Tropical Forest Even in an Advanced Stage of Recovery" Remote Sensing 7, no. 7: 8348-8367. https://doi.org/10.3390/rs70708348
APA StyleKent, R., Lindsell, J. A., Laurin, G. V., Valentini, R., & Coomes, D. A. (2015). Airborne LiDAR Detects Selectively Logged Tropical Forest Even in an Advanced Stage of Recovery. Remote Sensing, 7(7), 8348-8367. https://doi.org/10.3390/rs70708348







